Keywords

1 Introduction

Assortment selection is one of the most important and difficult decisions that retailers face. Assortments are typically chosen subjectively, often before any sales have been observed for some candidate products. Compared to pricing or advertising decisions, assortment decisions are more difficult to adjust later on. For multi-featured items such as consumer electronics and durable goods, the large number of product options, together with limited display space and financial constraints all contribute to the complexity of this decision. Consumer preferences for the various product attributes may also be heterogeneous, which requires assessing tradeoffs between the products that appeal to diverse customer segments. Because of these complexities, intuitively chosen retail assortments are likely to be suboptimal.

This paper develops an operational methodology for selecting optimal retail assortments based on an underlying multinomial logit (MNL) choice model for each customer’s selection of product and retailer. A formulation is developed for optimizing the retailer’s expected profit across customers with heterogeneous preferences. The formulation can also include a variety of additional merchandising constraints, such as display space, price point coverage or brand offerings.

Choice models have been successfully applied in consumer package goods to predict customers’ response to assortment changes, based on observing repeat purchase behavior. The increased use of the Internet as a shopping guide for more complex, less frequently purchased products provides an opportunity to obtain detailed preference information for broader classes of merchandise. A commercial data base of consumer preferences for attributes and features of DVD players, which was obtained through interactive Internet sessions, is used to illustrate the methodology. Consumer surveys or past buying behavior of individuals might also be used as alternative sources for the preference information needed for this assortment optimization methodology.

The methods in this paper provide a basis for several strategic retailer decisions including: (1) determining the optimal set of SKUs to offer and their estimated selling proportions; (2) how the retailer’s relative market strength affects the contents of the optimal assortment; (3) how changing the contents of the assortment affects the probability that customers choose a given retailer and (4) how the customers’ preference structure affects the optimal assortment and the corresponding expected profits. In analyzing our sample data set, it was found that accounting for preference heterogeneity and customers’ use of consideration sets both had significant impacts on the retailer’s expected profits.

1.1 Literature Review

Kok et al. (2015) provide a comprehensive survey of recent papers in retail assortment planning, and thus this paper’s literature review will focus on a few papers that are particularly relevant for the optimization model developed here. Several recent papers have developed models for assortment optimization based on a newsvendor type model for inventory cost. van Ryzin and Mahajan (1999), Cachon and Gurhan Kok (2007) and Cachon et al. (2005) use a multinomial logit (MNL) model in which customers have homogeneous expected utilities. In Mahajan and van Ryzin (2001), customers are heterogeneous with regard to utility and their paper explicitly models the substituted demand that results from random stockouts of the retailer’s inventory, but optimizing the assortment requires solution heuristics that are based on the set of possible inventory trajectories over the season. Guar and Honhon (2006) used a Lancaster type of model of substitution for products distributed along a single attribute dimension, and analyzed the impacts of static and dynamic substitution under this preference structure. Honhon et al. (2010) consider assortment optimization with stockout based substitution for more general deterministic preference structures. This leads to a dynamic programming formulation, for which they develop solution heuristics. Rusmevichientong and Topaloglu (2012) consider a generalized version of the MNL in which the model parameters are random, and show that the optimal assortments satisfy the nested set properties that hold for the MNL choice model with fixed parameters. Sauré and Zeevi (2013) develop a retail assortment optimization model that incorporates learning through experimentation with alternative assortments, and study the tradeoff between gaining information and maximizing current revenue. Smith and Agrawal (2000) used a probability of substitution matrix across products to optimize assortments in combination with an approximate newsvendor inventory model. Miller et al. (2010) provide a method for optimizing assortments for infrequently purchased products and compare the results for several simple assortment selection heuristics. Kok and Fisher (2007) develop a heuristic for optimizing the allocation of shelf facings and inventory levels for a supermarket based on a particular substitution structure that also considers stockouts. Chong et al. (2001) developed a more general hierarchical market model for retail assortment planning for repeat purchase items, but due to the complexity of the resulting objective function, used a local improvement heuristic for optimization.

Only two of the above papers address the issue of retailer choice. Cachon et al. (2005) investigates how three different consumer models for the value of additional search at alternative retailers can affect the optimal assortment. Cachon and Gurhan Kok (2007) develop a more general category management model based on the retailer choice probabilities obtained from the nested logit model, but require mean utilities that are homogeneous across customers.

Product line optimization models have used mathematical programming formulations to solve a related problem. In this setting, a manufacturer decides which set of products to produce, where each potential product is viewed as a collection of adjustable product attributes. Chen and Hausman (2000) considered product line selection based on the MNL choice model, with homogenous customer preferences. Green and Krieger (1985), McBride and Zufryden (1988), Dobson and Kalish (1988, 1993) and Kohli and Sukumar (1990) consider heterogeneous customer utilities, but assume deterministic product choices. Green and Krieger treat discrete price options as product attributes, as is done in this paper, while Dobson and Kalish treat product prices as separate decision variables. With the exception of Chen and Hausman, these mathematical programming formulations are computationally difficult to solve, in part because they assume strict utility maximization by customers. Some product line selection papers developed solution heuristics (Kohli and Sukumar 1990; Dobson and Kalish 1993) or suggested clustering of customer preferences to reduce the problem size (Green and Krieger 1985) so that iterative search methods can be applied. These product line optimization methods do not model retailer choice, nor do they include inventory management costs.

1.2 Summary of Results

This paper provides an operational assortment optimization model that includes general heterogeneous consumer preferences as well as the customer’s choice of retailer within the MNL framework. It is shown that the input parameters required for modeling product choice and retailer choice can be estimated separately, which facilitates their use in an operational model for assortment optimization. Assuming homogeneous mean utilities, van Ryzin and Mahajan (1999) showed that the optimal assortments form nested sets as the assortment size increases. Rusmevichientong and Topaloglu (2012) extend this result for the case of unknown MNL parameters. For heterogeneous customer utilities and competing retailers, this chapter shows that this nested set property no longer holds, but that nested optimal assortment sets do occur for two limiting cases: (1) a monopoly retailer and (2) perfect competition among retailers. An optimization formulation is developed, which can include linear retailer constraints on the contents of the assortment, such as brand coverage and display space limitations. Finally, a commercial data base of preferences for DVD players is analyzed to illustrate the sensitivity of the expected profit and optimal assortment to the customer preference structure. The results for this data set illustrate the importance of including preference heterogeneity and customers’ use of considerations sets in assortment optimization, as well as the sensitivity of the retailer’s profit to assortment size.

2 Model Description

This paper focuses on the assortment decision for a particular retailer r, whose objective is to maximize the expected profit over a fixed time period, e.g., the Fall season. It is assumed that other retailers do not react competitively to this retailer’s decisions. The retailer’s assortment is defined by a binary vector y = y 1, y 2, …, y n, where y j  = 1 if the retailer’s assortment includes product j and 0 otherwise. Then let

$$ {D}_j(y)=\mathrm{the}\ \mathrm{r}\mathrm{andom}\ \mathrm{demand}\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{product}\ j, $$

which depends on y as well as other factors that affect demand. We now develop a choice model that determines the probability distribution for D j (y).

2.1 Modeling the Consumer’s Purchase Decision

First, suppose that customers are classified according to n distinct customer types indexed by i = 1, …, n. It is assumed that customers of the same type assign the same expected values to various choice alternatives, but their actual purchase decisions also reflect individual random variations.

Actual purchases are the result of a sequential process that can be diagramed as follows:

figure a

The choice decisions in each of these steps can be described in terms of the iPACE model for retail shopping decisions that has been developed in the marketing literature, where iPACE stands for information, Price, Assortment, Convenience and Entertainment, (see e.g., Hanson and Kalyanam 2006, Chap. 13) By becoming an active shopper, the customer is sufficiently interested in the product category to gather information. Using a variety of sources, which may include both Internet research and store visits, customers assess their utilities for the available products and the relative values of purchasing from the alternative retailers. This process allows a customer to narrow the set of choices to a “consideration set” of products. The customer selects a retailer based on the retailer’s assortment, as well as the assessed convenience and entertainment values of shopping at that retailer. Finally, the customer makes a product selection from the choice set, which is defined as the intersection of the consideration set and the chosen retailer’s assortment. Although this description is sequential, these decisions do not necessarily need to be made in any specific order. For example, the customer might choose the most preferred product first, and then select the retailer from which to purchase. The key assumption is that the combination of the utility of the retailer and utility of the chosen product jointly determine the customer’s decision. This chapter assumes that these decisions are made normatively by customers, based on maximizing expected utility.

From the perspective of a particular retailer r, the customer may also choose the “no purchase” option for two reasons: (1) no product in the consideration set has positive net value, i.e., the choice set is empty or (2) the combined value of shopping and purchasing from this particular retailer’s assortment either does not exceed the product’s price, or is less than the combined value obtained from another retailer.

The mathematical models for each of these steps can be summarized as follows. The assortment decision is made for a fixed period of time, e.g., one season, and the time dependent parameters correspond to the length of this season. A random number N i of customers of type i will become “active shoppers,” i.e., they will gather information and make a purchase decision this season for this product category. We assume that N i is a Poisson random variable with rate parameter λ i . For the N i shoppers, define

$$ {q}_{ij}(y)=\mathrm{P}\left\{\mathrm{customer}\ \mathrm{type}\ i\ \mathrm{chooses}\ \mathrm{product}\ j\ \mathrm{from}\ \mathrm{this}\ \mathrm{retailer}\Big|\mathrm{assortment}\ y\right\}. $$

This implies that D j (y), the random demand for product j defined previously, has a Poisson distribution with mean

$$ {\mu}_j(y)={\displaystyle \sum_i{\lambda}_i}{q}_{ij}(y). $$
(11.1)

The remaining customer decisions, which determine q ij (y), are based on the following utility model. The underlying choice model is a multinomial logit (MNL) in which customer i’s combined utility for product j and retailer r is a random variable of the form

$$ {U}_{ij}^r={U}_{ij}+{V}_{ir}+{\varepsilon}_{ijr}, $$
(11.2)

where ε ijr  = Gumbel distributed error terms with mean 0 and scale parameter ξ i, ,

U ij  = the expected (net) utility obtained from purchasing product j,

V ir  = the additional utility obtained by purchasing from retailer r.

For this paper’s analysis, the product price is included in U ij as a fixed attribute, rather than a decision variable. For many retailers, this is justified based on operational practice. At the individual product level, tactical pricing decisions such as temporary markdowns are typically made by the retailer later on during the selling season, as part of promotional and advertising activities. Strategic pricing decisions, such as how to price relative to competitors, are typically made less frequently and at a higher level than just one product category. For assortment planning purposes, the product price is therefore the estimated average price for the season. A combined model that simultaneously optimizes product prices and the retail assortment is conceptually superior to separate decision models, but it cannot feasibly include all the other aspects of customers’ purchasing decisions that are analyzed here.

Additive MNL models of the form (11.2) are frequently used for two dimensional choice decisions. (See, e.g., Ben Akiva and Lerman 1985 for further discussion.) In the context of this application, the error terms ε ijr can capture both the customer’s imprecise knowledge of his or her own utilities, as well as the retailer’s imperfect knowledge of customers’ utilities. It is common practice to rescale the utilities for each customer i so that the scale parameters ξ i  = 1 for all i. This is possible because dividing all utilities with subscript i by the same scalar ξ i does not change which utility is the maximum for customer i. That is, probability statements about the maximum utility for customer i are not affected by this rescaling.

2.1.1 Narrowing the Product Choices

Narrowing the product choices is a “prescreening” step that does not change the fundamental structure of the underlying logit model. When there are many product alternatives to consider, marketing researchers have found that customers typically use some criteria to narrow their choices to a “consideration set” of products, which are then investigated in more detail. (See, e.g., Roberts and Lattin 1991; Andrews and Srinivasan 1995; Siddarth et al. 1995). In a normative framework, customer i would form a consideration set by eliminating all products with expected utility less than some threshold u i , where the threshold is based on his or her cost of considering additional alternatives. Thus we define

$$ {u}_i = \mathrm{customer}\ i'\mathrm{s}\ \mathrm{minimum}\ \mathrm{a}\mathrm{cceptable}\ \mathrm{expected}\ \mathrm{utility}\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{considering}\ \mathrm{a}\ \mathrm{product}, $$
$$ {X}_{ij}=1\kern0.5em \mathrm{if}\kern0.5em {U}_{ij}\ge {u}_i\kern0.5em \mathrm{and}\kern0.5em 0\kern0.5em \mathrm{o}\mathrm{therwise},\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\kern0.5em i,j. $$

Consideration sets can have a significant impact on the assortment optimization, as the numerical analysis in Sect. 3 illustrates.

2.1.2 Determining qij(y)

The definition of conditional probability implies that

$$ \begin{array}{l}\hfill {q}_{ij}(y)=\mathrm{P}\left\{\mathrm{customer}\ i\ \mathrm{purchases}\ \mathrm{product}\ j\ \mathrm{from}\ \mathrm{retailer}\ r\Big|y\right\}\hfill \\ {}\hfill \kern2.18em =\mathrm{P}\left\{\mathrm{customer}\ i\ \mathrm{purchases}\ \mathrm{product}\ j\Big|\mathrm{purchases}\ \mathrm{from}\ \mathrm{retailer}\ r,\ y\right\}\hfill \\ {}\hfill {\kern4.2em }^{*}\mathrm{P}\left\{\mathrm{customer}\ i\ \mathrm{purchases}\ \mathrm{from}\ \mathrm{retailer}\ r\Big|y\right\}\hfill \end{array} $$
(11.3)

This equation does not necessarily imply that the customer chooses the retailer first, but this decomposition allows a separable estimation of the required model parameters, as will be discussed later.

Given that customer i selects retailer r’s assortment for a purchase, his or her choice set is defined as the intersection of the consideration set and retailer r’s assortment, i.e.,

$$ {S}_{ri}=\left\{j\Big|{y}_j{X}_{ij}=1\right\},\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\kern0.5em i. $$

Given any choice set S ri , the probability of selecting item j ε S ri is the standard MNL probability, which in this case is

$$ P\left\{\mathrm{customer}\kern0.5em i\ \mathrm{purchases}\ \mathrm{product}\kern0.5em j\Big|\mathrm{chooses}\ \mathrm{retailer}\kern0.5em r,y\right\}=\frac{e^{U_{ij}}}{{\displaystyle \sum_{k\in {S}_{ri}}{e}^{U_{ik}}}}. $$
(11.4)

Ben Akiva and Lerman (1985, p. 282) show that the maximum utility that customer i obtains from the choice set S ri has a Gumbel distribution, with mean

$$ {V}_{ir}^{*}= \ln \left({\displaystyle \sum_{\kern0.2em j\in {S}_{ri}}{e}^{U_{ij}}}\right), $$

and the same scale parameter as the individual utilities. Thus, the total utility of purchasing from retailer r’s assortment is Gumbel distributed with mean v ir  = V ir  + V ir *. The analogous result holds for all other retailers’ assortments, which we index by ρ. Therefore, the maximum utility that customer i could obtain from shopping at other retailers also has a Gumbel distribution with mean

$$ {v}_{io}= \ln \left({\displaystyle \sum_{\rho \ne r}{e}^{V_{i\rho }+{V}_{i\rho}^{*}}}\right), $$

and the same scale parameter ξ i  = 1 as the individual utilities. This allows the retailer choice probability to be written as a binary logit probability

$$ \begin{array}{l}{f}_i=P\left\{\mathrm{customer}\kern0.5em i\kern0.5em \mathrm{selects}\ \mathrm{retailer}\kern0.5em r\Big|y\right\}=\frac{e^{v_{ir}}}{e^{v_{ir}}+{e}^{v_{io}}}\\ {}\kern.65em =\frac{{\displaystyle \sum_{j\in {S}_{ri}}{e}^{U_{ij}}}}{e^{a_{ir}}+{\displaystyle \sum_{j\in {S}_{ri}}{e}^{U_{ij}}}}\kern0.5em \mathrm{with}\kern0.5em {a}_{ir}={v}_{io}-{V}_{ir}.\end{array} $$
(11.5)

The second fraction results if we multiply top and bottom by exp{−V ir }. From this point onward, we focus on the particular retailer r and simply write a i for a ir .

Combining the two probabilities in (11.3) using the assortment y for retailer r and the X ij for customer i to define the choice set S ri , we obtain the formula

$$ {q}_{ij}(y)=\frac{y_j{X}_{ij}{e}^{U_{ij}}}{e^{a_i}+{\displaystyle \sum_k{y}_k{X}_{ik}{e}^{U_{ik}}}}, $$
(11.6)

\( \mathrm{after}\ \mathrm{cancelling}\ \mathrm{the}\ \mathrm{term}\kern0.5em {\displaystyle \sum_{j\in {S}_{ri}}{e}^{U_{ij}}} \). A key result in (11.6) is that a i is a constant that is independent of retailer r’s assortment decision y.

The size of a i indicates the relative strength of retailer r’s competitors for customer type i. The value of a i can be obtained in various ways. One method is to assume that customer i knows the contents of all the retailers’ assortments and chooses the best retailer by maximizing the total utility as described above. Alternatively, the customer might simply decide whether to continue shopping at other retailers based on an estimated value a i , which corresponds to the estimated maximum utility improvement obtained from other retailers’ products, plus the improvement in value obtained by buying from an alternative retailer versus buying from retailer r. For assortment optimization using (11.6), retailer r does not need to know which behavioral model applies to customer i, since a i is simply a parameter to be estimated, as discussed below.

Kahn and Lehmann (1991) and others have suggested adding terms to V ir to capture the additional customer value associated with properties of the assortment that increase its “breadth,” such as the total number of products or the number of brands offered. The structure of the optimization model in this chapter does not allow these additional variables to be included in the retailer’s objective function. But features such as the total number of products or the number of brands in the assortment can be included as constraints for the assortment optimization model, with their corresponding values being added as constant terms to V ir . This allows a sensitivity analysis to be done with respect to these assortment parameters.

2.1.3 Estimation and Empirical Testing

An estimate for a i can be obtained using (11.5) from the observed fraction f i of customers of type i who choose retailer r for any particular given assortment. Assuming that f i can be obtained approximately from market research data for the current assortment, we can solve for the corresponding a i as follows

$$ {a}_i=\left(\frac{1}{f_i}-1\right){\displaystyle \sum_{j\in {S}_{ri}}{e}^{U_{ij}}.} $$

This formula requires utility estimates for each product, which can be obtained from (11.4) as discussed previously. Thus, (11.4) and (11.5) allow the {U ij } and {a i } to be estimated separately, and they could in fact be obtained from different assortments.

Purchasing behavior for consumer package goods based on multi-stage logit models has been studied empirically for a variety of model forms. For example, Cintagunta (1993) provides a summary of articles that include empirical studies of three stages of consumer purchase decision making: (a) whether or not to purchase from this retailer (b) item choice from a retailer and (c) purchase quantity. See also Roberts and Lattin (1997) for a literature review. In forecasting demand for consumer package goods, “purchase incidence,” which is defined as the probability that the customer makes a shopping trip to a given retailer that results in a purchase from the category, plays a role that is similar to retailer choice in this paper. [See, e.g., Bucklin and Lattin 1991 for a discussion of using the binary logit model for purchase incidence.]

2.1.4 Elasticity Comparisons

Formula (11.6) shows that adding another product to the assortment increases the probability that customer i purchases from this retailer, but decreases the probability that each of the original products in the assortment is selected. The magnitudes of these effects depend on a i , as shown below.

Let Q i (y) = P{customer i purchases from this retailer}, where

$$ {Q}_i(y)={\displaystyle \sum_j{q}_{ij}(y)}=\frac{P_i(y)}{e^{a_i}+{P}_i(y)},\kern0.75em \mathrm{with}\kern0.5em {P}_i(y)={\displaystyle \sum_j{y}_j{X}_{ij}{e}^{U_{ij}}}. $$

Interpreting partial derivatives as changes in y k from 0 to 1, we can define the two elasticities

$$ \frac{1}{Q_i(y)}\frac{\partial {Q}_i(y)}{\partial {y}_k}=\frac{e^{a_i}{X}_{ik}{e}^{U_{ik}}}{P_i(y)\left[{e}^{a_i}+{P}_i(y)\right]}\kern0.5em \mathrm{and}\kern0.5em \frac{1}{q_{ij}(y)}\frac{\partial {q}_{ij}(y)}{\partial {y}_k}=-\frac{X_{ij}{e}^{U_{ij}}}{{\left[{e}^{a_i}+{P}_i(y)\right]}^2}. $$

The first and second elasticities show, respectively, that:

  1. 1.

    The percentage increase in total sales to customer i from adding product k is greater when a i is larger.

  2. 2.

    The percentage of cannibalization of product j’s sales due to adding product k is smaller when as a i is larger.

Taken together, these results imply that including additional products in the assortment is more advantageous to the retailer when the retailer’s competition is stronger.

2.2 Retailer’s Assortment Optimization

The profit function Π j (D j (y)) for each product j is based on a newsvendor type model. In general, a fixed cost

F j  = the fixed cost of stocking product j

should also be included. The expected profit Π(y) for the planning period as a function of y can therefore be written as the sum of the expected profits for the various products

$$ \Pi (y)={\displaystyle \sum_j\left\{E\left[{\Pi}_j\right({D}_j(y)\right)}\left]-{F}_j{y}_j\right\}. $$

[It should be noted that even though the random variables Π j (D j (y)) are not independent, their expectations are still additive.] A more general optimization problem can be defined if there are nonlinear cost interactions between the products, but that formulation will not be developed in this chapter.

The newsvendor expected profit for product j for a fixed time period as a function of the assortment y can be written as

$$ E\left[{\Pi}_j\left({D}_j(y)\right)\right]=\underset{S_j}{ \max}\left\{{m}_j{\mu}_j(y)-{c}_{uj}E{\left[{D}_j(y)-{s}_j\right]}^{+}-{c}_{oj}E{\left[{s}_j-{D}_j(y)\right]}^{+}\right\} $$
(11.7)

where E[x]+ denotes the expected value of max{0, x} and

  • s j  = the base stock level for product j for the time period

  • m j  = unit profit margin for product j

  • μ j (y) = expected demand during the time period = E[D j (y)]

  • c uj  = “understock” cost per unit c oj  = “overstock” cost per unit

The financial input quantities can be calculated in the usual way, i.e.,

  • m j  = selling price − unit cost,

  • c uj  = shortage loss − unit cost

  • c oj  = unit cost − salvage value.

From (11.6), we see that y j  = 0 implies D j (y) = 0 with probability 1, which implies that the expected profit is 0. That is, there is no specific shortage cost c uj that results from not including a given item in y, but there is a net loss of expected utility for the retailer’s assortment, which increases the likelihood that the customer will choose another retailer. This is because when a customer’s most preferred item is missing, the customer either substitutes another item from this retailer’s assortment or chooses another retailer. The demand that results from substitutions for items not in the retailer’s assortment is captured in μ j (y). Substitutions from stockouts are ignored, as discussed below. From the standpoint of this retailer r, the probability of choosing another retailer is lumped together with the “no purchase” option.

Using the newsvendor critical ratio formula, the optimal base stock level s j * satisfies

$$ {s}_j^{*}= \arg \underset{S}{ \min}\left\{s\Big|P\left\{{D}_j(y)\le s\right\}\ge {\alpha}_j=\frac{c_{uj}}{c_{uj}+{c}_{oj}}\right\}. $$

The overstock cost c oj above can have a variety of interpretations. For continuing products that will be offered in subsequent seasons, it is the unit holding cost for the season, while for “seasonal” products, it is the unit cost minus the expected salvage value per unit for any excess inventory at the end of the season.

There are various fixed costs F j that can be associated with stocking items in a product category. For larger items such as furniture, it is common to display one unit in the store and hold additional inventory elsewhere, for example. In this case, F j would include the required floor space for display. For smaller items, there may be a shelf facing with one item viewable, and the remaining items stored behind it. In both these cases, F j would include the fixed cost of the required display space in the store when the item is in the assortment.

2.2.1 Incremental Demand Arising from Substitution

Kok et al. (2015) define two kinds of substitution-based demand: (1) assortment based substitution in which a customer switches to another product when a more preferred product is not carried in the assortment and (2) stockout-based substitution in which the customer substitutes another product if a more preferred alternative is in the assortment, but it is out of stock. This chapter captures assortment-based substitution through the MNL choice model discussed previously, but it ignores stockout-based substitution. Some recent papers have modeled stockout-based substitutions, but this generally leads to complex optimizations, and thus solution heuristics are required. Mahajan and van Ryzin (2001) and Guar and Honhon (2006) and Honhon et al. (2010) assume that customers maximize utility over the items that are currently available, i.e., they treat the retailer’s assortment as dynamic. These approaches are quite general, but require heuristic solutions for most customer preference structures. The other assortment optimization models discussed previously in the literature review have either not treated this stockout-based substitution or have bounded its effects.

This chapter assumes that the customer chooses the retailer based on the complete assortment y, and that product demands which encounter stockouts of products in the retailer’s assortment become lost sales. Thus the demand arising from stockout-based substitutions is ignored. Smith and Agrawal (2000) argue using bounds, that the absolute percentage error in expected demand that results from ignoring demand from stockout based substitutions is bounded by (1 − α)(1 − L), where α is the target service level and L is the probability that the customer is unwilling to substitute. For retailers that set high service level targets for most products during the normal selling season, this bound implies that stockout substitutions will rarely occur. The stockout based demand needs to be counted only if the customer is willing to switch to another product from the same retailer. Given that alternative retailers exist for many items, customers who choose another retailer instead of substituting a different product will be correctly captured by the lost sales assumption. Also, when the service level is defined as the probability of no stockout using the normal distribution, the fraction of demand served is typically larger than the service level. For example, for the normal distribution with P{no stockout} = α = 0.9, approximately 96 % of demand will be served, and with α = 0.95 approximately 98 % of demand will be served before a stockout occurs. The error corresponding to the unserved demand is further reduced by eliminating those customers who do not substitute another product from this retailer. Thus, for retail products that have high service levels such as 0.9 or 0.95, it seems reasonable to ignore substitution demand arising from stockouts.

2.2.2 Two Variants of the Objective Function

Products that may have purchase quantities larger than one can be handled in a variety of ways. One method is to use a compound Poisson distribution for demand, in which customers arrive according to a Poisson process and then select their purchase quantities randomly. For example, Poisson arrivals with a purchase quantity selected from a logarithmic distribution result in a negative binomial distribution for total demand during any fixed period. Smith and Agrawal (2000) used the negative binomial distribution and found that a linear approximation to the newsvendor objective function worked well in that case. Other papers on assortment optimization (e.g., van Ryzin and Mahajan 1999; Mahajan and van Ryzin 2001; Guar and Honhon 2006) have used a normal approximation for demand to obtain a newsvendor expected profit function.

When there are time based holding costs, it may be advantageous for retailers to restock more frequently than once per season. This feature can be added to the newsvendor model (11.7), provided that the assortment does not change in midseason. If there is an additional cost h = unit holding cost for one restocking period, a cost term of the form \( 0.5h\left[s+{\left|s-{D}_j(y)\right|}^{+}\right] \) is subtracted from the objective function. The critical ratio stock level formula still holds, where c oj is replaced by c oj  + h and c uj is replaced by c uj  − 0.5 h. The costs c oj and c uj may also be allowed to vary by time period.

2.2.3 A Linear Approximation for the Objective Function

It can be verified by numerical calculation that for common ratios of profit margin to overstock and understock costs, the newsvendor expected profit function (11.7) is approximately linear in the expected demand μ j (y) for the Poisson distribution. That is, when the various costs are held fixed and expected demand increases, the target service level remains constant and the safety stock increases in such a way that the sum of the terms in (11.7) increases approximately linearly as a function of the mean.

For the Poisson demand distribution, this approximation is illustrated for a range of parameter ratios in Fig. 11.1. To simplify the graph, all F j  = 0 and all profits have been divided by c u . That is, when all cost parameters are expressed as multiples of c u , the graphs can be expressed as (expected profit)/c u , which implies that the only required variables are the service level α and the mean demand. Using linear regression, the R2 values for all the linear fits to the points in this figure are at least 0.998.

Fig. 11.1
figure 1

Maximum profit vs. mean demand m = cu, co = cu(1/α−1)

Full size image

The linear approximation implies that are constants π j and b j derived from the slope and intercept of the regression line for product j such that the expected profit can be approximated as follows

$$ E\left[{\Pi}_j\left({D}_j(y)\right)\right]\approx {\pi}_j{\mu}_j(y)-{y}_j\left({b}_j+{F}_j\right). $$

In general, it appears that the quality of the fit improves as the mean increases and as the service level α increases. When F j  = 0, Fig. 11.1 shows that the b j values are positive. This is because the expected profit becomes negative for low enough mean demand, but in these cases y j  = 0 will be optimal.

Using C j  = b j  + F j to combine the constants b j with the fixed costs F j , and recalling that \( {\mu}_j(y)={\displaystyle \sum_i{\lambda}_i}{q}_{ij}(y) \), the retailer’s approximate objective function can therefore be written as

$$ {\Pi}^{*}(y)={\displaystyle \sum_j{\pi}_j{\displaystyle \sum_i{\lambda}_i}{q}_{ij}(y)}-{\displaystyle \sum_j{C}_j}{y}_j. $$
(11.8)

This objective can be maximized with respect to y, subject to various constraints such as display space or brand representation in the assortment.

2.3 Properties of the Optimal Assortment

When customers’ utilities are Gumbel distributed with homogeneous means, van Ryzin and Mahajan (1999) showed that the optimal assortments form nested sets. This case corresponds to U ij  = U j for all i in this paper’s notation. That is, if S K is the best assortment of size K, then \( {S}^K\subseteq {S}^{K+1} \) for all K. With nonhomogeneous means U ij , however, this property no longer holds, as demonstrated by the following counterexample. Let λ i  = 1 and exp(a i ) = 10 for all i and consider the following matrix of exp(U ij ) values

  

Products

1

2

3

Customers

1

1,000

2

1,000

2

1,000

1,000

2

3

2

1,000

2

4

2

2

1,000

Let the unit profits for the three products be 10, 9, 9 respectively. Clearly, the best single product is Product 1. But it can be seen from the table of expected profits below that the best two products are 2 and 3.

 

y

 

Expected Profit

0

1

1

35.6

1

1

0

31.0

1

0

1

31.0

Thus, although Product 1 is the best single product, it is not part of the best set of two products.

Nested set properties do hold for two limiting cases, however. First, let us consider the case in which a i  = a for all i and a is very large. Then rewrite Π*(y) as

$$ {\Pi}^{*}(y)={e}^{-a}{\displaystyle \sum_{i,j}{\lambda}_i{\pi}_j\left(\frac{y_j{X}_{ij}{e}^{U_{ij}}}{1+{e}^{-a}{P}_i(y)}\right)}-{\displaystyle \sum_j{C}_j}{y}_j. $$
(11.9)

As a becomes sufficiently large, the term in parenthesis approaches y ij X ij e Uij. Thus, if the products are ordered so that

$$ {\pi}_1{\displaystyle \sum_i{\lambda}_i{X}_{i1}{e}^{U_{i1}}-{C}_1\ge }\ {\pi}_2{\displaystyle \sum_i{\lambda}_i{X}_{i2}{e}^{U_{i2}}-{C}_2\ge}\dots, $$
(11.10)

then the optimal assortments will be {1}, {1, 2}, … for a sufficiently large. This implies that there is an optimal product ordering for the assortment, if the retailer’s competition is sufficiently strong, even when consumer preferences are heterogeneous. In microeconomic terms, this might be called the “perfectly competitive” case.

A second special case arises when exp(a i ) approaches 0 for all i. In this case, the retailer is effectively a monopolist, since any consumer who purchases will choose this retailer. For the case in which X ij  = 1 for all i, j, every product in the retailer’s assortment is in every customer i’s choice set. Thus, the optimal strategy for a monopoly retailer is to rank products in order of profitability, based on ranking the expected profits as follows

$$ {\pi}_1{\displaystyle \sum_i{\lambda}_i-{C}_1\ge }{\pi}_2{\displaystyle \sum_i{\lambda}_i-{C}_2\ge}\dots . $$
(11.11)

But if some X ij  = 0, this property may not hold, because some customers may not consider the retailer’s most profitable product and thus would not choose it. Thus, with considerations sets, there may be no specific nested set property when exp(a i ) approaches 0, for all i.

2.3.1 Sensitivity to the Retailer’s Market Strength

To illustrate the difference in the two rankings (11.10) and (11.11), let us consider an example with 5 customer types and 20 products, where the utilities U ij were generated by taking samples from a uniform distribution on [0, 2]. Let all X ij  = 1 and all λ i  = 1 in this example. The 20 products are assigned gradually decreasing unit profits π j : $10.00, $9.90, $9.80, …, $8.10 and fixed costs C j  = 0 for all j. Thus, for the case in which the retailer’s competitive position is very strong, the products’ ranking is based on (11.11), which implies that the products would be ranked in order of the unit profits, 1, 2, 3, .... Therefore, for a retailer with a dominant market position, the optimal assortment of K products is {1, 2, …, K}.

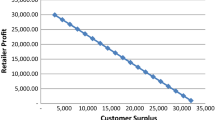
On the other hand, for a retailer in a weak competitive position, the product rankings are based on the rankings in (11.10). The calculated results for (11.10) are illustrated in Fig. 11.2.

Fig. 11.2
figure 2

Profitability calculations for 20 randomly generated products

Full size image

The height of the bars in Fig. 11.2 shows that the expected values for this case are quite different from those that would produce the ranking of 1, 2, 3, .... determined by (11.11). For example, the top 5 products based on ranking the values in Fig. 11.2 are: {9, 11, 20, 13, 7}.

2.4 Solving the Optimization Problem

If the total number of products is small, optimal assortments can be obtained by an exhaustive search, but this becomes more difficult for larger numbers of products. Based on the structure of the problem, certain products may be eliminated from the assortment a priori, which reduces the problem size. Substituting the definition (11.6) of q ij (y) into (11.8), the objective function can be written as

$$ \begin{array}{l}\mathrm{Max}\kern0.5em {\Pi}^{*}(y)={\displaystyle \sum_{j\ge 1}{y}_j\Big\{{\pi}_j}{r}_j(y)-{C}_j\Big\}\kern0.75em \mathrm{with}\kern0.5em {y}_j=0,1\kern0.5em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\kern0.5em j\ge 1,\\ {}\mathrm{where}\kern0.5em {r}_j(y)={\displaystyle \sum_i{\lambda}_i\left(\frac{y_j{X}_{ij}{e}^{U_{ij}}}{e^{a_i}+{\displaystyle \sum_{k\ge 1}{y}_k{X}_{ij}{e}^{U_{ij}}}}\right)}\end{array} $$
(11.12)

For any y such that y k  = 0, define

$$ {\Delta}_k{r}_j(y)={r}_j\left(y+{e}_k\right)-{r}_j(y),\kern1em \mathrm{where}\kern0.5em {e}_k = \mathrm{t}\mathrm{h}\mathrm{e}\ \mathrm{unit}\ \mathrm{vector}\ \mathrm{with}\ \mathrm{k}\mathrm{t}\mathrm{h}\ \mathrm{e}\mathrm{lement} = 1. $$

It can be verified that

$$ \mathrm{If}\kern0.5em {y}_k=0,\ \mathrm{then}\kern0.5em {\Delta}_k{y}_j\left[{r}_j(y)-{C}_j\right]\le 0\kern0.5em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\kern0.75em j\ne k. $$

This has the implication that if \( {\pi}_k{r}_k\left({e}_k\right)-{C}_k\le 0\kern0.5em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{any}\kern0.5em k,\kern0.5em \mathrm{then}\kern0.5em {y}_k = 0\kern0.5em \mathrm{must}\ \mathrm{hold}. \) That is, y k  = 1 cannot be optimal since y k could be changed to 0 and all terms in the objective function will improve or stay the same. This observation can used to eliminate some products before searching on y. However, it appears that an exhaustive search over the remaining 0,1 variables is required to optimize the assortment.

Retailer imposed constraints, such as the number of products must be at least K, or at least one product of Brand B must be included, can be added as linear constraints on y. For example, if the assortment must include at least one product of Brand B, define the logical inputs

I Bj  = 1 if product j is of brand B, and 0 otherwise.

Then the brand constraint is of the form

$$ {\displaystyle \sum_j{y}_j{I}_{Bj}\ge 1\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{band}\ B}. $$

We can also include a display space constraint of the form

$$ {\displaystyle \sum_j{d}_j{y}_j\le D,\ \mathrm{where}} $$

  • d j  = the space required for product j

  • D = total available display space for this category.

These additional constraints also reduce the number of alternatives to be searched.

3 Illustrative Application for a DVD Player Data Base

This section illustrates the application of the optimization model to a set of customer utilities derived from a conjoint analysis of actual consumer Internet responses. The preference data were collected through the Active Decisions’ Active Buyers Guide Sales Assistant website. [See www.activedecisions.com. This company has been acquired by Knova Systems, who plan to offer conjoint utility encoding as a consulting service.] Visitors to activebuyersguide.com, yahoo.com and other e-commerce sites completed an interactive survey to elicit their preference tradeoffs for product attributes. These preferences are defined so as to be independent of the specific set of products in the market. Product utilities were then derived from additive conjoint analysis of 2,213 customer responses for the DVD player category. That is, each customer’s net utility for a particular product was calculated as the sum of his or her “part worths” for the attributes of that product, including the price. (See Green and Srinivasan 1978; Cattin and Wittink 1982; Wittink and Cattin 1989 for discussions of conjoint analysis methods. The conjoint analysis of this data was performed by Active Decisions and the author is indebted to them for sharing their results).

The utility values were then normalized by dividing each utility U ij by customer i’s maximum utility to obtain

$$ {S}_{ij}=\frac{U_{ij}}{\underset{k\in \Omega}{ \max }{U}_{ik}}\kern0.75em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\kern0.5em i,j. $$

After this normalization, it was assumed that ξ i  = 1 for all i. Consideration sets based on utility thresholds can then be defined as a fixed fraction θ of each customer’s maximum utility over all products. That is,

$$ {u}_i=\underset{j\in \Omega}{\theta\ \max }{U}_{ij},\kern0.5em \mathrm{where}\kern0.5em \Omega =\mathrm{the}\ \mathrm{set}\ \mathrm{of}\ \mathrm{all}\ \mathrm{products}\ \mathrm{in}\ \mathrm{the}\ \mathrm{market}. $$

Thus, X ij  = 1 if and only if S ij  > θ.

Assortment optimization for this example was done for the case of “large” a i , i.e., the retailer’s competitive position is weak. Thus, the optimal assortments will form nested sets according to (11.10), as discussed previously. Because of the highly competitive nature of the DVD player market and because this retailer was not a dominant player in consumer electronics, this assumption seemed appropriate. However, the database had no data available on retailer preference so this assumption could not be tested.

3.1 Comparing the Model’s Predictions to a Retailer’s Sales Data

In order to test the predictive accuracy of utilities in the data base and the MNL choice models, we obtained data on the observed selling proportions for an assortment of 30 DVD payers offered by a major retail chain. These selling proportions were compared to those predicted by the MNL choice model fitted to the product attribute utilities in the DVD Player data base. The actual selling proportions of the products ranged from 0.2 to 16 %. [There were 117 different DVD player products at the time the data set was collected, and the retailer data was obtained for the same time period.] A variety of θ values were tested to obtain the correlations and the R-square values are shown below in the table below.

3.1.1 Actual vs. Predicted Selling Proportions for 30 Products

θ

Correlation

R-square

0

69 %

47 %

0.9

78 %

60 %

0.95

79 %

62 %

1.0

72 %

53 %

This table indicates that the fit is reasonably good for all θ values, but the accuracy improves somewhat when customers are assumed to use moderately restrictive consideration sets. Further investigation also revealed that most of the error in these predictions resulted from over-predictions for three products, which the retailer reported were unavailable in some stores. This test supports the use of the utilities in the data base, and also suggests a fairly high θ value such as θ = 0.9 or 0.95 may be appropriate for this data set.

3.2 Comparing the Expected Revenue of the Retailer’s Assortment vs. the Optimal Assortment

The objective function in (11.12) was then applied to the set of 117 DVD player products available at that point in time to determine the optimal assortment of 30 products. For the optimization, it was assumed that each of the 2,213 respondents to the online survey represents a customer segment of equal size, i.e., the λ i were assumed to be equal for all i. The fixed costs C j were set to zero and the product prices from the DVD Player data base were used to compute the expected revenue from a given assortment. Since the revenue comparisons will be done on a percentage basis, it is not necessary to know the actual number of buyers per segment. For percentage calculations with λ i  = λ for all i, the λ will cancel out of the profit comparisons. Therefore, for the case of “very large” a i , the objective function in (11.12) can be maximized by substituting a linear objective function that is similar to the ranking calculation in (11.10),

$$ \begin{array}{l}\mathrm{Max}\kern0.5em {\Pi}_0(y)={\displaystyle \sum_{j\ge 1}{y}_j{\pi}_j}{X}_{ij}{e}^{U_{ij}},\\ {}\mathrm{subject}\ \mathrm{t}\mathrm{o}\kern0.5em {y}_j=0,1\kern0.5em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\kern0.5em j\ge 1\kern0.75em \mathrm{and}\kern0.75em {\displaystyle \sum_{j=1}^n{y}_j}=30.\ \end{array} $$
(11.13)

The optimal assortments were then determined for various values of θ = 0.9, 0.95 and 1.0, which are captured by changes in the X ij . The table below compares the percentage improvements achieved by the optimal assortment over the retailer’s current assortment, for the various θ choices.

θ

Revenue improvement

Common products

0.9

169 %

11 (37 %)

0.95

185 %

 9 (30 %)

1.0

208 %

 7 (23 %)

The revenue improvements in this table are optimistic because they assume that each customer i’s buying behavior exactly matches the MNL model. However, even recognizing this, it appears that using the MNL-based optimal assortment with consideration sets has substantial potential to improve this retailer’s revenues.

3.3 The Impact of Customer Preference Structure

The analysis above is based on the use of both consideration sets and heterogeneous customer market segments. To test the impact of these structural assumptions, we focus on three sensitivity questions:

  1. 1.

    What is the impact of including customer preference heterogeneity in determining optimal assortments?

  2. 2.

    How does customers’ use of consideration sets impact the optimal assortments and expected profits?

  3. 3.

    How does the expected profit increase with assortment size, i.e., how does the optimal assortment size depend on the fixed costs of offering additional products

3.3.1 Customer Heterogeneity

To examine the role of customer preference heterogeneity in developing the optimal assortment, optimal assortments for homogeneous preferences were generated by replacing the S ij with “average” values S j , which equal the average S ij value over all customer types i. The expected profits for these optimal assortments were then compared to the profits for the optimal assortment with heterogeneous preferences S ij in Fig. 11.3.

Fig. 11.3
figure 3

Including preference heterogeneity in assortment optimization

Full size image

The potential revenues of the two optimal assortments converge when essentially all positive utility products are carried by the retailer. However, for assortment sizes 10–30 that are relevant to most retailers, the optimal assortments for heterogeneous preferences result in profits almost twice as large. Examining the contents of the assortments produced by the two methods found only about 5 % common items in the assortments of sizes 5–30. Thus, for this data set, ignoring customer heterogeneity has significant financial consequences and major impacts on the optimal assortment.

3.3.2 The Use of Consideration Sets

To analyze the impact of consideration sets, the optimal assortments for θ = 0, 0.9 and 1.0 are compared in Fig. 11.4, where θ = 0 corresponds to “no consideration sets.” Figure 11.4 shows that when customers use consideration sets and the retailer uses this information correctly in developing the optimal assortments, a substantial increase in expected profit results for typical assortment sizes. For assortments in the 5–10 item range, the θ = 0.9 or 1.0 cases yielded two to three times the profit of the optimal assortment without consideration sets.

Fig. 11.4
figure 4

The effect of consideration sets on expected profit

Full size image

Consideration sets allow the retailer to use a more focused assortment. When customers use consideration sets, the retailer can achieve 80–90 % of the maximum possible profit with an assortment sizes of only about 30 items, while these assortment sizes can achieve only about 50 % of the maximum without consideration sets. For θ = 1, all customers can receive their first choice product with an assortment size of 66, but for θ = 0 additional products always increase expected sales.

The shape of the curves in Fig. 11.4 also determines the impact of the fixed costs C j on the optimal assortment size. For an assortment of size 30, for example, the slopes of the lines are approximately, $3,500, $5,000 and $6,000, respectively, which correspond to the marginal benefits of an additional product. [These dollar figures correspond to one purchase by each of the 2,213 active shoppers in the category. This level of sales would correspond to an aggregate across multiple stores.] Thus, consideration sets allow high fixed costs to be justified for small numbers of products, but tend to limit the optimal assortment size as the number of products increases.

It was assumed in Fig. 11.4 that the optimal assortment was determined for the correct θ value in each case. But since customers’ behavior with regard to consideration sets may be difficult to predict, it is interesting to consider the impact of incorrect assumptions about consideration sets. This calculation is illustrated in Fig. 11.5, where the optimal assortment for θ = 0 was used when the correct value was θ = 0.9, and vice versa.

Fig. 11.5
figure 5

Percentage profit loss for incorrect consideration set assumption with θ = 0, 0.9

Full size image

This shows that if customers form consideration sets based on θ = 0.9, the optimal assortment for θ = 0 results in a reduction in expected profit of 12–50 % for assortments in the range of 10–30. On the other hand, if customers do not use consideration sets to prescreen the products, i.e., θ = 0 is correct, the optimal assortment for θ = 0.9 results in a 10–20 % reduction in expected profit. Thus, for this data set, the less risky alternative is to assume that customers do use considerations sets.

4 Summary and Conclusion

This chapter has developed an operational model for assortment optimization, based a multinomial logit choice model with general heterogeneous customer preferences. The structure of the model allows the required input parameters for product choice and retailer choice to be estimated separately from product sales and retailer market shares. These estimates can be based on observed consumer choices for previous assortments, which need not be optimal. The linear approximation of the newsvendor cost function assumes that temporary stockouts result in lost sales, which restricts the model’s use to retailers or categories of products with relatively high service levels. However, this assumption leads to a closed form objective function that captures the impact of the assortment on both retailer choice and product choice. While the optimal assortments may no longer form nested sets for heterogeneous preferences, it is shown that the special cases of perfect competition and retailer monopoly do lead to different sequences of optimal nested sets, and it is illustrated how the optimal assortment transitions between these two extremes as the retailer’s market share increases.

The optimization model can accommodate a variety of additional retailer constraints. For example, it may be important to: (1) require that certain top brands be represented in the assortment; (2) provide some level of assortment stability across time for customers; (3) stay within a given display space constraint; or (4) carry products with the full range of price points to promote the image of a category killer. The analysis of the DVD player data base illustrated the decreasing marginal benefits associated with increasing assortment size and also the sensitivity of the optimal assortment to the input assumptions regarding the customer choice process. Including customer heterogeneity had significant impacts on both the optimal assortments and the expected profits. Consideration sets, which have been studied in the context of modeling customer choice, but have not previously been included in assortment optimization, were found to strongly influence the optimal assortment for the DVD player data base. This analysis supports the importance of using a consumer choice model that includes heterogeneous preferences and consideration sets in obtaining optimal assortments. The sensitivity analysis also illustrates the potential profit improvement for additional selling effort designed to influence customers’ product choices.

There are a number of promising avenues for future research. Clustering customers into fewer classes can reduce the problem size and lead to shorter computation times for the general competitive case. Analytical methods for choosing the best customer clusters for a given database of utilities could therefore extend the applicability of the optimization model. Clusters based on customers’ preferences for product attributes, as opposed to individual product utilities, may lead to clusters that are more stable over time. Better optimization approaches that exploit the specific structure of the assortment problem may also exist. It is hoped that this chapter will also lead to additional research on the development of decision support systems for assortment planning that implement this optimization model for choosing assortments, taking into account both product choice and retailer choice.