A Finite Volume Element Method for a Nonlinear Parabolic Problem

Abstract

We study a finite volume element discretization of a nonlinear parabolic equation in a convex polygonal domain. We show the existence of the discrete solution and derive error estimates in L ₂- and H ¹-norms. We also consider a linearized method and provide numerical results to illustrate our theoretical findings.

Mathematics Subject Classification (2010): 65M60, 65M15

1 Introduction

We consider the nonlinear parabolic problem for t ∈ [0, T], T > 0,

$$\displaystyle{ u_{t} -\nabla \cdot (A(u)\nabla u) = f,\ \text{in}\ \Omega,\quad u = 0,\ \text{on}\ \partial \Omega,\quad \text{with}\ u(0) = {u}^{0},\ \text{in}\ \Omega, }$$

(1)

where Ω is a bounded convex polygonal domain in ${\mathbb{R}}^{2}$ and $A(v) = \text{diag}\,(a_{1}(v),a_{2}(v))$, a strictly positive definite and bounded real-valued matrix function, such that there exists β > 0.

$$\displaystyle{ \vert {x}^{\top }{A}^{{\prime}}(y)x\vert \leq \beta {x}^{\top }x,\quad \forall y \in \mathbb{R},\ \forall x \in {\mathbb{R}}^{2}. }$$

(2)

Further, we assume that A ^′ is Lipschitz continuous, i.e., ∃ L > 0

$$\displaystyle{ \vert a_{i}^{{\prime}}(y) - a_{ i}^{{\prime}}(\tilde{y})\vert \leq L\vert y -\tilde{ y}\vert,\quad \forall y,\tilde{y} \in \mathbb{R},\ i = 1,2, }$$

(3)

and that there exists a sufficiently smooth unique solution u of (1).

Questions about the existence and regularity of solutions for (1) have been intensively investigated, for example, in [7, Chap. 5]. Nonlinear parabolic problems such as (1) occur in many applied fields. To name a few, in the chemotaxis model, see Keller and Segel [6]; in groundwater hydrology, see L.A. Richards [10]; and in modeling and simulation of oil recovery techniques in the presence of capillary pressure, see [3].

We shall study fully discrete approximations of (1) by the finite volume element method (FVEM). The FVEM, which is also called finite volume method or covolume method in some literatures, is a class of important numerical methods for solving differential equations, especially those arising from conservation laws including mass, momentum, and energy, because this method possesses local conservation property, which is crucial in many applications. It is popular in computational fluid mechanics, groundwater hydrology, reservoir simulations, and others. Many researchers have studied this method for linear and nonlinear problems. We refer to the monographs [5, 9] for the general presentation of this method and references therein for details.

The approximate solution will be sought in the space of piecewise linear functions

$$\displaystyle{\mathcal{X}_{h} =\{\chi \in \mathcal{C} :\ \chi \vert _{K}\ \text{ linear},\ \forall K \in \mathcal{T}_{h};\ \chi \vert _{\partial \Omega } = 0\},}$$

where $\mathcal{T}_{h}$ is a family of quasiuniform triangulations T _h  = { K} of Ω, with h denoting the maximum diameter of the triangles $K \in \mathcal{T}_{h}$ and $\mathcal{C} = \mathcal{C}(\Omega )$ the space of continuous functions on $\bar{\Omega }$.

The FVEM is based on a local conservation property associated with the differential equation. Namely, integrating (1) over any region $V \subset \Omega$ and using Green’s formula we obtain for t ∈ [0, T]

$$\displaystyle{ \int _{V }u_{t}\,dx -\int _{\partial V }(A(u)\nabla u) \cdot n\,d\sigma =\int _{V }f\,dx, }$$

(4)

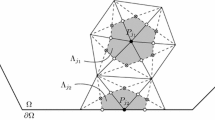
where n denotes the unit exterior normal vector to ∂ V. The semidiscrete FVEM approximation $u_{h}(t) \in \mathcal{X}_{h}$ will satisfy (4) for V in a finite collection of subregions of Ω called control volumes, the number of which will be equal to the dimension of the finite element space $\mathcal{X}_{h}$. These control volumes are constructed in the following way. Let z _K be the barycenter of $K \in \mathcal{T}_{h}$. We connect z _K with line segments to the midpoints of the edges of K, thus partitioning K into three quadrilaterals K _z , z ∈ Z _h (K), where Z _h (K) are the vertices of K. Then with each vertex $z \in Z_{h} = \cup _{K\in \mathcal{T}_{h}}Z_{h}(K)$ we associate a control volume V _z , which consists of the union of the subregions K _z , sharing the vertex z (see Fig. 1). We denote the set of interior vertices of Z _h by Z _h ⁰. The semidiscrete FVEM for (1) is then to find $u_{h}(t) \in \mathcal{X}_{h}$, for t ∈ [0, T], such that

$$\displaystyle{ \int _{V _{z}}u_{h,t}\,dx -\int _{\partial V _{z}}(A(u_{h})\nabla u_{h}) \cdot n\,ds =\int _{V _{z}}f\,dx,\quad \forall z \in Z_{h}^{0}, }$$

(5)

with $u_{h}(0) = u_{h}^{0}$, where $u_{h}^{0} \in \mathcal{X}_{h}$ is a given approximation of u ⁰. Note that different choices for z _K , e.g., the circumcenter of K, lead to other methods than the one considered here; see [8, 12].

Fig. 1

Left: a union of triangles that have a common vertex z; the dotted line shows the boundary of the corresponding control volume V _z . Right: a triangle K partitioned into the three subregions K _z

In our analysis of the FVEM we use existing results associated with the finite element method approximation $\tilde{u}_{h}(t) \in \mathcal{X}_{h}$ of u(t), defined by

$$\displaystyle{ (\tilde{u}_{h,t},\chi ) + a(\tilde{u}_{h};\tilde{u}_{h},\chi ) = (f,\chi ),\quad \forall \chi \in \mathcal{X}_{h},\quad \text{for}\ t > 0, }$$

(6)

with $(f,g) =\int _{\Omega }fg\,dx$, $a(w;v,g) = (A(w)\nabla v,\nabla g)$ and $\|w\| = {(w,w)}^{1/2}$ the norm in $L_{2} = L_{2}(\Omega )$. Further let $H_{0}^{1} = H_{0}^{1}(\Omega )$ be the standard Sobolev space with zero boundary conditions. Thus, in order to rewrite (5) in a weak formulation, we introduce the finite dimensional space of piecewise constant functions

$$\displaystyle{\mathcal{Y}_{h} =\{\eta \in L_{2} :\ \eta \vert _{V _{z}}\ \text{= constant},\ \forall z \in Z_{h}^{0};\ \eta \vert _{ V _{z}} = 0,\ \forall z \in Z_{h} \setminus Z_{h}^{0}\}.}$$

We now multiply (5) by η(z) for an arbitrary $\eta \in \mathcal{Y}_{h}$ and sum over all $z \in Z_{h}^{0}$ to obtain the Petrov–Galerkin formulation for t ∈ [0, T]

$$\displaystyle{ (u_{h,t},\eta ) + a_{h}(u_{h};u_{h},\eta ) = (f,\eta ),\quad \forall \eta \in \mathcal{Y}_{h},\quad \text{with}\ u_{h}(0) = u_{h}^{0}, }$$

(7)

where $a_{h}(\cdot ;\cdot,\cdot ) : \mathcal{X}_{h} \times \mathcal{X}_{h} \times \mathcal{Y}_{h} \rightarrow \mathbb{R}$ is defined by

$$\displaystyle{ a_{h}(w;v,\eta ) = -\sum _{z\in Z_{h}^{0}}\eta (z)\int _{\partial V _{z}}(A(w)\nabla v) \cdot n\,d\sigma,\quad \forall v,w \in \mathcal{X}_{h},\ \eta \in \mathcal{Y}_{h}. }$$

(8)

We shall now rewrite the Petrov–Galerkin method (7) as a Galerkin method in $\mathcal{X}_{h}$. For this purpose, we introduce the interpolation operator $J_{h} : \mathcal{C}\mapsto \mathcal{Y}_{h}$ by

$$\displaystyle{J_{h}w =\sum _{z\in Z_{h}^{0}}w(z)\Psi _{z},}$$

where Ψ _z is the characteristic function of the control volume V _z . It is known that J _h is self-adjoint and positive definite (see [4]), and hence the following defines an inner product $\langle \cdot,\cdot \rangle$ on $\mathcal{X}_{h}$:

$$\displaystyle{ \langle \chi,\psi \rangle = (\chi,J_{h}\psi ),\quad \forall \chi,\psi \in \mathcal{X}_{h}. }$$

(9)

Further, in [4] it is shown that the corresponding norm is equivalent to the L ₂norm, uniformly in h, i.e., with C ≥ c > 0,

$$\displaystyle{ c\|\chi \| \leq \vert \vert \vert \chi \vert \vert \vert \leq C\|\chi \|,\quad \forall \chi \in \mathcal{X}_{h},\quad \text{where}\ \vert \vert \vert \chi \vert \vert \vert \equiv {\langle \chi,\chi \rangle }^{1/2}. }$$

With this notation, (7) may equivalently be written in Galerkin form as

$$\displaystyle{ \langle u_{h,t},\chi \rangle +a_{h}(u_{h};u_{h},J_{h}\chi ) = (f,J_{h}\chi ),\quad \forall \chi \in \mathcal{X}_{h},\quad \text{for}\ t \geq 0. }$$

(10)

Then let $N \in \mathbb{N}$, N ≥ 1, $k = T/N$, and t ⁿ = n k, $n = 0,\ldots,N$. Discretizing in time (10), with the backward Euler method, we approximate u(t ⁿ) by ${U}^{n} \in \mathcal{X}_{h}$, for $n = 1,\ldots,N$, such that

$$\displaystyle{ \langle \bar{\partial }{U}^{n},\chi \rangle +a_{ h}({U}^{n};{U}^{n},J_{ h}\chi ) = ({f}^{n},J_{ h}\chi ),\quad \forall \chi \in \mathcal{X}_{h},\quad \text{with}\ {U}^{0} = u_{ h}^{0}, }$$

(11)

where $\bar{\partial }{U}^{n} = ({U}^{n} - {U}^{n-1})/k$ and ${f}^{n} = f({t}^{n})$.

To show the existence of the semidiscrete solution $\tilde{u}_{h}$ of the finite element method (6), one can employ Brouwer’s fixed point theorem and the coercivity property of a( ⋅;  ⋅,  ⋅):

$$\displaystyle{ a(w;\chi,\chi ) \geq \alpha \|{\nabla \chi \|}^{2},\quad \forall \chi \in \mathcal{X}_{ h},\ \forall w \in L_{2} }$$

(12)

(see [11]). However, the corresponding coercivity property for a _h ( ⋅;  ⋅,  ⋅),

$$\displaystyle{ a_{h}(w;\chi,J_{h}\chi ) \geq \tilde{\alpha }\|{\nabla \chi \|}^{2},\quad \forall \chi \in \mathcal{X}_{ h}, }$$

(13)

holds for $\|\nabla w\|_{L_{\infty }}$ in a bounded ball, where $\|w\|_{L_{\infty }} =\mathrm{ sup}_{x\in \Omega }\vert w(x)\vert$. For this reason, we will employ a different argument than the one in [11] to show the existence of U ⁿ. It is known that for fixed w, in general, the bilinear form $a_{h}(w;\psi,J_{h}\chi )$ is nonsymmetric on S _h , but (for a linear problem) it is not far from being symmetric, or $\vert a_{h}(\chi,J_{h}\psi ) - a_{h}(\psi,J_{h}\chi )\vert \leq Ch\|\nabla \chi \|\,\|\nabla \psi \|$, cf. [4]. Note that if z _K is the circumcenter of K, it is shown in [8] that (13) is satisfied for w ∈ L ₂, and thus, one may show the existence of the solution of the finite volume method analogously to the one for the finite element method. We show the existence and uniqueness of the solution U ⁿ of (11) and derive error estimates in L ₂- and H ¹-norms; see Theorems 3.1 and 4.1. Recently in [12], a two-grid FVEM was considered, for circumcenter-based control volumes, with suboptimal estimates in L ₂- and H ¹-norms.

Our analysis follows the corresponding one for the FVEM nonlinear elliptic and linear parabolic problems in [1, 2]. This is based in bounds for the error functionals $\varepsilon _{h}(\cdot,\cdot )$ defined by

$$\displaystyle{ \varepsilon _{h}(f,\chi ) = (f,J_{h}\chi ) - (f,\chi ),\quad \forall f \in L_{2},\ \chi \in \mathcal{X}_{h}, }$$

(14)

and $\varepsilon _{a}(\cdot ;\cdot,\cdot )$ defined by

$$\displaystyle{ \varepsilon _{a}(w;v_{h},\chi ) = a_{h}(w;v_{h},J_{h}\chi ) - a(w;v_{h},\chi )\quad \forall v_{h},\chi \in \mathcal{X}_{h},\ w \in L_{2}. }$$

(15)

Following [11], we introduce the projection $R_{h} : H_{0}^{1} \rightarrow \mathcal{X}_{h}$ defined by

$$\displaystyle{ a(v;R_{h}v,\chi ) = a(v;v,\chi ),\quad \forall \chi \in \mathcal{X}_{h}. }$$

(16)

In [11] optimal order error estimates in L ₂- and H ¹-norms were established for the difference R _h u(t) − u(t). Here we combine these error estimates with bounds for the difference ${\vartheta }^{n} = {U}^{n} - R_{h}{u}^{n}$, which satisfies

$$\displaystyle{ \begin{array}{cc} \langle \bar{{\partial }\vartheta }^{n},\chi \rangle +a_{h}({U}^{n}{;\vartheta }^{n},J_{h}\chi )& =\delta ({t}^{n};{U}^{n},\chi ),\quad \text{for}\ \chi \in \mathcal{X}_{h}, \end{array} }$$

(17)

with

$$\displaystyle{ \begin{array}{cc} \delta ({t}^{n};v,\chi )& \equiv -{(\omega }^{n},J_{h}\chi ) -\varepsilon _{h}({f}^{n} - u_{t}^{n},\chi ) +\varepsilon _{a}(v;R_{h}{u}^{n},\chi ) \\ & \qquad + ((A({u}^{n}) - A(v))\nabla R_{h}{u}^{n},\nabla \chi ) \equiv \sum _{j=1}^{4}I_{j}, \end{array} }$$

(18)

and ${\omega }^{n} = (R_{h} - I)\bar{\partial }{u}^{n} + (\bar{\partial }{u}^{n} - u_{t}^{n})$. Further we analyze a linearized fully discrete scheme and provide numerical examples to illustrate our results.

The rest of the paper is organized as follows. In Sect. 2 we recall known results and derive error bounds for the error functional δ. In Sect. 3 we derive error estimates and in Sect. 4 existence of the nonlinear fully discrete method. In Sect. 5 we consider a linearized version of the backward Euler scheme, and finally in Sect. 6 we present our numerical examples.

2 Preliminaries

In this section we recall known results about the projection R _h defined by (16) and the error functionals $\varepsilon _{h}$ and $\varepsilon _{a}$ introduced in (14) and (15). We also derive bounds for the error functional δ defined in (18).

We consider quasiuniform triangulations $\mathcal{T}_{h}$ for which the following inverse inequalities hold (see, e.g., [11]):

$$\displaystyle{ \|\nabla \chi \|\leq C{h}^{-1}\|\chi \|,\quad \text{and}\quad \|\nabla \chi \|_{ L_{\infty }} \leq C{h}^{-1}\|\nabla \chi \|,\quad \text{for}\ \chi \in \mathcal{X}_{ h}. }$$

(19)

In such meshes, it is shown in [11, Lemma 13.2] that there exists M ₀ > 0, independent of h, such that

$$\displaystyle{ \|\nabla u(t)\|_{L_{\infty }} +\| \nabla R_{h}u(t)\|_{L_{\infty }} \leq M_{0},\quad \text{for}\ t \leq T, }$$

(20)

and the following error estimates for R _h u − u.

Lemma 2.1.

With R _h defined by (16) and $\varrho = R_{h}u - u$ , we have under the appropriate regularity assumptions on u, with C _u > 0 independent of t,

$$\displaystyle{ \begin{array}{c} \|{\nabla }^{s}D_{t}^{\ell}\varrho (t)\| \leq C_{u}{h}^{2-s},\quad 0 < t \leq T,\quad \text{and}\quad s,\ell= 0,1,\quad \text{where}\ D_{t} = \partial /\partial t.\end{array} }$$

Our analysis is based on error estimates for the difference ${\vartheta }^{n} = {U}^{n} - R_{h}{u}^{n}$. Thus, in view of the error equation (17) for ${\vartheta }^{n}$, we recall necessary bounds for the error functionals $\varepsilon _{h}$ and $\varepsilon _{a}$ derived in [1, 2].

Lemma 2.2.

For the error functional $\varepsilon _{h}$ , defined by (14) , we have

$$\displaystyle{ \vert \varepsilon _{h}(f,\chi )\vert \leq C{h}^{2}\|\nabla f\|\,\|\nabla \chi \|,\quad \forall f \in {H}^{1},\ \chi \in \mathcal{X}_{ h}. }$$

To this end, for $M =\max (2M_{0},1)$, we consider

$$\displaystyle{\mathcal{B}_{M} =\{\chi \in \mathcal{X}_{h} :\| \nabla \chi \|_{L_{\infty }} \leq M\}.}$$

Lemma 2.3.

For the error functional $\varepsilon _{a}$ , defined in (15) , we have

$$\displaystyle{ \vert \varepsilon _{a}(w_{h};v_{h},\chi )\vert \leq Ch\|\nabla w_{h} \cdot \nabla v_{h}\|\,\|\nabla \chi \|,\ \forall w_{h},v_{h},\chi \in \mathcal{X}_{h}. }$$

(21)

Further, if u is the solution of (1) , then for $v \in \mathcal{B}_{M}$,

$$\displaystyle{ \begin{array}{c} \vert \varepsilon _{a}(v;R_{h}u(t),\chi )\vert \leq C{h}^{2}\|\nabla \chi \|.\end{array} }$$

(22)

Proof.

The first bound is shown in [1, Lemma 2.3]. The second bound is a direct result of Lemma 2.1, [1, Lemma 2.4], and the fact that $v \in \mathcal{B}_{M}$. □ 

Then, in view of Lemma 2.3 there exists a constant c > 0 such that for h sufficiently small, the coercivity property (13) for a _h holds for $w \in \mathcal{B}_{M}$. Further, in [1] we showed the following “Lipschitz”-type estimation for $\varepsilon _{a}$.

Lemma 2.4.

For the error functional $\varepsilon _{a}$ , defined in (15) , there exists a constant C, independent of h, such that for $\chi,\psi \in \mathcal{X}_{h}$

$$\displaystyle{ \vert \varepsilon _{a}(v;\psi,\chi ) -\varepsilon _{a}(w;\psi,\chi )\vert \leq Ch\|\nabla \psi \|_{L_{\infty }}(1 + \|\nabla w\|_{L_{\infty }})\|\nabla (v - w)\|\,\|\nabla \chi \|. }$$

Finally, we show appropriate bounds for the functional δ, defined by (18).

Lemma 2.5.

For δ defined by (18) , we have for $\chi \in \mathcal{X}_{h}$ and $v \in \mathcal{B}_{M}$

$$\displaystyle{ \vert \delta ({t}^{n};v,\chi )\vert \leq C(k+{h}^{2})\|\chi \|+C{h}^{2}\|\nabla \chi \|+\left \{\begin{array}{@{}l@{\quad }l@{}} \quad &C\|v - R_{h}{u}^{n}\|\,\|\nabla \chi \| \\ \quad &C\|\nabla (v - R_{h}{u}^{n})\|\,\|\chi \|. \end{array} \right. }$$

Proof.

Using the splitting in (18) we bound each of the terms I _j , $j = 1,\ldots,4$. Recall that ${\omega }^{n} = (R_{h} - I)\bar{\partial }{u}^{n} + (\bar{\partial }{u}^{n} - u_{t}^{n})$; then in view of Lemma 2.1, we have

$$\displaystyle{{ \|\omega }^{n}\| \leq C{k}^{-1}\int _{{ t}^{n-1}}^{{t}^{n} }\|\varrho _{t}\|\,ds + C\int _{{t}^{n-1}}^{{t}^{n} }\|u_{tt}\|\,ds \leq C(k + {h}^{2}), }$$

(23)

and hence

$$\displaystyle{ \vert I_{1}\vert \leq C(k + {h}^{2})\|\chi \|. }$$

(24)

To bound $I_{2} + I_{3}$, we use Lemma 2.2 and (22) to get

$$\displaystyle{ \vert I_{2} + I_{3}\vert \leq C{h}^{2}\|\nabla \chi \|. }$$

(25)

Finally, employing (2) and (20) and adding and subtracting $R_{h}{u}^{n}$ and using Lemma 2.1, we get

$$\displaystyle\begin{array}{rcl} \vert I_{4}\vert & =& \vert ((A({u}^{n}) - A(v))\nabla R_{ h}{u}^{n},\nabla \chi )\vert \leq C\|v - {u}^{n}\|\,\|\nabla \chi \| \\ &\leq & C{h}^{2}\|\nabla \chi \| + C\|v - R_{ h}{u}^{n}\|\|\nabla \chi \|. {}\end{array}$$

(26)

Combining now (24)–(26) we get the first one of the desired bounds. To show the second estimate of this lemma, we bound I ₄ differently. Using integration by parts, we rewrite I ₄ as

$$\displaystyle\begin{array}{rcl} I_{4}& =& ((A({u}^{n}) - A(R_{ h}{u}^{n}))\nabla R_{ h}{u}^{n},\nabla \chi ) + ((A(R_{ h}{u}^{n}) - A(v))\nabla R_{ h}{u}^{n},\nabla \chi ) {}\\ & =& ((A({u}^{n}) - A(R_{ h}{u}^{n}))\nabla R_{ h}{u}^{n},\nabla \chi ) + (\text{div}\,[(A(R_{ h}{u}^{n}) - A(v))\nabla R_{ h}{u}^{n}],\chi ) {}\\ & =& I_{4}^{i} + I_{ 4}^{ii}. {}\\ \end{array}$$

Then, in view of (2), Lemma 2.1, and (20), we have

$$\displaystyle{ \vert I_{4}^{i}\vert \leq C{h}^{2}\|\nabla \chi \|. }$$

(27)

Further, employing (2), (3), and (20), we obtain

$$\displaystyle\begin{array}{rcl} \vert I_{4}^{ii}\vert & \leq & C(\|({A}^{{\prime}}(R_{ h}{u}^{n}) - {A}^{{\prime}}(v))\nabla R_{ h}{u}^{n}\| +\| {A}^{{\prime}}(v)\nabla (R_{ h}{u}^{n} - v)\|)\|\chi \| \\ & \leq & C(\|v - R_{h}{u}^{n}\| +\| \nabla (v - R_{ h}{u}^{n})\|)\|\chi \|. {}\end{array}$$

(28)

Therefore combining (27) and (28), we have

$$\displaystyle{ \begin{array}{c} \vert I_{4}\vert \leq C\|\nabla (v - R_{h}{u}^{n})\|\|\chi \| + C{h}^{2}\|\nabla \chi \|.\end{array} }$$

(29)

Thus, combining (24), (25), (29), and (26), we obtain the second of the desired estimates of the lemma. □ 

3 Error Estimates for the Backward Euler Method

In this section we derive error estimates for the FVEM (11) in L ₂- and H ¹-norms, under the assumption that ${U}^{j} \in \mathcal{B}_{M}$, for $j = 0,\ldots,n$. In Sect. 4 we will show the existence of ${U}^{n} \in \mathcal{B}_{M}$.

Theorem 3.1.

Let U ⁿ and u be the solutions of (11) and (1) , with ${U}^{0} = R_{h}{u}^{0}$ . If ${U}^{j} \in \mathcal{B}_{M}$ , for $j = 0,\ldots,n$ , n ≥ 1, and k, h be sufficiently small, then there exist C > 0, independent of k and h, such that

$$\displaystyle{ \|{\nabla }^{s}({U}^{n} - {u}^{n})\| \leq C(k + {k}^{-s/2}{h}^{2-s}),\quad \text{for}\ s = 0,1. }$$

(30)

Proof.

Using the error splitting ${U}^{n} - {u}^{n} = ({U}^{n} - R_{h}{u}^{n}) + (R_{h}{u}^{n} - {u}^{n}) {=\vartheta }^{n} {+\varrho }^{n}$ and Lemma 2.1, it suffices to show

$$\displaystyle{ \|{\nabla {}^{s}\vartheta }^{n}\| \leq C_{ s}(k + {k}^{-s/2}{h}^{2-s}),\quad \text{for}\ s = 0,1. }$$

(31)

We start with the estimation of ${\|\vartheta }^{n}\|$. Due to the symmetry of $\langle \chi,\psi \rangle$, we have the following identity:

$$\displaystyle{ \langle \bar{{\partial }\vartheta }^{n}{,\vartheta }^{n}\rangle = \dfrac{1} {2k}{(\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2} {-\vert \vert \vert \vartheta {}^{n-1}\vert \vert \vert }^{2}) +{ \dfrac{1} {2k}\vert \vert \vert \vartheta }^{n} {-\vartheta {}^{n-1}\vert \vert \vert }^{2}. }$$

(32)

Choosing $\chi {=\vartheta }^{n}$ in (17) and using the fact that ${U}^{n} \in \mathcal{B}_{M}$, (13), and (32), we get after eliminating ${\vert \vert \vert \vartheta }^{n} {-\vartheta }^{n-1}\vert \vert \vert$

$$\displaystyle{ \begin{array}{cc} \dfrac{1} {2k}{(\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2} {-\vert \vert \vert \vartheta {}^{n-1}\vert \vert \vert }^{2}) +\tilde{\alpha }\| {\nabla \vartheta {}^{n}\|}^{2} & \leq \delta ({t}^{n};{U}^{n}{,\vartheta }^{n}).\end{array} }$$

(33)

Employing now the first estimate of Lemma 2.5, with v = U ⁿ and $\chi {=\vartheta }^{n}$, to bound the right-hand side of (33), we obtain

$$\displaystyle{ \frac{1} {2k}{(\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2} {-\vert \vert \vert \vartheta {}^{n-1}\vert \vert \vert }^{2}) +\tilde{\alpha }\| {\nabla \vartheta {}^{n}\|}^{2} \leq C{(k + {h}^{2})\|\vartheta }^{n}\| + C({k\|\vartheta }^{n}\| + {h}^{2})\|{\nabla \vartheta }^{n}\|. }$$

Then, after eliminating $\|{\nabla \vartheta {}^{n}\|}^{2}$ and moving ${\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2}$ to the left, we have for k sufficiently small

$$\displaystyle\begin{array}{rcl} \vert \vert \vert \vartheta {}^{n}\vert \vert \vert ^{2}& \leq & {(1 + Ck)\vert \vert \vert \vartheta {}^{n-1}\vert \vert \vert }^{2} + CkE,\quad \text{with}\ E = O({k}^{2} + {h}^{4}). {}\\ \end{array}$$

Hence, using the fact that ${\vartheta }^{0} = 0$, we obtain

$${\displaystyle{\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2} \leq CkE\sum _{\ell =0}^{n}{(1 + Ck)}^{n-\ell+1} \leq C({k}^{2} + {h}^{4}).}$$

Thus, there exists C ₀ > 0, such that ${\vert \vert \vert \vartheta }^{n}\vert \vert \vert \leq C_{0}(k + {h}^{2})$. Since $\vert \vert \vert \cdot \vert \vert \vert$ and $\|\cdot \|$ are equivalent norms, the first part of the proof is complete.

Next we turn to the estimation of $\|{\nabla \vartheta }^{n}\|$. Choosing this time $\chi =\bar{ {\partial }\vartheta }^{n}$ in (17), we obtain

$$\displaystyle{ \vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + a({U}^{n}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n}) =\delta ({t}^{n};{U}^{n},\bar{{\partial }\vartheta }^{n}) +\varepsilon _{ a}({U}^{n}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n}). }$$

(34)

Note now that since a( ⋅;  ⋅,  ⋅) is symmetric, we have the identity

$$\displaystyle{2ka({U}^{n}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n}) = a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) - a({U}^{n}{;\vartheta }^{n-1}{,\vartheta }^{n-1}) + {k}^{2}a({U}^{n};\bar{{\partial }\vartheta }^{n},\bar{{\partial }\vartheta }^{n}).}$$

Using now this and (12) in (34), we get, after subtracting $a({U}^{n-1}{;\vartheta }^{n-1}{,\vartheta }^{n-1})$ from both parts of (34),

$$\displaystyle\begin{array}{rcl} & & 2k\vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) - a({U}^{n-1}{;\vartheta }^{n-1}{,\vartheta }^{n-1}) +\alpha {k}^{2}\|\nabla \bar{{\partial }\vartheta {}^{n}\|}^{2} \\ & & \leq 2k\delta ({t}^{n};{U}^{n},\bar{{\partial }\vartheta }^{n}) + 2k\varepsilon _{ a}({U}^{n}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n})] \\ & & \ +\{a({U}^{n}{;\vartheta }^{n-1}{,\vartheta }^{n-1}) - a({U}^{n-1}{;\vartheta }^{n-1}{,\vartheta }^{n-1})\} = I + II + III.{}\end{array}$$

(35)

s Employing the second bound of Lemma 2.5, with v = U ⁿ and $\chi =\bar{ {\partial }\vartheta }^{n}$, we have

$$\displaystyle{ \begin{array}{cc} \vert I\vert \leq &Ck(k + {h}^{2})\|\bar{{\partial }\vartheta }^{n}\| + Ck{h}^{2}\|\nabla \bar{{\partial }\vartheta }^{n}\| + Ck\|{\nabla \vartheta }^{n}\|\,\|\bar{{\partial }\vartheta }^{n}\| \\ & \leq k\vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + Ck\|{\nabla \vartheta {}^{n}\|}^{2} + \frac{\alpha {k}^{2}} {2} \|\nabla \bar{{\partial }\vartheta {}^{n}\|}^{2} + CkE,\end{array} }$$

(36)

with $E = O({k}^{2} + {k}^{-1}{h}^{4})$. Next, using Lemma 2.3 and the fact that ${U}^{n} \in \mathcal{B}_{M}$, we obtain

$$\displaystyle{ \vert II\vert \leq Ckh\|\nabla {U}^{n}\|_{ L_{\infty }}\,\|{\nabla \vartheta }^{n}\|\,\|\nabla \bar{{\partial }\vartheta }^{n}\| \leq C{h}^{2}\|{\nabla \vartheta {}^{n}\|}^{2} + \frac{\alpha {k}^{2}} {2} \|\nabla \bar{{\partial }\vartheta {}^{n}\|}^{2}. }$$

(37)

Finally, using again (2), the fact that ${\vartheta }^{n-1} \in \mathcal{B}_{2M}$, and (23), we have

$$\displaystyle\begin{array}{rcl} \vert III\vert & \leq & Ck\|\,\vert {\nabla \vartheta }^{n-1}\vert \,\vert \bar{\partial }{U}^{n}\vert \,\|\,\|{\nabla \vartheta }^{n-1}\| \\ & \leq & Ck(\|\,\vert {\nabla \vartheta }^{n-1}\vert \,\vert \bar{{\partial }\vartheta }^{n}\vert \,\|\, +\|\, \vert {\nabla \vartheta }^{n-1}\vert \,\vert R_{ h}\bar{\partial }{u}^{n}\vert \,\|)\,\|{\nabla \vartheta }^{n-1}\| \\ & \leq & k\vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + Ck\|{\nabla \vartheta {}^{n-1}\|}^{2}. {}\end{array}$$

(38)

Therefore applying (36)–(38), in (35), eliminating $\vert \vert \vert \bar{{\partial }\vartheta }^{n}\vert \vert \vert$ and $\|\nabla \bar{{\partial }\vartheta }^{n}\|$ and using (12), we obtain for k and h sufficiently small,

$$\displaystyle{ a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) \leq (1 + Ck)a({U}^{n-1}{;\vartheta }^{n-1}{,\vartheta }^{n-1}) + CkE. }$$

Thus, using the fact that ${\vartheta }^{0} = 0$ and A is strictly positive definite, we get

$$\displaystyle{ c\|{\nabla \vartheta {}^{n}\|}^{2} \leq a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) \leq CkE\sum _{\ell =0}^{n}{(1 + Ck)}^{n-\ell+1} \leq C({k}^{2} + {k}^{-1}{h}^{4}). }$$

Thus, there exists C ₁ > 0, such that

$$\displaystyle{ \|{\nabla \vartheta }^{n}\| \leq C_{ 1}(k + {k}^{-1/2}{h}^{2}), }$$

(39)

which completes the second part of the proof. □ 

4 Existence of the Backward Euler Approximation

Here we show the existence of the solution of the nonlinear fully discrete scheme (11), if ${U}^{0} = R_{h}{u}^{0}$ and the discretization parameters k and h are sufficiently small and satisfy $k = O({h}^{1+\epsilon })$, with 0 < ε < 1.

Let $G_{n} : \mathcal{X}_{h} \rightarrow \mathcal{X}_{h}$, be defined by

$$\displaystyle{ \langle G_{n}v - {U}^{n-1},\chi \rangle +ka_{ h}(v;G_{n}v,J_{h}\chi ) = k({f}^{n},J_{ h}\chi ),\quad \forall \chi \in \mathcal{X}_{h}. }$$

(40)

Obviously, if G _n has a fixed point v, then U ⁿ = v is the solution of (11).

In view of (39), recall that if ${U}^{n-1} \in \mathcal{B}_{M}$, then

$$\displaystyle{ \|\nabla ({U}^{n-1} - R_{ h}{u}^{n-1})\| \leq C_{ 1}(k + {k}^{-1/2}{h}^{2}). }$$

(41)

Then the following two lemmas hold:

Lemma 4.6.

Let ${U}^{n-1} \in \mathcal{B}_{M}$ such that (41) holds. Then for $k = O({h}^{1+\epsilon })$ with 0 < ε < 1, there exists a constant C ₂ > 0, independent of h, sufficiently large such that ${U}^{n-1} \in \tilde{\mathcal{B}}$ , where

$$\displaystyle{ \tilde{\mathcal{B}}_{n} =\{ w \in \mathcal{X}_{h} :\ \| \nabla (w - R_{h}{u}^{n})\| \leq C_{ 2}{h}^{1+\tilde{\epsilon }}\},\quad \text{with}\ \tilde{\epsilon } =\min (\epsilon, \frac{1-\epsilon } {2} ). }$$

(42)

Proof.

Using the stability property of R _h and the fact that $k = O({h}^{1+\epsilon })$, we have

$$\displaystyle\begin{array}{rcl} \|\nabla ({U}^{n-1} - R_{ h}{u}^{n})\|& \leq & \|\nabla ({U}^{n-1} - R_{ h}{u}^{n-1})\| + k\|\nabla R_{ h}\bar{\partial }{u}^{n}\| {}\\ & \leq & C_{1}(k + {k}^{-1/2}{h}^{2}) + k\|\nabla \bar{\partial }{u}^{n}\| \leq C_{ 2}{h}^{1+\tilde{\epsilon }}. {}\\ \end{array}$$

 □ 

Lemma 4.7.

Let ${U}^{n-1},v \in \mathcal{B}_{M}$ such that (41) holds and $v \in \tilde{\mathcal{B}}_{n}$ , with $\tilde{\mathcal{B}}_{n}$ defined by (42) . Then for $k = \mathcal{O}({h}^{1+\epsilon })$ , with 0 < ε < 1, $G_{n}v \in \tilde{\mathcal{B}}_{n}$.

Proof.

Let us now denote by ${\xi }^{n} = G_{n}v - R_{h}{u}^{n}$ and ${\xi }^{n-1} = {U}^{n-1} - R_{h}{u}^{n-1}$. Then, using (40), (1), and (16), ξ ⁿ satisfies a similar equation to (17), with ξ ⁿ and v instead of ${\vartheta }^{n}$ and U ⁿ; hence,

$$\displaystyle{ \begin{array}{cc} \langle \bar{{\partial }\xi }^{n},\chi \rangle +a_{h}(v{;\xi }^{n},J_{h}\chi )& =\delta ({t}^{n};v,\chi ),\quad \text{for}\ \chi \in \mathcal{X}_{h}. \end{array} }$$

(43)

Choosing $\chi =\bar{ {\partial }\xi }^{n}$ in (43) and following the proof of Theorem 3.1, we obtain the corresponding inequality to (35), without the last term I I I, with ξ ⁿ and v in the place of ${\vartheta }^{n}$ and U ⁿ:

$$\displaystyle{ \begin{array}{cc} &2k\vert \vert \vert \bar{{\partial }\xi {}^{n}\vert \vert \vert }^{2} + a(v{;\xi }^{n}{,\xi }^{n}) - a(v{;\xi }^{n-1}{,\xi }^{n-1}) +\alpha {k}^{2}\|\nabla \bar{{\partial }\xi {}^{n}\|}^{2} \\ & \leq 2k\delta ({t}^{n};v,\bar{{\partial }\xi }^{n}) + 2k\varepsilon _{a}(v{;\xi }^{n},\bar{{\partial }\xi }^{n}) = I + II.\end{array} }$$

(44)

Similarly as before we obtain the corresponding estimates to (36) and (37), with ξ ⁿ and v in the place of ${\vartheta }^{n}$ and U ⁿ. Thus,

$$\displaystyle{ \begin{array}{c} \vert I\vert \leq 2k\vert \vert \vert \bar{{\partial }\xi {}^{n}\vert \vert \vert }^{2} + \frac{\alpha {k}^{2}} {2} \|\nabla \bar{{\partial }\xi {}^{n}\|}^{2} + Ck\|\nabla {(v - R_{ h}{u}^{n})\|}^{2} + CkE, \end{array} }$$

(45)

with $E = O({k}^{2} + {k}^{-1}{h}^{4})$ and

$$\displaystyle{ \vert II\vert \leq C{h}^{2}a(v{;\xi }^{n}{,\xi }^{n}) + \frac{\alpha {k}^{2}} {2} \|\nabla \bar{{\partial }\xi {}^{n}\|}^{2}. }$$

(46)

Then using (45) and (46) in (44) and eliminating $\vert \vert \vert \bar{{\partial }\xi {}^{n}\vert \vert \vert }^{2}$ and $\|\nabla \bar{{\partial }\xi {}^{n}\|}^{2}$, we get for h sufficiently small

$$\displaystyle{ a(v{;\xi }^{n}{,\xi }^{n}) \leq (1 + Ck)a(v{;\xi }^{n-1}{,\xi }^{n-1}) + Ck\|\nabla {(v - R_{ h}{u}^{n})\|}^{2} + CkE. }$$

Finally, using in this inequality, (41), the facts that $v \in \tilde{\mathcal{B}}_{n}$ and ε < 1 and (13), we obtain the desired bound for k sufficiently small. □ 

Theorem 4.1.

Let $\mathcal{T}_{h}$ satisfy the inverse assumption (19) and ${U}^{n-1},v \in \mathcal{B}_{M}$ such that (41) holds. Then for h sufficiently small and $k = \mathcal{O}({h}^{1+\epsilon })$ , with 0 < ε < 1, there exists ${U}^{n} \in \mathcal{B}_{M}$ satisfying (11).

Proof.

Obviously, in view of Lemmas 4.6 and 4.7, starting with $v_{0} = {U}^{n-1}$, through G _n , we obtain a sequence of elements $v_{j+1} = G_{n}v_{j} \in \tilde{\mathcal{B}}_{n}$, j ≥ 0. Thus, combining this with (20) and the facts that M > M ₀ and $\tilde{\epsilon }> 0$, we get $G_{n}v_{j} \in \mathcal{B}_{M}$ for h sufficiently small, i.e.,

$$\displaystyle{ \|\nabla G_{n}v_{j}\|_{L_{\infty }} \leq \|\nabla R_{h}{u}^{n}\|_{ L_{\infty }} + C{h}^{-1}\|\nabla (G_{ n}v_{j} - R_{h}{u}^{n})\| \leq M,\ j \geq 0. }$$

To show now the existence of ${U}^{n} \in \mathcal{B}_{M}$, it suffices that

$$\displaystyle{\vert \vert \vert G_{n}v - G_{n}w\vert \vert \vert < L\vert \vert \vert v - w\vert \vert \vert,\quad \forall v,w \in \mathcal{B}_{M},\quad \text{with}\ 0 < L < 1.}$$

Employing (40) for $v,w \in \mathcal{B}_{M}$ and $\chi \in \mathcal{X}_{h}$, we obtain

$$\displaystyle{\langle G_{n}v - G_{n}w,\chi \rangle +ka_{h}(v;G_{n}v,J_{h}\chi ) - ka_{h}(w;G_{n}w,J_{h}\chi ) = 0.}$$

Hence, for $\chi = G_{n}v - G_{n}w$, this gives

$$ \displaystyle\begin{array}{rcl} \vert \vert \vert \chi \vert \vert \vert ^{2}& +& ka_{ h}(w;\chi,J_{h}\chi ) = k(a_{h}(w;G_{n}v,J_{h}\chi ) - a_{h}(v;G_{n}v,J_{h}\chi )) \\ & =& k(a(w;G_{n}v,\chi ) - a(v;G_{n}v,\chi )) \\ & & \quad + k(\varepsilon _{a}(v;G_{n}v,\chi ) -\varepsilon _{a}(w;G_{n}v,\chi )) = I + II. {}\end{array}$$

(47)

To bound I we use (2) and the fact that $G_{n}v \in \mathcal{B}_{M}$ to get

$$\displaystyle{ \vert I\vert \leq Ck\,\|\nabla G_{n}v\|_{L_{\infty }}\,\|v - w\|\,\|\nabla \chi \|\leq Ck\,\|v - w\|\,\|\nabla \chi \|. }$$

(48)

For I I, we use Lemma 2.4, the inverse inequality (19), and the fact that $v,G_{n}v \in \mathcal{B}_{M}$ to obtain

$$\displaystyle{ \vert II\vert \leq Ckh\|\nabla (v - w)\|\,\|\nabla \chi \|\leq Ck\|v - w\|\,\|\nabla \chi \|. }$$

(49)

Employing now (13), (48), and (49) into (47), we have

$$\displaystyle{{ \vert \vert \vert \chi \vert \vert \vert }^{2} + k\tilde{\alpha }\,\|{\nabla \chi \|}^{2} \leq Ck\,\|v - w\|\,\|\nabla \chi \|\leq Ck\|v - {w\|}^{2} + k\tilde{\alpha }\,\|{\nabla \chi \|}^{2}, }$$

which in view of the fact that $\|\cdot \|$ and $\vert \vert \vert \cdot \vert \vert \vert$ are equivalent norms gives for sufficiently small k the desired bound. □ 

5 A Linearized Fully Discrete Scheme

In this section we analyze a linearized backward Euler (LBE) scheme for the approximation of (1). This time for ${U}^{0} = R_{h}{u}^{0}$, we define the nodal approximations ${U}^{n} \in \mathcal{X}_{h}$ to u ⁿ, $n = 1,\ldots,N$, by

$$\displaystyle{ \begin{array}{cc} \langle \bar{\partial }{U}^{n},\chi \rangle + a_{h}({U}^{n-1};{U}^{n},J_{h}\chi )& = ({f}^{n},J_{h}\chi ),\quad \forall \chi \in \mathcal{X}_{h},\ n \geq 1.\end{array} }$$

(50)

Theorem 5.2.

Let U ⁿ and u be the solutions of (50) and (1) , with ${U}^{0} = R_{h}{u}^{0}$ . Then, for ${U}^{n-1} \in \mathcal{B}_{M}$ , h sufficiently small and $k = O({h}^{1+\epsilon })$ , with 0 < ε < 1, we have ${U}^{n} \in \mathcal{B}_{M}$ and

$$\displaystyle{\|{\nabla }^{s}({U}^{n} - u({t}^{n}))\| \leq C(k + {k}^{-s/2}{h}^{2-s}),\quad \text{with}\ s = 0,1.}$$

Proof.

Since the discrete scheme (50) is linear, the existence of ${U}^{n} \in \mathcal{X}_{h}$ is obvious. The proof is analogous to that for Theorem 3.1; thus, it suffices to bound $\|{\nabla {}^{s}\vartheta }^{n}\|$, s = 0, 1. This time ${\vartheta }^{n}$ satisfies a similar equation to (17) with U ^n − 1 in the place of U ⁿ:

$$\displaystyle{ \langle \bar{{\partial }\vartheta }^{n},\chi \rangle +a_{ h}({U}^{n-1}{;\vartheta }^{n},J_{ h}\chi ) =\delta ({t}^{n};{U}^{n-1},\chi ),\quad \forall \chi \in \mathcal{X}_{ h}. }$$

We start with the estimation for ${\|\vartheta }^{n}\|$. In an analogous way to (33), we obtain the following inequality:

$$\displaystyle{ \frac{1} {2k}{({\vert \vert \vert \vartheta }^{n}\vert \vert \vert }^{2} {-{\vert \vert \vert \vartheta }^{n-1}\vert \vert \vert }^{2}) +\tilde{\alpha }\| {\nabla \vartheta {}^{n}\|}^{2} \leq \delta ({t}^{n};{U}^{n-1}{,\vartheta }^{n}). }$$

To bound now the right-hand side of this inequality we employ the first estimate of Lemma 2.5, with $v = {U}^{n-1}$ and $\chi {=\vartheta }^{n}$, using the fact that ${U}^{n-1} - R_{h}{u}^{n} {=\vartheta }^{n-1} - kR_{h}\bar{\partial }{u}^{n}$ and the stability of R _h , to get

$$\displaystyle\begin{array}{rcl} & & \frac{1} {2k}{(\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2} {-\vert \vert \vert \vartheta {}^{n-1}\vert \vert \vert }^{2}) +\tilde{\alpha }\| {\nabla \vartheta {}^{n}\|}^{2} {}\\ & & \quad \leq C{(k + {h}^{2})\|\vartheta }^{n}\| + C(k\|{U}^{n-1} - R_{ h}{u}^{n}\| + {h}^{2})\|{\nabla \vartheta }^{n}\| {}\\ & & \quad \leq {C\vert \vert \vert \vartheta {}^{n}\vert \vert \vert }^{2} +\tilde{\alpha }\| {\nabla \vartheta {}^{n}\|}^{2} + C{k\vert \vert \vert \vartheta {}^{n-1}\vert \vert \vert }^{2} + CE,\quad \text{with}\ E = O({k}^{2} + {h}^{4}). {}\\ \end{array}$$

Next, after eliminating $\|{\nabla \vartheta }^{n}\|$, we get for k sufficiently small

$$\displaystyle{{{ \vert \vert \vert \vartheta }^{n}\vert \vert \vert }^{2} \leq {(1 + Ck){\vert \vert \vert \vartheta }^{n-1}\vert \vert \vert }^{2} + CkE. }$$

Hence, since ${\vartheta }^{0} = 0$, we have by repeated application ${\vert \vert \vert \vartheta }^{n}\vert \vert \vert \leq C(k + {h}^{2})$, which, in view of the fact that $\vert \vert \vert \cdot \vert \vert \vert$ and $\|\cdot \|$ are equivalent norms, completes the first part of the proof. Next we turn to the bound for $\|{\nabla \vartheta }^{n}\|$. In an analogous way to (34), we get

$$\displaystyle{ \vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + a({U}^{n-1}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n}) =\delta ({t}^{n};{U}^{n-1},\bar{{\partial }\vartheta }^{n}) +\varepsilon _{ a}({U}^{n-1}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n}). }$$

Hence, similarly as in (35), we have

$$\displaystyle\begin{array}{rcl} & & 2k\vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) - a({U}^{n-1}{;\vartheta }^{n-1}{,\vartheta }^{n-1}) +\alpha {k}^{2}\|\nabla \bar{{\partial }\vartheta {}^{n}\|}^{2} \\ & & \leq 2k\delta ({t}^{n};{U}^{n-1},\bar{{\partial }\vartheta }^{n}) + 2k\varepsilon _{ a}({U}^{n-1}{;\vartheta }^{n},\bar{{\partial }\vartheta }^{n}) \\ & & \qquad +\{ a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) - a({U}^{n-1}{;\vartheta }^{n}{,\vartheta }^{n})\} = I. {}\end{array}$$

(51)

Thus, in a similar way that we obtained (36)–(38), we have

$$\displaystyle\begin{array}{rcl} \vert I\vert & \leq & 2k\vert \vert \vert \bar{{\partial }\vartheta {}^{n}\vert \vert \vert }^{2} + Ck\|\nabla {({U}^{n-1} - R_{ h}{u}^{n})\|}^{2} + C(k + {h}^{2})\|{\nabla \vartheta {}^{n}\|}^{2} {}\\ & & \quad +\alpha {k}^{2}\|\nabla \bar{{\partial }\vartheta {}^{n}\|}^{2} + CkE, {}\\ \end{array}$$

with $E = O({k}^{2} + {k}^{-1}{h}^{4})$. Combining these in (51), using the fact that ${U}^{n-1} - R_{h}{u}^{n} {=\vartheta }^{n-1} - kR_{h}\bar{\partial }{u}^{n}$ and the stability of R _h , we obtain for k sufficiently small

$$\displaystyle{ a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) \leq (1 + Ck)a({U}^{n-1}{;\vartheta }^{n-1}{,\vartheta }^{n-1}) + CkE. }$$

Therefore, since ${\vartheta }^{0} = 0$, we obtain

$$\displaystyle{ \alpha \|{\nabla \vartheta {}^{n}\|}^{2} \leq a({U}^{n}{;\vartheta }^{n}{,\vartheta }^{n}) \leq CkE\sum _{\ell =0}^{n}{(1 + Ck)}^{n-\ell+1} \leq C({k}^{2} + {k}^{-1}{h}^{4}), }$$

which gives the desired bound. Finally, this estimate, the inverse inequality (19), and the fact that $k = O({h}^{1+\epsilon })$ give, for sufficiently small h, that ${U}^{n} \in \mathcal{B}_{M}$, which completes the proof. □ 

6 Numerical Examples

In this section we give numerical examples to illustrate the error estimates presented in the previous sections. Let $\{\phi _{i}\}_{i=1}^{d}$ be the standard piecewise linear basis functions of $\mathcal{X}_{h}$ and for $\chi \in \mathcal{X}_{h}$, let $\tilde{\chi }= (\tilde{\chi }_{1},\ldots,\tilde{\chi }_{d}) \in {\mathbb{R}}^{d}$ be the vector such that $\chi =\sum _{ i=1}^{d}\tilde{\chi }_{i}\phi _{i}$. Then the backward Euler method (11) can be written as

$$\displaystyle{ (D + kS(\tilde{{U}}^{n}))\tilde{{U}}^{n} = D\tilde{{U}}^{n-1} + k{Q}^{n}, }$$

where D is the mass matrix with elements $D_{ij} =\int _{V _{i}}\,\phi _{j}\,dx$, Q the vector with entries $Q_{i} =\int _{V _{i}}\,f\,dx$, and $S(\tilde{\chi })$ the resulting stiffness matrix for $\chi \in \mathcal{X}_{h}$, i.e.,

$$\displaystyle{ S_{ij}(\tilde{\chi }) = -\int _{\partial V _{i}}\,A(\chi )\,\nabla \,\phi _{j} \cdot n\,ds,\quad \quad \text{for}\ \chi \in \mathcal{X}_{h}. }$$

Since, this is a nonlinear problem, we employ the following iteration: Set ${\tilde{\xi }}^{0} =\tilde{ {U}}^{n-1}$ and for $m = 1,2,\ldots,$ we solve

$$\displaystyle{ {(D + kS{(\tilde{\xi }}^{m-1}))\tilde{\xi }}^{m} = D\tilde{{U}}^{n-1} + k{Q}^{n}, }$$

until some specified convergence. We note that if the iteration is stopped at m = 1, we recover the LBE method. For all examples below, we use as a stopping criteria

$$\displaystyle{ \Vert {(D + kS{(\tilde{\xi }}^{m-1}))\tilde{\xi }}^{m} - D\tilde{{U}}^{n-1} - k{Q}^{n}\Vert _{ l_{\infty }} \leq \epsilon, }$$

for some preassigned small number ε, with $\|\tilde{\chi }\|_{l_{\infty }} =\max _{i}\vert \tilde{\chi }_{i}\vert.$

We consider Ω = [0, 1] ×[0, 1] and partition [0, 1] into N equidistant intervals; thus, N ² squares are formed and divide each one into two triangles, which results in a mesh with size $h = \sqrt{2}/N$. Once the spatial mesh size is determined, the time step k is computed in such a way that k = h ^1. 01. Note that our numerical examples indicate that we could choose k = h; however, we do not know at this point how to proceed with the analysis under this assumption. We consider $u(x,y,t) = 8{e}^{-t}(x - {x}^{2})(y - {y}^{2})$ and use the nonlinear coefficient $A(u) = 1/(1 - 0.{8\sin }^{2}(4u))$, with forcing function f such that u satisfies the parabolic equation (1). We compute the error at final time T = 1 and the results are shown in Table 1. In both methods, the error convergence rate does follow the a priori estimates. We also see that in the LBE, that as we decrease h, the error contribution from k starts to dominate. This is indicated by the decrease of the convergence order in the L ₂-norm.

Table 1 Comparison of errors of backward Euler (BE) and LBE methods for various h withk = h ^1. 01