A New Shape Memory Alloy-Based Damping Device Dedicated to Civil Engineering Cables

Abstract

Most of civil engineering cable structures are subjected to potential damages mainly due to dynamic oscillations induced by wind, rain or traffic. If vibration amplitudes of bridge cables for example are too high, it may cause a fatigue phenomenon. Recently, researches had been conducted dealing with the use of damping devices in order to reduce vibration amplitudes of cables. Thin shape memory alloy (SMA) NiTi (Nickel-Titanium) wires were used as a simplified damping device on a realistic full scale 50 m long cable specimen in Ifsttar (Nantes - France) laboratory facility, and its efficiency was shown. It has been done using finite element simulations, as well as experimental test methods. The aim of this work is to link the wire material behavior with the local damping induced along the cable qualitatively. Indeed, thermomechanical energy dissipation of the NiTi-based wires enables their damping power. The hysteretic behavior in NiTi-based alloys demonstrates a consequent dissipation because of an exothermic martensitic transformation and then an endothermic reverse transformation.

11.1 Introduction

Cables of civil engineering structures are subjected to two kinds of damage mechanisms : fatigue and corrosion. Furthermore, when cables are subjected to high amplitude vibrations, there is friction between steel wires or between wires and the anchorages [1–6]. This phenomenon is called fretting-fatigue [7, 8].

To avoid fatigue and fretting-fatigue phenomena, one needs to reduce cable oscillation amplitudes by increasing the cable damping ratio. Indeed, stay cables have quite a low intrinsic damping capacity (less than 0.01%). The most conventional way of limiting or eliminating high amplitudes cable-stay vibration consists in increasing their structural damping capacity by fitting special devices. Currently, different sorts of passive damping devices have been set up on bridges on duty [9, 10].

However, the damping systems described in [10] are not appropriate for too high amplitudes and frequencies. To expand the damping range and to get a better efficiency, a Ni-Ti-based Shape Memory Alloys damping device (SMA) was used as a damping device in the same way as the external dampers kind presented in [11, 12] and [13].

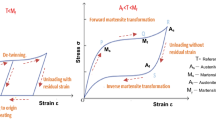
SMA are part of the smart material class, because they accommodate their response (mechanical and thermomecanical behaviors) according to the stimulations (natural or induced). In particular, NiTi SMA owns interesting properties because of the solid-solid martensitic transformation : the superelastic behavior (significant reversible strains at fixed temperature, Fig. 11.1) and a strong damping capacity, especially during the martensite transformation. The first one offers a structural fatigue resistance, whereas the second one enables the material to reach faster the threshold stress of the vibrating components. Some studies have been dealt with damping power of NiTi-based structures. A study led by Piedboeuf and Gauvin in [14] deals with the strain amplitude, the frequency and the temperature effects on the damping behavior of a NiTi alloy and a recent paper of Branco [15] deals with the NiTi applications in civil engineering, in particular with the cycling behavior of NiTi wires. A paper of Zbiciak was about the dynamic analysis of a pseudoelastic NiTi beam [16]. Recently, the efficiency of the SMA damper in controlling the cable displacement was assessed and compared with the tuned mass damper (TMD) device, using numerical models. The numerical results presented by Ben Mekki in [17] show the efficiency of the SMA damper to mitigate the high free vibrations and the harmonic vibrations on short cables (less than 5 m) better than an optimal Tuned Mass Damper (TMD).

Fig. 11.1

Superelastic behavior of NiTi at fixed temperature T > T _{A u s t e n i t e F i n i s h}

The first aim of this paper, consists of the numerical approach of the dynamic response of a pre-stressed horizontal civil engineering steel-made cable, after the release of a transverse force induced in the middle of the cable.

The second aim is to model the NiTi-based damper device effect set up perpendicular to the cable. The device is located at the same level as the induced force. The emphasis is layed on the wire energy dissipation effect on the dynamic behavior of the system, thanks to the finite element simulation. In particular, the SMA superelastic behavior is modelled in a different way than the Auricchio’s model used in [17]. The model developped by Bouvet et al. in [18] is adapted to a NiTi-based alloy and is implemented in a Finite Element code MSC Marc & Mentat, thanks to a user subroutine.

11.2 Finite Element Analysis

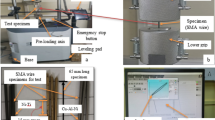
The Finite Element simulations are modelled on experimental tests realized in Ifsttar Laboratory facilities (Fig. 11.2a, b).

Fig. 11.2

(a) Experimental set up (b) Bench test (Ifsttar facilities)

11.2.1 Numerical Modelling of a Civil Engineering Cable

In the experimental set up, two laser sensors were used in order to get the vertical displacement of the cable. The first one was located near the damper location and the second one near the force location. Hence, the interest of the finite element simulations is to get information at each element node. In order to validate the simulation, the attention is focused on the transverse displacement of the cable, on the modal frequency values and on the damping ratio along the cable.

The finite element model was computed using Marc & Mentat finite element code. The cable is modelled using beam elements. This beam element is a straight, Euler-Bernoulli beam in space, which allows linear elastic and nonlinear elastic and inelastic material response. Indeed, two nodes element is the most common element used in the model of high pre-stressed cables according to Thai and Kim [19]. Large curvature changes are neglected in the large displacement formulation. Linear interpolation is used along the axis of the beam (constant axial force) with cubic displacement normal to the beam axis (linear variation in curvature). For this type of element, three parameters need to be defined: the section area A, the moment of inertia of section about local x-axis (I _{x x} ) and the moment of inertia of section about local y-axis (I _{y y} ). Input model parameters are calculated in agreement with the experimental cable values. Thus, Young’s modulus E is lower than steel modulus (E=190 GPa) cause of the slip between the wires, which affects the stiffness of the cable, and Poisson’s ratio ν is the 0.3 steel value [20]. The bending stiffnesses of the section are calculated as E I _{x x} and E I _{y y} . The torsional stiffness of the section is calculated as $\frac{E} {2(1+\nu )}(I_{xx} + I_{yy})$. The effective cross-section A ^∗ must take in account the empty space between the wires. The bending stiffness is assumed to be 33% lower than in steel case, according to experimental tests [20].

$$\displaystyle{ {(EI)}^{{\ast}} = \left (\frac{2} {3}\right ).EI }$$

(11.1)

So the effective cross-section of the beam and the corresponding diameter have to be reevaluated. Table 11.1 reports the parameters used on the numerical model compared to real cable characteristics.

Table 11.1 Physical and geometrical characteristics of the “experimental cable” specimen and the “numerical cable”

The 50m-long numerical cable is meshed into fifty 1m-long beam elements. The mechanical behavior of these elements is supposed to be elastic and linear. Initially, a vertical force is applied around the middle point of a horizontal cable. To put the “numerical cable” on vibration, the force is suddenly released in 0.05 s, according to the experimental tests. The force took several values during the experimental tests (2kN, 3kN, 4kN and 5kN). The “numerical cable” is assumed to be fixed-end : the end nodes have no degrees of freedom. An initial stress affected to the whole elements corresponds to an axial tension T of 900kN, in accordance with the experimental value. The sag-effect in the cable is neglected unlike in the Ben Mekki’s work.

Figure 11.3 show a figure of the vibrating numerical set up.

Fig. 11.3

Numerical set up

Anatically, the following differential equilibrium equation of a chord, governs the mechanical behavior of the cable.

$$\displaystyle{ EI \frac{{\partial }^{4}y(x,t)} {\partial {x}^{4}} - T \frac{{\partial }^{2}y(x,t)} {\partial {t}^{2}} + \frac{\mu } {L} \frac{{\partial }^{2}y(x,t)} {\partial {x}^{2}} = 0 }$$

(11.2)

where E I is the bending stiffness.

When the dimensionless parameter $\zeta = \frac{1} {L}\sqrt{\frac{EI} {T}}$, obtained from the previous equation (11.2), is well below 1, the bending stiffness can be neglected. Thus, the cable can be considered as a chord on the dynamic behavior aspect. Thanks to this assumption, the modal frequencies values can be determined from the equation (11.3).

$$\displaystyle{ f_{n} = \frac{n} {2L}\sqrt{\frac{T} {\mu }} }$$

(11.3)

where n is the mode rank, T is the tension in the cable, L is the cable length and μ is the mass per unit length of the cable. Anatically, the value of 2. 34 Hz is found for the 1^st mode of the “cable system” from equation (11.3).

Two preliminary analysis were conducted with different dynamic methods (such as modal and transient analysis) in order to validate the cable modeling. Modal analysis and transient dynamic analysis give approximatively the same first mode frequency values : 2. 43 Hz (modal) and 2. 39 Hz (transient dynamics), against 2. 34 Hz experimentally, according to the Fast Fourier Transform (FFT) spectrum (Fig. 11.4-b)).

Fig. 11.4

(a) Displacement at the middle of the cable (b) Fourier frequency spectrum at the middle of the cable

Furthermore, a second study plots the vertical displacement of each node on the cable thanks to a transient dynamic analysis, based on the Newmark-Beta dynamic operator [21]. It reveals an intrinsic damping ratio of 10^− 6 which will be neglected compared to the cable intrinsic damping ratio. This integration scheme is less dissipative than that of Houbolt [22] and therefore better suited to the solve of the linear and non-linear problems of mechanical vibration [23]. Furthermore, Newmark-Beta is a very stable method.

Initially, a Rayleigh viscous damping, corresponding to the first mode damping ratio of the free cable experimental configuration, is assigned on the whole cable elements to represent the intrinsic damping of a cable, due to the friction between the strand wires [24]. Indeed, the damping ratio (corresponding to the 1^st mode) evaluated from the experimental curves does not depend on the location along the cable. The Rayleigh viscous damping is presented in relation (11.4).

$$\displaystyle{ \left [C\right ] =\alpha \left [M\right ] +\beta \left [K\right ] = 2\xi \omega }$$

(11.4)

With C the Rayleigh damping matrix, M the mass matrix and K the stiffness matrix of the system “cable”, ξ the modal damping ratio and ω the natural pulsation. The mass coefficient α and the stiffness coefficient β are determined respectively by $\alpha =\xi \frac{2\omega _{i}\omega _{j}} {\omega _{i}+\omega _{j}}$ and $\beta =\xi \frac{2} {\omega _{i}+\omega _{j}}$ with ω _{k = i, j} the natural angular frequency of the k ^th mode of vibration. Here, $\alpha = 7.521{0}^{-3}$ and $\beta = 1.431{0}^{-5}$, for $\omega _{1} = 15.016rad.{s}^{-1}$ and $\omega _{2} = 30.032\mathit{rad}.{s}^{-1}$, and ξ = 0. 00033.

The evaluation of the experimental and the numerical transient analysis damping ratios ξ consisted of plotting the logarithmic decrement δ from the Hilbert envelop of the displacement signal.

$$\displaystyle{ \xi = \frac{\delta } {2\pi f_{k}T} }$$

(11.5)

With f _k the natural frequency of the n ^th considered vibration mode.

Figure 11.4a, b show the comparison between experimental and numerical curves of the vertical displacement at the middle of the cable and the associated Fast Fourier Transform spectrum. The finite element model adequately approaches the experimental signal in terms of amplitude and damping ratio (Fig. 11.4a). The error, which is reflected in the amplitude, is resulting from the difficulty of representing the distribution of the force along the cable, which is not well-extracted from the experimental tests. The numerical Fourier spectrum is coherent with experimental results and gives closed modal frequency values (Fig. 11.4b). Even-number ranking modes are not visible in the numerical spectrum because the signal was taken and the force was exerted at L ∕ 2 (common nodes of all even-number ranking nodes), which is not exactly right in the experimental case for practical reasons : the displacement sensor and the force could not be exactly located in the cable middlepoint. The first mode is the main mode (or the most energetic according to the FFT spectrum) because the signal is taken at its antinode, exactly where the force was located.

11.2.2 Action of the NiTi-Based Damping Device

11.2.2.1 Presentation of the Damping Device Model

The final aim of this study is to evaluate the consequences of the set up of a damping device on the cable damping behavior. The damping device consists of two NiTi-based alloy wires, fixed at the ground on one hand and at a specific location on the cable on the other hand. The wire is 1. 20m long and its cross-section area is 5.3 10^− 6 m ².

The material used for all the experimental tests is a NiTi polycristalline SMA (Ni : 56.3 % at., C : 40ppm, N+O : 0.0210 % at., Co ≤ 0.005 % at., Cu ≤ 0.005 % at.,Cr ≤ 0.005 % at., Nb ≤ 0.005 % at., H ≤ 0.001 % at., Ti : balance) provided by Memry (Bethel, Connecticut). Wires are in austenite state at room temperature and above. The real mass density is affected to the “numerical wire”. Before its use, the NiTi wire specimen was trained in the Ifsttar Laboratory in order to stabilize the hysteretic stress-strain curve (Fig. 11.5).

Fig. 11.5

Training of the NiTi wire realized in IFSTTAR

The wire is modelled by a single truss element. A truss element is defined as a deformable, two-nodes element with a linear interpolation along the length that is subjected to loads in the axial direction. The loads can be tensile or compressive. The element has three degrees of freedom per node. There is a single integration point at the centroid of the element. The mass matrix uses two-points integration. The element is 1.20m long and its cross-section-area is equal to the cross-section area of the two experimental wires (10.6 10^− 6 m ²) to simplify the model.

11.2.2.2 Superelastic Model General Description

The superelastic behavior available at a fixed temperature is implemented in the Marc & Mentat code via a user’s subroutine. Superelasticity means the possibility for a material to be significantly stretched without any remaining strain after loading. In NiTi, this behavior is possible thanks to a crystal rearranging. The phenomenological model was developped by Bouvet et al. [18] from the generalized plasticity frameworks with two yield surfaces corresponding respectively to the martensitic and austenitic elastic domains. The intersection of the two surfaces is associated to the elastic domain for the mixture of both phases.

The hardening functions corresponding to the direct and reverse martensitic transformations are determined from the 100^th cycle (not visible in the Fig. 11.5). The hardening directe g _dir and the hardening reverse g _rev of the model are governed respectively by a polynomial function and a hyperbolic sinus-based function.

We have to note that dynamic behavior change of NiTi alloy, induced by strain rate and temperature effects, are not taken in account in the model, and this aspect will be the topic of future works.

In the following parts, the parameters adopted, as shown in the Fig. 11.6, are given in Table 11.2.

Table 11.2 Parameters of the material modeled

Fig. 11.6

Description of model parameters

11.2.3 Numerical Model of a Civil Engineering Cable Equipped with a “Damping Device”

One node of the “numerical” wire is linked to the middle point node of the cable constitutive elements. Displacement and force are totally transmitted between the two linked nodes. The other node of the wire truss element has no degree of freedom because it is assumed to be clamped in the ground.

The truss which follows the superelastic behavior is initially pre-stressed by a force of 1kN, in order to stretch it and to increase the mean value of displacements subjected by the wire, in the same way as the experimental tests. It enables the shape memory alloy to undergo the martensitic transformation faster.

Because of a low diameter, the wire has to avoid any compression load because of the buckling phenomena which could be disastrous for its mechanical resistance. Indeed, a special device was established to impose that the device works only in tension during experimental tests. The outline of the real damper was presented in a previous study [12]. Thus, the model does not allow any compressive behavior : if the stress is a compression stress, the code removes the stress. This point involves an assymetric oscillation of the damping device, as shown in the section 11.3.

11.3 Numerical Results

The aim of this section is to compare the numerical with the experimental results in the case where the applied force (of 4kN) and the damper is located at the cable middlepoint.

11.3.1 Qualitative Comparison Between Experimental and Numerical Results

Experimental and numerical displacements of the cable midpoint, with and without the damping device, are represented in the time domain in Fig. 11.7a, b and in the frequency domain in Figs. 11.8a, b and 11.9a, b. The Fig. 11.8a, b represent the Fast Fourier Transform spectrum for the ten first seconds, whereas the Fig. 11.9a, b represent the five following seconds. Indeed, two phases of vibration are considered because of the shape of the decrement logarithmic where two damping phases (two straight lines) can be observed, as shown in Fig. 11.10.

Fig. 11.7

(a) Experimental signal (b) Numerical signal

Fig. 11.8

(a) Experimental signal (b) Numerical signal

Fig. 11.9

(a) Experimental signal (b) Numerical signal

Fig. 11.10

(a) Experimental signal (b) Numerical signal

The SMA damper allows a very fast reduction of the amplitude of the displacement after less than 10 seconds of vibration. In the “whithout damper” case, the cable is still vibrating after 120 seconds, according to numerical and experimental approaches. One can note that the logarithmic decrement is higher (Fig. 11.10a, b), and amplitudes of vibration are hardly limited from the beginning of oscillations (Fig. 11.7a, b), with the introduction of the damper. Furthermore, the symmetry does not exist any more because of the set up of the one-way damping device, even if the phenomenon is more obvious on the experimental curve.

The frequency spectrum response obtained by FFT shows the value of the first mode frequency (2.34 Hz), when the device is not introduced. The signal spectrum “With damper” contains only one main frequency at about 3Hz and noise (Fig. 11.8). The random presence of other peaks seems to predict an evolution of the first mode frequency indirectly related to time.

Wigner-Ville Transform (Fig. 11.11a, b) is used to study the frequency evolution : it shows an increase of the first modal value during damping effect. In Fig. 11.11, the maximum of Wigner-Ville Transform value at each given increment time and the corresponding frequency was extracted from the Wigner-Ville spectrogram. The Fig. 11.11a, b show the decrease of the Wigner-Ville Transform values, corresponding to an energy dissipation. The signal spectrum of the second phase corresponds to the end of the frequency evolution (Fig. 11.8a, b), and the first mode peak has clearly decreased.

Fig. 11.11

(a) Experimental signal (b) Numerical signal

For the cable with SMA damper, f ₁ increases from about 2.7 to 3.5 Hz, during the fifteen seconds after releasing of the cable. An interesting observation can be done about the time evolution of the numerical first modal frequency according to the Wigner-Ville Transform : the average frequency increases in the same way than in the experimental case but the frequency takes the “whithout damper” value of 2.4Hz at each oscillation, during the period when the damper is disabled (stress removed by the code).

On the qualitative point of view, numerical model is in good accordance with experimental observations. One can observe a small difference between the two initial amplitudes which can be explained by an imprecise spatial and time load distribution on the cable at t=0, in the numerical model. Once the cable is released by the force, the cable takes a coherent chord-like shape and the two signals become similar.

11.3.2 Modal Parameters Extraction

The relation (11.6) is one solution of the differential equilibrium equation of a chord given in equation (11.2) [10].

$$\displaystyle{ y(t) =\sum _{ n=1}^{N}A_{ n}\sin \left (\frac{n\pi x} {L} \right )\exp \left (-2\xi _{n}\pi f_{n}t\right )\sin \left (2\pi f_{n}\sqrt{1 -\xi _{ n }^{2}}t +\phi _{n}\right ) }$$

(11.6)

The parameters of the analytical equation (11.6) providing the displacement of each cable point according to time are : the modal frequencies f _n , the modal damping ratios ξ _n and the amplitudes A _n , associated to each node rank n. One can add the magnitudes of the Fourier frequency spectrum F _n . These parameters are chosen to compare experimental and numerical results. ϕ _n is the modal phase. Only modal parameters values of the first mode (n = 1) are presented in the Table 11.3, while its contribution in terms of amplitude is more important in this damper configuration.

Table 11.3 Modal parameters

Qualitatively, the same phenomenon can be observed, between numerical and experimental results, which shows a coherence between the two approaches of the study. In both approaches for the case “with damper”, the first frequency increases, damping ratio is high and decreases during the signal. The damping phenomenon can be illustrated by the FFT magnitude values.

Quantitatively, numerical results are in good accordance with experimental results, which enables to certify the finite element model. One can observe that the damping ratio is higher for the numerical approach despite low precision offered by the logarithmic decrement method. This comparison can be illustrated by a stronger Wigner-Ville Transform decrease in the previous Fig. 11.11b than in Fig. 11.11a. Furthermore, the NiTi superelastic model whose the parameters are determined on average, overestimates the damping ratio at the beginning of the signal because the strain rate is high and its effects on the hysteresis area are not taken in account. Indeed, the more the strain rate (beyond about 30%/min that is the case here), the less the strain dissipated energy density [15, 25]. The last part of the paper is dealing with the link between damping power and hysteresis loop area, thanks to the Finite Element simulation.

11.3.3 Effect of Energy Dissipation on the Damping Power for the Numerical Approach

The additional damping ratio of the numerical modeling “cable + damper” compared to the numerical cable only can be directly linked to the mechanical energy dissipation of the NiTi wire. The energy dissipation can be quantified by measuring the hysteresis area of the different loops that one can see on the stress-strain curve of the wire in Fig. 11.12. Thus, Piedboeuf et Gauvin defined, according to the defined variables, presented in Fig. 11.13, the loss factor for a non-linear material by the equation (11.7).

$$\displaystyle{ \eta = \frac{1} {2\pi } \frac{2\Delta W} {W -\frac{1} {2}\Delta W} }$$

(11.7)

Fig. 11.12

Mechanical behavior of NiTi wire during damping (finite elements)

Fig. 11.13

Physical description of energy dissipation

The approximation of the damping ratio ξ is:

$$\displaystyle{ \eta = 2\xi }$$

(11.8)

For the loops in Fig. 11.12, ξ evolution is given in Fig. 11.14.

Fig. 11.14

Comparison of damping ratio according to time by two means

Damping ratio calculated for each loop hysteresis area slightly decreases, according to the relation (11.7), but not directly with the loop area evolution. This shows that the damping ratio is not directly proportional to the hysteresis loops area but also depends on their “height” on the σ − ε plane. The damping ratio evolution can be related with the frequency evolution as considered by Schmidt and Lammering in [26]. Furthermore, the approximated damping ratio purposed by Piedboeuf and Gauvin agrees with the classical damping power calculation of a NiTi-based damping device, given in the previous section, as shown in Fig. 11.14.

One can draw a parallele between the damping ratio phases identified in Fig. 11.10a, b and the two domains undergone. During the first phase, when the damper is established, one can observe the martensitic transformation and a strong damping ratio. During the second phase, only the elastic austenitic domain is undergone and the slope of the decrement logarithmic is equivalent to for the “without damper” configuration (Fig. 11.10). In the second phase, the cable can be considered as totally damped. Here, the border between the two phases is exactly the exit of the last loop, i.e. the end of the last oscillation when the wire stress has reached the yield stress. The second phase can not be plotted in Fig. 11.14 by “hysteresis area damping ratio” method because there is no hysteresis loop left.

Better results could be obtained, knowing perfectly the mechanical behavior of the NiTi wires at the start of the experimental tests, which is not the case here for instrumentation practical reasons.

11.4 Conclusion

In this paper, a NiTi-based damping device dedicated to civil engineering cables is presented. A brief description of an application of a simplified SMA damper to mitigate oscillations artificially induced in realistic cables, as well as the corresponding finite element model are detailed. The cable consists of an assembly of beams, while NiTi wire is a single truss element whose a SMA superelastic model is attached. The efficiency of the system is shown and the corresponding finite element transient analysis is validated, as regards modal analysis. The emphasis is layed on the wire mechanical behavior effect on the device damping power, and on its dissipation energy in particular. The points to pay attention to and the future leads to optimize the damper set up on civil engineering cables are mentionned. The improvement of the SMA model could be the key of future works, in order to take in account NiTi strain rate and self-heating phenomena. set up of simplified damping devices could be done on bridges in use.