Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

The objective of this chapter is to present an analytic element approach for the simulation of transient groundwater flow in multilayer systems. The approach allow for the simulation of transient flow in systems consisting of an arbitrary number of layers. The storage in both aquifer layers and leaky layers is taken into account. In this chapter, the flow system may contain an arbitrary number of wells and line-sinks. Wells and line-sinks may be open to an arbitrary number of layers, which allows for the simulation of multi-aquifer wells, abandoned wells, partially penetrating streams, and linear fractures that provide a hydraulic connection between aquifer layers.

Application of an analytic approach has three major benefits over the application of commonly used grid-based models. First, the model domain does not have to be discretized areally in, for example, triangles or rectangles. This means that the accuracy of the solution does not depend on the size of the computational grid, hydrogeological features do not have to be fitted to the computational grid or vice versa, and the hydraulic head may be computed at any location in the aquifer. Second, the head may be evaluated at any time while the accuracy does not depend on a selected time step. And third, the model domain is infinite, avoiding the problem of selecting boundary conditions along the boundaries of the model domain, which is often difficult in the phreatic aquifer and almost impossible in deeper aquifers. Meaningful results are obtained only when significant head changes do not extend beyond hydrogeologic features that are not included in the model.

The approach for transient multilayer modeling presented in this chapter is a culmination and extension of a number of techniques. It applies the theory for transient multi-aquifer flow of Hemker and Maas [1987] and uses concepts of the analytic element method for single aquifer flow (Haitjema 1995, Strack 1989, 2003) and multi-aquifer flow (Bakker and Strack 2003) and the Laplace-transform analytic element method (Bakker and Kuhlman 2011, Furman and Neuman 2003, Kuhlman and Neuman 2009). Analytic element solutions are computed in the Laplace domain. A solution in the physical domain is obtained through numerical Laplace inversion using the algorithm of De Hoog et al. [1982]. The presented approach has been implemented in the computer program TTim (ttim.googlecode.com). Several benchmark problems are discussed, and a detailed example of a pumping well near a meandering river in a multilayer setting is discussed at the end of this chapter.

5.2 Main Approximations

Aquifer systems are conceptualized as consisting of two types of horizontal layers: aquifer layers and leaky layers. The Dupuit approximation is adopted for flow in aquifer layers which means that the resistance to flow in the vertical direction is neglected within an aquifer layer (e.g., Strack 2003), but flow is still three-dimensional (Strack 1984). Flow in leaky layers is approximated as vertical. Each layer is approximated as homogeneous. Changes in the transmissivity due to unconfined conditions are not taken into account, as the transmissivity is constant within an aquifer layer in both space and time. The presented approach is applicable to systems that may be approximated as linear. Nonlinear conditions such as streams that carry water only part of the year are not simulated.

5.3 Previous Work

Several approaches have been developed for the analytic solution of specific problems of transient flow in multilayer systems (i.e., no time stepping or areal discretization). Notwithstanding the elegance of many of these solutions, they are not reviewed here. Only a few general approaches have been published that allow for the analytic simulation of transient flow to wells in multilayer systems. Hemker and Maas [1987] and Hemker [1999a,b] present a series of solutions for flow to wells with different types of boundary conditions using a Laplace-transform approach. Superposition of these solutions is allowed as long as the boundary conditions do not interfere with each other. Application of the approach of Hemker and Maas [1987] for the simulation of abandoned wells (multi-aquifer wells with a net zero discharge) is presented in Cihan et al. [2011]. Veling and Maas [2009] presented a solution strategy for three-dimensional flow in multilayer systems, i.e., the Dupuit approximation is not adopted and the head varies horizontally and vertically within a layer. In all these papers, the inverse Laplace transform was carried out numerically using either the Schapery or Stehfest algorithms (Schapery 1962, Stehfest 1970). Nordbotten et al. [2004] presented an analytic approximate approach for the simulation of pumping wells and abandoned wells in aquifers that are separated by aquicludes. Strack [2009] presented the generating analytic element approach, which may also be used for the simulation of transient flow (Strack 2006). Fitts [2010] developed a multilayer analytic element approach for the simulation of transient flow that approximates both the areal leakage between aquifers and the release from storage with radial basis functions but relaxes some of the approximations adopted in this chapter, including a transmissivity that varies with the head in unconfined aquifers and horizontal anisotropy. Furman and Neuman [2003] and Kuhlman and Neuman [2009] developed the Laplace-transform analytic element method for single-aquifer flow, which allows for the general simulation of transient flow, and present examples of pumping wells near circular inhomogeneities. Bakker and Kuhlman [2011] apply the Laplace-transform analytic element method to simulate transient flow around impermeable walls in a single aquifer and transient flow between a well and a stream in a two-aquifer system. The cited papers on the Laplace-transform analytic element method compute the inverse Laplace transform numerically with the algorithm of De Hoog et al. [1982], which is also used in this chapter. Some advantages of this algorithm over, for example, Stehfest and Schapery, are discussed later on in this chapter.

5.4 Mathematical Model

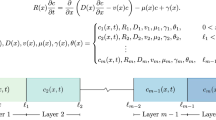
The governing system of differential equations in the Laplace domain is derived here. The derivation is given in term of potentials and essentially follows the derivation in terms of heads given in Hemker and Maas [1987]. Consider aquifer layer n sandwiched between leaky layers n on top and n + 1 at the bottom (Fig. 5.1). Three-dimensional Dupuit flow in aquifer layer n is governed by

$$T_{n}{\nabla }^{2}h_{ n} = S_{n}\frac{\partial h_{n}} {\partial t} + q_{b,n} - q_{t,n+1}$$
(5.1)

where h n (x, y) [L] is the head in aquifer layer n, T n [L2/T] and S n [ − ] are the transmissivity and storage coefficient of aquifer layer n, q b, n [L/T] is the upward leakage through the bottom of leaky layer n, q t, n + 1 is the upward leakage through the top of leaky layer n + 1, ∇ 2 is the two-dimensional horizontal Laplacian, and t is time. The horizontal components of the specific discharge vector, q x, n and q y, n , may be obtained with Darcy’s law and do not vary vertically within an aquifer layer:

$$q_{x,n} = -k_{n}\frac{\partial h_{n}} {\partial x} \qquad q_{y,n} = -k_{n}\frac{\partial h_{n}} {\partial y}$$
(5.2)

where k n is the horizontal hydraulic conductivity of layer n. The vertical component of the specific discharge vector varies linearly within an aquifer layer between q t, n + 1 at the bottom and q b, n at the top (see Fig. 5.1).

Fig. 5.1
figure 1

Numbering of aquifer layers and leaky layers in a multilayer system

Full size image

The discharge vector in layer n, with components Q x, n and Q y, n , is the vertically integrated horizontal specific discharge vector. Q x, n and Q y, n may be written as

$$Q_{x,n} = H_{n}q_{x,n} = -\frac{\partial \phi _{n}} {\partial x}\qquad Q_{y,n} = H_{n}q_{y,n} = -\frac{\partial \phi _{n}} {\partial y}$$
(5.3)

where ϕ n  = T n h n is the discharge potential, H n is the thickness of aquifer layer n, and T n  = k n H n . Equation (5.1) may now be written as

$${\nabla }^{2}\phi _{ n} = \frac{1} {D_{n}} \frac{\partial \phi _{n}} {\partial t} + q_{b,n} - q_{t,n+1}$$
(5.4)

where \(D_{n} = T_{n}/S_{n}\) is the aquifer diffusivity. Laplace transformation of (5.4) gives

$${\nabla }^{2}\bar{\phi }_{ n} = \frac{p} {D_{n}}\bar{\phi }_{n} +\bar{ q}_{b,n} -\bar{ q}_{t,n+1}$$
(5.5)

where Laplace-transformed variables are indicated with a bar and p is the complex Laplace-transform parameter.

Once a solution is obtained for the Laplace-transformed potential, a solution for the potential in the physical domain is obtained through solution of the Bromwich contour integral (e.g., Sneddon 1972):

$$\phi _{n} = {\mathcal{L}}^{-1}\{\bar{\phi }_{ n}\} = \frac{1} {2\pi \mathrm{i}}\displaystyle\int _{\gamma -\mathrm{i}\infty }^{\gamma +\mathrm{i}\infty }\bar{\phi }_{ n}{\text{e}}^{pt}\text{d}p$$
(5.6)

where γ is chosen to the right of any singularities in \(\bar{\phi }_{n}\). Integration of the Bromwich integral is carried out numerically in the complex plane using the algorithm of De Hoog et al. [1982].

5.5 Flow Between Aquifer Layers

An equation is derived for the upward flux from aquifer layer n through leaky layer n to aquifer layer n − 1 by considering one-dimensional vertical flow through leaky layer n (Fig. 5.1); this derivation closely follows (Hemker and Maas 1987). Flow in the leaky layer is governed by

$$\frac{{\partial }^{2}\eta } {\partial {z}^{2}} = \frac{\sigma _{n}} {\kappa _{n}} \frac{\partial \eta } {\partial t}$$
(5.7)

where η is the head in leaky layer n and κ n [LT − 1] and σ n [L − 1] are the vertical hydraulic conductivity and specific storage of leaky layer n, respectively. The head at the top and bottom of the leaky layer are equal to the head in the overlying and underlying aquifers:

$$\eta (z = 0) = h_{n}\qquad \eta (z = B_{n}) = h_{n-1}$$
(5.8)

where B n is the thickness of leaky layer n (see Fig. 5.1). Laplace transformation of the differential equation and boundary conditions leads to the ordinary differential equation and boundary conditions:

$$\displaystyle\begin{array}{rcl} & \frac{{\text{d}}^{2}\bar{\eta }} {\text{d}{z}^{2}} =\alpha _{ n}^{2}\bar{\eta }&\end{array}$$
(5.9)
$$\displaystyle\begin{array}{rcl} & \bar{\eta }(z = 0) =\bar{ h}_{n}\qquad \bar{\eta }(z = B_{n}) =\bar{ h}_{n-1}&\end{array}$$
(5.10)

where \(\alpha _{n} = \sqrt{p\sigma _{n } /\kappa _{n}}\). The solution for \(\bar{\eta }\) is straightforward (e.g., Strack 1989)

$$\bar{\eta }= \frac{\bar{h}_{n-1}\sinh (\alpha _{n}z) +\bar{ h}_{n}\sinh [\alpha _{n}(B_{n} - z)]} {\sinh (\alpha _{n}B_{n})}$$
(5.11)

so that

$$\frac{\text{d}\bar{\eta }} {\text{d}z} = \frac{\alpha _{n}\bar{h}_{n-1}\cosh (\alpha _{n}z) -\alpha _{n}\bar{h}_{n}\cosh [\alpha _{n}(B_{n} - z)]} {\sinh (\alpha _{n}B_{n})}$$
(5.12)

The Laplace-transformed vertical flux \(\bar{q}_{t,n}\) at the top of leaky layer n is obtained with Darcy’s law as

$$\bar{q}_{t,n} = -\kappa _{n} \frac{\text{d}\bar{\eta }} {\text{d}z}(z = B_{n}) = -\frac{\kappa _{n}\alpha _{n}\bar{h}_{n-1}} {\tanh (\alpha _{n}B_{n})} + \frac{\kappa _{n}\alpha _{n}\bar{h}_{n}} {\sinh (\alpha _{n}B_{n})}$$
(5.13)

The following new variables are introduced:

$$a_{n} = \frac{\alpha _{n}B_{n}} {\tanh (\alpha _{n}B_{n})}\qquad b_{n} = \frac{\alpha _{n}B_{n}} {\sinh (\alpha _{n}B_{n})}$$
(5.14)

The flux at the top of leaky layer n (5.13) may now be written as

$$\bar{q}_{t,n} = \frac{-a_{n}\bar{h}_{n-1} + b_{n}\bar{h}_{n}} {c_{n}}$$
(5.15)

where \(c_{n} = B_{n}/\kappa _{n}\) is the resistance to vertical flow of leaky layer n. Similarly, the flux at the bottom of leaky layer n is

$$\bar{q}_{b,n} = \frac{-b_{n}\bar{h}_{n-1} + a_{n}\bar{h}_{n}} {c_{n}}$$
(5.16)

For the special case that the top of the leaky layer is impermeable, a similar derivation gives for \(\bar{\eta }\) and its derivative:

$$\displaystyle\begin{array}{rcl} \bar{\eta }& =& \frac{\cosh [\alpha _{n}(B_{n} - z)]} {\cosh (\alpha _{n}B_{n})} \bar{h}_{n}\end{array}$$
(5.17)
$$\displaystyle\begin{array}{rcl} \frac{\text{d}\bar{\eta }} {\text{d}z}& =& -\frac{\alpha _{n}\sinh [\alpha _{n}(B_{n} - z)]} {\cosh (\alpha _{n}B_{n})} \bar{h}_{n}\end{array}$$
(5.18)

so that the vertical flux at the bottom of the leaky layer is

$$\bar{q}_{b,n} = d_{n}\frac{\bar{h}_{n}} {c_{n}}$$
(5.19)

where

$$d_{n} =\alpha _{n}B_{n}\tanh (\alpha _{n}B_{n})$$
(5.20)

When aquifer layers n and n + 1 are not separated by a leaky layer, the vertical flux between aquifer layers is computed with a standard finite difference scheme. The resistance to vertical flow c n between aquifer layers n and n − 1 is computed as

$$c_{n} = \frac{H_{n}} {2k_{v,n}} + \frac{H_{n+1}} {2k_{v,n+1}}$$
(5.21)

where k v, n and H n are the vertical hydraulic conductivity and thickness of aquifer layer n, respectively. The vertical flux between the aquifer layers is now computed as

$$\bar{q}_{t,n} =\bar{ q}_{b,n} = \frac{-\bar{h}_{n-1} +\bar{ h}_{n}} {c_{n}}$$
(5.22)

Comparison with (5.15) and (5.16) shows that for this case, \(a_{n} = b_{n} = 1\).

5.6 System of Differential Equations

Consider once again the differential equation for aquifer layer n (5.5). Use of (5.15) and (5.16) for the flux through the bottom and top of the aquifer layer, respectively, gives

$${\nabla }^{2}\bar{\phi }_{ n} = \frac{p} {D_{n}}\bar{\phi }_{n} - b_{n}\frac{\bar{h}_{n-1}} {c_{n}} + a_{n}\frac{\bar{h}_{n}} {c_{n}} + a_{n+1} \frac{\bar{h}_{n}} {c_{n+1}} - b_{n+1}\frac{\bar{h}_{n+1}} {c_{n+1}}$$
(5.23)

or in terms of the transformed discharge potential

$${\nabla }^{2}\bar{\phi }_{ n} = - \frac{b_{n}\bar{\phi }_{n-1}} {c_{n}T_{n-1}} + \left ( \frac{a_{n}} {c_{n}T_{n}} + \frac{a_{n+1}} {c_{n+1}T_{n}} + \frac{p} {D_{n}}\right )\bar{\phi }_{n} - \frac{b_{n+1}\bar{\phi }_{n+1}} {c_{n+1}T_{n+1}}$$
(5.24)

This differential equation is valid for any aquifer layer, except for the top layer (n = 1) and the bottom layer (n = N).

The differential equation for aquifer layer 1 is obtained by substituting n = 1 into Eq. (5.24). Three options are considered for the top of aquifer layer 1. First, aquifer layer 1 may be bounded on top by an impermeable layer in which case the vertical resistance of leaky layer 1 may be specified as c 1 = ∞ and division by ∞ gives zero. Second, aquifer layer 1 may be covered by a leaky layer, which is bounded on top by a fixed water level equal to zero, in which case \(\bar{\phi }_{0} = 0\). And third, aquifer layer 1 may be covered by a leaky layer, which is bounded on top by an impermeable layer, in which case \(\bar{q}_{b,1}\) reduces to (5.19) and the differential equation for aquifer layer 1 becomes

$${\nabla }^{2}\bar{\phi }_{ 1} = \left ( \frac{d} {c_{1}T_{1}} + \frac{a_{2}} {c_{2}T_{1}} + \frac{p} {D_{1}}\right )\bar{\phi }_{1} - \frac{b_{2}\bar{\phi }_{2}} {c_{2}T_{2}}$$
(5.25)

Finally, the bottom aquifer layer is considered to be bounded at the bottom by an impermeable layer (although the other two conditions as applied to the top aquifer layer may be incorporated as well), which means that \(c_{N+1} = \infty \) in the differential equation for aquifer layer N.

The system of differential equations (5.24) for n = 1, …, N may be written as a matrix differential equation

$${\nabla }^{2}\boldsymbol{\bar{\phi }} = \mathbf{A}\boldsymbol{\bar{\phi }}$$
(5.26)

where \(\boldsymbol{\bar{\phi }}\) is a vector of which component n is \(\bar{\phi }_{n}\). As may be seen from (5.24), matrix A is a tri-diagonal N by N matrix. For complex Laplace parameters p, A has N complex eigenvalues w n (n = 1, …, N) and N corresponding complex eigenvectors v n (n = 1, …, N) and may be factorized as

$$\mathbf{A} = \mathbf{V}\mathbf{W}{\mathbf{V}}^{-1}$$
(5.27)

where column n of V is formed by eigenvector v n and W is a diagonal matrix with corresponding eigenvalue w n on the diagonal of row n. Substitution of (5.27) for A in (5.26) and multiplication of both sides with V  − 1 gives

$${\nabla }^{2}\mathbf{f} = \mathbf{W}\mathbf{f}$$
(5.28)

where

$$\mathbf{f} ={ \mathbf{V}}^{-1}\boldsymbol{\bar{\phi }}.$$
(5.29)

Equation (5.28) represents a system of N uncoupled differential equations, which may be written as

$${\nabla }^{2}f_{ n} = f_{n}/\lambda _{n}^{2}\qquad n = 1,\ldots ,N$$
(5.30)

where \(\lambda _{n}^{2} = 1/w_{n}\) is introduced for convenience. This differential equation is referred to as the modified Helmholtz equation. The problem has now been reduced to the solution of N uncoupled modified Helmholtz equations.

Once a solution for all f n is determined, a solution for \(\boldsymbol{\bar{\phi }}\) is obtained as a linear combination

$$\boldsymbol{\bar{\phi }}=\displaystyle\sum _{ n=1}^{N}\beta _{ n}f_{n}\mathbf{v_{n}}$$
(5.31)

where β n are coefficients that are chosen to meet desired boundary conditions.

5.7 Laplace-Transformed Potential for Multilayer Wells and Line-sinks

Two types of analytic elements are used in this chapter: wells and line-sinks. Equations are discussed here for elements with either a unit impulse discharge or a unit step discharge screened in layer s. The function f n for a well with discharge Q(t) (positive for taking water out of the aquifer) and radius r w that fulfills (5.30) is (e.g., Strack 1989)

$$f_{n} = -\frac{\bar{Q}} {2\pi } \frac{\lambda _{n}\text{K}_{0}(r/\lambda _{n})} {r_{w}\text{K}_{1}(r_{w}/\lambda _{n})}$$
(5.32)

The Laplace transform of a unit impulse discharge at t = 0 is

$$\bar{Q} = 1$$
(5.33)

while the Laplace transform of a unit step discharge at t = 0 is

$$\bar{Q} = \frac{1} {p}$$
(5.34)

For a well with an infinitely small radius, (5.32) reduces to

$$f_{n} = -\frac{\bar{Q}} {2\pi } \text{K}_{0}(r/\lambda _{n})$$
(5.35)

The function f n for a line-sink is obtained through integration of the function for a point sink with infinitely small radius along a line. This integration may be carried out analytically near the line-sink using an infinite series expansion of K0(r ∕ λ n ) (Gusyev and Haitjema 2011), even when λ n is complex (Bakker and Kuhlman 2011). Farther away from the line-sink, accurate results are obtained with Gaussian quadrature integration, as the series expansion does not converge on a computer with commonly used finite precision arithmetic (Bakker and Kuhlman 2011).

For both wells and line-sinks, the potential in the Laplace domain may be written as (5.31). The coefficients β n need to be chosen such that the well or line-sink is screened in the desired layer s by making sure that

$$\mathbf{V}\boldsymbol{\beta } = \mathbf{e_{s}}$$
(5.36)

where β is a vector of which component n equals β n and e s is a unit vector with all zeros except for component s, which is equal to 1. To show that this does indeed give the desired result, consider, for example, the behavior of (5.35) for r approaching zero (Digital Library of Mathematical Functions, 2012, Eq. 10.30.3):

$$-\frac{\bar{Q}} {2\pi } \text{K}_{0}(r/\lambda _{n}) \sim \frac{\bar{Q}} {2\pi } \ln (r)\qquad \text{for }r \rightarrow 0$$
(5.37)

Substitution of (5.37) for f n in (5.31) and application of (5.36) gives

$$\boldsymbol{\bar{\phi }}\sim \frac{\bar{Q}} {2\pi } \ln (r)\displaystyle\sum _{n=1}^{N}\beta _{ n}\mathbf{v_{n}} = \frac{\bar{Q}} {2\pi } \ln (r)\mathbf{e_{s}}\qquad \text{for }r \rightarrow 0$$
(5.38)

so that near the well \(\boldsymbol{\bar{\phi }}\) indeed behaves as a well in layer s and not in the other layers.

5.8 Analytic Element Solution

In the previous section, equations were presented for the Laplace-transformed potential for a well and line-sink with unit impulse or step discharge screened in one layer. A solution in the Laplace domain is obtained though superposition of these potentials. The discharge of each potential is a free parameter. The free parameter may be specified (e.g., the discharge of a well) or may be computed to meet a certain boundary condition (e.g., the inflow into a stream segment is computed so that the head at the center of a stream segment has a certain value). All free parameters are determined simultaneously as, for example, the inflow of one stream segment influences the head at another stream segment and vice versa. The construction of the system of linear equations that needs to be solved to determine the free parameters of an analytic element model is discussed elsewhere (e.g., Strack 1989). Alternatively, a solution may be obtained iteratively by computing the parameters of one element at a time while keeping the parameters of the other elements fixed and by looping through all elements until the solution converges (Janković and Barnes 1999).

Multilayer wells and line-sinks may be used to model a variety of boundary conditions, including the following five:

  1. 1.

    A well or stream with a head that is fixed through time.

  2. 2.

    A well or stream with a head that varies through time.

  3. 3.

    Wells or stream segments that are screened in a single layer for which the total discharge is known.

  4. 4.

    A well that is screened in an arbitrary number of layers and for which only the net discharge is specified. The discharge of the well in each screened layer needs to be determined such that the head at the well screen is the same in each screened layer. For an abandoned well, the net discharge is zero.

  5. 5.

    A linear fault with a negligible resistance to vertical flow that cuts through multiple aquifer layers. Such a fault may be simulated with a string of line-sinks. Each line-sink is open to multiple layers and has a zero net discharge.

Once an analytic element solution is obtained in the Laplace domain, it is converted back to the physical domain through numerical integration of the Bromwich integral (5.6) using the algorithm of De Hoog et al. [1982]. One of the major advantages of using this algorithm is that an accurate solution may be obtained for one base-10 log cycle of time using a single set of M optimal Laplace parameters p, where M is commonly between 30 and 40. This means that M analytic element solutions need to be computed for each log cycle. Once these M solutions are stored, the potential can be evaluated for any time within the log cycle. It is pointed out that this is a major benefit of the De Hoog et al. algorithm. Most other commonly used algorithms, including Stehfest and Schapery, require a solution in the Laplace domain for a different set of p values for each time t, although Schapery only uses 1 real value of p and Stehfest uses on the order of 10–15 real p values.

Stepwise variation of the specified discharge or head of an element through time is simulated using superposition. It is noted that the function f n for flow to a well (5.35) may be evaluated for any Laplace-transformed discharge \(\bar{Q}\). However, back transformation for a step function that starts at an arbitrary time t 0 is difficult for most if not all existing algorithms for inverse Laplace transformations, including the ones mentioned in this chapter.

Superposition through time is fast, however, when the De Hoog et al. algorithm is used. The Laplace-transform solution needs to be computed for a few log cycles after which superposition through time only requires the repeated back transformation of a different linear combination of the Laplace-transform solution.

5.9 Benchmarking

The presented approach has been implemented in the free and open-source computer program TTim, which is written in Python using the packages NumPy and SciPy (Oliphant 2007, Pérez et al. 2011), among others. Some computationally demanding functions are written in FORTRAN and compiled into Python extensions using f2py. The design of TTim is based on the object-oriented design for analytic element models developed by Bakker and Kelson [2009].

Implementation of transient multilayer wells in TTim was benchmarked against results from MLU Lite, the free two-layer version of the commercial MLU code (www.microfem.com/products/mlu.html), which is an implementation of the papers by Hemker referred to earlier. Single layer and multilayer well solutions were also benchmarked against numerical solutions (Louwyck et al. 2011). The line-sink solution has been benchmarked against a row of wells and against a high-resolution numerical solution obtained with MODFLOW (Harbaugh 2005). These benchmarks are presented in the TTim manual (Bakker 2010). Two benchmark problems are presented here. First, TTim is benchmarked against a solution for transient three-dimensional flow in an unconfined aquifer by Neuman [1972], which shows the delayed response of the water table. Second, TTim is benchmarked against an analytic solution for periodic pumping in a multi-aquifer system, which tests the capabilities of TTim for wells with a time-varying discharge in aquifer-aquitard systems.

5.10 Benchmark Against Pumping Well in an Unconfined Aquifer

Consider transient three-dimensional flow to a pumping well in an unconfined aquifer. The well penetrates the aquifer fully, and the inflow is uniform over the thickness of the aquifer. An analytical solution was presented by Neuman [1972], who approximates the aquifer thickness as constant, which is reasonable when the drawdown is small compared to the saturated thickness. Phreatic storage is taken into account through the boundary condition at the top of the aquifer.

Neuman’s problem is solved with TTim by also using a constant transmissivity. An unconfined aquifer is divided into ten model layers each with a thickness of 1 m, a hydraulic conductivity of 1 m/d, and elastic storage. A thin eleventh layer of 1 cm thickness is added on top of the aquifer and has phreatic storage S = 0. 1. Five different values of the elastic storage coefficient are considered (see Fig. 5.2). The ratio of elastic and phreatic storage is called σ.

Fig. 5.2
figure 2

Dimensionless drawdown vs. dimensionless time at one aquifer thickness from a well in an unconfined aquifer. \(\sigma = S_{\text{elastic}}/S_{\text{phreatic}}\). Black lines are copied from Fig. 2 of Neuman [1972], while the crosses are computed with TTim. The dashed line is for the case \(\sigma = 1{0}^{-3}\) when the well drawdown is uniform rather than the inflow

Full size image

In the TTim model, one well is screened in layers 2–11. The discharge is specified for each layer to be 1 m3/d for a total of 10 m3/d. This facilitates comparison with the solution of Neuman, who specifies a uniform inflow along the well face. A comparison between the TTim solution and the Neuman solution is made for the curves of Fig. 2 in Neuman [1972]. This graph (shown in Fig. 5.2) shows dimensionless drawdown vs. dimensionless time, both on a log scale, at the bottom of the aquifer at a distance of one aquifer thickness from the well for an isotropic aquifer. The effect of the delayed response of the water table is clearly visible in Fig. 5.2, but it is noted that this effect is much less pronounced when the curves are plotted on a linear scale rather than a log scale. The curves represent different values of σ. The crosses in Fig. 5.2 represent the drawdown computed with TTim in the bottom layer of the model; they compare well to the Neuman solution. The dashed line is for the case that \(\sigma = 1{0}^{-3}\) when the well drawdown is uniform (computed with TTim) and only differs slightly from the uniform inflow case. The difference between uniform head and uniform inflow may be larger for partially penetrating wells, especially near the well.

5.11 Benchmark Against Periodic Pumping in a Multi-aquifer System

Consider periodic pumping in a system of three aquifers separated by two leaky layers (aquitards). All aquifer layers are 10 m thick and all leaky layers are 2 m thick. Aquifer and leaky layer properties are given in Table 5.1; the storage coefficient of the leaky layer is set to zero to facilitate comparison with an exact solution. A well is screened in aquifer 1 and has a discharge that varies periodically on a daily basis as

$$Q = 1,000\cos (2\pi t)$$
(5.39)

In TTim, each day is divided into 100 equal intervals with constant discharge. The head variation computed with TTim at a distance of five aquifer thicknesses from the well is shown by the solid line in Fig. 5.3; the largest amplitude represents aquifer 1, while the smallest amplitude represents aquifer 3. The exact solution for this problem is obtained through application of matrix functions, as described by Maas [1986], and is shown with dashed lines in Fig. 5.3. The exact solution is for a well that has been pumping with a periodic discharge forever, while the well in TTim starts pumping at time t = 0. Within a day, the effect of the different initial conditions is negated and TTim matches the exact periodic solution closely.

Fig. 5.3
figure 3

Head vs. time at five aquifer thicknesses from periodic well. TTim solution (solid) vs. exact solution (dash). TTim well starts at t = 0. Largest amplitude is aquifer 1; smallest amplitude is aquifer 3

Full size image
Table 5.1 Aquifer data for periodic pumping benchmark
Full size table

The same aquifer system is used to demonstrate the effect of an abandoned multi-aquifer well near a pumping well with a variable discharge. The pumping well is located at (x, y) = (0, 0) in layer 1. The discharge is 100 m3/d for 100 days, followed by 100 days with a discharge of 200 m3/d, after which the pump is turned off. An abandoned multi-aquifer well with a radius of 0.1 m is located at (x, y) = (50, 0) and is screened in all three aquifers. The head in the aquifer at \((x,y) = (-50,0)\) is shown as a function of time in the upper graph of Fig. 5.4; the drawdown is smaller in deeper aquifers. In the lower graph of Fig. 5.4, the head is shown along the line y = 0 at the end of pumping (t = 200 days). The drawdown is again smaller in deeper aquifers. Note that the head is equal in all three aquifers in the abandoned well at (x, y) = (50, 0). The dotted line represents the same situation for the case that the abandoned well is properly sealed.

Fig. 5.4
figure 4

Head vs. time in all three aquifers at \((x,y) = (-50,0)\); drawdown decreases with depth (upper graph). Head along y = 0 at t = 200 days for all three aquifers; drawdown decreases with depth. Dots represent same case but with properly sealed abandoned well (lower graph)

Full size image

5.12 Drawdown and Stream Depletion for a Well Pumping near a Meandering River

The hypothetical problem of a pumping well near a meandering river is solved to demonstrate some of the capabilities of the method (Fig. 5.5). Consider a stratified aquifer that consists of 5 layers, each with a thickness of 2 m. The aquifer properties of the five layers are given in Fig. 5.5. The top layer contains the phreatic surface and has phreatic storage. The vertical hydraulic conductivity is 10% of the horizontal one. The river is narrow and penetrates the top 4 m of the aquifer. The water level in the river is constant, and there is no leaky bed, which means that along the river the head in aquifer layers 1 and 2 equals the river level. The well is screened from 4 to 8 m below the top. The well starts pumping with a discharge 100 m3/d at time t = 0. The head is uniform along the well bore and the radius of the well is 0.3 m.

Fig. 5.5
figure 5

A pumping well and an observation well near a meandering river (left). A cross section along the dotted line (right)

Full size image

The change of the head in the aquifer caused by the pumping well is simulated. The aquifer is discretized vertically in 5 model layers. The river is modeled with 25 line-sinks that are screened in layers 1 and 2. The modeled part of the river is continued (straight) for another 300 m south and 350 m north of the section shown in Fig. 5.5. The outflow is uniform along each line-sink but varies with time such that the head is zero at the centers of the line-sinks at all times. The well is screened in layers 3 and 4, and the discharge in each layer varies such that the head is the same at the well screen in both layers at all times.

The head change at point \(\mathcal{A}\) is shown vs. time for all layers in Fig. 5.6. The horizontal axis represents the time since pumping started and has a log scale. The delayed response of the water table is clearly visible. The head decrease in layers 2–5 seems to plateau after about an hour, but the head decrease continues again after the water table at point \(\mathcal{A}\) starts to decrease. It seems that a steady-state situation is approached after 1 year of pumping.

Fig. 5.6
figure 6

Head vs. time at point \(\mathcal{A}\)

Full size image

Contour plots of the head in layers 1 and 3 after 100 days of pumping are shown in Fig. 5.7. In the left contour plot of Fig. 5.7, it may be seen that there is drawdown on both sides of the river in layer 1. The maximum drawdown in layer 1 is approximately 55 cm and occurs slightly southeast of the well rather than exactly above the well. The maximum drawdown in layer 1 on the opposite side of the river is slightly more than 20 cm. The drawdown in layer 3 is shown in the right contour plot of Fig. 5.7 and extends well beyond the river, which is screened in layers 1 and 2 only. The drawdown at the well is 2.5 m after 100 days of pumping. Head contours after 100 days of pumping in a cross-sectional view along part of the dotted line in Fig. 5.5 are shown in Fig. 5.8. The lines are created by contouring the heads at the centers of the aquifer layers. The contour lines clearly show the drawdown below the river and around the well screen.

Fig. 5.7
figure 7

Head contours in layer 1 (left) and layer 3 (right) after 100 days of pumping

Full size image
Fig. 5.8
figure 8

Head contours in cross-section along part of the dotted line shown in Fig. 5.5 after 100 days of pumping. Horizontal and vertical scale are equal. Layer discretization is shown on left and right axes

Full size image

The stream depletion, the induced recharge from the modeled river segment into the aquifer, is shown vs. time in Fig. 5.9. In addition to the total river recharge, the river recharge into layers 1 and 2 is shown separately. It takes approximately 6 days until the recharge from the river segment has reached 50% of the well discharge and 55 days until it has reached 80%. In the absence of any other aquifer features, it is expected that the induced recharge will eventually be equal to the discharge of the well. The induced recharge has only reached 96% of the well discharge after 100 years of pumping. It needs to be realized, however, that only part of the river is simulated in the model (the north–south length is 900 m). At the end of the simulation, the first and last line-sink of the string start to supply water to the aquifer. The remaining 4% of water is supplied by parts of the river or other hydrogeologic features that are not in the model and is supplied in TTim through the release of storage. The omission of these distant features has a minor effect on the solution at later time only.

Fig. 5.9
figure 9

Stream depletion vs. time

Full size image

5.13 Conclusions and Future Direction

An analytic element approach was presented for the modeling of transient flow in multilayer systems. The approach is based on the Laplace-transform analytic element method and may be applied to simulate transient flow in multilayer systems consisting of an arbitrary number of layers while taking storage within both aquifer layers and leaky layers into account. Analytic element solutions are computed in the Laplace domain while the solution in the physical domain is obtained numerically through application of the algorithm by De Hoog et al. [1982]. This algorithm may be applied to obtain an accurate solution for one log cycle of time using a single set of ∼ 40 complex Laplace parameters, which allows for the efficient computation of analytic element solutions including boundary conditions that vary stepwise through time. Benchmark problems were presented for three-dimensional flow to a fully penetrating well in an unconfined aquifer and for a periodic well in a three-aquifer system. An example was shown for a multilayer well near a partially penetrating meandering stream. The example consists of five aquifer layers with different properties. The delayed response of the water table was simulated and the stream depletion was computed. The presented approach is implemented in the free and open-source computer program TTim (ttim.googlecode.com).

Application of the approach will benefit from development of analytic elements for impermeable or leaky walls, infiltration areas, inhomogeneities, lakes or other surface water features with a leaky bed, and vertical faults with different types of boundary conditions. These elements have all been developed for steady multi-aquifer flow (Anderson and Bakker 2008, Bakker 2006, 2007) and may be modified for transient flow. Application of an integrated flux boundary condition, using the approach of Strack [2009], and applied by Gusyev and Haitjema [2011] may improve performance of some of these new elements.

Extension of the presented approach to nonlinear systems such as ephemeral streams, drains, or aquifer layers that dry up may not be feasible. Some of these problems may be simulated semi-analytically using, for example, the approach of Strack [2006] or Fitts [2010]. Strack [2009] presented an approach that allows for analytic element modeling of flow in aquifers with continuously varying properties, which has the potential to rival grid-based methods where a cell-by-cell variation of aquifer properties is trivial.

Analytic element modeling of transient multi-aquifer flow is attractive, as the input files are short and easy, and no grid, time-stepping, or closed model boundaries are needed. Analytic element models are inherently parallel, so that models with large numbers of analytic elements may be run on computer clusters (Janković et al. 2006). The one-to-one correspondence between analytic elements and hydrogeologic features naturally allow for step-wise modeling to gain insight in the flow system.