Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Blood flow patterns in the aorta are highly complex but may be characterized by two basic features. First, after receiving intermittent jet-like flows from the left heart ventricle, the aortic flow is highly pulsatile, and second, the pulsatile aortic flow is dampened and partly “contained” in the elastic aorta. These two effects, i.e. the vascular resistance and compliance, were modeled in a simple WindKessel model by Frank more than one century ago and its variants are still being used to this day [1].

This simple lumped parameter model, of course, cannot be used to simulate the extremely complicated three-dimensional (3D) flow patterns in the aorta, which is supported by surrounding tissue and organs [2]. This is due to a number of reasons, particularly the complex vascular anatomy and the nonlinear properties of the arterial wall [2, 3]. Consequently most computational studies of aorta (or elastic arteries) have made substantial simplifications, either by treating the vessel wall as rigid [3, 4] or by using ideal arterial wall geometries (e.g. cylinders [5]). From a physiological perspective, the rigid wall assumption is too simplified for the aorta, where compliance/elasticity plays a major role in the WindKessel effects.

The fluid–structure interaction (FSI) problem considers effect of the fluid forces (pressure and wall shear stresses) as loads on the vessel walls and the effects of the subsequent vessel deformations as a change in the geometry of the fluid flow. This necessitates the use of a mesh deforming process for the fluid region. A basic computational technique to address this problem is the Arbitrarily Lagrangian–Eulerian (ALE) method [2, 6]. However, the ALE method is computationally expensive because updating of the fluidic and structural geometry is required at each time step. Various approaches have been proposed to alleviate the computational load, e.g., Figueroa et al. [2] proposed a coupled momentum method, which applied a conventional finite element formulation of the Navier–Stokes equations to the rigid fluid domain, and treated the blood vessel as a linear elastic membrane. This method was applied to an anatomically accurate model of the abdominal aorta [2].

The aim of this work is to develop a fully coupled FSI model of an anatomically accurate aortic arch, whose geometry is digitized directly from a 3D CT image. A commercial ANSYS FSI framework is used to address the complex interactions between the pulsatile aortic flow and elastic wall.

2 Methods

2.1 Geometric Model of the Aortic Arch

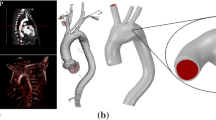
The geometry of a patient-specific aortic arch was adopted from the public vascular model repository of cardiovascular simulation, Inc. (www.vascularmodel.org) and is shown in Fig. 1. The three branches arising from the arch are the right brachiocephalic artery (with outlets A1 and A2), the left common carotid artery (with outlet B) and the left subclavian artery (with outlet C). These arteries supply blood to the head, neck, and upper limbs. The distal end of the arch is truncated proximal to the renal hepatic arteries. The descending aorta, which receives more than 70% of the cardiac output, supplies blood to the torso, abdominal organs, and lower limbs. The unloaded diameters of the ascending aorta (inlet) and descending aorta (outlet) are 25.8 mm and 14.0 mm, respectively.

Fig. 1
figure 1

Schematic diagram of aortic arch geometry: the aortic arch is supported by a virtual spring system whose stiffness is adjustable; the red square indicates an ascending aorta cross section whose velocity streamlines will be visualized in Fig. 4

Full size image

Since the aortic arch is supported by tissues, body fluids, and organs inside the chest, the arterial wall is assumed to be supported by virtual springs (as seen in Fig. 1) to simulate this scenario. The spring support is applied uniformly over the surface of the vessel walls with a stiffness of 135 kPa/m used here—this value is low enough that these backing spring supports do not act to constrain the vessel dilatation and compliance (this is effectively determined only by the vessel wall stiffness) but is adequate to resist large lateral displacements of the entire vessel. It should be noted that the main results are not particularly sensitive to the exact value of this spring support. The wall thickness is taken as 1.5 mm, which is approximately 6% of the aortic diameter.

The aortic geometry of Fig. 1 requires computational grid generation for both structure and fluid domains. The computational mesh of the solid domain contains approximately 11,000 quadrilateral elements; the grid for the fluid domain contains approximately 550,000 tetrahedral elements with 15 near-wall layered cells to provide good resolution of the boundary layer. The resulting meshes are shown in Fig. 2.

Fig. 2
figure 2

Computational grid generation for the aorta arch: (left) quadrilateral elements for the solid wall domain; and (right) tetrahedral elements with layered boundary cells for the fluid (blood) domain

Full size image

2.2 Fluid–Structure Interaction

The commercial structural finite element analysis code ANSYS and computational fluid dynamics (CFD) code CFX (ANSYS Inc., Canonsburg, PA) are used in the coupled FSI analysis. The solution is obtained in a time-marching manner, and within each time step there are a series of stagger loops, which allows coupling of the load fields from the CFD intermediate solutions to a deflected geometry from the structural code. The deflection is assumed to be relatively small so that the fluid mesh is simply stretched and deformed by the deflection of the wall surface (i.e. no remeshing of either the structural or fluidic meshes takes place). Convergence of the FSI coupling in the stagger loops is determined by monitoring changes in the displacement variants, after which the solution progresses to the following time step.

2.3 Turbulence Modeling for the Blood Flow

While the blood flow in most blood vessels in the human cardiovascular system is laminar, turbulence can occur in the aortic arch [7]. The peak Reynolds number in the aorta can reach 4,000, exceeding the critical value ( ∼ 2,300) for turbulent flow in straight pipes. Because adverse pressure gradients and possible flow separation occur at the arch portion of aorta as well as aortic bifurcations, the k − ω / k − ε blended shear stress transport (SST) turbulence model [8, 9] is used to capture the flow behavior in the aorta, similar to that used by Tan [10] (for aortic flow without fluid structure coupling). In such eddy-viscosity models, a turbulent viscosity μ t is used to account for the turbulent transport of fluid momentum. In the SST model, it is determined as: \(\mu _{t} = \frac{\rho k} {\omega }\), where ω is determined from a blend of the k − ω model using the standard constants [11] near the wall, and that using constants based on the k − ε model farther from the wall [8]. Limiters are also used to improve near wall performance in adverse pressure gradients and separated flows [8, 9] both in the production term of the transport equation for the turbulent kinetic energy k, and in the equation for eddy viscosity itself:

$$\displaystyle{ \mu _{t} = \frac{\rho k} {\max \left [\omega ,C\Omega F\right ]} }$$
(1)

where Ω is the vorticity magnitude, C a constant, and F a near wall blending function. Detailed description of the model and its various terms and their physical/mathematical definitions are lengthy, and so we refer the interested reader to literature [8, 9] for more details.

2.4 Linear Elastic Shell Model for the Aortic Wall

The arterial wall is assumed to behave like a linear elastic shell because the wall thickness is relatively small ( ∼ 6%) compared to the artery diameter. In the finite element analysis, shell elements governed by the Kirchhoff–Love theory are used due to the thin aortic wall as well as its small bending deformation. The applied shell elements are 4-noded with six degrees of freedom at each node: translation in the x, y, and z directions, and rotation about the x, y, and z axes.

The behaviour of aortic wall is nonlinear; however, here a linear constant elasticity assumption is made as the range of pressure loading is small compared to the nonlinear behaviour seen in tensile testing of cadavar samples. A Young’s modulus of 2 MPa is used, approximately in the middle of the wide range of aorta wall Young’s moduli that have been reported [2, 5]. Much of the literature variation is apparently due to real differences along the length of the aorta [5], as well as the wide range of loadings imposed on the samples (i.e. where a linear fit is made to the nonlinear behaviour). A Poisson’s ratio of 0.45 was used, typical of arterial walls [12].

2.5 Boundary and Initial Conditions

The inlet volumetric flow rate waveform of the pulsatile blood flow is adopted from [13], as shown in Figs. 3 and 6, and implemented as a uniform velocity profile at the inlet. In this waveform, a cardiac cycle was one second, with the division between systole and diastole at approximately 0.48 s. The mean flow rate of this waveform is 4.94 l/min, which is the approximate cardiac output of a healthy adult [14]. Fourier analysis was performed for this periodic function, and the first ten harmonics of the waveform are taken to prescribe a function defining the inflow velocity boundary condition in the fluids solver.

Fig. 3
figure 3

Time points T1–T4 identified through the cardiac cycle shown as a trace of the time-varying inlet velocity

Full size image
Fig. 4
figure 4

Velocity streamlines at the 4 time points T1–T4 from left to right: (top row) streamlines throughout the entire computational domain; (bottom row) the velocity streamlines on the cross-section plane identified in Fig. 1

Full size image
Fig. 5
figure 5

Principal stress at T2 and T4 (left) and mesh displacement at T2 and T4 (right)

Full size image
Fig. 6
figure 6

Volumetric flow rate vs. time at each outlet

Full size image

For the outlets’ boundary conditions, a real time back pressure from a previous hemodynamic study in a large arterial tree [4] is imposed on each outlet synchronized to the inlet flow cycle. The back pressure differences between outlets in this model are assumed to be small enough that the same back pressure can be used at each outlet. The outflow pressure data was prescribed in the fluids solver as a function of time using a Fourier analysis similar to the inlet flowrate. It is recognized that this assumption is valid only for this geometry with its limited lengths, and in particular is sensitive to the lengths of the three branch artery stubs; however, the split in the bulk (time-averaged) flow rate between the descending aorta and the branch arteries is realistic.

The inlet of the aorta is assumed to be clamped to aid numerical convergence, similar to that of Gerbeau et al. [6]. The outlet of the descending aorta is fixed in the z (caudal) direction and in the x and y directions (i.e. on the transverse plane), representative of the rigid attachment of the aorta by the intercostal arteries (see Fig. 1). The branch outlets were set to be fixed to avoid large oscillations induced by the pulsatile blood flow in the vessel and is consistent with the anatomy of branch artery attachments. The internal surface of the aorta was defined as the FSI interface, across which structural FEA code and fluid CFD code transfer load and boundary deflection data to each other. Structural damping was imposed to ensure convergence. In vivo structural damping is expected to be very high, due to both the vessel wall structure and the adjacent tissue and fluid outside the aorta.

3 Results

The blood is assumed to be a Newtonian fluid (valid for these larger Reynolds numbers) with a dynamic viscosity and density of 0.00388 Pas and 1,050 kg/m3, respectively. The simulation was run for 3 s (i.e. three complete cardiac cycles) with a time step of 0.02 s, and an initial flow at t = 0 of zero. After two full cardiac cycles, the flow exhibits cycle-to-cycle consistency (there is less than a 2% difference in all local velocities between the third and fourth cycles). Flow data in the third cardiac cycle was used for post-processing. Four time points (t = 0.08 s, 0.22 s, 0.5 s, 0.9 s) that span both systole and diastole were selected for post-processing the simulation results, as shown in Fig. 3.

Flow velocity streamlines were visualized for these specific time steps. From Fig. 4 we see that the flow pattern is essentially laminar at the ascending phase of systole with, turbulent flow developing during the descending phase of the systole. Helical blood flow is evident during diastole. The streamline visualization of the blood flow on crosssection of the ascending aorta (Fig. 4 at the location indicated by the red square in Fig. 1) shows the start of the development of the vortices at the descending phase of systole. The highest instantaneous velocity in the aorta, which occurs at systole, reaches 1.5 m/s. At the end phase of diastole, the aortic wall recoils to push blood downstream, albeit at a much lower velocity (less than 0.15 m/s). These phenomena are consistent with in vivo canine [7] and human [15] observations.

Figure 5(left) shows the calculated principal stress distributions on the aortic arch surface at the time points T2 and T4. The cross-section area averaged stress at T2 of systole is approximately 1.5 times that of the trough point T4. These stresses are dominated by the pressure loading (rather than the wall shear stress). Figure 5(right) also shows the displacement contours of the aortic surface at the corresponding times T2 and T4. The stresses and deformations are largest in the ascending aorta and smallest in the descending aorta. The cross-sectional area of the slice through the ascending aorta (shown in Figs. 1 and 4) is 442 mm2 at T2 and 405 mm2 at T4. The model is predicting the elastic chamber behaviour of the aorta (i.e. Windkessel effects) [7] in the 10% area increase from diastole to systole seen. Stress concentrations and large displacements occur at the transition between the aortic sinuses and the ascending aorta where the geometry has its largest deviation from a cylindrical pipe. Stress concentrations can also be seen at the proximal ends of subclavian and common carotids arteries. The displacement of these points is large through the cycle, although the stress concentrations seen here are exaggerated by the assumed uniform spring attachment of all of the vessel walls (in reality, the arteries are relatively stiffly attached at their distal ends of the lengths in the model, and much less stiffly from the aortic arch to these outlet points.

Temporal flow rate waveforms are shown in Fig. 6 for each outlet and the inlet over a cardiac cycle. Given the boundary conditions used, the split between the descending aorta outflow (taking over 78% of the total cardiac output) and the common carotid and subclavian arteries (almost equally dividing the remainder) are realistic. A comparison can also made between the time-varying flow rates simulated by the elastic wall model and the same model but with a rigid wall, also shown in Fig. 6. We observe that the waveform differences between the outlets A1, A2, B and C are small—mainly consisting of a delay in the time of peak flow. This makes physiological sense as the aortic wall is dilated by the high blood pressure in systole, and thus a portion of blood is “contained” by the aorta in systole and released in diastole. Interestingly, a decrease in peak flow rates is not seen—there is a delay in the peak, but no peak broadening is seen.

Figure 7 shows the variation of the wall shear stress (WSS) during a cardiac cycle due to the pulsatility of blood flow. The highest WSS in the aorta itself approaches 17 Pa at the narrowing of the ascending aorta at systole (t = 0.24 s). High values are also seen on the inner arch wall of the aorta at systole. The highest WSS in the aorta at diastole was about 0.5 Pa, also located at the inner arch wall. Low WSS regions form at the outer wall of the arch as well as the inner wall of the descending aorta immediately after the arch. The WSS with the turbulent model used here was much higher (2–3x) than that seen in an earlier purely laminar model due to the turbulence viscosity reducing the thickness of the boundary layers (the unpublished laminar results are not shown here). The highest WSS levels naturally occur when the flow rate (and so Reynolds number and turbulence level) is highest, showing the importance in including the turbulent nature of the flow in the aorta. Locations of high and low WSS were similar in both the turbulent model here and the earlier laminar model.

Fig. 7
figure 7

Wall shear stress distributions on the vessel walls at the four time points T1–T4 from left to right

Full size image

4 Discussion and Conclusions

The purpose of this study was to simulate fluid–structure interaction in the aortic arch with realistic pulsatile inlet blood flow and a realistic 3D aortic arch geometry. A 3D computational fluid dynamics simulation of the blood flow in the aorta was performed and the resulting fluid pressures and wall shear stresses used as input to a structural finite element analysis of the vessel walls. The resulting deformation of the walls due to these forces was then applied as new boundary conditions to the fluids solver.

Using such an approach, the WSS, velocity, mass/volume flow rate and total pressure in the fluid domain, as well as the von-Mises stress distributions and elastic wall deflections in the solid domain were calculated throughout a cardiac cycle. Since in vivo measurements for these quantities is sparse (and variable between test subjects and studies), validation was mainly made by qualitative comparison with aortic arch studies [3, 5, 6, 12, 15]. The comparison shows that the computational results such as flow transition from laminar to turbulence, the high and low WSS regions, and the wall displacement are consistent with that reported in literature. Limitations of the current model include the linearly elastic wall model, which should be anisotropic and nonlinear. Also, the uneven vessel thickness and supporting issues distributions around the aorta arch were not considered. Moreover, the outflow boundary condition was simply treated as real time back pressure—future work is needed to consider the downstream truncated arterial tree as a combined resistance and compliance (Windkessel) boundary condition. Nevertheless, the 3D FSI aortic model presented in this paper has established an initial platform to conduct further physiological/pathological flow analysis in the aorta