Stability of Marginally Outer Trapped Surfaces and Applications

Abstract

Marginally outer trapped surfaces (MOTS) are special types of codimension-two space-like surfaces in Lorentzian space-times defined by the vanishing of one of its future null expansions. Such surfaces play an important role in gravitational theory as indicators of strong gravitational fields and share some of the properties of minimal hypersurfaces, in particular the existence of a useful notion of stability. In this contribution I describe this notion and present some of its consequences. In particular I will summarize the implications of stability on the topology of MOTS, their role as barriers, the interplay between stability and space–times symmetries and the stability of Killing horizons.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In geometric theories of gravity, the gravitational field is a manifestation of the curvature of a spacetime, namely, an n-dimensional smooth manifold with a metric of Lorentzian signature $\{-,+\cdots \,,+\}$. An immediate consequence is that freely falling observers feel no gravitational field at sufficiently small scales. This is similar to the fact that any Riemannian manifold is infinitesimally flat, and hence any sufficiently local geometric measurement can be approximated by a Euclidean measurement. As a consequence, the notion of strong gravitational field becomes necessarily a subtle one in any geometric theory of gravity. This implies, in particular, that no useful notion of intense gravitational field can be attached to one single space–time point and that a less local notion becomes necessary. A reasonable possibility that has proved very successful is the use of space like, codimension-two embedded surfaces. Such surfaces have the distinctive feature that may serve as initial events for sending pulses of light. Since the codimension is two (and assuming orientability of various objects), two independent future-directed surface-orthogonal pulses of light can be emitted, one towards one side of the surface (say inwards) and another towards the other side (say outwards). These pulses of light (i.e. null geodesics starting on the surface with tangent vector orthogonal to the surface) will generate two null hypersurfaces which are smooth sufficiently near the starting surface. In this situation, one may analyse the dependence in time of the area of those light fronts. In a “normal” situation, i.e. when the gravitational field is weak, the pulse of light sent outwards will increase its area, while the pulse of light sent inwards will have decreasing area. However, light is bent by the gravitational field (which in geometric terms translates into the obvious statement that geodesics depend on the geometry). Consequently, if the gravitational field near the surface is intense and directed, say inwards, it is possible that the outward light geodesics may bend inwards sufficiently so that the area of the light fronts decreases. This geometric fact may be taken as a convincing indication that the gravitational field is intense. Surfaces where this behaviour (or a variant thereof) occurs are typically called trapped surfaces. Surfaces exhibiting a behaviour which is borderline between the “normal” situation and the strong gravitational field situation are typically called “marginally trapped”. In the literature, several specific definitions have been used, each one with their peculiarities (see, e.g. [41] for a classification). However, they all share the general pattern described above. The marginal-type surfaces are of particular interest because they may, in principle, locate transition zones from strong to weak gravitational fields. It should be emphasized that, for the discussion above to be physically sound, it is necessary to restrict the surfaces to being compact (in the non-compact case, the area element may increase due to physical reasons different from those exposed above, in fact non-compact spacelike surfaces with decreasing area element in both orthogonal null directions exist even in the Minkowski spacetime, see Example 4.1 in [40]).

Another completely different approach to define, and locate, strong gravitational fields is to consider causally disconnected regions. The motion of particles, and more generally of any signals, is restricted to lie within the null cones of the space–time metric at any point. This is one of the ways in which the gravitational field affects to propagation of particles and fields. Intuitively (although difficult to put in precise terms), one may think that the gravitational field bends the null cones towards the source of the gravitational field. If the field is sufficiently strong, the null cones will bend so much that no particle or signal will be able to escape from a predetermined space–time region. This general idea leads to the concept of black hole spacetime and of black hole region (i.e. the non-escape region in a black hole spacetime). The precise definition of black hole is, however, not simple because one needs to define the “non-escape” region in a sensible way (for instance, the causal future of an event is by construction a non-escape region, but this does not capture the idea of non-escaping a predetermined region). The most natural framework admitting such definition is the class of spacetimes which contain a large region that qualifies as “infinity”. In deliberately vague terms, a black hole region is then a region that cannot be observed from infinity. As a consequence, the notion of black hole requires imposing strong global causal assumptions on a spacetime. Black holes are certainly among the most interesting space–time objects (or rather spacetimes). They have very interesting physical and geometrical properties. However, they also have a fundamental drawback. With our present understanding of the gravitational field equations, it is not possible to know if a black hole will form during the evolution of a given initial configuration. This is because the very concept of black hole needs complete and detailed knowledge of the causal properties of the maximal Cauchy development of the given initial configuration.

It should be clear so far that the two notions of strong gravitational fields outlined above are very different from each other. However, they share the basic fact that “bending” of light is involved in one way or another. It is reasonable to ask whether, despite all appearances, there is a relationship between those two concepts. This relationship indeed exists. It is well-known (see Propositions 12.2.3 and 12.2.4 in [42] and Theorem 6.1 in [13], and also [15]) that trapped surfaces lie necessarily inside the black hole region in a black hole spacetime satisfying the so-called dominant energy condition (DEC). This last notion (defined below) states, physically, that any observer measures energy fluxes which propagate at most at the speed of light. This confinement result is very satisfactory because, in some sense, it shows that the global notion of strong gravitational field (black holes) captures the quasi-local notion (trapped surfaces). It is most natural to ask whether the converse is also true, namely: are spacetimes containing trapped surfaces (and satisfying suitable reasonable conditions) always black hole spacetimes? In view of what has been said above on our present impossibility of determining whether a given initial data evolves to form a black hole or not, it is clear that this question cannot be answered so far. There are, however, indications that it might be true. The most important one comes from the so-called singularity theorems. These are fundamental results in gravity that predict geodesic causal incompleteness of all spacetimes satisfying suitable properties. The detailed statements of the various singularity theorems do not concern us here (see, e.g. [40, 42]). However, they all share three basic conditions, namely an energy condition, a causality condition and a quasi-local condition that guarantees that the gravitational field is sufficiently strong in some space–time region. One of this quasi-local conditions is the existence of a trapped surface. Thus, spacetimes containing trapped surfaces (and satisfying a number of additional physically reasonable conditions) are singular in the sense that they are causally geodesically incomplete. The previous question can therefore be rephrased as follows:

Are singularities that form during the evolution of a regular initial data set visible from infinity?

In this form, the question is even more fundamental and important than before because it addresses the basic issue of whether the gravity theory involved (say, e.g. general relativity) is predictable, at least, in the asymptotic region at infinity. It is widely believed that the question above has a negative answer (for generic initial data). This is the content of the weak cosmic censorship conjecture put forward by Penrose [38]. This problem is very difficult indeed, and little is known at present on its validity (see [1, 43] for reviews and [12, 18] for rigorous results in spherical symmetry). It is clear, however, that there is a close connection between the validity of the weak cosmic censorship conjecture and the fact that trapped surfaces may signal the presence of a black hole spacetime.

In fact, in evolutionary approaches to spacetimes (most notably in approaches where the gravitational field equations are solved via numerical methods) marginally outer trapped surfaces (MOTS) (defined below) are routinely taken as good indicators of the location of the black hole boundary (the so-called event horizon). In numerical relativity, it is even customary to abuse notation and call these surfaces “black holes” even though no global information is available to make sure that a black hole spacetime will indeed form. This is just a manifestation of the widespread opinion among general relativists that MOTSs are good indicators of the eventual formation of a black hole spacetime. Even more, it is expected that MOTSs should approximate the event horizon at late times after all dynamical processes have taken place and an equilibrium configuration is eventually approached.

In order to see whether these expectations are confirmed, it becomes necessary to study in detail the geometry of MOTSs. Although many issues remain open, a number of results have been obtained in the last years. In particular, the notion of stability of MOTSs has proved to be important and useful. The aim of this chapter is to describe this notion and to review various places where it has turned out to be relevant.

2 Definition of Marginally Outer Trapped Surface

In this work, (M, g ⁽ⁿ⁾) will denote an n-dimensional (n ≥ 4) oriented manifold M together with a smooth metric g ⁽ⁿ⁾ of Lorentzian signature $\{-,+,\cdots \,,+\}$. $(M,{g}^{(n)})$ is always assumed to be time-oriented. We take all manifolds to be smooth and connected. Manifolds are without boundary unless otherwise stated, in which case $\partial M$ will be used for its boundary. Scalar product with g ⁽ⁿ⁾ is denoted by <, >. If necessary, Greek indices will be used for space–time tensors. The Lie derivative on M will be denoted by $\mathcal{L}$. For any metric h, we use Ric(h), Ein(h) and Scal(h) respectively for the Ricci, Einstein and scalar curvatures of h. For the space–time metric g ⁽ⁿ⁾, we simply write Ric, Ein, Scal for the corresponding curvature tensors and ∇ for the Levi–Civita covariant derivative.

The notation for submanifolds is as follows: If Σ is a smooth manifold of dimension s ≤ n and $\Phi : \Sigma \rightarrow M$ is an immersion, we say that Φ(Σ) is an immersed submanifold. If Φ is injective, we say that Φ(Σ) is a submanifold. If moreover, the two topologies inherited by Φ(Σ) from Φ and from the inclusion map onto M agree, then Φ(Σ) is an embedded submanifold. In this latter case, we often identify Σ and Φ(Σ) whenever appropriate. An (immersed/embedded) submanifold is space like if the first fundamental from ${\Phi }^{\star }({g}^{(n)})$ is positive definite. Throughout this work, we use the following definition for surface.

Definition 1.

A surface S is a smooth, orientable, closed (i.e. compact and without boundary), codimension-two, space like embedded submanifold of $(M,{g}^{(n)})$ (with embedding Φ _S ). Moreover, a surface will be connected unless otherwise stated.

2.1 Geometry of Spacelike Surfaces

It is straightforward to show that the normal bundle NS of a surface admits a basis of future null normals $\{{\mathcal{l}}^{+},{\mathcal{l}}^{-}\}$. More specifically, denoting by $\mathfrak{X}{(S)}^{\perp }$ the set of sections of the normal bundle, there exist ${\mathcal{l}}^{\pm }\in \mathfrak{X}{(S)}^{\perp }$ such that $\{{\mathcal{l}}^{+}{\vert }_{p},{\mathcal{l}}^{-}{\vert }_{p}\}$ are future directed, null and linearly independent at each point p ∈ S. This null basis is obviously not unique. We will partially fix the basis by demanding $< {\mathcal{l}}^{+},{\mathcal{l}}^{-} >= -2$ everywhere on S. The remaining freedom are the “boosts”, namely, transformations ${\mathcal{l}}^{\pm }\rightarrow {F}^{\pm 1}{\mathcal{l}}^{\pm }$ where F is a smooth positive function $F \in {C}^{\infty }(S, {\mathbb{R}}^{+})$.

S being space like, the tangent space T _p M, p ∈ S, admits a direct sum decomposition ${T}_{p}M = {T}_{p}S \oplus {N}_{p}S$, where T _p S and N _p S are, respectively, the tangent and normal spaces to S at p, see Fig. 1. According to this direct sum, a vector $V \in {T}_{p}M$ decomposes as $V = {V }^{\parallel } + {V }^{\perp }$. The first fundamental form on S, called h in the following, is a positive definite Riemannian metric. The corresponding Levi–Civita covariant derivative is denoted by ∇ _h .

Fig. 1

Schematic representation of a surface in a four-dimensional spacetime. The vertical plane represents the normal space N _p S orthogonal to S at p. The null basis ${\mathcal{l}}^{\pm }$ of the normal space is also depicted. The representation is obviously not accurate because the tangent space T _p S and the normal space N _p S intersect only at the zero vector

As usual, we define the second fundamental form vector as the symmetric, bilinear map:

$$\begin{array}{rcl} \chi (X,Y ) = -{({\nabla }_{X}Y )}^{\perp },\quad \quad X,Y \in \mathfrak{X}(S).& & \\ \end{array}$$

The null extrinsic curvatures are the projections of χ(X, Y ) along the null normals, ${\chi }_{\pm }(X,Y ){ \mathbf{def} \atop =} < \chi (X,Y ),{\mathcal{l}}^{\pm } >$. Taking traces on S we have the mean curvature vector, $H ={ \mbox{ tr}}_{S}\chi$, and the null expansions ${\theta }_{\pm } =< H,{\mathcal{l}}^{\pm } >$. These definitions imply the decomposition

$$\begin{array}{rcl} H = -\frac{1} {2}\left ({\theta }_{+}{\mathcal{l}}^{-} + {\theta }_{ -}{\mathcal{l}}^{+}\right ).& & \\ \end{array}$$

The remaining extrinsic information of the embedded surface S is encoded in the normal connection. Given $\zeta \in \mathfrak{X}{(S)}^{\perp }$, its covariant derivative along a tangent vector $X \in \mathfrak{X}(S)$ is defined as ${\nabla }_{X}^{\perp }\zeta { \mathbf{def} \atop =} {({\nabla }_{X}\zeta )}^{\perp }$. Since the scalar products of basis vectors ${\mathcal{l}}^{\pm }$ are constant, the normal covariant derivative is fully determined by the connection one-form ${s}(X){ \mathbf{def} \atop =} -\frac{1} {2} < {\mathcal{l}}^{-},{\nabla }_{ X}{\mathcal{l}}^{+} >$.

Regarding orientability issues, a choice of orientation on S fixes the orientation of the normal bundle NS. More specifically, assume that a choice of orientation on S has been made and let ${{\eta }_{S}}$ be the corresponding volume form. The volume form ${{\eta }_{{S}^{\perp }}}$ on the normal space is defined as follows: Let ${\eta }$ be the space–time volume form (recall that all spacetimes are oriented here). For any pair of normal vector fields ${\zeta }_{1},{\zeta }_{2} \in \mathfrak{X}{(S)}^{\perp }$ define ${{\eta }_{{S}^{\perp }}}({\zeta }_{1},{\zeta }_{2}){ \mathbf{def} \atop =} {\eta }\left ({\zeta }_{1},{\zeta }_{2},{X}_{1},{X}_{2}\right )/{{\eta }_{S}}({X}_{1},{X}_{2})$, where ${X}_{1},{X}_{2} \in \mathfrak{X}(S)$ are arbitrary except for the condition of being linearly independent at each point. Alternatively, a choice of orientation on the normal space fixes uniquely an orientation on S satisfying the previous relationship.

Assume that an orientation has been chosen on S (or on its normal space) and let $\xi \in \mathfrak{X}{(S)}^{\perp }$. The dual vector ${\xi }^{\star } \in \mathfrak{X}{(S)}^{\perp }$ is defined (c.f. [8]) as $< {\xi }^{\star },\zeta >{ \mathbf{def} \atop =} {{\eta }_{{S}^{\perp }}}(\xi,\zeta )$ for any vector $\zeta \in \mathfrak{X}{(S)}^{\perp }$. The following properties are immediate:

$$\begin{array}{rcl} < {\xi }^{\star },\xi >= 0,\quad < {\xi }^{\star },{\xi }^{\star } >= - < \xi,\xi >.& &\end{array}$$

(1)

Note that, given a non-null ξ | _p , Eqs. (1) admit a unique solution ${\xi }^{\star }{\vert }_{p}$ up to sign. This sign reflects the freedom in choosing the orientation on NS (or equivalently on TS).

2.2 Marginally Outer Trapped Surfaces

As discussed in the introduction, a possible way of determining the strength of a gravitational field at a quasi-local level is by studying the behaviour of light fronts of pulses originating on a surface S. The collection of null geodesics starting on S along the orthogonal null direction ${\mathcal{l}}^{+}$ (${\mathcal{l}}^{-}$) define a null hypersurface ${\mathcal{N}}^{+}$ (${\mathcal{N}}^{-}$) which is smooth near S. Light fronts are sections of ${\mathcal{N}}^{\pm }$ (i.e. smooth embedded surfaces in ${\mathcal{N}}^{\pm }$ intersecting each null geodesic orthogonal to S precisely once). Taking the light fronts sufficiently close to S, we can evaluate their area by using the first variation of area of submanifolds.

Let ν be a normal variation vector on S, i.e. a vector field defined in a space–time neighbourhood of S which is orthogonal to S on the surface. Choose ν to be compactly supported (this entails no restriction since S itself is compact). This vector field generates a one-parameter local group of transformations $\{{\varphi {}_{\tau }\}}_{\tau \in I}$, where $I \subset \mathbb{R}$ is an interval containing τ = 0 and τ is the canonical parameter of the group. The variation of S along ν is the one-parameter family of surfaces ${S}_{\tau } \equiv {\varphi }_{\tau }(S)$. Obviously we have ${S}_{\tau =0} = S$. For any covariant tensor Γ defined on S and depending on its geometry (intrinsic or extrinsic), let us denote by ${\Gamma }_{\tau }$ the corresponding (formally analogous) tensor defined on the surface ${S}_{\tau } = {\varphi }_{\tau }(S)$. The variation of Γ along ν is defined as ${\delta }_{\nu }\Gamma \equiv {\left. \frac{d} {d\tau }\left [{\varphi }_{\tau }^{{_\ast}}({\Gamma }_{ \tau })\right ]\right \vert }_{\tau =0}$, where ${\varphi }_{\tau }^{{_\ast}}$ denotes the pull-back of ${\varphi }_{\tau }$. It is immediate to check that this variation only depends on the values of ν on S and not on its extension off S.

For the first variation of area, let $\vert {S}_{\tau }\vert$ denote the area of the surface S _τ. The formula of the first variation of area states (see e.g. [11])

$${\delta }_{\nu }\vert S\vert { \mathbf{def} \atop =} { \left.\frac{d\vert {S}_{\tau }\vert } {d\tau } \right \vert }_{\tau =0} ={ \int \limits }_{S} < H,\nu >{ {\eta }_{S}}.$$

(2)

Variations of S along ${\mathcal{N}}^{\pm }$ are defined by vector fields ν satisfying $\nu {\vert }_{S} = \psi {\mathcal{l}}^{\pm }$ where $\psi \in {C}^{\infty }(S, {\mathbb{R}}^{+} \cup 0)$. A necessary condition for the area of the light fronts to decrease along ${\mathcal{N}}^{\pm }$ is that ${\delta }_{\psi {\mathcal{l}}^{\pm }}\vert S\vert \leq 0$ for any such ψ. By the first variation of area, this is equivalent to $< H,{\mathcal{l}}^{\pm } >\leq 0$, i.e. that the mean curvature vector H is future causal on S. This, in turn, is equivalent to the null expansion ${\theta }_{\pm }$ being non-positive, ${\theta }_{\pm }\leq 0$. If these inequalities are strict (i.e. if H is future time like) then the area of S is strictly larger than that of ${S}_{\tau }$, for $\tau > 0$ sufficiently small. This is the condition defining a future trapped surface and which signals the presence of a strong gravitational field as discussed in the introduction, see Fig. 2. The marginal case corresponds to the situation when the area is stationary along one of the null directions and non-increasing along the other null direction, i.e. $\{{\theta }_{+} = 0,{\theta }_{-}\leq 0\}$ or $\{{\theta }_{-} = 0$, ${\theta }_{+} \leq 0\}$.

Fig. 2

Schematic figure showing the behaviour of light pulses emitted from S along its two independent orthogonal directions. In the weak gravitational field case, the area of one of the pulses increases and the other decreases. In the strong gravitational field case, light rays are bent “inwards” and the area of the light fronts decreases in both directions

The fact that the definition of marginally trapped surfaces involves both equalities and inequalities makes them somewhat cumbersome to study. It is natural to ask whether relaxing the inequality part still defines a class of surfaces where the gravitational field is strong. More specifically, the question is whether surfaces satisfying $H \propto {\mathcal{l}}^{+}$ (or $H \propto {\mathcal{l}}^{-}$) are still useful to define strong gravitational fields. In physical terms, one expects this to be true provided the surface S admits a well-defined notion of “exterior”, and that the null expansion which vanishes is the one along the exterior direction. This is because light pulses emitted to the exterior are bent inwards by the gravitational attraction and even more so are the light pulses emitted in the inward direction. If the gravitational field is sufficiently intense, the corresponding outer null expansion will be negative (i.e. the outward directed light pulses will focus) or zero in the borderline case. However, this physical expectation is tied to the existence of a sensible notion of “exterior”, which may easily be a non-trivial problem in itself. A convenient approach is to study all surfaces for which one of the null expansions vanishes and, later on, restrict the class further in order to ensure that an adequate notion of exterior exists. These considerations lead to the notion of MOTS.

Definition 2.

A marginally outer trapped surface (MOTS, for short) is a surface with stationary area with respect to variations along ${\mathcal{N}}^{+}$ or along ${\mathcal{N}}^{-}$. Equivalently, a surface is a MOTS if and only if $H \propto {\mathcal{l}}^{+}$ or $H \propto {\mathcal{l}}^{-}$ everywhere.

Remark. After renaming ℓ ⁺ and ℓ  ⁻ if necessary, we can always assume that a MOTS satisfies $H \propto {\mathcal{l}}^{+}$, or equivalently ${\theta }_{+} = 0$. For MOTS, we will always choose the orientation of the normal bundle so that ${{\eta }_{{S}^{\perp }}}({\mathcal{l}}^{+},{\mathcal{l}}^{-}) < 0$. As discussed above, this also fixes the orientation on S.

3 Stability of MOTS

MOTS are by definition critical points of the area functional for a certain class of variations. Minimal surfaces, on the other hand, are stationary points of area with respect to all possible variations. Thus, although both concepts involve properties of the area functional, there are fundamental differences between them. In the Lorentzian case, a codimension-two spacelike surface admits a normal bundle with two very special directions, namely the null normal directions. For codimension-two embedded submanifolds in a Riemannian ambient space, all normal directions are, in principle, equivalent and there is no intrinsic way of selecting specific directions along which to perform particular variations. It is clear that minimal codimension-two embedded surfaces (which must satisfy two scalar conditions, namely the vanishing of the whole mean curvature vector) are much more restrictive than MOTS. In view of this fundamental difference, one should expect very few similarities between MOTS and minimal codimension-two surfaces. Consider, on the other hand, minimal hypersurfaces in a Riemannian ambient manifold. They are also critical points of the area functional and now the space of variations has the same dimensionality as for MOTS. Since MOTS are (n − 2)-dimensional objects in n-dimensional spacetimes, one might hope that MOTS could share important similarities with minimal hypersurfaces in (n − 1)-dimensional Riemannian ambient spaces. This, in principle, rather vague relationship has turned out to be much deeper than originally expected. One instance where such close similarities arise involves the notion of stability.

We define “minimal hypersurface” as a codimension-one closed, orientable, embedded submanifold with vanishing mean curvature. We take the ambient manifold to be Riemannian although everything below would also hold for non-degenerate codimension-one submanifolds in an ambient space of arbitrary signature. The area functional is stationary on a minimal hypersurface. The second variation of area gives information about the extremal (minimum or saddle point) properties of the area functional on a minimal hypersurface S _m . Let m be a unit normal to S _m and $\psi \in {C}^{\infty }({S}_{m}, \mathbb{R})$, see Fig. 3.

Fig. 3

Variation along ψm of a minimal hypersurface S _m . The space of variation vectors contains one arbitrary smooth function ψ on S _m

The second variation of area defines the stability operator L ₀ via

$$\begin{array}{rcl}{ \delta }_{\psi m}^{2}\vert {S}_{ m}\vert ={ \int \limits }_{{S}_{m}}\psi {\delta }_{\psi m}H{{\eta }_{{S}_{m}}} ={ \int \limits }_{{S}_{m}}\psi {L}_{0}\left (\psi \right ){{\eta }_{{S}_{m}}}.& &\end{array}$$

(3)

Its explicit form reads (see, e.g. [11])

$${L}_{0}\left (\psi \right ) = -{\Delta }_{h}\psi -\left (\mbox{ Ric}(h)(m,m) + \vert \vert \kappa \vert {\vert }_{h}^{2}\right )\psi,$$

(4)

where Δ _h is the Laplacian on $({S}_{m},h)$ and κ is the second fundamental form of S _m along m. The operator L ₀ is linear, elliptic and formally self-adjoint with respect to the L ² product with the metric volume form ${{\eta }_{{S}_{m}}}$. This implies that the principal eigenvalue λ₀ can be represented by the Rayleigh–Ritz formula

$$\begin{array}{rcl}{ \lambda }_{0} ={ \mbox{ inf} \atop { \psi \neq 0 \atop \psi \in {C}^{\infty }({S}_{m},\mathbb{R})} } \frac{< \psi,L\psi {>}_{{L}^{2}}} {< \psi,\psi {>}_{{L}^{2}}}.& & \\ \end{array}$$

This immediately gives a lower bound for any second variation of area

$${\delta }_{\psi m}^{2}\vert {S}_{ m}\vert \geq {\lambda }_{0}{ \int \limits }_{{S}_{m}}{\psi }^{2}{{\eta }_{{ S}_{m}}}.$$

Equality occurs if and only if ψ is a principal eigenfunction i.e ${L}_{0}\psi = {\lambda }_{0}\psi$. Thus, ${\delta }_{\psi m}^{2}\vert {S}_{m}\vert \geq 0$ is equivalent to ${\lambda }_{0} \geq 0$. A minimal surface satisfying ${\lambda }_{0} \geq 0$ is called stable minimal surface.

MOTS are codimension-two surfaces, and the area functional is critical only for variations along ℓ ⁺. It is natural to evaluate the second variation of area along ℓ ⁺. The result is then given by the well-known Raychaudhuri equation (see e.g. [42]) and reads

$$\begin{array}{rcl}{ \delta }_{\psi {\mathcal{l}}^{+}}^{2}\vert S\vert = -{\int \limits }_{S}{\psi }^{2}\left (\mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{+}) +{ \mbox{ tr}}_{ h}({\chi }_{+}^{2})\right ){{\eta }_{ S}}.& & \\ \end{array}$$

The result is algebraic in ψ, so no differential operator similar to the stability operator above can be defined in this way. Moreover, if the spacetime $(M,{g}^{(n)})$ satisfies the so-called null energy condition (NEC), namely, $\mbox{ Ein}(\mathcal{l},\mathcal{l}) \geq 0$ for all null vector fields ℓ, then the second variation is always non-positive and MOTS are always local maxima of area. No useful notion of stability can be obtained from this second variation and any connection between stability and area is lost. However, as discussed in [3, 4], the second variation of area for minimal surfaces is essentially equivalent to the first variation of its mean curvature H (this is already apparent from the first equality in (3)). MOTS are defined by the vanishing of the scalar quantity ${\theta }_{+}$, so its first variation may give useful information for MOTS related to the stability properties for minimal surfaces. As already mentioned, it turns out to be useful to restrict the class of variations to dimension one. This amounts to choosing a section of the bundle of normal directions to S. Since the variation of ${\theta }_{+}$ along ${\mathcal{l}}^{+}$ is algebraic (instead of differential), it is convenient to restrict to sections which are nowhere tangent to ℓ ⁺. Given a fixed ${\mathcal{l}}^{+}$, such a section is uniquely represented by a vector field $v \in \mathfrak{X}{(S)}^{\perp }$ satisfying (see Fig. 4)

$$\begin{array}{rcl} v = -\frac{1} {2}{\mathcal{l}}^{-} + V {\mathcal{l}}^{+},\quad V \in {C}^{\infty }(S, \mathbb{R}).& &\end{array}$$

(5)

Fig. 4

The vector field v is a (unique) representative of a section of the bundle of normal directions to S provided this section is nowhere tangent to ℓ ⁺. Note that if a section is somewhere tangent to ℓ ⁺, the corresponding vector v would diverge to infinity. This restriction on the section is dictated by the fact that the first variation of θ₊ along ℓ ⁺ gives an algebraic operator instead of a differential operator; see [4] (in particular Lemma 3.1) for further details

Thus, these sections may be labelled by smooth functions V on S. Note that the variation direction v is not restricted to being of any specific causal character. For instance, the choice V = 0 gives $v = -{\mathcal{l}}^{-}/2$, i.e. variations along the null direction ℓ  ⁻.

For any function ψ on S, we can calculate the first-order variation ${\delta }_{\psi v}{\theta }_{+}$. This defines [4] the so-called stability operator L _v via ${L}_{v}\left (\psi \right ){ \mathbf{def} \atop =} {\delta }_{\psi v}{\theta }_{+}$. A formula for the first variation of ${\theta }_{+}$ was derived by Newman in [37] for arbitrary immersed spacelike submanifolds. The derivation was simplified in [4] (see also [28] and [9]). The explicit form of the stability operator reads

$$\begin{array}{rcl}{ L}_{v}\left (\psi \right )& =& -{\Delta }_{h}\psi + 2{s}({\nabla }_{h}\psi ) \\ & & +\left (\frac{\mbox{ Scal}(h)} {2} -\mbox{ Ein}({\mathcal{l}}^{+},{v}^{\star }) - V{ \mbox{ tr}}_{ h}({\chi }_{+}^{2}) -\vert \vert {s}\vert {\vert }_{ h}^{2} +{ \mbox{ div}}_{ h}{s}\right )\psi,\end{array}$$

(6)

where ${v}^{\star } = \frac{1} {2}{\mathcal{l}}^{-} + V {\mathcal{l}}^{+}$ in accordance with the general definition of the ⋆ operation and our choice of orientation for the normal space of MOTS. Since $< {v}^{\star },v >= 0$ and $< {v}^{\star },{v}^{\star } >= - < v,v >$, it follows that ${v}^{\star }$ is time like if and only if v is space like, and vice versa (and hence that ${v}^{\star }$ is null if and only if v is null). Recall the following definition of dominant energy condition.

Definition 3.

A spacetime $(M,{g}^{(n)})$ satisfies the DEC if $-\mbox{ Ein}(u,\cdot )$ is future causal for any future causal vector field u.

It follows that the term $\mbox{ Ein}({\mathcal{l}}^{+},{v}^{\star })$ is non-negative in spacetimes satisfying the DEC provided v is space like or null. Obviously, this term is also non-negative in Ricci-flat spacetimes irrespectively of the choice of direction v.

3.1 Principal Eigenvalue of the Stability Operator

The operator L _v plays a similar role for MOTS as the stability operator L ₀ for minimal surfaces. Like L ₀, L _v is an elliptic, second-order operator. However, L _v is not self-adjoint in general (not even allowing for different measures in the definition of the L ² product). Nevertheless, as a consequence of the Krein–Rutman theorem [34] there exists a unique principal eigenvalue defined as follows. L _v being not self-adjoint, its eigenvalues lie on the complex plane. It turns out however, that the infimum λ _v of the real parts of all eigenvalues is finite. Moreover, there exists one single eigenvalue whose real part is λ _v . This eigenvalue is called principal eigenvalue [22] and it has the property that it is always real (and hence coincides with λ _v ). The eigenspace of λ _v is one-dimensional [7] and all eigenfunctions in this space have constant sign [21, 22]. All these properties were originally obtained for bounded domains in ${\mathbb{R}}^{n}$ and for the Dirichlet problem. However, they extend easily to the compact manifold case (see Appendix B in [4] for more details).

Let us show next in which sense can the sign of the principal eigenvalue of the stability operator for MOTS be related to stability properties of such surfaces. Returning to minimal surfaces, stability means that the area functional does not decrease to second-order. If the second variation is positive (as opposed to non-negative) for non-zero variations, then the minimal surface is said to be strictly stable. In terms of the principal eigenvalue, strict stability corresponds to ${\lambda }_{0} > 0$. It is a well-known fact that minimal hypersurfaces are stable (strictly stable) if and only if there exists a positive variation along the normal m which, to first order, does not decrease (does increase) the mean curvature.

For MOTS the second variation of area along directions tangent to v gives no useful information because the first variation is nonzero along those directions and this term is dominant. However, by comparison with the previous discussion, one may ask under which conditions there exist nearby surfaces exterior to S (“exterior” being defined as the direction to which v points) which have positive null expansion. The answer is closely tied to the sign of the principal eigenvalue [4], as follows:

Lemma 1.

The principal eigenvalue λ _v of the stability operator L _v of a MOTS S is non-negative if and only if there exists an outward variation ψv ( $\psi \geq 0$, $\psi \not\equiv 0$ ) such that ${\delta }_{\psi v}{\theta }_{+} \geq 0$ .

The principal eigenvalue is positive if and only if there exists an outward variation such that ${\delta }_{\psi v}{\theta }_{+} > 0$ .

This lemma leads to the following definition [4] of stable and strictly stable MOTS.

Definition 4.

A MOTS S is called:

• Strictly stable along v if ${\lambda }_{v} > 0$.

• Stable along v if ${\lambda }_{v} \geq 0$.

• Marginally stable along v if it is stable but not strictly stable along v (i.e. ${\lambda }_{v} = 0$).

• Unstable along v if ${\lambda }_{v} < 0$.

In order to study stability of MOTS, it becomes necessary to understand under which conditions the principal eigenvalue is non-negative (or positive) and analyse its consequences. Despite the similarities between the properties of the principal eigenvalue of general second-order elliptic operators and standard properties of the lowest eigenvalue of self-adjoint operators, there are also fundamental differences. One of them comes from the possible ways of characterizing the principal eigenvalues. For self-adjoint operators, the Rayleigh–Ritz quotient characterization is of paramount importance. For MOTS, this characterization is no longer true. However, Donsker and Varadhan [21] were able to obtain two alternative min-max characterizations of the principal eigenvalue as follows

$$\begin{array}{rcl}{ \lambda }_{v}& =& \inf {}_{{\mu }_{S}\in \mathcal{P}(S)}{\sup }_{\psi \in {C}^{\infty }(S,{\mathbb{R}}^{+})}{ \int \limits }_{S}\frac{{L}_{v}\left (\psi \right )} {\psi }{ \mbox{ $\mu $}}_{S}, \\ \quad {\lambda }_{v}& =& {\sup }_{\psi \in {C}^{\infty }(S,{\mathbb{R}}^{+})}{\inf }_{x\in S}\,\frac{{L}_{v}\left (\psi \right )(x)} {\psi (x)}. \end{array}$$

Here $\mathcal{P}(S)$ denotes the space of probability measures on S.

Despite its interest, these characterizations are in general difficult to work with (because they involve a minimization of suprema, or vice versa). On the other hand, the Rayleigh–Ritz characterization is of the main technical tools for studying properties of stable minimal surfaces (see, e.g. [16]). It is natural to ask whether some type of characterization that resembles the Rayleigh–Ritz characterization can also be obtained for MOTS. This was done in [4] based on the Hodge decomposition of one-forms on compact manifolds. Indeed, the obstruction to being self-adjoint for the stability operator for MOTS is encoded in the connection one-form $\mbox{ $s$}$ of the normal bundle. For any (smooth) one-form $\mbox{ $s$}$ on a compact Riemannian manifold, the Hodge decomposition asserts that there exists a smooth function f and a smooth, divergence-free one-form ${z}$ (i.e. a one-form satisfying ${\mbox{ div}}_{h}{z} = 0$), such that

$$\begin{array}{rcl} {s} = df +\rm{ z},& & \\ \end{array}$$

(note that this decomposition can be refined further because ${z}$ can be written as a sum of co-exact one-form and a harmonic form, but the decomposition above is more useful for our purposes here). This decomposition is unique up to an arbitrary additive constant in f. In [4], the following lemma was proved.

Lemma 2.

Let (S,h) be a compact Riemannian manifold and ${L}_{v}\left (\psi \right ){ \mathbf{def} \atop =} - {\Delta }_{h}\psi + 2{s}({\nabla }_{h}\psi ) + c\psi$ where ${s}$ and c are, respectively, a smooth one-form and a smooth scalar on S. Then, the principal eigenvalue ${\lambda }_{v}$ of L _v admits the Rayleigh–Ritz type characterization

$$\begin{array}{rcl}{ \lambda }_{v} {=\inf }_{u}{ \int \limits }_{S}\left (\vert \vert {\nabla }_{h}u\vert {\vert }_{h}^{2} + Q{u}^{2} -\vert \vert d{\omega }_{ u} +{ z}\vert {\vert }_{h}^{2}{u}^{2}\right ){\mbox{ $\eta $}}_{ S},\quad u \in {C}^{\infty }(S, {\mathbb{R}}^{+}),\quad \vert \vert u\vert {\vert }_{{ L}^{2}} = 1,& & \\ \end{array}$$

where $Q{ \mathbf{def} \atop =} c + \vert \vert {s}\vert {\vert }_{h}^{2} -{\mbox{ div}}_{ h}{s}$ and ω _u is the unique solution of

$$\begin{array}{rcl} -{\Delta }_{h}{\omega }_{u} - 2{u}^{-1} < {\nabla }_{ h}{\omega }_{u},{\nabla }_{h}u >= 2{u}^{-2}1{z}\left ({\nabla }_{ h}u\right ),\quad {\int \limits }_{S}{u}^{-1}{\omega }_{ u}{\mbox{ $\eta $}}_{S} = 0.& &\end{array}$$

(7)

When ${s}$ is a gradient, then we have ${z} \equiv 0$ and the elliptic problem (7) has unique solution ${\omega }_{u} = 0$ for all functions u and we recover the standard Rayleigh–Ritz quotient for self-adjoint operators.

A simple consequence of this lemma is that the principal eigenvalue of a non-self-adjoint operator L _v can be bounded above and below by the principal eigenvalues of two canonically defined self-adjoint operators. Given L _v as in Lemma 2, let ${L}_{s}\left (\psi \right ){ \mathbf{def} \atop =} - {\Delta }_{h}\psi + Q\psi$ and ${L}_{z}\left (\psi \right ) = -{\Delta }_{h}\psi + \left (Q -\vert \vert {z}\vert {\vert }_{h}^{2}\right )\psi$ and denote by λ _s and λ _z the corresponding principal eigenvalues. It follows [4].

Lemma 3.

Let ${\lambda }_{s},{\lambda }_{v}$ and ${\lambda }_{s}$ be defined as before. Then ${\lambda }_{s} \geq {\lambda }_{v} \geq {\lambda }_{z}$ .

It is clear that the “symmetrized stability operator” L _s is non-negative (i.e. has a non-negative principal eigenvalue) on any stable MOTS. The converse is, however, not true, so it makes sense to define the notion of a MOTS being symmetrized stable along a direction v whenever the symmetrized stability operator L _s has non-negative principal eigenvalue. It is well-known that the topology of stable minimal hypersurfaces is restricted when the ambient Riemannian manifold satisfies curvature inequalities. It may be expected that similar topological restrictions should exist for stable MOTS provided the ambient spacetime satisfies also suitable curvature inequalities. Galloway and Schoen have shown [27] that this is the case and that, in fact, the notion of symmetrized stability suffices.

Theorem 1 (Galloway and Schoen [27]).

Let $(M,{g}^{(n)})$ be a spacetime satisfying the DEC and S is a MOTS which is symmetrized stable with respect to a direction v satisfying $\vert \vert v\vert {\vert }_{{g}^{(n)}} \geq 0$ everywhere. Then S is of non-negative Yamabe type (i.e. admits a metric of non-negative constant curvature). Moreover, the Yamabe type is positive unless (S,h) is Ricci flat, $\mbox{ Ein}({\mathcal{l}}^{+},{v}^{\star }) = 0$ and ${\chi }^{+} = 0$ .

Remark. This theorem was stated in [27] only for stable MOTS along spacelike directions. However, stability of the MOTS was only used to show (by direct estimates) that the Rayleigh–Ritz quotient is non-negative:

$$\begin{array}{rcl}{ \mbox{ inf} \atop { \psi \neq 0 \atop \psi \in {C}^{\infty }(S,\mathbb{R})} } \frac{{\int \limits }_{S}\psi {L}_{s}\left (\psi \right ){{\eta }_{S}}} {{\int \limits }_{S}{\psi }^{2}{{\eta }_{S}}} \geq 0.& & \\ \end{array}$$

This inequality states precisely that the principal eigenvalue of the symmetrized stability operator L _s is non-negative, so the theorem covers this case as well. It can also be checked that the proof extends to the more general case of “achronal” directions (i.e. $\vert \vert v\vert {\vert }_{{g}^{(n)}} \geq 0$), as stated above.

Remark. In the case of four dimensional spacetimes, Theorem 1 states that stable MOTS are of spherical topology, or else are a flat torus with vanishing null second fundamental form ${\chi }^{+}$. This result extends a previous theorem by Hawking [29].

3.2 Dependence of the Stability Properties on the Direction

In the definition of the stability operator, the direction v along which the variations are performed is fixed. It is of interest to study how the stability operator depends on the direction v. A natural possibility is to fix one direction and to compare the stability operator along any direction v with respect to this fixed direction. The choice of reference direction v ₀ will depend on the geometric structure available. For instance, imagine that S is known to lie within a codimension-one embedded submanifold Σ ₀ and that ℓ ⁺ is nowhere tangent to Σ ₀. Then there is a unique vector field v ₀ along S which is normal to S, tangent to Σ ₀ and satisfying (5) (note that we are not making any causality assumption on Σ ₀ besides the fact that it is nowhere tangent to ${\mathcal{l}}^{+}$). In this context, it is natural to choose v ₀ as the reference vector and compare all other stability operators with ${L}_{{v}_{0}}$. If no additional structure of this sort exists, or if one wishes to work exclusively with space–time information, then the only privileged direction v is the unique null direction orthogonal to S which is linearly independent to ${\mathcal{l}}^{+}$, namely, ${v}_{0} = -\frac{1} {2}{\mathcal{l}}^{-}$. This direction being geometrically distinguished, we simplify its notation and write L ₋ instead of ${L}_{-{\mathcal{l}}^{-}/2}$. We also write ${\lambda }_{-}$ instead of ${\lambda }_{-{\mathcal{l}}^{-}/2}$. Since the function V vanishes for this vector, it follows from (6) that

$$\begin{array}{rcl}{ L}_{-}\left (\psi \right )& =& -{\Delta }_{h}\psi + 2{s}({\nabla }_{h}\psi ) + \frac{1} {2}\left (\mbox{ Scal}(h) -\mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{-}) - 2\vert \vert {s}\vert {\vert }_{ h}^{2} + 2{\mbox{ div}}_{ h}{s}\right )\psi, \\ {L}_{v}\left (\psi \right )& =& {L}_{-}\left (\psi \right ) - V W\psi. \end{array}$$

(8)

where we have defined the function

$$\begin{array}{rcl} W{ \mathbf{def} \atop =} { \mbox{ tr}}_{h}({\chi }_{+}^{2}) + \mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{+}).& & \\ \end{array}$$

If $(M,{g}^{(n)})$ satisfies the NEC, then W ≥ 0. Thus, making V larger (more positive) will tend to decrease the principal eigenvalue. Increasing V makes the direction of v closer to the direction of ${\mathcal{l}}^{+}$, so the decreasing of the principal eigenvalue is consistent with the fact that the second variation of area along ${\mathcal{l}}^{+}$ is always non-positive (provided NEC holds). In fact, if $W\not\equiv 0$, then there necessarily exists a direction sufficiently close to ${\mathcal{l}}^{+}$ for which the principal eigenvalue is negative. Conversely, for directions sufficiently close to $-{\mathcal{l}}^{+}$ (in the sense that $V \rightarrow -\infty$), then the zero-order term in L _v can be made as large and positive as desired. This implies that, as long as $W\not\equiv 0$, there always exists directions (close to $-{\mathcal{l}}^{+}$) for which the principal eigenvalue is positive. More quantitatively, the following estimate is easily derived [4].

Lemma 4.

Let v,v′ define directions nowhere tangent to ${\mathcal{l}}^{+}$ and let $V,V \prime$ be the corresponding functions according to (5). Then, the eigenvalues ${\lambda }_{v}$, ${\lambda }_{v\prime }$ satisfy the estimates

$$\begin{array}{rcl}{ \lambda }_{v\prime } {+\inf }_{S}[(V \prime - V )W] \leq {\lambda }_{v} \leq {\lambda }_{v\prime } {+\sup }_{S}[(V \prime - V )W].& & \\ \end{array}$$

The following facts can be easily deduced from this lemma (see Fig. 5 for a schematic representation of the various vectors involved):

• (a) If $W \equiv 0$, then λ _v is independent of direction.

• (b) Assume that v′ is tilted towards ${\mathcal{l}}^{+}$ with respect to v, i.e. the function $V \prime \geq V$ everywhere (see Fig. 5) and that $(M,{g}^{(n)})$ satisfies the NEC, then ${\lambda }_{v\prime } \leq {\lambda }_{v}$.

• (c) Under NEC, a MOTS which is stable with respect to a spacelike direction, is also stable with respect to the null direction $-{\mathcal{l}}^{-}/2$.

• (d) Under NEC, a marginally stable MOTS along $-{\mathcal{l}}^{-}/2$ (i.e. ${\lambda }_{-} = 0$) is unstable along any spacelike direction v unless $\mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{+}) = 0$ and ${\chi }_{+} = 0$ on S.

• (e) If the NEC is satisfied and $W\not\equiv 0$ then ${\lambda }_{v\prime \prime } < 0$ for some direction v′ sufficiently close to ${\mathcal{l}}^{+}$.

Fig. 5

The direction v′′ is more tilted towards ℓ ⁺ than v′ and the same holds for v′ with respect to v. Note that one dimension has been suppressed in S and two have been suppressed when plotting normal directions. It is clear that, in general, given two normal directions, neither is tilted towards ${\mathcal{l}}^{+}$ with respect to the other

The following corollary follows directly from Theorem 1 and Lemma 4 and appears to have been unnoticed before.

Corollary 1.

Let S be a MOTS in a spacetime $(M,{g}^{(n)})$ satisfying the DEC. Assume that S is stable with respect to some spacelike direction v and that its Yamabe type is zero. Then, in addition to Ricci flatness, ${\chi }^{+} = 0$ , and $\mbox{ Ein}({\mathcal{l}}^{+},{v}^{\star }) = 0$ on S (as stated in Theorem 1), we also have $\mbox{ Ein}({\mathcal{l}}^{+},u){\vert }_{S} = 0$ for any vector u orthogonal to S.

Proof.

The DEC implies the NEC. So S is also stable with respect to the null direction $-{\mathcal{l}}^{-}/2$. Since its Yamabe type is zero and ${({\mathcal{l}}^{-})}^{\star } = -{\mathcal{l}}^{-}$ it follows from Theorem 1 that $\mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{-}) = 0$. Since v is spacelike, ${v}^{\star }$ is time like and hence linearly independent to ${\mathcal{l}}^{-}$ at every point, from which the claim follows.

Remark. In fact this corollary also holds for MOTS which are merely symmetrized stable with respect to some spacelike direction v. This follows from the fact that Lemma 4 also holds if we replace λ _v by λ _s and ${\lambda }_{v\prime }$ by ${\lambda }_{s\prime }$, where λ _s and ${\lambda }_{s\prime }$ are, respectively, the principal eigenvalue of the symmetrized stability operator corresponding to v and to v′. This, in turn, is a direct consequence of the fact that the transformation from the stability operator into its symmetrized counterpart only involves the connection one-form $\mathbf{s}$, which is independent of v.

Remark. A simple consequence of this corollary is that a stable (or even symmetrized stable) MOTS with respect to an achronal direction can be of zero Yamabe type and satisfy at the same time $\mbox{ Ein}({\mathcal{l}}^{+},u){\vert }_{S}\not\equiv 0$ for some normal field $u \in \mathfrak{X}{(S)}^{\perp }$ only if S is marginally stable along $-{\mathcal{l}}^{-}/2$ and $\mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{+}){\vert }_{S}\not\equiv 0$.

4 Barrier Properties of MOTS

An important property of minimal hypersurfaces is that they act as barriers for other hypersurfaces. In its simplest form, this is a consequence of the maximum principle for minimal surfaces, which states that two distinct minimal surfaces cannot touch (recall that two surfaces S ₁ and S ₂ “touch” each other if their intersection is non-empty, and there exists a neighbourhood ${U}_{1} \subset {S}_{1}$ of ${S}_{1} \cap {S}_{2}$ and a tubular neighbourhood of U ₁ such that S ₂ intersects U ₁ only on one side).

MOTSs are codimension-two objects and the notion of “touching” is necessarily subtler because one needs to define the meaning of “being on one side”. As mentioned above, given a spacelike surface S, one can generate a null hypersurface ${\mathcal{N}}^{+}$ by sending pulses of light orthogonally to S along the direction ${\mathcal{l}}^{+}$. Null hypersurfaces, like any other hypersurface in a manifold with a metric, admit a well-defined notion of second fundamental form. Despite the fact that the first fundamental form on a null hypersurface is degenerate (and hence cannot be inverted), it is nevertheless possible to define the trace of the second fundamental form by passing to a suitable quotient space (see e.g. [25] for details). This defines a scalar function θ on the null hypersurface ${\mathcal{N}}^{+}$ called “null expansion” of ${\mathcal{N}}^{+}$. Let $p \in {\mathcal{N}}^{+}$ be arbitrary and $\theta {\vert }_{p}$ be the null expansion with respect to the normal vector ${\mathcal{l}}^{+}$. It is a remarkable consequence of the degeneracy of the induced metric that any spacelike surface $\hat{S}$ embedded in ${\mathcal{N}}^{+}$ and passing through p has null expansion along ${\mathcal{l}}^{+}$ (note that this vector is necessarily orthogonal to $\hat{S}$) with exactly the same value as the hypersurface null expansion $\theta {\vert }_{p}$. The maximum principle for null hypersurfaces [24]¹ implies a maximum principle for MOTS. The appropriate notion of “touching” is that the surfaces intersect and, locally near the intersection set, one of the surfaces lies to the future of the null hypersurface ${\mathcal{N}}^{+}$ generated by the other surface. The precise statement is as follows (cf. Proposition 3.1 in [6] and Proposition 2.4 in [5] when the surfaces are restricted to lying on a spacelike hypersurface).

Theorem 2 (Maximum principle for null expansions).

Let S ₁ , S ₂ be codimension-2, spacelike surfaces intersecting at a point p and assume that their corresponding tangent planes at p coincide. Let ${\mathcal{l}}_{+}({S}_{1})$, ${\mathcal{l}}_{+}({S}_{2})$ be future-directed null normals which agree at p.

Assume that there exists a space–time neighbourhood U _p of p. Which is causal (i.e. free of closed causal curves) and satisfying ${\sup }_{{S}_{1}\cap {U}_{p}}{\theta }_{+}({S}_{1}) \leq 0 \leq {\inf }_{{S}_{2}\cap {U}_{p}}{\theta }_{+}({S}_{2})$ . Suppose that ${S}_{1} \cap {U}_{p}$ lies in the causal future of ${\mathcal{N}}^{+}({S}_{2})$ (in U _p ) and S ₁ and S ₂ are contained in a hypersurface Σ transverse to ${\mathcal{N}}^{+}({S}_{2})$ . Then S ₁ and S ₂ coincide on U _p .

This theorem states, in particular, that MOTS cannot touch each other (in the sense of this theorem) if their null normals agree at the touching point.

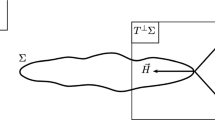
Let us, for the remainder of this section, restrict the discussion to MOTS lying on a fixed hypersurface Σ. More precisely, consider an embedded hypersurface Σ with no a priori restriction on its causal character. We say that a surface S is a MOTS lying on Σ if there is an embedding $\Phi : S \rightarrow \Sigma$ and a future null normal ℓ ⁺ to $S$ such that ${\mathcal{l}}^{+}$ is nowhere tangent to Σ and the null expansion ${\theta }_{+}$ of S along ${\mathcal{l}}^{+}$ vanishes. Obviously, when Σ is space like, the condition that ${\mathcal{l}}^{+}$ is nowhere tangent to Σ is automatically satisfied. Let S be a MOTS lying on Σ with corresponding null normal ℓ ⁺. Let v be the unique normal to S which is tangent to Σ and satisfies $< v,{\mathcal{l}}^{+} >= 1$. A rescaling of ${\mathcal{l}}^{+}$ changes v but without affecting its orientation. Given a two sided neighbourhood D of S in Σ, define the exterior part D ⁺ as the one one-sided part of D which lies in the positive direction of v. Similarly, we define the interior part D  ⁻ as the one-sided part of D which lies in the negative direction of v. Thus, a MOTS with a selected ℓ ⁺ defines locally near S a unique notion of exterior and interior within Σ. Note that if the MOTS has non-zero mean curvature somewhere, this notion of exterior/interior is unambiguous (because then ℓ ⁺, and hence v, are uniquely fixed up to positive rescaling). However, if $H \equiv 0$ on S then a choice of null normal ℓ ⁺ is necessary in order to define exterior/interior in Σ. Conversely, let S be an embedded surface in Σ with a selected normal v tangent to Σ. We define ${\theta }_{+,v}$ to be the null expansion along the unique future directed null normal ${\mathcal{l}}^{+}$ to $S$ satisfying $< {\mathcal{l}}^{+},v >= 1$. The following definition is natural in this context [4].

Definition 5.

Let Σ be an embedded hypersurface in $(M,{g}^{(n)})$ and S a MOTS lying on Σ. Assume that a future null normal ${\mathcal{l}}^{+}$ satisfying ${\theta }_{+}[S] = 0$ has been chosen. S is called locally outermost in Σ if there exists a two-sided neighbourhood ${D}^{+} \cup {D}^{-}\subset \Sigma$ of S such that the exterior D ⁺ contains no surface S ₁satisfying:

• (a) $S \cup {S}_{1}$ bounds a domain $\mathcal{D}$ in D ⁺.

• (b) ${\theta }_{+,v}[{S}_{1}] \leq 0$ where v is a normal to S ₁ in Σ pointing outside the domain $\mathcal{D}$.

This notion of locally outermost (see Fig. 6) captures the idea of a surface being (locally) an outer barrier for weakly trapped surfaces (i.e. surfaces with non-positive null expansion with respect to the outer null direction). In the case of minimal surfaces, a similar notion of barrier turns out to be intimately related to stability properties of the surface. For MOTS, an analogous result holds [4].

Fig. 6

This figure shows a MOTS S lying on a hypersurface Σ. If S is locally outermost, then there exists a sufficiently small two-sided neighbourhood D of S such that any surface S ₁ fully contained in the exterior part D ⁺ and homologous to S must have positive null expansion somewhere with respect to the outer direction ${\mathcal{l}}^{+}$

Proposition 1.

Let Σ be an embedded hypersurface in $(M,{g}^{(n)})$ and S a MOTS lying on Σ with a selected null normal ${\mathcal{l}}^{+}$ for which ${\theta }_{+} = 0$ . Let v be the unique normal to S which is tangent to Σ and satisfies $< v,{\mathcal{l}}^{+} >= 1$.

• (a) If S is strictly stable along v, then S is locally outermost in Σ.

• (b) If S is locally outermost in Σ, then S is stable along v.

For locally outermost MOTS lying on a spacelike hypersurface, the topological result [27] (Theorem 1 above) can be strengthened [26].

Theorem 3 (Galloway [26]).

Let $(M,{g}^{(n)})$ be a spacetime satisfying the DEC and Σ a space like embedded hypersurface. If S is a locally outermost MOTS in Σ then S is of positive Yamabe type.

From a space–time perspective, it is natural to ask whether this theorem extends to the case of hypersurfaces which are either space like or null at every point. As far as I know, neither a proof nor a counterexample to such a statement is known. It would be of interest to settle this point.

A most natural question regarding barrier properties of MOTS is whether there exists a globally outermost MOTS in a given hypersurface. A fundamental theorem along these lines has been proved by Andersson and Metzger [5] in space–time dimension four and extended to dimension up to and including eight by Eichmair using different methods [23]. We need some notation first.

Consider a compact space like embedded hypersurface Σ with smooth boundary $\partial \Sigma$. Assume that this boundary can be split in two non-empty disjoint component $\partial \Sigma = {\partial }^{-}\Sigma \cup {\partial }^{+}\Sigma$. A (not necessarily connected) surface S embedded in $\Sigma \setminus {\partial }^{+}\Sigma$ is called bounding if $S \cup {\partial }^{+}\Sigma$ is the boundary of a domain ${\Omega }^{+}(S)$ in Σ. This domain is called “exterior” of S in $\Sigma$. For bounding surfaces (in particular for ${\partial }^{-}\Sigma$), we always denote by θ₊ the null expansion with respect to the (unique) outer null normal ${\mathcal{l}}^{+}$ satisfying that its tangential projection on Σ has unit norm and points towards the exterior of S in Σ. For ${\partial }^{+}\Sigma$, the null normal is chosen so that its tangential projection is unit and points outside Σ. Combining the results of Andersson and Metzger [5] and Eichmair [23], the next existence and uniqueness result of an outermost MOTS in Σ follows (Theorem 3.3 in [2]).

Theorem 4 (Andersson et al. [2]).

Let $(M,{g}^{(n)})$ be a spacetime of dimension $4 \leq n \leq 8$ . Let Σ be a compact, space like embedded hypersurface with smooth boundary $\partial \Sigma = {\partial }^{+}\Sigma \cup {\partial }^{-}\Sigma$ , as before. Assume that ${\theta }_{+}[{\partial }^{-}\Sigma ] \leq 0$ and ${\theta }_{+}[{\partial }^{+}\Sigma ] > 0$ . Then there exists a unique (not necessarily connected) bounding MOTS S in Σ satisfying the property that no bounding surface in Σ with ${\theta }_{+} \leq 0$ intersects the exterior ${\Omega }^{+}(S)$ .

Being globally outermost, S is also locally outermost and hence stable and of positive Yamabe type.

4.1 MOTS and Symmetries

Spacetimes with symmetries play an important role in gravitational theories. For instance, the gravitational collapse that necessarily occurs when an initial data set contains a trapped surface is believed to settle down to a stationary black hole once all relevant dynamical processes (like, e.g. accretion of matter into the black hole or emission of gravitational waves) have already taken place. It is clear that a proper analysis of MOTS in stationary spacetimes is important in order to understand whether this type of surfaces are useful as quasi-local replacements for black holes. A first natural step is to study the restrictions on MOTS arising from the presence of space–time symmetries. Since symmetries of various sorts are typically defined by imposing restrictions on its vector field generators, it is convenient to study MOTS, and in particular their stability properties, in spacetimes containing special types of vector fields. Let us start with the following simple observation [10]:

Assume that a spacetime admits a Killing vector ξ and let S be a MOTS. It is clear that the motion along the local one-parameter group of transformations ${\varphi }_{\tau }$ generated by ξ changes no geometric properties of S. Hence, the surface ${S}_{\tau } = {\varphi }_{\tau }(S)$ is also a MOTS, which implies that the first variation of ${\theta }_{+}$ along ξ vanishes. Assume that ξ is nowhere tangent to S and linearly independent to ${\mathcal{l}}^{+}$ on S. Then, there exists a unique vector v orthogonal to S and satisfying $< v,{\mathcal{l}}^{+} >= 1$ such that $\xi = Fv + {\xi }^{\parallel }$, where ${\xi }^{\parallel }$ is tangent to S. It follows

$$\begin{array}{rcl} 0 = {\delta }_{\xi \,}{\theta }_{+} = {\delta }_{Fv+{\xi }^{\parallel }\,}{\theta }_{+} = {\delta }_{Fv}{\theta }_{+} = {L}_{v}\left (F\right ),& & \\ \end{array}$$

where the third equality follows because tangential variations of a vanishing quantity are obviously zero. Thus, by this symmetry argument, it follows that the stability operator L _v admits 0 as an eigenvalue with eigenfunction $F =< \xi,{\mathcal{l}}^{+} >$. However, the stability operator (6) is written in terms of the geometry of S, and it is far from obvious by looking at that expression that ${L}_{v}\left (F\right )$ should vanish. The lesson is that the form (6) of the stability operator may not be the most convenient one for studying the interplay of MOTS and symmetries. One needs an alternative expression of L _v adapted to space–time information. Since generators of symmetries are typically defined in terms of conditions on the Lie derivative of the metric along the generator (as, for instance, for Killing vector, homotheties, conformal Killing vectors, Kerr–Schild vectors [17], etc.), the following definition turns out to be useful.

Definition 6.

Let ξ be a vector field in a spacetime $(M,{g}^{(n)})$. The metric deformation tensor ${a}^{\xi }$ is the symmetric, two-covariant tensor defined as

$$\begin{array}{rcl}{ a}^{\,\xi \,}{ \mathbf{def} \atop =} {\mathcal{L}}_{\xi }\,{g}^{(n)}.& & \\ \end{array}$$

The following lemma [10] gives an explicit form for the variation of ${\theta }_{+}$ on a MOTS along an arbitrary vector ξ in terms of its deformation tensor. A more general version valid for any normal expansion (not necessarily along ${\mathcal{l}}^{\pm }$) and for arbitrary surfaces (not necessarily MOTS) can be found in [10].

Lemma 5.

Let ξ be a vector field with deformation tensor ${a}^{\,\xi \,}$ in a spacetime $(M,{g}^{(n)})$ . Let S be a MOTS with embedding Φ _S , then

$$\begin{array}{rcl}{ \delta }_{\xi \,}\,{\theta }_{+} ={ \left.-\frac{1} {4}{\theta }_{-}{a}^{\,\xi \,}({\mathcal{l}}^{+},{\mathcal{l}}^{+}) -{\mbox{ tr}}_{ h}\left ({a}^{\,\xi,S} \cdot {\chi }_{ +}\right ) + {h}^{\alpha \beta }{\mathcal{l}}^{+\,\gamma }\left [\frac{1} {2}{\nabla }_{\gamma }{a}_{\alpha \beta }^{\,\xi \,} -{\nabla }_{ \alpha }{a}_{\gamma \beta }^{\,\xi \,}\,\right ]\right \vert }_{ S}.& & \\ \end{array}$$

where ${a}^{\,\xi,\,S}{ \mathbf{def} \atop =} {\Phi }_{S}^{\star }({a}^{\,\xi \,})$, ${\mbox{ tr}}_{h}({a}^{\,\xi,S} \cdot {\chi }_{+})$ is the double trace (with the metric h) of ${a}^{\,\xi,S} \otimes {\chi }_{+}$ in the first-third indices and in the second-fourth indices, and ${h}^{\alpha \beta }$ is the projector tangent to S.

When the vector field ξ is Killing, then its deformation tensor vanishes identically and the expression above gives ${\delta }_{\xi \,}{\theta }_{+} = 0$. We already knew this, but the difference is that the conclusion now follows from an explicit calculation rather than from a symmetry argument. For vector fields generating symmetries other than isometries, the expression above is necessary because no direct symmetry invariance argument is available.

Several results can be obtained by studying the interplay between stable MOTS and special types of vector fields by means of Lemma 5. Here only two examples of the type of results that can be derived are included. I refer to [10] for details and further results (see also [6, 35] for previous works on the interplay between different types of trapped surfaces and symmetries).

Theorem 5.

Let S be a stable MOTS with respect to a direction v. Suppose that $(M,{g}^{(n)})$ admits a conformal Killing vector ξ, i.e. ${\mathcal{L}}_{\xi \,\,}{g}^{(n)} = 2\phi {g}^{(n)}$ (including homotheties ϕ = C and isometries ϕ = 0):

• (a) If $0\not\equiv 2{\mathcal{l}}^{+}(\phi )- < \xi,{v}^{\star } >W{\vert }_{S} \leq 0$ , then $< \xi,{\mathcal{l}}^{+} >{\vert }_{S} < 0$ .

• (b) If S is strictly stable and $2{\mathcal{l}}^{+}(\phi )- < \xi,{v}^{\star } >W{\vert }_{S} \leq 0$ , then $< \xi,{\mathcal{l}}^{+} >{\vert }_{S} \leq 0$ and vanishes at one point only if it vanishes everywhere.

This result is true also if all inequalities are reversed (this follows immediately by applying the theorem to − ξ). This result can be particularized for Killing vector fields or homotheties in spacetimes satisfying the NEC. Then ${\mathcal{l}}^{+}(\phi ) = 0$ and $W \geq 0$, so the theorem gives restrictions directly on the scalar product $< \xi,{v}^{\star } >$, i.e. on the relative position of ξ with respect to the normal stability direction v. Figure 7 describes the restrictions in this case.

Fig. 7

The planes ${T}_{p}\Sigma$ and $P \equiv {T}_{p}S \oplus \mbox{ span}\{{\mathcal{l}}^{+}\,{\vert }_{p}\}$ divide the tangent space T _p M in four regions. Theorem 5 implies that if S is strictly stable and ξ is a Killing vector or a homothety in a spacetime satisfying the NEC which points above Σ everywhere, then ξ cannot enter into the forbidden region at any point (and, similarly, if ξ points below Σ everywhere). The allowed region includes the plane P. However, if there is a point with W≠0 where ξ is not tangent to Σ, then the result is also valid for stable MOTS with P belonging to the forbidden region

If the Killing vector is future or past, the result can be strengthened [10].

Theorem 6.

Let S be a MOTS stable with respect to $-{\mathcal{l}}^{+}/2$ . Assume that $(M,{g}^{(n)})$ satisfies the NEC and admits a causal Killing vector or homothety ξ which is future directed everywhere on S:

• (a) Then ${\chi }_{+} = 0$ and $\mbox{ Ein}({\mathcal{l}}^{+},{\mathcal{l}}^{+}) = 0$ at every point p where $\xi (p)\neq 0$ .

• (b) If S is strictly stable, then $\xi \propto {\mathcal{l}}^{+}$ everywhere.

5 MOTS and Killing Horizons

Stationary black holes have the property that the stationary Killing vector is tangent to the event horizon. If the Killing vector is hypersurface orthogonal, then the event horizon is in fact a Killing horizon, i.e. a null hypersurface where the Killing vector is tangent, null and nonzero. More generally, event horizons are also Killing horizons in stationary and axially symmetric four-dimensional black holes. As already mentioned several times, in the context of cosmic censorship, one expects collapsing, asymptotically flat spacetimes to settle down to a stationary black hole. One also expects that tubes of MOTS eventually approach the event horizon (see however [44]), which by the uniqueness theorems of stationary black holes should in turn be an approximate Killing horizon (at least in four space–time dimensions, and possibly also in higher dimensions).

A first step towards this aim would be understanding the interplay between MOTS and Killing horizons. This is the aim of a recent investigation [36]. Here I only summarize some of the results. The reader is referred to [36] for the proofs and for further details.

5.1 Killing Horizons

Let us assume that the spacetime $(M,{g}^{(n)})$ admits a Killing vector ξ which is nonzero and null along a smooth null hypersurface ${\mathcal{H}}_{\xi }$, a so-called Killing horizon. To be more precise, we adopt the following definition of Killing horizon, which includes a topological restriction (c.f. Condition 2.1 in [39]).

Definition 7 (Killing horizon).

A Killing horizon ${\mathcal{H}}_{\xi }$ of a Killing vector ξ is a smooth hypersurface embedded in (M, g ⁽ⁿ⁾) with embedding ${\Phi }_{\xi } : {\mathcal{H}}_{\xi } \rightarrow M$, satisfying the following properties:

• (a) ${\mathcal{H}}_{\xi }$ is diffeomorphic to $S \times \mathbb{R}$ where S is a closed (n − 2)-manifold.

• (b) The first fundamental form ${g}_{{\mathcal{H}}_{\xi }}{ \mathbf{def} \atop =} {\Phi }_{\xi }^{\star }({g}^{(n)})$ is degenerate along the $\mathbb{R}$ factor at every point $p \in {\mathcal{H}}_{\xi }$.

• (c) For each $p \in {\mathcal{H}}_{\xi }$, the Killing vector $\xi {\vert }_{{\Phi }_{\xi }(p)}$ is non-zero, null, future directed and tangent to ${\Phi }_{\xi }({\mathcal{H}}_{\xi })$.

Being null and tangent to ${\mathcal{H}}_{\xi }$ it follows that ξ points along the $\mathbb{R}$ factor at every point $p \in {\mathcal{H}}_{\xi }$. The condition of ξ being future directed is adopted here only for notational simplicity later (in particular when we choose ${\mathcal{l}}^{+} = \xi$ on any section of a Killing horizon). Obviously, if ${\mathcal{H}}_{\xi }$ satisfies all properties above except for the condition of ξ being future directed, then ${\mathcal{H}}_{\xi }$ is a Killing horizon with respect to − ξ.

The degeneracy of the first fundamental form of ${\mathcal{H}}_{\xi }$ implies that ξ is a nowhere zero normal vector to ${\mathcal{H}}_{\xi }$. The square norm of ξ vanishes on ${\mathcal{H}}_{\xi }$, which implies that its gradient is normal to ${\mathcal{H}}_{\xi }$. The proportionality factor between this gradient and ${\xi }$ defines the surface gravity. More precisely (see e.g. [42]).

Definition 8.

The surface gravity ${\kappa }_{\xi }$ of a Killing horizon ${\mathcal{H}}_{\xi }$ is a function ${\mathcal{H}}_{\xi } \rightarrow \mathbb{R}$ defined by

$$\begin{array}{rcl} \nabla \lambda {\vert }_{p} = 2{\kappa }_{\xi }\xi \,{\vert }_{p},\quad \forall p \in {\mathcal{H}}_{\xi },\quad \quad \mbox{ where}\quad \lambda { \mathbf{def} \atop =} - < \xi,\xi >.& & \\ \end{array}$$

The surface gravity can be equivalently defined by

$$\begin{array}{rcl}{ \nabla }_{\xi }\xi { \mbox{ ${\mathcal{H}}_{\xi }$} \atop =} {\kappa }_{\xi }\xi,& &\end{array}$$

(9)

i.e. ${\kappa }_{\xi }$ measures the departure of the Killing parametrization of the orbits of ξ on ${\mathcal{H}}_{\xi }$ (which, from general properties of null hypersurfaces, are necessarily null geodesics) from being an affine parametrization. The following definition is standard.

Definition 9.

A Killing horizon ${\mathcal{H}}_{\xi }$ is degenerate if ${\kappa }_{\xi } \equiv 0$ and non-degenerate if ${\kappa }_{\xi }{\vert }_{p}\neq 0$ for some point $p \in {\mathcal{H}}_{\xi }$.

Killing horizons are well-studied objects. I summarize some well-known properties (see e.g. [31, 42] for details).

Since ${\mathcal{H}}_{\xi }$ is a (trivial) bundle over S, we can define $\pi : {\mathcal{H}}_{\xi } \simeq S \times \mathbb{R} \rightarrow S$ as the projection onto S. The fact that ξ is a Killing vector implies that there exists a Riemannian metric on S, denoted by h, such that ${g}_{{\mathcal{H}}_{\xi }} = {\pi }^{\star }(h)$. Moreover, for any section S ₁ of $({\mathcal{H}}_{\xi },S,\pi )$ (see Fig. 8) the space–time metric (or equivalently the first fundamental form ${g}_{{\mathcal{H}}_{\xi }}$) induces a Riemannian metric h ₁ on S ₁. The Riemannian spaces $({S}_{1},{h}_{1})$ and (S, h) are isometric with isometry $\pi {\vert }_{{S}_{1}}$. As a simple consequence of this fact (see e.g. [25]), the second fundamental form vector $\chi ({S}_{1})$ of any section S ₁ (as a space–time submanifold) satisfies ${\chi }_{\xi }({S}_{1}){ \mathbf{def} \atop =} < \chi ({S}_{1}),\xi >= 0$. In particular, the null expansion along ξ vanishes:

$$\begin{array}{rcl}{ \theta }_{\xi }({S}_{1}){ \mathbf{def} \atop =} { \mbox{ tr}}_{{S}_{1}}{\chi }_{\xi }({S}_{1}) = 0.& & \\ \end{array}$$

The Raychaudhuri equation for the null expansion ${\theta }_{\xi }({S}_{1})$ combined with ${\chi }_{\xi }({S}_{1}) = 0$ immediately implies $\mbox{ Ein}(\xi,\xi ) = 0$ everywhere on a Killing horizon ${\mathcal{H}}_{\xi }$.

Fig. 8

Schematic figure for a Killing horizon. The vector field ξ is null, tangent to ${\mathcal{H}}_{\xi }$ and nowhere zero. Furthermore, it is the restriction on ${\mathcal{H}}_{\xi }$ of a Killing vector of the spacetime. A section of the Killing horizon is a smooth spacelike surface embedded in ${\mathcal{H}}_{\xi }$

All sections of a Killing horizon are therefore MOTS with respect to the null normal ξ. On a given section S ₀, let us define k as the unique future directed null normal satisfying $< k,\xi >= -2$.

Regarding the surface gravity ${\kappa }_{\xi }$, it is well-known (see, e.g. [42]) that ${\kappa }_{\xi }$ is constant on any Killing horizon in a spacetime satisfying the DEC. The surface gravity is also constant on any Killing horizon of an integrable Killing vector (i.e. a Killing vector satisfying ${\xi } \wedge d{\xi } = 0$), irrespectively of any energy condition. In fact, both statements are a simple consequence of the identity (see [42] p. 334 for a derivation in four dimensions which holds true in any dimension):

$$\begin{array}{rcl} {\xi } \wedge d{\kappa }_{\xi }{ \mbox{ ${\mathcal{H}}_{\xi }$} \atop =} -{ \xi } \wedge {{\mbox{ Ric}}_{\xi }},& & \\ \end{array}$$

where ${{\mbox{ Ric}}_{\xi }}{ \mathbf{def} \atop =} \mbox{ Ric}(\xi,\cdot )$ and ${\kappa }_{\xi }$ stands for any smooth extension of the surface gravity to a neighbourhood of ${\mathcal{H}}_{\xi }$.

5.2 Stability Operator of MOTS in Killing Horizons

The aim of this subsection is to study the stability properties of MOTS embedded in Killing horizons. The first immediate observation is that the stability operator L _v is independent of the direction v. This follows from (8) and the fact that $W ={ \mbox{ tr}}_{h}({\chi }_{+}^{2}) + \mbox{ Ein}(\xi,\xi )$ vanishes identically on a Killing horizon. So, the stability operator is a property of the section itself, not of the normal direction along which the variations are performed. Let us write ${L}_{{S}_{1}}$ for this stability operator. The following lemma follows from combining properties of Killing horizons with the general expression for the stability operator in terms of deformation tensors (see [36] for details).

Proposition 2 (Stability operator of a section of a Killing horizon).

Let ${\mathcal{H}}_{\xi }$ a Killing horizon and S ₀ a section of ${\mathcal{H}}_{\xi }$ . Let $\mbox{ $s$}$ be the connection one-form of the normal bundle of S ₀ in the basis $\{\xi (= {\mathcal{l}}^{+}),k = ({\mathcal{l}}^{-})\}$ , namely $\mbox{ $s$}(X) \equiv -\frac{1} {2} < k,{\nabla }_{X}\xi >$ . Let $\mbox{ $s$} = dF + z$ be the Hodge decomposition of $\mbox{ $s$}$ and define $u{ \mathbf{def} \atop =} {e}^{2F}$ . Then, the stability operator of S ₀ is

$$\begin{array}{rcl}{ L}_{{S}_{0}}(\psi ) = -{\mbox{ div}}_{h}\left (u{\nabla }_{h}\left (\frac{\psi } {u}\right )\right ) + 2{z}({\nabla }_{h}\psi ) -\frac{1} {2}{\kappa }_{\xi }{\theta }_{k}\psi.& &\end{array}$$

(10)

A natural question is to ask how does the stability operator (or, more generally, the stability properties) depend on the section S ₀. The case of degenerate horizons is an easy consequence of Proposition 2.

Lemma 6.

Let S ₀ be a section of a degenerate horizon ${\mathcal{H}}_{\xi }$ . Then ${S}_{0}$ is marginally stable.

In order to determine the dependence of the stability on the section for non-degenerate horizons, we need to compare two arbitrary sections of ${\mathcal{H}}_{\xi }$. Let us therefore fix a section S ₀ of ${\mathcal{H}}_{\xi }$. Any other section S[f] is defined by a graph over S ₀, $f : {S}_{0} \rightarrow \mathbb{R}$, see Fig. 9. Let ${\pi }_{f} : S[f] \rightarrow {S}_{0}$ be the natural projection along orbits of the Killing vector. π _f is a diffeomorphism between these two spaces (in fact an isometry with their respective induced metrics).

Fig. 9

An arbitrary section S[f] of a Killing horizon is defined uniquely by a graph function $f : {S}_{0} \rightarrow \mathbb{R}$ on a fixed section S ₀. Lemma 7 establishes how the geometric properties of S[f] relate to the geometric properties of S ₀

In order to determine the behaviour of the stability operator, we need to relate the one-forms ${s}$ of S ₀ and ${s[f]}$ of S[f] and the null expansions θ _k of S ₀ and ${\theta }_{k}[f]$ of S[f]. The following lemma [36] establishes these relationships.

Lemma 7.

Let S ₀ , S[f] and ${\pi }_{f}$ as before. Let k _f be the null normal to S[f] satisfying $< \xi,{k}_{f} >{ \mbox{ $S$}[f] \atop =} - 2$ . Denote by ${s[f]}$ the connection of S[f] with respect to k _f , by ${\chi }_{f}^{{k}_{f}}$ the second fundamental form of S[f] along k _f and by ${\theta }_{k}[f]$ its trace. Then

$$\begin{array}{rcl} {s[f]}& =& {\pi }_{f}^{\star }\left ({s} + {\kappa }_{ \xi }df\right ),\end{array}$$

(11)

$$\begin{array}{rcl}{ \chi }_{f}^{{k}_{f} }& =& {\pi }_{f}^{\star }\left ({\chi }^{k} + 2{\mbox{ Hess}}_{ h}f + 2{\kappa }_{\xi }df \otimes df + 2df \otimes {s} + 2{s} \otimes df\right ),\end{array}$$

(12)

$$\begin{array}{rcl}{ \theta }_{k}[f]& =& \left ({\theta }_{k} + 2{\Delta }_{h}f + 2{\kappa }_{\xi }\vert \vert {\nabla }_{h}f\vert {\vert }_{h}^{2} + +4{s}\left ({\nabla }_{ h}f\right )\right ) \circ {\pi }_{f},\end{array}$$

(13)

where ${\mbox{ Hess}}_{h}$ denotes the Hessian with the h-metric connection and ${s}$, ${\chi }^{k}$ and ${\theta }_{k}$ are, respectively, the connection one-form, the second fundamental form and the null expansion of S ₀ along the null normal k satisfying $< \xi,k >{ { \mbox{ $S$}}_{0} \atop =} - 2$ .

This transformation lemma allows us to obtain the relationship between the stability operator of S ₀ and S[f] in the case of constant surface gravity.

Proposition 3 (Dependence of stability operator on the section).

Assume that ${\kappa }_{\xi }$ is constant. The stability operator of S[f] is related to the stability operator of S ₀ by

$$\begin{array}{rcl}{ L}_{S[f]}\left (\psi \circ {\pi }_{f}\right ) = {e}^{-{\kappa }_{\xi }f}{L}_{{ S}_{0}}\left ({e}^{{\kappa }_{\xi }f}\psi \right ) \circ {\pi }_{ f},\quad \quad \forall \psi \in {C}^{2}({S}_{ 0}, \mathbb{R}).& & \\ \end{array}$$

The following is an immediate consequence.

Corollary 2.

Let ${\mathcal{H}}_{\xi }$ be a Killing horizon with constant surface gravity. Then the principal eigenvalue is independent of the section.

Although the case of constant surface gravity is the most interesting one (because ${\kappa }_{\xi }$ is constant if the DEC is satisfied), it is natural to ask whether the result above extends to the case of general ${\kappa }_{\xi }$. It turns out that the constancy of the surface gravity is a necessary condition for the validity of the conclusion of Corollary 2 [36].

The analysis of stability of MOTS lying on Killing horizons can be used to clarify the relationship between area–angular momentum inequalities obtained in different contexts. The first one was obtained by Hennig, Ansorg and Cederbaum [30] in the context of stationary and axially symmetric black holes. The second was obtained by Jaramillo, Reiris and Dain [33] for stable MOTS along the null direction $-{\mathcal{l}}^{-}/2$. A similar inequality for minimal surfaces lying on maximal spacelike hypersurfaces was also obtained by Dain and Reiris [19]. The relationship between the result for black holes and the result for minimal surfaces has been clarified recently by Chruściel, Eckstein, Nguyen and Szybka [14]. I refer to [36] for a discussion on how the analysis of the stability properties of Killing horizons (in four dimensions) allows for a clarification of the relationship between the results in [30] and [33]. Here I only summarize the statement of the inequality as given by Jaramillo, Reiris and Dain. For more details on this beautiful inequality, see [32] and the recent review article [20].

6 Axially Symmetric MOTS and Angular Momentum

A remarkable consequence of stability of MOTS is that, in the axially symmetric case and in spacetimes satisfying the DEC, the area of the MOTS is always bounded below by a universal expression involving the angular momentum of the surface. We start with the definition of “axial symmetry” in this context. This definition captures the minimal ingredients needed for the proof of the inequality as given in [33].

Definition 10.

A MOTS S is axially symmetric if there exists a vector field $\eta \in \mathfrak{X}(S)$ with closed orbits satisfying

• (a) ${\mathcal{L}}_{\eta \,}h = 0$.

• (b) ${\mathcal{L}}_{\eta \,}{s} = 0$, for some choice of basis $\{{\mathcal{l}}^{+},{\mathcal{l}}^{-}\}$.

• (c) η commutes with the stability operator L _v for some choice of normal vector v.

The following standard definition of “angular momentum” is motivated by the Komar expression of conserved quantities associated to Killing vectors.

Definition 11.

The angular momentum of an axially symmetric, two-dimensional MOTS is the integral

$$\begin{array}{rcl} J = \frac{1} {8\pi }{\int \limits }_{S}{s}(\eta ){{\eta }}_{S}.& & \\ \end{array}$$

The following theorem establishes a remarkable inequality between area and angular momentum for stable, axially symmetric MOTS in four-dimensional spacetimes.

Theorem 7 (Jaramillo et al. [33]).

Let $(M,{g}^{(4)})$ be a spacetime satisfying the DEC. Let S be a MOTS in $(M,{g}^{(4)})$ and assume S to be axially symmetric and stable with respect to the null direction $-{\mathcal{l}}^{-}/2$ . Then

$$\begin{array}{rcl} \vert S\vert \geq 8\pi \vert J\vert.& & \\ \end{array}$$