Abstract
Availability is a very important measure of system performance. A great deal of research works on it have been done. This article reviews the recent major results in this field. Systems whose failures are either self-announcing or not self-announcing are considered in these works, various repair methods and different inspection policies are explored as well. Some of these studies derive the expressions of the steady-state availability, limiting average availability, and others give the expressions of the instantaneous availability explicitly or recursively.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Let \(S\) be a system that is designed for implementing certain function and is put into field operation at time \(t = 0\). It is desired that the system performs excellently in field use. To measure its performance naturally, we can use its reliability characteristics such as survival probability, mean lifetime, mean residual life, or hazard rate etc., as criteria. If, however, we look at this process dynamically, then we will have to consider whether the system will be still functioning at any given time \(t > 0\).
No matter how reliable the system is, it will fail sooner or later. So a problem is how to deal with failed system. Commonly, there are two ways to restore the failed system to operation. One is to repair the failed system if the system is repairable. Two types of repair methods are commonly studied in reliability literature. One method is called perfect or complete repair which repairs the failed system as good as new, i.e., the lifetime of the repaired system has the same distribution function as the original system \(S\). Of course, it is implicitly assumed that the lifetime of the repaired system is independent of that of the original system \(S\). The other type of repair method is named imperfect or incomplete repair with which the distribution function of the repaired system is not exactly the same as that of the original system. There is a special imperfect repair-minimal repair that repairs the failed system as good as it was prior to the failure of the original system. The other way to restore the failed system to operation is to replace it by a system that is iid as the original \(S\). Both perfect repair and replacement change the failed system to be as good as new, they are equivalent in this regard and so we will use them alternatively later.
In addition to different types of repair methods, another related problem is how we can know whether a system is failed or unfailed. With respect to this, systems can be classified into two categories. Systems in one category can be under continuously monitoring, and consequently their failures are self-announcing, whereas systems in the other category cannot be continuously monitored due to either technical difficulties or expensive costs and therefore their failures are not self-announcing. In this case, system failure can only be detected by applying inspections. Two inspection policies, calendar-based and age-based policy will be described in Sect. 3.
Maintenance policies of both repair/replacement and inspection will be considered. With the help of these maintenance policies, it becomes more meaningful to measure the likelihood for a system to be functioning at any given time \(t > 0\). To this purpose, we consider a system which can be in one of two states, namely ‘unfailed’ (or ‘up’) and ‘failed’ (or ‘down’). By ‘up,’ we mean the system is still functioning and by ‘down,’ we mean the system is not working. Suppose that the status of system in field use can be revealed through certain way. Depending on the status of the system, the unfailed system may be upgraded or modified, and the failed system will be repaired or replaced. Let a system (the original system) starts operation at time \(t = 0\) and works until certain maintenance measures, which includes but not limited to minimal repair, perfect repair, replacement, and many others, are going to take place. At this time, the first up period is over and the first down period begins. The first up and down periods constitute the first cycle of the system. At the end of each subsequent down period, a new cycle of the system will be completed and the system will resume operating, and so on and so forth. Let \(U_{j}\) and \(D_{j}\) denote the duration of the \(j\)th up and down periods, respectively. Basically \(U_{j}\) is the lifetime of the system after the \((j - 1)\)th down period, while \(D_{j}\) is the length of time required to finish the planned maintenances like repairing or replacement. For any time \(t \ge 0\), we can use binary random variable \(\xi (t)\) to indicate the status of the system, namely \(\xi (t) = 1\) meaning the system is unfailed or still working, and \(\xi (t) = 0\) meaning the system failed or is not working. The probability that the system is still working at time \(t\) called instantaneous availability is denoted as \(A(t) = P(\xi (t) = 1)\). This review will focus on the recent research works on \(A(t)\) and some other related quantities such as the steady-state availability \(A(\infty )\), the limiting average availability \(A_{av} (\infty )\) defined later. The focus of Sect. 2 is the availability of systems whose failures are self-announcing, and so there is no need of applying inspections. Section 3 reviews major works on availability of systems whose failure are not self-announcing and hence inspections are necessary. The last section will mention some other works on system availability. There is a great vast of papers contributed to the topic of system availability, so it is inevitable that our review may miss some meaningful works or even very significant ones. But the authors hope this chapter can provide readers an overview about the progresses made in recent years toward the very important topic of system availability.
2 Availability of System Under Continuously Monitoring
It is assumed in this section that the failure of the system is self-announcing and thus inspection policy will not be involved.
Usually it is a formidable work to give explicit formula of \(A(t)\) except for a few simple cases, so other measures have been proposed, and more attention is being paid to the limiting behavior of these quantities, i.e., engineers are more interested in the extent to which the system will be available after it has been run for a long time.
In the case, when \(\{ (U_{j} ,D_{j} ),j \ge 1\}\) consists of a sequence of iid random variables and \(U_{j}\) is independent of \(D_{j}\) for each \(j \ge 1\) (for convenience we will call this as the IID Model in the following), some desirable properties have been obtained using results from alternative renewal processes. For instance, it has been proved that \(A(t)\) is the unique solution of the renewal equation
where \(H(t)\) is the convolution of \(F(t)\) and \(G(t)\) due to the assumed independence of \(U_{i}\) and \(D_{i}\), i.e., \(H(t) = \int_{0}^{t} F(t - x){\text{d}}G(x)\) for any \(t \ge 0\). The solution can actually be expressed explicitly as
where \(H^{(n)}\) is the n fold convolution of \(H\). However, in the most cases this equation does not help much. In the case, when both \(F\) and \(G\) have density functions \(f\) and \(g\) the function \(H\) also has density given be \(h(t) = H^{\prime}(t) = \int_{0}^{t} g(t - x)f(x){\text{d}}x\) and consequently \(A(t)\) is the unique solution of the renewal equation
Moreover, as \(t \to \infty\) both the instantaneous and the average availability
converge to a common limit \({\mathbb{E}}(U)/[{\mathbb{E}}(U) + {\mathbb{E}}(D)]\) where \((U,D)\) is iid as \((U_{1} ,D_{1} )\). More details can be found in Barlow and Proschan (1975).
In addition, Takács (1957), Rényi (1957), Rise (1979), and Gut and Janson (1983) discussed the asymptotic normality property of \(A(t)\) for the IID Model.
Mi (1995) studies the case when \(\{ (U_{j} ,D_{j} ),j \ge 1\}\) are independent but not necessarily identically distributed. The concepts that a sequence of random variables or their CDFs are dominated by a function and the average availability in the first \(n\) cycles defined by the ratio of accumulated up time in the first \(n\) cycles to the total length of time in the \(n\) cycles
were introduced there. Assuming that \(\{ (U_{j} ,D_{j} ),j \ge 1\}\) are dominated by a function and that
it was shown that
and
where \(A_{av} (\infty )\) is called the limiting average availability.
Furthermore, under some additional mild conditions both \(\bar{A}_{n}\) and \(\bar{A}(t)\) are asymptotically normal as \(n \to \infty\) or \(t \to \infty\).
Assuming the IID Model, Sarkar and Chaudhuri (1999) found the Fourier transform \(\tilde{b}(z)\) of the derivative \(b(t)\) of unavailability \(B(t) = 1 - A(t)\) defined by
where \(i = \sqrt{ - 1}\) is the imaginary unit. Then they defined function \(c_{u} (z) = {\text{e}}^{ - iuz} \tilde{b}(z)\) for any \(u > 0\). The function \(c_{u} (z)\) is analytic except at finite number of isolated singularities, say \(z_{j} ,1 \le j \le k\), and the authors further expressed \(b(u)\) as a sum of residues
where \(Im(z_{j} )\) is the imaginary part of the complex number \(z_{j}\), and \(Im(z_{j} ) < 0\) means \(z_{j}\) locates in lower half of the complex plane. Finally the instantaneous availability \(A(t)\) was expressed in terms of the integral of \(b(u)\)
In that paper, Fourier transformation is applied instead of Laplace transformation in order to avoid problem with inverting the Laplace transform of \(A(t)\). As an example, let the lifetime of the system have gamma distribution with density
where \(\alpha\) is a positive integer, and let the repair time have exponential distribution with density
Then \(A(t)\) is obtained as
where \(\theta_{0} = 1,\theta_{1} , \ldots ,\theta_{\alpha }\) are the \((\alpha + 1)\)-th roots of 1. That is, \(\theta_{j} = [\exp \{ i2\pi /(\alpha + 1)\} ]^{j}\).
Example 2.1
Suppose that \(T{ \sim }Gamma(4,\alpha )\) and \(D{ \sim }Gamma(2,\alpha )\).
In this case, we have
There are 4 singularities of \(c_{u} (z)\):
We can calculate the residue at \(z = z_{1}\):
The residues at \(z = z_{2} ,z_{3}\) and \(z_{4}\) can be calculated similarly. Thus, we have
and
Without using Fourier or Laplace transformation, it seems not likely to obtain this expression through directly solving the renewal equation mentioned above.
Keeping the assumption of independence of all \(U_{j}\) and \(D_{j},\, j \ge 1\), Biswas and Sarkar (2000) modified the IID model as follows. A positive integer \(k\) is fixed in advance. At the \((k + 1)\) th failure of the system, either it is replaced by a new system that is iid to the original one and the replacement is finished instantly without taking any time (Model A), or it is perfectly repaired that takes time \(D_{k + 1}\) (Model B). Obviously, in either case, the system is brought back to a condition as good as new and so the time when \(D_{k + 1}\) ends is the renewal point. Afterward, the process will evolve in the same pattern. In other words, the two models allow \(k\) imperfect repairs before a complete repair or replacement that will bring the process to a renewal point. It is natural to further assume that
and
This paper employed the same Fourier transformation approach in Sarkar and Chaudhuri (1999). Denote the instantaneous system availability as \(A_{j} (t)\) when at time \(t = 0\) the system with lifetime \(U_{j}\) and then again take the ending time of \(D_{k + 1}\) as the renewal point. The equations satisfied by the Fourier transforms of the derivatives \(b_{j} (t)\) of unavailability \(B_{j} (t) = 1 - A_{j} (t),1 \le j \le k + 1\) were derived for both Model A and Model B. Upon determination of \(\tilde{b}(u) \equiv \tilde{b}_{1} (u)\), the desired availability \(A(t) \equiv A_{1} (t)\) then can be obtained by (7). The explicit expression of \(A(t)\) were shown for the case of exponential lifetimes and repair times.
In the above studies at each system failure, it is deterministic that the failed system undergoes either perfect repair or imperfect repair. Brown and Proschan (1983) considered a model according to which a perfect repair is implemented with probability \(p\) and an imperfect repair, which is actually a minimal repair restoring the failed system to its condition just prior to failure, is performed with probability \(1 - p\) at each system failure. Their model has been generalized by Block et al. (1985) to the case in which the probability of perfect repair is state dependent. Lim et al. (1998) proposed the Bayesian imperfect repair model, according to which the probability of performing a perfect repair is a random variable \(P\) with distribution function \(\varPi (p)\) on \((0,1] ,\) and the probability of applying minimal repair is \(1 - P\) at each system failure. Cha and Kim (2001) examined the same model under the assumptions that the perfect repair times are iid, the minimal repair times are iid, and these times are independent of each other. Under these assumptions the steady-state system availability \(A(\infty )\) was derived as
where \(\Lambda (t) = \int_{0}^{t} \lambda (x){\text{d}}x\), \(\lambda (x)\) is the failure rate function of the system, \(\nu_{1}\) is the mean perfect repair time, and \(\nu_{2}\) is the mean minimal repair time.
In the special case of \(P = 1\) with probability one, that is, only perfect repair is performed at each system failure, this model is reduced to the IID one. Certainly in this case \(\nu_{2} = 0\) and so \(A(\infty )\) becomes
which is exactly the same as in the classic IID model since
In the previous works on availability, only one type failure was taken into consideration, Cha et al. (2004) generalizes the study of Mi (1994) and considered repairable system with two types of failures: one is Type I failure (minor failure) that occurs with probability \(1 - p(t)\), where \(t\) is the age of the system at failure, the other is Type II failure (catastrophic failure, i.e., the usual failure) that occurs with probability \(p(t)\). The failed system with Type I failure can be restored to operation by a minimal repair, whereas the failed system with Type II failure can be restored to operation only by a perfect repair (or a replacement). This model is called the general failure model. The study on availability in Cha et al. (2004) combined burn-in policy \(b\) and age replacement \(T\) together and obtained the expression of the steady-state availability \(A(\infty )\) as follows:
Suppose that a new system is burned-in for time \(b\), and it will be put in field operation if it survives the burn-in. In the field use, the system is replaced by another system, which has also survived the same burn-in time \(b\), either at the use ‘‘age’’ \(T\) or at the time of the first Type II failure, whichever occurs first. However, for each Type I failure occurring during field use, only minimal repair will be performed.
It is further assumed that the repair times are not negligible. Let \(\nu_{1}\), \(\nu_{2}\), and \(\nu_{3}\) be the means of a minimal repair time, time for an unplanned replacement caused by the Type II failure, and time for a replacement done at the system field use age T by planned preventive maintenance policy, respectively. For technique reason, it is required that \(\int_{0}^{\infty } p(t)r(t){\text{d}}t = \infty\) where \(r(t)\) is the hazard rate function of the lifetime of a new system. Under these assumptions, then by similar arguments described in Cha and Kim (2002), it can be shown that the steady-state availability of the system under the policy \((b,T)\) is given by
where
Letting \(b = 0\) and \(p(t) = 1,\forall t \ge 0\), we see that \(\bar{G}_{b} (t) = \bar{F}(t)\). It also implies that there is only perfect repair but no minimal repair and so \(\nu_{1} = 0\), and \(\nu_{2} = \nu_{3} \equiv \nu\). Thus \(A(\infty )\) is reduced to
If further let the age replacement policy \(T = \infty\), that is replacement can only take place at system failure, then finally \(A(\infty )\) is obtained as
which is exactly the result in the case of the IID Model.
Mi (2006a, b) reconsidered the system with nonidentical lifetime distributions and nonidentical repair time distributions studied in Mi (1995). Let \(U_{j}\) and \(D_{j}\) have distribution functions \(F_{j}\) and \(G_{j} ,\) respectively, for each \(j \ge 1\). Assuming that both sequences \(\{ U_{j} \} ,j \ge 1\) and \(\{ D_{j} ,j \ge 1\}\) are dominated, there exist two CDFs \(F\) and \(G\) such that \(F_{j} \to F\) and \(G_{j} \to G\) in distribution as \(j \to \infty\), and some other technical requirements, Mi (2006a, b) gave three sets of conditions under which the steady-state availability \(A(\infty )\) exists and is given by
where
Moreover, it was shown there that if there exists an integer \(k \ge 0\) such that \(F_{\text{nk} + j} (t) = F_{j} (t)\), \(G_{\text{nk} + j} (t) = G_{j} (t)\), for any \(1 \le j \le k\), \(t \ge 0\), then it holds that
where \(\mu_{j}\) and \(\nu_{j}\) are the means associated with \(F_{j}\) and \(G_{j} ,\quad 1 \le j \le k\). Clearly, the results of both Model A and Model B discussed in Biswas and Sarkar (2000) can be obtained as special cases of this result in Mi (2006a, b).
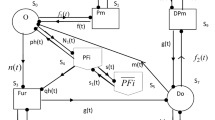
In the models reviewed above, there is no spare system on cold standby and there is only one repair facility so failed system can be placed for repairing without any waiting time. However, in the model considered in Sarkar and Li (2006) in addition to the original system, there are \(s \ge 1\) identical spares remain on cold standby, and there are \(r \ge 1\) repair facilities which serves the failed systems in the order in which they join the repair queue. The lifetimes of the original system and the \(s\) spares are iid; the repair times of the \(r\) repair facilities are also iid; further, these lifetimes and repair times are independent of each other.
At time \(t = 0 ,\) the original system is put on operation and at its failure one spare is placed on operation immediately without taking any time and the failed system is sent for repairing. In general, at the instant of failure of an operating system, the failed system always joins the repair queue and its repair starts as soon as one of the repair facilities is free, in the mean time one spare, if available, is placed to operation immediately without taking any time. If, however, at the failure of an operating system, there is no any spare available, that is all the \((s + 1)\) systems are either undergoing or awaiting repair, then the entire system enter the down state. It is obvious that \(r \le s + 1\) since otherwise at any time, there are always some repair facilities remain idle.
Let the original system be supported by \(r \ge 1\) repair facilities and \(s \ge r - 1\) spare systems. Assuming that the lifetime distribution is exponential with mean \(\alpha^{ - 1}\) and repair time distribution is exponential with mean \(\beta^{ - 1}\), the authors derived the limiting average availability as
where \(\rho = \beta /\alpha\) and
In a more general case, if again there are at least one repair facilities (\(r \ge 1\)), repair time has exponential distribution with mean \(\beta^{ - 1}\), but the number of spare systems satisfies \(s \ge \hbox{max} \{ 1,r - 1\}\), and the lifetime distribution of systems has density and is arbitrary other than this. Based on these assumptions, the limiting average availability was obtained as
where \(\mu\) denotes the mean system lifetime, \((1, \ldots ,1)^{\prime}\) is a \(s \times 1\) column vector with all components of 1, and the \(s \times s\) matrix \(Q\) can be determined by some equations given in Sarkar and Li (2006).
Sarkar and Biswas (2010) employed the same Fourier transformation approach proposed in Sarkar and Chaudhuri (1999) to the model studied in Sarkar and Li (2006). Keeping the same assumption of the exponential system lifetimes and repair times, the authors expressed the instantaneous availability \(A(t)\) as
for the case of \(s \ge 1\) and \(r = 1\) and \(r = 2\), where the function \(b_{0} (u)\) is the derivative of \(B_{0} (u)\), and \(B_{0} (u)\) denotes the unavailability of the system at time \(u > 0\) when there is no failure of spares. Actually, \(A(t) = 1 - B_{0} (t)\). It turns out that \(b_{0} (u)\) is the sum of residues of a complex-valued function that is analytic except finite number of isolated singularities. For details, the readers are referred to the Appendix of Sarkar and Biswas (2010).
At the end of this section recall that usually it is difficult to obtain a closed-form expression for \(A(t)\) as mentioned before. As a matter of fact, the behavior of \(A(t)\) can also be very complicate as shown in the following example.
Example 2.2
Consider a system that has \(U{ \sim }Gamma(p,\alpha )\) and \(D{ \sim }\ln {\mathcal{N}}(\mu ,\sigma )\) with density functions
In the following figure, the left panel shows the system availability functions \(A(t)\) corresponding to different parameters \(p = 2,4,8\) and \(p = 10\). The right panel shows the availability functions with different parameters \(\sigma = 0.25,0.50\) and \(\sigma = 0.75\). The function \(A(t)\) for all these cases does not have closed form and thus are obtained numerically.

3 Availability of System with Inspections
In this section, we will review research works on availability of systems that can be maintained through inspections. Inspection policy was proposed in Barlow and Proschan (1975) or even earlier. Inspections are important for systems whose failures are not self-announcing. This type of systems is common in industries. For instance, some industrial safety and protection system such as circuit breakers, fire detectors, gas detectors, pressure detectors, and safety valves are installed to prevent various specific risks. Depending on the status of the system being inspected the system will be repaired, replaced, upgraded, or modified. The system then will be restored to operation upon completion of these maintenances.
Two types of inspection policies are widely applied in practice. The first type called calendar-based inspection policy schedules inspections at fixed calendar intervals, say at times \(\tau ,2\tau , \ldots ,\) where \(\tau > 0\) is a predetermined constant. This policy is also named as periodic inspection policy. According to the calendar-based inspection policy, a system starting its operation at time \(t = 0\) is inspected at time \(t = \tau\), then at time \(t = 2\tau\) and so on.
The second type of inspection polity, the age-based inspection policy schedules inspections at fixed age intervals. Suppose that constant \(\tau > 0\) is determined in advance. Let the system be inspected at time \(t = \tau\) and resume operation at time \(\tau + m ,\) where \(m\) represents the required time to complete the above-mentioned maintenances. According to the age-based inspection policy, the system will be inspected at time \(t = \tau + m\) and this pattern will be continued in the same way.
Much has been done in studying availability of systems that are maintained through inspection. For example, Wortman et al. (1994), Wortman and Klutke (1994), Yeh (1995), Klutke et al. (1996), Dieulle (1999), Vaurio (1999), Ito and Nakagawa (2000), Chelbi and Ait-Kadi (2000), Yang and Klutke (2000, 2001) and Yadavalli et al. (2002), among others. But we will focus on the following papers.
Sarkar and Sarkar (2000) studied two models: Model A and Model B. In both models the periodic inspection policy is applied and a failed system is repaired as good as new (i.e., the repair is complete or perfect), and the repair takes constant time \(\nu \in [0,\tau ]\).
Specifically, under Model A an unfailed system found by inspection is considered as good as new. That is, necessary actions such as upgrading or modifying are taken to make the unfailed system as good as new. This is equivalent to an instantaneous perfect repair and automatically holds if the lifetime distribution of the system is exponential due to its memoryless property; whereas, a failed system revealed by inspection is completely repaired or replaced by an iid system under Model A. Thereafter, the completely repaired/replaced system is immediately restored to operation. Model A extends the case of instantaneous repair with \(\nu = 0\) in Høyland and Rausand (1994).
On the other hand, under Model B an unfailed system continues its operation without any intervention, i.e., the system remains as good as it is; a failed system will undergo perfect repair or replacement as under Model A, but the operation of the repaired system will start at the next scheduled inspection time after the repair/replacement, not immediately which is different from Model A.
To display the results in Sarkar and Sarkar (2000) we denote the life time of a given system starting operation at time \(t = 0\) as \(U\), the distribution function of \(U\) as \(F( \cdot )\). This notation will be kept in the rest of this paper.
For Model A with constant repair/replacement time \(0 \le \nu \le \tau\) the availability \(A(k\tau )\) is given as
Based on it the instantaneous availability \(A(t)\) is given as
It is easy to see that when \(\nu = 0\) the expression of \(A(t)\) has the form
where \(\left\lfloor x \right\rfloor\) is the largest integer part of \(x\). This is exactly the result in Høyland and Rausand (1994). For the same Model A, the limiting average availability of the system is
where
and
For Model B, in the case of \(\nu = 0\), the instantaneous availability \(A(t)\) is given as
where \(c_{0} = 1\) and \(c_{j} ,j \ge 1\) are determined recursively by
with \(p_{i} = F(i\tau ) - F((i - 1)\tau )\).
In addition, the limiting average availability of the system is
where \(\left\lceil x \right\rceil\) is the smallest integer satisfying \(\left\lceil x \right\rceil \ge x\).
In the case of \(\nu > 0\), without loss of generality it can be assumed that \(\nu = m\tau\) for some integer \(m \ge 1\). This holds because under Model B the failed system is restored to operation only at the next scheduled inspection time following its perfect repair or replacement; that is, if repair/replacement is completed during the time interval \(((m - 1)\tau ,m\tau ]\), then the repaired/replaced system is restored to operation at time \(m\tau\).
In the case of \(\nu > 0\) suppose \(\nu = m\tau\) for an integer \(m \ge 1\), it wan shown that
where \(d_{0} = 1\), \(d_{1} = d_{2} = \cdots = d_{m} = 0\), and \(d_{j} ,\quad j \ge m\) is determined by
with \(q_{1} = q_{2} = \cdots = q_{m} = 0\) and \(q_{m + i} = F(i\tau ) - F((i - 1)\tau ),\quad \forall i \ge 1\). Moreover, the limiting average availability of the system is
Example 3.1
Consider Model A in Sarkar and Sarkar (2000). The system availability \(A(t)\) is determined by (25) and (26).
Specifically, let \(\overline{F} (t) = {\text{e}}^{ - t}\) for all \(t \ge 0\), \(\nu = \ln 2\) and \(\tau = 2\ln 2\). According to (25)
From (26) it follows that
Obviously \(A(t)\) does not converge as \(t \to \infty\) but the limiting average availability \(A_{av} (\infty )\) exists and is given by (28). We have
and
Mi (2002) discussed a model which is similar to Model B with \(\nu = 0\) in Sarkar and Sarkar (2000) except that the system will undergo complete repair or replacement at time \(\eta \tau\) regardless whether the system is failed or unfailed from the result of inspection, where \(\eta\) is either an integer or \(\eta = \infty\). Under this assumption, the limiting average availability of the system was derived as
Note that assuming \(\nu = 0\) then the limiting average availability of the system under Model B in Sarkar and Sarkar (2000) is the special case of \(\eta = \infty\) in Mi (2002). As a matter of fact, we have
Example 3.2
Let the system lifetime distribution be exponential \(F(t) = 1 - exp( - \lambda t)\). The following figures show the limiting average availabilities obtained from (35) at fixed \(\lambda\) (left panel) and at fixed \(\tau\) (right panel).

In the model studied by Sarkar and Sarkar (2001), the system in application is periodically inspected with inspection interval \(\tau > 0\) and is supported by an iid spare system which is in cold standby. At time \(t = \tau ,\) the spare system takes over the operation no matter whether the status of the inspected system is failed or unfailed. If the inspection found the inspected system failed then it is sent for repair/replacement; otherwise, it is upgraded. Both the repair and upgrade are perfect meaning that repaired or upgraded system becomes as good as new. At time \(t = 2\tau ,\) the inspection is performed again. The system being repaired/replaced or upgraded at time \(t = \tau\) will take over operation if the repair/replacement or upgrade has been completed before \(t = 2\tau\), and the system inspected at \(t = 2\tau\) will undergo either repair/replacement or upgrade; otherwise, the inspection will be suspended and only after completion of repair/replacement or upgrade the repaired or upgraded system will take over the operation at the next scheduled inspection time. Denote the random time needed for repair/replacement and upgrade as \(Y_{r}\) and \(Y_{w}\), respectively. It can be assumed that the random times \(Y_{r}\) and \(Y_{w}\) have \(\{ \tau ,2\tau , \ldots \}\) as their support sets because of the assumption about the inspection policy. Furthermore, it is assumed naturally that \(Y_{w} \mathop \le \limits^{st} Y_{r}\).
Let \(P(Y_{w} = i\tau ) = p_{i}\) and \(P(Y_{r} = i\tau ) = q_{i}\) for \(i \ge 1\). Under their model, the authors obtain the instantaneous system availability \(A(t)\) as follows:
Where \(A_{1} (s) = {\mathbb{P}}(\xi (s + \tau ) = 1)\) and has the form
with \(w_{kj}\) determined by (2.1a), (2.1b) of Sarkar and Sarkar (2001). Based on the expression of \(A(t)\), the limiting average availability is also obtained as
where \(R_{0} = 0\),
and
Cui and Xie (2001) investigated two models: Model A and Model B similar to those of Sarkar and Sarkar (2000). But the models in Cui and Xie (2001) allow a perfect repair or a replacement that takes a random time \(Y\) with distribution \(G(y)\) and density function \(g(y)\). Special case when \(Y\) is a constant \(\nu\) that was assumed in Sarkar and Sarkar (2000) is also discussed in Cui and Xie (2001).
Using a random walk approach, Cui and Xie (2001) established the relationship between the random walk in a plane and the periodically inspected system. Based on this relationship, both the explicit and recursive formulas of \(A(t)\) for the case of constant perfect repair time or replacement time were displayed for the two models. In the case of random time \(Y\), the recursive formula of \(A(t)\) for the two models were obtained too. All these expressions and formulas of \(A(t)\) are complicate, so the readers are referred to their paper for details.
The model proposed in Biswas et al. (2003) assumed that for \(1 \le i \le h\), where \(h \ge 1\) is a given integer, at the time the \(i\)th system failure is detected by inspection, the failed system will undergo an incomplete repair and the lifetime distribution of the repaired system may not be the same as \(F\), the lifetime distribution of the original system. At the time, when the \((h + 1)\)th system failure is detected, the failed system will be repaired perfectly or replaced by one whose lifetime is iid as that of the original system. Here, the times needed for performing incomplete repair, perfect repair, and replacement can be either constants or random variables. It is also assumed that the repaired system will be restored to operation at the next scheduled inspection time but not immediately. As a consequence of this assumption, the support set of the random perfect repair time, replacement time, incomplete repair time can be limited on the set \(\{\uptau,2\uptau, \ldots \}\), and constant repair/replacement times can be limited to multiples of \(\uptau\).
Under these assumptions, both the instantaneous system availability \(A(t)\) and limiting average availability are obtained when there is only a single incomplete repair, i.e., \(h = 1\). The expression of \(A(t)\) is complicate, so we display only the limiting average availability \(A_{\text{av}} (\infty )\). In the deterministic case, that is repair/replacement times are constant, \(A_{\text{av}} (\infty )\) is given as
where \(U_{1}\) is the lifetime of the original system and \(U_{2}\) is the lifetime of the system upon completion of the first incomplete repair, constants \(m_{1} \tau\) and \(m_{2} \tau\) are the required times for perfect repair (or replacement) and incomplete repair, respectively.
In the stochastic case, denote the required times of perfect repair and incomplete repair as random variables \(D_{1}\) and \(D_{2} ,\) respectively. Then the limiting average availability is
Obviously, if \({\mathbb{P}}(D_{i} = m_{i} \tau ) = 1,\quad i = 1,2\) for two integers \(m_{1}\) and \(m_{2}\), then Eq. (43) becomes (42).
Note that the expression of \(A_{\text{av}} (\infty )\) shown in (43) becomes that one in Sarkar and Sarkar (2000) if \(U_{1} \mathop = \limits^{st} U_{2}\) and \(m_{1} = m_{2}\) which is equivalent to the case \(h = 0\).
Consider the case of single incomplete repair (\(h = 1\)) but the repair/replacement times are random. This time the expressions for \(A(t)\) and \(A_{av} (\infty )\) were also derived in Biswas et al. (2003). For example,
where \(D_{1}\) represents the random time required for an incomplete repair and \(D_{2}\) represents the random time required for a perfect repair. Clearly, if \(P(D_{i} = m_{i} \tau ) = 1,\quad i = 1,2\), then (43) is reduced to (42).
Cui and Xie (2005) assumed the following: failed system found by inspection is completely repaired or replaced; the times required for a perfect repair or replacement is either a constant \(\nu \ge 0\) or a random variable \(Y\) which has distribution \(G(y)\) and density function \(g(y)\), the repaired or replaced system is restored to operation immediately, i.e., it does not take any time, and treating the time at the completion of the perfect repair or replacement as a new starting point then the periodic inspection will be resumed. In their Model A, it is also assumed that unfailed system determined by inspection is upgraded as good as new, whereas in Model B unfailed system continues operation without any intervention.
Under Model A with constant repair/replacement time \(\nu\), the instantaneous system availability \(A(t)\) is determined recursively as follows
From this recursive equation, it was shown there that the limit of \(A(t)\) as \(t \to \infty\) does not exist if \(\nu = 0\) or \(\tau /\nu\) is a rational number when \(\nu > 0\), i.e., the steady-state availability does not exist. If the repair/replacement time is random, \(A(t)\) can be determined by two different recursive equations:
and
Moreover, in this case the steady-state availability and consequently the limiting average availability exist and are given as
For Model B with constant repair/replacement time \(\nu\), the instantaneous availability \(A(t)\) is given in a recursive way
On the other hand when the repair/replacement time \(Y\) has density function \(g(y)\) then \(A(t)\) satisfies equation
The steady-state availability and consequently the limiting average availability exist and are given by
It is interesting that if we let \(\eta = \infty\) in Mi (2002), \(Y = 0\) in Cui and Xie (2005), and notice that
then the results in Mi (2002) and Cui and Xie (2005) are the same as that one given in (50).
Example 3.3
Assume that system lifetime has Weibull distribution \(F(t) = 1 - \text{exp}( - (x/\lambda )^{k} )\) with mean \(\lambda\Gamma (1 + 1/k)\) and \(G(t) = 1 - \text{exp}( - \beta t)\). The following figures show the limiting average availabilities given by Eqs. (47) and (50) with different parameters \(\tau ,\lambda\) and \(\beta\) when \(k = 2\).

Different from most of previous research work on system availability, Tang et al. (2013) considered both calendar-based and age-based inspection policy. In their study, not only the downtime due to repair or replacement but also the downtime due to inspection are taken into consideration. In the past, only few works considered both nonnegligible times, for instance, Barroeta (2005), Jardine and Tsang (2006), Jiang and Jardine (2006), and Pak et al. (2006).
In the following, we use \(\nu_{w}\) to denote the constant downtime due to inspection for unfailed system and constant \(\nu_{f}\) to denote the total time when a failed system is detected including the downtime due to repair/replacement for failed system.
Model A studied in Tang et al. (2013) assumes that unfailed system found by inspection is upgraded or modified to be as good as new. But Model B assumes that unfailed system is put back to operation, i.e., the unfailed system remains as good as it is.
For Model A, the instantaneous system availability \(A(t)\) with a calendar-based inspection polity is given recursively by
for \(k = 1,2, \ldots\). And the limiting average availability is given as
where
Under Model A if the age-based inspection policy is applied, then \(A(t)\) is recursively determined by the following equation:
and the limiting average availability is
For Model B, the instantaneous system availability \(A(t)\) with a calendar-based inspection policy is determined recursively as follows:
The equations for determining \(B(s)\) appearing in the above expression can be found in Tang et al. (2013) and is omitted here because it is tedious to display them. The limiting average availability in this case is obtained as
where \(s_{0} = 0\), and \(s_{k} = k(\tau - \nu_{w} ) + \nu_{w} - \nu_{f} ,\forall k \ge 1\).
In the age-based inspection policy is applied under Model B, then \(A(t)\) is determined recursively by
where
and
Under the same assumptions the limiting average availability is obtained as
Note that when \(\nu_{w} = 0\) it holds that
and it turns out to be the same as the expression of \(A_{av} (\infty )\) in Sarkar and Sarkar (2000).
Example 3.4
Suppose that system lifetime has exponential distribution \(F(t) = 1 - exp( - \alpha t)\), the following figures show the limiting average availabilities determined by Eqs. (53), (58) and (56), (62), respectively, when \(\alpha = 0.05,\nu_{w} = 1\) and \(\nu_{f} = 2\). The left panel corresponds to the calendar-base inspection policy, and the right panel corresponds to the age-base inspection policy.

4 Other Works on System Availability
The previous two sections address availability of systems without specifying their configurations. In the field of reliability, the \(k\)-out-of-\(n\) system has particular importance since it is widely used in practice. Recent research works on the availability of \(k\)-out-of-\(n\) system include, for example, Fawzi (1991), Frostig (2002), De Smidt-Destombes et al. (2004, 2006, 2007, 2009), Li et al. (2006), Yam et al. (2003), and Zhang et al. (2000, 2006) among others.
There are also lots of studies on availability of various other systems appearing in industry. For instance, Berrade (2012), Chung (1994), Dhillon (1993), Dhillon and Yang (1992), Klutke et al. (1996, 2002), Lau et al. (2004), Mishra (2013), Pascual (2011), Pham-Gia and Turkkan (1999), Vaurio (1997, 1999), Wang et al. (2006), Wang and Chen (2009), and works referred therein. In these works warm standby, imperfect switch, reboot delay, common cause failures, and random deterioration were considered. Specifically, Mi (2006a, b) introduced the concept of pseudo availability which differs from the traditional availabilities in that once the system is in ‘up’ state, it will remain there forever without change.
It is worthy of mentioning that in addition to \(A(t)\), the interval availability and the steady-state interval availability are probably as important as the instantaneous system availability or even more important for certain situations. For any \(w \ge 0\) the interval availability is defined as \(A_{w} (t) = P(\xi (s) = 1,\quad t \le s \le t + w)\). It is the probability that the system is functioning during the interval \([t,t + w]\). Of course, if \(w = 0\) then \(A_{w} (t)\) becomes the instantaneous system availability \(A(t)\). Mi (1999) and Huang and Mi (2013) discussed interval availability. We think it would be worthwhile studying those models mentioned above to derive more results about interval availability.
References
Barlow, R. E., & Proschan, F. (1975). Statistical theory of reliability and life testing. New York: Holt, Rinehart & Winston.
Barroeta, C. E. (2005). Risk and economic estimation of inspection policy for periodically tested repairable components, MS thesis.
Berrade, M. D. (2012). A two-phase inspection policy with imperfect testing. Applied Mathematical Modelling, 36, 108–114.
Biswas, J., & Sarkar, J. (2000). Availability of a system maintained through several imperfect repairs before a replacement or a perfect repair. Statistics & Probability Letters, 50, 105–114.
Biswas, A., Sarkar, J., & Sarkar, S. (2003). Availability of a periodically inspected system, maintained under an imperfect-repair policy. IEEE Transactions on Reliability, 52(3).
Block, H. W., Borges, W. S., & Savits, T. H. (1985). Age-dependent minimal repair. Journal of Applied Probability, 22, 370–385.
Brown, M., & Proschan, F. (1983). Imperfect repair. Journal of Applied Probability, 20, 851–859.
Cha, J. H., & Kim, J. J. (2001). On availability of Bayesian imperfect repair model. Statistics & Probability Letters, 53, 181–187.
Cha, J. H., & Kim, J. J. (2002). On the existence of the steady state availability of imperfect repair model. Sankhya Series B, 64, 76–81.
Cha, J. H., Lee, S., & Mi, J. (2004). Bounding the optimal burn-in time for a system with two types of failure. Naval Research Logistics: An International Journal, 51, 1090–1101.
Chelbi, A., & Ait-Kadi, D. (2000). Generalized inspection strategy for randomly failing systems subjected to random shocks. International Journal of Production Economics, 64, 379–384.
Chung, W. K. (1994). Reliability and availability analysis of warm standby systems with repair and multiple critical errors. Microelectronics Reliability, 34(1), 153–155.
Cui, L. R. & Xie, M. (2001). Availability analysis of periodically inspected systems with random walk model 38, 860–871.
Cui, L. R., & Xie, M. (2005). Availability of a periodically inspected system with random repair or replacement times. Journal of Statistical Planning and Inference, 131, 89–100.
De Smidt-Destombes, K. S., van der Heijdenb, M. C., & van Harten, A. (2004). On the availability of a k-out-of-N system given limited spares and repair capacity under a condition based maintenance strategy. Reliability Engineering and System Safety, 83, 287–300.
De Smidt-Destombes, K. S., van der Heijden, M. C., & van Harten, A. (2006). On the interaction between maintenance, spare part inventories and repair capacity for a k-out-of-N system with wear-out. European Journal of Operational Research, 174, 182–200.
De Smidt-Destombes, K. S., van der Heijdenb, M. C., & van Harten, A. (2007). Availability of k-out-of-N systems under block replacement sharing limited spares and repair capacity. International Journal of Production Economics, 107, 404–421 (2007)
De Smidt-Destombes, K. S., vander Heijden, M. C., & van Harten, A. (2009). Joint optimization of spare part inventory, maintenance frequency and repair capacity for k-out-of-N systems. International Journal of Production Economics, 118, 260–268.
Dhillon, B. S., & Yang, N. (1992). Reliability and availability analysis of warm standby systems with common-cause failures and human errors. Microelectron Reliability, 32(4), 561–575.
Dhillon, B. S. (1993). Reliability and availability analysis of a system with warm standby and common cause failures. Microelectron Reliability, 33(9), 1343–1349.
Dieulle, L. (1999). Reliability of a system with Poisson inspection times. Journal of Applied Probability, 36, 1140–1154.
Fawzi, B. B., & Hawkes, A. G. (1991). Availability of an R-out-of-N system with spares and repairs. Journal of Applied Probability, 28, 397–408.
Frostig, E., & Levikson, B. (2002). On the availability of R out of N repairable systems. Naval Research Logistics, 49(5), 483–498.
Gut, A., & Jansons, S. (1983). The limiting behaviour of certain stopped sums and some applications. Scandinavian Journal of Statistics, 10, 281–292.
Høyland, A., & Rausand, M. (1994). System reliability theory. New York: Wiley.
Huang, K., & Mi, J. (2013). Properties and computation of interval availability of system. Statistics and Probability Letter, 83, 1388–1396.
Ito, K., & Nakagawa, T. (2000). Optimal inspection policies for a storage system with degradation at periodic tests. Mathematical and Computer Modelling, 31, 191–195.
Jardine, A. K. S., & Tsang, A. H. C. (2006). Maintenance, replacement, and reliability: Theory and applications. Boca Raton: CRC Press.
Jiang, R. Y., & Jardine, A. K. S. (2006). Optimal failure-finding interval through maximizing availability. International Journal of Plant Engineering and Management, 11, 174–178.
Klutke, G. A., Wortman, M. A., & Ayhan, H. (1996). The availability of inspected systems subject to random deterioration. Probability in the Engineering and Informational Sciences, 10, 109–118.
Klutke, G. A., & Yang, Y. J. (2002). The availability of inspected systems subject to shocks and graceful degradation. IEEE Transactions on Reliability, 51(3), 371–374.
Lau, H. C., Song, H. W., See, C. T., & Cheng, S. Y. (2004). Evaluation of time-varying availability in multi-echelon spare parts systems with passivation. European Journal of Operational Research, 170(1), 91–105.
Li, X., Zuo, M. J., & Yam, R. C. M. (2006). Reliability analysis of a repairable k-out-of-n system with some components being suspended when the system is down. Reliability Engineering and System Safety, 91, 305–310.
Lim, J. H., Lu, K. L., & Park, D. H. (1998). Bayesian imperfect repair model. Communication in Statistics Theory, 27(4), 965–984.
Mi, J. (1994). Burn-in and maintenance policies. Advanced Applied Probability, 26, 207–221.
Mi, J. (1995). Limiting behavior of some measures of system availability. Journal of Applied Probability, 32, 482–493.
Mi, J. (1999). On measure of system interval availability. Probability in the Engineering and Informational Sciences, 13, 359–375.
Mi, J. (2002). On bounds to some optimal policies in reliability. Journal of Applied Probability, 39, 491–502.
Mi, J. (2006a). Limiting availability of system with non-identical lifetime distributions and non-identical repair time distributions. Statistics & Probability Letter, 76, 729–736.
Mi, J. (2006b). Pseudo availability of repairable system. Methodology and Computing in Applied Probability, 8, 93–103.
Mishra, A., & Jain, M. (2013). Maintainability policy for deteriorating system with inspection and common cause failure. International Journal of Engineering Transactions C: Aspects, 26(6), 631–640.
Pak, A., Pascual, R., & Jarding, A. K. S. (2006). Maintenance and replacement policies for protective devices with imperfect repairs, Technical report.
Pascual, R., Louit, D., & Jardine, A. K. S. (2011). Optimal inspection intervals for safety systems with partial inspections. Journal of the Operational Research Society, 62, 2051–2062.
Pham-Gia, T., & Turkkan, N. (1999) System availability in a gamma alternating renewal process. Naval Research Logistics, 46
Rényi, A. (1957). On the asymptotic distribution of the sum of a random number of independent random variables. Acta Mathematica Academiae Scientiarum Hungaricae, 8, 193–199.
Rise, J. (1979). Compliance test plans for reliability. In Proceedings of the 1979 annual reliability and maintenance symposium.
Sarkar, J., & Biswas, A. (2010). Availability of a one-unit system supported by several spares and repair facilities. Journal of the Korean Statistical Society, 39, 165–176.
Sarkar, J., & Chaudhuri, G. (1999). Availability of a system with gamma life and exponential repair time under a perfect repair policy. Statistics & Probability Letters, 43, 189–196.
Sarkar, J., & Li, F. (2006). Limiting average availability of a system supported by several spares and several repair facilities. Statistics & Probability Letters, 76, 1965–1974.
Sarkar, J., & Sarkar, S. (2000). Availability of a periodically inspected system under perfect repair. Journal of Statistical Planning and Inference, 91, 77–90.
Sarkar, J., & Sarkar, S. (2001). Availability of a periodically inspected system supported by a spare unit, under perfect repair or perfect upgrade. Statistics & Probability Letters, 53, 207–217.
Takács, L. (1957). On certain sojourn time problems in the theory of stochastic processes. Acta Mathematica Academiae Scientiarum Hungaricae, 8, 169–191.
Tang, T. Q., Lin, D. M., Banjevic, D., & Andrew, K. S. J. (2013). Availability of a system subject to hidden failure inspected at constant intervals with non-negligible downtime due to inspection and downtime due to repair/replacement. Journal of Statistical Planning and Inference, 143, 176–185.
Vaurio, J. K. (1997). On time-dependent availability and maintenance optimization of standby units under various maintenance policies. Reliability Engineering and System Safety, 56, 79–89.
Vaurio, J. K. (1999). Availability and cost functions for periodically inspected preventively maintained units. Reliability Engineering and Systems Safety, 63, 133–140.
Wang, K. H., Dong, W. L., & Jyh-Bin Ke, J. B. (2006). Comparison of reliability and the availability between four systems with warm standby components and standby switching failures. Applied Mathematics and Computation, 183, 1310–1322.
Wang, K. H., & Chen, Y. J. (2009). Comparative analysis of availability between three systems with general repair times, reboot delay and switching failures. Applied Mathematics and Computation, 215, 384–394.
Wortman, M. A., & Klutke, G. A. (1994). On maintained systems operating in a random environment. Journal of Applied Probability, 31, 589–594.
Wortman, M. A., Klutke, G. A., & Ayhan, H. (1994). A maintenance strategy for systems subjected to deterioration governed by random shocks. IEEE Transaction on Reliability, 43, 439–445.
Yadavalli, V. S. S., Botha, M., & Bekker, A. (2002). Asymptotic confidence limits for the steady state availability of a two-unit parallel system with preparation time for the repair facility. Asia-Pacific Journal of Operational Research, 19, 249–256.
Yam, R. C. M., Zuo, M. J., & Zhang, Y. L. (2003). A method for evaluation of reliability indices for repairable circular consecutive-k-out-of-n: F systems. Reliability Engineering and System Safety, 79(1), 1–9.
Yang, Y. J., & Klutke, G. A. (2000). Improved inspection schemes for deteriorating equipment. Probability Engineering Information Sciences, 14(4), 445–460.
Yang, Y. J., & Klutke, G. A. (2001). A distribution-free lower bound for availability of quantile-based inspection schemes. IEEE Transactions on Reliability, 50(4), 419–421.
Yeh, L. (1995). An optimal inspection-repair-replacement policy for standby systems. Journal of Applied Probability, 32, 212–223.
Zhang, T. L., & Horigome, M. (2000). Availability of 3-out-of-4: G warm standby system. IEEE Transactions on Fundamentals of Electronics Communications and Computer, E83-A(5), 857–862.
Zhang, T. L., Xie, M., & Horigome, M. (2006). Availability and reliability of k-out-of-(M+N): G warm standby systems. Reliability Engineering and System Safety, 91, 381–387.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag London
About this chapter
Cite this chapter
Huang, K., Mi, J. (2016). Availability of Systems with or Without Inspections. In: Pham, H. (eds) Quality and Reliability Management and Its Applications. Springer Series in Reliability Engineering. Springer, London. https://doi.org/10.1007/978-1-4471-6778-5_9
Download citation
DOI: https://doi.org/10.1007/978-1-4471-6778-5_9
Published:
Publisher Name: Springer, London
Print ISBN: 978-1-4471-6776-1
Online ISBN: 978-1-4471-6778-5
eBook Packages: EngineeringEngineering (R0)