A Comparative Study of Periodic-Review Order-Up-To (T, S) Policy and Continuous-Review (s, S) Policy in a Serial Supply Chain Over a Finite Planning Horizon

Abstract

In this paper, we consider a serial supply chain (SC) operating with deterministic and known customer demands and costs of review or orders, holding, and backlog at every installation over a finite planning horizon. We present an evaluation of two order policies: Periodic-review order-up-to S policy (i.e., (T, S) policy), and (s, S) policy. We first present a mathematical programming model to determine optimal re-order point and base-stock for every member in the SC. By virtue of the computational complexity associated with the mathematical model, we present genetic algorithms (GAs) to determine the order policy parameters, s and S for every stage. We compare the performances of GAs (for obtaining installation s and S) with the mathematical model for the periodic-review order-up-to (T, S) policy that obtains in its class optimal review periods and order-up-to levels. It is observed that the (s, S) policy emerges to be mostly better than the (T, S) policy.

1 Introduction

Supply chain (SC) decisions are broadly classified into strategic, tactical, and operational decisions, and the operational perspective can be addressed in terms of four problem areas, namely, inventory management and control; production, planning, and scheduling; information sharing and coordination monitoring; and operation tools (Ganeshan et al. 1999). Inventory is held by installations or members in a SC in different forms so as to provide continuous service to the respective downstream customer and finally to customers/consumers. Love (1979) defined inventory as goods or materials in the control of an enterprise, and held for a time in a relatively idle or unproductive state, awaiting its intended use or sale. Efficient and effective management of inventory throughout the SC significantly improves the service provided to the customer (Lee and Billington 1992). Nahmias (2008) listed out the motivation for holding inventories in view of economies of scale, uncertainties, smoothing, transportation, control cost, and logistics. Some issues that are critical in the SC inventory management include the inventory order policy such as the periodic-review order-up-to policy (T, S) and continuous-review (s, S) policy. These order policies help answer basically two questions: When to order and how much to order? The objective is to minimize the sum of costs, mostly consisting of costs of review or order, holding, and shortage at different members in the SC. In this paper, a serial SC that manufactures a single product with discrete customer demands known a priori over the finite planning horizon is considered, and a relative evaluation of two inventory order polices, namely, periodic-review order-up-to policy (i.e., (T, S) policy) and the (s, S) policy, is presented by considering many SC settings. It is possibly for the first time in the literature that such a relative evaluation of such order policies is undertaken in a serial SC over a finite time horizon.

2 Literature Review

Clark and Scarf (1960) addressed the problem of determining optimal purchasing quantities in a serial multi-echelon system so as to minimize the long-run average cost, and showed that an echelon base-stock policy is optimal for the finite horizon problem. Federgruen and Zipkin (1984) extended Clark and Scarf’s work to infinite horizon problem, and proved that a stationary order-up-to-level policy is optimal. Lee and Billington (1993) developed a decision support system for Hewlett-Packard company to aid inventory and service benchmarking, operational planning and control, and what-if analyses. Axsäter and Rosling (1993) compared the installation and echelon stock policy, and proved that when every stock-point in a multi-echelon inventory system is controlled by an order-up-to policy, an installation stock policy can always be replaced by an equivalent echelon stock policy, and vice versa. Glasserman and Tayur (1995) developed simulation-based methods to estimate sensitivities of inventory costs with respect to policy parameters. Gallego and Zipkin (1999) discussed the issue of stock positioning, and constructed heuristics to minimize the system average cost. Zipkin (2000) presented discussions on base-stock levels for series systems, assembly systems, and distributed systems with local control and central control.

Min and Zhou (2002) classified SC models into inventory theoretic and simulation hybrids, and stressed the need of mathematical programming models to explore multi-echelon and multi period issues in the SC. Shang and Song (2003) developed an easily implementable heuristic to determine the echelon base-stock levels for an N-stage serial system by solving 2 N single stage news vendor-type problems. Daniel and Rajendran (2005a) developed a simulation-based heuristic that attempts to optimize (in the class of base-stock policy) the base-stocks in a serial SC with the objective of minimizing the total SC cost consisting of holding costs and shortage costs at all installations in the SC. They proposed a genetic algorithm (GA) to determine the best installation base-stocks for a serial SC. Daniel and Rajendran (2005b) developed a problem-specific heuristic and a simulated annealing (SA) heuristic for finding the best installation base-stocks in a serial SC. Daniel and Rajendran (2006) developed different variants of GA to obtain the best installation base-stocks for a serial SC, and compared these variants with the complete enumeration and the best-move local search technique. However, they did not consider the presence of order costs in the SC.

Another application of GAs to SC inventory optimization was reported by Haq and Kannan (2006) by considering a two-echelon distribution-inventory SC for the bread industry. Cheng et al. (2006) proposed using a fuzzy inventory controller to determine the ordering quantity for the members in a SC. Axsäter (2006) provided discussions on multi-echelon inventory ordering policies including the determination of optimal lot sizing and re-order points. van Houtum et al. (2007) considered a single-item, periodic-review, serial inventory/production system, with linear inventory-holding and penalty costs, and proved the optimality of base-stock policies by deriving newsboy equations for the optimal base-stock levels, and described an efficient exact solution procedure for the case with mixed Erlang demands. Shang and Song (2007) considered two models of stochastic serial inventory systems and showed that the optimal policy parameters can be bounded and approximated by a series of independent, single-stage optimal policy parameters. Cheung and Zhang (2008) considered a SC with one supplier and multiple retailers in which base-stock policies are practiced, specifically two replenishment strategies: Synchronized ordering and balanced ordering. Johansen and Thorstenson (2008) extended the problem of determination of optimal base-stock of the inventory system with continuous review and constant lead time to the case with periodic review and stochastic and sequential lead times. For a detailed review of literature, see Sethupathi and Rajendran (2010).

Most studies considered only holding and shortage costs, and they did not consider the order costs to be significant which may not be true in all SCs; in that case, the total costs consist of holding, shortage, and order costs at various echelons in the SC. Sethupathi and Rajendran (2010) modeled a serial SC with periodic-review order-up-to policy (i.e., (T, S) policy), and determined the optimal and heuristic review periods and base-stocks at installations in the SC (with deterministic customer demands over a fine planning horizon) respectively using a mathematical programming model and two GAs. It is evident that the determination of order-up-to levels in SCs and the minimization of the total SC cost are quite complex and computationally quite tedious (e.g., see Lee and Billington 1993; Petrovic et al. 1998; Shang and Song 2003; Daniel and Rajendran 2006; Sethupathi and Rajendran 2010); it is also evident from the literature review that the determination of optimal order quantity and re-order level or re-order point is computationally difficult with the consideration of the exact total costs in SC, and that no attempt has been made to determine such optimal order policy parameters in a SC in a deterministic demand environment over a finite planning horizon (also see the related observations of researchers in the case of determination of inventory order policy parameters with respect to periodic-review base-stock policy in a serial SC).

The present study aims to model a serial SC operating with dynamic, known, and deterministic customer demands over a finite planning horizon: First with the consideration of (s, S) policy with re-order point to determine the installation base-stock and re-order point for every member in the SC; and compare its performance with that of periodic review order-up-to S policy (i.e., (T, S) policy) that operates with base-stock and review period for every installation. We make use of mathematical programming models to determine the optimal parameter values in the respective class of inventory order policies, and subsequently three GAs to determine the heuristic parameter values (via deterministic simulation) in view of the computational complexity associated with the mathematical programming models. We consider the installation inventory order policy and its parameters in view of the ease of implementation in the proposed mathematical programming model and the GAs. Our model consists of a serial SC with a supplier, a manufacturer, a distributor, and a retailer, and a time unit is assumed to be discrete and it corresponds to a day, though not restrictive. The present work employs the SC model similar to the one by Sethupathi and Rajendran (2010); however differs in terms of the order policy i.e., (s, S) policy considered in this study.

3 Mathematical Programming Model for the (s, S) Policy

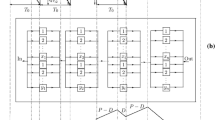
The SC framework considered in this study comprises four members, namely, retailer, distributor, manufacturer, and supplier, and the material flow is shown in Fig. 1. This study primarily focuses on the determination of the optimal or heuristic best installation base-stocks and re-order points, i.e., S and s respectively at every installation, and hence we do not treat the customer as a member in the context of the current problem, except that a customer demand triggers the information flow and hence the material flow in the SC. All four members add value to the product as it passes through the SC before it is delivered to the customer. The members are linked through information flow in both directions and products flow from the most upstream member to the lowest downstream member. The whole SC works with a pull strategy and the customer demand arising at member 1 (i.e., retailer) pulls the product from the subsequent upstream member. Inventory is controlled by the SC members by using the (s, S) policy with a re-order point. This review mechanism triggers replenishment orders at every member depending upon the inventory on hand, pre-specified installation base-stock, re-order point, outstanding orders, and backorders at that member. Every member continuously monitors its installation inventory position; when it equals or falls below the re-order point s, an order is triggered to the immediate upstream member. Different holding and shortage cost-rates and ordering costs exist at different SC members. Every member has a deterministic replenishment lead time equal to the sum of production lead time and transportation lead time with respect to the upstream member.

Fig. 1

Material flow in the serial supply chain

3.1 Model Assumptions

• 1. A single product flows through the SC.

• 2. Time is assumed to be discrete, and the unit of discrete time is assumed to be a day.

• 3. We consider a serial SC model comprising N installations with a finite time horizon and with known discrete customer demands varying over time.

• 4. All the N installations or stages or members in the SC operate under an installation (s, S) policy with the respective re-order points and base-stocks for every member in the SC.

• 5. Inventory order policy parameters such as the base-stock (S) and re-order point (s) for a given member remain the same across the entire finite time horizon.

• 6. Base-stock and re-order point for a given member or installation in the SC take integer values as the customer demands are assumed to be integers.

• 7. The retailer faces a customer demand, which is assumed to be stationary and uniformly distributed in the interval [20, 60] in the computational experiments considered in this study (though this demand distribution is not restrictive). Customer demands are sampled from the given distribution, and they are assumed to be discrete and known over the finite planning horizon in this study.

• 8. Lead time for information or order processing is zero.

• 9. Processing (procurement/production/packing) lead time and transportation lead time are combined accordingly at each stage and considered together as one component, called replenishment lead time for that installation or member in the SC, and is assumed to be deterministic.

• 10. There is no lot-size or discount policy for members in the SC.

• 11. Every member in the SC has its own installation or local holding and shortage cost rates, and an order cost per order.

• 12. Re-order point of a member is assumed to be less than or equal to the base-stock of that member.

• 13. If the demand exceeds on-hand inventory at a member, then the excess demand is backlogged.

• 14. Availability of raw material for installation N, i.e., the supplier, is unlimited.

• 15. All installations have infinite capacity.

• 16. The entire customer demand on day t is assumed to occur during the time epoch $\Updelta t$ within day t itself; the demand from installation j gets transmitted to upstream member (j + 1) immediately at the end of time epoch $\Updelta t$, if the installation inventory position equals or falls below the re-order point $s_{j}$ at installation j. Hence, relevant inventory information gets updated at the beginning of and at the end of t at every installation.

3.2 Supply Chain Model Description with (s, S) Policy

The sequence of events taking place at installation or member j, for j = 1 to N in the same order, in time (or during day) t, where N is the number of installations in the SC, is as follows.

• (1) The receipt of material at member j (shipped from member (j + 1) to member j) takes place if the material is due to arrive at the beginning of current time instant t. The installation’s inventory information, namely, on-hand inventory, is updated.

• (2) Member 1 receives the customer demand; for member j, j > 1, the order from the immediate downstream member is received, when the inventory position of installation (j − 1) has reached or has fallen below its re-order level.

• (3) The possible order fulfillment (combining both installation’s backorder as of the previous day and the current day’s demand received from downstream member (j − 1)) takes place, depending upon the available on-hand inventory at stage j. If sufficient on-hand inventory is not there with member j to meet this combined demand, then the unsatisfied demand is backlogged. The downstream member (j − 1) receives a partially or fully fulfilled order quantity after a delay corresponding to replenishment lead time of member (j − 1). If the downstream member is the customer, then the customer receives it in the current day t itself. Installation inventory at stage j is updated.

• (4) With the available local inventory information, member j triggers an order to the upstream member (j + 1) only if the inventory position of j has reached or fallen below the re-order level of j; otherwise no order placement takes place. The order placement depends upon the inventory on hand, pre-specified base-stock $S_{j}$, re-order point $s_{j}$, outstanding order, and backorder at that member j. If order placement takes place, member (j + 1) realizes the order placed by member j immediately, since the information/order processing lead time is assumed to be zero.

• (5) Installation inventory such as on-hand inventory, on-order inventory, and backorder are updated, and the sum of local holding cost, shortage cost, and order cost, if an order takes place, are computed with respect to member j.

Since it is assumed in this study that a day corresponds to a unit time, t is incremented and the same sequence of events gets repeated on the following day; the same sequence of events takes place at all members in the SC, for j = 1, 2,.., N. The total supply chain cost (TSCC) is computed over the given finite-time horizon of T days.

3.3 Formulation of the Mathematical Model for the (s, S) Policy

The notations used in the mathematical model are as follows:

TSCC:

total supply chain cost

$j$ :

installation/stage index

$N$ :

number of installations in the SC

$T$ :

total number of days (planning horizon) over which TSCC is computed

t :

current time or current day

$S_{j}$ :

installation base-stock at installation j

$s_{j}$ :

installation re-order point for installation j

$h_{j}$ :

installation holding cost-rate for installation j

$b_{j}$ :

installation shortage cost-rate for installation j

$O_{j}$ :

installation ordering cost for installation j

${\text{LT}}_{j}$ :

installation replenishment lead time with respect to installation j /* note that the member j receives on t, the possible shipment from (j + 1) that has taken place at the end of $(t - {\text{LT}}_{j} )$; hence in this study, when we assume ${\text{LT}}_{j} = 1$, it means that member j receives on day t the shipment that has been shipped from member (j + 1) on day (t − 1), though theoretically ${\text{LT}}_{j}$ equals 0; however, we set ${\text{LT}}_{j} = 1$ and we carry on with this setting of ${\text{LT}}_{j}$ for the sake of correctness of mathematical formulation in this study; also see Daniel and Rajendran (2005a, b, 2006) */

$I_{j,t}$ :

end installation on-hand inventory at installation j at t

$I_{j,t}^{*}$ :

installation on-hand inventory at installation j at the beginning of t, after the possible replenishment from installation (j +1) arrives at installation j

${\text{OI}}_{j,t}$ :

end on-order inventory at installation j at t

${\text{OI}}_{j,t}^{*}$ :

on-order inventory at installation j at the beginning of t

${\text{SUMDEM}}_{j,t}$ :

sum of demand at (i.e., received by) installation j up to t

${\text{SUMORD}}_{j,t}$ :

sum of orders placed by installation j up to t

$B_{j,t}$ :

backorder at installation j at the end of t

$D_{j,j + 1,t}$ :

demand placed by installation j to upstream installation (j + 1) at t /* this demand is assumed to be immediately realized by installation (j + 1) at t itself; $D_{0,1,t}$ corresponds to customer demand at installation 1 on day t; as for other installations, $D_{j,j + 1,t}$ equals zero if ($I_{j,t}$ + ${\text{OI}}_{j,t}^{*}$ − $B_{j,t}$ > $s_{j}$); otherwise it equals ($S_{j}$ − ($I_{j,t}$ + ${\text{OI}}_{j,t}^{*}$ − $B_{j,t}$)) that is same as the sum of demands received by the installation up to t minus the sum its order quantities up to (t − 1). */

$\delta_{j,t}^{*}$ :

a binary variable that assumes the value of 1, whenever there is an order placement at installation j at t; else it is 0

${\text{QS}}_{j,j - 1,t}$ :

quantity shipped from installation j to (j − 1) at the end of t

${\text{QS}}_{N + 1,N,t}$ :

raw material shipped to installation N at the end of t /* installation N + 1 is assumed to have raw material supply of infinite capacity */

The objective is to minimize the total system-wide cost given as follows:

$$ {\text{Minimize}}\;{\text{TSCC}} = \sum\limits_{t = 1}^{T} {\sum\limits_{j = 1}^{N} {\left( {h_{j} \,I_{j,t} + b_{j} \,B_{j,t} + O_{j} \delta_{j,t}^{*} } \right)} } $$

(1)

subject to the following:

• {

  • {

    • $$ {\text{OI}}_{j,t}^{*} = {\text{OI}}_{j,t - 1} - {\text{QS}}_{{j + 1,j,t - LT_{j} }} $$

      (2)
      $$ I_{j,t}^{*} = I_{j,t - 1} + {\text{QS}}_{{j + 1,j,t - LT_{j} }} $$

      (3)
      $$ I_{j,t} - B_{j,t} = I_{j,t}^{*} - B_{j,t - 1} - D_{j - 1,j,t} $$

      (4)
      $$ {\text{SUMDEM}}_{j,t} = {\text{SUMDEM}}_{j,t - 1} + D_{j - 1,j,t} $$

      (5)
      $$ {\text{OI}}_{j,t}^{*} + I_{j,t}^{{}} - B_{j,t} \le s_{j} + M(1 - \delta_{j,t}^{*} ) $$

      (6)
      $$ {\text{OI}}_{j,t}^{*} + I_{j,t}^{{}} - B_{j,t} \ge s_{j} + 1 - M\delta_{j,t}^{*} $$

      (7)
      $$ D_{j,j + 1,t} \le {\text{SUMDEM}}_{j,t} - {\text{SUMORD}}_{j,t - 1} + M\left( {1 - \delta_{j,t}^{*} } \right) $$

      (8)
      $$ D_{j,j + 1,t} \ge {\text{SUMDEM}}_{j,t} - {\text{SUMORD}}_{j,t - 1} - M\left( {1 - \delta_{j,t}^{*} } \right) $$

      (9)
      $$ D_{j,j + 1,t} \le M\delta_{j,t}^{*} $$

      (10)
      $$ {\text{QS}}_{j,j - 1,t} \, = I_{j,t}^{*} - I_{j,t} $$

      (11)
      $$ {\text{SUMORD}}_{j,t} = {\text{SUMORD}}_{j,t - 1} + D_{j,j + 1,t} $$

      (12)
      $$ {\text{OI}}_{j,t} = {\text{OI}}_{j,t}^{*} + D_{j,j + 1,t} $$

      (13)

  • }, for j = 1, 2, …, N

• $$ {\text{QS}}_{N + 1,N,t} = D_{N,N + 1,t} $$

  (14)

• }, for t = 1, 2, …, T

• with initial conditions as

  $$ I_{j,0} = S_{j} ,\quad \forall \,j \le N $$

  (15)
  $$ s_{j} \le S_{j} ,\quad {\text{for}}\;\forall \,j \le N $$

  (16)
  $$ {\text{OI}}_{j,0} = 0,\quad \forall \,j \le N $$

  (17)
  $$ B_{j,0} = 0,\quad \forall \,j \le N $$

  (18)
  $$ {\text{SUMDEM}}_{j,0} = 0,\quad \forall \,j \le N $$

  (19)
  $$ {\text{SUMORD}}_{j,0} = 0,\quad \forall \,j \le N $$

  (20)
  $$ {\text{QS}}_{{j + 1,j,t - LT_{j} }} = 0,\quad \forall t \le LT_{j} \;{\text{and}}\;\,\forall \,j \le N $$

  (21)
  $$ \delta_{j,t}^{*} \in \left\{ {0,1} \right\} \,\forall \,j\, \le \,N\,{\text{and}}\,\forall \,t\, \le \,T \; \text{and all other variables}\;\ge \,0,\,\,\,\forall \,j\, \le \,N\;\text{and}\;\forall \,t\, \le \,T. $$

  (22)

Equation 1 shows the objective function to minimize the TSCC comprising the holding, shortage, and ordering costs for all installation over T days. Equation 2 updates the on-order inventory at j at the beginning of t. Equation 3 updates the on-hand inventory at j at the beginning of t. Equation 4 updates the on-hand inventory/backorder at j after the demand realization. This equation holds, in view of our assumption that $b_{j} \ge \,h_{j + 1}$. However, if this assumption does not hold, both terms may co-exist in Eq. 4, and hence we need to have the following expressions introduced to avoid the co-existence of $I_{j,t} \,$ and $B_{j,t}$:

$$ I_{j,t} \le M\delta_{j,t}^{**} \;{\text{and}}\;B_{j,t} \le M(1 - \delta_{j,t}^{**} ),{\text{with}}\;\delta_{j,t}^{*} \in \left\{ {0,1} \right\},{\text{for}}\;\forall \,j \le N\;{\text{and}}\;\forall \,t \le T $$

(23)

where M denotes a large positive integer value.

Equation 5 updates the sum of demand up to t. Expressions 6 and 7 monitor inventory position at stage j (i.e., ${\text{OI}}_{j,t}^{*} + I_{j,t}^{{}} - B_{j,t}$) and trigger the order if the end-inventory position equals or falls below the re-order level at j (and in this case $\delta_{j,t}^{*}$ becomes equal to one and hence $D_{j,j + 1,t} = {\text{SUMDEM}}_{j,t} - {\text{SUMORD}}_{j,t - 1}$, i.e., ($S_{j}$ − ($I_{j,t}$ + ${\text{OI}}_{j,t}^{*}$ − $B_{j,t}$)); else $\delta_{j,t}^{*}$ becomes zero and hence $D_{j,j + 1,t} = 0$, indicating no order placement. Expressions 8, 9, and 10 set the order to the upstream member accordingly (note that the order quantity equals zero if no order placement is there). Note that since we assume demands to be integers, we have ‘1’ in Expression 7, and all variables in an optimal solution are also integers. Equation 11 shows the shipment quantity from member j to the downstream member. Equation 12 updates the sum of orders placed (or on-order inventory) at stage j up to t. Equation 13 computes the end on-order inventory at j at t. Equation 14 shows the immediate shipment of quantity from the raw material supplier (who has infinite raw material availability) to the supplier, namely, installation N. Equations 15–21 are constraints which are used for initial conditions. Equation 22 refers to the binary variable used to represent the order placement and non-negativity constraints.

3.4 Supply Chain Settings

Tables 1 and 2 show the experimental settings of the SC test problems with lead time settings and cost settings considered in this study.

Table 1 Lead time settings

Table 2 Supply chain settings with respect to supply chain members

We sample daily integer customer demands that are uniformly distributed between [20, 60], and treat them as known and deterministic over the finite planning horizon. We establish two different demand streams or patterns. One long stream of demands spanning over 1200 days (called FD in this study) is directly generated from a seed value through a uniform random number generator for sampling customer demands. Another long stream spanning over 1200 days (called AD in this study) of customer demands is generated by the antithetic uniform random number from the same seed value. For example, if one demand in the first run is 30, and then in the antithetic run demand equals 50 (in view of the demand distribution being U [20, 60]). The method of antithetic sampling is a commonly used procedure for negatively correlated pair of samples (Deo 1999). These demand streams are long and sufficient for substantive experiments. We assume three different deterministic lead time settings as given in Table 1. The different cost settings are assumed as follows:

• Installation shortage cost rate, $b_{j} \, = C \times h_{j}$, where C = 2, 4, 8, 16; and

• installation ordering cost $O_{j\,} = K \times E(D) \times h_{j}$,

where E(D) is the expected customer demand with respect to the customer demand distribution and K = 2, 4, 8, 16.

The rationale for this setting of $O_{j}$ is that we relate the ordering cost to the setting of holding cost at stage j, and that we take the holding cost as the basis for the ordering cost because normally we deal with a SC with a very high service level (see Silver et al. 1998). See Table 2 for details of different cost settings where S, M, D, and R represent supplier, manufacturer, distributor, and retailer, respectively.

In all, we create 96 SC test problem instances in the present study $( 1 6 {\text{ cost settings }} \times 3 {\text{ lead time settings}} \times {\text{ 2 demand patterns)}} .$ It is to be noted that we increase the ratio of $b_{j} \,/h_{j}$ with the installation order costs remaining the same (e.g., see CS1–CS4), and that we increase installation order costs with the ratio of $b_{j} \,/h_{j}$ remaining the same (e.g., see CS1, CS5, CS9, and CS13). This is done in order to discover a possible pattern in the behavior of order policies (in terms of their base-stocks and re-order points) as a function of order costs and ratios of $b_{j} \,/h_{j}$.

3.5 Results of Execution of Mathematical Model Through an Optimization Solver and the Need for Heuristic Algorithm

The proposed model considering problem instances with T = 10, T = 15, T = 20, T = 25, and T = 30 and with the consideration of CS1 and LT1 has been executed with CPLEX, an optimization solver, using a computer with an Intel Pentium IV processor of 3.0 GHz speed and 1 GB RAM. The solver is able to solve the problems with T = 10, T = 15, T = 20, and T = 25. When we set T = 30, the solver could obtain only an upper bound and not the optimal solution, and the solver could not solve this test problem even after 6 h of execution, and its execution got terminated due to its memory limitations. The base-stocks and re-order points, which lead to minimum SC costs, and the CPU times for the five test problems, are reported in Table 3, where S, M, D, and R represent supplier, manufacturer, distributor, and retailer, respectively. We have also obtained the LP-relaxed solution, i.e., a lower bound on TSCC, by relaxing the binary constraints in the mathematical programming model (i.e., by treating $\delta_{j,t}^{*}$’s as continuous variables in the interval (0,1)). The lower bounds thus obtained for the test problems are also reported in Table 3. As the lower bounds obtained in these problems appear to be weak, we do not consider the lower bound through the LP-relaxation in our further analyses.

Table 3 Results obtained for the test problems using the solver

Figure 2 shows the computational effort of the solver for test problems with T = 10, 15, 20, and 25. From Fig. 2, it can be noted that the computational time taken for obtaining solutions appears to increase exponentially. This is not unexpected due to the presence of binary variables in the mathematical programming model. Wang (2011) also presented a similar observation that when time is discrete, the large dimension of the inventory state for the exact formulation usually precludes an exact solution and hence the focus is shifted to approximate solutions. Hence, we resort to the use of a heuristic algorithm in the present study to obtain the best inventory parameters in the SC.

Fig. 2

Computational experience with test problems (setting CS1 + LT1)

4 Proposed Genetic Algorithms for the (s, S) Policy

GAs are search algorithms based on the mechanism of natural selection and natural genetics. Simplicity of operation and power of effect are two of the main attractions of the GA approach (Goldberg 1989). GA is applied as an optimization tool to a variety of SC problems. Attempts had been made to develop meta-heuristics such as GA for SC inventory optimization. Daniel and Rajendran (2006) developed simulation-based heuristics to obtain inventory levels (base-stock levels) in a serial SC with the objective of minimizing the total SC cost in the class of base-stock policy. They proposed GAs to determine the best base-stock levels for a serial SC, and their findings indicated the performance of GAs based on gene-wise crossover operators superior to the SA algorithm by Daniel and Rajendran (2005b). They found their GGA (gene-wise GA) to perform very well. Haq and Kannan (2006) and Kumanan et al. (2007) employed GAs for minimizing the total cost consisting of production, inventory, and distribution costs. Some applications of GAs in SCs/multi-echelon inventory systems were discussed by Berry et al. (1998), Zhou et al. (2002), Lee et al.(2002), Hong and Kim (2009), and Rom and Slotnick (2009); and Sethupathi and Rajendran (2010) considering (T, S) policy. For all these reasons, we have gone for GAs to obtain the best heuristic order policy parameters in our study in view of the well-established performance of GAs in supply-chain operations optimization. In this study, we present the modified gene-wise GA (called MGGA), and two hybrid GAs, called HGA1 and HGA2 (GAs with the hybridization of gene-wise crossover operator and arithmetic crossover operator), to determine the best installation base-stocks and re-order points in the present case of (s, S) policy. It is to be noted that our present study is different from earlier works such as those by Daniel and Rajendran (2005a, 2006) in that earlier researchers did not consider the presence of order costs and hence they did not investigate the performance of policies such as (s, S) policy.

4.1 Notations and Terminologies for the Proposed GAs

The notations and terminologies used in the proposed GAs are as follows:

no_gen :

number of generations

l :

length of a chromosome (or the number of genes)

pop_size :

population size

n :

number of chromosomes (equal to pop_size)

par_pop :

parent population, consisting of n parent chromosomes

$S_{j}$ :

installation base-stock at member j, where j = 1 to N

$s_{j}$ :

installation re-order point at installation j /* it is ensured in the implementation of all GAs that $s_{j} \le \,S_{j}$*/

$S_{j}^{\text{UL}}$ :

upper limit on the base-stock at installation j /*(set rather loose to 1,000 in this study)*/

$S_{j}^{\text{LL}}$ :

lower limit on the base-stock at installation j /*(set to 20 in view of demand distribution assumed in the computational experiments in this study)*/

$s_{j}^{\text{UL}}$ :

upper limit on the re-order point /*(set to $S_{j}$ in this study)*/

$s_{j}^{\text{LL}}$ :

lower limit on re-order point

/*(set to 0 in this study)*/

f _k :

fitness value for the kth chromosome

P _k :

probability of selecting chromosome k into the mating pool (relative fitness of the kth chromosome)

u :

a uniform random number between 0 and 1

CR:

probability of crossover or Crossover Rate (CR)

/*(set to 1 in our study)*/

MR:

probability of mutation or Mutation Rate (MR)

R _m :

merging rate used in HGA2

P _m :

merging probability used in HGA2

int_pop :

intermediate population consisting of child chromosomes or offspring that are obtained from the crossover of parent chromosomes in par_pop

res_pop :

resultant population consisting of offspring after mutation

$S_{j}^{\text{old}}$ :

base-stock at installation j before mutation

$S_{j}^{\text{new}}$ :

base-stock at installation j after mutation

$s_{j}^{\text{old}}$ :

re-order point at installation j before mutation

$s_{j}^{\text{new}}$ :

re-order point at installation j after mutation

4.2 Mechanism of the Proposed GAs

The mechanism of MGGA, HGA1, and HGA2 is same except they vary in their respective crossover operators. All other steps are common for these three GAs.

4.2.1 Representation of a Chromosome

GA is a population-based search technique that works on a population represented by several individual chromosomes (solutions). Figure 3 shows the representation of a chromosome in our study as an example. It has eight genes of which the first four genes represent base-stocks, and the next four genes represent the corresponding re-order points of the supplier, manufacturer, distributor, and retailer, respectively. Genes 1 and 5 correspond to the supplier (representing respectively its base-stock and re-order point); genes 2 and 6 correspond to the manufacturer (representing respectively base-stock and re-order point), and so on.

Fig. 3

Representation of the chromosome

4.2.2 Initialization of Population

The initial population par_pop is created by generating solutions randomly within limits with respect to base-stock and re-order point of the corresponding member. The lower limit on base-stock $S_{j}^{\text{LL}}$ for every member j is set as their minimum customer demand which is equal to 20 in our computational experiments. The upper limit on base-stock $S_{j}^{\text{UL}}$ for every member j is set as 1,000. We have fixed such a loose upper limit for base-stocks in order to test the robust performance of GAs in the large search space across all settings. The upper limit on the re-order point $s_{j}^{\text{UL}}$ is set to $S_{j}$ and the lower limit on re-order point $s_{j}^{\text{LL}}$ is set to 0 in this study. The number of chromosomes (n) generated in the initial population, pop_size, is fixed as 40 (five times the length of the chromosome). For all n chromosomes, base-stocks and re-order points are generated randomly between their respective lower and upper limits. Figure 4 shows one such generated initial population.

Fig. 4

Initialization of population

4.2.3 Evaluation and Selection of Chromosomes for Crossover

Chromosomes in par_pop are evaluated through the deterministic simulation of SC using the demands sampled from the uniform distribution [20, 60] and known apriori over T days and their respective objective function values in terms of TSCC are obtained. For the sake of generality, let us use TSCC _k corresponding to chromosome k. Fitness value f _k is computed for the kth chromosome by making use of the objective function value, i.e., set f _k  = 1/(1 + TSCC _k ). Based on f _k values, the chromosomes are selected probabilistically for placement in the mating pool for crossover operation. The selection of chromosomes for the mating pool is done by using the roulette-wheel procedure (Goldberg 1989). The probability of selecting the kth chromosome from par_pop to the mating pool, P _k (i.e., relative fitness), is obtained by computing $\left( {{{f_{k} } \mathord{\left/ {\vphantom {{f_{k} } {\sum\nolimits_{{k^{\prime} = 1}}^{n} {f_{{k^{\prime}}} } }}} \right. \kern-0pt} {\sum\nolimits_{{k^{\prime} = 1}}^{n} {f_{{k^{\prime}}} } }}} \right)$. Similarly, P _k ’s are calculated for all n chromosomes in par_pop and their respective cumulative probabilities are obtained.

4.2.4 Crossover Operators

We present three crossover operators in our GAs that employ arithmetic and gene-wise crossover operators either separately or in combination. The crossover rate CR is set to one in this study because the crossover operators are population-based crossover operators and we generate as many offspring as the number of parent chromosomes.

4.2.4.1 Modified Gene-wise Genetic Algorithm (MGGA)

The MGGA makes use of the crossover operator, called gene-wise crossover operator (see Daniel and Rajendran (2006)) that makes use of the information of genes of all the chromosomes that are present in par_pop, and builds an offspring out of those chromosomes. In their study, Daniel and Rajendran presented the superiority of the GGA to other crossover operators. We have chosen to adapt their GGA in our work (called the MGGA in our study) and the modified gene-wise crossover operator is explained with the example in Fig. 5. Assume that five chromosomes C1 to C5 are present in par_pop for the sake of illustration.

Fig. 5

An example of MGGA crossover operator and arithmetic operator with their parent population and the resultant offspring

The gene-wise crossover operator constructs a child chromosome or offspring by considering the genes of all the chromosomes on the basis of its respective fitness function values. Assume that the probabilities of selection (or relative fitness values) of chromosomes (P _k ) are 0.30, 0.25, 0.20, 0.15, and 0.10, respectively. Four uniform random numbers are generated because we need to construct one offspring with the first four genes representing the base-stocks and the next four corresponding genes representing re-order points. Let the random numbers be 0.61, 0.42, 0.93, and 0.14. Four parent chromosomes corresponding to these random numbers are selected as follows. The chromosome corresponding to u = 0.61 is chromosome C3 as seen from the cumulative probabilities of choosing chromosomes. Similarly, the chromosomes selected corresponding to the other three random numbers are chromosomes C2, C5, and C1, respectively. The offspring is now constructed gene-by-gene, by using the selected above four chromosomes in the same order. The first and fifth genes for the offspring are picked from the first selected chromosome C3, namely, {28, 10}. To construct the offspring’s second and sixth genes, the second and sixth gene positions of the second selected chromosome C2 are chosen, i.e., {66, 15}. In this way we have the resultant offspring {28, 66, 220, 245, 10, 15, 115, 125}. Thus the generated offspring inherits eight genes from the four selected chromosomes in par_pop based on their fitness values. As the base-stock and re-order point of each member have inter-relationship ($s_{j} \le \,S_{j}$), we inherit both base-stock and re-order point of a given member from the same parent into the offspring. In this way, the GGA proposed by Daniel and Rajendran (2006) is modified in our study taking into account both base-stocks and re-order points of members. The proposed gene-wise crossover operator may produce a good-quality offspring as the gene-wise crossover operator builds an offspring gene-by-gene, by making use of the fitness function values of all chromosomes in the parent population. This feature of the crossover operator leads to the generation of an offspring with proper and logical inheritance of both base-stock and re-order point from a given parent chromosome. This process is repeated until n offspring are generated.

4.2.4.2 Hybrid Genetic Algorithm 1 (HGA1)

Hybrid Genetic Algorithm 1 (HGA1) is an adapted version of the HGA proposed by Sethupathi and Rajendran (2010). In their work, Sethupathi and Rajendran employed a crossover operator using a combination of the arithmetic crossover operator and the gene-wise crossover operator to obtain the best heuristic order-up-to levels and review periods at installations. In the present work, we adapt their HGA to determine the best base-stocks and re-order points at installations. A chromosome is first obtained from the entire population by using the arithmetic crossover operator as follows. Assume that five chromosomes C1 to C5 are present in par_pop as shown in Fig. 5. Let the relative fitness values of these chromosomes be 0.30, 0.25, 0.20, 0.15, and 0.10. We make use of these values to construct the arithmetic offspring. The first gene in the offspring is constructed by an arithmetic operation (i.e., the first gene value of the first chromosome multiplied by its relative fitness plus the first gene value of the second chromosome multiplied by its relative fitness, and so on to obtain the first gene value of the offspring). For example, the value of first gene in the offspring is as follows:

$$ ( ( 2 0 0\times 0. 3 ) + (142 \times 0. 2 5 ) + (28 \times 0. 2 ) + (190 \times 0. 1 5 ) + (165 \times 0. 1 ) ) = 146 $$

Likewise, every gene in the offspring is obtained by using this arithmetic operation on respective gene values of the respective chromosomes in par_pop. This offspring is placed first in the intermediate population int_pop, and this arithmetic chromosome is shown in Fig. 5. All the other offspring are constructed by the combination of gene-wise crossover operator and arithmetic crossover operator, as shown with examples in Fig. 6. For this, we proceed as follows: First, as per the procedure of the crossover operator in the MGGA, a chromosome is constructed by using the gene-wise crossover operator; then by selecting a set of positions, the respective arithmetic gene value gets superimposed on the gene value obtained by gene-wise crossover operator. By this procedure, we can obtain different offspring by filling up a set of genes with arithmetic crossover operator and the remaining genes by gene-wise crossover operator. For example, we can fill up one couple of positions by the arithmetic crossover operator and the remaining by the gene-wise crossover operator, and we can thus construct a total of 15 offspring in int_pop by the combination of both crossover operators. The remaining 25 offspring are built by using the gene-wise crossover operator presented in the MGGA. Figure 6 shows examples of thus constructed offspring by using the crossover operations in HGA1.

Fig. 6

Examples of the constructed offspring by the hybrid genetic algorithm 1 (HGA1)

4.2.4.3 Hybrid Genetic Algorithm 2 (HGA2)

Hybrid Genetic Algorithm 2 (HGA2) employs a crossover operator which uses a combination of the arithmetic crossover operator and the gene-wise crossover operator. As in HGA1, a unique chromosome is first obtained from the entire population by using the arithmetic crossover operator (see Fig. 5). After the construction of a chromosome using the arithmetic crossover operator, the remaining chromosomes in int_pop are constructed as follows: First, a chromosome is constructed by using the gene-wise crossover operator as done in MGGA; then, every gene in this constructed chromosome is subjected to a probability of merging P _m and merging rate R _m (set as 0.25 and 0.3 respectively after a pilot study). Considering the first four genes corresponding to order quantities, one by one, a uniform random number u is generated; if u is ≤P _m, then the corresponding gene value will be altered as follows:

$$ {\text{value}}\,{\text{of}}\,{\text{new}}\,{\text{gene}} = \left( \begin{aligned} &\left( {R_{\text{m}} \times {\text{ value of the gene obtained by arithmetic crossover operator}}} \right) \hfill \\ &+ \left( {1 - R_{\text{m}} } \right) \times \left( {{\text{value of the gene obtained by gene-wi}}\text{se} {\text{ crossover operator}}} \right) \hfill \\ \end{aligned} \right) \, $$

otherwise, the old gene value constructed by the gene-wise crossover operator remains. Note that the value of the re-order point is also altered if the corresponding installation’s base-stock is altered. For example, let the chromosomes 3, 2, 5, and 1 be randomly selected in the gene-wise crossover operation, and four uniform random numbers sampled be 0.21, 0.38, 0.62, and 0.53. Gene positions 1 and 5 are altered, because the corresponding random number generated is less than or equal to P _m (i.e., 0.25). So the value of the first gene becomes $\left( {(0. 3\times 1 4 6 )+ (0. 7\times 2 8 )= 6 3} \right) \,$ and 5th gene becomes $\left( {(0. 3\times 6 7 )+ (0. 7\times 10) = 2 7} \right)$, and the remaining genes are retained as constructed by the gene-wise crossover operator. The rationale of this approach of constructing offspring is to exploit the goodness of both arithmetic and gene-wise crossover operators. Figure 7 shows an example of the mechanism of the proposed hybrid crossover operator in HGA2. This process is repeated until all the offspring are built for int_pop.

Fig. 7

An example of constructed offspring by the proposed hybrid genetic algorithm 2 (HGA2)

4.2.5 Mutation Operation

The mutation operator used in this study is a gene-wise mutation. As the chromosomes are represented in a phenotypic manner, the first four genes are subjected to mutation with a probability of MR. When a gene is subjected to mutation, the value of the gene is altered as follows:

$$ S_{j}^{\text{new}} = \left( {\hbox{min} \left\{ {\hbox{max} \left\{ {(S_{j}^{\text{old}} \times (1 - x)) + (S_{j}^{\text{old}} \times 2 \times x \times u);S_{j}^{\text{LL}} } \right\};S_{j}^{\text{UL}} } \right\}} \right) $$

(24)

where u is a sampled uniform random number and $0 < x < 1$. We set x = 0.2 (after a pilot study). At the same time, we also mutate the corresponding gene containing the re-order point for that member which is altered as follows using the same u:

$$ s_{j}^{\text{new}} = \left( {\hbox{min} \left\{ {\hbox{max} \left\{ {(s_{j}^{\text{old}} \times (1 - x)) + (s_{j}^{\text{old}} \times 2 \times x \times u);s_{j}^{\text{LL}} } \right\};S_{j}^{\text{new}} } \right\}} \right) $$

(25)

For example, consider the offspring shown in Fig. 8; let four random numbers be generated corresponding to the first four genes, and let them be 0.55, 0.46, 0.12, and 0.79, respectively. When the mutation rate (MR) is 0.2, the genes selected for mutation are the third gene and the seventh gene corresponding to this offspring. Again, a random number u is generated; let the value be 0.25. By using Equations 24 and 25, the values of third and seventh gene become 162 and 90, respectively. Here we use the same u that is sampled for mutating both base-stock and re-order point of the chosen installation so as to maintain proportionate perturbations in the base-stock and the corresponding re-order point. Figure 8 shows an example of how mutation is being carried out. As a result of mutation operation on the offspring in int_pop, we obtain the resultant pool called res_pop.

Fig. 8

Mutation operation

4.2.6 Survival of Chromosomes into the Next Generation

Now that there are n chromosomes in par_pop and n chromosomes in res_pop, we choose the best n distinct chromosomes out of these 2n chromosomes (present in par_pop and res_pop), on the basis of their TSCC values. The selected n distinct chromosomes become the parent chromosomes for the next generation. At the end of every generation, the best chromosome with the best TSCC value is subjected to a local search technique and updated.

4.2.7 Local Search Technique

We propose a local search on the best chromosome to enhance the convergence process. The best chromosome obtained at the end of Sect. 4.2.6 is removed from the population set and subjected to the following local search technique. We alter only one position randomly and with that generated neighborhood solution evaluate this setting of base-stocks and re-order points in the SC over the finite time horizon to find whether this neighborhood solution is better or worse than or same as that the seed solution. If the solution is better, the neighborhood solution replaces the seed solution; otherwise the seed chromosome is retained. For this purpose, a uniform random number u is generated between 0 and 1, and the couple of genes to be altered is decided as follows:

• if $0 \le u \le 0.25,$ then the gene-couple to be altered is 1 and 5;

• if $0.25 < u \le 0.50,$ then the gene-couple to be altered is 2 and 6;

• if $0.50 < u \le 0.75,$ then the gene-couple to be altered is 3 and 7; and

• if $0.75 < u \le \,1,$ then the gene-couple to be altered is 4 and 8.

Again, a uniform random number u is generated between 0 and 1, and by using Equations 24 and 25 (similar to the mutation process), the selected gene positions are altered. Then the resultant chromosome is evaluated. If its TSCC value has a better value than seed chromosome’s TSCC, then the seed chromosome is replaced by the generated chromosome; otherwise the same chromosome is retained. This procedure is repeated eight times (corresponding to the length of chromosome). The final chromosome thus obtained is placed in par_pop for the next generation.

4.2.8 Termination

The termination criterion is fixed in terms of number of generations. After 500 generations, the algorithm is terminated and the best chromosome at the end of termination provides the best base-stocks and re-order points for respective members in the SC which lead to the minimum TSCC of the solutions generated.

4.3 Step-By-Step Procedure of the GAs for the (s, S) Policy

• Step 1 Initialize no_gen = 0.

• Step 2 Generate the initial population with the number of chromosomes (n) equal to pop_size (5 × l), and each chromosome representing base-stocks and re-order points at N installations in the SC.

• Step 3 Evaluate every chromosome in par_pop by evaluating them over the given finite time horizon in the SC, and hence obtain the objective function TSCC.

• Step 4 Obtain the fitness value f _k for every chromosome k, selection probabilities P _k ’s and cumulative probabilities.

• Step 5 Do crossover operator as follows to obtain int_pop:

  • (a) In the MGGA, generate n offspring, by constructing each offspring directly from the chromosomes in par_pop by using the modified gene-wise crossover operator.

  • (b) In HGA1, construct one chromosome by the arithmetic crossover operator; generate (n − 1) offspring by constructing each offspring directly from the chromosomes in par_pop by using the combination of both gene-wise crossover operator and arithmetic crossover operator or using gene-wise crossover, as appropriate.

  • (c) In HGA2, construct one chromosome by the arithmetic operator; generate (n − 1) offspring, by constructing each offspring directly from the chromosomes in par_pop, with the possible combination of both gene-wise crossover operator and arithmetic crossover operator and by using the probability of merging P _m and merging rate R _m.

• Step 6 Subject n chromosomes in int_pop to gene-wise mutation, with a probability of MR.

• Step 7 Call the resultant n chromosomes as res_pop; Evaluate them with respect to TSCC, corresponding to every chromosome in res_pop.

• Step 8 From both par_pop and res_pop, select the best n distinct chromosomes (equal to pop_size), based on the value of TSCC, to form par_pop for the next generation.

• Step 9 Remove the best chromosome among par_pop.

• Step 10 Do the proposed local search eight times on the best chromosome, and update the best chromosome, if it improves through local search, place the same chromosome in par_pop for the next generation.

• Step 11 Increment no_gen = no_gen + 1;

  If no_gen is $\le$ 500, then return to Step 4; else proceed to Step 12.

• Step 12 Stop. The best solution (i.e., the best chromosome) among the chromosomes in the final par_pop and its TSCC constitute the solution to the problem.

5 Performance Analysis of (s, S) Policy Under Consideration

As mentioned earlier, this paper attempts to determine best base-stocks and re-order points with (s, S) policy in a serial SC operating with deterministic demands over a finite planning horizon and make a comparative evaluation between policies, namely, periodic-review order-up-to S policy (i.e., (T, S) policy), and (s, S) policy. As for the determination of the optimal order-up-to S policy, Sethupathi and Rajendran (2010) proposed a mathematical programming model that can be executed with T = 1200 days, a substantive long time horizon. In view of the limitation in executing the proposed mathematical programming models for (s, S) policy over such a long time horizon, we present three GAs that are not constrained by such limitations even though GAs cannot guarantee optimal solutions in the respective class of inventory order policies. We can therefore compare the optimal solution from the mathematical model for order-up-to S policy and heuristic solutions from GAs in order to have an idea about the relative evaluation of the respective order policies in a serial SC.

As for SC settings, we consider the same settings presented in Sect. 3.4, with T set to 1200 days. Before embarking on this relative evaluation of control polices, we first present the details of a pilot study involving parameter settings for the MGGA in respect of (s, S) policy. We wish to state that similar observations with respect to GA parameters in HGA1 and HGA2 have been made in the case of (s, S) policy and all these details of the pilot study are not presented here for saving space.

5.1 Parameter Settings for GAs

The crossover rate CR is set to one in this study because the crossover operators are population-based crossover operators and we generate as many offspring as the number of parent chromosomes. For fixing the MR and parameter x which are used in the mutation operator, we conduct a pilot study with the consideration of the MGGA and with lead time setting LT1. As for (MR, x), we have experimented respectively with the values of (0.1, 0.1), (0.2, 0.1), (0.1, 0.2), and (0.2, 0.2); we have chosen these values as in most experiments involving GAs, MR is usually small and we have set x not to exceed 0.2 in order to search in a limited neighborhood. The TSCC values corresponding to these parameter settings with their relative percentage deviations from the best solution among them are evaluated in a pilot study. After evaluating the four settings, we have found that the setting (MR = 0.2, x = 0.2) performs the best.

As for fixing the probability of merging P _m and merging rate R _m for the case of HGA2, we have conducted a pilot study with the values of (0.2, 0.25), (0.2, 0.3), (0.25, 0.25), and (0.25, 0.3). The reasoning of these settings are as follows: since there are four genes corresponding to the base-stocks/re-order points at four installations, the probability of altering a gene’s value (obtained by gene-wise crossover operator) is not to exceed 0.25; and the relative importance given to the gene values obtained by arithmetic crossover operator is set not to exceed one-third in relation to the gene-wise crossover operator as otherwise we may not have a diversity in the generated offspring. The TSCC values corresponding to the lead time setting LT1 with their relative percentage deviations from the best solution among them are evaluated. After evaluating the four settings, we have found that the setting (P _m = 0.25, and R _m = 0.3) performs the best.

5.2 Performance of Local Search Technique in the Search Process

We have employed a local search technique to search in the neighborhood of the best solution at the end of every generation in our GAs. The introduction of local search into the GA mechanism is seen to hasten the convergence and hence the local search technique appears effective.

5.3 Run Length Concerning the Execution of GAs

Almost all the three GAs converge within 50 generations which is the common phenomenon observed over all SC settings. However, we executed the GAs over 500 generations because the CPU time is in the order of few seconds only.

5.4 Results of Execution of GAs for (s, S) Policy

The GAs for the (s, S) policy have been executed with the consideration of various SC and lead time settings with T = 1200 days, and with two customer demand streams, namely, first demand stream (FD) and antithetic demand stream (AD). Tables 4, 5, 6, 7, 8, and 9 show the consolidated results obtained with the respective TSCC values with best base-stocks and re-order points for all members by the three GA variants, and their performance comparison. Tables 4 and 5 show the performance of the proposed GA variants with respective TSCC values, and base-stocks and re-order points in respect of lead time setting 1 (LT1) with FD and AD, respectively. Tables 6 and 7 show the performance of the GA variants with respective TSCC values, and base-stocks and re-order points in respect of lead time setting 2 (LT2) with the FD and AD demand stream, respectively. Tables 8 and 9 show the performance of the proposed GA variants with respective TSCC values, and base-stocks and re-order points in respect of lead time setting 3 (LT3) with the FD and AD demand stream, respectively.

Table 4 Performance of the different approaches, in respect of TSCC values, base-stocks and re-order points at different members with the lead time setting 1 (LT1) with the first demand stream (FD) using the (s, S) policy

Table 5 Performance of the different approaches, in respect of TSCC values, base-stocks and re-order points at different members with the lead time setting 1 (LT1) with the antithetic demand stream (AD) using the (s, S) policy

Table 6 Performance of the different approaches, in respect of TSCC values, base-stocks and re-order points at different members with the lead time setting 2 (LT2) with the first demand stream (FD) using the (s, S) policy

Table 7 Performance of the different approaches, in respect of TSCC values, base-stocks and re-order points at different members with the lead time setting 2 (LT2) with the antithetic demand stream (AD) using the (s, S) policy

Table 8 Performance of the different approaches, in respect of TSCC values, base-stocks and re-order points at different members with the lead time setting 3 (LT3) with the first demand stream (FD) using the (s, S) policy

Table 9 Performance of the different approaches, in respect of TSCC values, base-stocks and re-order points at different members with the lead time setting 3 (LT3) with the antithetic demand stream (AD) using the (s, S) policy

The relative percentage deviation for a given GA variant’s solution from the best GA solution is calculated as follows:

$$ {\text{Relative percentage deviation}} = \left( {\left\{ {{{\left( {{\text{TSCC}}_{\text{GA}} - {\text{TSCC}}_{\text{best}} } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{TSCC}}_{\text{GA}} - {\text{TSCC}}_{\text{best}} } \right)} {\left( {{\text{TSCC}}_{\text{best}} } \right)}}} \right. \kern-0pt} {\left( {{\text{TSCC}}_{\text{best}} } \right)}}} \right\} \times 100} \right) $$

(26)

where ${\text{TSCC}}_{\text{GA}}$ is the TSCC value obtained by the respective GA variant and ${\text{TSCC}}_{\text{best}}$ is the best TSCC obtained from the three GA variants for the particular cost and lead time settings. The computational time taken by GA variants are also reported in the tables. For every SC setting and lead time setting, the number of solutions enumerated by the respective GA variant to obtain the best solution is also given in the tables. The average relative percentage deviation with respect to every GA variant across all the SC setting and lead time setting are found, and reported in Table 10. From the results, we find that HGA2 performs very well with an average relative percentage of only 0.455 %, when compared with HGA1 with an average relative percentage of 1.18 %, and MGGA with an average relative percentage of 1.747 %.

Table 10 Performance of the different GA approaches in terms of their average relative percentage deviations

We find that as the ratio of $(b_{j} /h_{j} )$ increases for the given order costs at installations (e.g., CS1–CS4; CS5–CS8; CS9–CS12; CS13–CS16), re-order points mostly increase so as to increase the order frequency in order to replenish faster and hence reduce shortage costs across members in the SC. We also find that as the order costs increase across the SC for the given ratio of $(b_{j} /h_{j} )$ (e.g., see CS1, CS5, CS9, and CS13; CS2, CS6, CS10, and CS14; and so on), base stock also increases at every installation to bring down the costs of orders at installations in the SC over the finite-time horizon.

5.5 Relative Performance Evaluation of (s, S) Policy with the Order-Up-To S Policy with Periodic Review

As for the determination of the optimal base-stock policy, Sethupathi and Rajendran (2010) proposed a mathematical programming model that can be executed with time horizon T = 1200 days. We compare these optimal TSCC values in the class of order-up-to S policy (i.e., (T, S) policy) with periodic review obtained through the execution of the above model in CPlex Solver with the best TSCC values obtained through the execution of GAs for the (s, S) policy. Tables 11, 12, 13, 14, 15, and 16 show the comparison of optimal TSCC values obtained for order-up-to S policy with periodic review (Policy I) with best TSCC values obtained by GAs for (s, S) policy (Policy II) for all SC settings and their relative percentage deviations.

Table 11 Performance of inventory order policies, in respect of TSCC values, with lead time setting 1 (LT1) and with the first demand stream (FD)

Table 12 Performance of inventory order policies, in respect of TSCC values, with lead time setting 1 (LT1) and with the antithetic demand stream (AD)

Table 13 Performance of inventory order policies, in respect of TSCC values, with lead time setting 2 (LT2) and with the first demand stream (FD)

Table 14 Performance of inventory order policies, in respect of TSCC values, with lead time setting 2 (LT2) and with the antithetic demand stream (AD)

Table 15 Performance of inventory order policies, in respect of TSCC values, with lead time setting 3 (LT3) and with the first demand stream (FD)

Table 16 Performance of inventory order policies, in respect of TSCC values, with lead time setting 3 (LT3) and with the antithetic demand stream (AD)

The relative percentage deviation of a given TSCC value for an order policy is computed with respect to the best TSCC value among two order policies for given SC and LT settings.

$$ {\text{Relative percentage deviation}} = \left( {\left\{ {\left( {{\text{TSCC}}_{\begin{subarray}{l} {\text{given }} \\ {\text{policy}} \end{subarray} } - {\text{TSCC}}_{\begin{subarray}{l} {\text{best}} \\ {\text{across}} \\ {\text{two}} \\ {\text{policies }} \\ \end{subarray} } } \right) /\left( {{\text{TSCC}}_{\begin{subarray}{l} {\text{best}} \hfill \\ {\text{across}} \hfill \\ {\text{two}} \hfill \\ {\text{policies}} \hfill \\ \end{subarray} } } \right)} \right\} \times 100} \right) $$

(27)

where ${\text{TSCC}}_{\begin{subarray}{l} {\text{given }} \\ {\text{policy}} \end{subarray} }$ is the TSCC value obtained by the respective model, and ${\text{TSCC}}_{\begin{subarray}{l} {\text{best}} \hfill \\ {\text{across}} \hfill \\ {\text{two}} \hfill \\ {\text{policies}} \hfill \\ \end{subarray} }$is the best TSCC value obtained among the three models for the given cost and lead time settings. The average relative percentage deviation with respect to two policies across all SC settings and lead time settings are found, and reported in Table 17.

Table 17 Overall performance comparison of inventory order policies in respect of average relative percentage deviations of their TSCC from the best TSCC

6 Managerial Implications and Further Work of this Study

It is evident that on the whole, Policy-II, namely, the (s, S) policy emerges to be better with an average relative percentage deviation of 0.151 %, when compared with Policy-I namely, order-up-to S policy with periodic review with an average relative percentage deviation of 2.678 % over the SC settings. This finding is interesting in the sense that the (s, S) policy that capitalizes on the tight control by using the re-order point at every installation yields the least TSCC in most cases, as opposed to the periodic review system operating with order-up-to S policy. We observe that the (s, S) policy performs better than the (T, S) policy on the whole over a number of SC settings. However, at relatively larger lead times with low cost settings, we find that the (T, S) policy becomes competitive. This is because of demand aggregation over large lead times coupled with low costs lead to less sensitivity with order policy. Hence, we can resort to the (T, S) policy under these circumstances. Further work can look at comparative study involving more inventory order policies such as (R, Q) policy, which the authors are investigating using approaches and algorithms similar to the ones presented here.

7 Summary

In this paper, we have considered the (s, S) policy and developed a mathematical model to determine the optimal base-stocks and re-order points in the class of (s, S) policy in a SC operating with deterministic demands over a finite time horizon in order to minimize the sum of holding costs, shortage costs, and order costs. In view of the computational complexity associated with this policy, we have presented three GAs to obtain the best heuristic base-stocks and re-order points across members in a SC. We have carried out a relative evaluation of the periodic review order-up-to S policy ((T, S) policy) and (s, S) policy by considering many SC costs and lead time settings. We have found that the (s, S) policy performs mostly better, in comparison to the periodic review order-up-to S policy.