Abstract
The chapter begins with the axiomatic construction of the probability space in the general case where the number of outcomes of an experiment is not necessarily countable. The concepts of algebra and sigma-algebra of sets are introduced and discussed in detail. Then the axioms of probability and, more generally, measure are presented and illustrated by several fundamental examples of measure spaces. The idea of extension of a measure is discussed, basing on the Carathéodory theorem (of which the proof is given in Appendix 1). Then the general elementary properties of probability are discussed in detail in Sect. 2.2. Conditional probability given an event is introduced along with the concept of independence in Sect. 2.3. The chapter concludes with Sect. 2.4 presenting the total probability formula and the Bayes formula, the former illustrated by an example leading to the introduction of the Poisson process.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
- Total Probability Formula
- Elementary General Properties
- Bernoulli Scheme
- Discrete Measurable Spaces
- Nonnegative Countably Additive Measure
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
2.1 The Axioms of Probability Theory. A Probability Space
So far we have been considering problems in which the set of outcomes had at most countably many elements. In such a case we defined the probability P(A) using the probabilities P(ω) of elementary outcomes ω. It proved to be a function defined on all the subsets A of the space Ω of elementary events having the following properties:
-
(1)
P(A)≥0.
-
(2)
P(Ω)=1.
-
(3)
For disjoint events A 1,A 2,…
$$\mathbf{P} \Bigl(\,\bigcup A_j \Bigr)=\sum \mathbf{P}(A_j ). $$
However, as we have already noted, one can easily imagine a problem in which the set of all outcomes is uncountable. For example, choosing a point at random from the segment [t 1,t 2] (say, in an experiment involving measurement of temperature) has a continuum of outcomes, for any point of the segment could be the result of the experiment. While in experiments with finite or countable sets of outcomes any collection of outcomes was an event, this is not the case in this example. We will encounter serious difficulties if we treat any subset of the segment as an event. Here one needs to select a special class of subsets which will be treated as events.
Let the space of elementary events Ω be an arbitrary set, and  be a system of subsets of Ω.
be a system of subsets of Ω.
Definition 2.1.1
 is called an algebra if the following conditions are met:
is called an algebra if the following conditions are met:
- A1.:
-
 .
. - A2.:
-
If
 and
and
 , then
, then

- A3.:
-
If
 then
then
 .
.
It is not hard to see that in condition A2 it suffices to require that only one of the given relations holds. The second relation will be satisfied automatically since
An algebra  is sometimes called a ring since there are two operations defined on
is sometimes called a ring since there are two operations defined on  (addition and multiplication) which do not lead outside of
(addition and multiplication) which do not lead outside of  . An algebra
. An algebra  is a ring with identity, for
is a ring with identity, for  and AΩ=ΩA=A for any
and AΩ=ΩA=A for any  .
.
Definition 2.1.2
A class of sets \(\mathfrak{F}\) is called a sigma-algebra (σ-algebra, or σ-ring, or Borel field of events) if property A2 is satisfied for any sequences of sets:
- A2′.:
-
If {A n } is a sequence of sets from \(\mathfrak{F}\), then
$$\bigcup_{n=1}^{\infty} A_n \in \mathfrak{F},\qquad\bigcap_{n=1}^{\infty} A_n \in\mathfrak{F}. $$
Here, as was the case for A2, it suffices to require that only one of the two relations be satisfied. The second relation will follow from the equality
Thus an algebra is a class of sets which is closed under a finite number of operations of taking complements, unions and intersections; a σ-algebra is a class of sets which is closed under a countable number of such operations.
Given a set Ω and an algebra or σ-algebra \(\mathfrak{F}\) of its subsets, one says that we are given a measurable space \(\langle\varOmega,\mathfrak{F}\rangle\).
For the segment [0,1], all the sets consisting of a finite number of segments or intervals form an algebra, but not a σ-algebra.
Consider all the σ-algebras on [0,1] containing all intervals from that segment (there is at least one such σ-algebra, for the collection of all the subsets of a given set clearly forms a σ-algebra). It is easy to see that the intersection of all such σ-algebras (i.e. the collection of all the sets which belong simultaneously to all the σ-algebras) is again a σ-algebra. It is the smallest σ-algebra containing all intervals and is called the Borel σ-algebra. Roughly speaking, the Borel σ-algebra could be thought of as the collection of sets obtained from intervals by taking countably many unions, intersections and complements. This is a rather rich class of sets which is certainly sufficient for any practical purposes. The elements of the Borel σ-algebra are called Borel sets. Everything we have said in this paragraph equally applies to systems of subsets of the whole real line.
Along with the intervals (a,b), the one-point sets {a} and sets of the form (a,b], [a,b] and [a,b) (in which a and b can take infinite values) are also Borel sets. This assertion follows, for example, from the representations of the form
Thus all countable sets and countable unions of intervals and segments are also Borel sets.
For a given class  of subsets of Ω, one can again consider the intersection of all σ-algebras containing
of subsets of Ω, one can again consider the intersection of all σ-algebras containing  and obtain in this way the smallest
σ-algebra containing
and obtain in this way the smallest
σ-algebra containing  .
.
Definition 2.1.3
The smallest σ-algebra containing  is called the σ-algebra generated by
is called the σ-algebra generated by
 and is denoted by
and is denoted by  .
.
In this terminology, the Borel σ-algebra in the n-dimensional Euclidean space \(\mathbb{R}^{n}\) is the σ-algebra generated by rectangles or balls. If Ω is countable, then the σ-algebra generated by the elements ω∈Ω clearly coincides with the σ-algebra of all subsets of Ω.
As an exercise, we suggest the reader to describe the algebra and the σ-algebra of sets in Ω=[0,1] generated by: (a) the intervals (0,1/3) and (1/3,1); (b) the semi-open intervals (a,1], 0<a<1; and (c) individual points.
To formalise a probabilistic problem, one has to find an appropriate measurable space \(\langle\varOmega,\mathfrak{F}\rangle\) for the corresponding experiment. The symbol Ω denotes the set of elementary outcomes of the experiment, while the algebra or σ-algebra \(\mathfrak{F}\) specifies a class of events. All the remaining subsets of Ω which are not elements of \(\mathfrak{F}\)
are not events. Rather often it is convenient to define the class of events \(\mathfrak{F}\) as the σ-algebra generated by a certain algebra  .
.
Selecting a specific algebra or σ-algebra \(\mathfrak{F}\) depends, on the one hand, on the nature of the problem in question and, on the other hand, on that of the set Ω. As we will see, one cannot always define probability in such a way that it would make sense for any subset of Ω.
We have already noted in Chap. 1 that, in probability theory, one uses, along with the usual set theory terminology, a somewhat different terminology related to the fact that the subsets of Ω (belonging to \(\mathfrak{F}\)) are interpreted as events. The set Ω itself is often called the certain event. By axioms A1 and A2, the empty set ∅ also belongs to \(\mathfrak{F}\); it is called the impossible event. The event \(\overline{A}\) is called the complement event or simply the complement of A. If A∩B=∅, then the events A and B are called mutually exclusive or disjoint.
Now it remains to introduce the notion of probability. Consider a space Ω and a system  of its subsets which forms an algebra of events.
of its subsets which forms an algebra of events.
Definition 2.1.4
A probability on  is a real-valued function defined on the sets from
is a real-valued function defined on the sets from  and having the following properties:
and having the following properties:
-
P1.
P(A)≥0 for any
 .
. -
P2.
P(Ω)=1.
-
P3.
If a sequence of events {A n } is such that A i A j =∅ for i≠j and
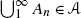 , then $$ \mathbf{P} \Biggl(\, \bigcup_{n=1}^{\infty} A_n \Biggr) =\sum_{n=1}^{\infty} \mathbf{P}(A_n). $$(2.1.1)
, then $$ \mathbf{P} \Biggl(\, \bigcup_{n=1}^{\infty} A_n \Biggr) =\sum_{n=1}^{\infty} \mathbf{P}(A_n). $$(2.1.1)
These properties can be considered as an axiomatic definition of probability.
An equivalent to axiom P3 is the requirement of additivity (2.1.1) for finite collections of events A j plus the following continuity axiom.
- P3′.:
-
Let {B n } be a sequence of events such that B n+1⊂B n and
 . Then
P(B
n
)→P(B) as
n→∞.
. Then
P(B
n
)→P(B) as
n→∞.
Proof of the equivalence
Assume P3 is satisfied and let B
n+1⊂B
n
,  . Then the sequence of the events B, \(C_{k} =B_{k} \overline{B}_{k+1}\), k=1,2,…, consists of disjoint events and \(B_{n} =B+\bigcup_{k=n}^{\infty} C_{k}\) for any n. Now making use of property P3 we see that the series \(\mathbf {P}(B_{1})=\mathbf{P} (B)+\sum_{k=n}^{\infty} \mathbf{P}(C_{k})\) is convergent, which means that
. Then the sequence of the events B, \(C_{k} =B_{k} \overline{B}_{k+1}\), k=1,2,…, consists of disjoint events and \(B_{n} =B+\bigcup_{k=n}^{\infty} C_{k}\) for any n. Now making use of property P3 we see that the series \(\mathbf {P}(B_{1})=\mathbf{P} (B)+\sum_{k=n}^{\infty} \mathbf{P}(C_{k})\) is convergent, which means that
as n→∞. This is just the property P3′.
Conversely, if A n is a sequence of disjoint events, then
and one has
The last equality follows from P3′. □
Definition 2.1.5
A triple  is called a wide-sense probability space. If an algebra \(\mathfrak{F}\) is a σ-algebra (\(\mathfrak {F}=\sigma(\mathfrak{F})\)), then condition \(\bigcup_{n=1}^{\infty} A_{n} \in\mathfrak{F}\) in axiom P3 (for a probability on \(\langle\varOmega,\mathfrak{F}\rangle\)) will be automatically satisfied.
is called a wide-sense probability space. If an algebra \(\mathfrak{F}\) is a σ-algebra (\(\mathfrak {F}=\sigma(\mathfrak{F})\)), then condition \(\bigcup_{n=1}^{\infty} A_{n} \in\mathfrak{F}\) in axiom P3 (for a probability on \(\langle\varOmega,\mathfrak{F}\rangle\)) will be automatically satisfied.
Definition 2.1.6
A triple \(\langle\varOmega,\mathfrak {F},\mathbf{P}\rangle\), where \(\mathfrak{F}\) is a σ-algebra, is called a probability space.
A probability P on \(\langle\varOmega,\mathfrak{F}\rangle\) is also sometimes called a probability distribution on Ω or just a distribution on Ω (on \(\langle\varOmega,\mathfrak{F}\rangle\)).
Thus defining a probability space means defining a countably additive nonnegative measure on a measurable space such that the measure of Ω is equal to one. In this form the axiomatics of Probability Theory was formulated by A.N. Kolmogorov. The system of axioms we introduced is incomplete and consistent.
Constructing a probability space \(\langle\varOmega,\mathfrak{F},\mathbf {P}\rangle\) is the basic stage in creating a mathematical model (formalisation) of an experiment.
Discussions on what should one understand by probability have a long history and are related to the desire to connect the definition of probability with its “physical” nature. However, because of the complexity of the latter, such attempts have always encountered difficulties not only of mathematical, but also of philosophical character (see the Introduction). The most important stages in this discussion are related to the names of Borel, von Mises, Bernstein and Kolmogorov. The emergence of Kolmogorov’s axiomatics separated, in a sense, the mathematical aspect of the problem from all the rest. With this approach, the “physical interpretation” of the notion of probability appears in the form of a theorem (the strong law of large numbers, see Chaps. 5 and 7), by virtue of which the relative frequency of the occurrence of a certain event in an increasingly long series of independent trials approaches (in a strictly defined sense) the probability of this event.
We now consider examples of the most commonly used measurable and probability spaces.
1. Discrete measurable spaces. These are spaces \(\langle\varOmega, \mathfrak{F} \rangle\) where Ω is a finite or countably infinite collection of elements, and the σ-algebra \(\mathfrak {F}\) usually consists of all the subsets of Ω. Discrete probability spaces constructed on discrete measurable spaces were studied, with concrete examples, in Chap. 1.
2. The measurable space \(\langle\mathbb{R} ,\mathfrak {B}\rangle\), where \(\mathbb{R}\) is the real line (or a part of it) and \(\mathfrak{B}\) is the σ-algebra of Borel sets. The necessity of considering such spaces arises in situations where the results of observations of interest may assume any values in \(\mathbb{R}\).
Example 2.1.1
Consider an experiment consisting of choosing a point “at random” from the interval [0,1]. By this we will understand the following. The set of elementary outcomes Ω is the interval [0,1]. The σ-algebra \(\mathfrak{F}\) will be taken to be the class of subsets B for which the notion of length (Lebesgue measure) μ(B) is defined—for example, the σ-algebra \(\mathfrak{B}\) of Borel measurable sets. To “conduct a trial” means to choose a point ω∈Ω=[0,1], the probability of the event ω∈B being μ(B). All the axioms are clearly satisfied for the probability space \(\langle[0,1],\mathfrak{B},\mu \rangle\). We obtain the so-called uniform distribution on [0,1].
Why did we take the σ-algebra of Borel sets \(\mathfrak{B}\) to be our \(\mathfrak{F}\) in this example? If we considered on Ω=[0,1] the σ-algebra generated by “individual” points of the interval, we would get the sets of which the Lebesgue measure is either 0 or 1. In other words, the obtained sets would be either very “dense” or very “thin” (countable), so that the intervals (a,b) for 0<b−a<1 do not belong to this σ-algebra.
On the other hand, if we considered on Ω=[0,1] the σ-algebra of all subsets of Ω, it would be impossible to define a probability measure on it in such a way that P([a,b])=b−a (i.e. to get the uniform distribution).Footnote 1
Turning back to the uniform distribution P on Ω=[0,1], it is easy to see that it is impossible to define this distribution using the same approach as we used to define a probability on a discrete space of elementary events (i.e. by defining the probabilities of elementary outcomes ω). Since in this example the ωs are individual points from [0,1], we clearly have P(ω)=0 for any ω.
3. The measurable space \(\langle\mathbb{R}^{n} ,\mathfrak{B}^{n} \rangle\) is used in the cases when observations are vectors. Here \(\mathbb{R}^{n}\) is the n-dimensional Euclidean space (\(\mathbb{R}^{n} =\mathbb{R}_{1}\times\cdots\times\mathbb{R}^{n} \), where \(\mathbb{R}_{1} ,\ldots,\mathbb{R}_{n}\) are n copies of the real line), \(\mathfrak{B}^{n}\) is the σ-algebra of Borel sets in \(\mathbb{R}^{n}\), i.e. the σ-algebra generated by the sets B=B 1×⋯×B n, where \(B_{i} \subset \mathbb{R}_{i}\) are Borel sets on the line. Instead of \(\mathbb{R}^{n}\) we could also consider some measurable part \(\varOmega\in\mathfrak{B}^{n}\) (for example a cube or ball), and instead of \(\mathfrak{B}^{n}\) the restriction of \(\mathfrak{B}^{n}\) onto Ω. Thus, similarly to the last example one can construct a probability space for choosing a point at random from the cube Ω=[0,1]n. We put here P(ω∈B)=μ(B), where μ(B) is the Lebesgue measure (volume) of the set B. Instead of the cube [0,1]n we could consider any other cube, for example [a,b]n, but in this case we would have to put
This is the uniform distribution on a cube.
In Probability Theory one also needs to deal with more complex probability spaces. What to do if the result of the experiment is an infinite random sequence? In this case the space \(\langle \mathbb{R}^{\infty} ,\mathfrak{B}^{\infty} \rangle\) is often the most appropriate one.
4. The measurable space \(\langle\mathbb{R}^{\infty} ,\mathfrak{B} ^{\infty} \rangle\), where
is the space of all sequences (x 1,x 2,…) (the direct product of the spaces \(\mathbb{R}_{j}\)), and \(\mathfrak{B}^{\infty}\) the σ-algebra generated by the sets of the form

for any N,j 1,…,j N , where \(\mathfrak{B}_{j}\) is the σ-algebra of Borel sets from \(\mathbb{R}_{j}\).
5. If an experiment results, say, in a continuous function on the interval [a,b] (a trajectory of a moving particle, a cardiogram of a patient, etc.), then the probability spaces considered above turn out to be inappropriate. In such a case one should take Ω to be the space C(a,b) of all continuous functions on [a,b] or the space \(\mathbb{R}^{[a,b]}\) of all functions on [a,b]. The problem of choosing a suitable σ-algebra here becomes somewhat more complicated and we will discuss it later in Chap. 18.
Now let us return to the definition of a probability space.
Let a triple  be a wide-sense probability space (
be a wide-sense probability space ( is an algebra). As we have already seen, to each algebra
is an algebra). As we have already seen, to each algebra  there corresponds a σ-algebra
there corresponds a σ-algebra  generated by
generated by  . The following question is of substantial interest: does the probability measure P on
. The following question is of substantial interest: does the probability measure P on  define a measure on
define a measure on  ? And if so, does it define it in a unique way? In other words, to construct a probability space
? And if so, does it define it in a unique way? In other words, to construct a probability space  , is it sufficient to define the probability just on some algebra
, is it sufficient to define the probability just on some algebra  generating \(\mathfrak {F}\) (i.e. to construct a wide-sense probability space
generating \(\mathfrak {F}\) (i.e. to construct a wide-sense probability space  , where
, where  )? An answer to this important question is given by the Carathéodory theorem.
)? An answer to this important question is given by the Carathéodory theorem.
The measure extension theorem
Let
 be a wide-sense probability space. Then there exists a unique probability measure
Q
defined on
be a wide-sense probability space. Then there exists a unique probability measure
Q
defined on
 such that
such that

Corollary 2.1.1
Any wide-sense probability space
 automatically defines a probability space
\(\langle\varOmega,\mathfrak{F},\mathbf {P}\rangle\)
with
automatically defines a probability space
\(\langle\varOmega,\mathfrak{F},\mathbf {P}\rangle\)
with
 .
.
We will make extensive use of this fact in what follows. In particular, it implies that to define a probability measure on the measurable space \(\langle\mathbb{R},\mathfrak{B}\rangle\), it suffices to define the probability on intervals.
The proof of the Carathéodory theorem is given in Appendix 1.
In conclusion of this section we will make a general comment. Mathematics differs qualitatively from such sciences as physics, chemistry, etc. in that it does not always base its conclusions on empirical data with the help of which a naturalist tries to answer his questions. Mathematics develops in the framework of an initial construction or system of axioms with which one describes an object under study. Thus mathematics and, in particular, Probability Theory, studies the nature of the phenomena around us in a methodologically different way: one studies not the phenomena themselves, but rather the models of these phenomena that have been created based on human experience. The value of a particular model is determined by the agreement of the conclusions of the theory with our observations and therefore depends on the choice of the axioms characterising the object.
In this sense axioms P1, P2, and the additivity of probability look indisputable and natural (see the remarks in the Introduction on desirable properties of probability). Countable additivity of probability and the property A2′ of σ-algebras are more delicate and less easy to intuit (as incidentally are a lot of other things related to the notion of infinity). Introducing the last two properties was essentially brought about by the possibility of constructing a meaningful mathematical theory. Numerous applications of Probability Theory developed from the system of axioms formulated in the present section demonstrate its high efficiency and purposefulness.
2.2 Properties of Probability
1. P(∅)=0. This follows from the equality ∅+Ω=Ω and properties P2 and P3 of probability.
2. \(\mathbf{P}(\overline{A})=1-\mathbf{P}(A)\), since \(A+\overline{A} =\varOmega\) and \(A \cap{\overline{A}}=\varnothing\).
3. If A⊂B, then P(A)≤P(B). This follows from the relation \(\mathbf{P}(A)+ \mathbf{P}(\overline{A} B)=\mathbf{P}(B)\).
4. P(A)≤1 (by properties 3 and P2).
5. P(A∪B)=P(A)+P(B)−P(AB), since A∪B=A+(B−AB) and P(B−AB)=P(B)−P(AB).
6. P(A∪B)≤P(A)+P(B) follows from the previous property.
7. The formula
has already been proved and used for discrete spaces Ω. Here the reader can prove it in exactly the same way, using induction and property 5.
Denote the sums on the right hand side of the last formula by Z 1, Z 2,…,Z n , respectively. Then statement 7 for the event \(B_{n}=\bigcup_{j=1}^{n}A_{j}\) can be rewritten as \(\mathbf{P}(B_{n})= \sum_{j=1}^{n} (-1)^{j-1} Z_{j}\).
8. An important addition to property 7 is that the sequence \(\sum_{j=1}^{k} (-1)^{j-1} Z_{j}\) approximates P(B n ) by turns from above and from below as k grows, i.e.

This property can also be proved by induction on n. For n=2 this property is ascertained in 5. Let (2.2.1) be valid for any events A 1,…,A n−1 (i.e. for any B n−1). Then by 5 we have
where, in view of (2.2.1) for k=1,
Hence, for B n =B n−1∪A n , we get
This proves (2.2.1) for k=1. For k=2,3,… the proof is similar.
9. If A n is a monotonically increasing sequence of sets (i.e. A n ⊂A n+1) and \(A= \bigcup_{n=1}^{\infty} A_{n}\), then
This is a different form of the continuity axiom equivalent to P3′.
Indeed, introducing the sets B n =A−A n , we get B n+1⊂B n and \(\bigcap_{n=1}^{\infty} B_{n}=\varnothing\). Therefore, by the continuity axiom,
as n→∞. The converse assertion that (2.2.2) implies the continuity axiom can be obtained in a similar way. □
2.3 Conditional Probability. Independence of Events and Trials
We will start with examples. Let an experiment consist of three tosses of a fair coin. The probability that heads shows up only once, i.e. that one of the elementary events htt, tht, or tth occurs, is equal in the classical scheme to 3/8. Denote this event by A. Now assume that we know in addition that the event B={the number of heads is odd} has occurred.
What is the probability of the event A given this additional information? The event B consists of four elementary outcomes. The event A is constituted by three outcomes from the event B. In the framework of the classical scheme, it is natural to define the new probability of the event A to be 3/4.
Consider a more general example. Let a classical scheme with n outcomes be given. An event A consists of r outcomes, an event B of m outcomes, and let the event AB have k outcomes. Similarly to the previous example, it is natural to define the probability of the event A given the event B has occurred as
The ratio is equal to P(AB)/P(B), for
Now we can give a general definition.
Definition 2.3.1
Let \(\langle\varOmega,\mathfrak {F},\mathbf{P}\rangle\) be a probability space and A and B be arbitrary events. If P(B)>0, the conditional probability of the event A given B has occurred is denoted by P(A|B) and is defined by
Definition 2.3.2
Events A and B are called independent if
Below we list several properties of independent events.
1. If P(B)>0, then the independence of A and B is equivalent to the equality
The proof is obvious.
2. If A and B are independent, then \(\overline{A}\) and B are also independent.
Indeed,
3. Let the events A and B 1 and the events A and B 2 each be independent, and assume B 1 B 2=∅. Then the events A and B 1+B 2 are independent.
The property is proved by the following chain of equalities:
As we will see below, the requirement B 1 B 2=∅ is essential here.
Example 2.3.1
Let event A mean that heads shows up in the first of two tosses of a fair coin, and event B that tails shows up in the second toss. The probability of each of these events is 1/2. The probability of the intersection AB is
Therefore the events A and B are independent.
Example 2.3.2
Consider the uniform distribution on the square [0,1]2 (see Sect. 2.1). Let A be the event that a point chosen at random is in the region on the right of an abscissa a and B the event that the point is in the region above an ordinate b.
Both regions are hatched in Fig. 2.1. The event AB is squared in the figure. Clearly, P(AB)=P(A)P(B), and hence the events A and B are independent.
It is also easy to verify that if B is the event that the chosen point is inside the triangle FCD (see Fig. 2.1), then the events A and B will already be dependent.
Definition 2.3.3
Events B 1,B 2,…,B n are jointly independent if, for any 1≤i 1<i 2<⋯<i r ≤n, r=2,3,…,n,
Pairwise independence is not sufficient for joint independence of n events, as one can see from the following example.
Example 2.3.3
(Bernstein’s example)
Consider the following experiment. We roll a symmetric tetrahedron of which three faces are painted red, blue and green respectively, and the fourth is painted in all three colours. Event R means that when the tetrahedron stops, the bottom face has the red colour on it, event B that it has the blue colour, and G the green. Since each of the three colours is present on two faces, P(R)=P(B)=P(G)=1/2. For any two of the introduced events, the probability of the intersection is 1/4, since any two colours are present on one face only. Since \(\frac{1}{4}=\frac{1}{2}\times\frac{1}{2}\), this implies the pairwise independence of all three events. However,
Now it is easy to construct an example in which property 3 of independent events does not hold when B 1 B 2≠∅.
An example of a sequence of jointly independent events is given by the series of outcomes of trials in the Bernoulli scheme.
If we assume that each outcome was obtained as a result of a separate trial, then we will find that any event related to a fixed trial will be independent of any event related to other trials. In such cases one speaks of a sequence of independent trials.
To give a general definition, consider two arbitrary experiments G 1 and G 2 and denote by \(\langle\varOmega_{1} ,\mathfrak{F}_{1} ,\mathbf {P}_{1} \rangle\) and \(\langle\varOmega_{2} ,\mathfrak{F}_{2} ,\mathbf{P}_{2} \rangle\) the respective probability spaces. Consider also the “compound” experiment G with the probability space \(\langle\varOmega,\mathfrak{F},\mathbf{P}\rangle\), where Ω=Ω 1×Ω 2 is the direct product of the spaces Ω 1 and Ω 2, and the σ-algebra \(\mathfrak{F}\) is generated by the direct product \(\mathfrak{F}_{1}\times\mathfrak {F}_{2}\) (i.e. by the events B=B 1×B 2, \(B_{1}\in\mathfrak{F}_{1}\), \(B_{2}\in\mathfrak{F}_{2}\)).
Definition 2.3.4
We will say that the trials G 1 and G 2 are independent if, for any B=B 1×B 2, \(B_{1}\in\mathfrak{F}_{1}\), \(B_{2}\in\mathfrak{F}_{2}\) one has
Independence of n trials G 1,…,G n is defined in a similar way, using the equality
where B=B 1×⋯×B n , \(B_{k} \in\mathfrak{F}_{k}\), and \(\langle\varOmega_{k} ,\mathfrak{F}_{k} ,\mathbf{P}_{k} \rangle\) is the probability space corresponding to the experiment G k , k=1,…,n.
In the Bernoulli scheme, the probability of any sequence of outcomes consisting of r zeros and ones and containing k ones is equal to p k(1−p)r−k. Therefore the Bernoulli scheme may be considered as a result of r independent trials in each of which one has 1 (success) with probability p and 0 (failure) with probability 1−p. Thus, the probability of k successes in r independent trials equals \({r\choose k}p^{k} (1-p)^{r-k}\).
The following assertion, which is in a sense converse to the last one, is also true: any sequence of identical independent trials with two outcomes makes up a Bernoulli scheme.
In Chap. 3 several remarks will be given on the relationship between the notions of independence we introduced here and the common notion of causality.
2.4 The Total Probability Formula. The Bayes Formula
Let A be an event and B 1,B 2,…,B n be mutually exclusive events having positive probabilities such that
The sequence of events B 1,B 2,… can be infinite, in which case we put n=∞. The following total probability formula holds true:
Proof
It follows from the assumptions that
Moreover, the events AB 1, AB 2,…,AB n are disjoint, and hence
□
Example 2.4.1
In experiments with colliding electron-positron beams, the probability that during a time unit there will occur j collisions leading to the birth of new elementary particles is equal to
where λ is a positive parameter (this is the so-called Poisson distribution, to be considered in more detail in Chaps. 3, 5 and 19). In each collision, different groups of elementary particles can appear as a result of the interaction, and the probability of each group is fixed and does not depend on the outcomes of other collisions. Consider one such group, consisting of two μ-mesons, and denote by p the probability of its appearance in a collision. What is the probability of the event A k that, during a time unit, k pairs of μ-mesons will be born?
Assume that the event B j that there were j collisions during the time unit has occurred. Given this condition, we will have a sequence of j independent trials, and the probability of having k pairs of μ-mesons will be \({j\choose k}p^{k} (1-p)^{j-k}\). Therefore by the total probability formula,
Thus we again obtain a Poisson distribution, but this time with parameter λp.
The solution above was not formalised. A formal solution would first of all require the construction of a probability space. The space turns out to be rather complex in this example. Denote by Ω j the space of elementary outcomes in the Bernoulli scheme corresponding to j trials, and let ω j denote an element of Ω j . Then one could take Ω to be the collection of all pairs \(\{(j,\omega_{j}) \}^{\infty}_{j=0}\), where the number j indicates the number of collisions, and ω j is a sequence of “successes” and “failures” of length j (“success” stands for the birth of two μ-mesons). If ω j contains k “successes”, one has to put
To get P(A k ), it remains to sum up these probabilities over all ω j containing k successes and all j≥k (the idea of the total probability formula is used here tacitly when splitting A k into the events (j,ω j )).
The fact that the number of collisions is described here by a Poisson distribution could be understood from the following circumstances related to the nature of the physical process. Let B j (t,u) be the event that there were j collisions during the time interval [t,t+u). Then it turns out that:
-
(a)
the pairs of events B j (v,t) and B k (v+t,u) related to non-overlapping time intervals are independent for all v,t,u,j, and k;
-
(b)
for small Δ the probability of a collision during the time Δ is proportional to Δ:
$$\mathbf{P}\bigl(B_1(t,\varDelta )\bigr)=\lambda \varDelta +o(\varDelta ), $$and, moreover, P(B k (t,Δ))=o(Δ) for k≥2.
Again using the total probability formula with the hypotheses B j (v,t), we obtain for the probabilities p k (t)=P(B k (v,t)) the following relations:

Transforming the last equation, we find that
Therefore the derivative of p 0 exists and is given by
In a similar way we establish the existence of
Now note that since the functions p k (t) are continuous, one should put p 0(0)=1, p k (0)=0 for k≥1. Hence
Using induction and substituting into (2.4.1) the function \(p_{k-1}(t)=\frac{(\lambda t)^{k-1}e^{-\lambda t}}{(k-1)!}\), we establish (it is convenient to make the substitution p k =e −λt u k , which turns (2.4.1) into \(u'_{k}=\frac{\lambda(\lambda t)^{k-1}}{(k-1)!}\)) that
This is the Poisson distribution with parameter λt.
To understand the construction of the probability space in this problem, one should consider the set Ω of all non-decreasing step-functions x(t)≥0, t≥0, taking values 0,1,2,…. Any such function can play the role of an elementary outcome: its jump points indicate the collision times, the value x(t) itself will be the number of collisions during the time interval (0,t). To avoid a tedious argument related to introducing an appropriate σ-algebra, for the purposes of our computations we could treat the probability as given on the algebra
 (see Sect. 2.1) generated by the sets {x(t)=k}, t≥0; k=0,1,… (note that all the events considered in this problem are just of such form). The above argument shows that one has to put
(see Sect. 2.1) generated by the sets {x(t)=k}, t≥0; k=0,1,… (note that all the events considered in this problem are just of such form). The above argument shows that one has to put
(See also the treatment of Poisson processes in Chap. 19.) □
By these examples we would like not only to illustrate the application of the total probability formula, but also to show that the construction of probability spaces in real problems is not always a simple task.
Of course, for each particular problem, such constructions are by no means necessary, but we would recommend to carry them out until one acquires sufficient experience.
Assume that events A and B 1,…,B n satisfy the conditions stated at the beginning of this section. If P(A)>0, then under these conditions the following Bayes’ formula holds true:
This formula is simply an alternative way of writing the equality
where in the numerator one should make use of the definition of conditional probability, and in the denominator, the total probability formula. In Bayes’ formula we can take n=∞, just as for the total probability formula.
Example 2.4.2
An item is manufactured by two factories. The production volume of the first factory is k times the production of the second one. The proportion of defective items for the first factory is P 1, and for the second one P 2. Now assume that the items manufactured by the factories during a certain time interval were mixed up and then sent to retailers. What is the probability that you have purchased an item produced by the second factory given the item proved to be defective?
Let B 1 be the event that the item you have got came from the first factory, and B 2 from the second. It easy to see that
These are the so-called prior probabilities of the events B 1 and B 2. Let A be the event that the purchased item is defective. We are given conditional probabilities P(A|B 1)=P 1 and P(A|B 2)=P 2. Now, using Bayes’ formula, we can answer the posed question:
Similarly, \(\mathbf{P}(B_{1} | A)= \frac{P_{1}}{P_{1} +kP_{2}}\). □
The probabilities P(B 1| A) and P(B 2| A) are sometimes called posterior probabilities of the events B 1 and B 2 respectively, after the event A has occurred.
Example 2.4.3
A student is suggested to solve a numerical problem. The answer to the problem is known to be one of the numbers 1,…,k. Solving the problem, the student can either find the correct way of reasoning or err. The training of the student is such that he finds a correct way of solving the problem with probability p. In that case the answer he finds coincides with the right one. With the complementary probability 1−p the student makes an error. In that case we will assume that the student can give as an answer any of the numbers 1,…,k with equal probabilities 1/k.
We know that the student gave a correct answer. What is the probability that his solution of the problem was correct?
Let B 1 (B 2) be the event that the student’s solution was correct (wrong). Then, by our assumptions, the prior probabilities of these events are P(B 1)=p, P(B 2)=1−p. If the event A means that the student got a correct answer, then
By Bayes’ formula the desired posterior probability P(B 1| A) is equal to
Clearly, P(B 1|A)>P(B 1)=p and P(B 1|A) is close to 1 for large k.
Notes
- 1.
See e.g. [28], p. 80.
References
Natanson, I.P.: Theory of Functions of a Real Variable. Ungar, New York (1961)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag London
About this chapter
Cite this chapter
Borovkov, A.A. (2013). An Arbitrary Space of Elementary Events. In: Probability Theory. Universitext. Springer, London. https://doi.org/10.1007/978-1-4471-5201-9_2
Download citation
DOI: https://doi.org/10.1007/978-1-4471-5201-9_2
Publisher Name: Springer, London
Print ISBN: 978-1-4471-5200-2
Online ISBN: 978-1-4471-5201-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 .
. and
and
 , then
, then

 then
then
 .
. .
.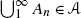 , then
, then  . Then
P(B
n
)→P(B) as
n→∞.
. Then
P(B
n
)→P(B) as
n→∞.