The Thermodynamic and Kinetic Aspects of Power Ultrasound Processes

Abstract

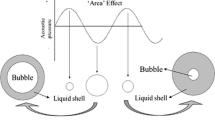
Most high intensity or power ultrasound applications involve a special transmission mode of sound waves in a medium that is composed of consecutive compressions and rarefactions. Since the propagation of such longitudinal waves is normally associated with a liquid medium, the use of power ultrasound is often termed as sonication. When the negative pressure in the rarefaction phase surpasses the tensile stress of the liquid, the liquid will be torn apart and cavities will be formed (Leighton, 1994). The inception of cavitation and the subsequent mechanical and chemical effects rising from the cavitation activity enable interactions between the acoustic energy and food and biological systems being processed. Such interactions take place at microscopic levels as the average diameters of cavitation bubbles are at 150–170 μm, for bubbles generated in water by 20 kHz ultrasound transducers (Awad, 1996; Vago, 1992).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

4.1 Introduction

Most high intensity or power ultrasound applications involve a special transmission mode of sound waves in a medium that is composed of consecutive compressions and rarefactions. Since the propagation of such longitudinal waves is normally associated with a liquid medium, the use of power ultrasound is often termed as sonication. When the negative pressure in the rarefaction phase surpasses the tensile stress of the liquid, the liquid will be torn apart and cavities will be formed (Leighton, 1994). The inception of cavitation and the subsequent mechanical and chemical effects rising from the cavitation activity enable interactions between the acoustic energy and food and biological systems being processed. Such interactions take place at microscopic levels as the average diameters of cavitation bubbles are at 150–170 μm, for bubbles generated in water by 20 kHz ultrasound transducers (Awad, 1996; Vago, 1992). How to link the cavitation events at the micrometer scale to overall ultrasonic processing parameters is an important question that has not been touched upon in previous ultrasound research. In addition, the effect of changing system parameters, such as temperature and pressure, on microscale events during a sonication treatment also remains to be fully understood. If an ultrasonic process can be treated as a process of transmitting acoustic energy into a food or biological system to facilitate a target operation, the principles established in thermodynamics may be used to gain a better understanding of the process. In this chapter, a thermodynamic method will be used to shed light on an abnormality encountered in microbial inactivation when ultrasonic and thermal energies are combined, with the hope of triggering more investigations in the field.

Kinetics, which provide important information about reaction rate and kinetic data, have been used in the design of a number of food processing processes. Pasteurization and sterilization are two typical processes where first-order microbial inactivation kinetics are used to obtain D- and z-values. With the D- and z-values, the treatment time of a thermal process can be determined to achieve a target microbial count reduction. Scientists working on power ultrasound have also attempted to provide similar D- and z-values to guide the design of, for instance, an ultrasound-assisted liquid food pasteurization process. Compared with traditional thermal processing and other non-thermal processing technologies, however, the kinetic data for ultrasound inactivation of bacteria and food enzymes are insufficient, especially for data in food systems. There are very limited reports about the reaction kinetics of food components during sonication. Moreover, the situation is compounded by the fact that most ultrasound treatments involve multiple parameters and most ultrasound applications employ the hurdle concept by employing a combination of ultrasound with other preservation methods. Nevertheless, a short summary about this important topic will be presented in this chapter based on currently available data.

4.2 Abnormality in Thermo-sonication Inactivation

Passing ultrasonic waves through a liquid was first reported to cause irreversible inactivation of bacteria in the 1920s (Harvey and Loomis, 1929). In the early years, to reach the five-log cycle reduction in the survival count of pathogenic cells as currently required by Food and Drug Administration (FDA) for food pasteurization (U.S. Food and Drug Administration, 2001), a relatively long process time and high acoustic power density (APD) were required when an ultrasonic treatment was performed at sublethal temperatures (or sonication). Because of the limitations of the hardware then in use, early sonication tests were conducted at relatively low APD and a low inactivation rate of microbial cells was reported, with one log reduction achieved between 3 to over 80 min, depending on the bacteria species and properties of the suspension medium (Jacobs and Thornley, 1954; Kinsloe et al., 1954). With the progress in the development of robust piezoelectric elements for power ultrasound generation, recent ultrasound inactivation studies have employed relatively high APD and, as a result, a five-log reduction was achieved in 12–22 min (Rodgers and Ryser, 2004; Ugarte-Romero et al., 2007). However, the time (12–22 min) needed to achieve a five-log reduction was still long for any practical pasteurization operations. Alternatively, a combination of sonication and heat was exploited in a process termed thermo-sonication (TS) to increase the microbial or enzyme inactivation rate (Earnshaw et al., 1995; López-Malo et al., 1999; Ordoñez et al., 1987). When treating the samples at TS mode, inactivation is a result of the combined action of heat and ultrasound, and usually additive or even synergistic effects can be observed. In a TS test at 61°C, for example, the D-value of Escherichia coli K12 in buffer was 0.13 min, which represents a sixfold increase in inactivation rate compared to a thermal-only treatment at the same temperature (Lee et al., 2009b). However, there is an upper temperature limit for TS inactivation of bacteria (Fig. 4.1). Due to a cushioning effect when vapor-filled bubbles implodes at a relatively high temperature, TS inactivation above this temperature do not result in any additional killing compared to a treatment using only heat at the same temperature (Ugarte-Romero et al., 2007). This temperature effect is found in the inactivation of yeast, spore formers, and Gram-positive and Gram-negative cells. Sometimes, inactivation beyond the threshold temperature exhibits some degree of uncertainty and is hard to explain with only the vapor-filled bubble cushioning effect theory. This phenomenon is therefore examined under the framework of thermodynamics in this chapter.

Fig. 4.1

Resistance of L. monocytogenes (a: Ugarte-Romero et al., 2007), S. cerevisiae (b: López-Malo et al., 1999), Aspergillus flavus (c: López-Malo et al., 2005), and Bacillus subtilis spores (d: Sala et al., 1999) to thermo-sonication treatment in comparison with thermal alone treatment. There are two lines for each microorganism, with the upper one denoting the thermal treatment and the lower one representing a thermo-sonication treatment. Thick solid lines represent the temperature range reported in the literature, while the thin solid lines are an extrapolation from the date reported

4.3 Non-equilibrium Thermodynamic Theory for Biological Systems

Classic thermodynamic theories apply only to equilibrium systems. Since no biological system is at equilibrium, non-equilibrium theories have been used to extend the useful domain of thermodynamics to biological applications (Singh, 1998). For microbial growth via biochemical reactions of catabolic nature, for instance, it is known that a Gibbs energy dissipation takes place, which is a combined process of entropy reduction through entropy exchange associated with heat $(Q/T < 0)$ and by yielding products of higher entropy (von Stockar and Liu, 1999). Not much published information is available regarding the thermodynamic basis of microbial death or microbial inactivation, as the thermodynamic definition of biological death has been a challenge in biology (Nahle, 2009). One hypothesis proposed by Heinz and Knorr (2005) states that changes in the Gibbs energy correspond to either a recoverable or non-recoverable state of a bacterial spore, and hence $\Delta G = 0$ can be used to indicate pressure–temperature combinations for irreversible bacterial inactivation or killing. The conception of Heinz and Knorr is further developed in this work to take into account the energy input from the environment into a system, which hence can be used to provide a non-equilibrium thermodynamic explanation for microbial inactivation using acoustic energy.

To obtain Gibbs free energy changes in a microbial inactivation process, let us start with the definition of Gibbs free energy $G = H - TS$, where H is the enthalpy, T is the temperature, and S is the entropy. The enthalpy H is given by $H = U + pV$, where U is the internal energy, p the pressure, and V the volume. One C-mol of microbial cells is taken as a non-steady open thermodynamic system for the analysis. For an infinitesimal change, the general entropy balance is given by (von Stockar et al., 2006)

$$\textrm{d}U = \textrm{d}Q + \textrm{d}W - pdV + \Sigma h_i {\textrm{d}}n_i $$

((4.1))

where h _i and n _i are the partial molar enthalpy and number of moles of i-th species in the system, respectively. In the above equation, the dW refers to the work done on the system not accounted for by the pdV term.

With 1 C-mol of cellular mass as the system boundary, the balance of entropy is

$${\textrm{d}}S = {\textrm{d}}Q/T + \Sigma s_i \cdot {\textrm{d}}n_i $$

((4.2))

where s _i refers to the partial molar enthalpy of i-th species. From Equation (4.2), an expression for the infinitesimal change in heat imported can be obtained:

$${\textrm{d}}Q = T({\textrm{d}}S - \Sigma s_i \cdot {\textrm{d}}n_i )$$

((4.3))

For an infinitesimal change in Gibbs energy, the following is available:

$${\textrm{d}}G = {\textrm{d}}H - {\textrm{d}}(TS) = {\textrm{d}}H - T{\textrm{d}}S - S{\textrm{d}}T$$

((4.4))

On the other hand, the definition for enthalpy gives the following:

$${\textrm{d}}H = {\textrm{d}}U + {\textrm{d}}(pV) = {\textrm{d}}U + p{\textrm{d}}V + V{\textrm{d}}p$$

((4.5))

Substitute Equation (4.3) into Equation (4.1) and eliminate dQ resulting in the following:

$${\textrm{d}}U = T{\textrm{d}}S + {\textrm{d}}W - p{\textrm{d}}V + \Sigma \mu _i \cdot {\textrm{d}}n_i $$

((4.6))

where $\mu _i = h_i - Ts_i$ is the chemical potential of the i-th species. Then, substitute Equation (4.6) into Equation (4.5) to eliminate dU, yielding

$${\textrm{d}}H = T{\textrm{d}}S + {\textrm{d}}W + \Sigma \mu _i \cdot {\textrm{d}}n_i + V{\textrm{d}}p$$

((4.7))

Finally, Equation (4.7) is substituted into Equation (4.4), eliminating dH to obtain the following expression:

$${\textrm{d}}G = V{\textrm{d}}p - S{\textrm{d}}T + {\textrm{d}}W + \Sigma \mu _i \cdot {\textrm{d}}n_i $$

((4.8))

In a similar fashion, when only changes in free energy ΔG are considered, Equation (4.8) becomes

$${\textrm{d}}\Delta G = \Delta V{\textrm{d}}p - \Delta S{\textrm{d}}T + {\textrm{d}}\Delta W + \Sigma \Delta \mu _i \cdot {\textrm{d}}n_i $$

((4.9))

Equation (4.9) applies to living microbial open systems. dn _i is the exchange rate of the chemical species. For a microbial inactivation process, species exchanges to the environment can be ignored, and hence $\sum {\Delta \mu _i \cdot {\textrm{d}}n_i } \; = \;0$. Similar to Heinz and Knorr (2002), Equation (4.9) can be integrated using a Taylor series expansion up to the second-order term, which gives the following:

$$ \begin{aligned} \Delta G = \Delta G_0 &+ \Delta V_0 (p - p_0 ) - \Delta S_0 (T - T_0 ) + \raisebox{3.5pt}{\scriptsize 1}\hbox{/}\raisebox{-2pt}{\scriptsize 2} \Delta \beta (p - p_0 )^2 \\ & - \raisebox{3.5pt}{\scriptsize 1}\hbox{/}\raisebox{-2pt}{\scriptsize 2} \Delta cp/T_0 (T - T_0 )^2 + \Delta \alpha (T - T_0 )\;(p - p_0 ) + (\Delta W - \Delta W_0 ) \end{aligned}$$

((4.10))

In particular, the conditions where $\Delta G = 0$, corresponding to irreversible microbial inactivation, are of interest. In this case, Equation (4.10) reduces to the equation of a quadratic curve. To find the conditions that satisfy $\Delta G = 0$, let

$$ \begin{aligned} A = - \raisebox{3.5pt}{\scriptsize 1}\hbox{/}\raisebox{-2pt}{\scriptsize 2} \Delta c_p /T_0 ,\;2b &= \Delta \alpha ,\;c = \raisebox{3.5pt}{\scriptsize 1}\hbox{/}\raisebox{-2pt}{\scriptsize 2} \Delta \beta ,\;2d = - \Delta S_0 ,\;2f = \Delta V_0 ,\;\\ g &= \Delta G_0 + (\Delta W - \Delta W_0 ) \end{aligned} $$

((4.11))

where α is the thermal expansion coefficient of the microbial cells, β is the compressibility, and c _p is the heat capacity. The $\Delta G = 0$ conditions are then transformed to the standard form for the equation of a quadratic curve, as shown in Fig. 4.2.

$$ax^2 + 2bxy + cy^2 + 2dx + 2fy + g = 0,x = (T - T_0 )\;{\textrm{and }}y = (p - p_0 )$$

((4.12))

Fig. 4.2

The plane P–T corresponding to $\Delta G = 0$

Equation (4.12) would describe an ellipse when the following conditions are satisfied:

$${\textrm{0}} \ne \Delta = \left| {\begin{array}{*{20}c} a &\,\,\, b &\,\,\, d \\ b &\,\,\, c &\,\,\, f \\ d &\,\,\, f &\,\,\, g \\\end{array}} \right|,0 \ne \Delta = \left| {\begin{array}{*{20}c} a & b \\ b & c \\\end{array}} \right|$$

((4.13))

$I = a + c$ with $\Delta /I < 0$

In this case, the center of the ellipse will be at the point $(x_0 ,y_0 )$ at an incline of

$$\begin{array}{l} \displaystyle x_0 = \displaystyle\frac{{cd - bf}}{{b^2 - ac}} \\ \displaystyle y_0 = \displaystyle\frac{{af - bd}}{{b^2 - ac}} \\ \displaystyle \phi = \displaystyle \frac{1}{2}\cot ^{ - 1} \left( {\frac{{c - a}}{{2b}}} \right) \\ \end{array}$$

((4.14))

The lengths of the major axes are given by

$$A = \sqrt {\frac{{2(af^2 + cd^2 + gb^2 - 2bdf - acg)}}{{(b^2 - ac)\left[ {(c - a)\sqrt {1 + \frac{{4b^2 }}{{(a - c)^2 }}} - (c + a)} \right]}}}$$

((4.15))

$$B = \sqrt {\frac{{2(af^2 + cd^2 + gb^2 - 2bdf - acg)}}{{(b^2 - ac)\left[ {(a - c)\sqrt {1 + \frac{{4b^2 }}{{(a - c)^2 }}} - (c + a)} \right]}}}$$

Of particular interest is the value of g that will shrink the ellipse into a point; this is realized when $A = B = 0$, which implies the following:

$$af^2 + cd^2 + gb^2 - 2bdf - acg = 0 \quad g = \frac{{af^2 + cd^2 - 2bd}}{{b^2 - ac}}$$

((4.16))

In terms of the physical variables, this yields the following:

$$\Delta G_0 + \Delta W - \Delta W_0 = \frac{{ - \Delta c_p \Delta V_0 ^2 + T_0 \Delta \beta \Delta S_0 ^2 + 4T_0 \Delta \alpha \Delta S_0 }}{{2T_0 \Delta \alpha ^2 + 2T_0 \Delta c_p \Delta \beta }}$$

((4.17))

In Equation (4.12), in order to achieve a maximum for the function z (and hence a minimum for −ΔG), it requires the coefficients a < 0 and c < 0, since for either p or V being fixed, Equation (4.12) represents a parabola.

Furthermore, it is noted that for non-zero d and/or f, allow $X = ax - d/a$ and $Y = cy - f/c$, such that a non-zero d and/or f amounts only to a translation of the quadratic curve in the xy plane. Likewise, a non-zero g merely results in the translation of the quadratic curve in a direction parallel to the $z\,( - \Delta G)$ axis.

In Fig. 4.3, the effects of the coefficients a, b, and c on the shape of the ellipse as described by Equation (4.12) are presented, with the restriction that $a < 0,\;c < 0$ and $d = f = 0$, by plotting contour lines of the function as given by Equation (4.12), for various values of a, b, and c.

Fig. 4.3

The effect of a, b, and c on the shape and orientation of the ellipse defined by $\Delta G = 0$

As can be seen from Fig. 4.3, the relative magnitude of the coefficients a and c determines the ratio of the lengths of the major axis A and B, while the coefficient b determines the direction of the major axis. In 3D, the plot of Equation (4.10) for $z\,( - \Delta G)$ as a function of $x = (T - T_0 )$ and $y = (p - p_0 )$ is given in Fig. 4.4.

Fig. 4.4

Three-dimensional plot of the Gibbs free energy (G) function

4.4 Cut-Off Temperature for Thermo-sonication Inactivation

When the pressure of the system is fixed, as in the case for most ultrasound inactivation studies, a parabola in the $\Delta G - T$ plane can be obtained.

Consider now two different systems, one with ultrasound treatment and one without. The action of adding acoustic energy into the system corresponds to introducing a ΔW in Equation (4.10). Therefore, these two systems will have identical phase diagrams on the $\Delta G - T$ plane, except that the system with ultrasound treatment (termed as US+T) will be lying above the system without (denoted by T) by a difference of ΔW in z direction (Fig. 4.5).

Fig. 4.5

The Gibbs free energy at the $\Delta G - T$ plane showing with (US + T) and without (T) ultra-sonication

When $T < T_1$, the application of ultrasound lowers the Gibbs energy of the system and allows $\Delta G < 0$ to be achieved over a wider temperature range on the $\Delta G - T$ plane. According to Heremans (2002), a certain constant free-energy difference $(\Delta G)$ region can be defined on the P−T plane where the T−P combinations can cause protein denaturation. If we allow the constant ΔG to be at a specific value of $\Delta G = 0$ and thus $\Delta G < 0$ corresponds to irreversible microbial inactivation, the conditions can also be extended to more complicated situations such as killing of bacteria. At $T > T_1$, however, the system without ultrasound treatment already has $\Delta G < 0$. As a result, any additional treatment by ultrasound will not cause the conditions to be more favorable than they are already. Consequently, no more additional killing in the US+T treatment will result from further temperature increase beyond T ₁ as compared to a heat-only treatment at the same temperature. Therefore, $T = T_1$ defines a cut-off temperature whereby there will be no observable gain in killing efficiency above T ₁.

Since the $\Delta G - T$ plane is built on information from non-steady open thermodynamic microbial systems, for different organisms, it is foreseeable that there exists a different T ₁. Responses of bacteria to TS inactivation as shown in Fig. 4.1 thus can be attributed to the existence of T ₁, which equals to approximately 64°C for Listeria monocytogenes, 53°C for Saccharomyces cerevisiae, 67°C for Aspergillus flavus, and 99°C for Bacillus subtilis spores (Ugarte-Romero et al., 2007).

4.5 A Note on Inactivation Kinetics

Similar to the thermal processing counterpart, most ultrasound inactivation studies have attempted to use first-order inactivation kinetics to describe the survival curves of microorganisms or activity reduction of enzymes. An advantage of using log-linear inactivation kinetic equations is that the well-established design procedure in thermal processing (pasteurization or sterilization) can be used in the design of an ultrasound-assisted treatment. When the first-order inactivation kinetics are valid, the survival count of a bacterium can be estimated by

$$- \frac{{{\textrm{d}}N}}{{{\textrm{d}}t}}\; = \;kN\;\;{\textrm{or}}\;\;\frac{N}{{N_0 }}\; = \;\exp \left( { - \frac{t}{D}} \right)\;\;{\textrm{or}}\;\;\log N\; - \;\log N_0 = \; - \frac{t}{D}$$

((4.18))

where D is the decimal reduction time in min, k is a constant, N is survival count at time t, and N ₀ is initial count. The survival count reduction in a treatment can be caused by a number of chemical or mechanical lethal factors, such as temperature, pressure, electric field intensity, acoustic energy intensity, ultraviolet light, irradiation, sanitizer concentration, etc. In ultrasound inactivation of microorganisms, the lethal factors could be a combination of different chemical and physical effects related to cavitation activity, which imparts ultrasound inactivation an inherent complexity compared to other non-thermal processing technologies. From a process operation point of view, the parameters that appear to affect the efficacy of an ultrasound treatment include the amplitude of the ultrasonic waves, treatment time, frequency, reactor shape, shape and location of the ultrasound emitting element, temperature, static pressure, and properties of the liquid food, such as viscosity, surface tension, dissolved gas, solid concentration, pH, and water activity, as well as the type of organism, the growth phase, among others. When conducting an ultrasound kinetic study, it is critical to hold other factors constant when examining the effect of one parameter. It is also important to report the details about hardware set-up and the medium and treatment conditions. Unfortunately, not all of the above-mentioned information is provided in published reports on ultrasound applications, rendering a direct comparison of the data produced by different research groups difficult. Currently, there are two types of models for ultrasound inactivation kinetic studies: linear models and non-linear models.

4.5.1 First-Order Kinetic Models

Most ultrasonic inactivation studies have either employed first-order kinetic parameters (D-values and z-values) to describe microbial survival count reduction, or have simply reported the log-cycle reduction without using any kinetic parameters. To document the resistance of a microorganism to ultra-sonication, it is not a bad choice to only report the log reduction, since an ideal linear relation across the entire inactivation curve without a shoulder and a tail is rarely observed, especially when the microbial count reduction is over five log in the inactivation test. However, for process design purposes, kinetic parameters will be preferred, as long as the D-values are not giving an overestimate of the inactivation rate, which will result in an unsafe design. When processing the inactivation data with a first-order kinetic model, D values, which is the time used to cause 90% reduction in the number of microbial survival count or enzyme activity, are reported. From the published ultrasound inactivation results, the inactivation rate as indicated by the D values for a specific bacterium is influenced by a number of factors. Different bacteria and even different strains of the same organism exhibit different resistance to an ultrasonic treatment (Baumann et al., 2005). When temperature and pressure are fixed, the D-values are in the sequence of spores > fungi > yeasts > Gram-positive > Gram-negative cells, as can be seen in Fig. 4.6. As a result, the inactivation rate (log CFU/min) in ultra-sonication is in the sequence of Gram-negative cells > Gram-positive cells > yeasts > fungi > spores.

Fig. 4.6

D-values of bacteria with respect to temperature. Data for each bacterial group were collected from the literature. For spore formers, the data are from ultrasonic inactivation of Bacillus cereus, Bacillus licheniformis, and Bacillus subtilis (Burgos et al., 1972; Sala et al., 1999). The inactivation data for Aspergillus flavus, Penicillium digitatium and Zygosaccharomyces bailii are from López-Malo et al. (2005), and López-Malo and Palou (2005). The data for Saccharomyces cerevisiae are from López-Malo et al. (1999, 2005) and Guerrero et al. (2001). Streptococcus faecium, Staphylococcus carnosus, Lactobacillus acidophilus, and Listeria monocytogenes inactivation data were collected from the work of Pagán et al. (1999), Earnshaw et al. (1995), Zenker et al. (2003), Rodgers and Ryser (2004), Baumann et al. (2005), and D’Amico et al. (2006). The data of Gram-negative cells, i.e., Yersinia, Flavobacterium spp., Salmonella enterica serovar enteritidis, Acinetobacter bauxmaii, Escherichia coli, and Shigella boydii are from Ordóñez et al. (1987), Chamul and Silva (1999), Zenker et al. (2003), Cabeza et al. (2004), D’Amico et al. (2006), Rodríguez-Calleja et al. (2006), Ugarte-Romero et al. (2007), and Patila et al. (2009)

The temperature sensitivity of different bacteria is clearly shown in Fig. 4.6. An increase in temperature results in a fast decrease in D-values for all of the five types of organisms. The slope on a log D-value versus temperature curve is defined as z-value when a linear relation on a semi-log plot can be observed. Since the data in Fig. 4.6 were collected from inactivation data of different bacteria and treated under different conditions, the slope only functions as an indication of the changes in D-value as affected by sonication temperature. A few studies have reported z values for ultrasound inactivation of microorganisms. In a sonication test, in buffer with different acoustic power densities (APDs), Ugarte-Romero et al. (2007) estimated that the z-value for Shigella boydii was 1.8 W/mL, while that for Listeria monocytogenes was 1.5 W/mL. At a given APD, the z value for thermo-sonication of L. monocytogenes was 23.4°C, while that for a thermal inactivation at the same temperature was 10.5°C. The higher z-value for the thermo-sonication corresponds to a less sensitive change in D-value when increasing temperature. As a result, when plotting the log D-values of the thermo-sonication and that for the thermal alone treatment on a D-value versus temperature chart, at a relatively high temperature, the curve for the thermo-sonication will traverse that for the thermal-only treatment. This is the root cause for the existence of the cut-off temperature, a phenomenon previously discussed in this chapter (see Fig. 4.6). The z-values corresponding to pressure changes during sonication have not been reported in the literature. This is partially because the treatment must be performed in a mano-thermo-sonication (MTS) mode with reliable temperature and pressure controls, and only very few groups have developed the capacity to conduct MTS tests. Nevertheless, the limited data published until now seem to indicate that there exists an upper pressure in an MTS test (Lee et al., 2009b; Raso et al., 1998a). The effect of pressurization on ultrasonic microbial inactivation will diminish above the threshold pressure.

When examining the effect of temperature and pressure on sonication treatments, another method that utilizes linear inactivation kinetic models has been used (Raso et al., 1998a, b). This method assumes that the heat- and pressure-related lethal processes follow a log-linear relation and that the overall lethal effect is the addition of individual lethal effects. A detailed description of this method is given in Chapter 11 of this book. For inactivation curves with an obvious tail, a two-sectional linear inactivation model has also been used to describe the bacterial response to sonication treatments. An advantage of using two linear sections to fit the inactivation curve is that a D-value can be produced for each linear section, which may be used to compare with D values obtained from other inactivation tests. In addition, the inactivation in the first and fast reduction section is more efficient and of practical importance in real world applications. The inactivation in the second section is slow and ineffective, and should be avoided. This approach has been employed in the inactivation kinetic studies of L. monocytogenes in a thermo-sonication test in apple cider (Baumann et al., 2005) and E. coli K12 in an MTS test in a buffer (Lee et al., 2009b).

The inactivation of enzymes has been reported to mainly follow a log-linear relation for MTS inactivation of peroxidase (López and Burgos, 1995b) and lipoxygenase (López and Burgos, 1995a), thermo-sonication of peroxidase (De Gennaro et al., 1999), MTS of pectin methylesterase and polygalacturonase (López et al., 1998), and thermo-sonication of tomato pectin methylesterase (Raviyan et al., 2005). In contrast with most microbial inactivation data sets where an over five-log reduction in the survival count of a bacterium can often be seen, most enzyme inactivation tests have reported an enzyme activity reduction over a range of less than 2 log cycles (99% reduction). This may contribute to the dominant linearity observed on enzyme inactivation curves.

Reports on the reaction kinetics of nutrients and other quality attributes in foods during sonication treatment are especially limited. The few recent reports have documented the degradation of ascorbic acid in orange juice after sonication and during storage (Lee et al., 2005; Tiwaria et al., 2009), and a first-order degradation kinetics were observed during storage for the reduction of the ascorbic acid concentration (Tiwaria et al., 2009).

4.5.2 Non-linear Inactivation Models

There has been growing evidence that inactivation of microorganisms may not follow first-order kinetics, especially for inactivation with non-thermal processing methods, with more than one lethal factor, or with a log reduction of near or over five-log cycles (Klotz et al., 2007; Peleg and Cole, 1998). Shoulders and/or tails have been observed on the inactivation curves for a combined treatment of ultrasound with chitasan (Guerrero et al., 2005), ultrasound with vanillin (Gastelum et al., 2010), ultrasound with lethal temperature (Baumann et al., 2005), and ultrasound with pressure (Lee et al., 2009a, b). For tested microorganisms, non-linear inactivation behavior has been observed for the inactivation of L. monocytogenes (Baumann et al., 2005; D’Amico et al., 2006), E. coli (Allison et al., 1996; D’Amico et al., 2006; Stanley et al., 2004; Ugarte-Romero et al., 2006), Alicyclobacillus acidophilus, and A. acidoterrestris (Wang et al., 2010), Bacillus subtilis spores (Raso et al., 1998b), natural flora in raw milk (D’Amico et al., 2006), and Saccharomyces cerevisiae (Guerrero et al., 2005). To describe non-linear inactivation kinetics, several models, including Weibull, modified Gompertz, biphasic linear, and log-logistic models have been used to fit non-linear inactivation data of several microorganisms for inactivation by heat, high pressure processing or pulsed electric field (Gómez et al., 2005; Lee et al., 2009a, b; Raso et al., 2000). Table 4.1 tabulates a few selected non-linear inactivation models. Non-linear regression methods are normally used to fit the inactivation data to the models for the estimation of parameters in the model equations. Statistical parameters and methods, such as mean square error of model (MSE), coefficient of determination (R ²), accuracy factor (A _f ), F test, and Akaike information criterion (Akaike, 1973) can be employed to evaluate the goodness of fit of the models to the inactivation data. In the reports of Lee et al. (2009a, b), the biphasic linear, log-logistic, and modified Gompertz kinetic models produced better fitting of the inactivation data for MTS, thermo-sonication, and mano-sonication treatments of E. coli K12 than the first-order and Weibull models.

Table 4.1 Selected non-linear inactivation kinetic models

In ultrasound inactivation, the non-linearity could be attributed to subpopulations of different resistance and physiological reactions of the cells to a lethal factor (Heldman and Newsome, 2003). The break-up of cell aggregates during sonication by cavitation has also been considered as a cause for shoulders in bacterial survival curves. The tails, in some cases, may be caused by a gradual change in the properties of the liquid medium during sonication. For instance, in a probe system open to air, air may be entrained into the liquid, which would induce a progressive decrease in the cavitation activity and hence a reduction in inactivation rate. For a treatment for a relatively long time, the output power of the generator would decrease over time, which will also result in a decrease in inactivation efficacy.

The potential use of non-linear kinetic models in process design has raised concerns (Heldman and Newsome, 2003). Since most non-linear models are either empirical or with assumption(s) about the resistance distribution of cells to certain lethal factor, the results cannot be used outside the range of inactivation conditions employed to obtain the model parameters. No extrapolation is recommended. Suggestions have been proposed to follow the conventions adopted by the industry for a log-linear model when applying non-linear models. A practice of only reporting the end-point log reduction has been recommended to control the delivery of an expected log reduction in a process, which can minimize the non-linear survivor issues and provide consistency with the log-linear kinetic model (Heldman and Newsome, 2003).