9.1 Introduction

System reliabilities can be calculated from individual component (or subsystem) reliabilities, if the series–parallel reliability relationships are known.

Series reliability refers to the situation where the system fails if any individual component, the weakest link, fails and is given for a system of n components by:

$$ {R_{\it{SS}}} = \prod\limits_{i = 1}^n {{R_i} = {R_1} \cdot {R_2} \cdot {R_3} \cdots \cdot {R_n}}, $$
(9.1)

with system hazard rate:

$$ {\lambda_{\it{SS}}} = \sum\limits_1^n {{\lambda_i}}, $$
(9.2)

and mean time to failure:

$$ {\it{MTT}}{{\it{F}}_{\it{SS}}} = \frac{1}{{{\lambda_{\it{SS}}}}}. $$
(9.3)

Table 9.1 shows how rapidly system reliability can degrade in a series system of equal component reliabilities.

Table 9.1 System reliability reduction with complexity
Full size table

Parallel reliability applies to redundant systems and is given for a system of n components by:

$$ {R_{\it{PS}}} = 1 - {Q_{\it{PS}}} = 1 - \prod\limits_{i = 1}^n {(1 - {R_i})}. $$
(9.4)

Formula for system hazard rate and MTTF escalate rapidly in complexity, so for n = 2, for example,

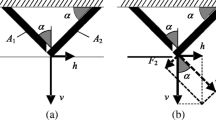
$$ {\lambda_{\it{PS}}} = \frac{{{\lambda_1}{{\it e}^{ - {\lambda_1}t}} + {\lambda_2}{{\it e}^{ - {\lambda_2}t}} - ({\lambda_1} + {\lambda_2}){{\it e}^{ - ({\lambda_1} + {\lambda_2})t}}}}{{{{\it e}^{ - {\lambda_1}t}} + {{\it e}^{ - {\lambda_2}t}} - {{\it e}^{ - ({\lambda_1} + {\lambda_2})t}}}}. $$
(9.5)

Examples of the next level of complexity are shown in Fig. 9.1, which contrasts (a) the series combination of redundant elements with (b) a redundant arrangement of series elements. Real systems are often designed to include redundant combinations of low-reliability elements. More generalized series–parallel systems can be analyzed by a quasi-Boolean algebraic approach, as demonstrated here for the system of Fig. 9.2. Table 9.2 lists all the possible operational (and nonoperational) conditions in terms of functional and nonfunctional elements, indicated for example by A and A respectively. Considering all the possible operational states, the complex system reliability can be written in terms of the component reliabilities R A, R B, R C, and R D, as:

$$ R = {R_{\it{A}}}{R_{\it{B}}}{R_{\it{C}}}{R_{\it{D}}} + {R_{\it{A}}}{R_{\it{B}}}\left( {{1} - {R_{\it{C}}}} \right){R_{\it{D}}} + {R_{\it{A}}}\left( {{1} - {R_{\it{B}}}} \right){R_{\it{C}}}{R_{\it{D}}} + \ldots {\hbox{etc}}{.}, $$
(9.6)

which can be simplified to show that:

$$ R = {R_{\it{D}}} + {R_{\it{A}}}\left( {{R_{\it{B}}} + {R_{\it{C}}} - {R_{\it{B}}}{R_{\it{C}}}} \right)\left( {{1} - {R_{\it{D}}}} \right). $$
(9.7)
Fig. 9.1
figure 1_9

(a) Series–parallel and (b) parallel–series reliability systems

Full size image
Fig. 9.2
figure 2_9

Complex (mixed) reliability system

Full size image
Table 9.2 Determination of system reliability
Full size table

It is well known that only the exponential distribution has a constant hazard rate. The constant hazard rate is related to some random effects that take place during the lifetime of a component (bathtub curve with β = 1 in Fig. 9.3).

Fig. 9.3
figure 3_9

Bathtub curve and the different failure regions

Full size image

When Weibull shape parameter β < 1, failures are predominantly of early failure type, and when β = 1, random failures are dominant, and when β > 1, wearout is mostly responsible for failures.

An exponential distribution assumption with constant hazard rate is used quite a lot due to the resulting simplicity in system level reliability analyses. When utilizing a constant hazard rate assumption in parts-count type reliability estimates, the hazard rates of individual components λ comp,i can be summed up, and the end result is the system level hazard rate λ system [1]:

$$ {\lambda_{\it{system}}} = \sum\limits_{i = 1}^n {{\lambda_{{\it{comp}},i}}}. $$
(9.8)

The reciprocal of the system hazard rate is the MTTF (Mean Time to Failure) of the system:

$$ {\it{MTTF}} = \frac{1}{{{\lambda_{\it{system}}}}}. $$
(9.9)

Quite a lot of component lifetime data that have been gathered are presented in terms of constant hazard rate. Many system level reliability prediction methods also give lifetime predictions in terms of constant hazard rates [2]. However, in reality, the constant hazard rate assumption is often not valid. Therefore, applying exponential distribution may not always be an appropriate choice [3]. Assuming a constant hazard rate makes the mathematical analyses easy, but assuming a constant hazard rate is in contradiction with the fact that most components fail either in the early failure or the wearout regime, where the hazard rate is either decreasing or increasing, respectively. The hazard rate in those regimes can be taken into account, for example, by utilizing Weibull statistics, but not by an exponential distribution. Owing to this fact, there seems to be an unbridgeable situation, as component level reliability data can be interpreted by applying Weibull statistics, but these results cannot be utilized later on in simplistic system level MTTF calculations.

The relationship between the exponential and the Weibull distributions has already been studied in the past, and the so-called Weibull-to-exponential transformation has been created [4–6]. The use of this transformation simplifies the estimation of the confidence bounds and some other parameters of the Weibull distribution. When using the transformation, the Weibull data is first transformed into an exponential form where the mathematical analyses, (e.g., the determination of the confidence bounds) are done. After that, the results are converted back to Weibull form.

In our case, the Weibull data (hazard rate) is converted into exponential type data format (constant hazard rate) by time-averaging the hazard rate within certain time intervals. The approximate information created is readily applicable in parts-count type system level reliability analyses. Conversion back to the Weibull regime is not needed.

9.2 Some Constant Hazard Rate Approximations of the Weibull Distribution

The exponential distribution and Weibull distributions are of different forms, and they have a different time dependency. The only exception is the case when the Weibull distribution shape parameter β = 1, in which case the two distributions are identical, with η = θ = 1/λ. In this case, the Weibull distribution characteristic lifetime η is equal to the MTTF (θ) value of the exponential distribution. At all other times, the distributions are not identical and therefore, some approximation is needed in order to present the Weibull distribution data in terms of an exponential distribution.

There may be different strategies to create a suitable approximation of the Weibull distribution. Although it is impossible to match all the distribution functions (hazard function h(t), probability density function f(t), cumulative density function F(t), and reliability function R(t)) between the two distributions simultaneously, there is a possibility to match perfectly some individual functions.

After the two-parameter Weibull data are transformed into constant hazard rate form, it can be utilized in MTTF calculations for the whole system. Therefore, it would be beneficial if the reliability function of the approximate exponential distribution R(t)WB→EXP would imitate the reliability function of the original Weibull distribution R(t)WB as closely as possible, in other words:

$$ R{(t)_{{\it{WB}} \to }}_{\it{EXP}} \approx R{(t)_{\it{WB}}}. $$
(9.10)

Another criterion to be fulfilled is that the form of the hazard function h(t)WB→EXP should be kept as simple as possible, but it should still present the main characteristics of the original distribution. This means that preferably h(t)WB→EXP = constant at least for some time intervals. Still, oversimplification should be avoided when trying to satisfy this criterion. Otherwise, some false conclusions might be drawn from the MTTF calculations. Typically, the reliability test results of components are of increasing hazard rate type.

Weibull distribution with two parameters, shape parameter β and the characteristic lifetime η, can fit the data satisfactorily many times.

The Weibull hazard rate is of the form [7]:

$$ h(t) = {{\beta \cdot {t^{\beta - 1}}} \mathord{\left/{\vphantom {{\beta \cdot {t^{\beta - 1}}} {{\eta^\beta }}}} \right.} {{\eta^\beta }}}. $$
(9.11)

In order to approximate this function, one of the below strategies can be chosen:

  • Option 1: Pick some representative value of the hazard function at some selected time t.

  • Option 2: Calculate a time-averaged hazard rate value for the whole lifetime.

  • Option 3: Calculate a time-averaged hazard rate value for some time intervals.

  • Option 4: Pick values from the time-averaged hazard rate curve (Option 2) between selected time intervals.

  • Option 5: Calculate time-averaged reliability function values for selected time intervals and based on those, calculate equivalent hazard rate values λ eq for each time interval.

The actual procedure is explained later on in more detail.

In the following section, the five strategies above are discussed in light of the criteria given earlier in this chapter.

First, give the formal definitions for Options 2–5:

  • Option 2

    The hazard rate of the option 2 is defined as the time-averaged value over the whole lifetime of the component:

    $$ {\left\langle {h(t)} \right\rangle_t} = \frac{ {\int\limits_0^t {h(t^\prime){\rm d} t^\prime} }}{{\int\limits_0^t {{\rm d} t^\prime} }} = \frac{{{t^{\beta - 1}}}}{{{\eta^\beta }}}. $$
    (9.12)

    It is noted that this value is dependent on time t. The above approximation is useful, if the expected lifetime or lifetime requirement for the component t = t lifetime is known. By inserting this value into (9.12), it results in one constant hazard rate value for the whole lifetime of the component.

  • Option 3

    The third option can be calculated in a similar way as above, but this time, the time-averaged hazard rate will be calculated for selected time intervals \( \Delta t = {t_{i + 1}}-{t_i} \):

    $$ {\left\langle {h(t)} \right\rangle_{\Delta t}} = \frac{{\int\limits_{{t_i}}^{{t_{i + 1}}} {h(t){\rm d} t} }}{{\int\limits_{{t_i}}^{{t_{i + 1}}} {{\rm d} t} }} = \frac{1}{{{\eta^\beta }}} \cdot \frac{{\left( {t_{_{i + 1}}^\beta - t_{_i}^\beta } \right)}}{{{t_{i + 1}} - {t_i}}}. $$
    (9.13)

    In this case, the hazard rate has a constant value in a selected time interval from t i to t i+1 i = 0, 1, 2, …, n, where n is the number of time intervals.

  • Option 4

    This option makes use of time-averaged hazard rate function defined by (9.12). The hazard rate values used are defined as \( {\left\langle {{\hbox{h}}\left( {{t_i}_{ + {1}}} \right)} \right\rangle_t} \) during selected time intervals:

    $$ \Delta t = {t_i}_{ + 1} - {t_i} $$

  • Option 5

    Utilizing Option 5 requires a little more rigorous analysis. The strategy is to first solve the time-averaged value of the reliability function RWB for selected time intervals t i …t i+1.

    This can be accomplished by writing:

    $$ \eqalign{ \left\langle {{R_{\rm{WB}}}} \right\rangle = \frac{{\int\limits_{{t_i}}^{{t_{i + 1}}} {R(t){\it d} t} }}{{\int\limits_{{t_i}}^{{t_{i + 1}}} {{\it d} t} }} = \frac{{\int\limits_{{t_i}}^{{t_{i + 1}}} {{{\rm e}^{ - {{\left( {t/\eta } \right)}^\beta }}}{\rm d} t} }}{{{t_{i + 1}} - {t_i}}} \\ = \frac{\eta }{{\beta ({t_{i + 1}} - {t_i})}}\left\{ {\Gamma \left( {\frac{1}{\beta },{{\left( {\frac{{{t_{i + 1}}}}{\eta }} \right)}^\beta }} \right) - \Gamma \left( {\frac{1}{\beta },{{\left( {\frac{{{t_i}}}{\eta }} \right)}^\beta }} \right)} \right\}, \\}<!endgathered> $$
    (9.14)

    where Γ(·,·) is the incomplete gamma function. In Fig. 9.4, the time-averaged reliability function is depicted.

    Fig. 9.4
    figure 4_9

    The Weibull reliability function R(t) (WB), the time-averaged reliability function \( {R_{\it{WB}}}\left( {\left\langle {\hbox{WB}} \right\rangle } \right) \), and the approximate exponential reliability function R EXP(EXP) for time interval t i …t i+1

    Full size image

The instant in time t eq (t i  ≤ t eq ≤ t i+1), at which the time-averaged reliability function is equal to the reliability function of the original Weibull distribution, may be written as:

$$ {t_{\it{eq}}} = \eta {\left[ {\ln \left( {\frac{1}{{\left\langle {{R_{\it{WB}}}} \right\rangle }}} \right)} \right]^{1/\beta }}. $$
(9.15)

In order to obtain the corresponding equivalent constant hazard rate λ eq, the exponential reliability function R EXP can be utilized:

$$ {R_{\it{EXP}}} = {{\it e}^{ - {\lambda_{\it{eq}}}t}}. $$
(9.16)

To satisfy (9.10), it can be required that when t = t eq, R EXP = R WB. After solving for λ eq, the following is obtained:

$$ {\lambda_{{eq}}} = \frac{{\ln \left( {{1 \mathord{\left/{\vphantom {1 {\left\langle {{R_{\rm{WB}}}} \right\rangle }}} \right.} {\left\langle {{R_{{WB}}}} \right\rangle }}} \right)}}{{{t_{{eq}}}}}. $$
(9.17)

In Fig. 9.5, the Weibull and time-averaged hazard rate λ eq are depicted.

Fig. 9.5
figure 5_9

Hazard rate of Weibull distribution (WB) and the time-averaged value \( \left( {\left\langle {\hbox{WB}} \right\rangle } \right) \)

Full size image

Later on, it is shown that Option 5 best fulfills the requirement given by (9.10).

However, it may be demanding to calculate numerically the incomplete gamma function values accurately when time has large values, especially if β is large. In general, this is due to the lack of numerical solutions that are accurate enough for the incomplete gamma function, when variables have very large values.

9.3 Resulting Functions and Hazard Rates

In Fig. 9.6, all five approximate hazard rate options depicted for a component having η = 3,677 days and β = 20 can be seen. The time interval selected in the time averaging was 5 years. The hazard rate for Options 3–5 is, therefore, constant in time intervals 0…5 years, 5…10 years, 10…15 years, and 15…20 years.

Fig. 9.6
figure 6_9

Weibull hazard rate and five approximate options. The selected time interval used in time averaging is 5 years

Full size image

The hazard rate for Option 1 is selected to be 10,000 FITs corresponding to the hazard rate value of Weibull distribution in the middle of the lifetime (10 years = 20 years/2). However, some other choice might have been justified as well. The hazard rate for Option 2 is the time-averaged value for the whole 20-year lifetime obtained by utilizing (9.12). The hazard rate for Option 3 was obtained by utilizing (9.13) with time-interval t i+1 − t i  = 5 years. Values for Option 4 are picked from the curve plotted according to (9.12) at time instants of 5, 10, 15, and 20 years. The hazard rate for Option 5 is calculated by utilizing the above-described method (9.13)–(9.17), which is based on the time averaging of the reliability function.

It is noted that the actual hazard rate obtains values from 0 FIT to 1 × 1011 FIT during the component’s lifetime. Therefore, it might not be a good idea to use one single hazard rate value, as is the case in Option 1. If doing so, there is a danger that the value picked is not representative of the risk level of the component at all instants of time. Also, utilizing Option 2 with only one single hazard rate value results in a similar problem, although in this case the selection of the hazard rate is not arbitrary.

Keeping in mind the criterion stated in (9.10), the reliability function of the different options (Fig. 9.7) should also be studied. Doing so, it can be noted that a perfect fit between the original Weibull reliability function and Option 2 exists. The next best choices are Options 5, 4, and 3. Option 1 has the worst performance. Therefore, it is not a suitable choice.

Fig. 9.7
figure 7_9

Reliability functions of the different approximation options. Option 2 data is overlapping with the Weibull data. The time interval used in the time averaging is 5 years

Full size image

If the exact lifetime expectancy t lifetime of a component were known prior to the product launch, then Option 2 would match exactly the original Weibull reliability function at t = t lifetime. In this case, one would just pick h(t lifetime) and use that in the MTTF calculations. This would represent the time-averaged value over the whole lifetime. However, in practice the true expected lifetime is not always known. Moreover, if wearout is expected to take place during the operational lifetime, averaging over the whole lifetime may result in a very large hazard rate value. This would not give a proper picture of the reliability of the component during its early life period. Therefore, Option 2 is attractive only if the hazard rate does not change much during the lifetime of a component. Keeping in mind that:

$$ F(t) = {1} - R(t). $$
(9.18)

It is expected that the approximate options behave similarly when cumulative failure function F(t) is concerned.

Looking at the density function f(t), it may be noted that all the approximate solutions are a poor fit for the original Weibull distribution function (Fig. 9.8). One can also show, that:

$$ \int_0^\infty {f(t){ d} t} \,<\, 1, $$
(9.19)

in the case of Options 2–4. Therefore, those options cannot be considered as true statistical distribution functions. The integration of a true distribution density function over time should always be equal to 1 [8].

Fig. 9.8
figure 8_9

Reliability density function of the Weibull and those related to the approximate solutions

Full size image

When using Options 3–5, simple constant hazard rate values can be found for some selected time intervals, for example, in a tabulated form. This is demonstrated in Table 9.3 where the data of the above example is listed. Using Option 4 does not gain a hazard rate value during time interval 15…20 years due to the lack of accurate numerical solutions to the incomplete gamma function, as discussed earlier.

Table 9.3 Time-averaged hazard rate values for different approximate options
Full size table

This kind of data can be utilized directly in parts-count type system level MTTF calculations.

9.4 Properties of Different Options

Let us first look at Option 2 in detail. The definitions of the statistical functions of Option 2 are based on the exponential distribution function using the hazard rate obtained from (9.12). This is accomplished just by replacing the constant hazard rate value λ by the hazard rate value given by the above definition (9.12). The functions of the exponential distribution and Option 2 are listed below in Table 9.4. The distribution functions derived for other options were also derived by replacing the exponential hazard rate function with the time-averaged hazard rate values.

Table 9.4 Exponential distribution functions and Option 2 related functions
Full size table

As already shown, the reliability function of Option 2 is equal to the original Weibull reliability function at any selected instant in time t. Simple relations can be written between all statistical functions of the two-parameter Weibull distribution and those of Option 2. Table 9.5 lists these relations. Inserting the hazard rate defined by (9.19) into Option 2 distribution functions in Table 9.2 can verify that the relations are correct.

Table 9.5 Statistical functions of the Weibull distribution, and their relationship to those of Option 2
Full size table

An important note is that although closed form results can be derived for Option 2, Option 2 is not a true distribution function, as it does not satisfy all the criteria required from a true reliability statistical function (9.19). Actually, it can be shown that the integration of this function, over time, is equal to 1/β. This may sound a bit odd, as both the cumulative distribution function and the reliability function for Option 2 get reasonable values and reach values in the whole scale (0…1). The explanation for this apparent contradiction is simply the fact that the cumulative distribution function, in this case, is defined by making use of the exponential function – not by actually integrating the distribution density function of the Option 2 over time.

Option 3 fitted both to hazard rate and reliability functions of the true Weibull distribution (Figs. 9.6 and 9.7) relatively accurately. Looking more carefully at the hazard rate function of this option, it is noted that at the end of the first time interval, the value of the hazard rate function is equal to the time-averaged value of the hazard rate (Option 2). During the next time intervals, the hazard rate of Option 3 starts to approach the original (instantaneous) Weibull distribution hazard rate. In actual fact, it can be shown that when the number of time intervals n approaches infinity, the hazard rate functions of Option 3 and the instantaneous Weibull distribution approach each other. The reliability function of Option 3 has always got smaller values than the true Weibull distribution (Fig. 9.7).

Option 4 is making use of the time-averaged hazard rate function defined by (9.12) at the end points of the time intervals. The reliability function is smaller than, or equal to, the original Weibull distribution function at all instants in time. At the end points of the time intervals, the reliability function is equal to the values given by the Weibull distribution and is smaller elsewhere. Option 4 is a better match to the original Weibull reliability function than Option 3.

Option 5 resembles most the original Weibull reliability function among those approximations that utilize time intervals. However, for very large time values, the calculation of the hazard rate may become cumbersome due to numerical solution accuracy limitations discussed earlier.

9.5 Comparison of the Selected Options

There are at least two things that must be taken into account, when making practical choices about the hazard rate approximation function. The first one is that the reliability function of the approximation should closely imitate the original Weibull reliability function. Option 2 is superior to the others in this respect as it matches perfectly the original Weibull reliability function. The next best choices are Options 5, 4, and 3. The use of a single, constant hazard rate value (Option 1) has the worst accuracy over the lifetime.

The other important criterion is to keep the expression of the hazard rate as simple as possible. By doing so, it is possible to apply the calculated hazard rate values directly into the system level parts-count type MTTF calculations. In this respect, Option 2 might not be a suitable choice, as it cannot be used in a tabulated form. All other options can be presented in a simple table form having constant hazard rate values either for the whole lifetime or for part of it.

To satisfy both criteria, Option 5 seems to be the best choice, having the possibility to be used in a simplistic form (for example, table) and still match reasonably well the true reliability behavior of the component.

9.6 Selection of Time Intervals

When using the simplistic time-averaged hazard rates, the time intervals should be selected in a way that the reliability behavior can be imitated with acceptable accuracy. In order to be able to satisfy this criterion, the reliability function should be plotted in conjunction with the hazard rate of the component and then the lifetime should be divided into suitable time intervals. There should be at least one, but preferably several, time intervals in which wearout has not yet fully occurred (let us say, F(t) < 1%). The following time intervals may already include the wearout phenomena related to high hazard rate values, and therefore, the resulting time-averaged hazard rate value may be large in those intervals. When wearout has occurred almost completely, the hazard rate gets values of infinite magnitude and using those in the MTTF calculations will result in a clear message; this component will fail at latest in the selected time interval. One interval indicating the end of the life of the component is enough for practical purposes.

9.7 The Motivation for Selecting Two-Parameter Weibull Distribution

In this chapter, the two-parameter Weibull distribution was selected to present the statistical behavior of components that face wearout phenomena. Some other choice might have been possible, too. The selection of a suitable statistical distribution has raised some discussion in the science community. In [9] the two-parameter, Weibull distribution is recommended, whereas in [10, 11] the three-parameter, Weibull is considered superior over two-parameter Weibull. Also, lognormal distribution is considered to fit the test results better than two-parameter Weibull distribution. The conclusion that two-parameter Weibull distribution is not very accurately presenting the test data is based on least squares curve fitting results and the related small correlation coefficients obtained when fitting the test data to two-parameter Weibull distribution.

Another argumentation used against the two-parameter Weibull distribution is that it is expected that there is a failure-free period of time (presented by the failure-free time γ in the three-parameter Weibull distribution) when testing solder attachments. One fact supporting this is that according to Darveaux [12], it takes some finite time to initiate a crack in the solder material. One further observation made is that when fitting the test data to a two-parameter Weibull distribution, the test data has a tendency to have a downward sloping in the beginning of the wear-out period [10]. This is believed to indicate that there is a failure-free time that a two-parameter Weibull distribution cannot satisfactorily take into account. Furthermore, it is noted that if a two-parameter Weibull distribution is used, the reliability requirement based on it will be very demanding [10, 11].

Now, we try if we can verify that the two-parameter Weibull distribution is accurate enough for practical purposes. The author is aware that using the two-parameter Weibull distribution will result in a more demanding reliability requirement if very small percentages of failed items are considered. This is evident if comparing the behavior of cumulative distribution functions. It is also “natural” to consider that there is a failure-free period of time until the first items start failing in the test. However, we think that in reality, it is not impossible that items may fail very early. This may happen if the test vehicles are inherently very weak or if the test itself is very harsh. One should remember that as lifetime is often monitored in terms of number of cycles, this measure used is discretized, as the length of thermal cycle is finite. The first cycle may include the incubation period of some weak components. Still, from a number-of-cycles viewpoint, it would seem that the failure occurs instantly.

Therefore, the assumption of an incubation period is not necessarily in conflict with the selection of the two-parameter Weibull distribution. Furthermore, it is not known that there would be well-documented tests that would prove either two-parameter or three-parameter Weibull statistics to best describe the behavior of a test population, especially when very small cumulative failure percentages, such as 0.01%, are considered. This would require testing of thousands of items, which is very difficult to arrange in practice. Therefore, the discussion on the distribution function selection is at least partly speculative, as no actual proof exists.

9.8 Constant Failure Rate and Its Origin in the Field Failure Data

In the field environment, constant hazard rate at the product level is often recorded, although components may fail due to wearout phenomena. The reason that the exponential portion of the bathtub curve for a population of products is observed is in part because of repairs, and in part because of random overstress events through the lifetime of the population. If the data is grouped by failure mechanisms, then it is highly doubtful to find an exponential distribution for each group. It is more likely to find a collection of Weibull distributions, each with β ≠ 1, indicating that either early failures or wearout mechanisms are taking place. However, at the system level, this can be represented with an averaged quasi-constant hazard rate.