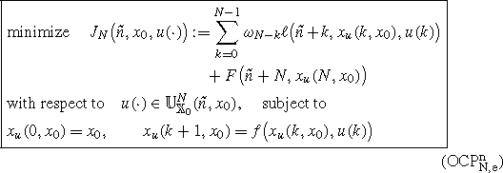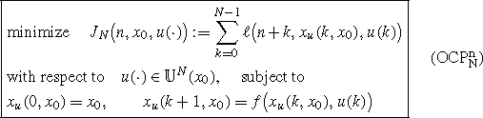Variants and Extensions

Abstract

The results developed so far in this book can be extended in many ways. In this chapter we present a selection of possible variants and extensions. Some of these introduce new combinations of techniques developed in the previous chapters, others relax some of the previous assumptions in order to obtain more general results or strengthen assumptions in order to derive stronger results. Several sections contain algorithmic ideas which can be added on top of the basic NMPC schemes from the previous chapters. Parts of this chapter contain results which are somewhat preliminary and are thus subject to further research. Some sections have a survey like style and, in contrast to the other chapters of this book, proofs are occasionally only sketched with appropriate references to the literature.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The results developed so far in this book can be extended in many ways. In this chapter we present a selection of possible variants and extensions. Some of these introduce new combinations of techniques developed in the previous chapters, others relax some of the previous assumptions in order to obtain more general results or strengthen assumptions in order to derive stronger results. Several sections contain algorithmic ideas which can be added on top of the basic NMPC schemes from the previous chapters. Parts of this chapter contain results which are somewhat preliminary and are thus subject to further research. Some sections have a survey like style and, in contrast to the other chapters of this book, proofs are occasionally only sketched with appropriate references to the literature.

7.1 Mixed Constrained–Unconstrained Schemes

The previous Chaps. 5 and6 have featured two extreme cases, namely NMPC schemes with terminal constraints$\mathbb{X}_{0}$ and costsF on the one hand and schemes without both$\mathbb{X}_{0}$ andF on the other hand. However, it appears natural to consider also intermediate or mixed cases, namely schemes in which (nonequilibrium) terminal constraint sets$\mathbb{X}_{0}$ but no terminal costsF are used and schemes in which terminal costsF but no terminal constraints sets$\mathbb{X}_{0}$ are used.

Schemes with terminal constraints$\mathbb{X}_{0}$ but without terminal costsF appear as a special case of Algorithm 3.10 (or its time varying counterpart 3.11) with (OCP_N,e) = (5.15) andF≡0. For this setting, it is not reasonable to expect that Assumption 5.9(ii) holds. Consequently, the argument used in the proof of Theorem 5.13 does not apply; in fact, we are not aware of results in the literature analyzing such schemes with the techniques from Chap. 5.

Fortunately, the stability analysis in Chap. 6 provides a remedy to this problem. Observe that the main structural assumption on the control sequences from Assumption 6.4 needed in the fundamental Lemmas 6.9 and 6.10 in Chap. 6 is that each admissible control sequence$u\in \mathbb{U}^{N}(x)$ can be extended to an admissible control sequence$\hat{u}\in \mathbb{U}^{N+K}(x)$ for eachK≥1. Since Lemma 5.2(i) ensures this property for$\mathbb{U}_{\mathbb{X}_{0}}^{N}(x)$ provided$\mathbb{X}_{0}$ is viable, we can incorporate the terminal constraint set$\mathbb{X}_{0}$ into the analysis from Chap. 6.

As a consequence, replacing$\mathbb{U}^{N}(x)$ by$\mathbb{U}^{N}_{\mathbb{X}_{0}}(x)$ in Assumption 6.4 and assuming Assumption 5.9(i), i.e., viability of$\mathbb{X}_{0}$, all results in Chap. 6 carry over to the scheme with terminal constraint set. In particular, the stability results Theorem 6.18, Corollary 6.19, Theorem 6.21 and Theorem 6.33 remain valid. However, like in Theorem 5.13 the resulting controllerμ _N is only defined on the feasible set$\mathbb{X}_{N}$ from Definition 3.9.

This combined scheme inherits certain advantages and disadvantages from both schemes. From the terminal constrained scheme we inherit that the resulting controllerμ _N is only defined on the feasible set$\mathbb{X}_{N}$. On the other hand, as discussed before Lemma 5.3, we do not need to assume viability of$\mathbb{X}$ but only for the terminal constraint set$\mathbb{X}_{0}$ (further methods to avoid the viability assumption on$\mathbb{X}$ will be discussed in Sects. 8.1–8.3).

From the unconstrained scheme we inherit the advantage that no terminal cost satisfying Assumption 5.9(ii) needs to be constructed. On the other hand, we need to ensure that the assumptions of one of the mentioned stability results from Chap. 6 hold whose rigorous verification may be involved, cf. also Sect. 6.6. For a more comprehensive discussion on advantages and disadvantages of different NMPC schemes we refer to Sect. 8.4.

Another way of imposing terminal constraints without terminal costs which can be found in the literature is via so-calledcontractive constraints. Here the terminal constraint set depends on the initial valuex ₀ of the optimal control problem (OCP_N,e) via

$$\mathbb{X}_0 = \bigl\{ x \in \mathbb{X}\bigm| |x|_{x_*} \le \gamma |x_0|_{x_*} \bigr\}$$

for some constantγ∈(0,1); see, e.g., the book of Alamir [1] or the works of de Oliveira Kothare and Morari [28] and De Nicolao, Magni and Scattolini [5]. However, for these constraints stability is only guaranteed if either the whole optimal control sequence (as opposed to only the first element) is applied or if the optimization horizon is treated as an optimization variable and the contractivity condition is incorporated into the optimization objective [1, Chap. 4]. Since these approaches do not conform with the MPC paradigm used throughout this book, we do not discuss their analysis in detail.

Schemes with terminal costF but without terminal constraint$\mathbb{X}_{0}$ have been investigated in several places in the literature, for instance in Grimm, Messina, Tuna and Teel [13] and Jadbabaie and Hauser [22] (for more information on these references see also the discussions at the end of Sect. 6.1 and in Sect. 6.9). In both references stability results for such schemes are derived in which only positive definiteness ofF is assumed. Roughly speaking, these references show that the addition ofF does not destroy stability. While the authors emphasize the potential positive effects of adding such costs, they do not rigorously analyze these positive effects. In contrast to this, in the work of Parisini and Zoppoli [30] the specific properties of the terminal cost described in Remark 5.15 were exploited in order to show stability. The proof in [30] uses that under suitable conditions and for sufficiently large optimization horizonN for all initial values from a given region the open-loop optimal trajectories end up in the terminal constraint set without actually imposing this as a condition. The same proof idea has been generalized later by Limón, Alamo, Salas and Camacho [24] for a more general terminal cost.

Here we outline an approach from Grüne and Rantzer [17] which we combine with the analysis technique from Chap. 6. This approach rigorously shows the positive effect of adding a terminal cost also in the absence of stabilizing terminal constraints. In contrast to [30] or [24] the stability property is not restricted to sets of initial values for which the open-loop optimal trajectories end up in a terminal constraint set. However, the fact that this happens for a set of initial values around the origin will be used in our proof. We start from a terminal cost functionF satisfying Assumption 5.9(ii) with a forward invariant neighborhood$\mathbb{X}_{0}$ ofx _∗, however, we will not use$\mathbb{X}_{0}$ as a terminal constraint set. Instead, we assume thatF≡c>0 holds on the boundary$\partial \mathbb{X}_{0}$ with$c\ge \sup_{x\in \mathbb{X}_{0}}F(x)$. This is, for instance, satisfied ifF is constructed from a linearization via linear–quadratic techniques according to Remark 5.15 and$\mathbb{X}_{0}$ is a sublevel set ofF. Then we may extendF continuously to the whole set$\mathbb{X}$ by settingF(x):=c for all$x\in \mathbb{X}\setminus \mathbb{X}_{0}$.

With this setting we obtain the following theorem.

Theorem 7.1

Let the assumptions of Theorem 6.33be satisfied for the NMPC Algorithm 3.1without terminal cost.Let $F:\mathbb{X}\to \mathbb{R}_{0}^{+}$ and assume that Assumption 5.9holds for some set $\mathbb{X}_{0}$ containing a ball $\mathcal{B}_{\eta}(x_{*})$ for some η>0.Assume,furthermore,that F≡c holds outside $\mathbb{X}_{0}$ with $c\ge \sup_{x\in \mathbb{X}_{0}}F(x)$ and that $F(x)\le \tilde{\alpha}_{2}(|x|_{x_{*}})$ holds for all $x\in \mathbb{X}_{0}$ and some $\tilde{\alpha}_{2}\in \mathcal{K}_{\infty}$.Consider the NMPC Algorithm 3.10with (OCP_N,e) = (5.15)for this F but without terminal constraints,i.e.,with $\mathbb{X}_{0}=\mathbb{X}$ in (5.15).

Then the nominal NMPC closed-loop system (3.5)with NMPC feedback law μ _N is semiglobally asymptotically stable on $\mathbb{X}$ with respect to the parameter N in the sense of Definition 6.28(i).

Proof

We consider the following three optimal control problems

• (a) (5.15) with$\mathbb{X}_{0}=\mathbb{X}$, which generatesμ _N in this theorem

• (b) (5.15) with$\mathbb{X}_{0}$ from Assumption 5.9 forF, which generatesμ _N in Theorem 5.5

• (c) (OCP_N), which generatesμ _N in Theorem 6.18

and denote the respective optimal value functions by$V_{N}^{(a)}$,$V_{N}^{(b)}$ and$V_{N}^{(c)}$. For each$x\in \mathbb{X}$ we obtain the inequalities$V_{N}^{(c)}(x) \le V_{N}^{(a)}(x) \le V_{N}^{(c)}(x) + c$ and, for$x\in \mathbb{X}_{N}$ (where$\mathbb{X}_{N}$ denotes the feasible set from Definition 3.9 for Problem (b)), we have$V_{N}^{(a)}(x)\le V_{N}^{(b)}(x)$.

In order to show semiglobal asymptotic stability, i.e., Definition 6.28(i), we fix Δ>0. For an arbitrary$x\in \mathbb{X}$ we consider the optimal controlu ^⋆ for Problem (a) (which impliesμ _N (x)=u ^⋆(0) forμ _N from this theorem) and distinguish two cases:

(i)$x_{u^{\star}}(N,x) \in \mathbb{X}_{0}$: This implies$u^{\star}\in \mathbb{U}_{\mathbb{X}_{0}}^{N}(x)$ and hence$x\in \mathbb{X}_{N}$ and$V_{N}^{(a)}(x)=V_{N}^{(b)}(x)$. Using$x_{u^{\star}}(1,x)=f(x,\mu_{N}(x))\in \mathbb{X}_{N}$ and$V_{N}^{(a)}\le V_{N}^{(b)}$ on$\mathbb{X}_{N}$, the proof of Theorem 5.5 yields

$$ \begin{array}{l} V_N^{(a)} (x) = V_N^{(b)} (x) \ge \ell (x,\mu _N (x)) + V_N^{(b)} (f(x,\mu _N (x))) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \ge \ell (x,\mu _N (x)) + V_N^{(a)} (f(x,\mu _N (x))). \\ \end{array} $$

(7.1)

This inequality will be used below in order to conclude asymptotic stability. Before we turn to case (ii) we show that case (i) applies to all points$x\in \mathcal{B}_{\delta}(x_{*})$ for someδ>0:

Since (5.20) shows$V_{N}^{(b)}(x) \le F(x)$ on$\mathbb{X}_{0}$, we obtain$V_{N}^{(a)}(x) \le V_{N}^{(b)}(x) \le \tilde{\alpha}_{2}(|x|_{x_{*}})$ for$x\in \mathcal{B}_{\eta}(x_{*})\subseteq \mathbb{X}_{0}$. For$\delta=\min\{ \eta, \tilde{\alpha}_{2}^{-1}(c/2)\}$ this implies$V_{N}^{(a)}(x) \le c/2$ for all$x\in \mathcal{B}_{\delta}(x_{*})$. On the other hand,$x_{u^{\star}}(N,x) \notin \mathbb{X}_{0}$ implies$F(x_{u^{\star}}(N,x))=c$ and thus$V_{N}^{(a)}(x) \ge c$. Hence, case (i) occurs for all$x\in \mathcal{B}_{\delta}(x_{*})$.

(ii)$x_{u^{\star}}(N,x) \notin \mathbb{X}_{0}$: This implies$F(x_{u^{\star}}(N,x))=c$ and thus$V_{N}^{(a)}(x) = V_{N}^{(c)}(x) + c$. This implies thatu ^⋆ is an optimal control for$V_{N}^{(c)}(x)$ and from the proof of Theorem 6.33 we obtain that (5.1), i.e.,

$$V_N^{(c)}(x) \ge \alpha\ell\bigl(x,\mu_N(x)\bigr) +V_{N}^{(c)}\bigl(f\bigl(x,\mu_N(x)\bigr)\bigr)$$

holds for allx∈Y=S∖P withS andP chosen as in the proof of Theorem 6.33. The setsS andP are forward invariant and by choosingN∈ℕ sufficiently large we obtainα>0,$\overline{ \mathcal{B}}_{\Delta}(x_{*})\subseteq S$ and$P\subset \mathcal{B}_{\delta}(x_{*})$ for Δ fixed above andδ defined at the end of case (i). Since$V_{N}^{(a)}(x) =V_{N}^{(c)}(x) + c$ and$V_{N}^{(a)}(f(x,\mu_{N}(x))) \le V_{N}^{(c)}(f(x,\mu_{N}(x))) + c$ we obtain

$$V_N^{(a)}(x) \ge \alpha\ell\bigl(x,\mu_N(x)\bigr) +V_{N}^{(a)}\bigl(f\bigl(x,\mu_N(x)\bigr)\bigr) $$

(7.2)

for ally∈Y and someα>0.

Now, the choice ofN andP implies that for$x\in S\setminus \mathcal{B}_{\delta}(x_{*})$ Inequality (7.2) holds while for$x\in \mathcal{B}_{\delta}(x_{*})$ Inequality (7.1) holds. This implies that Theorem 4.14 is applicable withS(n)=S which yields semiglobal practical stability using Lemma 6.29(i). □

Comparing Theorem 7.1 with Theorem 6.33, one sees that the benefit of including the terminal costF is that here we obtain semiglobal asymptotic stability while withoutF we can only guarantee semiglobalpractical asymptotic stability. Loosely speaking, the unconstrained scheme guarantees stability up to the neighborhood$\mathcal{B}_{\delta}(x_{*})$, whileF ensures asymptotic stability inside this neighborhood.

7.2 Unconstrained NMPC with Terminal Weights

Our next extension analyzes the effect of inclusion of terminal weights in (OCP_N), i.e., in NMPC schemes without stabilizing terminal constraints and costs. Both in numerical simulations and in practice one can observe that adding terminal weights can improve the stability behavior of the NMPC closed loop. Formally, adding terminal weights can be achieved by replacing the optimization criterion in (OCP_N) by

$$J_N\bigl(x_0,u(\cdot)\bigr) := \sum_{k=0}^{N-2} \ell \bigl(x_u(k,x_0),u(k)\bigr) + \omega \ell\bigl(x_u(N-1,x_0),u(N-1)\bigr) $$

(7.3)

for someω≥1. Forω=1 we thus obtain the original problem (OCP_N). This extension is a special case of (OCP_N,e) in which we specify$\mathbb{X}_{0}=\mathbb{X}$,F≡0,ω ₁=ω andω ₂=ω ₃=⋅⋅⋅=ω _N =1. In a similar way, such a terminal weight can be added to the respective time variant problem ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$) leading to a special case of ($\mathrm{OCP}_{\mathrm{N},\mathrm{e}}^{\mathrm{n}}$). Thus, all results developed in Chap. 3 apply to this problem. Given that the optimal control valueu(N−1) in (7.3) will minimizeℓ(x _u (N−1,x ₀),u(N−1)), this approach is identical to choosingF(x)=ωℓ ^∗(x) andN=N−1 in the terminal cost approach discussed in the previous section, withℓ ^∗ from (6.2). However, the specific structure of the terminal cost allows for applying different and more powerful analysis techniques which we explain now.

The terminal weight leads to an increased penalization ofℓ(x _u (N−1,x ₀),u(N−1)) inJ _N and thus to an increased penalization of the distance ofx _u (N−1,x ₀) tox _∗. Thus, forω>1 the optimizer selects a finite time optimal trajectory whose terminal state$x_{u^{\star}}(N-1,x_{0})$ has a smaller distance tox _∗. Since our goal is that the NMPC-feedback lawμ _N steers the trajectory tox _∗, this would intuitively explain better stability behavior.

Formally, however, the analysis is not that easy because in closed loop we never actually applyu ^⋆(1),…,u ^⋆(N−1) and the effect ofω onu ^⋆(0) is not that obvious. Hence, we extend the technique developed in Chap. 6 in order to analyze the effect ofω. To this end, we change the definition (6.8) ofB _N to

$$B_N(r) := \sum_{n=0}^{N-2}\beta(r,n) + \omega\beta(r,N-1).$$

With this definition, all results in Sect. 6.3 remain valid for the extended problem. Proposition 6.12 remains valid, too, if we change (6.11) to

$$\sum_{n=k}^{N-2}\lambda_n + \omega\lambda_{N-1} \le B_{N-k}(\lambda_k), \quad k=0,\ldots,N-2.$$

If, furthermore, in the subsequent statements we replace$\sum_{n=0}^{N-1}\lambda_{n}$ by$\sum_{n=0}^{N-2}\lambda_{n} +\omega\lambda_{N-1}$, then it can be shown that Proposition 6.17 remains valid if we replace (6.19) by

$$\underline{\alpha}_{N}^\omega := 1 - \frac { (\gamma_N - 1)(\gamma_{2}-\omega)\prod_{i=3}^N (\gamma_i - 1)}{\prod_{i=2}^N \gamma_{i} -(\gamma_{2}-\omega) \prod_{i=3}^{N}(\gamma_{i}-1)}. $$

(7.4)

The proof is similar to the proof of Proposition 6.17 and can be found in Grüne, Pannek, Seehafer and Worthmann [20].

With this expression, Theorem 6.18 and its corollaries remain valid, except for the inequalitiesV _N (x)/α≤V _∞(x)/α andCV _N (x)≤CV _∞(x), which do in general no longer hold because of the additional weight which is present inV _N but not in V _∞.

Figure7.1 shows the values from (7.4) for an exponentialβ of type (6.3) withC=2 andσ=0.55, optimization horizonN=5 and terminal weightsω=1,2,…,20. The figure illustrates that our analysis reflects the positive effect the terminal weight has on the stability: while forω=1,2 we obtain negative values forα and thus stability cannot be ensured, forω≥3 stability is guaranteed. However, one also sees that forω≥10 the value ofα is decreasing, again. For more examples for the effect of terminal weights we refer to [20] and Example 7.14, below.

Fig. 7.1

Suboptimality indexα depending on terminal weightω

7.3 Nonpositive Definite Running Cost

In many regulator problems one is not interested in driving the whole state to a reference trajectory or point. Rather, often one is only interested in certain output quantities. The following example illustrates such a situation.

Example 7.2

We reconsider Example 2.2, i.e.,

with running cost

$$\ell(x,u) = x_1^2+ u^2.$$

In contrast to our standing assumption (3.2), no matter how we choosex _∗∈ℝ², this function does not satisfyℓ(x,u)>0 for allx∈X andu∈U withx≠x _∗. Instead, following the interpretation ofx ₁ andx ₂ as position and velocity of a vehicle in a plane, the running cost only penalizes the distance of the positionx ₁ from 0 but not the velocity.

However, the only way to put the system at rest withx ₁=0 is to setx ₂=0. Hence, one may expect that the NMPC controller will “automatically” steerx ₂ to 0, too. The numerical simulation shown in Fig. 7.2 (performed with optimization horizonN=5 without stabilizing terminal constraints and with state constraints$\mathbb{X}=[-1,1]^{2}$ and control constraints$\mathbb{U}=[-1/4,1/4]$) confirms that this is exactly what happens: the system is perfectly stabilized atx _∗=0 even though the running cost does not “tell” the optimization problem to steerx ₂ to 0.

Fig. 7.2

MPC closed-loop trajectory withN=5

How can this behavior be explained theoretically? The decisive difference ofℓ from this example toℓ used in the theorems in the previous chapters is that the lower bound$\ell(x,u) \ge \alpha_{3}(|x|_{x_{*}})$ imposed in all our results is no longer valid. In other words, the running cost is no longer positive definite.

For NMPC schemes with stabilizing terminal constraints and costs satisfying Assumption 5.9, the notion of input/output-to-state stability (IOSS) provides a way to deal with this setting. IOSS can be seen as a nonlinear detectability condition which ensures that the state converges tox _∗ if both the output and the input converge to their steady state values, which can in turn be guaranteed by suitable bounds onℓ. We sketch this approach for time invariant referencex ^ref≡x _∗ with corresponding control valueu _∗ satisfyingf(x _∗,u _∗)=x _∗.

To this end, we relax the assumptions of Theorem 5.13 as follows: instead of assuming (5.2) we consider an output functionh:X→Y for another metric spaceY. In Example 7.2 we haveX=ℝ²,Y=ℝ andh(x)=x ₁.

Now we change (5.2) to

$$\everymath{\displaystyle}\begin{array}{l}\alpha_1\bigl(\big|h(x)\big|_{y_*}\bigr) \le V_N(x) \le \alpha_2\bigl(|x|_{x_*}\bigr)\quad \mbox{and} \quad \\[6pt]\ell(x,u) \ge \alpha_3\bigl(\big|h(x)\big|_{y_*}\bigr)+ \alpha_3\bigl(|u|_{u_*}\bigr)\end{array} $$

(7.5)

withy _∗=h(x _∗) and$|h(x)|_{y_{*}}=d_{Y}(h(x),y_{*})$, whered _Y (⋅,⋅) is the metric onY. Furthermore, we assume that the system with outputy=h(x) is IOSS in the following sense: There exist$\beta\in \mathcal{KL}$ and$\gamma_{1},\gamma_{2}\in \mathcal{K}_{\infty}$ such that for each$x\in \mathbb{X}$ and each admissible control$u\in \mathbb{U}^{\infty}(x)$ the inequality

$$ \begin{array}{*{20}l} {|x_u (n,x)|x_* } & { \le \max \left\{ {\beta (|\beta (|x|x_* ,n),\gamma _1 \left( {\mathop {\max }\limits_{k = 0,...,n - 1} |u(k)|u_* } \right)} \right.} \\ {} & {\gamma _2 \left( {\mathop {\max }\limits_{k = 0,...,n - 1} |y(k)|_{y_* } } \right)\} } \\ \end{array} $$

holds for alln∈ℕ₀ withy(k)=h(x _u (k,x)).

With these changed assumptions, the assertion of Theorem 5.13 remains valid. The proof relies on the fact that the functionV _N still satisfies

$$V_N(x) \ge \ell\bigl(x,\mu_N(x)\bigr) + V_{N}\bigl(f\bigl(x,\mu_N(x)\bigr)\bigr).$$

This implies that$V_{N}(x_{\mu_{N}}(n,x))$ is monotone decreasing inn and since it is bounded from below by 0 it converges to some value asn→∞, although not necessarily to 0. However, the convergence of$V_{N}(x_{\mu_{N}}(n,x))$ implies convergence of$\ell(x_{\mu_{N}}(n,x), \mu_{N}(x_{\mu_{N}}(n,x)))\to 0$ which by means of the last inequality in (7.5) yields$h(x_{\mu_{N}}(n,x))\to 0$ and$\mu_{N}(x_{\mu_{N}}(n,x))\to 0$. Now the IOSS property can be used to conclude asymptotic stability of the closed loop. For more details of this approach, we refer to the book of Rawlings and Mayne [31, Sect. 2.7 and the references therein].

While the approach just sketched relies on stabilizing terminal constraints, the simulation in Example 7.2 shows that asymptotic stability can also be expected without such constraints. For this setting, a stability proof was given in the work of Grimm, Messina, Tuna and Teel [13] and the main result in this reference extends Theorem 6.33. Again, a detectability condition is used, but this time it is formulated via a suitable auxiliary functionW: we assume the existence of a function$W:X\to \mathbb{R}_{0}^{+}$ which satisfies the inequalities

$$\everymath{\displaystyle}\begin{array}{rcl} W(x) & \le & \overline{\alpha}_W\bigl(|x|_{x_*}\bigr),\\[6pt]W\bigl(f(x,u)\bigr) - W(x) & \le & -\alpha_W\bigl(|x|_{x_*}\bigr) +\gamma_W\bigl(\ell(x,u)\bigr)\end{array} $$

(7.6)

for all$x\in \mathbb{X}$,$u\in \mathbb{U}(x)$ and suitable functions$\overline{\alpha}_{W}, \alpha_{W}, \gamma_{W}\in \mathcal{K}_{\infty}$.

In turn, we remove the lower bound$\alpha_{3}(|x|_{x_{*}}) \le \ell^{*}(x)$ forℓ ^∗ from (6.2) from the assumptions of Theorem 6.33. Observe that whenever this lower bound holds, the detectability condition is trivially satisfied withW≡0,γ _W (r)=r andα _W =α ₃.

Under these modified assumptions, it is shown in [13, Theorem 1] that the semiglobal practical stability assertion of Theorem 6.33 remains valid. Furthermore, [13, Corollary 2 and Corollary 3] provide counterparts to Theorems 6.31 and 6.21 which prove semiglobal and “real” asymptotic stability, respectively. In contrast to the IOSS-based result for stabilizing terminal constraints, the proof of [13, Theorem 1] yields a Lyapunov function constructed from the optimal value functionV _N and the functionW from the detectability condition. In the simplest case, which occurs under suitable bounds on the involved$\mathcal{K}_{\infty}$-functions, this Lyapunov function is given byV _N +W. In general, a weighted sum has to be used.

In Example 7.2, numerical evaluation suggests that the detectability condition is satisfied for$W(x)=\max\{-|x_{1}x_{2}|+x_{2}^{2},0\}/2$ andγ _W (r)=r. Plots of the differenceW(x)−W(f(x,u))+ℓ(x,u) in MAPLE indicate that this expression is positive definite and can hence be bounded from below by some function$\alpha_{W}(|x|_{x_{*}})$; a rigorous proof of this property is, however, missing up to now.

As discussed in Sect. 6.9, the analysis in [13] uses a condition of the formV _N (x)≤α _V (r) in order to show stability, which compared to our Assumptions 6.4 or 6.30 has the drawback to yield fewer information for the design of “good” running costsℓ. Furthermore, suboptimality estimates are not easily available. It would hence be desirable to extend the statement and proof of Theorem 6.18 to the case of nonpositive definite running costs. A first attempt in this direction is the following: suppose that we are able to find a function$W:X\to \mathbb{R}_{0}^{+}$ satisfying (7.6) withγ _W (r)=r. Then the function

$$\ell_W(x,u) := W(x) - W\bigl(f(x,u)\bigr) + \ell(x,u)$$

satisfies a lower bound of the form

$$\ell_W^*(x) := \min_{u\in U} \ell_W(x,u) \ge \alpha_W\bigl(|x|_{x_*}\bigr)$$

for allx∈X. Letu ^⋆ be an optimal control forV _N (x), i.e.,

$$V_N(x) = J_N\bigl(x,u^\star\bigr) = \sum_{k=0}^{N-1} \ell \bigl(x_{u^\star}(k,x),u^\star(k)\bigr)$$

and define

$$\widetilde{V}_N(x) := \sum_{k=0}^{N-1} \ell_W\bigl(x_{u^\star}(k,x),u^\star(k)\bigr).$$

The definition ofℓ _W then implies

$$\widetilde{V}_N(x) = W(x) - W\bigl(x_{u^\star}(N,x)\bigr) + V_N(x).$$

Changing the inequality in Assumption 6.30 to

$$V_k(x) \le B_k\bigl(\ell_W^*(x)\bigr) - W(x)$$

then implies

$$\widetilde{V}_k(x) \le B_k\bigl(\ell_W^*(x)\bigr).$$

Using this inequality, it should be possible to carry over all results in Sect. 6.3 to$\widetilde{V}_{N}$ usingℓ _W in place ofℓ. A rigorous investigation of this approach as well as possible extensions will be the topic of future research.

In this context we would like to emphasize once again that even if the running costℓ only depends on an outputy, the resulting NMPC-feedback law is still a state feedback law because the full state information is needed in order to compute the predictionx _u (⋅,x ₀) forx ₀=x(n).

7.4 Multistep NMPC-Feedback Laws

Next we investigate what happens if instead of only the first control valueu ^⋆(0) we implement the firstm valuesu ^⋆(0),…,u ^⋆(m−1) before optimizing again. Formally, we can write this NMPC variant as a multistep feedback law

$$\mu_N(x,k) := u^\star(k),\quad k=0,\ldots,m-1,$$

whereu ^⋆ is an optimal control sequence for problem (OCP_N,e) (or one of its variants) with initial valuex ₀=x. The resulting generalized closed-loop system then reads

$$x(n+1) = f\bigl(x(n),\mu_N\bigl(x\bigl([n]_m\bigr),n-[n]_m\bigr)\bigr), $$

(7.7)

where [n] _m denotes the largest productkm,k∈ℕ₀, withkm≤n. The valuem∈{1,…,N−1} is called thecontrol horizon.

When using stabilizing terminal constraints, the respective stability proofs from Chap. 5 are easily extended to this setting which we illustrate for Theorem 5.13. Indeed, fromV _N (x)≤V _N−1(x) one immediately gets the inequalityV _N (x)≤V _N−m (x) for eachm∈{1,…,N−1} and each$x\in \mathbb{X}_{N-m}$. Proceeding as in the proof of Theorem 5.13 using Equality (3.20) inductively forN,N−1,…,N−m+1 andV _N (x)≤V _N−m (x) one obtains

$$V_N(x) \ge \sum_{k=0}^{m-1} \ell\bigl(x_{\mu_N}(k,x),\mu_N(k,x)\bigr) + V_{N}\bigl(x_{\mu_N}(m,x)\bigr).$$

This shows thatV _N is a Lyapunov function for the closed-loop system at the times 0,m,2m,…. Since a similar argument shows that$V_{N}(x_{\mu_{N}}(k,x))$ is bounded byV _N (x) fork=1,…,m−1, this proves asymptotic stability of the closed loop.

Without stabilizing terminal constraints, our analysis can be adjusted to the multistep setting, too, by extending Proposition 6.17 as well as the subsequent stability results, accordingly. The respective extension of Formulas (6.19) and (7.4) (including both control horizonsm≥1 and terminal weightsω≥1) is given by

$$\underline{\alpha}_{N,m}^\omega = 1 - \tfrac {(\gamma_{m+1}-\omega)\prod_{i=m+2}^N (\gamma_i - 1) \prod_{i=N-m+1}^{N}(\gamma_i - 1)}{ (\prod_{i=m+1}^N \gamma_{i} -(\gamma_{m+1}-\omega) \prod_{i=m+2}^{N}(\gamma_{i}-1) ) ( \prod_{i=N-m+1}^N \gamma_{i} -\prod_{i=N-m+1}^N (\gamma_{i}-1) )}.$$

Again, the proof proceeds along the lines of the proof of Proposition 6.17 but becomes considerably more involved, cf. the paper by Grüne, Pannek, Seehafer and Worthmann [20].

It is worth noting that these extended stability and performance results remain valid ifm is time varying, i.e., if the control horizon is changed dynamically, e.g., by a network induced perturbation. This has interesting applications in NMPC for networked control systems, cf. the work of Grüne, Pannek and Worthmann [18].

Figure7.3 shows how$\alpha=\underline{\alpha}_{N,m}^{\omega}$ depends onm for an exponentialβ of type (6.3) withC=2 andσ=0.75, optimization horizonN=11, terminal weightω=1 and control horizonsm=1,…,10. Here one observes two facts: first, theα-values are symmetric, i.e.,$\underline{\alpha}_{N,m}^{\omega}= \underline{\alpha}_{N,N-m}^{\omega}$ and second, the values increase untilm=(N−1)/2 and then decrease, again. This is not a particular feature of this example. In fact, it can be rigorously proved for a general class of$\beta\in \mathcal{KL}_{0}$; see [20] for details.

Fig. 7.3

Suboptimality indexα depending on control horizonm

It is interesting to compare Fig. 7.3 withα-values which have been obtained numerically from an NMPC simulation for the linear inverted pendulum, cf. Example 2.10 and Sect. A.2 or [18] for the precise description of the problem. Figure 7.4 shows the resulting values for a set of different initial values. These values have been computed by Algorithm 7.8 described in Sect. 7.7, below.

Fig. 7.4

Numerically measured values forα for a linear inverted pendulum and various initial values. Thethick line represents the minimum

While the monotonicity is—at least approximately—visible in this example, the perfect symmetry from Fig. 7.3 is not reflected in Fig. 7.4. A qualitatively similar behavior can be observed for the nonlinear inverted pendulum; see Example 7.14, below. In fact, so far we have not been able to find an example for which the symmetry could be observed in simulations. This may be due to the fact that our stability estimate is tight not for a single system but rather for the whole class of systems satisfying Assumption 6.4, cf. Theorem 6.23. Our numerical findings suggest that the conservativity induced by this “worst case approach” is higher for smallm than for largem. This is also supported by Monte Carlo simulations performed by Grüne in [14].

7.5 Fast Sampling

Let us now turn to the special case of sampled data systems. In this case, according to (2.12) the discrete time solutionx _u (n,x ₀) represents the continuous time solutionϕ(t,0,x ₀,v) at sampling timest=nT. In this setting, it is natural to define the optimization horizon not in terms of the discrete time variablen but in terms of the continuous timet. Fixing an optimization horizonT _opt>0 and picking a sampling periodT>0 where we assume for simplicity of exposition thatT _opt is an integer multiple ofT, the discrete time optimization horizon becomesN=T _opt/T, cf. also Sect. 3.5.

Having introduced this notation, an interesting question is what happens to stability and performance of the NMPC closed loop if we keepT _opt fixed but vary the sampling periodT. In particular, it is interesting to see what happens if we sample faster and faster, i.e., if we letT→0. Clearly, in a practical NMPC implementation we cannot arbitrarily reduceT because we need some time for solving the optimal control problem (OCP_N) or its variants online. Still, in particular in the case of zero order hold it is often desirable to sample as fast as possible in order to approximate the ideal continuous time control signal as good as possible, cf., e.g., the paper of Nešić and Teel [26], and thus one would like to make sure that this does not have negative effects on the stability and performance of the closed loop.

In the case of equilibrium endpoint constraint from Sect. 5.2 it is immediately clear that the stability result itself does not depend onT, however, the feasible set$\mathbb{X}_{N}$ may change withT. In the case of zero order hold, i.e., when the continuous time control function ν is constant on each sampling interval [nT,(n+1)T), cf. the discussion after Theorem 2.7, it is easily seen that each trajectory for sampling periodT is also a trajectory for each sampling periodT/k for eachk∈ℕ. Hence, the feasible set$\mathbb{X}_{kN}$ for sampling periodT/k always contains the feasible set$\mathbb{X}_{N}$ for sampling periodT, i.e., the feasible set cannot shrink fork→∞ and hence for sampling periodT/k we obtain at least the same stability properties as for sampling periodT.

In the case of Lyapunov function terminal costsF as discussed in Sect. 5.3 either the terminal costs or the running costs need to be adjusted to the sampling periodT in order to ensure that Assumption 5.9 remains valid. One way to achieve this is to choose a running cost in integral form (3.4) and the terminal costF such that the following condition holds: for each$x\in \mathbb{X}_{0}$ and someT ₀>0 there exists a continuous time controlv satisfying$\varphi(t,0,x,v)\in \mathbb{X}_{0}$ and

$$V\bigl(\varphi(t,0,x,v)\bigr) - V(x) \le - \int_0^t L\bigl(\varphi(\tau,0,x,v),v(\tau)\bigr)\, d\tau $$

(7.8)

for allt∈[0,T], cf. also Findeisen [9, Sect. 4.4.2]. Under this condition one easily checks that Assumption 5.9 holds forℓ from (3.4) and allT≤T ₀, provided the control functionv in (7.8) is of the formv|_[nT,(n+1)T)(t)=u(n)(t) for an admissible discrete time control sequenceu(⋅) withu(n)∈U. IfU=L ^∞([0,T],ℝ^m) then this last condition is not a restriction but if we use some smaller space forU (as in the case of zero order hold, cf. the discussion after Theorem 2.7), then this may be more difficult to achieve; see also [9, Remark 4.7].

Since the schemes from Chap. 6 do not use stabilizing terminal constraints$\mathbb{X}_{0}$ and terminal costsF, the difficulties just discussed vanish. However, the price to pay for this simplification is that the analysis of the effect of small sampling periods which we present in the remainder of this section is somewhat more complicated.

FixingT _opt and lettingT→0 we obtain thatN=T _opt/T→∞. Looking at Theorem 6.21, this is obviously a good feature, because this theorem states that the largerN becomes, the better the performance will be. However, we cannot directly apply this theorem because we have to take into account thatβ in the Controllability Assumption 6.4 will also depend onT.

In order to facilitate the analysis, let us assume that in our discrete time NMPC formulation we use a running costℓ that only takes the statesϕ(nT,0,x ₀,v) at the sampling instants and the respective control values into account.¹ For the continuous time system, the controllability assumption can be formulated in discrete time. We denote the set of admissible continuous time control functions (in analogy to the discrete time notation) by$\mathbb{V}^{\tau}(x)$. More precisely, for the admissible discrete time control values$\mathbb{U}(x) \subseteq U\subseteq L^{\infty}([0,T],\mathbb{R}^{m})$ (recall that these “values” are actually functions on [0,T], cf. the discussion after Theorem 2.7) and anyτ>0 we define

$$ \begin{array}{l} V^\tau (x): = \{ \nu \in L^{^\infty } ([0,\tau ],R^m )|\,\,\,\,{\rm there exists }u \in U^N (x)\,\,\,{\rm with}\,\,N \ge \tau /T + 1 \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm such that }u(n) = \nu |[nT,(n + 1)T( \cdot + nT) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm holds for all }n \in N_0 {\rm with }nT< \tau \} . \\ \end{array} $$

Then, the respective assumption reads as follows.

Assumption 7.3

We assume that the continuous time system is asymptotically controllable with respect toℓ with rate$\beta\in \mathcal{KL}_{0}$, i.e., for each$x\in \mathbb{X}$ and eachτ>0 there exists an admissible control function$v_{x}\in \mathbb{V}^{\tau}(x)$ satisfying

$$\ell\bigl(\varphi(t,0,x,v_x),v_x(t)\bigr) \le \beta\bigl(\ell^*(x),t\bigr)$$

for allt∈[0,τ].

For the discrete time system (2.8) satisfying (2.12) the Controllability Assumption 7.3 translates to the discrete time Assumption 6.4 as

$$\ell\bigl(x_{u_x}(n,x),u_{x}(n)\bigr) \le \beta\bigl(\ell^*(x),nT\bigr).$$

In the special case of exponential controllability,β in Assumption 7.3 is of the form

$$\beta(r,t) = C e^{-\lambda t}r $$

(7.9)

forC≥1 andλ>0. Thus, for the discrete time system, the Controllability Assumption 6.4 becomes

$$\ell\bigl(x_{u_x}(n,x),u_{x}(n)\bigr) \le Ce^{-\lambda nT}\ell^*(x) = C \bigl(e^{-\lambda T} \bigr)^n \ell^*(x)$$

and we obtain a$\mathcal{KL}_{0}$-function of type (6.3) withC from (7.9) andσ=e ^−λT.

Summarizing, if we change the sampling periodT, then not only the discrete time optimization horizonN but also the decay rateσ in the exponential controllability property will change, more precisely we haveσ→1 asT→0. When evaluating (6.19) with the resulting values

$$\gamma_k = \sum_{j=0}^{k-1} Ce^{-\lambda jT},$$

it turns out that the convergenceσ→1 counteracts the positive effect of the growing optimization horizonsN→∞. In fact, the negative effect ofσ→1 is so strong thatα diverges to −∞ asT→0. Figure 7.5 illustrates this fact (which can also be proven rigorously, cf. [21]) forC=2,λ=1 andT _opt=5.

Fig. 7.5

Suboptimality indexα from (6.19) for fixedT _opt and varying sampling period T

This means that whenever we choose the sampling periodT>0 too small, then performance may deteriorate and eventually instability may occur. This predicted behavior is not consistent with observations in numerical examples. How can this be explained?

The answer lies in the fact that our stability and performance estimate is only tight for one particular system in the class of systems satisfying Assumption 6.4, cf. Theorem 6.23 and the discussion preceding this theorem, and not for the whole class. In particular, the subclass of sampled data systems satisfying Assumption 6.4 may well behave better than general systems. Thus, we may try to identify the decisive property which makes sampled data systems behave better and try to incorporate this property into our computation ofα.

To this end, note that so far we have not imposed any continuity properties off in (2.1). Sampled data systems, however, are governed by differential equations (2.6) for which we have assumed Lipschitz continuity in Assumption 2.4. Let us assume for simplicity of exposition that the Lipschitz constant in this assumption is independent ofr. Then, for a large class of running costsℓ the following property for the continuous time system can be concluded from Gronwall’s Lemma; see [21] for details.

Assumption 7.4

There exists a constantL>0 such that for each$x\in \mathbb{X}$ and eachτ>0 there exists an admissible control function$v_{x}\in \mathbb{V}^{\tau}(x)$ satisfying

$$\ell\bigl(\varphi(t,0,x,v_x),v_x(t)\bigr) \le e^{Lt}\ell^*(x)$$

for allt∈[0,τ].

The estimates onℓ induced by this assumption can now be incorporated into the analysis in Chap. 6. As a result, the valuesγ _k in Formula (6.19) change to

$$\gamma_k = \min \Biggl\{\,\sum_{j=0}^{k-1} Ce^{-\lambda jT},\sum_{j=0}^{k-1} e^{LjT} \Biggr\}.$$

The effect of this change is clearly visible in Fig. 7.6. Theα-values from (6.19) no longer diverge to −∞ but rather converge to a finite—and for the chosen parameters also positive—value asT→0. Again, this convergence behavior can be rigorously proved; for details we refer to [21].

Fig. 7.6

α for fixedT _opt and varying sampling periodT without Assumption 7.4 (lower graphs) and with Assumption 7.4 (upper graphs) withL=2 (left) andL=10 (right)

7.6 Compensation of Computation Times

Throughout the previous chapters we assumed that the solution of the optimal control problems (OCP_N,e) and its variants in Step (2) of Algorithms 3.1, 3.7, 3.10 and 3.11 can be obtained instantaneously, i.e., with negligible computation time. Clearly, this is not possible in general, as the algorithms for solving such problems, cf. Chap. 10 for details, need some time to compute a solution. If this time is large compared to the sampling periodT, the computational delay caused by Step (2) is not negligible and needs to be considered. One way for handling these delays would be to interpret them as perturbations and use techniques similar to the robustness analysis in Sects. 8.5–8.9. In this section we pursue another idea in which a delay compensation mechanism is added to the NMPC scheme.

Taking a look at the structure of the NMPC algorithm from Chap. 3, we see that Steps (1)–(3) correspond to different physical tasks: measuring, computing and applying the control. These tasks are operated by individual components as shown schematically in Fig. 7.7. Note that in the following actuator, sensor and controller are not required to be physically decomposed, however, this case is also not excluded.

Fig. 7.7

Scheme of the NMPC closed-loop components

While it is a necessity to consider different clocks in a decomposed setting, it may not be the case if the components are physically connected. Here, we assume that every single component possesses its own clock and, for simplicity of exposition, that these clocks are synchronized (see the work of Varutti and Findeisen [34, Sect. III.C] for a possible way to relax this assumption). To indicate that a time instantn is considered with respect to a certain clock, we indicate this by adding indicess for the sensor,c for the NMPC controller anda for the actuator.

The idea behind the compensation approach is to run the NMPC controller component with a predefined time offset. This offset causes the controller to compute a control ahead of time, such that the computed control value is readily available at the time it is supposed to be applied, cf. Fig. 7.8. In this figure,τ _c denotes the actual computational delay and$\tau_{c}^{\max}$ denotes the predefined offset. In order to be operable, this offset needs to be chosen such that it is larger than the maximal computing time required to solve the optimal control problem in Step (2) of the considered NMPC algorithm. At timen _c this optimal control problem is solved with a prediction$\tilde{x}(n_{a})$ of the initial valuex(n _a ) based on the available measurementx(n _c )=x(n _s ). This prediction is performed using the same model which is used for the NMPC prediction in (OCP_N,e) or its variants, i.e., using (2.1).

Fig. 7.8

Operation of time decoupled NMPC scheme

In order to perform this prediction, the control valuesμ _N (n,x(n)),n∈{n _s ,…,n _a } which are to be applied at the plant during the time interval [n _s ,n _a ] and which have been computed before by the NMPC controller are needed and are therefore buffered. Thus, we extend the scheme given in Fig. 7.7 by adding the required predictor to the controller. The structure of the resulting scheme is shown in Fig. 7.9.

Fig. 7.9

Scheme of the time decoupled NMPC closed-loop components

Observe that in this scheme we buffer the control values twice: within the predictor, but also at the actuator since the computation ofμ(n _a ,x(n _a )) will be finished ahead of time if$\tau_{c}<\tau_{c}^{\max}$, which is the typical case. Alternatively, one could use only one buffer at the controller and send each control value “just in time”. Using two buffers has the advantage that further delays induced, e.g., by network delays between the controller and the actuator can be compensated; see also the discussion at the end of this section.

The corresponding algorithm has the following form. Since all NMPC algorithms stated in Chap. 3 can be modified in a similar manner, we only show the algorithm for the most general form given in Algorithm 3.11:

Algorithm 7.5

(Time decoupled NMPC algorithm for time varying reference)

At each sampling timet _n ,n=0,1,2,…:

• (1) Measure the statex(n _s ):=x(n)∈X of the system and send pair (n _s ,x(n _s )) to controller.

• (2a) Delete pair (n _c −1,μ _N (n _c −1,x(n _c −1))) from bufferB _c and compute the predicted state$\tilde{x}(n_{c} + \tau_{c}^{\max})$ from the measured statex(n _c ).

• (2b) Set$\tilde{n} := n_{c} + \tau_{c}^{\max}$,$x_{0} = \tilde{x}(\tilde{n})$ and solve the optimal control problem

  

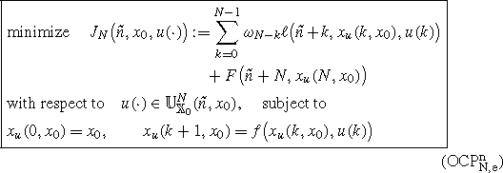
  and denote the obtained optimal control sequence by$u^{\star}(\cdot) \in \mathbb{U}_{\mathbb{X}_{0}}^{N}(\tilde{n},x_{0})$.

• (2c) Add pair$(\tilde{n},\mu_{N}(\tilde{n}, \tilde{x}(\tilde{n}))) :=(\tilde{n}, u^{\star}(0))$ to BufferB _c and send it to actuator.

• (3a) Delete pair$(n_{a} - \tau_{c}^{\max} - 1,\mu_{N}(n_{a} - \tau_{c}^{\max} - 1, \tilde{x}(n_{a} - \tau_{c}^{\max}- 1)))$ and add received pair$(n_{a}, \mu_{N}(n_{a},\tilde{x}(n_{a})))$ to bufferB _a .

• (3b) Use$\mu_{N}(n_{a} - \tau_{c}^{\max}, \tilde{x}(n_{a} - \tau_{c}^{\max}))$ in the next sampling period.

At a first glance, writing this algorithm using three different clocks and sending time stamped information in Steps (1) and (2c) may be considered as overly complicated, given thatn _s in Step (1) is always equal ton _c in Step (2a) andn _c in Step (2c) always equalsn _a in Step (3a). However, this way of writing the algorithm allows us to easily separate the components—sensor, predictor/controller and actuator—of the NMPC scheme and to assume that the “sending” in Steps (1) and (2c) is performed via a digital network. Then, we can assign Step (1) to the sensor, Steps (2a)–(2c) to the controller and Steps (3a) and (3b) to the actuator. Assuming that all transmissions between the components can be done with negligible delay, we can run these three steps as separate algorithms in parallel. Denoting the real time byn, the resulting scheduling structure is sketched in Fig. 7.10 for$\tau_{c}^{\max}=2$. For comparison, the structure of the NMPC Algorithm 3.11 without prediction is indicated by the dashed lines.

Fig. 7.10

Comparison of scheduling structure between NMPC Algorithms 3.11 (dashed lines) and 7.5 (solid lines) with$\tau_{c}^{\max} = 2T$

Since the algorithm is already applicable to work in parallel, it can be extended to a more complex networked control context in which transmission delays and packet loss may occur. To this end, such delays have to be considered in the prediction and an appropriate error handling must be added for handling dropouts; see, e.g., the paper by Grüne, Pannek and Worthmann [19]. In the presence of transmission delays and dropouts, we cannot expect that all control values are actually available at the actuator when they are supposed to be applied. Using NMPC, this can be compensated easily using the multistep feedback concept and the respective stability results from Sect. 7.4 as presented by Grüne et al. in [18].

Besides [19], which forms the basis for the presentation in this section, model based prediction for compensating computational delay in NMPC schemes has been considered earlier, e.g., in the works of Chen, Ballance and O’Reilly [4] and Findeisen and Allgöwer [10]. Note that the use of the nominal model (2.1) for predicting future states may lead to wrong predictions in case of model uncertainties, disturbances etc. In this case, the predicted state$\tilde{x}(\tilde{n})$ may differ from the actual statex(n _a ) at time$n_{a}=\tilde{n}$ and hence (OCP_N,e) is solved with a wrong initial value. In the paper of Zavala and Biegler [35] a method for correcting this mismatch based on NLP sensitivity techniques is presented, cf. also Sect. 10.5.

7.7 Online Measurement ofα

In the analysis of NMPC schemes without stabilizing terminal constraints in Chap. 6, one of the central aims was to establish conditions to rigorously guarantee the existence ofα∈(0,1] such that the inequality

$$ V_N(n,x) \ge \alpha\ell\bigl(n,x,\mu_N(n,x)\bigr) + V_N\bigl(n+1,f\bigl(x,\mu_N(n,x)\bigr)\bigr) $$

(5.1)

holds for all$x \in \mathbb{X}$ andn∈ℕ₀. While Theorem 6.14 and Proposition 6.17 provide computational methods for estimatingα from the problem data, the assumptions needed for these computations—in particular Assumption 6.4—may be difficult to check.

In this section we present methods from Grüne and Pannek [15] and Pannek [29] which allow for the online computation or estimation ofα along simulated NMPC closed-loop trajectories. There are several motivations for proceeding this way. First, as already mentioned, it may be difficult to check the assumptions needed for the computation ofα using Theorem 6.14 or Proposition 6.17. Although a simulation based computation ofα for a selection of closed-loop trajectories cannot rigorously guarantee stability and performance for all possible closed-loop trajectories, it may still give valuable insight into the performance of the controller. In particular, the information obtained from such simulations may be very useful in order to tune the controller parameters, in particular the optimization horizonN and the running cost ℓ.

Second, requiring (5.1) to hold for all$x\in \mathbb{X}$ may result in a rather conservative estimate forα. As we will see in Proposition 7.6, below, for assessing the performance of the controller along one closed-loop trajectory it is sufficient that (5.1) holds only for those points$x\in \mathbb{X}$ which are actually visited by this trajectory.

Finally, the knowledge ofα may be used for an online adaptation of the optimization horizonN; some ideas in this direction are described in the subsequent Sect. 7.8.

Our first result shows that for assessing stability and performance of the NMPC controller along one specific closed-loop trajectory it is sufficient to findα such that (5.1) holds for the points actually visited by this trajectory.

Proposition 7.6

Consider the feedback law $\mu_{N}: \mathbb{N}_{0} \times \mathbb{X}\rightarrow \mathbb{U}$ computed from Algorithm 3.7and the closed-loop trajectory $x(\cdot)=x_{\mu_{N}}(\cdot)$ of (3.9)with initial value $x(0) \in \mathbb{X}$ at initial time 0.If the optimal value function $V_{N}:\mathbb{N}_{0} \times \mathbb{X}\rightarrow \mathbb{R}_{0}^{+}$ satisfies

$$ V_N (n,x(n)) \ge V_N (n + 1,x(n + 1)) + \alpha \ell (n,x(n))) $$

(7.10)

for some α∈(0,1]and all n∈ℕ₀,then

$$ \alpha V_\infty (n,x(n)) \le \alpha J_\infty (n,x(n),\mu _N ) \le V_N (n,x(n)) \le V_\infty (n,x(n)) $$

(7.11)

holds for all n∈ℕ₀.

If,in addition,there exist $\alpha_{1},\alpha_{2},\alpha_{3} \in \mathcal{K}_{\infty}$ such that (5.2)holds for all $(n,x)\in \mathbb{N}_{0}\times \mathbb{X}$ with n∈ℕ₀ and x=x(n),then there exists $\beta\in \mathcal{KL}$ which only depends on α ₁,α ₂,α ₃ and α such that the inequality

$$\big|x(n)\big|_{x^{\mathrm{ref}}(n)} \le \beta\bigl(\big|x(0)\big|_{x^{\mathrm{ref}}(0)},n\bigr)$$

holds for all n∈ℕ₀,i.e.,x behaves like a trajectory of an asymptotically stable system.

Proof

The proof of (7.11) is similar to the proof of Theorem 4.11.

The existence ofβ follows with the same construction as in the proof of Theorem 2.19, observing that the definition ofβ in this proof only depends onα ₁,α ₂ andα _V =αα ₃ and not on the specific form ofV=V _N . □

Proposition 7.6 gives us a way to computeα from the data available at runtime and guarantees the performance estimate (7.11) as well as—under the additional assumption that (5.2) holds—asymptotic stability-like behavior for the considered closed-loop trajectory ifα>0. Moreover, under this additional assumption (7.10) immediately implies thatV _N strictly decreases along the trajectory, i.e., it behaves like a Lyapunov function.

Since the values ofα for which (5.1) holds for all$x\in \mathbb{X}$ and for which (7.10) holds along a specific trajectory$x_{\mu_{N}}$ will be different in general, we introduce the following definition.

Definition 7.7

• (1) We call$\alpha := \max \{ \alpha \mid \mbox{ (5.1) holds for all}\ x \in \mathbb{X}\}$ theglobal suboptimality degree.

• (2) For fixed$x \in \mathbb{X}$ the maximal value ofα satisfying (5.1) for thisx is calledlocal suboptimality degree inx.

• (3) Given a closed-loop trajectory$x_{\mu_{N}}(\cdot)$ of (3.9) with initial time 0 we call$\alpha := \max \{ \alpha \mid \mbox{ (7.10) holds forall}\ n \in \mathbb{N}_{0}\ \mbox{with}\ x(\cdot)=x_{\mu_{N}}(\cdot)\}$ theclosed-loop suboptimality degree along$x_{\mu_{N}}(\cdot)$.

An algorithm to evaluateα from (7.10) can easily be obtained and integrated into Algorithm 3.7:

Algorithm 7.8

(NMPC algorithm for time varying referencex ^ref with a posteriori suboptimality estimate)

Setα=1. At each sampling timet _n ,n=0,1,2,…:

• (1) Measure the statex(n)∈X of the system.

• (2) Setx ₀=x(n) and solve the optimal control problem

  

  and denote the obtained optimal control sequence by$u^{\star}(\cdot) \in \mathbb{U}^{N}(x_{0})$.

• (3) Define the NMPC-feedback valueμ _N (n,x(n)):=u ^⋆(0)∈U and use this control value in the next sampling period.

• (4) Ifn≥1 computeα via

  

Proposition 7.6 and Algorithm 7.8 are easily extended to the multistep NMPC case described in Sect. 7.4. In this case, (7.10) is replaced by

$$ \begin{array}{*{20}l} {V_N (n,x(n)) \ge } & {V_N (n + m + 1,x(n + m + 1))} \\ {} & { + \alpha \sum\limits_{k = 0}^m {\ell (n + k,x_u (k,x(n)),u^* (k,x(n)))} } \\ \end{array} $$

and the definition ofα _l in Step (4) is changed, accordingly.

Note that in Step (4) of Algorithm 7.8, the computation ofα _l does not provide the value ofα in (7.10) for the current time instantn but forn−1. This is why we callα from Algorithm 7.8 ana posteriori estimate. The distinction between the current value ofα _l andα in Step (4) is required in order to be consistent with Proposition 7.6 sinceα _l corresponds to the local suboptimality degree inx(n−1) while the suboptimality degree according to Proposition 7.6 is the minimum over allα _l along the closed loop.

While Algorithm 7.8 is perfectly suited in order to evaluate the performance of an NMPC controller via numerical simulations, its a posteriori nature is not suitable if we want to use the estimatedα in order to adjust the optimization horizonN. For instance, if we detect that at some timen the value ofα in (7.10) is too small—or even negative—then we may want to increaseN in order to increaseα (see Sect. 7.8 for more details on such procedures). However, in Algorithm 7.8 the value ofα in (7.10) only becomes available at timen+1, which is too late in order to adjustN.

A simple remedy for this problem is to solve at timen a second optimal control problem ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$) with initial valuex _u (1,x(n)) and initial timen:=n+1. However, since solving the problem ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$) is the computationally most expensive part of the NMPC algorithm, this solution would be rather inefficient.

In order to obtain ana priori estimate with reduced additional computing costs, a few more insights into the local NMPC problem structure are required. The main tool we are going to use is the following lemma.

Lemma 7.9

Consider the feedback law $\mu_{N}: \mathbb{N}_{0} \times \mathbb{X}\rightarrow \mathbb{U}$ computed from Algorithm 3.7and the closed-loop trajectory $x(\cdot)=x_{\mu_{N}}(\cdot)$ of (3.9)with initial value $x(0) = x_{0} \in \mathbb{X}$ at initial time 0.If

$$ \begin{array}{l} V_N (n + 1,x(n + 1)) - V_{N - 1} (n + 1,x(n + 1)) \\ \le (1 - \alpha )\ell (n,x(n),\mu _N (n,x(n))) \\ \end{array} $$

(7.12)

holds for some α∈[0,1]and some n∈ℕ₀,then (7.11)holds for this n.

Proof

Using the dynamic programming principle (3.16) withK=1 we obtain

Hence, (7.10) holds and Proposition 7.6 guarantees the assertion. □

Now, we would not gain much if we tried to computeα using (7.12) directly, since we would again need the future informationV _N (n+1,x(n+1)), i.e., the solution of another optimal control problem (in contrast to thatV _N−1(n+1,x(n+1)) is readily available at timen since by the dynamic programming principle it can be computed fromV _N (n,x(n)) andℓ(x(n),μ _N (x(n)))). There is, however, a way to reduce the size of the additional optimal control problem that needs to be solved. To this end, we introduce the following assumption which will later be checked numerically in our algorithm.

Assumption 7.10

For givenN,N ₀∈ℕ,N≥N ₀≥2, there exists a constantγ>0 such that for the optimal open-loop solution$x_{u^{\star}}(\cdot, x(n))$ of ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$) in Algorithm 3.7 the inequalities

$$ \frac{{V_{N0} (n + N - N_0 ,x_{u*} (N - N_0 x(n)))}}{{\gamma + 1}} $$

hold for allk∈{N ₀+1,…,N} and alln∈ℕ₀.

Note that computingγ for which this assumption holds requires only the computation ofμ _j forj=1,…,N ₀−1 in the first inequality, sinceμ _k in the second inequality can be obtained fromu ^⋆ via (3.23). This corresponds to solvingN ₀−2 additional optimal control problems which may look like a step backward, but since these optimal control problems are defined on a significantly smaller horizon, the computing costs are actually reduced. In fact, in the special case thatℓ does not depend onu, no additional computations have to be performed, at all. In this assumption, the valueN ₀ is a design parameter which affects the computational effort for checking Assumption 7.10 as well as the accuracy of the estimate forα obtained from this assumption.

Under Assumption 7.10 we can relate the minimal values of two optimal control problems with different horizon lengths.

Proposition 7.11

Suppose that Assumption 7.10holds for N≥N ₀≥2.Then

$$ \frac{{(\gamma + 1)^{N - N_0 } }}{{(\gamma + 1)^{N - N_0 } + \gamma ^{N - N_0 + 1} }}V_N (n,x(n)) \le V_{N - 1} (n,x(n)) $$

holds for all n∈ℕ₀.

Proof

In the following we use the abbreviationx _u (j):=x _u (j,x(n)),j=0,…,N, since all our calculations use the open-loop trajectory with fixed initial valuex(n).

Set$\tilde{n} := N - k$. Using the principle of optimality and Assumption 7.10 we obtain

$$ \begin{array}{l} V_{k - 1} (n + \tilde n + 1,f(x_u (\tilde n),\mu k(n + \tilde n,x_u (n \\ \le \gamma \ell (n + \tilde n,x_u (\tilde n),\mu k(n + \tilde n,x_u (\tilde n))) \\ \end{array} $$

(7.13)

for allk∈{N ₀+1,…,N} and alln∈ℕ₀.

We abbreviate$\eta_{k} = \frac{(\gamma + 1)^{k - N_{0}}}{(\gamma + 1)^{k -N_{0}} + \gamma^{k - N_{0} + 1}}$ and prove the main assertion$\eta_{k}V_{k}(n+\tilde{n}, x_{u}(\tilde{n})) \leq V_{k-1}(n+\tilde{n},x_{u}(\tilde{n}))$ by induction overk=N ₀,…,N. By choosingx _u (0)=x(n) withn being arbitrary but fixed we obtain

$$ \begin{array}{l} V_{N_0 } (n + N - N_0 ,x_u (N - N_0 )) \\ \le (\gamma + 1)\mathop {\max }\limits_{j = 2,...,N_0 } \ell (n + N - j,x_u (N - j),\mu _{j - 1} (n + N - j,x_u (N - j))) \\ \le (\gamma + 1)\sum\limits_{j = 2}^{N_0 } {\ell (n + N - j,x_u (N - j),\mu _{j - 1} (n + N - j,x_u (N - j)))} \\ = \frac{1}{{\eta N_0 }}V_{N_0 - 1} (n + N_0 ,x_u (N - N_0 )). \\ \end{array} $$

For the induction stepk→k+1 the following holds, using (7.13) and the induction assumption:

$$ \begin{array}{*{20}l} {v_k (n + \tilde n,x_u (\tilde n))} \\ { = V_{k - 1} (n + \tilde n + 1,f(x_u (\tilde n),\mu _k (n + \tilde n,x_u (\tilde n))))} \\ { + \ell (n + \tilde n,x_u (\tilde n),\mu _k (n + \tilde n,x_u (\tilde n))} \\ { \ge \eta k\left( {1 + \frac{{1 - \eta k}}{{\gamma + \eta k}}} \right)V_k (n + \tilde n + 1,f(x_u (\tilde n),\mu _k (n + \tilde n,x_u (\tilde n))))} \\ { + \left( {1 - \gamma \frac{{1 - \eta k}}{{\gamma + \eta k}}} \right)\ell (n + \tilde n + 1,f(x_u (\tilde n),\mu k(n + \tilde n,x_u (\tilde n)))} \\ { = \eta k\frac{{\gamma + 1}}{{\gamma + \eta k}}(V_k (n + \tilde n + 1,f(x_u (\tilde n),\mu k(n + \tilde n,x_u (\tilde n))))} \\ { + \ell (n + \tilde n,x_u (\tilde n),\mu k(n + \tilde n,x_u (\tilde n))))} \\ \end{array} $$

using the dynamic programming principle (3.16) withK=1 in the last step. Hence, we obtain$V_{k}(n+\tilde{n},x_{u}(\tilde{n})) \geq \eta_{k} \frac{\gamma + 1}{\gamma +\eta_{k}} V_{k + 1}(n+\tilde{n}, x_{u}(\tilde{n}))$ with

$$ \begin{array}{*{20}l} {\eta k\frac{{\gamma + 1}}{{(\gamma + \eta k}}} & { = \frac{{(\gamma + 1)^{k - 2} }}{{(\gamma + 1)^{k - 2} + \gamma ^{k - 1} }}\frac{{\gamma + 1}}{{\gamma + \frac{{(\gamma + 1)^{k - 2} }}{{(\gamma + 1)^{k - 2} + \gamma ^{k - 1} }}}}} & { = \frac{{(\gamma + 1)^{k - 1} }}{{(\gamma + 1)^{k - 1} + \gamma ^k }} = \eta k + 1.} \\ \end{array} $$

If we choosek=N then we get$\tilde{n} = 0$. Inserting this into our induction result we can usex _u (0)=x _u (0,x(n))=x(n) and the assertion holds. □

Finally, we can now use Proposition 7.11 within the NMPC closed loop. This allows us to verify Condition (7.12) and to estimateα directly from Assumption 7.10.

Theorem 7.12

Consider γ>0and N,N ₀∈ℕ,N≥N ₀ such that $(\gamma + 1)^{N - N_{0}} > \gamma^{N - N_{0} + 2}$ holds.If Assumption 7.10is fulfilled for these γ,N and N ₀,then the estimate (7.11)holds for all n∈ℕ₀ where

$$ \alpha : = \frac{{(\gamma + 1)^{N - N_0 } - \gamma ^{N - N_0 + 2} }}{{(\gamma + 1)^{N - N_0 } }}. $$

(7.14)

Proof

From Proposition 7.11 we know

$$ V_N (n,x,(n) - V_{N - 1} (n,x(n)) \le \frac{{\gamma ^{N - N_0 + 1} }}{{(\gamma + 1)^{N - N_0 } }}V_{N - 1} (n,x(n)). $$

Settingj=n−1, we can reformulate this and obtain

$$ \begin{array}{l} {\rm V}_{\rm N} (j + 1,x(j + 1)) - V_{N - 1} (j + 1,x(j + 1)) \\ \,\,\,\,\,\, \le \frac{{\gamma ^{N - N_0 + 1} }}{{(\gamma + 1)^{N - N_0 } }}V_{N - 1} (j + 1,f(x_u (0,x(j)),\mu N(j,x_u (0,x(j))))) \\ \end{array} $$

using the dynamics of the optimal open-loop solution. Now, we can use (7.13) withk=N and get

$$ \begin{array}{l} V_N (j + 1,x(j + 1)) - V_{N - 1} (j + 1)) \\ \,\,\,\,\,\, \le \frac{{\gamma ^{N - N_0 + 2} }}{{(\gamma + 1)^{N - N_0 } }}\ell (j,x(j),\mu N(j,x(j))). \\ \end{array} $$

Hence, the assumptions of Lemma 7.9 are fulfilled with

$$ \alpha = 1 - \frac{{\gamma ^{N - N_0 + 2} }}{{(\gamma + 1)^{N - N_0 } }} = \frac{{(\gamma + 1)^{N - N_0 + 2} }}{{(\gamma + 1)^{N - N_0 } }} $$

and the assertion follows. □

Similar to Proposition 7.6, the required values ofγ andα are easily computable and allow us to extend Algorithm 3.7 in a similar manner as we did in Algorithm 7.8.

Algorithm 7.13

(NMPC algorithm for time varying referencex ^ref with a priori suboptimality estimate)

Setα=1. At each sampling timet _n ,n=0,1,2,…:

• (1) Measure the statex(n)∈X of the system.

• (2) Setx ₀=x(n) and solve the optimal control problem

  

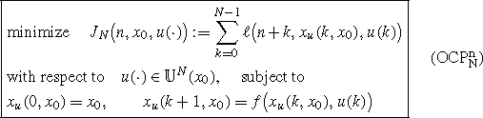
  and denote the obtained optimal control sequence by$u^{\star}(\cdot) \in \mathbb{U}^{N}(x_{0})$.

• (3) Define the NMPC-feedback valueμ _N (n,x(n)):=u ^⋆(0)∈U and use this control value in the next sampling period.

• (4) Computeα via

  

Note that checking the additional condition$(\gamma + 1)^{N - N_{0}} >\gamma^{N - N_{0} + 2}$ from Theorem 7.12 is unnecessary, since a violation would lead to a negativeα in which case asymptotic stability cannot be guaranteed by means of Theorem 7.12, anyway.

Similar to Proposition 7.6, the results from Theorem 7.12 are easily carried over to the multistep NMPC case described in Sect. 7.4 by extending Assumption 7.10.

Example 7.14

To illustrate these results, we consider the inverted pendulum on a cart problem from Example 2.10 with parametersg=9.81,l=10 andk _R =k _L =0.01 and control constraint set$\mathbb{U}= [-15, 15]$. Our aim is to stabilize one of the upright positions$x \in \mathcal{S} := \{((k + 1) \pi, 0, 0,0)^{\top}\mid k \in 2 \mathbb{Z} \}$. For this example we will provide online measurements ofα using Algorithm 7.8 for one fixed initial value and varying terminal weightsω, cf. Sect. 7.2, and control horizons, cf. Sect. 7.4. For a comparison of Algorithms 7.8 and 7.13 we refer to [15] and [29].

In order to obtain a suitable cost function, we follow the guidelines from Sect. 6.6 and construct a cost function for which—at least in the first two components—the overshoot ofℓ along a typical stable trajectory becomes small. To this end, we have used the geometry of the vector field of the first two differential equations representing the pendulum, see Fig. 7.11(a), and shaped the cost function such that it exhibits local maxima at the downward equilibria and “valleys” along the stable manifolds of the upright equilibria to be stabilized. The resulting cost functionℓ is of the integral type (3.4) with

$$ \begin{array}{*{20}l} {L(x,u): = } & {10^{ - 4} u^2 + (3.52\sin (x_1 - \pi )^2 + 4.82\sin (x_1 - \pi )x_2 } \\ {} & { + 2.31x_2^2 + 0.1((1 - \cos (x_1 - \pi )) \cdot (1 + \cos (x_2 )^2 ))^2 } \\ {} & { + 0.01x_3^2 + 0.1x_4^2 )^2 ,} \\ \end{array} $$

cf. Fig. 7.11(b). Using the terminal weights from Sect. 7.2, the cost functional becomes

$$ J_N (x_0 ,u) = \sum\limits_{i = 0}^{N - 2} {\ell (x(i),u(i)) + \omega \ell (xN - 1),u(N - 1)).} $$

Fig. 7.11

Vector field and cost function

This way of adjusting the cost function to the dynamics allows us to considerably reduce the length of the optimization horizon for obtaining stability in the NMPC scheme without stabilizing terminal constraints compared to simpler choices ofℓ. However, for the initial valuex ₀=(2π+1.5,0,0,0) and sampling periodT=0.05, which have been used in the subsequent computations, we still need a rather large optimization horizon ofN=70 to obtain stability of the closed loop.

Since the cost function is 2π-periodic it does not penalize the distance to a specific equilibrium in$\mathcal{S}$; rather, it penalizes the distance to the whole set. For a better comparison of the solutions for different parameters we want to force the algorithm to stabilize one specific upright position in$\mathcal{S}$. To this end, we add box-constraints to$\mathbb{X}$ limiting thex ₁-component to the interval [−π+0.01,3π−0.01]. The tolerances of the optimization routine and the differential equation solver are set to 10⁻⁶ and 10⁻⁷, respectively. The NMPC closed-loop trajectories displayed in Fig. 7.12 are simulated for terminal weightsω=1,…,10, cf. Sect. 7.2, and control horizonsm=1,…,10, cf. Sect. 7.4. The resultingα-values from Algorithm 7.8, denoted by$\alpha_{N,m}^{\omega}$, are shown in Fig. 7.12.

Fig. 7.12

Computed value for$\alpha_{70,m}^{\omega}$ for the nonlinear inverted pendulum example 2.10 with control horizonsm∈{1,…,20} and terminal weightsω∈{1,…,10}

Note that forω=1 theα values are negative for control horizonsm=1,…,4. Still, larger control horizons exhibit a positiveα value such that stability is guaranteed. This is in accordance with the theoretical results from Sect. 7.4, even though these simulation based results do not share the monotonicity of the theoretical bounds from Fig. 7.3. Additionally, an increase ofα can be observed for all control horizonsm ifω is increased. This confirms the stabilizing effect of terminal costs shown theoretically in Sect. 7.2; cf. Fig. 7.1.

Summarizing, these results show that the online measurement ofα yields valuable insights into the performance analysis of NMPC schemes without terminal constraints and thus nicely complements the theoretical results from Chap. 6 and Sects. 7.2 and7.4.

7.8 Adaptive Optimization Horizon

In the previous Sect. 7.7 we have shown how the suboptimality degreeα can be computed at runtime of the NMPC scheme without stabilizing terminal constraints. If the horizon lengthN is not chosen adequately, then it is likely that during runtime a valueα<0 is obtained. In this case, stability of the closed loop cannot be guaranteed by Proposition 7.6 or Theorem 7.12. However, the ability to computeα for each pointx(n) on the closed-loop trajectory using the techniques from Sect. 7.7 naturally leads to the idea of adapting the optimization horizonN at each timen such that stability and desired performance can be guaranteed. In this section, we will show some algorithms for this purpose, taken from Pannek [29]. Here we restrict ourselves to the basic idea and refer to [29] for more sophisticated approaches.

The fundamental idea of such an adaptive algorithm is rather simple: introducing a stability and suboptimality threshold$\overline{\alpha}> 0$, at each sampling instantn we prolong the optimization horizon ifα for the current horizon is smaller than$\overline{\alpha}$. If$\alpha > \overline{\alpha}$ holds, then we may reduceN in order to save computational time. This leads to the following algorithm.

Algorithm 7.15

(Adaptive horizon NMPC algorithm for time varying reference)

SetN ₀>0 and$\overline{\alpha} > 0$. At each sampling timet _n ,n=0,1,2,…:

• (1) Measure the statex(n)∈X of the system and setα=0.

• (2) While$\overline{\alpha} > \alpha$

  • (a) Setx ₀=x(n),N=N _n and solve the optimal control problem

    

    Denote the obtained optimal control sequence by$u^{\star}(\cdot) \in \mathbb{U}^{N}(x_{0})$.

  • (b) Computeα via Proposition 7.6 or Theorem 7.12.

  • (c) If$\alpha > \overline{\alpha}$ call reducing strategy forN _n , else call increasing strategy forN _n ; obtainu ^⋆(⋅) for the newN=N _n and an initial guess forN _n+1.

• (3) Define the NMPC-feedback valueμ _N (n,x(n)):=u ^⋆(0)∈U and use this control value in the next sampling period.

Here, the initial guessN _n+1 in Step (2c) will typically beN _n+1=N _n , however, as we will see below, in the case of reducingN _n the choiceN _n+1=N _n −1 is more efficient, cf. the discussion after Proposition 7.18.

If this algorithm is successful in ensuring$\alpha \ge \overline{\alpha}$ for eachn, then the assumptions of Proposition 7.6 or Theorem 7.12 are satisfied. However, these results require the optimization horizonN to be fixed and hence do not apply to Algorithm 7.15 in whichN _n changes with time.

To cope with this issue, we generalize Proposition 7.6 to varying optimization horizons. To this end, for each$x\in \mathbb{X}$ andN∈ℕ we denote the maximalα from (7.10) byα(N). We then introduce the following assumption, which guarantees that for any horizonN satisfying$\alpha(N) \geq \overline{\alpha}$ the controller shows a bounded guaranteed performance if the horizon length is increased.

Assumption 7.16

Givenn∈ℕ₀,$x \in \mathbb{X}$,N<∞ and a value$\overline{\alpha} \in (0, 1)$ with$\alpha(N) \geq \overline{\alpha}$, we assume that there exist constantsC _l ,C _α >0 such that the inequalities

$$ \begin{array}{l} C_l \ell (n,x,\mu _N (n,x)) \\ \le \ell (n,x,\mu _{\tilde N} (n,x)) = \frac{{V_{\tilde N} (n,x) - V_{\tilde N} (n + 1,f(x,\mu _N (n,x)))}}{{V_{\tilde N} (n,x) - V_{\tilde N} (n + 1,f(x,\mu _{\tilde N} (n,x)))}}, \\ \end{array} $$

(7.15)

$$ C_\alpha \alpha (N) \le \alpha (\tilde N) $$

(7.16)

hold for all$\widetilde{N} \geq N$.

The reason for Assumption 7.16 is that it is possible that the performance of the controllerμ _N may not improve monotonically asN increases; see Di Palma and Magni [6]. Consequently, we cannot expect$\alpha(\widetilde{N})\ge \alpha(N)$ for$\widetilde{N} > N$. Still, we need to ensure that$\alpha(\widetilde{N})$ does not become too small compared toα(N), in particular,$\alpha(\widetilde{N})$ should not drop below zero if the horizon length is increased; this is ensured by (7.16). Furthermore, we need an estimate for the dependence ofℓ(n,x,μ _N (n,x)) onN which is given by (7.15). Unfortunately, for both inequalities so far we were not able to provide sufficient conditions in terms of the problem data, like, e.g., a controllability condition similar to Assumption 6.4. Still, numerical evaluation for several examples showed that these inequalities are satisfied and thatC _l andC _α attain reasonable values.

Using Assumption 7.16, we obtain a stability and performance estimate of the closed loop in the context of changing horizon lengths similar to Proposition 7.6. Since the closed-loop control resulting from Algorithm 7.15 now depends on a sequence of horizons$(N_{n})_{n \in \mathbb{N}_{0}}$ we obtain a sequence of control laws$(\mu_{N_{n}})_{n\in \mathbb{N}_{0}}$. The closed-loop trajectory generated by this algorithm is then given by

$$x(n+1) = f\bigl(x(n),\mu_{N_n}\bigl(n,x(n)\bigr)\bigr). $$

(7.17)

Theorem 7.17

Consider the sequence of feedback laws $(\mu_{N_{n}})$ computed from Algorithm 7.15and the corresponding closed-loop trajectory x(⋅)from (7.17).Assume that for optimal value functions $V_{N_{n}}:\mathbb{N}_{0} \times \mathbb{X}\rightarrow \mathbb{R}_{0}^{+}$ of ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$)with N=N _n the inequality

$$ V_{N_n}\bigl(n, x(n)\bigr) \geq V_{N_n}\bigl(n + 1, x(n+1)\bigr) + \overline{\alpha} \ell \bigl(n, x(n), \mu_{N_n}\bigl(n, x(n)\bigr)\bigr)$$

(7.18)

holds for all n∈ℕ₀ and that Assumption 7.16is satisfied for all triplets (n,x,N)=(n,x(n),N _n ),n∈ℕ₀,with constants $C_{l}^{(n)}$,$C_{\alpha}^{(n)}$.Then

$$ \alpha _C V_\infty (n,x(n)) \le \alpha _C J_\infty (n,x(n),\mu _{(N_n )} ) \le V_{N^* } (n,x(n)) \le V_\infty (n,x(n)) $$

(7.19)

holds for all n∈ℕ₀ where $\alpha_{C} := \min_{i\in \mathbb{N}_{\geq n}} C_{\alpha}^{(i)} C_{l}^{(i)}\overline{\alpha}$.

Proof

Given (i,x(i),N _i ) for somei∈ℕ₀, Assumption 7.16 for (n,x,N)=(i,x(i),N _i ) guarantees$\alpha(N_{i}) \leq \alpha(\widetilde{N})/C_{\alpha}^{(i)}$ for$\widetilde{N} \geq N_{i}$. Choosing$\widetilde{N} = N^{\star}$, we obtain$\overline{\alpha} \leq \alpha(N_{i}) \leq \alpha(N^{\star})/C_{\alpha}^{(i)}$ using the relaxed Lyapunov Inequality (7.18). Multiplying by the stage cost$\ell(i,x(i), \mu_{N_{i}}(i,x(i)))$, we can conclude

$$ \begin{array}{*{20}l} {\bar \alpha \ell (i,x(i),\mu _{N_i } (i,x(i)))} \\ { \le \frac{{\alpha (N^* )}}{{C_{^\alpha }^{(i)} }}\ell (i,x(i),\mu _{N_i } (i,x(i)))} \\ { = \frac{{V_{N^* } (i,x(i)) - V_{N^* } (i + 1,f(x(i),\mu _{N^* } (i,x(i))))}}{{C_{^\alpha }^{(i)} \ell (i,x(i),\mu _{N^* } (i,x(i)))}}\ell (i,x(i),\mu _{Ni} (i,x(i)))} \\ { \le \frac{{V_{N^* } (i,x(i)) - V_{N^* } (i + 1,f(x(i),\mu _{Ni} (i,x(i))))}}{{C_{^a }^{(i)} C_l^{(i)} }}} \\ \end{array} $$

using (7.18) and (7.15). In particular, the latter condition allows us to use an identical telescope sum argument as in the proof of Proposition 7.6 since it relates the closed-loop varying optimization horizon to a fixed one. Hence, summing the running costs along the closed-loop trajectory reveals

$$ \alpha c\sum\limits_{i = n}^k {\ell (i,x(i),\mu N_i (i,x(i))) \le V_{N^* } (n,x(n)) - V_{N^* } (K + 1,x(K + 1))} $$

where we defined$\alpha_{C} := \min_{i \in [n, \ldots, K]} C_{\alpha}^{(i)} C_{l}^{(i)} \overline{\alpha}$. Since$V_{N^{\star}}(K+1, x(K+1)) \geq 0$ holds, we can neglect it in the last inequality. TakingK to infinity yields

$$ \alpha cV_\infty ^{\mu (N_i )} (n,x(n)) = \alpha c\mathop {\lim }\limits_{K \to \infty } \sum\limits_{i = n}^K {\ell (i,x(i),\mu _{N_i } (i,x(i))) \le V_{N^* } (n,x(n)).} $$

Since the first and the last inequality of (7.19) hold by definition ofV _N andV _∞, the assertion follows. □

If the conditions of this theorem hold, then stability-like behavior of the closed loop can be obtained analogously to Proposition 7.6.

Having shown the analytical background, we now present adaptation strategies which can be used for increasing or reducing the optimization horizonN in Step (2c) of Algorithm 7.15. For simplicity of exposition, we restrict ourselves to two simple strategies and consider a posteriori estimates based variants only. Despite their simplicity, these methods have shown to be reliable and fast in numerical simulations. A more detailed analysis, further methods and comparisons can be found in [29]. The following proposition yields the basis for a strategy for reducing N _n .

Proposition 7.18

Consider the optimal control problem ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$)with initial value x ₀=x(n),N _n ∈ℕ,and denote the optimal control sequence by u ^⋆.For fixed $\overline{\alpha} \in (0, 1)$,suppose there exists an integer $\overline{i} \in \mathbb{N}_{0}$,$0 \leq \overline{i}< N$ such that

$$ \begin{array}{*{20}l} {V_{N_n - i} (n + i + 1,x_{u^* } (i + 1,x(n)))} \\ { + \bar \alpha \ell (n + i,x_{u^* } (i,x(n)),\mu _{N_n - i} (n + i,x_{u^* } (i,x(n))))} \\ { \le V_{N_n - i} (n + i,x_{u^* } (i,x(n)))} \\ \end{array} $$

(7.20)

holds for all $0 \leq i \leq \overline{i}$.Then,setting N _n+i =N _n −i and $\mu_{N_{n+i}}(n+i,x(n+i))= u^{\star}(i)$ for $0 \leq i\leq \overline{i}-1$,Inequality (7.18)holds for $n =n,\ldots,n+\overline{i}-1$.

Proof

The proof follows immediately from the fact that for$\mu_{N_{n+i}}(n+i,x(n+i))= u^{\star}(i)$ the closed-loop trajectory (7.17) satisfies$x(n+i)=x_{u^{\star}}(i,x(n))$. Hence, (7.18) follows from (7.20). □

Observe that Proposition 7.18 is quite similar to the results from Sect. 7.4, since$\mu_{N_{n+i}}(n+i,x(n+i))$ as defined in this theorem coincides with the multistep feedback law from Sect. 7.4. Thus, Proposition 7.18 guarantees that if$\overline{i} > 1$, then the multistep NMPC feedback from Sect. 7.4 can be applied with$m = \overline{i}$ steps such that the suboptimality threshold$\overline{\alpha}$ can be guaranteed. With the choiceN _n+i =N _n −i, due to the principle of optimality we obtain that the optimal control problems within the next$\overline{i} - 1$ NMPC iterations are already solved since$\mu_{N_{n+i}}(n+i,x(n+i))$ can be obtained from the optimal control sequence$u^{\star}(\cdot) \in \mathbb{U}^{N}(x(n))$ computed at timen. This implies that the most efficient way for the reducing strategy in Step (2c) of Algorithm 7.15 is not to reduceN _n itself but rather to reduce the horizonsN _n+i byi for the subsequent sampling instants$n+1,\ldots,n+\overline{i}$, i.e., we choose the initial guess in Step (2c) asN _n+1=N _n −1. Still, if the a posteriori estimate is used, the evaluation of (7.20) requires the solution of an additional optimal control problem in each step in order to compute$V_{N_{n}-i}(n + i+1, x_{u^{\star}}(i+1, x(n)))$.

In contrast to this efficient and simple shortening strategy, it is quite difficult to obtain efficient methods for prolonging the optimization horizonN in Step (2c) of Algorithm 7.15. In order to understand why this is the case, we first introduce the basic idea behind any such prolongation strategy: at each sampling instant we iteratively increase the horizonN _n until (7.18) is satisfied and use this horizon for the next NMPC step. In order to ensure that iteratively increasingN _n will eventually lead to a horizon for which (7.18) holds, we make the following assumption.

Assumption 7.19

Given$\overline{\alpha} \in (0, 1)$, for all$x_{0} \in \mathbb{X}$ and alln∈ℕ₀ there exists a finite horizon length$\overline{N} = \overline{N}(n, x_{0}) \in \mathbb{N}$ such that (7.18) holds with$\alpha(N_{n}) \geq \overline{\alpha}$ forx(n)=x ₀ and$N_{n} \ge \overline{N}$.

Assumption 7.19 can be seen as a performance assumption which requires the existence of a horizon lengthN _n such that the predefined threshold$\overline{\alpha}$ can be satisfied. If no such horizon exists, no prolongation strategy can be designed which can guarantee closed-loop suboptimality degree$\alpha >\overline{\alpha}$. Assumption 7.19 is, for instance, satisfied if the conditions of Theorem 6.21 hold.

The following proposition shows that under this assumption any iterative strategy which increases the horizon will terminate after finitely many steps with a horizon lengthN for which the desired local suboptimality degree holds.

Proposition 7.20

Consider the optimal control problem ($\mathrm{OCP}_{\mathrm{N}}^{\mathrm{n}}$)with initial value x ₀=x(n)and N _n ∈ℕ.For fixed $\overline{\alpha} \in (0, 1)$ suppose that Assumption 7.19holds.Then,any algorithm which iteratively increases the optimization horizon N _n and terminates if (7.18)holds will terminate in finite time with an optimization horizon N _n for which (7.18)holds.In particular,Theorem 7.17is applicable provided Assumption 7.16holds.

Proof

The proof follows immediately from Assumption 7.19. □

Unfortunately, if (7.18) does not hold it is in general difficult to assess by how muchN _n should be increased such that (7.18) holds for the increasedN _n . The most simple strategy of increasingN _n by one in each iteration shows satisfactory results in practice, however, in the worst case it requires us to check (7.18)$\overline{N} - N_{n}+ 1$ times at each sampling instant. In contrast to the shortening strategy, the principle of optimality cannot be used here to establish a relation between the optimal control problems for differentN _n and, moreover, these problems may exhibit different solution structures which makes it a hard task to provide a suitable initial guess for the optimization algorithm; see also Sect. 10.5.

In order to come up with more efficient strategies, different methods have been developed [29] which utilize the structure of the suboptimality estimate itself to determine by how muchN _n should be increased. Compared to these methods, however, the performance of the simple strategy of increasingN _n by one is still acceptable. In the following example we illustrate the performance of this strategy for Example 2.11.

Example 7.21

For the ARP system (2.19)–(2.26) we have already analytically derived a continuous time tracking feedback in (2.28). However, this feedback law performs poorly under sampling, in particular, for the sampling periodT=0.2 which we consider here we obtain an unstable closed-loop sampled data system.

In order to obtain a sampled data feedback law which shows better performance we use the digital redesign technique proposed by Nešić and Grüne in [27]: given a signalv(t) to track, we numerically simulate the continuous time controlled system in order to generate the outputx ^ref which in turn will be used as the reference trajectory for an NMPC tracking problem. The advantage of proceeding this way compared to the direct formulation of an NMPC tracking problem lies in the fact that—according to our numerical experience—the resulting NMPC problem is much easier to solve and in particular requires considerably smaller optimization horizons in order to obtain a stable NMPC closed loop.

Specifically, we consider the piecewise constant reference function

$$ \nu (t) = \left\{ {\begin{array}{*{20}l} {10,} & {t \in [0,5) \cup [9,10),} \\ {0,} & {t \in [5,9) \cup [10,15)} \\ \end{array}} \right. $$

for thex ₅-component of the trajectory of the system. In order to obtain short transient times for the continuous time feedback, we set the design parametersc _i in (2.28) to (c ₀,c ₁,c ₂,c ₃)=(10 000,3500,500,35). Then, we incorporate the resulting trajectory displayed in Fig. 7.13 as referencex ^ref(⋅) in the NMPC algorithm. Since our goal is to track the reference with thex ₅-component of the trajectory, we use the simple quadratic cost function

$$ J(x_0 ,u) = \sum\limits_{j = 0}^N {\int_{t_j }^{t_{j + 1} } {|x_{5,u} (t,x_0 ) - x_{5,{\rm ref}} (t)|dt} } $$

within the adaptive horizon NMPC Algorithm 7.15. Moreover, we select the sampling periodT=0.2 and fix the initial valuex(0)=(0,0,0,0,10,0,0,0) for both the continuously and the sampled-data controlled system.

Fig. 7.13

Reference function for the continuous time feedback (solid) and state trajectory using the continuous time feedback (dashed). The latter will be used as reference function within the NMPC algorithm

Using the a posteriori and a priori estimation techniques within the adaptive NMPC Algorithm 7.15, we obtain the evolutions of horizonsN _n along the closed loop for the suboptimality bound$\overline{\alpha} =0.1$ as displayed in Fig. 7.14. Comparing the horizons chosen by the a priori and the a posteriori estimates, one sees that the a posteriori algorithms yields smaller optimization horizons which makes the resulting scheme computationally more efficient, however, at the expense that the evaluation of the a posteriori criterion itself is computationally more demanding; see also Fig. 7.15, below.

Fig. 7.14

Optimization horizons computed by the adaptive NMPC Algorithm 7.15 for the ARP problem using the a posteriori estimate (solid) and the a priori estimate (dashed)

Fig. 7.15

Computing times of the adaptive NMPC Algorithm 7.15 for the ARP problem using the a posteriori estimate (solid) and the a priori estimate (dashed)

It is also interesting to compare these horizons to the standard NMPC Algorithm 3.7 with fixedN which needs a horizon ofN=6 in order to guarantee$\alpha \geq \overline{\alpha}$ along the closed loop. Here, one observes that the required horizonN _n for the adaptive NMPC approach is typically smaller thanN=6 for both the a posteriori and the a priori estimate based variant. One also observes that the horizon is increased at the jump points of the reference functionv(⋅), which is the behavior one would expect in a “critical” situation and nicely reflects the ability of the adaptive horizon algorithm to adapt to the new situation.

Although the algorithm chooses to modify the horizon length throughout the run of the closed loop, one can barely see a difference between the resultingx ₅ trajectories and the (dashed) reference trajectory given in Fig. 7.13. For this reason, we do not display the closed-loop solutions. Instead, we additionally plotted the computing times of the two adaptive NMPC variants in Fig. 7.15. Again, one can immediately see the spikes in the graph right at the points in whichv(⋅) jumps. This figure also illustrates the disadvantage of the algorithm of having to solve multiple additional optimal control problems wheneverN is increased, which clearly shows up in the higher computation times at these points, in particular for the computationally more expensive a posteriori estimation.

While the adaptive optimization horizon algorithm produces good results in this example, we would like to mention that there are other examples—like, e.g., the swing-up of the inverted pendulum—for which the algorithm performs less convincing. We conjecture that a better understanding of Assumption 7.16 may provide the insight needed in order to tell the situations in which the adaptive algorithms provides good results from those in which it does not.

7.9 Nonoptimal NMPC

In the case of limited computational resources and/or fast sampling, the time available for solving the optimization problems (OCP_N) or its variants may not be sufficient to obtain an arbitrary accurate solution. Typically, the algorithms for solving these problems, i.e., for obtainingu ^⋆ and thusμ _N (x(n))=u ^⋆(0), work iteratively² and with limited computation time may we may be forced to terminate this algorithm prior to convergence to the optimal control sequence u ^⋆.

It is therefore interesting to derive conditions which ensure stability and performance estimates for the NMPC closed loop in this situation. To this end, we modify Algorithm 3.1 as follows.

Algorithm 7.22

We replace Steps (2) and (3) of Algorithm 3.1 (or its variants) by the following:

• (2′) For initial valuex ₀=x(n), given an initial guess$u_{n}^{0}(\cdot)\in U^{N}$ we iteratively compute$u_{n}^{j}(\cdot)\in U^{N}$ by an iterative optimization algorithm such that

  $$J_N\bigl(x_0, u_n^{j+1}(\cdot)\bigr) \le J_N\bigl(x_0,u_n^{j}(\cdot)\bigr).$$

  We terminate this iteration afterj ^∗∈ℕ iterations, set$u_{n}(\cdot) := u_{n}^{j^{*}}(\cdot)$ and$\widetilde{V}_{N}(n) :=J_{N}(x_{0}, u_{n}(\cdot))$.

• (3′) Define the NMPC-feedback valueμ _N (x(n)):=u _n (0)∈U and use this control value in the next sampling period.

One way to ensure proper operation of such an algorithm is by assuming that the sampling period is so small such that the optimal control from sampling instantn−1 is still “almost optimal” at timen. In this case, one iteration starting from$u_{n}^{0}=u_{n-1}$, i.e.,j ^∗=1, may be enough in order to be sufficiently close to an optimal control, i.e., to ensure$J_{N}(x(n),u_{n}^{1})\approx V_{N}(x(n))$. This procedure is, e.g., investigated by Diehl, Findeisen, Allgöwer, Bock and Schlöder in [8].

An alternative but conceptually similar idea is presented in work of Graichen and Kugi [11]. In this reference a sufficiently large number of iterationsj ^∗ is fixed and conditions are given under which the control sequences$u^{j^{*}}_{n}$ become more and more optimal asn increases, i.e., they satisfy$J_{N}(x(n),u_{n}^{j^{*}})\approx V_{N}(u^{\star})$ for sufficiently largen. Using suitable bounds during the transient phase in which this approximate optimality does not yet hold then allows the authors to conclude stability estimates.

While these results use that$u_{n}^{j^{*}}$ is close tou ^⋆ in an appropriate sense, here we investigate the case in which$u_{n}^{j^{*}}$ may be far away from the optimal solution. As we will see, asymptotic stability in the sense of Definition 2.14 is in general difficult to establish in this case. However, it will still be possible to prove the following weaker property.

Definition 7.23

Given a set$S\subseteq \mathbb{X}$, we say that the NMPC closed loop (2.5) isattractive on S if for eachx∈S the convergence

$$\lim_{k\to\infty } x_{\mu_N}(k,x) = x_*$$

holds.

Contrary to asymptotic stability, a merely attractive solution$x_{\mu_{N}}$ which starts close to the equilibriumx _∗ may deviate far from it before it eventually converges to x _∗. In order to exclude this undesirable behavior, one may wish to require the following stability property in addition to attraction.

Definition 7.24

Given a set$S\subseteq \mathbb{X}$, we say that the NMPC closed loop (2.5) isstable on S if there exists$\alpha_{S}\in \mathcal{K}$ such that the inequality

$$\big|x_{\mu_N}(k,x)\big|_{x_*} \le \alpha_S\bigl(|x|_{x_*}\bigr)$$

holds for allx∈S and allk=0,1,2,….

It is well known that under suitable regularity conditions attractivity and stability imply asymptotic stability; see, e.g., the book of Khalil [23, Chap. 4]. Since this is not the topic of this book, we will not go into technical details here and rather work with the separate properties attractivity and stability in the remainder of this section.

The following variant of Proposition 7.6 will be used in order to ensure attractivity and stability.

Proposition 7.25

Consider the solution $x(n)=x_{\mu_{N}}(n,x_{0})$ of the NMPC closed loop (2.5),a set $S\subseteq \mathbb{X}$,a value α∈(0,1].Assume that ℓ satisfies

$$\ell^*(x) \ge \alpha_3\bigl(|x|_{x_*}\bigr) $$

(7.21)

for some $\alpha_{3} \in \mathcal{K}_{\infty}$ and all x∈S and that for each x ₀∈S there exists a function $\widetilde{V}_{N}:\mathbb{N}_{0}\to \mathbb{R}_{0}^{+}$ which for all n∈ℕ₀ satisfies

$$\widetilde{V}_N(n) \geq \widetilde{V}_N(n + 1) + \alpha \ell\bigl(x(n), \mu_N\bigl(x(n)\bigr)\bigr). $$

(7.22)

Then the closed loop (2.5)is attractive on S and the inequality

$$J_\infty(x_0,\mu_N) \le \widetilde{V}_N(0) $$

(7.23)

holds for J _∞(x ₀,μ _N )from Definition 4.10.

If,in addition,there exists $\tilde{\alpha}_{2}\in \mathcal{K}_{\infty}$ independent of x ₀ such that the functions $\widetilde{V}_{N}$ satisfy

$$\widetilde{V}_N(0) \le \tilde{\alpha}_2\bigl(\big|x(0)\big|_{x_*}\bigr), $$

(7.24)

then the closed loop (2.5)is stable on S.

Proof

Iterating Inequality (7.22) forn=0,…,k and using$\widetilde{V}_{N}(n)\ge 0$ yields

$$\sum_{n=0}^{k} \ell\bigl(x(n),\mu_N\bigl(x(n)\bigr)\bigr)\le \widetilde{V}_N(0) - \widetilde{V}_N(k+1) \le \widetilde{V}_N(0).$$

Lettingk→∞ we obtain

$$J_\infty(x,\mu_N) = \lim_{k\to\infty} \sum_{n=0}^{k} \ell \bigl(x(n),\mu_N\bigl(x(n)\bigr)\bigr) \le \widetilde{V}_N(0),$$

i.e., (7.23). Now nonnegativity ofℓ implies lim  _n→∞ ℓ(x(n),μ _N (x(n)))=0 and thus (7.21) impliesx(n)→0, i.e., attractivity.

In order to prove stability under the additional assumption (7.24), observe that (7.22) together with the nonnegativity of$\widetilde{V}_{N}$ and (7.21) implies

$$\widetilde{V}_N(n) \ge \alpha \ell\bigl(x(n),\mu_N\bigl(x(n)\bigr)\bigr) \ge \alpha\, \alpha_3\bigl(\big|x(n)\big|_{x_*}\bigr) =:\tilde{\alpha}_1\bigl(\big|x(n)\big|_{x_*}\bigr).$$

Furthermore, (7.22) implies that$\widetilde{V}_{N}(n)$ is decreasing inn. Using these properties, stability immediately follows from

$$\big|x(n)\big|_{x_*} \le \tilde{\alpha}_1^{-1}\bigl(\widetilde{V}_N(n)\bigr) \le \tilde{\alpha}_1^{-1}\bigl(\widetilde{V}_N(0)\bigr) \le \tilde{\alpha}_1^{-1}\bigl(\tilde{\alpha}_2\bigl(|x_0|_{x_*}\bigr)\bigr) =:\alpha_S\bigl(|x_0|_{x_*}\bigr).$$

 □

The precise conditions on$u_{n}^{j}$ andu _n in Algorithm 7.22 which ensure attractivity, stability and suboptimality estimates now depend on whether stabilizing terminal constraints are used or not. We first consider the case of stabilizing terminal constraints which was investigated, e.g., by Michalska and Mayne [25], Scokaert, Mayne and Rawlings [32] and Rawlings and Mayne [31, Sect. 2.8] which all use conceptually similar ideas. Here, we follow the latter reference.

The approach in [31, Sect. 2.8] can be written as a variant of Theorem 5.13. In particular, we assume that Assumption 5.9 is satisfied. In order to obtain a more convenient notation, on the terminal constraint set$\mathbb{X}_{0}$ we define a map$\kappa:\mathbb{X}_{0}\to \mathbb{U}$ which assigns to each$x\in \mathbb{X}_{0}$ the control value$u_{x}\in \mathbb{U}(x)$ from Assumption 5.9(ii). With this notation, the corresponding theorem reads as follows.

Theorem 7.26

Assume that the conditions of Theorem 5.13are satisfied.Consider Algorithm 3.10with Steps (2)and (3)replaced by Steps (2′)and (3′)of Algorithm 7.22under the following assumptions for a set $S\subseteq \mathbb{X}_{N}$.

• (i) For n=0,we are able to find an admissible initial guess $u_{0}^{0}(\cdot)\in \mathbb{U}_{\mathbb{X}_{0}}^{N}(x_{0})$ for each initial value x ₀=x(0)∈S.

• (ii) For n=1,2,…,the initial guess $u_{n}^{0}(\cdot)$ is chosen as $u_{n}^{0}(k)=u_{n-1}(k+1)$,k=0,…,N−2and $u_{n}^{0}(N-1) =\kappa(x_{u_{n}^{0}}(N-1,x_{0}))$.

• (iii) For all n=0,1,2,…the control sequences $u_{n}(\cdot) = u_{n}^{j^{*}}(\cdot)$ satisfy $u_{n}^{j^{*}}(\cdot)\in \mathbb{U}_{\mathbb{X}_{0}}^{N}(x_{0})$,i.e.,they are admissible.

Then the NMPC closed loop (2.5)is attractive on S and the inequality

$$J_\infty(x,\mu_N) \le \widetilde{V}_N(0)$$

holds.If,in addition,there exists $\tilde{\alpha}_{3}\in \mathcal{K}_{\infty}$ such that the inequality $J_{N}(x_{0},u_{0}^{0}(\cdot)) \le \tilde{\alpha}_{3}(|x|_{x_{*}})$ holds for $u_{0}^{0}(\cdot)$ from (i),then (2.5)is also stable on S.

Proof

First note that (i) ensures that$u_{0}^{0}$ is admissible at timen=0 and that (iii) ensures that$u_{n}^{0}$ in (ii) is admissible forn=1,2,…, cf. also Lemma 5.10(i).

We abbreviate$x(n)=x_{\mu_{n}}(n)$. Then, (ii) and the same computation as in the proof of Lemma 5.12 yield the inequality$J_{N}(x(n+1),u_{n+1}^{0}(\cdot)) \le J_{N-1}(x(n+1),u_{n}(\cdot+1))$ for eachn≥0. On the other hand, the definition ofJ _N in Algorithm 3.10 implies

$$\widetilde{V}_N(n) = J_N\bigl(x(n), u_{n}(\cdot)\bigr) = \ell \bigl(x(n),u_{n}(0)\bigr) + J_{N-1}\bigl(f\bigl(x(n),u_{n}(x)\bigr),u_{n}(\cdot +1)\bigr).$$

The identitiesf(x(n),u _n (x))=x(n+1),u _n (0)=μ _N (x(n)) and the inequality$\widetilde{V}_{N}(n+1) \le J_{N}(x(n+1),u_{n+1}^{0}(\cdot))$ then lead to

$$\widetilde{V}_N(n) \ge \ell\bigl(x(n),u_{n}(0)\bigr) + J_N\bigl(x_0,u_n^0(\cdot)\bigr) \ge \ell\bigl(x(n),\mu_N\bigl(x(n)\bigr)\bigr) +\widetilde{V}_N(n+1),$$

i.e., (7.22). Now all properties follow directly from Proposition 7.25. □

Remark 7.27

• (i) If the assumptions of Proposition 5.14(ii) hold, then for$x_{0}\in \mathbb{X}_{0}$, the additional stability condition$J_{N}(x_{0},u_{0}^{0}(\cdot)) \le \tilde{\alpha}_{3}(|x|_{x_{*}})$ can be guaranteed if we define$u_{0}^{0}(\cdot)$ by$u_{0}^{0}(k):=\kappa(x_{u_{0}^{0}}(k,x_{0}))$,k=0,…,N−1. From Assumption 5.9(ii) it follows that this choice implies$J_{N}(x_{0},u_{0}^{0}(\cdot))\le F(x_{0})\le \tilde{\alpha}_{2}(|x|_{x_{*}})$ and thus the desired inequality follows with$\tilde{\alpha}_{3} =\tilde{\alpha}_{2}$. Hence, this choice guarantees stability locally aroundx _∗.

  One may also apply this definition to$u_{n}^{0}$ in (ii) for thosen in which$x(n)\in \mathbb{X}_{0}$ holds. This way, stability is ensured at least for the tail of the resulting closed-loop trajectory. If we use this choice of$u_{n}^{0}$ and do not perform the iterative optimization in Step (2′) of Algorithm 7.22, i.e., if we choosej ^∗=0, then we obtain an algorithm similar to the so-called dual mode strategy from [25].

• (ii) Iterative optimizations algorithms are usually designed such that the intermediate results satisfy the desired constraints as soon as the algorithm has succeeded in finding an admissible solution; see Sect. 10.6 for details. Since condition (ii) in Theorem 7.26 ensures that we already initialize the iterative optimization with an admissible solution, most common optimization algorithms will yield solutions$u_{n}^{j^{*}}(\cdot)$ satisfying condition (iii) of Theorem 7.26 regardless of howj ^∗ is chosen.

• (iii) Theorem 7.26 yields attractivity for arbitraryj ^∗∈ℕ₀. In particular, it applies toj ^∗=0, i.e., to the case in which we do not optimize at all. This means that attractivity follows readily from the stabilizing terminal constraints and the particular construction of the initial guesses. An important consequence of this property is that we can fixj ^∗ a priori, e.g., determined by the available computation time, which makes this approach suitable for real-time NMPC schemes.

Without stabilizing terminal constraints, stability is inherited from optimality and we can no longer expect attractivity or stability for arbitraryj ^∗. Instead, we need to make sure that$u_{n}^{j^{*}}$ is at least “good enough” to ensure (7.22). This is the idea of the following algorithm for determiningj ^∗ taken from Grüne and Pannek [16].

Algorithm 7.28

Givenα∈(0,1), in Step (2′) of Algorithm 7.22 we iterate over$u_{n}^{j}(\cdot)\in \mathbb{U}^{N}(x(n))$ forj=1,2,… until the termination criterion

$$J_N\bigl(x(n),u_{n}^{j^*}(\cdot)\bigr) \le \widetilde{V}_N(n - 1) -\alpha \ell\bigl(x(n-1), u_{n-1}(0)\bigr) $$

(7.25)

is satisfied.

The following theorem shows attractivity, suboptimality and stability for this algorithm.

Theorem 7.29

Consider a set $S\subseteq \mathbb{X}_{N}$,α∈(0,1]and Algorithm 3.1with Steps (2)and (3)replaced by Steps (2′)and (3′)of Algorithm 7.22.Assume that Algorithm 7.28is used in Step (2′)of Algorithm 7.22and that (7.25)is feasible for each n∈ℕ,i.e.,that for each n∈ℕthere exists $u_{n}^{j^{*}}\in \mathbb{U}^{N}(x(n))$ such that (7.25)holds.Assume furthermore that (7.21)holds for the running cost ℓ.

Then the NMPC closed loop (2.5)is attractive on S and the inequality

$$J_\infty(x,\mu_N) \le \widetilde{V}_N(0)$$

holds.If,in addition,there exists $\tilde{\alpha}_{3}\in \mathcal{K}_{\infty}$ such that the inequality $J_{N}(x_{0},u_{0}^{0}(\cdot)) \le \tilde{\alpha}_{3}(|x|_{x_{*}})$ holds for the initial guess $u_{0}^{0}(\cdot)$ in Step (2′)of Algorithm 7.22for each x(0)∈S,then (2.5)is also stable on S.

Proof

Under the stated assumptions, all properties follow directly from Proposition 7.25. □

Remark 7.30

In contrast to what was observed in Remark 7.27(iii) for the terminal constrained scheme, here we cannot in general fixj ^∗ a priori. Indeed, the number of iterations of the optimization algorithm which are needed until (7.25) is satisfied depends on various factors—particularly on the choice ofu _n−1 and$u_{n}^{0}$—and is in general unknown before the optimization is started. We assume that for sufficiently small sampling periods similar techniques as developed by Diehl, Findeisen, Allgöwer, Bock and Schlöder [8] or Graichen and Kugi [11] can be used in order to bound the number of needed iterations when setting$u_{n}^{0}=u_{n-1}$, but this has not yet been investigated rigorously.

In the general case, the feasibility assumption for (7.25) in Theorem 7.29 may not even be satisfied. Before we investigate this issue, we illustrate the performance of this algorithm by a numerical example.

Example 7.31

We consider the nonlinear pendulum from Example 2.10, where the task is now to stabilize the downward equilibriumx _∗=(0,0,0,0)^T. Figures7.16 and7.17 below show parts of the closed-loop trajectories ofx ₁ andx ₃ using Algorithm 7.22 and Algorithm 7.28 in Step (2′) for varyingα. The running cost is of type (3.4) with

$$ L(x,u) = 100\sin ^2 (0.5x_1 + x_2^2 + 10.0x_3^2 + x_4^2 + u^2 , $$

and sampling periodT=0.15 and the NMPC algorithm was run with optimization horizonN=17 and input constraints$\mathbb{U}= [-1, 1]$ using a recursive discretization and a line-search (SQP) method to solve the resulting optimization problem; see Chap. 10 for details on such methods.

Fig. 7.16

Angle of the pendulumx ₁ for varyingα

Fig. 7.17

Position of the cartx ₃ for varyingα

One can see clearly from Figs. 7.16 and7.17 that the closed-loop system is stable for all values ofα. Moreover, one can nicely observe the improvement of the closed-loop behavior visible in the decreasing time until the system comes to rest for increasing values ofα.

This is also reflected in the total closed-loop costs: While forα=0.1 the costs sum up to$V_{\infty}^{\tilde{\mu}_{N}}(x_{0})\approx 2512.74$, we obtain a total cost of$V_{\infty}^{\tilde{\mu}_{N}}(x_{0})\approx 2485.83$ forα=0.95. Note that the majority of the costs, i.e., approximately 2435, is accumulated on the interval [0,5] on which the trajectories for differentα are almost identical and which is therefore not displayed in Figs. 7.16 and7.17. However, the choice ofα has a visible impact on the closed-loop performance in the remaining part of the interval.

Regarding the computational cost, the total number of (SQP) steps which are executed during the run of the NMPC procedure reduces from 455 forα=0.95 and 407 forα=0.9, to 267 and 246 forα=0.5 andα=0.1, respectively. Hence, we obtain an average of approximately 2.5–4.5 optimization iterations per MPC step over the entire interval [0,15], while using standard termination criteria 9.5 optimization iterations per NMPC step are required.

A closer look at the numerical simulation in this example reveals that for eachα there were some sampling instantsn at which it was not possible to satisfy the suboptimality based termination criterion (7.25). In this case we simply iterated the SQP optimization routine until convergence.

While this fact is not visible in Figs. 7.16 and7.17 and obviously does not affect stability and performance in our example, this observation raises the question whether (7.25) is feasible, i.e., whether at timen we can ensure the existence of$u_{n}^{j^{*}}$ such that (7.25) is satisfied regardless of howu _n−1 was chosen, before. In order to analyze this question, let us suppose that Assumption 6.4 holds. Then, observing that for optimal controls (7.25) coincides with (5.1), Theorem 6.14 yields that (7.25) is feasible ifu _n−1 is an optimal control sequence andα in (7.25) is smaller thanα from (6.14). However, even with this choice ofα in (7.25), condition (7.25) may not be feasible for nonoptimal control sequencesu _n−1.

In order to understand why this is the case we investigate how Proposition 6.12—which provides the crucial ingredient for deriving (6.14)—changes if the optimal control sequenceu ^⋆ in this proposition is replaced by a nonoptimal control sequenceu _n−1. To this end, we fixn∈ℕ and set$x=x_{\mu_{N}}(n)$ andu=u _n−1. Now, first observe that the inequalities in (6.12) remain valid regardless of the optimality ofu ^⋆. All inequalities in (6.11), however, require optimality of the control sequenceu ^⋆ generating theλ _n . In order to maintain at least some of these inequalities we can pick an optimal control sequenceu ^⋆ for initial valuex _u (1,x) and horizon lengthN−1 and define a control sequence$\tilde{u}$ via$\tilde{u}(0)=u(0)$,$\tilde{u}(n)=u^{\star}(n-1)$,n=1,…,N−1. Then, abbreviating

$$\everymath{\displaystyle}\begin{array}{rcl}\tilde{\lambda}_n & =& \ell\bigl(x_{\tilde{u}}(n,x),\tilde{u}(n)\bigr), \quad n=0,\ldots, N-1 \quad \mbox{and}\\[6pt]\tilde{\nu}& =& V_N\bigl(x_{u}(1,x)\bigr)=V_N\bigl(x_{\tilde{u}}(1,x)\bigr),\end{array} $$

(7.26)

we arrive at the following version of Proposition 6.12.

Proposition 7.32

Let Assumption 6.4hold.Then the inequalities

$$\sum_{n=k}^{N-1} \tilde{\lambda}_n \le B_{N-k}(\tilde{\lambda}_k) \quad \mbox{and} \quad \tilde{\nu}\le \sum_{n=0}^{j-1}\tilde{\lambda}_{n+1} + B_{N-j}(\tilde{\lambda}_{j+1}) $$

(7.27)

hold for k=1,…,N−2and j=0,…,N−2.

Proof

Analogous to the proof of Proposition 6.12. □

The subtle but crucial difference of (7.27) to (6.11), (6.12) is that the left inequality in (7.27) is not valid fork=0. As a consequence,$\tilde{\lambda}_{0}$ does not appear in any of the inequalities, thus for any$\tilde{\lambda}_{1},\ldots,\tilde{\lambda}_{n}$ and$\tilde{\nu}$ satisfying (7.27) and anyδ>0 the values$\delta\tilde{\lambda}_{1},\ldots,\delta\tilde{\lambda}_{n}$ and$\delta\tilde{\nu}$ satisfy (7.27), too. Hence, unless (7.27) implies$\tilde{\nu}\le\sum_{n=0}^{N-1}\tilde{\lambda}_{n}$—which is a very particular case—replacing (6.11), (6.12) in (6.14) by (7.27) will lead to the optimal valueα=−∞. Consequently, feasibility of (7.25) cannot be concluded for any positiveα.

The following example shows that this undesirable result is not simply due to an insufficient estimate forα but that infeasibility of (7.25) can indeed happen.

Example 7.33

Consider the 1d system

$$x^+ = x/2 + u $$

(7.28)

withℓ(x,u)=|x|, input constraintu≥0 and optimization horizonN=3. A simple computation usingu _x ≡0 shows that for this system Assumption 6.4 is satisfied withβ(r,k)=Cσ ^k r withC=1 andσ=1/2. Hence, Corollary 6.19 applies and we can use (6.19) in order to compute that forN=3 Inequality (5.1) holds forα=7/8. Ifu _n−1 in the termination criterion (7.25) is chosen as the optimal controlu ^⋆, then (7.25) implies that (5.1) is feasible for thisα.

Forx(n−1)=0, it is obvious that the controlu ^⋆≡0 is optimal. Using the nonoptimal control given byu _n−1(0)=ε>0 andu _n−1(1)=u _n−1(2)=0 yields the trajectory$x_{u_{n-1}}(0)=x(n-1)=0$,$x_{u_{n-1}}(k)=\varepsilon 2^{-k+1}$,k=1,2, which impliesx(n)=ε and

$$J_3\bigl(x(n-1),u_{n-1}\bigr) = \sum_{k=0}^{1}\varepsilon 2^{-k} = 3\varepsilon /2.$$

On the other hand, for the initial valuex(n)=ε it is easily seen that for each controlu _n the inequality

$$J_3\bigl(x(n),u_n\bigr) \ge \sum_{k=0}^{2} \varepsilon 2^{-k} = 7\varepsilon /4 > 3\varepsilon /2 = J_N\bigl(x(n-1),u_{n-1}\bigr)$$

holds. Hence, for this choice ofu _n−1 the Inequality (7.25) is not feasible for anyα>0.

Clearly, in order to rigorously ensure attraction and guaranteed performance one should derive conditions which exclude these situations and we briefly discuss two possible approaches for this purpose.

One way to guarantee feasibility of (7.25) is to add the missing inequality in (7.27) (i.e., the left inequality fork=0) as an additional constraint in the optimization. This guarantees feasibility of (7.25) for anyα smaller than the value from (6.19). One drawback of this approach is that—similar to the terminal constraint case—an additional constraint in the optimization is needed which needs to be ensured for allj≥1 or at least forj ^∗. This makes the optimization more demanding, since in contrast to Remark 7.27(ii) here we do not have a canonical candidate for an admissible solution which can be used for initializing the iterative optimization. Another drawback is that the value$B_{N}(\tilde{\lambda}_{0})$ depends on the in general unknown functionβ from Assumption 6.4 and thus needs to be determined either by an a priori analysis or by a try-and-error procedure.

Another way to guarantee feasibility is to chooseℓ in such a way that there existsγ>0 for which

$$\gamma\ell(x,u) \ge \ell^*\bigl(f(x,u)\bigr) $$

(7.29)

holds for allx∈X and allu∈U. Then from (7.29) and the controllability Assumption 6.4 for$x=f(x(n-1),\tilde{u}_{n-1}(0))$ we get

$$\sum_{k=0}^{N-1} \tilde{\lambda}_k \le \tilde{\lambda}_0 +B_{N-1}\bigl(\ell^*\bigl(f\bigl(x(n-1),\tilde{u}_{n-1}(0)\bigr)\bigr)\bigr) \le \tilde{\lambda}_0+ B_{N-1}(\gamma\tilde{\lambda}_0).$$

Replacingβ(r,0) by$\max\{\beta(r,t), \tilde{\beta}(r,t)\}$ with$\tilde{\beta}(r,0) = \beta(\gamma r,0) + r$ and$\tilde{\beta}(r,k)=\beta(\gamma r,k)$ fork≥1, this right hand side is$\le B_{N}(\tilde{\lambda}_{0})$ which again yields the left inequality in (7.27) fork=0 and thus feasibility of (7.25). Note that (7.29) holds for our example (7.28) if we changeℓ(x,u)=|x| toℓ(x,u)=|x|+|u|/γ. For thisℓ and the points and control sequences considered in the example, we obtain

$$J_3\bigl(x(n-1),u_{n-1}\bigr) = 3\varepsilon /2 + \varepsilon = 5\varepsilon /2$$

from which one computes that (7.25) is now feasible.

The advantage of this method is that no additional constraints have to be imposed in the optimization. Its disadvantages are that constructingℓ satisfying (7.29) may be complicated for more involved dynamics and that the overshoot encoded inβ will in general increase for the re-designedℓ. As outlined in Sect. 6.6, this may lower the NMPC closed-loop performance and cause the need for larger optimization horizonsN in order to obtain stability.

An in depth study of these approaches and in particular their algorithmic implementation and numerical evaluation will be the topic of further research.

7.10 Beyond Stabilization and Tracking

All NMPC variants discussed so far have in common that the cost functionℓ penalizes the distance to some desired reference, either to an equilibriumx _∗ or to a time varying referencex ^ref. These variants may hence be calledstabilizing NMPC. There is, however, a large variety of optimal control problems where this is not the case. For instance, in economic applications one typically uses a running costℓ _e which reflects an economic cost rather than a distance to some reference, cf., e.g., Seierstad and Sydsæter [33]. In what follows we will refer toℓ _e as theeconomic cost. In such problems, the desired limit behavior of the optimal trajectories is not given a priori in terms of a referencex _∗ orx ^ref but is rather an outcome of the optimization itself. Even for rather simple nonlinear models, this limit behavior can be surprisingly complex, as, e.g., the examples in the book of Grass, Caulkins, Feichtinger, Tragler and Behrens [12]—for optimal control problems mainly motivated by social sciences—show.

One way to use stabilizing NMPC for such problems is as follows. In a first step, the optimal limit behavior for the economic running costℓ _e is identified. Assuming that this problem can be solved analytically or numerically we obtain an optimal reference solutionx ^ref which, however, does not need to be asymptotically stable. Hence, a stabilizing controller needs to be designed in order to stabilize the optimal reference. To this end, in a second step a cost functionℓ—which we will refer to asstabilizing cost—penalizing the distance tox ^ref is designed which is suitable for running a stabilizing NMPC scheme in order to obtain a stable closed loop.

Proceeding this way guarantees asymptotic stability of the optimal equilibrium (e.g., under the various conditions onf,ℓ and the particular NMPC scheme discussed in this book) but the resulting closed-loop trajectories based on the optimization of the stabilizing costℓ may be very different from the optimal trajectories using the economic costℓ _e . In particular, they may be far from optimal when performance is measured via the economic cost functionℓ _e .

Due to the fact that for running the NMPC Algorithms 3.1 and its variants no particular conditions onℓ are needed, it is a natural idea to try to run these algorithms using the economic costℓ _e in (OCP_N) and its variants instead of taking the detour via the stabilizing cost functionℓ. Formally, most usual NMPC algorithms (in particular those discussed in this book) are perfectly suited for doing so, however, the theoretical results ensuring stability and performance are in general not applicable, because the economic costℓ _e will not satisfy the conditions needed for these results. Hence, new conditions for ensuring stability and performance are needed.

Here we summarize some recent results in this direction. In [3] (see also the references in this paper for earlier research on this subject), Angeli, Amrit and Rawlings observe that if one adds the optimal limit behavior as a terminal constraint to the NMPC scheme, then performance estimates for the NMPC closed loop can be given. More precisely, assume that the optimal control problem exhibits an optimal equilibriumx _∗ with related control valueu _∗, i.e.,f(x _∗,u _∗)=x _∗ holds andℓ _e (x _∗,u _∗) is minimal among all possible equilibria. Then, using the NMPC scheme from Sect. 5.2 withℓ=ℓ _e and$\mathbb{X}_{0}=\{x_{*}\}$, for each$x\in \mathbb{X}_{N}$ one obtains the performance estimate

$$\overline{J}_\infty(x,\mu_N) \le \ell_e(x_*,u_*), $$

(7.30)

where$\overline{J}_{\infty}$ denotes the averaged infinite horizon cost functional

$$\overline{J}_\infty(x_0,\mu_N) := \lim_{K\to\infty} \frac{1}{K}\sum_{k=0}^K \ell_e\bigl( x_{\mu_N}(k,x_0),\mu \bigl(x_{\mu_N}(k)\bigr)\bigr). $$

(7.31)

Observe that$\overline{J}_{\infty}(x_{0},\mu_{N})$ is not simplyJ _∞(x ₀,μ _N ) from (4.10) withℓ replaced byℓ _e . The important difference betweenJ _∞ and$\overline{J}_{\infty}$ is that$\overline{J}_{\infty}$ contains the additional averaging term 1/K. This term is necessary since in general for economic running costsℓ _e we cannot expect the infinite sum in (4.10) to converge. This approach can be extended to periodic optimal trajectoriesx ^ref instead of equilibria by using suitable periodic terminal constraint sets; for details see [3].

It is interesting to note that—at least in the case of an optimal equilibriumx _∗ with control valueu _∗—the estimate (7.30) may also hold for controllersμ _N from stabilizing NMPC schemes. To this end, we use a stabilizing running costℓ satisfying

$$\ell(x,u) \ge \alpha_1\bigl(|x|_{x_*} + |u|_{u_*}\bigr) $$

(7.32)

for some$\alpha_{1}\in \mathcal{K}_{\infty}$ and assume thatJ _∞(x ₀,μ _N ) is finite and that the economic costℓ _e is continuous. Then, sinceJ _∞(x ₀,μ _N ) is finite,$\ell_{e}(x_{\mu_{N}}(n),\mu_{N}(x_{\mu_{N}}(n)))$ converges to 0 asn→∞ and hence the lower bound (7.32) implies$x_{\mu_{N}}(n) \to x_{*}$ and$\mu_{N}(x_{\mu_{N}}(n)) \to u_{*}$ asn→∞. This, in turn, implies$\ell_{e}(x_{\mu_{N}}(n), \mu_{N}(x_{\mu_{N}}(n))) \to \ell_{e}(x_{*},u_{*})$ asn→∞ from which (7.30) follows. Hence, although it seems reasonable to expect that for NMPC with economic running costℓ _e one obtains a better performance of the closed-loop trajectories in terms of the economic objectiveℓ _e , this is not reflected in the asymptotic estimate (7.30).

In the usual NMPC setting, a finite value ofJ _∞(x ₀,μ _N ) from (4.10) together with positive definiteness ofℓ allows one to conclude that the closed-loop trajectory must converge tox _∗, because otherwiseJ _∞(x ₀,μ _N ) would be unbounded. This is not the case for the averaged functional$\overline{J}_{\infty}(x_{0},\mu)$ from (7.31) and, indeed, one needs additional conditions in order to ensure that the closed-loop solution satisfying (7.30) does converge tox _∗. Such a condition has been presented in Diehl, Amrit and Rawlings [7] for the case of an optimal steady state and finite-dimensional state spaceX=ℝ^d. The condition, called strong duality, demands the existence of a valueλ _∗∈ℝ^d such thatx _∗ andu _∗ minimize the expression

$$\ell_e(x,u) +\bigl[x-f(x,u)\bigr]^T\lambda_*$$

over all admissible states$x\in \mathbb{X}$ and control values$u\in \mathbb{U}(x)$. Furthermore, the existence of$\alpha_{1}\in \mathcal{K}_{\infty}$ with

$$\ell_e(x,u) +\bigl[x-f(x,u)\bigr]^T\lambda_* - \ell_e(x_*,u_*) \ge \alpha_1\bigl(|x|_{x_*}\bigr)$$

is required. Under these conditions, a Lyapunov function can be constructed by adding suitable correction terms to the finite horizon optimal value functionV _N (corresponding to the economic running costℓ _e ). In [2], Angeli and Rawlings further observed that strong duality can be interpreted as a dissipativity condition, which links this condition to more classical concepts used in the stability analysis of control systems.

Summarizing, the results sketched in this section show that NMPC can be used for obtaining optimal feedback controllers also for optimal control problems different from the classical NMPC objectives stabilization and tracking. We conjecture that NMPC will prove valuable also for other types of optimization criteria, however, we are also convinced that there are problems which are not solvable using the receding horizon NMPC paradigm. An in depth analysis of the structural properties an optimal control problem needs to exhibit in order to be tractable with NMPC techniques would certainly be an interesting research project.