Abstract
A better title for this chapter might be “Computing the Weak Mordell–Weil Group,” since we will be concerned solely with the problem of computing generators for the group E(K)∕mE(K).
Access provided by Autonomous University of Puebla. Download chapter PDF
A better title for this chapter might be “Computing the Weak Mordell–Weil Group,” since we will be concerned solely with the problem of computing generators for the group E(K)∕mE(K). However, given generators for E(K)∕mE(K), a finite amount of computation yields generators for E(K); see (VIII.3.2) and Exercise 8.18. Unfortunately, there is no comparable algorithm currently known that is guaranteed to give generators for E(K)∕mE(K) in a finite amount of time!
We start in (X §1) by taking the proof of the weak Mordell–Weil theorem given in (VIII §1) and making it quite explicit. In this way the computation of the quotient E(K)∕mE(K) (in a special case) is reduced to the problem of determining whether each of a certain finite set of auxiliary curves, called homogeneous spaces, has a single rational point. The question whether a given homogeneous space has a rational point may often be answered either affirmatively by finding a point or negatively by showing that it has no points in some completion K v of K.
The subsequent two sections develop the general theory of homogeneous spaces (for elliptic curves). Then, in (X §4), we apply this theory to the problem of computing E(K)∕mE(K) or, more generally, \(E'(K)/\phi {\bigl (E(K)\bigr )}\) for an isogeny
Again this computation is reduced to the problem of the existence of a single rational point on certain homogeneous spaces. The only impediment to solving this latter problem occurs if some homogeneous space has a K v -rational point for every completion K v of K, yet fails to have a K-rational point. Unfortunately, this precise situation, the failure of the so-called Hasse principle, does occur. The extent of its failure is quantified by the elements of a certain group, called the Shafarevich–Tate group. The question of an effective algorithm for the computation of E(K)∕mE(K) is thus finally reduced to the problem of giving a bound for divisibility in the Shafarevich–Tate group, or, even better, proving the conjecture that the Shafarevich–Tate group is finite. In the last section we illustrate the general theory by studying in some detail the family of elliptic curves given by the equations
In particular, we compute the torsion subgroups and give an upper bound for the rank of \(E_{D}(\mathbb{Q})\), we give a large class of examples for which \(E_{D}(\mathbb{Q})\) has rank 0, and we show that in certain cases \(E_{D}(\mathbb{Q})\) has an associated homogeneous space that violates the Hasse principle, i.e., the homogeneous space has points defined over \(\mathbb{R}\) and over \(\mathbb{Q}_{p}\) for every prime p, but it has no \(\mathbb{Q}\)-rational points.
Unless explicitly stated to the contrary, the notation for this chapter is the same as for Chapter VIII. In particular, K is a number field and M K is a complete set of inequivalent absolute values on K. However, as indicated in the text, this specification is dropped in (X §§2,3,5), where K is allowed to be an arbitrary (perfect) field.
X.1 An Example
For this section we let E∕K be an elliptic curve and m ≥ 2 an integer, and we assume that
Recall from (VIII §1) that under this assumption there is a pairing
defined by
where \(Q \in E(\bar{K})\) is chosen to satisfy [m]Q = P. Further, (VIII.1.2) says that the kernel on the left is mE(K), so we may view κ as a homomorphism
(This is the connecting homomorphism for a group cohomology long exact sequence; see (VIII §2).)
We also observe from (III.8.1.1) that our assumption \(E[m] \subset E(K)\) implies that \(\boldsymbol{\mu }_{m} \subset K^{{\ast}}\). This follows from basic properties of the Weil pairing (III.8.1.1),
The Weil pairing will play a prominent role in this section.
Finally, since \(\boldsymbol{\mu }_{m} \subset K^{{\ast}}\), Hilbert’s Theorem 90 (B.2.5c) says that every homomorphism \(G_{\bar{K}/K} \rightarrow \boldsymbol{\mu }_{m}\) has the form
In other words, there is an isomorphism (cf. VIII §2)
defined by
where \(\beta \in \bar{K}^{{\ast}}\) is chosen to satisfy β m = b. Note the close resemblance in the definitions of δ E and δ K . This is no coincidence. The map δ E is the connecting homomorphism for the Kummer sequence associated to the group variety E∕K, and δ K is the connecting homomorphism for the Kummer sequence associated to the group variety \(\mathbb{G}_{m}/K\).
Using these maps, we can make the proof of the weak Mordell–Weil theorem much more explicit, and by doing so, derive formulas that allow us to compute the Mordell–Weil group in certain cases. We start with a theoretical description of the method.
Theorem 1.1.
-
(a)
With notation as above, there is a bilinear pairing
$$\displaystyle\begin{array}{rcl} b : E(K)/mE(K) \times E[m]\longrightarrow K^{{\ast}}/(K^{{\ast}})^{m}& & {}\\ \end{array}$$satisfying
$$\displaystyle\begin{array}{rcl} e_{m}{\bigl (\delta _{E}(P),T\bigr )} = \delta _{K}{\bigl (b(P,T)\bigr )}.& & {}\\ \end{array}$$ -
(b)
The pairing in (a) is nondegenerate on the left.
-
(c)
Let \(S \subset M_{K}\) be the union of the set of infinite places, the set of finite primes at which E has bad reduction, and the set of finite primes dividing m. Then the image of the pairing in (a) lies in the following subgroup of K ∗ ∕(K ∗ ) m :
$$\displaystyle{K(S,m) ={\bigl \{ b \in K^{{\ast}}/(K^{{\ast}})^{m} : \mbox{ $\mathop{\mathrm{ord}}\nolimits _{ v}(b) \equiv 0(\text{ mod}m)$ for all $v\notin S$}\bigr \}}.}$$ -
(d)
The pairing in (a) may be computed as follows. For each T ∈ E[m], choose functions f T ,g T ∈ K(E) satisfying the conditions
$$\displaystyle{\mathop{\mathrm{div}}\nolimits (f_{T}) = m(T) - m(O)\qquad \text{and}\qquad f_{T} \circ [m] = g_{T}^{m}}$$( cf. the definition of the Weil pairing (III §8) ) . Then for any point P ≠ T,
$$\displaystyle{b(P,T) \equiv f_{T}(P)\pmod (K^{{\ast}})^{m}.}$$( If P = T, we can compute b(T,T) using linearity. For example, if [2]T ≠ O, then b(T,T) = f T (−T) −1 . More generally, let Q ∈ E(K) be any point with Q ≠ T; then b(T,T) = f T (T + Q)f T (Q) −1 . )
Remark 1.2.
Why do we say that (X.1.1) provides formulas that help us to compute the Mordell–Weil group? First, the group K(S, m) in (c) is finite (see the proof of (VIII.1.6)), and in fact it is reasonably easy to explicitly compute K(S, m). Second, the functions f T in (d) are also fairly easy to compute from the equation of the curve. (This is true even for quite large values of m; see (XI.8.1).) Then the fact that the pairing in (a) is nondegenerate on the left means that in order to compute E(K)∕mE(K), it is necessary to do “only” the following:
Fix generators T 1 and T 2 for E[m]. For each of the finitely many pairs
check whether the simultaneous equations
have a solution (P, z 1, z 2) ∈ E(K) × K ∗× K ∗. We can be even more explicit if we express the function f T in terms of Weierstrass coordinates x and y. Then we are looking for a solution (x, y, z 1, z 2) ∈ K × K × K ∗× K ∗ satisfying
These equations define a new curve, called a homogeneous space for E∕K. (We discuss homogeneous spaces in more detail in (X §3).) What we have done is reduce the problem of calculating E(K)∕mE(K) to the problem of the existence or non-existence of a single rational point on each of an explicitly given finite set of curves. Frequently, many of these curves can be immediately eliminated from consideration because they have no points over some completion K v of K, which is an easy thing to check. On the other hand, a short search by hand or with a computer often uncovers rational points on some of the others. If, in this way, we can deal with all of the homogeneous spaces in question, then the determination of E(K)∕mE(K) is complete. The problem that arises is that occasionally there is a homogeneous space having points defined over every completion K v , yet having no K-rational points. It is this situation, the failure of the Hasse principle, that makes the Mordell–Weil theorem ineffective.
Remark 1.3.
Notice that the condition \(\mathop{\mathrm{div}}\nolimits (f_{T}) = m(T) - m(O)\) in (X.1.1d) is enough to specify f T only up to multiplication by an arbitrary element of K ∗. However, the equality f T ∘ [m] = g T m with g T ∈ K(E) means that in fact f T is well-determined up to multiplication by an element of (K ∗)m. Thus the value of f T (P) in (X.1.1d) is a well-defined element of K ∗∕(K ∗)m.
We now give the proof of (X.1.1), after which we study the case m = 2 in more detail and use it to compute E(K)∕2E(K) for an example.
Proof Proof of (X.1.1).
(a) Hilbert’s Theorem 90 (B.2.5c) shows that the pairing is well-defined. Bilinearity follows from bilinearity of the Kummer pairing (VIII.1.2b) and bilinearity of the Weil e m -pairing (III.8.1a).
(b)In order to prove nondegeneracy on the left, we suppose that b(P, T) = 1 for all T ∈ E[m]. This means that for all T ∈ E[m] and all \(\sigma \in G_{\bar{K}/K}\),
The nondegeneracy of the Weil pairing (III.8.1c) implies that \(\kappa (P,\sigma ) = 0\) for all \(\sigma\), and then (VIII.1.2c) tells us that P ∈ mE(K).
(c)Let β = b(P, T)1∕m . Tracing through the definitions, we see that the field K(β) is contained in the field \(K{\bigl ([m]^{-1}E(K)\bigr )}\) described in (VIII.1.2d). Further, applying (VIII.1.5b) tells us that the extension L∕K is unramified outside S. But it is easy to see that if v ∈ M K is a finite place with v(m) = 0, then the extension K(β)∕K is unramified at v if and only if
(Here \(\mathop{\mathrm{ord}}\nolimits _{v} : K^{{\ast}}\twoheadrightarrow \mathbb{Z}\) is the normalized valuation associated to v.) This says precisely that b(P, T) ∈ K(S, m).
(d)Choose \(Q \in E(\bar{K} )\) and \(\beta \in \bar{K}^{{\ast}}\) satisfying
Then for all \(\sigma \in G_{\bar{K}/K}\) we have by definition
Since δ K is an isomorphism, it follows that \(g_{T}(Q)^{m} \equiv \beta ^{m}\ (\text{ mod}\ (K^{{\ast}})^{m})\). (Note that g T (Q)m = f T (P) is in K ∗.) Therefore
□
We now consider the special case m = 2, which is by far the easiest with which to work. Under our assumption \(E[m] \subset E(K)\), we may take a Weierstrass equation for E of the form
The three nontrivial 2-torsion points are
Letting T = (e, 0) represent any one of these points, we claim that the associated function f T specified in (X.1.1d) is f T = x − e. It is clear that this function has the correct divisor,
It is then a calculation to check that
so x − e has both of the properties needed to be f T .
Now suppose that we have chosen a pair (b 1, b 2) ∈ K(S, m) × K(S, m) and that we want to determine whether there is a point P ∈ E(K)∕2E(K) satisfying
Such a point exists if and only if there is a solution
to the system of equations
We substitute the latter two equations into the former and define a new variable z 3 by y = b 1 b 2 z 1 z 2 z 3, which is permissible since b 1, b 2, z 1, and z 2 take only nonzero values. This yields the three equations
Finally, eliminating x gives the pair of equations
This gives a finite collection of equations, one for each pair (b 1, b 2), and we may use whatever techniques are at our disposal (e.g., v-adic, computer search) to determine whether they have a solution. Notice that if we do find a solution (z 1, z 2, z 3), then we immediately recover the corresponding point in E(K)∕2E(K) using the formulas
Finally we must deal with the fact that the definition b(P, T) = f T (P) cannot be used if it happens that P = T. In other words, there are two pairs (b 1, b 2) that do not arise from the above procedure, namely the pairs \({\bigl (b(T_{1},T_{1}),b(T_{1},T_{2})\bigr )}\) and \({\bigl (b(T_{2},T_{1}),b(T_{2},T_{2})\bigr )}\). These values may be computed using linearity as
and similarly
We summarize this entire procedure in the following proposition.
Proposition 1.4.
(Complete 2-Descent) Let E∕K be an elliptic curve given by a Weierstrass equation
Let \(S \subset M_{K}\) be a finite set of places of K including all archimedean places, all places dividing 2, and all places at which E has bad reduction. Further let
Then there is an injective homomorphism
defined by
Let (b 1 ,b 2 ) ∈ K(S,2) × K(S,2) be a pair that is not the image of one of the three points O, (e 1 ,0), (e 2 ,0). Then (b 1 ,b 2 ) is the image of a point
if and only if the equations
have a solution (z 1 ,z 2 ,z 3 ) ∈ K ∗ × K ∗ × K. If such a solution exists, then we can take
Proof.
As explained above, this is a special case of (X.1.1). □
Example 1.5.
We use (X.1.4) to compute \(E(\mathbb{Q})/2E(\mathbb{Q})\) for the elliptic curve
This equation has discriminant
so it has good reduction except at 2 and 5. Reducing the equation modulo 3, we easily check that \(\#\tilde{E}(\mathbb{F}_{3}) = 4\). Since \(E[2] \subset E_{\text{tors}}(\mathbb{Q})\) and \(E_{\text{tors}}(\mathbb{Q})\) injects into \(\tilde{E}(\mathbb{F}_{3})\) from (VII.3.5), we see that
Let \(S =\{ 2,5,\infty \}\subset M_{\mathbb{Q}}\). Then a complete set of representatives for
is given by the set
We identify this set with \(\mathbb{Q}(S,2)\). Now consider the map given in (X.1.4),
say with
There are 64 pairs \((b_{1},b_{2}) \in \mathbb{Q}(S,2) \times \mathbb{Q}(S,2)\), and for each pair, we must check to see whether it comes from an element of \(E(\mathbb{Q})/2E(\mathbb{Q})\). For example, using (X.1.4), we can compute the image of E[2] in \(\mathbb{Q}(S,2) \times \mathbb{Q}(S,2)\):
It remains to determine, for every other pair (b 1, b 2), whether the equations
have a solution \(z_{1},z_{2},z_{3} \in \mathbb{Q}\). For example, if b 1 < 0 and b 2 > 0, then (*) clearly has no rational solutions, since the first equation does not even have a solution in \(\mathbb{R}\).
Proceeding systematically, we list our results in Table 10.1. The entry for each pair (b 1, b 2) consists of either a point of \(E(\mathbb{Q})\) that maps to (b 1, b 2), or else a (local) field over which the equations listed in (*) have no solution. (Note that if (z 1, z 2, z 3) is a solution to (*), then the corresponding point of \(E(\mathbb{Q})\) is (b 1 z 1 2 + e 1, b 1 b 2 z 1 z 2 z 3).) The circled numbers in the table refer to the notes that explain each entry. Finally, we note that since the map \(E(\mathbb{Q})/2E(\mathbb{Q}) \rightarrow \mathbb{Q}(S,2) \times \mathbb{Q}(S,2)\) is a homomorphism, it is not necessary to check every pair (b 1, b 2). For example, if both (b 1, b 2) and (b 1′, b 2′) come from \(E(\mathbb{Q})\), then so does (b 1 b 1′, b 2 b 2′). Similarly, if (b 1, b 2) does and (b 1′, b 2′) does not, then (b 1 b 1′, b 2 b 2′) does not. This observation substantially reduces the number of cases of (*) that must be considered.
-
1.
If b 1 < 0 and b 2 > 0, then b 1 z 1 2 − b 2 z 2 2 = 2 has no solutions in \(\mathbb{R}\).
-
2.
If b 1 < 0 and b 2 < 0, then b 1 z 1 2 − b 1 b 2 z 3 2 = 10 has no solutions in \(\mathbb{R}\).
-
3.
The four 2-torsion points \({\bigl \{O,(0,0),(2,0),(10,0)\bigr \}}\) map respectively to the four points (1, 1), (5, −2), (2, −1), and (10, 2).
-
4.
(b 1, b 2) = (1, −1): By inspection, the equations
$$\displaystyle{z_{1}^{2} + z_{ 2}^{2} = 2\qquad \text{and}\qquad z_{ 1}^{2} + z_{ 3}^{2} = 10}$$have the solution (1, 1, 3). This gives the point \((1,-3) \in E(\mathbb{Q})\).
-
5.
Adding \((1,-3) \in E(\mathbb{Q})\) to the nontrivial two-torsion points corresponds to multiplying their (b 1, b 2) values. This gives three pairs (5, 2), (2, 1), and (10, −2) in \(\mathbb{Q}(S,2) \times \mathbb{Q}(S,2)\), which correspond to the three rational points (20, 60), (18, −48), and (10∕9, −80∕27) in \(E(\mathbb{Q})\).
-
6.
\(b_{1}\not\equiv 0\ (\text{ mod}\ 5)\) and \(b_{2} \equiv 0\ (\text{ mod}\ 5)\): The first equation in (*) implies that z 1 and z 2 must be 5-adically integral. Then the second equation shows that \(z_{1} \equiv 0\ (\text{ mod}\ 5)\), and so from the first equation we obtain \(0 \equiv 2\ (\text{ mod}\ 5)\). Therefore (*) has no solutions in \(\mathbb{Q}_{5}\).
-
7.
The eight pairs in (6) are \(\mathbb{Q}_{5}\)-nontrivial, i.e., there are no \(\mathbb{Q}_{5}\) solutions to (*). If we multiply these eight pairs by the \(\mathbb{Q}\)-trivial pair (5, 2), we obtain eight more \(\mathbb{Q}_{5}\)-nontrivial pairs.
-
8.
(b 1, b 2) = (1, 2): The two equations in (*) are
$$\displaystyle{z_{1}^{2} - 2z_{ 2}^{2} = 2\qquad \text{and}\qquad z_{ 1}^{2} - 2z_{ 3}^{2} = 10.}$$Since 2 is a quadratic nonresidue modulo 5, the second equation implies that \(z_{1} \equiv z_{3} \equiv 0\ (\text{ mod}\ 5)\). But then the second equation says that \(0 \equiv 10\ (\text{ mod}\ 25)\). Therefore there are no solutions in \(\mathbb{Q}_{5}\).
-
9.
Taking the \(\mathbb{Q}_{5}\)-nontrivial pair (1, 2) from (8) and multiplying it by the seven \(\mathbb{Q}\)-trivial pairs already in the table gives seven new \(\mathbb{Q}_{5}\)-nontrivial pairs that fill the remaining entries in the table.
Conclusion. \(E(\mathbb{Q})\mathop{\cong}\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}\).
X.2 Twisting—General Theory
For this section and the next we drop the requirement that K be a number field, so K will be an arbitrary (perfect) field. As we saw in (X §1), computation of the Mordell–Weil group of an elliptic curve E leads naturally to the problem of the existence or nonexistence of a single rational point on various other curves. These other curves are certain twists of E that are called homogeneous spaces. In this section we study the general question of twisting which, since it is no more difficult, we develop for curves of arbitrary genus. Then, in the next section, we look at the homogeneous spaces associated to elliptic curves.
Definition.
Let C∕K be a smooth projective curve. The isomorphism group of C, denoted by \(\mathop{\mathrm{Isom}}\nolimits (C)\), is the group of \(\bar{K}\)-isomorphisms from C to itself. We denote the subgroup of \(\mathop{\mathrm{Isom}}\nolimits (C)\) consisting of isomorphisms defined over K by \(\mathop{\mathrm{Isom}}\nolimits _{K}(C)\). To ease notation, we write composition of maps multiplicatively, thus α β instead of α ∘β.
Remark 2.1.
The group that we are denoting by \(\mathop{\mathrm{Isom}}\nolimits (C)\) is usually called the automorphism group of C and denoted by \(\mathop{\mathrm{Aut}}\nolimits (C)\). However, if E is an elliptic curve, then we have defined \(\mathop{\mathrm{Aut}}\nolimits (E)\) to be the group of isomorphisms from E to E that take O to O. Thus \(\mathop{\mathrm{Aut}}\nolimits (E)\neq \mathop{\mathrm{Isom}}\nolimits (E)\), since for example, the group \(\mathop{\mathrm{Isom}}\nolimits (E)\) contains translation maps τ P : E → E. We describe \(\mathop{\mathrm{Isom}}\nolimits (E)\) more fully in (X §5).
Definition.
A twist of C∕K is a smooth curve C′∕K that is isomorphic to C over \(\bar{K}\). We treat two twists as equivalent if they are isomorphic over K. The set of twists of C∕K, modulo K-isomorphism, is denoted by \(\mathop{\mathrm{Twist}}\nolimits (C/K)\).
Let C′∕K be a twist of C∕K. Thus there is an isomorphism ϕ : C′ → C defined over \(\bar{K}\). To measure the failure of ϕ to be defined over K, we consider the map
It turns out that \(\xi\) is a 1-cocycle and that the cohomology class of \(\xi\) is uniquely determined by the K-isomorphism class of C′. Further, every cohomology class comes from some twist of C∕K. In this way \(\mathop{\mathrm{Twist}}\nolimits (C/K)\) may be identified with a certain cohomology set. We now prove these assertions.
Theorem 2.2.
Let C∕K be a smooth projective curve. For each twist C′∕K of C∕K, choose a \(\bar{K}\) -isomorphism ϕ : C′ → C and define a map \(\xi _{\sigma } = \phi ^{\sigma }\phi ^{-1} \in \mathop{\mathrm{Isom}}\nolimits (C)\) as above.
-
(a)
The map \(\xi\) is a 1-cocycle, i.e.,
$$\displaystyle{\xi _{\sigma \tau } = (\xi _{\sigma })^{\tau }\xi _{\tau }\qquad \mbox{ for all $\sigma ,\tau \in G_{\bar{K}/K}$.}}$$The associated cohomology class in \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}\) is denoted by \(\{\xi \}\) .
-
(b)
The cohomology class \(\{\xi \}\) is determined by the K-isomorphism class of C′ and is independent of the choice of ϕ. We thus obtain a natural map
$$\displaystyle{\mathop{\mathrm{Twist}}\nolimits (C/K)\longrightarrow H^{1}{\bigl (G_{\bar{ K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}.}$$ -
(c)
The map in (b) is a bijection. In other words, the twists of C∕K, up to K-isomorphism, are in one-to-one correspondence with the elements of the cohomology set \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}\) .
Remark 2.3.
We emphasize that the group \(\mathop{\mathrm{Isom}}\nolimits (C)\) is often nonabelian, and indeed, it is always nonabelian for elliptic curves. Hence \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}\) is generally only a pointed set, not a group. See (B §3) for details. However, if \(\mathop{\mathrm{Isom}}\nolimits (C)\) has a \(G_{\bar{K}/K}\)-invariant abelian subgroup A, then \(H^{1}(G_{\bar{K}/K},A)\) is a group, and its image in \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}\) gives a natural group structure to some subset of \(\mathop{\mathrm{Twist}}\nolimits (C)\). We apply this observation in (X §3) when C is an elliptic curve, taking for A the group of translations, and in (X §5) we do the same with \(A =\mathop{ \mathrm{Aut}}\nolimits (E)\).
Proof.
(a) We compute
(b)Let C″∕K be another twist of C∕K that is K-isomorphic to C′. Choose a \(\bar{K}\)-isomorphism ψ : C″ → C. We must show that the cocycles \(\phi ^{\sigma }\phi ^{-1}\) and \(\psi ^{\sigma }\psi ^{-1}\) are cohomologous. By assumption there is a K-isomorphism \(\theta : C'' \rightarrow C'\!\). Consider the element \(\alpha =\phi \theta \psi ^{-1} \in \mathop{\mathrm{Isom}}\nolimits (C)\). We compute
This proves that \(\phi ^{\sigma }\phi ^{-1}\) and \(\psi ^{\sigma }\psi ^{-1}\) are cohomologous when viewed as elements of \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}\).
(c)Suppose that C′∕K and C″∕K are twists of C∕K that give the same cohomology class in \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (C)\bigr )}\). This means that if we choose \(\bar{K}\)-isomorphisms ϕ : C′ → C and ψ : C″ → C, then there is a map \(\alpha \in \mathop{\mathrm{Isom}}\nolimits (C)\) such that
In other words, the cocycles associated to ϕ and ψ are cohomologous. We now consider the map \(\theta : C'' \rightarrow C'\) defined by \(\theta = \phi ^{-1}\alpha \psi\). It is clearly a \(\bar{K}\)-isomorphism, and we claim that it is, in fact, defined over K. To prove this, for any \(\sigma \in G_{\bar{K}/K}\) we compute
Therefore C″ and C′ are K-isomorphic, and thus they give the same element of \(\mathop{\mathrm{Twist}}\nolimits (C/K)\). This proves that the map
is injective.
To prove surjectivity, we start with a 1-cocycle
and use it to construct a curve C′∕K and an isomorphism ϕ : C′ → C satisfying \(\xi _{\sigma } = \phi ^{\sigma }\phi ^{-1}\). To do this, we consider a field, denoted by \(\bar{K}(C)_{\xi }\), that is isomorphic, as an abstract field extension of \(\bar{K}\), to \(\bar{K}(C)\), say by an isomorphism that we denote by \(Z : \bar{K}(C) \rightarrow \bar{K}(C)_{\xi }\). The difference between \(\bar{K}(C)\) and \(\bar{K}(C)_{\xi }\) lies in the action of the Galois group \(G_{\bar{K}/K}\); the action on \(\bar{K}(C)_{\xi }\) is twisted by \(\xi\). What this means is that
In this equality we are viewing f as a map \(f : C \rightarrow \mathbb{P}^{1}\) as in (II.2.2), and \(f^{\sigma }\xi _{\sigma }\) is composition of maps. Equivalently, the map \(\xi _{\sigma } : C \rightarrow C\) of curves induces a map \(\xi _{\sigma }^{{\ast}} : \bar{K}(C) \rightarrow \bar{K}(C)\) of fields, and \(f^{\sigma }\xi _{\sigma }\) is an alternative notation for \(\xi _{\sigma }^{{\ast}}(f^{\sigma })\).
For this action of \(G_{\bar{K}/K}\) on \(\bar{K}(C)_{\xi }\), we consider the subfield \(\mathcal{F}\subset \bar{K}(C)_{\xi }\) consisting of the elements of \(\bar{K}(C)_{\xi }\) that are fixed by \(G_{\bar{K}/K}\). We now show, in several steps, that the field \(\mathcal{F}\) is the function field of the desired twist of C.
Suppose that \(Z(f) \in \mathcal{F}\cap \bar{K}\). In particular, since Z induces the identity on \(\bar{K}\), we have \(f \in \bar{K}\). Now the fact that \(Z(f) \in \mathcal{F}\), combined with the fact that f is a constant function and thus unaffected by isomorphisms of C, implies that
This holds for all \(\sigma \in G_{\bar{K}/K}\), and hence f ∈ K.
This is an immediate consequence of (II.5.8.1) applied to the \(\bar{K}\)-vector space \(\bar{K}(C)_{\xi }\).
It follows from Step (ii) that \(\mathcal{F}\) has transcendence degree one over K, and thus using Step (i) and (II.2.4c), we deduce that there exists a smooth curve C′∕K such that \(\mathcal{F}\mathop{\cong}K(C')\). Further, Step (ii) implies that
so (II.2.4.1) says that C′ and C are isomorphic over \(\bar{K}\). In other words, C′ is a twist of C, and the final step in proving surjectivity is to show that C′ gives the cohomology class \(\{\xi \}\).
Let ϕ : C′ → C be a \(\bar{K}\)-isomorphism, as described in (II.2.4b), whose associated map ϕ ∗ is the isomorphism of fields
Having identified ϕ ∗ with Z, the relation \(Z(f)^{\sigma } = Z(f^{\sigma }\xi _{\sigma })\) used to define the map Z can be rewritten as \((f\phi )^{\sigma } = f^{\sigma }\xi _{\sigma }\phi\). In other words,
This implies that \(\phi ^{\sigma } =\xi _{\sigma }\phi\), which is exactly the desired result. □
Example 2.4.
Let E∕K be an elliptic curve, let \(K(\sqrt{d}\,)\) be a quadratic extension of K, and let
be the quadratic character associated to \(K(\sqrt{d}\,)/K\). (Note that \(\mathop{\mathrm{char}}\nolimits (K)\neq 2\).) We use χ to define a 1-cocycle
Let C∕K be the corresponding twist of E∕K. We are going to derive an equation for C∕K.
We choose a Weierstrass equation for E∕K of the form y 2 = f(x) and we write \(\bar{K}(E) = \bar{K}(x,y)\) and \(\bar{K}(C) = \bar{K}(x,y)_{\xi }\). Since [−1](x, y) = (x, −y), the action of \(\sigma \in G_{\bar{K}/K}\) on \(\bar{K}(x,y)_{\xi }\) is determined by the formulas
Notice that the functions x′ = x and \(y' = y/\sqrt{d}\) in \(\bar{K}(x,y)_{\xi }\) are fixed by \(G_{\bar{K}/K}\), and they satisfy the equation
which is the equation of an elliptic curve defined over K. Further, the identification \((x',y')\mapsto (x',y'\sqrt{d}\,)\) shows that this curve is isomorphic to E over \(K(\sqrt{d}\,)\). It is now an easy matter to check that the associated cocycle is \(\xi\), and thus to verify that we have found an equation for C∕K. The curve C is a quadratic twist of E; more precisely, it is the twist of E by the quadratic character χ. We will return to this example in more detail in (X §5).
X.3 Homogeneous Spaces
We recall from (VIII §2) that associated to an elliptic curve E∕K is a Kummer sequence
The proof of the weak Mordell–Weil theorem hinges on the essential fact that the image of the first term in the second consists of elements that are unramified outside of a certain finite set of primes. In this section we analyze the third term in the sequence by associating to each element of \(H^{1}(G_{\bar{K}/K},E)\) a certain twist of E called a homogeneous space. However, rather than starting with cohomology, we instead begin by directly defining homogeneous spaces and describing their basic properties. We follow this with the cohomological interpretation, which says that homogeneous spaces are those twists that correspond to cocycles taking values in the group of translations.
Definition.
Let E∕K be an elliptic curve. A (principal) homogeneous space for E∕K is a smooth curve C∕K together with a simply transitive algebraic group action of E on C defined over K. In other words, a homogeneous space for E∕K consists of a pair (C, μ), where C∕K is a smooth curve and
is a morphism defined over K having the following three properties:
-
(i)
μ(p, O) = p for all p ∈ C.
-
(ii)
\(\mu {\bigl (\mu (p,P),Q\bigr )} =\mu (p,P + Q)\) for all p ∈ C and P, Q ∈ E.
-
(iii)
For all p, q ∈ C there is a unique P ∈ E satisfying μ(p, P) = q.
We will often replace μ(p, P) with the more intuitive notation p + P. Then property (ii) is just the associative law (p + P) + Q = p + (P + Q). Of course, one must determine from context whether + means addition on E or the action of E on C.
In view of the simple transitivity of the action, we may define a subtraction map on C by the rule
It is not clear, a priori, that the map ν is even a rational map, but we will soon see that ν is a morphism and is defined over K. (This fact also follows from elementary intersection theory on C × C.) In conjunction with our addition notation for μ, we often write ν(q, p) as q − p.
We now verify that addition and subtraction on a homogeneous space have the right properties.
Lemma 3.1.
Let C∕K be a homogeneous space for E∕K. Then for all p,q ∈ C and all P,Q ∈ E :
-
(a)
μ(p,O) = p and ν(p,p) = O.
-
(b)
\(\mu {\bigl (p,\nu (q,p)\bigr )} = q\quad and\quad \nu \bigl (\mu (p,P),p) = P\) .
-
(c)
\(\nu {\bigl (\mu (q,Q),\mu (p,P)\bigr )} =\nu (q,p) + Q - P\) .
Equivalently, using the alternative “addition” and “subtraction” notation :
-
(a)
p + O = p and p − p = O.
-
(b)
p + (q − p) = q and (p + P) − p = P.
-
(c)
(q + Q) − (p + P) = (q − p) + Q − P.
In other words, using + and − signs provides the right intuition.
Proof.
(a) The equality μ(p, O) = p is part of the definition of homogeneous space. Next, the definition of ν says that ν(p, p) is the unique point P ∈ E satisfying μ(p, P) = p. We know that this last equation is true for P = O, so ν(p, p) = O.
(b)The relation \(\mu {\bigl (p,\nu (q, p)\bigr )} = q\) is the definition of ν. Then, from
we conclude that ν(μ(p, P), p) = P.
(c)We start with
Adding Q to both sides gives
From the definition of ν, this is equivalent to
□
Next we show that a homogeneous space C∕K for E∕K is a twist of of E∕K as described in (X §2). We also describe addition and subtraction on C in terms of a given \(\bar{K}\)-isomorphism E → C.
Proposition 3.2.
Let E∕K be an elliptic curve, and let C∕K be a homogeneous space for E∕K. Fix a point p 0 ∈ C and define a map
-
(a)
The map \(\theta\) is an isomorphism defined over K(p 0 ). In particular, the curve C∕K is a twist of E∕K.
-
(b)
For all p ∈ C and all P ∈ E,
$$\displaystyle{p + P =\theta {\bigl (\theta ^{-1}(p) + P\bigr )}.}$$( N.B. The first + is the action of E on C, while the second + is addition on E. )
-
(c)
For all p,q ∈ C,
$$\displaystyle{q - p =\theta ^{-1}(q) -\theta ^{-1}(p).}$$ -
(d)
The subtraction map
$$\displaystyle{\nu : C \times C\longrightarrow E,\qquad \nu (q,p) = q - p,}$$is a morphism and is defined over K.
Proof.
(a) The action of E on C is defined over K. Hence for any \(\sigma \in G_{\bar{K}/K}\) satisfying \(p_{0}^{\sigma } = p_{0}\), we have
This shows that \(\theta\) is defined over K(p 0). Further, the simple transitivity of the action tells us that \(\theta\) has degree one, and then (II.2.4.1) allows us to conclude that \(\theta\) is an isomorphism.
(b)We compute
Note that we are using the fact that \(\theta ^{-1}(p)\) is the unique point of E that gives p when it is added to p 0.
(c)We compute
(d)The fact that ν is a morphism follows from (c), since (III.3.6) says that subtraction on E is a morphism. To check that ν is defined over K, we let \(\sigma \in G_{\bar{K}/K}\) and use (c) to compute
This completes the proof that ν is defined over K. □
Definition.
Two homogeneous spaces C∕K and C′∕K for E∕K are equivalent if there is an isomorphism \(\theta : C \rightarrow C'\) defined over K that is compatible with the action of E on C and C′. In other words,
The equivalence class containing E∕K, acting on itself by translation, is called the trivial class. The collection of equivalence classes of homogeneous spaces for E∕K is called the Weil–Châtelet group for E∕K and is denoted by \(\mathop{\mathrm{WC}}\nolimits (E/K)\). (We will see later why \(\mathop{\mathrm{WC}}\nolimits (E/K)\) is a group.)
The next result explains which homogeneous spaces are trivial.
Proposition 3.3.
Let C∕K be a homogeneous space for E∕K. Then C∕K is in the trivial class if and only if C(K) is not the empty set.
Proof.
Suppose that C∕K is in the trivial class. Then there is a K-isomorphism \(\theta : E \rightarrow C\), and thus \(\theta (O) \in C(K)\).
Conversely, suppose that p 0 ∈ C(K). Then from (X.3.2a), the map
is an isomorphism defined over K(p 0) = K. The required compatibility condition on \(\theta\) is
which is part of the definition of homogeneous space. □
Remark 3.4.
Notice that (X.3.3) says that the problem of checking the triviality of a homogeneous space is exactly equivalent to answering the fundamental Diophantine question whether the given curve has any rational points. Thus our next step, namely the identification of \(\mathop{\mathrm{WC}}\nolimits (E/K)\) with a certain cohomology group, may be regarded as the development of a tool to help us study this difficult Diophantine problem.
Lemma 3.5.
Let \(\theta : C/K \rightarrow C'/K\) be an equivalence of homogeneous spaces for E∕K. Then
Proof.
This is just a matter of grouping points so that the additions and subtractions are well-defined. Thus
□
Theorem 3.6.
Let E∕K be an elliptic curve. There is a natural bijection
defined as follows :
Let C∕K be a homogeneous space for E∕K and choose any point p 0 ∈ C. Then
( The braces indicate that we are taking the equivalence class of C∕K and the cohomology class of the 1-cocycle \(\sigma \mapsto p_{0}^{\sigma } - p_{0}\) . )
Remark 3.6.1.
Since \(H^{1}(G_{\bar{K}/K},E)\) is a group, we can use (X.3.6) to define a group structure on the set \(\mathop{\mathrm{WC}}\nolimits (E/K)\). It is also possible to describe the group law on \(\mathop{\mathrm{WC}}\nolimits (E/K)\) geometrically, without using cohomology, which in fact is the way that it was originally defined. See Exercise 10.2 and [307].
Proof.
First we check that the map is well-defined. It is easy to see that the map \(\sigma \mapsto p_{0}^{\sigma } - p_{0}\) is a cocycle:
Now suppose that C′∕K is another homogeneous space that is equivalent to C∕K. Let \(\theta : C \rightarrow C'\) be a K-isomorphism giving the equivalence, and let p 0′ ∈ C′. We use (X.3.5) to compute
Hence the cocycles \(p_{0}^{\sigma } - p_{0}\) and \(p_{0}^{{\prime}\sigma }- p_{0}'\) differ by the coboundary generated by the point \(\theta (p_{0}) - p_{0}' \in E\), so they give the same cohomology class in \(H^{1}(G_{\bar{K}/K},E)\).
Next we check injectivity. Suppose that the cocycles \(p_{0}^{\sigma } - p_{0}\) and \(p_{0}^{{\prime}\sigma }- p_{0}'\) corresponding to C∕K and C′∕K are cohomologous. This means that there is a point P 0 ∈ E satisfying
Consider the map
It is clear that \(\theta\) is a \(\bar{K}\)-isomorphism and that it is compatible with the action of E on C and C′. We claim that \(\theta\) is defined over K. In order to prove this, we compute
This proves that C and C′ are equivalent.
It remains to prove surjectivity. Let \(\xi : G_{\bar{K}/K} \rightarrow E\) be a 1-cocycle representing an element in \(H^{1}(G_{\bar{K}/K},E)\). We embed E into \(\mathop{\mathrm{Isom}}\nolimits (E)\) by sending P ∈ E to the translation map \(\tau _{P} \in \mathop{\mathrm{Isom}}\nolimits (E)\), and then we may view \(\xi\) as living in the cohomology set \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (E)\bigr )}\). From (X.2.2), there are a curve C∕K and a \(\bar{K}\)-isomorphism ϕ : C → E such that for all \(\sigma \in G_{\bar{K}/K}\),
(The reason for using \(-\xi\), rather than \(\xi\), will soon become apparent.)
Define a map
We now show that μ gives C∕K the structure of a homogeneous space over E∕K and that its associated cohomology class is \(\{\xi \}\).
First we check that μ is simply transitive. Let p, q ∈ C. Then by definition we have
so the only choice for P is P = ϕ(q) −ϕ(p). Second we verify that μ is defined over K. We take \(\sigma \in G_{\bar{K}/K}\) and compute
Finally, we compute the cohomology class associated to C∕K. To do this, we may choose any point p 0 ∈ C and take the class of the cocycle \(\sigma \mapsto p_{0}^{\sigma } - p_{0}\). In particular, if we take p 0 = ϕ −1(O), then
This completes the proof of (X.3.6). □
Remark 3.7.
Let E∕K be an elliptic curve and let \(K(\sqrt{d}\,)/K\) be a quadratic extension, so in particular \(\mathop{\mathrm{char}}\nolimits (K)\neq 2\). Let T ∈ E(K) be a nontrivial point of order 2. Then the homomorphism
is a 1-cocycle. We now construct the homogeneous space corresponding to the element \(\{\xi \}\in H^{1}(G_{\bar{K}/K},E)\).
Since T ∈ E(K), we may choose a Weierstrass equation for E∕K in the form
Then the translation-by-T map has the simple form
Thus if we let \(\sigma \in G_{\bar{K}/K}\) be the nontrivial automorphism of \(K(\sqrt{d}\,)/K\), then the action of \(\sigma\) on the twisted field \(\bar{K}(E)_{\xi }\) may be summarized by
We need to find the subfield of \(K(\sqrt{d}\,)(x,y)_{\xi }\) that is fixed by \(\sigma\).
The functions
are easily seen to be invariant. Anticipating the form of our final equation, we consider instead the functions
We find a relation between z and w by computing
Thus (z, w) are affine coordinates for the hyperelliptic curve
(See (II.2.5.1) and Exercise 2.14 for general properties of hyperelliptic curves.) We claim that C∕K is the twist of E∕K corresponding to the cocycle \(\xi\).
First, we recall from (II.2.5.1) that C is a smooth affine curve provided that the polynomial d 2 − 2adz 2 + (a 2 − 4b)z 4 has four distinct roots in \(\bar{K}\). Further, (II.2.5.2) says that if the quartic polynomial has distinct roots, then there is a smooth curve in \(\mathbb{P}^{3}\) that has an affine piece isomorphic to C. This smooth curve consists of C together with the two points
at infinity. (N.B. The projective closure of C in \(\mathbb{P}^{2}\) is always singular.) It is easy to check that the quartic has distinct roots if and only if b(a 2 − 4b) ≠ 0. On the other hand, since E is nonsingular, we know that Δ(E) = 16b 2(a 2 − 4b) ≠ 0. Therefore C is an affine piece of a smooth curve in \(\mathbb{P}^{3}\). To ease notation, we also use C to denote this smooth curve \(C \subset \mathbb{P}^{3}\).
There is a natural map defined over \(K(\sqrt{d}\,)\),
Note that since
the map ϕ may also be written as
This allows us to evaluate
To show that ϕ is an isomorphism, we compute its inverse:
This gives x in terms of z and w, and then \(y = \sqrt{d}\,x/z\). Thus
Since C and E are smooth, it follows from (II.2.4.1) that ϕ is an isomorphism.
Finally, in order to compute the element of \(H^{1}(G_{\bar{K}/K},E)\) corresponding to the curve C∕K, we may choose any point p ∈ C and compute the cocycle
For instance, we may take \(p = (0,\sqrt{d}\,) \in C\). It is clear that if \(\sigma\) fixes \(\sqrt{d}\), then \(p^{\sigma } - p = O\). On the other hand, if \(\sqrt{d}^{\,\sigma } = -\sqrt{d}\), then
Therefore \(p^{\sigma } - p =\xi _{\sigma }\) for all \(\sigma \in G_{\bar{K}/K}\), so \(\{C/K\} \in \mathop{\mathrm{WC}}\nolimits (E/K)\) maps to \(\{\xi \}\in H^{1}(G_{\bar{K}/K},E)\). Of course, it was just “luck” that we obtained an equality \(p^{\sigma } - p =\xi _{\sigma }\). In general, the difference of these two cocycles would be some coboundary.
We conclude this section by showing that if C∕K is a homogeneous space for E∕K, then \(\mathop{\mathrm{Pic}}\nolimits ^{0}(C)\) may be canonically identified with E. This means that E is the Jacobian variety of C∕K. Since every curve C∕K of genus one is a homogeneous space for some elliptic curve E∕K (Exercise 10.3), this shows that the abstract group \(\mathop{\mathrm{Pic}}\nolimits ^{0}(C)\) can always be represented as the group of points of an elliptic curve. The analogous result for curves of higher genus, in which \(\mathop{\mathrm{Pic}}\nolimits ^{0}(C)\) is represented by an abelian variety of dimension equal to the genus of C, is considerably harder to prove.
Theorem 3.8.
Let C∕K be a homogeneous space for an elliptic curve E∕K. Choose a point p 0 ∈ C and consider the summation map
-
(a)
There is an exact sequence

-
(b)
The summation map is independent of the choice of the point p 0 .
-
(c)
The summation map commutes with the natural actions of the Galois group \(G_{\bar{K}/K}\) on \(\mathop{\mathrm{Div}}\nolimits ^{0}(C)\) and on E. Hence it induces an isomorphism of \(G_{\bar{K}/K}\) -modules (also denoted by \(\mathop{\mathrm{sum}}\nolimits\) )
$$\displaystyle{\mathop{\mathrm{sum}}\nolimits :\mathop{ \mathrm{Pic}}\nolimits ^{0}(C)\mathop{\longrightarrow}\limits_{}^{\; \sim \;} E.}$$In particular,
$$\displaystyle{\mathop{\mathrm{Pic}}\nolimits _{K}^{0}(C)\mathop{\cong}E(K).}$$
Proof.
(a) Using (II.3.4), we see that we must check that the summation map is a surjective homomorphism and that its kernel is the set of principal divisors. It is clear that it is a homomorphism. Let P ∈ E and \(D = (p_{0} + P) - (p_{0}) \in \mathop{\mathrm{Div}}\nolimits ^{0}(C)\). Then
so \(\mathop{\mathrm{sum}}\nolimits\) is surjective.
Next suppose that \(D =\sum n_{i}(p_{i}) \in \mathop{\mathrm{Div}}\nolimits ^{0}(C)\) satisfies \(\mathop{\mathrm{sum}}\nolimits (D) = O\). Then the divisor \(\sum n_{i}(p_{i} - p_{0}) \in \mathop{\mathrm{Div}}\nolimits ^{0}(E)\) sums to O, so (III.3.5) tells us that it is principal, say
We have an isomorphism
and hence applying (II.3.6b),
Therefore D is principal.
Finally, if \(D =\mathop{ \mathrm{div}}\nolimits (g)\) is principal, then
and hence \(\mathop{\mathrm{sum}}\nolimits (D) = O\). This shows that the kernel of the summation map is the set of principal divisors.
(b)Let \(\mathop{\mathrm{sum } }\nolimits ' :\mathop{ \mathrm{Div } }\nolimits ^{0 } (C) \rightarrow E\) be the summation map defined using the base point p 0′ ∈ C. Then
since \(\sum n_{i} =\deg (D) = 0\).
(c)Let \(\sigma \in G_{\bar{K} /K }\). Then
since we know from (b) that the sum is the same if we use \(p_{0}^{\sigma }\) as our base point instead of p 0. Now (a) and the definition of \(\mathop{\mathrm{Pic}}\nolimits ^{0}(C)\) tell us that we have a group isomorphism \(\mathop{\mathrm{sum}}\nolimits :\mathop{ \mathrm{Pic}}\nolimits ^{0}(C) \rightarrow E\), and the fact that the summation map commutes with the action of \(G_{\bar{K}/K}\) says precisely that it is an isomorphism of \(G_{\bar{K}/K}\)-modules. Finally, the last statement in (X.3.8c) follows by taking \(G_{\bar{K}/K}\)-invariants. □
X.4 The Selmer and Shafarevich–Tate Groups
We return now to the problem of calculating the Mordell–Weil group of an elliptic curve E∕K defined over a number field K. As we have seen in (VIII.3.2) and Exercise 8.18, it is enough to find generators for the finite group E(K)∕mE(K) for any integer m ≥ 2.
Suppose that we are given another elliptic curve E′∕K and a nonzero isogeny ϕ : E → E′ defined over K. For example, we could take E = E′ and ϕ = [m]. Then there is an exact sequence of \(G_{\bar{K}/K}\)-modules
where E[ϕ] denotes the kernel of ϕ. Taking Galois cohomology yields the long exact sequence

and from this we form the fundamental short exact sequence
Note that (X.3.6) says that the last term in (*) may be identified with the ϕ-torsion in the Weil–Châtelet group \(\mathop{\mathrm{WC}}\nolimits (E/K)\).
The next step is to replace the second and third terms of (*) with certain finite groups. This is accomplished by local considerations. For each v ∈ M K we fix an extension of v to \(\bar{K}\), which serves to fix an embedding \(\bar{K} \subset \bar{K}_{v}\) and a decomposition group \(G_{v} \subset G_{\bar{K}/K}\). Now G v acts on \(E(\bar{K}_{v})\) and \(E'(\bar{K}_{v})\), and repeating the above argument yields exact sequences
The natural inclusions \(G_{v} \subset G_{\bar{K}/K}\) and \(E(\bar{K}) \subset E(\bar{K}_{v})\) give restriction maps on cohomology, and we thus end up with the following commutative diagram, in which we have replaced each H 1(G, E) with the corresponding Weil–Châtelet group:
Our ultimate goal is to compute the image of \(E'(K)/\phi {\bigl (E(K)\bigr )}\) in the cohomology group \(H^{1}{\bigl (G_{\bar{K}/K},E[\phi ]\bigr )}\), or equivalently, to compute the kernel of the map
Using (X.3.3), we see that this last problem is the same as determining whether certain homogeneous spaces possess a K-rational point, which may be a very difficult question to answer. On the other hand, by the same reasoning, the determination of each local kernel
is straightforward, since the question whether a curve has a point over a complete local field K v reduces, by Hensel’s lemma, to checking whether the curve has a point in some finite ring \(R_{v}^{}/\mathcal{M}_{v}^{e}\) for some easily computable integer e, which clearly requires only a finite amount of computation. This prompts the following definitions.
Definition.
Let ϕ : E∕K → E′∕K be an isogeny. The ϕ-Selmer group of E∕K is the subgroup of \(H^{1}{\bigl (G_{\bar{K}/K},E[\phi ]\bigr )}\) defined by
The Shafarevich–Tate group of E∕K is the subgroup of \(\mathop{\mathrm{WC}}\nolimits (E/K)\) defined by

(The Cyrillic letter  is pronounced “sha.”)
is pronounced “sha.”)
Remark 4.1.1.
The exact sequences (*
v
) require us to extend each v ∈ M
K
to \(\bar{K}\), so the groups S
(ϕ)(E∕K) and  might depend on this choice. However, in order to determine whether an element of \(\mathop{\mathrm{WC}}\nolimits (E/K)\) becomes trivial in \(\mathop{\mathrm{WC}}\nolimits (E/K_{v})\), we must check whether the associated homogeneous space, which is a curve defined over K, has any points defined over K
v
. This last problem is clearly independent of our choice of extension of v to \(\bar{K}\), since v itself determines the embedding of K into K
v
. Therefore S
(ϕ)(E∕K) and
might depend on this choice. However, in order to determine whether an element of \(\mathop{\mathrm{WC}}\nolimits (E/K)\) becomes trivial in \(\mathop{\mathrm{WC}}\nolimits (E/K_{v})\), we must check whether the associated homogeneous space, which is a curve defined over K, has any points defined over K
v
. This last problem is clearly independent of our choice of extension of v to \(\bar{K}\), since v itself determines the embedding of K into K
v
. Therefore S
(ϕ)(E∕K) and  depend only on E and K.
depend only on E and K.
Alternatively, one can check directly by working with cocycles that the cohomological definitions of S
(ϕ) and  do not depend on the extension of the v ∈ M
K
to \(\bar{K}\). We leave this verification for the reader. (See also Exercise B.6.)
do not depend on the extension of the v ∈ M
K
to \(\bar{K}\). We leave this verification for the reader. (See also Exercise B.6.)
Remark 4.1.2.
A good way to view  is as the group of homogeneous spaces for E∕K that possess a K
v
-rational point for every v ∈ M
K
.
Equivalently, the Shafarevich–Tate group
is as the group of homogeneous spaces for E∕K that possess a K
v
-rational point for every v ∈ M
K
.
Equivalently, the Shafarevich–Tate group  is the group of homogeneous spaces, modulo equivalence, that are everywhere locally trivial.
is the group of homogeneous spaces, modulo equivalence, that are everywhere locally trivial.
Theorem 4.2.
Let ϕ : E∕K → E′∕K be an isogeny of elliptic curves defined over K.
-
(a)
There is an exact sequence

-
(b)
The Selmer group S (ϕ) (E∕K) is finite.
Proof.
(a) This is immediate from the diagram (**) and the definitions of the Selmer and Shafarevich–Tate groups.
(b)If we take E = E′ and ϕ = [m], then (a) and the finiteness of S (m)(E∕K) imply the weak Mordell–Weil theorem. On the other hand, in order to prove that S (ϕ)(E∕K) is finite for a general map ϕ, we must essentially re-prove the weak Mordell–Weil theorem. The arguement goes as follows.
Let \(\xi \in S^{(\phi )}(E/K)\), and let v ∈ M K be a finite place of K not dividing \(m =\deg (\phi )\) and such that E∕K has good reduction at v. We claim that \(\xi\) is unramified at v. (See (VIII §2) for the definition of an unramified cocycle.)
To check this, let \(I_{v} \subset G_{v}\) be the inertia group for v. Since \(\xi \in S^{(\phi )}(E/K)\), we know that \(\xi\) is trivial in \(\mathop{\mathrm{WC}}\nolimits (E/K_{v})\). Hence from the sequence (* v ) given earlier, there is a point \(P \in E(\bar{K}_{v})\) such that
(Note that \(P^{\sigma } - P \in E[\phi ]\).) In particular, this holds for all \(\sigma\) in the inertia group. But if \(\sigma \in I_{v}\), then looking at the “reduction modulo v” map \(E \rightarrow \tilde{ E}_{v}\) yields
since by definition inertia acts trivially on \(\tilde{E}_{v}\). Thus \(P^{\sigma } - P\) is in the kernel of reduction modulo v. But \(P^{\sigma } - P\) is also in E[ϕ], which is contained in E[m]; and from (VIII.1.4) we know that E(K)[m] injects into \(\tilde{E}_{v}\). Therefore \(P^{\sigma } = P\), and hence
This proves that every element in S (ϕ)(E∕K) is unramified at all but a fixed, finite set of places v ∈ M K . The following lemma allows us to conclude that S (ϕ)(E∕K) is finite. □
Lemma 4.3.
Let M be a finite ( abelian ) \(G_{\bar{K}/K}\) -module, let \(S \subset M_{K}\) be a finite set of places, and define
Then \(H^{1}(G_{\bar{K}/K},M;S)\) is finite.
Proof.
Since M is finite and \(G_{\bar{K}/K}\) acts continuously on M, there is a subgroup of finite index in \(G_{\bar{K}/K}\) that fixes every element of M. Using the inflation–restriction sequence (B.2.4), it suffices to prove the lemma with K replaced by a finite extension, so we may assume that the action of \(G_{\bar{K}/K}\) on M is trivial. Then
Let m be the exponent of M, i.e., the smallest positive integer such that mx = 0 for all x ∈ M, and let L∕K be the maximal abelian extension of K having exponent m that is unramified outside of S. Since M has exponent m, the natural map
is an isomorphism. But we know from (VIII.1.6) that L∕K is a finite extension. Therefore \(\mathop{\mathrm{Hom}}\nolimits (G_{\bar{K}/K},M;S)\) is finite. □
We record as a corollary an important property of the Selmer group that was derived during the course of proving (X.4.2), where we use the fact (VII.7.2) that isogenous elliptic curves have the same set of primes of bad reduction.
Corollary 4.4.
Let ϕ : E∕K → E′∕K be as in (X.4.2), and let \(S \subset M_{K}\) be a finite set of places containing
Then
Remark 4.5.
Certainly in theory, and often in practice, the Selmer group is effectively computable. This is true because the finite group \(H^{1}(G_{\bar{K}/K},E[\phi ];S)\) is effectively computable. Then, in order to determine whether a given element \(\xi \in H^{1}(G_{\bar{K}/K},E[\phi ];S)\) is in S (ϕ)(E∕K), we take the corresponding homogeneous spaces \(\{C/K\} \in \mathop{\mathrm{WC}}\nolimits (E/K)\) and check, for each of the finitely many v ∈ S, whether C(K v ) ≠ ∅. This last problem may be reduced, using Hensel’s lemma, to a finite amount of computation.
Example 4.5.1.
We reformulate the example described in (X §1) in these terms, leaving some details to the reader. Let E∕K be an elliptic curve with \(E[m] \subset E(K)\), let \(S \subset M_{K}\) be the usual set of places (X.4.4), and let K(S, m) be as in (X.1.1c). We choose a basis for E[m] and use it to identify E[m] with \(\boldsymbol{\mu }_{m} \times \boldsymbol{\mu }_{m}\) as \(G_{\bar{K}/K}\)-modules. Then
where this map uses the isomorphism \(K^{{\ast}}/(K^{{\ast}})^{m}\mathop{\longrightarrow}\limits_{}^{\, \sim \,} H^{1}(G_{\bar{K}/K},\boldsymbol{\mu }_{m})\).
Restricting attention now to the case m = 2, the homogeneous space associated to a pair (b 1, b 2) ∈ K(S, m) × K(S, m) is the curve in \(\mathbb{P}^{3}\) given by the equations (cf. (X.1.4))
For any given pair (b 1, b 2) and any absolute value v ∈ S, it is easy to check whether C(K v ) ≠ ∅, and thus to calculate S (2)(E∕K). For example, the conclusion of (X.1.5) may be summarized by stating that the curve
satisfies

The conclusion about  follows from the exact sequence (X.4.2a), since in (X.1.5) we proved that every element of \(S^{(2)}(E/\mathbb{Q})\) is the image of a point in \(E(\mathbb{Q})\).
follows from the exact sequence (X.4.2a), since in (X.1.5) we proved that every element of \(S^{(2)}(E/\mathbb{Q})\) is the image of a point in \(E(\mathbb{Q})\).
Suppose that we have computed the Selmer group S
(ϕ)(E∕K) for an isogeny ϕ. Each \(\xi \in S^{(\phi )}(E/K)\) corresponds to a homogeneous space \(C_{\xi }/K\) that has a point defined over every local field K
v
. Suppose further that we are lucky and can show that  . This means that we are able to find a K-rational point on each \(C_{\xi }\). It then follows from (X.4.2a) that \(E'(K)/\phi {\bigl (E(K)\bigr )}\mathop{\cong}S^{(\phi )}(E/K)\), and all that remains is to explain how to find generators for \(E'(K)/\phi {\bigl (E(K)\bigr )}\) in terms of the points that we found in each \(C_{\xi }(K)\). This is done in the next proposition.
. This means that we are able to find a K-rational point on each \(C_{\xi }\). It then follows from (X.4.2a) that \(E'(K)/\phi {\bigl (E(K)\bigr )}\mathop{\cong}S^{(\phi )}(E/K)\), and all that remains is to explain how to find generators for \(E'(K)/\phi {\bigl (E(K)\bigr )}\) in terms of the points that we found in each \(C_{\xi }(K)\). This is done in the next proposition.
Proposition 4.6.
Let ϕ : E∕K → E′∕K be a K-isogeny, let \(\xi\) be a cocycle representing an element of \(H^{1}(G_{\bar{K}/K},E[\phi ])\) , and let C∕K be a homogeneous space representing the image of \(\xi\) in \(\mathop{\mathrm{WC}}\nolimits (E/K)\) . Choose a \(\bar{K}\) -isomorphism \(\theta : C \rightarrow E\) satisfying
-
(a)
The map \(\phi \circ \theta : C \rightarrow E'\) is defined over K.
-
(b)
Suppose that there is a point P ∈ C(K), so {C∕K} is trivial in \(\mathop{\mathrm{WC}}\nolimits (E/K)\) . Then the point \(\phi \circ \theta (P) \in E'(K)\) maps to \(\xi\) via the connecting homomorphism \(\delta : E'(K) \rightarrow H^{1}{\bigl (G_{\bar{K}/K},E[\phi ]\bigr )}\) .
Proof.
(a) Let \(\sigma \in G_{\bar{K}/K}\) and let P ∈ C. Then, since ϕ is defined over K and \(\xi _{\sigma } \in E[\phi ]\), we have
Therefore \(\phi \circ \theta\) is defined over K.
(b)This is just a matter of unwinding definitions. Thus
□
Remark 4.7.
We have been working with arbitrary isogenies ϕ : E → E′, but in order to compute the Mordell–Weil group of E′, we must find generators for E′(K)∕mE′(K) for some integer m; simply knowing \(E'(K)/\phi {\bigl (E(K)\bigr )}\) is not enough. The solution to this dilemma is to work with both ϕ and its dual \(\hat{\phi }: E' \rightarrow E\). Using the procedure described in this section, we compute both Selmer groups S (ϕ)(E∕K) and \(S^{(\hat{\phi })}(E'/K)\), and with a little bit of luck, we find generators for the two quotient groups \(E'(K)/\phi {\bigl (E(K)\bigr )}\) and \(E(K)/\hat{\phi }{\bigl (E'(K)\bigr )}\). It is then a simple matter to compute generators for E(K)∕mE(K), where \(m =\deg (\phi )\), using the elementary exact sequence (note that \(\hat{\phi }\circ \phi = [m]\))
Example 4.8.
Two-isogenies. We illustrate the general theory by completely analyzing the case of isogenies of degree 2. Let ϕ : E → E′ be an isogeny of degree 2 defined over K. Then the kernel E[ϕ] = { O, T} is defined over K, so T ∈ E(K). Moving this K-rational 2-torsion point to (0, 0), we can find a Weierstrass equation for E∕K of the form
Let \(S \subset M_{K}\) be the usual set of places (X.4.4). Identifying E[ϕ] with \(\boldsymbol{\mu }_{2}\) (as \(G_{\bar{K}/K}\)-modules), we see that \(K^{{\ast}}/(K^{{\ast}})^{2}\mathop{\cong}H^{1}(G_{\bar{K}/K},E[\phi ])\). Thus, using notation from (X.1.1c) and (X.4.3), we have
More precisely, if d ∈ K(S, 2), then tracing through the above identification shows that the corresponding cocycle is
The homogeneous space C d ∕K associated to this cocycle was computed in (X.3.7); it is given by the equation
We can now compute the Selmer group S (ϕ) by checking whether C d (K v ) = ∅ for each of the finitely many d ∈ K(S, 2) and v ∈ S.
The isogenous curve E′∕K has Weierstrass equation
and the isogeny ϕ : E → E′ is given by the formula (III.4.5)
In (X.3.7) we gave an isomorphism \(\theta : C_{d} \rightarrow E\) defined over \(K(\sqrt{d}\,)\). Computing the composition \(\phi \circ \theta\) yields the map
described in (X.4.6). Finally, just as we did in (X.1.4) (see also Exercise 10.1), we can compute the connecting homomorphism
It is given by
We summarize (X.4.8) in the next proposition.
Proposition 4.9.
(Descent via Two-Isogeny) Let E∕K and E′∕K be elliptic curves given by the equations
and let
be the isogeny of degree 2 with kernel \(E[\phi ] ={\bigl \{ O,(0,0)\bigr \}}\) . Let
Further, for each d ∈ K ∗ , let C d ∕K be the homogeneous space for E∕K given by the equation
Then there is an exact sequence
The ϕ-Selmer group is
Finally, the map
has the property that if P ∈ C d (K), then
Remark 4.9.1.
Note that since the isogenous curve E′ in (X.4.9) has the same form as E, everything in (X.4.9) applies equally well to the dual isogeny \(\hat{\phi }: E' \rightarrow E\). Then, using the exact sequence (X.4.7), we can try to compute E(K)∕2E(K).
Remark 4.9.2.
If E∕K is an elliptic curve that has a K-rational 2-torsion point, then (III.4.5) says that E automatically has an isogeny of degree 2 defined over K. Thus the procedure described in (X.4.8) may be applied to any elliptic curve satisfying E(K)[2] ≠ 0. In particular, (X.4.9) in some sense subsumes (X.1.4), which described how to try to compute E(K)∕2E(K) when \(E[2] \subset E(K)\).
Example 4.10.
We use (X.4.9) to compute \(E(\mathbb{Q})/2E(\mathbb{Q})\) for the elliptic curve
This equation has discriminant Δ = −147968 = −29172, so our set S is \(\{\infty ,2,17\}\) and we may identify \(\mathbb{Q}(S,2)\) with { ± 1, ±2, ±17, ±34}. The curve that is 2-isogenous to E has equation
and for \(d \in \mathbb{Q}(S,2)\), the corresponding homogeneous space is
From (X.4.9) we know that the point \((0,0) \in E'(\mathbb{Q})\) maps to
so \(-2 \in S^{(\phi )}(E/\mathbb{Q})\). It remains to check the other values of \(d \in \mathbb{Q}(S,2)\).
Dividing by 2 and letting z = Z∕2 gives the equation
which by inspection has the rational point (Z, w) = (1, 2). Then (X.4.9) tells us that the point \((z,w) = (\frac{1} {2},2) \in C_{2}(\mathbb{Q})\) maps to to \(\psi (\frac{1} {2},2) = (8,-32) \in E'(\mathbb{Q})\). Further, as the theory predicts, we have \(\delta (8,-32) = 8 \equiv 2\ (\text{ mod}\ (\mathbb{Q}^{{\ast}})^{2})\).
Suppose that \(C_{17}(\mathbb{Q}_{17})\neq \emptyset\). Since \(\mathop{\mathrm{ord}}\nolimits _{17}(17w^{2})\) is odd and \(\mathop{\mathrm{ord}}\nolimits _{17}(32z^{4})\) is even, we see that necessarily \(z,w \in \mathbb{Z}_{17}\). But then the equation for C 17 implies first that \(z \equiv 0\ (\text{ mod}\ 17)\), then that \(w \equiv 0\ (\text{ mod}\ 17)\), and finally that \(17^{2} \equiv 0\ (\text{ mod}\ 17^{3})\). This contradiction shows that \(C_{17}(\mathbb{Q}_{17}) =\emptyset\), and hence that \(17\notin S^{(\phi )}(E/\mathbb{Q})\).
We now know that
Since \(S^{(\phi )}(E/\mathbb{Q})\) is a subgroup of \(\mathbb{Q}(S,2)\), we have \(S^{(\phi )}(E/\mathbb{Q}) =\{ \pm 1,\pm 2\}\). Further, we have shown that \(E'(\mathbb{Q})\) surjects onto \(S^{(\phi )}(E/\mathbb{Q})\), and hence from (X.4.2a) we see that  .
.
We now repeat the above computation with the roles of E and E′ reversed. Thus for \(d \in \mathbb{Q}(S,2)\) we look at the homogeneous space
As above, the point \((0,0) \in E(\mathbb{Q})\) maps to \(\delta (0,0) = 272 \equiv 17\ (\text{ mod}\ (\mathbb{Q}^{{\ast}})^{2})\). Next, if d < 0, then clearly \(C_{d}'(\mathbb{R}) =\emptyset\), so \(d\notin S^{(\hat{\phi })}(E'/\mathbb{Q})\). Finally, for d = 2, if we let z = Z∕2, then C 2′ has the equation
If \(C_{2}'(\mathbb{Q}_{2})\neq \emptyset\), then necessarily \(Z,w \in \mathbb{Z}_{2}\), and then the equation allows us to deduce successively
Therefore \(C_{2}(\mathbb{Q}_{2}) =\emptyset\), and hence \(2\notin S^{(\hat{\phi })}(E'/\mathbb{Q})\). Thus \(S^{(\hat{\phi })}(E'/\mathbb{Q}) =\{ 1,17\}\) and  .
.
To recapitulate, we now know that
the former being generated by \({\bigl \{(0,0),\,(8,-32)\bigr \}}\) and the latter by \({\bigl \{(0,0)\bigr \}}\). The exact sequence (X.4.7) then yields
and hence
Remark 4.11.
In all of the examples up to this point, we have been lucky in the sense that for every locally trivial homogeneous space that has appeared, we were able to find (by inspection) a global rational point. Another way to say this is that we have yet to see a nontrivial element of the Shafarevich–Tate group. The first examples of such spaces are due to Lind [150] and independently, but a bit later, to Reichardt [207]. For example, they proved that the curve
has no \(\mathbb{Q}\)-rational points, while it is easy to check that it has a point defined over every \(\mathbb{Q}_{p}\). Shortly thereafter, Selmer [225, 227] made an extensive study of the curves ax 3 + by 3 + cz 3 = 0, which are homogeneous spaces for the elliptic curves x 3 + y 3 + dz 3 = 0. He gave many examples of locally trivial, globally nontrivial homogeneous spaces, of which the simplest is
It is a difficult problem, in general, to divide the Selmer group into the piece coming from rational points on the elliptic curve and the piece giving nontrivial elements of the Shafarevich–Tate group. At present there is no algorithm known that is guaranteed to solve this problem. The procedure that we now describe often works in practice, although it tends to lead to fairly elaborate computations in algebraic number fields.
Recall that for each integer m ≥ 2 there is an exact sequence (X.4.2a)

where at least in theory, the finite group S
(m)(E∕K) is effectively computable; see (X.4.5). If we knew some way of computing  , then we could find generators for E(K)∕mE(K), and thence for E(K). Unfortunately, a general procedure for computing
, then we could find generators for E(K)∕mE(K), and thence for E(K). Unfortunately, a general procedure for computing  is still being sought. However, for each integer n ≥ 1 we can combine different versions of the above exact sequence to form a commutative diagram
is still being sought. However, for each integer n ≥ 1 we can combine different versions of the above exact sequence to form a commutative diagram

Now at least in principle, the middle column of this diagram is effectively computable. This allows us to make the following refinement to the exact sequence in (X.4.2a).
Proposition 4.12.
Let E∕K be an elliptic curve. For any integers m ≥ 2 and n ≥ 1, let S (m,n) (E∕K) be the image of \(S^{(m^{n}) }(E/K)\) in S (m) (E∕K). Then there exists an exact sequence

Proof.
This is immediate from the commutative diagram given above. □
Now to find generators for E(K), we can try the following procedure. Compute successively the relative Selmer groups
and the rational-point groups
where T (m, r)(E∕K) is the subgroup of S (m)(E∕K) generated by all of the points P ∈ E(K) with height h x (P) ≤ r. Eventually, with sufficient perseverance, we hope to arrive at an equality
Once this happens, we know that  and that the points with height h
x
(P) ≤ r generate E(K)∕mE(K). The difficulty lies in the fact that as far as is currently known, there is nothing to prevent
and that the points with height h
x
(P) ≤ r generate E(K)∕mE(K). The difficulty lies in the fact that as far as is currently known, there is nothing to prevent  from containing an element that is infinitely m-divisible, i.e., a nonzero element
from containing an element that is infinitely m-divisible, i.e., a nonzero element  such that for every n ≥ 1 there is an element
such that for every n ≥ 1 there is an element  satisfying \(\xi = m^{n}\xi _{n}\). If such an element exists, then the above procedure never terminates. However, opposed to such a gloomy scenario is the following optimistic conjecture.
satisfying \(\xi = m^{n}\xi _{n}\). If such an element exists, then the above procedure never terminates. However, opposed to such a gloomy scenario is the following optimistic conjecture.
Conjecture 4.13.
Let E∕K be an elliptic curve. Then
 is finite.
!
is finite.
!
The finiteness of  has been proven for certain elliptic curves by Kolyvagin [130] and Rubin [215]. Note that the successful carrying out of the procedure described above shows only that the m-primary component of
has been proven for certain elliptic curves by Kolyvagin [130] and Rubin [215]. Note that the successful carrying out of the procedure described above shows only that the m-primary component of  is finite. This has, of course, been done in many cases. For example, in (X.4.10) we showed that
is finite. This has, of course, been done in many cases. For example, in (X.4.10) we showed that  for a particular elliptic curve.
for a particular elliptic curve.
We conclude this section with a beautiful result of Cassels, which says something interesting about the order of a group that is not known in general to be finite.
Theorem 4.14.
( [38] , [281] ) Let E∕K be an elliptic curve. There exists an alternating bilinear pairing

whose kernel on each side is exactly the subgroup of divisible elements of
 . In other words, if
\(\varGamma (\alpha ,\beta ) = 0\)
for all
. In other words, if
\(\varGamma (\alpha ,\beta ) = 0\)
for all
 , then for every integer N ≥ 1 there exists an element
, then for every integer N ≥ 1 there exists an element
 satisfying Nα
N
= α.
satisfying Nα
N
= α.
In particular, if
 is finite, then its order is a perfect square,
and the same is true of any p-primary component of
is finite, then its order is a perfect square,
and the same is true of any p-primary component of
 . (See Exercise
10.20
.)
. (See Exercise
10.20
.)
X.5 Twisting—Elliptic Curves
As in (X §§2,3), we let K be an arbitrary (perfect) field and we let E∕K be an elliptic curve. We saw in (X.2.2) that if we consider E merely to be a curve and ignore the base point O, then the twists of E∕K correspond to the elements of the (pointed) cohomology set \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Isom}}\nolimits (E)\bigr )}\). The group \(\mathop{\mathrm{Isom}}\nolimits (E)\) has two natural subgroups, namely \(\mathop{\mathrm{Aut}}\nolimits (E)\) and E, where we identify E with the set of translations {τ P } in \(\mathop{\mathrm{Isom}}\nolimits (E)\). We also observe that \(\mathop{\mathrm{Aut}}\nolimits (E)\) acts naturally on E. The next proposition describes \(\mathop{\mathrm{Isom}}\nolimits (E)\).
Proposition 5.1.
The map
is a bijection of sets. It identifies \(\mathop{\mathrm{Isom}}\nolimits (E)\) with the product of E and \(\mathop{\mathrm{Aut}}\nolimits (E)\) twisted by the natural action of \(\mathop{\mathrm{Aut}}\nolimits (E)\) on E. In other words, the group \(\mathop{\mathrm{Isom}}\nolimits (E)\) is the set of ordered pairs \(E \times \mathop{\mathrm{Aut}}\nolimits (E)\) with the group law
Proof.
Let \(\phi \in \mathop{\mathrm{Isom}}\nolimits (E)\). Then \(\tau _{-\phi (O)}\circ \phi \in \mathop{\mathrm{Aut}}\nolimits (E)\), so writing
shows that the map is surjective. On the other hand, if τ P ∘α = τ Q ∘β, then evaluating at O gives P = Q, and then also α = β. This proves injectivity. Finally, the twisted nature of the group law follows from the calculation
□
We have already extensively studied those twists of E∕K that arise from translations; these are the twists corresponding to elements of the group
that we studied in (X §§3,4). We now look at the twists of E∕K coming from isomorphisms of E as an elliptic curve, i.e., isomorphisms of the pair (E, O). In other words, we consider the twists of E corresponding to elements of the cohomology group \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\). We start with a general proposition and then, for \(\mathop{\mathrm{char}}\nolimits (K)\neq 2,3\), we derive explicit equations for the associated twists.
Remark 5.2.
In the literature, the phrase “let C be a twist of E” generally means that C corresponds to an element of \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\). More properly, such a C should be called a twist of the pair (E, O), since the group of isomorphisms of (E, O) with itself is the group we denote by \(\mathop{\mathrm{Aut}}\nolimits (E)\). However, one can generally resolve any ambiguity from context.
Proposition 5.3.
Let E∕K be an elliptic curve.
-
(a)
The natural inclusion \(\mathop{\mathrm{Aut}}\nolimits (E) \subset \mathop{\mathrm{Isom}}\nolimits (E)\) induces an inclusion
$$\displaystyle{H^{1}{\bigl (G_{\bar{ K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )} \subset H^{1}{\bigl (G_{\bar{ K}/K},\mathop{\mathrm{Isom}}\nolimits (E)\bigr )}.}$$Identifying the latter set with \(\mathop{\mathrm{Twist}}\nolimits (E/K)\) via (X.2.2), we denote the former by \(\mathop{\mathrm{Twist}}\nolimits {\bigl ((E,O)/K\bigr )}\) .
-
(b)
Let \(C/K \in \mathop{\mathrm{Twist}}\nolimits {\bigl ((E,O)/K\bigr )}\) . Then C(K) ≠ ∅ , so C∕K can be given the structure of an elliptic curve over K. N.B. The curve C∕K is generally not K-isomorphic to E∕K; cf. (X.3.3).
-
(c)
Conversely, if E′∕K is an elliptic curve that is isomorphic to E over \(\bar{K}\) , then E′∕K represents an element of \(\mathop{\mathrm{Twist}}\nolimits {\bigl ((E,O)/K\bigr )}\) .
Proof.
(a) Let \(i :\mathop{ \mathrm{Aut}}\nolimits (E) \rightarrow \mathop{\mathrm{Isom}}\nolimits (E)\) be the natural inclusion. From (X.5.1), there is a homomorphism \(j :\mathop{ \mathrm{Isom}}\nolimits (E) \rightarrow \mathop{\mathrm{Aut}}\nolimits (E)\) satisfying j ∘ i = 1. It follows that the induced map
is one-to-one.
(b)Let ϕ : C → E be an isomorphism defined over \(\bar{K}\) such that the cocycle
represents the element of \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\) corresponding to C∕K. Then we have \(\phi ^{\sigma } \circ \phi ^{-1}(O) = O\), so
Hence ϕ −1(O) ∈ C(K), so \({\bigl (C,\phi ^{-1}(O)\bigr )}\) is an elliptic curve defined over K.
(c)Let ϕ : E′ → E be a \(\bar{K}\)-isomorphism of elliptic curves, so in particular, ϕ(O′) = O, where O ∈ E(K) and O′ ∈ E′(K) are the respective zero points of E and E′. Then for any \(\sigma \in G_{\bar{K}/K}\) we have
Thus \(\phi ^{\sigma } \circ \phi ^{-1} \in \mathop{\mathrm{Aut}}\nolimits (E)\), so the cocycle corresponding to E′∕K lies in the group \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\) as desired. □
If the characteristic of K is not equal to 2 or 3, then the elements of the group \(\mathop{\mathrm{Twist}}\nolimits {\bigl ((E,O)/K\bigr )}\) can be described quite explicitly.
Proposition 5.4.
Assume that \(\mathop{\mathrm{char}}\nolimits (K)\neq 2,3\) , and let
Then \(\mathop{\mathrm{Twist}}\nolimits {\bigl ((E,O)/K\bigr )}\) is canonically isomorphic to K ∗ ∕(K ∗ ) n .
More precisely, choose a Weierstrass equation
for E∕K, and let D ∈ K ∗ . Then the elliptic curve \(E_{D} \in \mathop{\mathrm{Twist}}\nolimits {\bigl ((E,O)/K\bigr )}\) corresponding to \(D\ (\text{ mod}\ (K^{{\ast}})^{n})\) has Weierstrass equation
Corollary 5.4.1.
Define an equivalence relation on the set K × K ∗ by
where n(j) = 2 ( respectively 4, respectively 6 ) if j ≠ 0,1728 ( respectively j = 1728, respectively j = 0 ) . Then the K-isomorphism classes of elliptic curves E∕K are in one-to-one correspondence with the elements of the quotient
Proof.
From (III.10.2.) we have an isomorphism
of \(G_{\bar{K}/K}\)-modules. It follows from (B.2.5c) that
The calculation of an equation for the twist of E is straightforward. The case j(E) ≠ 0, 1728 was done in (X.2.4). We do j(E) = 1728 here and leave j(E) = 0 for the reader.
Thus let D ∈ K ∗, let \(\delta \in \bar{K}\) be a fourth root of D, and define a cocycle
We also fix an isomorphism
Then E D corresponds to the cocycle \(\sigma \mapsto [\xi _{\sigma }]\) in \(H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\).
The action of \(G_{\bar{K}/K}\) on the twisted field \(\bar{K}(E)_{\xi }\) is given by
The subfield fixed by \(G_{\bar{K}/K}\) thus contains the functions
and these functions satisfy the equation
This gives an equation for the twist E D ∕K, and the substitution
puts it into the desired form.
The corollary follows by combining the proposition and (X.5.3c) with (III.1.4bc), which says that up to \(\bar{K}\)-isomorphism, the elliptic curves E∕K are in one-to-one correspondence with their j-invariants j(E) ∈ K. □
X.6 The Curve Y 2 = X 3 + DX
Many of the deepest theorems and conjectures in the arithmetic theory of elliptic curves have had as their testing ground one of the families of curves given in (X.5.4). To illustrate the theory that we have developed, let’s see what we can say about the family of elliptic curves \(E/\mathbb{Q}\) with j-invariant j(E) = 1728.
One such curve is given by the equation
and then (X.5.3) and (X.5.4) tell us that every such curve has an equation of the form
where D ranges over representatives for the cosets in \(\mathbb{Q}^{{\ast}}/(\mathbb{Q}^{{\ast}})^{4}\). Thus if we specify that D is a fourth-power-free integer, then D is uniquely determined by E. We observe that the equation for E has discriminant Δ(E) = −64D 3, so E has good reduction at all primes not dividing 2D, and the given Weierstrass equation is minimal at all odd primes.
Let p be a prime not dividing 2D and consider the reduced curve \(\tilde{E}\) over the finite field \(\mathbb{F}_{p}\). From (V.4.1) we find that \(\tilde{E}\) is supersingular if and only if the coefficient of x p−1 in (x 3 + Dx)(p−1)∕2 is zero. In particular, if \(p \equiv 3\ (\text{ mod}\ 4)\), then \(\tilde{E}/\mathbb{F}_{p}\) is supersingular, and hence we conclude (see Exercise 5.10) that
(See Exercise 10.17 for an elementary derivation of this result.)
Next we recall from (VII.3.5) that if p ≠ 2 and if E has good reduction at p, then \(E_{\text{tors}}(\mathbb{Q})\) injects into the reduction \(\tilde{E}(\mathbb{F}_{p})\). It follows from this discussion that \(\#E_{\text{tors}}(\mathbb{Q})\) divides p + 1 for all but finitely many primes \(p \equiv 3\ (\text{ mod}\ 4)\), and hence that \(\#E_{\text{tors}}(\mathbb{Q})\) divides 4. Since \((0,0) \in E(\mathbb{Q})[2]\), the possibilities for \(E_{\text{tors}}(\mathbb{Q})\) are \(\mathbb{Z}/2\mathbb{Z}\), \((\mathbb{Z}/2\mathbb{Z})^{2}\), and \(\mathbb{Z}/4\mathbb{Z}\).
We have \(E[2] \subset E(\mathbb{Q})\) if and only if the polynomial x 3 + Dx factors completely over \(\mathbb{Q}\), so if and only if − D is a perfect square. Similarly, \(E(\mathbb{Q})\) has a point of order 4 if and only if \((0,0) \in 2E(\mathbb{Q})\). The duplication formula for E reads
so we see that
Hence assuming that D is a fourth-power-free integer, we conclude that
in which case (0, 0) = [2](2, ±4).
Next, since \(E(\mathbb{Q})\) contains a 2-torsion point, we can use (X.4.9) to try to calculate \(E(\mathbb{Q})/2E(\mathbb{Q})\). The curve E is isogenous to the curve
via the isogeny
The set \(S \subset M_{\mathbb{Q}}\) consists of \(\infty \) and the primes dividing 2D, and for each \(d \in \mathbb{Q}(S,2)\), the corresponding homogeneous space \(C_{d}/\mathbb{Q} \in \mathop{\mathrm{WC}}\nolimits (E/\mathbb{Q})\) is given by the equation
Similarly, working with the dual isogeny \(\hat{\phi }: E' \rightarrow E\) leads to the homogeneous spaces \(C_{d}'/\mathbb{Q} \in \mathop{\mathrm{WC}}\nolimits (E'/\mathbb{Q})\) with equations
(More precisely, using (X.4.9) leads to the equation dW 2 = d 2 + 16DZ 4, but we are free to replace Z with Z∕2.)
Let ν(2D) denote the number of distinct primes dividing 2D. The group \(\mathbb{Q}(S,2)\) is generated by − 1 and the primes dividing 2D, so we have the estimate
Here \(\dim _{2}\) denotes the dimension of an \(\mathbb{F}_{2}\)-vector space. We clearly have
In order to deal with the other two terms, we consider two cases.
-
(1)
\(E(\mathbb{Q})[2]\mathop{\cong}\mathbb{Z}/2\mathbb{Z}\). Then \(\phi {\bigl (E(\mathbb{Q})[2]\bigr )}\mathop{\cong}0\) and \(\dim _{2}E(\mathbb{Q})/2E(\mathbb{Q}) =\mathop{ \mathrm{rank}}\nolimits E(\mathbb{Q}) + 1\).
-
(2)
\(E(\mathbb{Q})[2]\mathop{\cong}\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}\). Then \(\phi {\bigl (E(\mathbb{Q})[2]\bigr )}\mathop{\cong}\mathbb{Z}/2\mathbb{Z}\) and \(\dim _{2}E(\mathbb{Q})/2E(\mathbb{Q}) =\mathop{ \mathrm{rank}}\nolimits E(\mathbb{Q}) + 2\).
Substituting these values into the above inequality yields in both cases the estimate
Notice that we have obtained this upper bound without having checked for local triviality of any of the homogeneous spaces C d and C d ′. By inspection, if d < 0, then either \(C_{d}(\mathbb{R}) =\emptyset\) or \(C_{d}'(\mathbb{R}) =\emptyset\). Thus the upper bound my be decreased by 1, giving the small improvement
The preceding discussion is summarized in the following proposition.
Proposition 6.1.
Let \(D \in \mathbb{Z}\) be a fourth-power-free integer, and let E D be the elliptic curve
-
(a)
$$\displaystyle{E_{D,\text{tors}}(\mathbb{Q})\mathop{\cong}\left \{\begin{array}{@{}l@{\quad }l@{}} \mathbb{Z}/4\mathbb{Z} \quad &\mbox{ if $D = 4$,} \\ \mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}\quad &\mbox{ if $ - D$ is a perfect square,} \\ \mathbb{Z}/2\mathbb{Z} \quad &\text{otherwise.}\\ \quad \end{array} \right .}$$
-
(b)
$$\displaystyle{\mathop{\mathrm{rank}}\nolimits E(\mathbb{Q}) \leq 2\nu (2D) - 1.}$$
Remark 6.1.1.
The estimate in (X.6.1b) cannot be improved in general. For example, the curve E : y 2 = x 3 − 82x has
while ν(−164) = ν(24 ⋅ 41) = 2. See Exercise 10.18.
We now restrict attention to the special case that D = p is an odd prime. The next proposition gives a complete description of the relevant Selmer groups and deduces corresponding upper bounds for the rank of \(E(\mathbb{Q})\) and the dimension of  .
.
Proposition 6.2.
Let p be an odd prime, let E p be the elliptic curve
and let ϕ : E p → E p ′ be the isogeny of degree 2 with kernel \(E_{p}[\phi ] ={\bigl \{ O,(0,0)\bigr \}}\).
-
(a)
$$\displaystyle{E_{p,\text{tors}}(\mathbb{Q})\mathop{\cong}\mathbb{Z}/2\mathbb{Z}.}$$
-
(b)
$$\displaystyle\begin{array}{rcl} S^{(\hat{\phi })}(E_{ p}'/\mathbb{Q})& \mathop{\cong}& \mathbb{Z}/2\mathbb{Z}. {}\\ S^{(\phi )}(E_{ p}/\mathbb{Q})& \mathop{\cong}& \left \{\begin{array}{@{}l@{\quad }l@{}} \mathbb{Z}/2\mathbb{Z} \quad &\mbox{ if $p \equiv 7,11(\text{ mod}16)$,} \\ (\mathbb{Z}/2\mathbb{Z})^{2}\quad &\mbox{ if $p \equiv 3,5,13,15(\text{ mod}16)$,} \\ (\mathbb{Z}/2\mathbb{Z})^{3}\quad &\mbox{ if $p \equiv 1,9(\text{ mod}16)$.}\\ \quad \end{array} \right . {}\\ & & {}\\ \end{array}$$
-
(c)
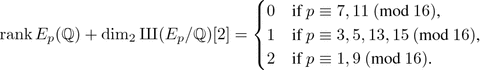
Proof.
To ease notation, we let E = E p and E′ = E p ′.
(a)This is a special case of (X.6.1a) .
(b)As usual, we take representatives { ± 1, ±2, ±p, ±2p} for the cosets in the finite group \(\mathbb{Q}(S,2)\). From (X.4.9) we know that the images of the 2-torsion points in the Selmer groups are given by
Further, if d < 0, then \(C_{d}(\mathbb{R}) =\emptyset\), so \(d\notin S^{(\hat{\phi })}(E'/\mathbb{Q})\).
Next we consider the homogeneous space
If \((Z,W) \in C_{2}'(\mathbb{Q}_{2})\), then necessarily \(Z,W \in \mathbb{Z}_{2}\), which allows us to conclude that \(Z \equiv 0\ (\text{ mod}\ 2)\), so \(W \equiv 0\ (\text{ mod}\ 2)\), and thus \(0 \equiv 4\ (\text{ mod}\ 8)\). Therefore \(C_{2}'(\mathbb{Q}_{2}) =\emptyset\), and hence \(2\notin S^{(\hat{\phi })}(E'/\mathbb{Q})\). We now know that
It follows that \(S^{(\hat{\phi })}(E'/\mathbb{Q}) =\{ 1,p\} \equiv \mathbb{Z}/2\mathbb{Z}\).
It remains to calculate \(S^{(\phi )}(E/\mathbb{Q})\), and from the form of the answer, it is clear that there will be many cases to be considered. The best approach is to look at the various \(d \in \mathbb{Q}(S,2)\) and check for which primes the homogeneous space is locally trivial. Note that (X.4.9) says that
i.e., it suffices to check whether C d is locally trivial at the primes p and 2. We make frequent use of Hensel’s lemma (Exercise 10.12), which gives a criterion for when a solution of an equation modulo q n lifts to a solution in \(\mathbb{Q}_{q}\).
-
(i)
If \((z,w) \in C_{-1}(\mathbb{Q}_{p})\), then necessarily \(z,w \in \mathbb{Z}_{p}\), so \(w^{2} \equiv -1\ (\text{ mod}\ p)\). Conversely, from Exercise 10.12 we see that any solution to the congruence \(w^{2} \equiv -1\ (\text{ mod}\ p)\) lifts to a point in \(C_{-1}(\mathbb{Q}_{p})\). Therefore
$$\displaystyle{C_{-1}(\mathbb{Q}_{p})\neq \emptyset \quad \Longleftrightarrow\quad p \equiv 1\pmod 4.}$$ -
(ii)
From (i) we may assume that \(p \equiv 1\ (\text{ mod}\ 4)\). If \(p \equiv 1\ (\text{ mod}\ 8)\), then we let
$$\displaystyle{\mbox{ $(z,w) = (Z/4,W/8)$}.}$$Our equation becomes W 2 + 64 = pZ 4, and the solution (1, 1) to the congruence
$$\displaystyle{W^{2} + 64 \equiv pZ^{4}\pmod 8}$$lifts to a point in \(C_{-1}(\mathbb{Q}_{2})\). Similarly, if \(p \equiv 5\ (\text{ mod}\ 8)\), then we let
$$\displaystyle{\mbox{ $(z,w) = (Z/2,W/2)$}}$$and consider the solution (Z, W) = (1, 1) to the congruence
$$\displaystyle{W^{2} + 4 = pZ^{4}\pmod 8.}$$This solution lifts to a point in \(C_{-1}(\mathbb{Q}_{2})\). This shows that if \(p \equiv 1\ (\text{ mod}\ 4)\), then \(C_{-1}(\mathbb{Q}_{2})\neq \emptyset\).
Combining (i) and (ii) yields
-
(i)
If \((z,w) \in C_{-2}(\mathbb{Q}_{p})\), then \(z,w \in \mathbb{Z}_{p}\) and \(w^{2} \equiv -2\ (\text{ mod}\ p)\). Conversely, a solution to \(w^{2} \equiv -2\ (\text{ mod}\ p)\) lifts to a point of \(C_{-1}(\mathbb{Q}_{p})\). Therefore
$$\displaystyle{C_{-2}(\mathbb{Q}_{p})\neq \emptyset \quad \Longleftrightarrow\quad p \equiv 1,3\pmod 8.}$$ -
(ii)
If \((z,w) \in C_{-2}(\mathbb{Q}_{2})\), then \(z,w \in \mathbb{Z}_{2}\) and \(w \equiv 0\ (\text{ mod}\ 2)\). So after setting (z, w) = (Z, 2W), we must check whether the equation
$$\displaystyle{2W^{2} + 1 = pZ^{4}}$$has any solutions \(Z,W \in \mathbb{Z}_{2}\). From (i) we see that it suffices to consider primes \(p \equiv 1,3\ (\text{ mod}\ 8)\). The congruence \(2W^{2} + 1 \equiv pZ^{4}\ (\text{ mod}\ 16)\) has no solutions if \(p \equiv 11\ (\text{ mod}\ 16)\), so
$$\displaystyle{p \equiv 11\pmod 16\quad \Longrightarrow\quad C_{-2}(\mathbb{Q}_{2}) =\emptyset .}$$On the other hand, if we can find solutions modulo 25 = 32, then Exercise 10.12 says that they lift to points in \(C_{-2}(\mathbb{Q}_{2})\). The following table gives solutions (Z, W) to the congruence
$$\displaystyle{2W^{2} + 1 \equiv pZ^{4}\pmod 32}$$for each of the remaining values of \(p\bmod 32\):
$$\displaystyle{\begin{array}{|c|c|c|c|c|c|c|} \hline p\bmod 32 & 1 & 3 & 9 & 17 & 19 & 25 \\ \hline (Z,W)&(1,0)&(3,11)&(1,2)&(3,0)&(1,3)&(3,2) \\ \hline\end{array} }$$
Combining (i) and (ii), we have proven that
This case is entirely similar to the case d = −2 that we just completed. A point \((z,w) \in C_{2}(\mathbb{Q}_{p})\) has \(z,w \in \mathbb{Z}_{p}\) and \(w^{2} \equiv 2\ (\text{ mod}\ p)\), and any such solutions lifts, so
Next, if \(p \equiv 1\ (\text{ mod}\ 8)\), then from above we have \(-1,-2 \in S^{(\phi )}(E/\mathbb{Q})\), so certainly \(2 \in S^{(\phi )}(E/\mathbb{Q})\). It remains to consider the case \(p \equiv 7\ (\text{ mod}\ 8)\).
A point \((z,w) \in C_{2}(\mathbb{Q}_{2})\) satisfies (z, w) = (Z, 2W) with \(Z,W \in \mathbb{Z}_{2}\) and
If \(p \equiv 7\ (\text{ mod}\ 16)\), then this equation has no solutions modulo 16. On the other hand, if \(p \equiv 15\ (\text{ mod}\ 16)\), then we have solutions
and these solutions lift to points in \(C_{2}(\mathbb{Q}_{2})\). Putting all of this together, we have shown that
We have now determined exactly which of the values − 1, 2, and − 2 are in \(S^{(\phi )}(E/\mathbb{Q})\) in terms of the residue of p modulo 16. Since we also know that \(-p \in S^{(\phi )}(E/\mathbb{Q})\), it is now a simple matter to reconstruct the table for \(S^{(\phi )}(E/\mathbb{Q})\) given in (b). In fact, we obtain more information, namely a precise list of which elements of \(\mathbb{Q}(S,2)\) are in \(S^{(\phi )}(E/\mathbb{Q})\).
(c)We use (X.4.7) and (X.4.2a) to compute

From (a) we see that
Further, since \(E(\mathbb{Q})/\hat{\phi }\bigl (E'(\mathbb{Q}))\mathop{\cong}S^{(\hat{\phi })}(E'/\mathbb{Q})\mathop{\cong}\mathbb{Z}/2\mathbb{Z}\) from (b), the exact sequence given in (X.4.2a) implies that  . Hence the exact sequence
. Hence the exact sequence

gives

and combining this with the above results yields

Now (c) is immediate from the calculation of \(S^{(\phi )}(E/\mathbb{Q})\) and \(S^{(\hat{\phi })}(E'/\mathbb{Q})\) given in (b). □
Corollary 6.2.1.
There are infinitely many elliptic curves \(E/\mathbb{Q}\) satisfying

Proof.
From (X.6.2), the elliptic curves y 2 = x 3 + px with \(p \equiv 7,11\ (\text{ mod}\ 16)\) have this property. □
Remark 6.3.
One of the consequences of (X.6.2) is that if p is a prime satisfying \(p \equiv 5\ (\text{ mod}\ 8)\), then the elliptic curve
has rank at most one. Further, examining the proof of (X.6.2) shows that the group \(E_{p}(\mathbb{Q})\) has rank 1 if and only if the homogeneous space
has a \(\mathbb{Q}\)-rational point, and if there is such a point, then we can find a point of infinite order in \(E(\mathbb{Q})\) by using the map
cf. (X.4.9). Taking the first few primes \(p \equiv 5\ (\text{ mod}\ 8)\), in each case we find points in \(C_{-1}(\mathbb{Q})\), and these give points of infinite order in \(E_{p}(\mathbb{Q})\) as listed in the following table:
Suppose that we knew, a priori, that the Shafarevich–Tate group  was finite, or even that its 2-primary component was finite.
Then the existence of the Cassels pairing (X.4.14) implies that
was finite, or even that its 2-primary component was finite.
Then the existence of the Cassels pairing (X.4.14) implies that  is even, and hence that \(E_{p}(\mathbb{Q})\) has rank 1 for all primes \(p \equiv 5\ (\text{ mod}\ 8)\). This also follows from a conjecture of Selmer [226] concerning the difference between the number of “first and second descents,” and it is also a consequence of the conjecture of Birch and Swinnerton-Dyer (C.16.5).
Bremner and Cassels [26, 27] have verified numerically that \(\mathop{\mathrm{rank}}\nolimits E_{p}(\mathbb{Q}) = 1\) for all such primes less than 20000,
and Monsky [182] has shown that \(\mathop{\mathrm{rank}}\nolimits E_{p}(\mathbb{Q}) = 1\) for all primes \(p \equiv 5\pmod 16\).
is even, and hence that \(E_{p}(\mathbb{Q})\) has rank 1 for all primes \(p \equiv 5\ (\text{ mod}\ 8)\). This also follows from a conjecture of Selmer [226] concerning the difference between the number of “first and second descents,” and it is also a consequence of the conjecture of Birch and Swinnerton-Dyer (C.16.5).
Bremner and Cassels [26, 27] have verified numerically that \(\mathop{\mathrm{rank}}\nolimits E_{p}(\mathbb{Q}) = 1\) for all such primes less than 20000,
and Monsky [182] has shown that \(\mathop{\mathrm{rank}}\nolimits E_{p}(\mathbb{Q}) = 1\) for all primes \(p \equiv 5\pmod 16\).
In order to give the reader an idea of the magnitude of the solutions that may occur, we mention that for p = 877, the Mordell–Weil group of the elliptic curve
is generated by the 2-torsion point (0, 0) and the point
Similarly, if \(p \equiv 3,15\ (\text{ mod}\ 16)\) and if the 2-primary component of  is finite, then (X.6.2) and (X.4.14) imply that \(E_{p}(\mathbb{Q})\) has rank exactly one. The fact that the rank is one for any particular prime p may be verified numerically by searching for a point in \(C_{-2}(\mathbb{Q})\) and \(C_{2}(\mathbb{Q})\) respectively. See, for example, the tables in [20] and [54] and online at [53] and [274].
is finite, then (X.6.2) and (X.4.14) imply that \(E_{p}(\mathbb{Q})\) has rank exactly one. The fact that the rank is one for any particular prime p may be verified numerically by searching for a point in \(C_{-2}(\mathbb{Q})\) and \(C_{2}(\mathbb{Q})\) respectively. See, for example, the tables in [20] and [54] and online at [53] and [274].
Remark 6.4.
If \(p \equiv 7,11\ (\text{ mod}\ 16)\), then (X.6.2c) says that \(E_{p}(\mathbb{Q})\) consists of only two points, while if \(p \equiv 3,5,13,15\ (\text{ mod}\ 16)\), then (X.6.2c) combined with the reasonable conjecture that  is finite tells us that \(E_{p}(\mathbb{Q})\mathop{\cong}\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}\). In the remaining case, namely \(p \equiv 1\ (\text{ mod}\ 8)\), there are two possibilities. First, \(E_{p}(\mathbb{Q})\) might have rank 2. This can certainly occur. For example, the curves
is finite tells us that \(E_{p}(\mathbb{Q})\mathop{\cong}\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}\). In the remaining case, namely \(p \equiv 1\ (\text{ mod}\ 8)\), there are two possibilities. First, \(E_{p}(\mathbb{Q})\) might have rank 2. This can certainly occur. For example, the curves
both have rank 2, independent points being given by
Second, \(E_{p}(\mathbb{Q})\) might have rank 0, in which case  . (Note that \(\mathop{\mathrm{rank}}\nolimits E_{p}(\mathbb{Q}) = 1\) is precluded if we assume that
. (Note that \(\mathop{\mathrm{rank}}\nolimits E_{p}(\mathbb{Q}) = 1\) is precluded if we assume that  is finite.) The next proposition gives a fairly general condition under which the second possibility holds. It also provides our first examples of homogeneous spaces that are everywhere locally trivial,
but have no global rational points.
is finite.) The next proposition gives a fairly general condition under which the second possibility holds. It also provides our first examples of homogeneous spaces that are everywhere locally trivial,
but have no global rational points.
Proposition 6.5.
Let \(p \equiv 1\ (\text{ mod}\ 8)\) be a prime for which 2 is not a quartic residue.
-
(a)
The curves
$$\displaystyle{w^{2} + 1 = 4pz^{4},\qquad w^{2} + 2 = 2pz^{4},\qquad w^{2} + 2pz^{4} = 2,}$$have points defined over every completion of \(\mathbb{Q}\) , but they have no \(\mathbb{Q}\) -rational points.
-
(b)
The elliptic curve
$$\displaystyle{E_{p} : y^{2} = x^{3} + px}$$satisfies

Remark 6.5.1.
Any prime \(p \equiv 1\ (\text{ mod}\ 8)\) can be written as p = A 2 + B 2 with \(A,B \in \mathbb{Z}\) satisfying \(AB \equiv 0\ (\text{ mod}\ 4)\). A theorem of Gauss, which we prove later in this section (X.6.6), says that 2 is a quartic residue modulo p if and only if \(AB \equiv 0\ (\text{ mod}\ 8)\). Thus, for example, 2 is a quartic nonresidue for the primes
so these primes satisfy the conclusion of (X.6.5).
Proof Proof of (X.6.5).
During the course of proving (X.6.2b), we showed that the Selmer group \(S^{(p)}(E_{p}/\mathbb{Q}) \subset \mathbb{Q}^{{\ast}}/(\mathbb{Q}^{{\ast}})^{2}\) is given by { ± 1, ±2, ±p, ±2p}. Further, we showed that − p is the image of the 2-torsion point \((0,0) \in E_{p}(\mathbb{Q})\). Thus in order to show that  has order 4, it suffices to prove that the homogeneous spaces C
−1, C
2, and C
−2 have no \(\mathbb{Q}\)-rational points. These are the three curves listed in (a), and so, once we prove that they have no \(\mathbb{Q}\)-rational points, all of (X.6.5) will follow from (X.6.2). Our proof is based on ideas of Lind and Mordell [150, 41]; see also [207, 184, 20].
has order 4, it suffices to prove that the homogeneous spaces C
−1, C
2, and C
−2 have no \(\mathbb{Q}\)-rational points. These are the three curves listed in (a), and so, once we prove that they have no \(\mathbb{Q}\)-rational points, all of (X.6.5) will follow from (X.6.2). Our proof is based on ideas of Lind and Mordell [150, 41]; see also [207, 184, 20].
Suppose that \((z,w) \in C_{\pm 2}(\mathbb{Q})\). Writing z and w in lowest terms, we see that they necessarily have the form (z, w) = (r∕t, 2s∕t 2), where \(r,s,t \in \mathbb{Z}\) satisfy
We write (a | b) for the Legendre symbol. Let q be an odd prime dividing s. Then (p | q) = 1, so (q | p) = 1 by quadratic reciprocity. Since also (2 | p) = 1, we see that (s | p) = 1, so (s 2 | p)4 = 1, i.e., s 2 is a quartic residue modulo p. Now the equation implies that (±2 | p)4 = 1. But − 1 is always a quartic residue for primes \(p \equiv 1\ (\text{ mod}\ 8)\), while by assumption 2 is a quartic nonresidue modulo p. This contradiction proves that \(C_{\pm 2}(\mathbb{Q}) =\emptyset\).
Writing \((z,w) \in C_{-1}(\mathbb{Q})\) in (almost) lowest terms as (z, w) = (r∕2t, s∕2t 2), we have
(We do not preclude the possibility that r is even.) Since \(p \equiv 1\ (\text{ mod}\ 4)\), there are integers \(A \equiv 1\ (\text{ mod}\ 2)\) and \(B \equiv 0\ (\text{ mod}\ 2)\) such that
It is a simple matter to verify the identity
from which we obtain the factorization
It is not difficult to check that \(\gcd (pr^{2} + 2Bt^{2} + As,pr^{2} + 2Bt^{2} - As)\) is either a square or twice a square; up to multiplication by 2, it is a square divisor of \(\gcd (A,s)^{2}\). Hence the above factorization implies that there are integers u and v satisfying
Eliminating s from these equations, we obtain two systems of equations:
We prove later (X.6.6) that the assumptions that 2 is a quartic nonresidue modulo p and that \(p \equiv 1\ (\text{ mod}\ 8)\) imply that \(B \equiv 4\ (\text{ mod}\ 8)\). Reducing each system of equations modulo 8, it is now a simple matter to verify that in both cases, any solution must satisfy \(r \equiv t \equiv 0\ (\text{ mod}\ 2)\). This contradicts our initial assumption that \(\gcd (r,t) = 1\), which completes the proof that \(C_{-1}(\mathbb{Q}) =\emptyset\). □
We close this section with the theorem of Gauss describing the quartic character of 2 that was used in the proof of (X.6.5). The proof that we give is due to Dirichlet [66]; see also [184].
Proposition 6.6.
Let p be a prime satisfying \(p \equiv 1\ (\text{ mod}\ 8)\) , and write p as a sum of two squares, p = A 2 + B 2 . Then
In other words, 2 is a quartic residue modulo p if and only if \(AB \equiv 0\ (\text{ mod}\ 8)\) .
Proof.
Using the fact that \(A^{2} + B^{2} \equiv 0\ (\text{ mod}\ p)\), we compute
Switching A and B if necessary, we may assume that A is odd, and then the fact that \(p \equiv 1\ (\text{ mod}\ 4)\) implies that
Hence
Finally, we observe that
since the identity
Substituting this above yields
□
Exercises
10.1. Let ϕ : E∕K → E′∕K be an isogeny of degree m of elliptic curves defined over an arbitrary (perfect) field K. Assume that \(E[\hat{\phi }] \subset E(K)\). Generalize (X.1.1) as follows:
-
(a)
Prove that there is a bilinear pairing
$$\displaystyle{b : E'(K)/\phi {\bigl (E(K)\bigr )} \times E'[\hat{\phi }]\longrightarrow K(S,m)}$$defined by
$$\displaystyle{e_{\phi }{\bigl (\delta _{\phi }(P),T\bigr )} = \delta _{K}{\bigl (b(P,T)\bigr )}.}$$Here e ϕ is the generalized Weil pairing (Exercise 3.15) and
$$\displaystyle{\delta _{\phi } : E'(K) \rightarrow H^{1}{\bigl (G_{\bar{ K}/K},E[\phi ]\bigr )}\qquad \text{and}\qquad \delta _{K} : K^{{\ast}}\rightarrow H^{1}(G_{\bar{ K}/K},\boldsymbol{\mu }_{m})}$$are the usual connecting homomorphisms.
-
(b)
Prove that the pairing in (a) is nondegenerate on the left.
-
(c)
For \(T \in E[\hat{\phi }]\), let f T ∈ K(E′) and g T ∈ K(E) be functions satisfying
$$\displaystyle{\mathop{\mathrm{div}}\nolimits (f_{T}) = m(T) - m(O)\qquad \text{and}\qquad f_{T}\circ \phi = g_{T}^{m}.}$$Prove that
$$\displaystyle{b(P,T) = f_{T}(P)\bmod (K^{{\ast}})^{m}\qquad \text{for all} P\neq O,T.}$$ -
(d)
In particular, if \(\deg (\phi ) = 2\), so \(E'[\hat{\phi }] =\{ O,T\}\), then
$$\displaystyle{b(P,T) = x(P) - x(T)\bmod (K^{{\ast}})^{2}.}$$We thus recover part of (X.4.9).
10.2. Let K be an arbitrary (perfect) field, let E∕K be an elliptic curve, and let C 1∕K and C 2∕K be homogeneous spaces for E∕K.
-
(a)
Prove that there exist a homogeneous space C 3∕K for E∕K and a morphism
$$\displaystyle{\phi : C_{1} \times C_{2} \rightarrow C_{3}}$$defined over K such that for all p 1 ∈ C 1, p 2 ∈ C 2, and P 1, P 2 ∈ E,
$$\displaystyle{\phi (p_{1} + P_{1},p_{2} + P_{2}) =\phi (p_{1},p_{2}) + P_{1} + P_{2}.}$$ -
(b)
Prove that C 3 is uniquely determined, up to equivalence of homogeneous spaces, by C 1 and C 2.
-
(c)
Prove that
$$\displaystyle{\{C_{1}\} +\{ C_{2}\} =\{ C_{3}\},}$$the sum taking place in \(\mathop{\mathrm{WC}}\nolimits (E/K)\).
10.3. Let C∕K be a curve of genus one defined over an arbitrary (perfect) field.
-
(a)
Prove that there exists an elliptic curve E∕K such that C∕K is a homogeneous space for E∕K. (Hint. Use Exercise 3.22 to show that \(C/K \in \mathop{\mathrm{Twist}}\nolimits (E/K)\). Then find an element \(\{\xi \}\in H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\) such that C∕K is the homogeneous space for the twist of E by \(\xi\).)
-
(b)
Prove that E is unique up to K-isomorphism.
10.4. Let K be an arbitrary (perfect) field and let E∕K be an elliptic curve.
-
(a)
Prove that there is a natural action of \(\mathop{\mathrm{Aut}}\nolimits _{K}(E)\) on \(\mathop{\mathrm{WC}}\nolimits (E/K)\) defined by letting an automorphism \(\alpha \in \mathop{\mathrm{Aut}}\nolimits _{K}(E)\) act on \(\{C/K,\mu \}\in \mathop{\mathrm{WC}}\nolimits (E/K)\) via
$$\displaystyle{\{C/K,\mu \}^{\alpha } ={\bigl \{ C/K,\mu \circ (1\times \alpha )\bigr \}}.}$$In other words, take the same curve, but define a new action of E on C by the rule
$$\displaystyle{\mu ^{\alpha }(p,P) =\mu (p,\alpha P).}$$ -
(b)
Conversely, if {C∕K, μ} and {C∕K, μ′} are elements of \(\mathop{\mathrm{WC}}\nolimits (E/K)\), prove that there exists an \(\alpha \in \mathop{\mathrm{Aut}}\nolimits _{K}(E)\) such that μ′ = μ ∘ (1 ×α).
-
(c)
Conclude that for a given curve C∕K of genus one, there are only finitely many inequivalent ways to make C∕K into a homogeneous space. In particular, if C satisfies j(C) ≠ 0, 1728, then there are at most two. (See also Exercise B.5.)
10.5. Let ϕ : E∕K → E′∕K be a separable isogeny of elliptic curves defined over an arbitrary (perfect) field K, and let C∕K be a homogeneous space for E∕K. The finite group E[ϕ] acts on C, and we let C′ = C∕E[ϕ] be the quotient curve (cf. Exercise 3.13).
-
(a)
Prove that C′ is a curve of genus one defined over K.
-
(b)
Prove that C′∕K is a homogeneous space for E′∕K and that the natural map
$$\displaystyle{\phi :\mathop{ \mathrm{WC}}\nolimits (E/K) \rightarrow \mathop{\mathrm{WC}}\nolimits (E'/K)}$$sends {C∕K} to {C′∕K}.
-
(c)
In particular, if \(\{C/K\} \in \mathop{\mathrm{WC}}\nolimits (E/K)[\phi ]\), then C′ is isomorphic to E′ over K. Prove that this isomorphism can be chosen so that the natural projection \(C \rightarrow C/E[\phi ]\mathop{\cong}E'\) is the map \(\phi \circ \theta\) defined in (X.4.6a).
10.6. WC Over Finite Fields. Let \(\mathbb{F}_{q}\) be a finite field with q elements, let \(C/\mathbb{F}_{q}\) be a curve of genus one, and pick any point of \(C(\bar{\mathbb{F}}_{q})\) as origin to make C into an elliptic curve. Let ϕ : C → C be the q th-power Frobenius map on C.
-
(a)
Prove that there are an endomorphism \(f \in \mathop{\mathrm{End}}\nolimits (C)\) and a point \(P_{0} \in C(\bar{\mathbb{F}}_{q})\) satisfying ϕ(P) = f(P) + P 0.
-
(b)
Prove that f is inseparable, and conclude that there exists a point \(P_{1} \in C(\bar{\mathbb{F}}_{q})\) satisfying (1 − f)(P 1) = P 0.
-
(c)
Prove that ϕ(P 1) = P 1, and hence that \(P_{1} \in C(\mathbb{F}_{q})\).
-
(d)
Let \(E/\mathbb{F}_{q}\) be an elliptic curve. Prove that \(\mathop{\mathrm{WC}}\nolimits (E/\mathbb{F}_{q}) = 0\).
10.7. WC Over \(\mathbb{R}\). Let \(E/\mathbb{R}\) be an elliptic curve.
-
(a)
Prove that
$$\displaystyle{\mathop{\mathrm{WC}}\nolimits (E/\mathbb{R}) = \left \{\begin{array}{@{}l@{\quad }l@{}} \mathbb{Z}/2\mathbb{Z}\quad &\mbox{ if $\varDelta (E/\mathbb{R}) > 0$,}\\ 0 \quad &\mbox{ if $\varDelta (E/\mathbb{R}) < 0$.} \\ \quad \end{array} \right .}$$ -
(b)
Assuming that \(\varDelta (E/\mathbb{R}) > 0\), find an equation for a homogeneous space representing the nontrivial element of \(\mathop{\mathrm{WC}}\nolimits (E/\mathbb{R})\) in terms of a given Weierstrass equation for \(E/\mathbb{R}\).
10.8. Let E∕K be an elliptic curve, let m ≥ 2 be an integer, and assume that \(E[m] \subset E(K)\). Let v ∈ M K 0 be a prime not dividing m. Prove that the restriction map
is surjective. (Hint. Show that the map on the \(H^{1}{\bigl (\,\cdot \,,E[m]\bigr )}\) groups is surjective.)
10.9. Let E∕K be an elliptic curve, let T ∈ E[m], and suppose that the field L = K(T) has maximal degree, namely [L : K] = m 2 − 1. (Note that L∕K is generally not a Galois extension.) Let e m denote the Weil pairing and consider the chain of maps
-
(a)
Let f T ∈ L(E) be as in (X.1.1d), i.e.,
$$\displaystyle{\mathop{\mathrm{div}}\nolimits (f_{T}) = m(T) - m(O)\qquad \text{and}\qquad f_{T} \circ [m] \in {\bigl ( L(E)^{{\ast}}\bigr )}^{m}.}$$Prove that
$$\displaystyle{\alpha (P) = f_{T}(P)\bmod (L^{{\ast}})^{m}.}$$ -
(b)
Prove that for all P ∈ E(K),
$$\displaystyle{\mathop{\mathrm{N}}\nolimits _{L/K}{\bigl (\alpha (P)\bigr )} \in (K^{{\ast}})^{m}.}$$ -
(c)
Let \(S \subset M_{L}\) be the set of places of L containing all archimedean places, all places dividing m, and all places at which E∕L has bad reduction. Show that if P ∈ E(K) and v ∈ M L with v ∉ S, then
$$\displaystyle{\mathop{\mathrm{ord}}\nolimits _{v}{\bigl (\alpha (P)\bigr )} \equiv 0\pmod m.}$$ -
(d)
For m = 2, prove that the kernel of α is exactly 2E(K). Hence in this case there is an injective homomorphism from E(K)∕2E(K) into the group
$$\displaystyle{{\bigl \{a \in L^{{\ast}}/(L^{{\ast}})^{2} : \mbox{ $\mathop{\mathrm{N}}\nolimits _{ L/K}(a) \in (K^{{\ast}})^{2}$ and $\mathop{\mathrm{ord}}\nolimits _{v}(a) \equiv 0(\text{ mod}2)$ for all $v\notin S$}\bigr \}}}$$given by the map
$$\displaystyle{P\longmapsto x(P) - x(T).}$$This map may often be used to compute E(K)∕2E(K). (Hint. Expand the quantity x(P) − x(T) = r + sx(T) + tx(T)2 and use the resulting relations on r, s, t ∈ K to show that P is in 2E(K).)
-
(e)
Use (d) to compute \(E(\mathbb{Q})/2E(\mathbb{Q})\) for the curve
$$\displaystyle{E : y^{2} + y = x^{3} - x.}$$(Hint. Let \(K/\mathbb{Q}\) be the totally real cubic field generated by a root of the polynomial 4x 3 − 4x + 1. Start by showing that K has class number one and that every totally positive unit in K is a square.)
10.10. Let C∕K be a curve of genus one, and suppose that C(K v ) ≠ ∅ for all v ∈ M K . Prove that the map
is surjective. (Hint. Take Galois cohomology of the exact sequence
Use Noether’s generalization of Hilbert’s Theorem 90,
and the (cohomological version) of the Brauer–Hasse–Noether theorem [288, §9.6], which says that an element of \(H^{2}(G_{\bar{K}/K},\bar{K}^{{\ast}})\) is trivial if and only if it is trivial in \(H^{2}(G_{\bar{K}_{v}/K_{v}},\bar{K}_{v}^{{\ast}})\) for every v ∈ M K .)
10.11. Index and Period in WC. Let K be an arbitrary (perfect) field, let E∕K be an elliptic curve, and let C∕K be a homogeneous space for E∕K. The period of C∕K is defined to be the exact order of {C∕K} in \(\mathop{\mathrm{WC}}\nolimits (E/K)\), and the index of C∕K is the smallest degree of an extension L∕K such that C(L) ≠ ∅. So for example, (X.3.3) says that the period is equal to 1 if and only if the index is equal to 1.
-
(a)
Prove that the period may also be characterized as the smallest integer m ≥ 1 such that there exists a point p ∈ C satisfying
$$\displaystyle{p^{\sigma } - p \in E[m]\qquad \mbox{ for every $\sigma \in G_{\bar{K}/K}$.}}$$ -
(b)
Prove that the index may also be characterized as the smallest degree among the positive divisors in \(\mathop{\mathrm{Div}}\nolimits _{K}(C)\).
-
(c)
Prove that the period divides the index.
-
(d)
Prove that the period and the index are divisible by the same set of primes.
-
(e)
* Give an example with \(K = \mathbb{Q}\) showing that the period may be strictly smaller than the index.
-
(f)
Prove that if K is a number field and if C∕K represents an element of
 ,
then the period and the index are equal. (Hint. Use (a), (b), (c), and Exercise 10.10.)
,
then the period and the index are equal. (Hint. Use (a), (b), (c), and Exercise 10.10.) -
(g)
* Let \(K/\mathbb{Q}_{p}\) be a finite extension. Prove that the period and the index are equal.
10.12. Hensel’s Lemma. The following version of Hensel’s lemma is often useful for proving that a homogeneous space is locally trivial. Let R be a ring that is complete with respect to a discrete valuation v.
-
(a)
Let f(T) ∈ R[T] be a polynomial and a 0 ∈ R a value satisfying
$$\displaystyle{v{\bigl (f(a_{0})\bigr )} > 2v{\bigl (f'(a_{0})\bigr )}.}$$Define a sequence of elements a n ∈ R recursively by
$$\displaystyle{a_{n+1} = a_{n} -\frac{f(a_{n})} {f'(a_{n})}\qquad \mbox{ for $n = 1, 2,\ldots \,$.}}$$Prove that a n converges to an element a ∈ R satisfying
$$\displaystyle{f(a) = 0\qquad \text{and}\qquad v(a - a_{0}) \geq v\left ( \frac{f(a_{0})} {f'(a_{0})^{2}}\right ) > 0.}$$ -
(b)
More generally, let F(X 1, …, X N ) ∈ R[X 1, …, X N ], and suppose that there are an index 1 ≤ i ≤ N and a point (a 1, …, a N ) ∈ R N satisfying
$$\displaystyle{v{\bigl (F(a_{1},\ldots ,a_{N})\bigr )} > 2v\left ( \frac{\partial F} {\partial X_{i}}(a_{1},\ldots ,a_{N})\right ).}$$Prove that F has a root in R N.
-
(c)
Show that the curve
$$\displaystyle{3X^{3} + 4Y ^{3} + 5Z^{3} = 0}$$in \(\mathbb{P}^{2}\) has a point defined over \(\mathbb{Q}_{p}\) for every prime p.
10.13. Use (X.1.4) to compute \(E(\mathbb{Q})/2E(\mathbb{Q})\) for each of the following elliptic curves.
-
(a)
E : y 2 = x(x − 1)(x + 3).
-
(b)
E : y 2 = x(x − 12)(x − 36).
10.14. Use (X.4.9) to compute \(E(\mathbb{Q})/2E(\mathbb{Q})\) for each of the following elliptic curves.
-
(a)
E : y 2 = x 3 + 6x 2 + x.
-
(b)
E : y 2 = x 3 + 14x 2 + x.
-
(c)
E : y 2 = x 3 + 9x 2 − x.
10.15. Let E∕K be an elliptic curve, let \(\xi \in H^{1}{\bigl (G_{\bar{K}/K},\mathop{\mathrm{Aut}}\nolimits (E)\bigr )}\), and let \(E_{\xi }\) be the twist of E corresponding to \(\xi\). Let v ∈ M K be a finite place at which E has good reduction. Prove that \(E_{\xi }\) has good reduction at v if and only if \(\xi\) is unramified at v. (See (VIII §2) for the definition of an unramified cocycle. Hint. If the residue characteristic is not 2 or 3, you can use explicit Weierstrass equations. In general, use the criterion of Néron–Ogg–Shafarevich (VII.7.1).)
10.16. Let E∕K be an elliptic curve, let D ∈ K ∗ be such that \(L = K(\sqrt{D}\,)\) is a quadratic extension, and let E D ∕K be the twist of E∕K given by (X.5.4). Prove that
10.17. Let \(p \equiv 3\ (\text{ mod}\ 4)\) be a prime and let \(D \in \mathbb{F}_{p}^{{\ast}}\).
-
(a)
Show directly that the equation
$$\displaystyle{C : v^{2} = u^{4} - 4D}$$has p − 1 solutions \((u,v) \in \mathbb{F}_{p} \times \mathbb{F}_{p}\). (Hint. Since \(p \equiv 3\ (\text{ mod}\ 4)\), the map u 2 ↦ u 4 is an automorphism of \((\mathbb{F}_{p}^{{\ast}})^{2}\).)
-
(b)
Let \(E/\mathbb{F}_{p}\) be the elliptic curve
$$\displaystyle{E : y^{2} = x^{3} + Dx.}$$Use the map
$$\displaystyle{\phi : C\longrightarrow E,\qquad \phi (u,v) = \left (\frac{u^{2} + v} {2} , \frac{u(u^{2} + v)} {2} \right ),}$$to prove that
$$\displaystyle{\#E(\mathbb{F}_{p}) = p + 1.}$$
10.18. Let p be an odd prime. Do a computation analogous to (X.6.2) to determine the Selmer groups and a bound for the ranks of the following families of elliptic curves \(E/\mathbb{Q}\).
-
(a)
E : y 2 = x 3 − 2px. (The curve with p = 41 has rank 3.)
-
(b)
E : y 2 = x 3 + p 2 x.
10.19. Let \(E/\mathbb{Q}\) be an elliptic curve with j(E) = 0.
-
(a)
Prove that there is a unique sixth-power-free integer D such that E is given by the Weierstrass equation
$$\displaystyle{E : y^{2} = x^{3} + D.}$$ -
(b)
Let \(p \equiv 2\ (\text{ mod}\ 3)\) be a prime not dividing 6D. Prove that
$$\displaystyle{\#E(\mathbb{F}_{p}) = p + 1.}$$ -
(c)
Prove that \(\#E(\mathbb{Q})_{\text{tors}}\) divides 6.
-
(d)
More precisely, prove that the following list gives a complete description of \(E_{\text{tors}}(\mathbb{Q})\):
$$\displaystyle{E_{\text{tors}}(\mathbb{Q})\mathop{\cong}\left \{\begin{array}{@{}l@{\quad }l@{}} \mathbb{Z}/6\mathbb{Z}\quad &\mbox{ if $D = 1$,} \\ \mathbb{Z}/3\mathbb{Z}\quad &\mbox{ if $D\neq 1$ is a square, or if $D = -432$,} \\ \mathbb{Z}/2\mathbb{Z}\quad &\mbox{ if $D\neq 1$ is a cube,} \\ 1 \quad &\text{otherwise.}\\ \quad \end{array} \right .}$$
10.20. Let A be a finite abelian group, and suppose that there exists a bilinear, alternating, nondegenerate pairing
Prove that # A is a perfect square.
10.21. Let E∕K be an elliptic curve defined over a field of characteristic not equal to 2 or 3, fix a Weierstrass equation for E∕K, and let c 4 and c 6 be the usual quantities (III §1) associated to the equation. Assuming that j(E) ≠ 0, 1728, we define
-
(a)
Prove that γ(E∕K) is well-defined as an element of K ∗∕(K ∗)2, independent of the choice of Weierstrass equation for E∕K.
-
(b)
Let E′∕K be another elliptic curve with j(E′) ≠ 0, 1728. Prove that E and E′ are isomorphic over K if and only if j(E) = j(E′) and γ(E∕K) = γ(E′∕K).
-
(c)
If j(E) = j(E′) ≠ 0, 1728, prove that E and E′ are isomorphic over the field
$$\displaystyle{K\left (\sqrt{\frac{\gamma (E/K)} {\gamma (E'/K)}}\right ).}$$
10.22. Let E∕K be an elliptic curve over an arbitrary (perfect) field, let L∕K be a finite Galois extension, and define a trace map
-
(a)
Prove that T L∕K is a homomorphism.
-
(b)
If K is a finite field, prove that T L∕K : E(L) → E(K) is surjective.
-
(c)
Assume that [L : K] = 2 and that \(\mathop{\mathrm{char}}\nolimits (K)\neq 2\), and write \(L = K(\sqrt{D}\,)\). Fix a Weierstrass equation for E∕K of the form
$$\displaystyle{E : y^{2} = x^{3} + ax^{2} + bx + c,}$$and let E D be the quadratic twist of E given by the equation (cf. (X.5.4))
$$\displaystyle{E_{D} : y^{2} = x^{3} + Dax^{2} + D^{2}bx + D^{3}c.}$$-
(i)
Prove that the kernel of T L∕K : E(L) → E(K) is isomorphic to E D (K).
-
(ii)
Prove that the image of T L∕K : E(L) → E(K) contains 2E(K).
-
(iii)
Deduce that there are an exact sequence

and a surjective homomorphism \(E(K)/2E(K) \twoheadrightarrow V\).
-
(iv)
Suppose further that K is a number field. Re-prove Exercise 10.16, i.e.,
$$\displaystyle{\mathop{\mathrm{rank}}\nolimits E(L) =\mathop{ \mathrm{rank}}\nolimits E(K) +\mathop{ \mathrm{rank}}\nolimits E_{D}(K).}$$
-
(i)
10.23. Let \(a \equiv 1\ (\text{ mod}\ 4)\) be an integer with the property that p = a 2 + 64 is prime. (It is conjectured, but not known, that there exist infinitely many such primes.) Let \(E_{a}/\mathbb{Q}\) be the elliptic curve
These are known as Neumann–Setzer curves.
-
(a)
Prove that \(\mathcal{D}_{E_{a}/\mathbb{Q}} = (p)\). More precisely, prove that E a has split multiplicative reduction at p and good reduction at all other primes. (N.B. The given Weierstrass equation is not minimal.)
-
(b)
Perform a two-descent (X.4.9) and prove that

-
(c)
* Let \(E/\mathbb{Q}\) be an elliptic curve with the following two properties: (i) \(E(\mathbb{Q})\) contains a 2-torsion point. (ii) E has multiplicative reduction at a single prime p > 17 and good reduction at all other primes. Prove that p has the form p = a 2 + 64 and that E is either isomorphic or 2-isogenous to the curve E a .
10.24. Let E∕K be an elliptic curve and let m ≥ 1. This exercise describes the Tate pairing
where \(\mathop{\mathrm{Br}}\nolimits (K) = H^{2}(G_{\bar{K}/K},\bar{K}^{{\ast}})\) is the Brauer group of K. (This exercise assumes that the reader is familiar with higher cohomology groups; see for example [9, 233].)
Let P ∈ E(K)∕mE(K) and let \(C \in \mathop{\mathrm{WC}}\nolimits (E/K)[m]\). We use the Kummer sequence (VIII §2)
to push forward the point P by δ and to pull back the homogeneous space C by ε to obtain 1-cocycles
We use δ P and ξ C to define a map
where e m is the Weil pairing.
-
(a)
Prove that the map λ P, C is a 2-cocycle.
-
(b)
Prove that changing either δ P or ξ C by a 1-coboundary has the effect of changing λ P, C by a 2-coboundary.
-
(c)
Prove that pulling back C to some other element ξ′ C changes λ P, C by a 2-coboundary.
-
(d)
Conclude that
$$\displaystyle{\langle P,\xi \rangle _{\text{Tate}} = \mbox{ cohomology class of $\lambda _{P,C}$}}$$gives a well-defined pairing
$$\displaystyle{\langle \,\cdot \,,\,\cdot \,\rangle _{\text{Tate}} : E(K)/mE(K) \times \mathop{\mathrm{WC}}\nolimits (E/K)[m]\longrightarrow \mathop{ \mathrm{Br}}\nolimits (K).}$$ -
(e)
Prove that the pairing in (d) is bilinear.
-
(f)
* Let K∕ℚ p be a finite extension. A basic result in local class field theory says that Br(K)≅ℚ∕ℤ; see [233, XII §3, Theorem 2]. Prove in this case that the Tate pairing is nondegenerate.
References
M. Abdalla, M. Bellare, and P. Rogaway. The oracle Diffie-Hellman assumptions and an analysis of DHIES. In Topics in cryptology—CT-RSA 2001 (San Francisco, CA), volume 2020 of Lecture Notes in Comput. Sci., pages 143–158. Springer, Berlin, 2001.
D. Abramovich. Formal finiteness and the torsion conjecture on elliptic curves. A footnote to a paper: “Rational torsion of prime order in elliptic curves over number fields” [Astérisque No. 228 (1995), 3, 81–100] by S. Kamienny and B. Mazur. Astérisque, (228):3, 5–17, 1995. Columbia University Number Theory Seminar (New York, 1992).
L. V. Ahlfors. Complex analysis. McGraw-Hill Book Co., New York, third edition, 1978. An introduction to the theory of analytic functions of one complex variable, International Series in Pure and Applied Mathematics.
T. M. Apostol. Introduction to analytic number theory. Springer-Verlag, New York, 1976. Undergraduate Texts in Mathematics.
T. M. Apostol. Modular functions and Dirichlet series in number theory, volume 41 of Graduate Texts in Mathematics. Springer-Verlag, New York, second edition, 1990.
N. Arthaud. On Birch and Swinnerton-Dyer’s conjecture for elliptic curves with complex multiplication. I. Compositio Math., 37(2):209–232, 1978.
E. Artin. Galois theory. Dover Publications Inc., Mineola, NY, second edition, 1998. Edited and with a supplemental chapter by Arthur N. Milgram.
M. F. Atiyah and I. G. Macdonald. Introduction to commutative algebra. Addison-Wesley Publishing Co., Reading, Mass.–London–Don Mills, Ont., 1969.
M. F. Atiyah and C. T. C. Wall. Cohomology of groups. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 94–115. Thompson, Washington, D.C., 1967.
A. O. L. Atkin and F. Morain. Elliptic curves and primality proving. Math. Comp., 61(203):29–68, 1993.
A. Baker. Transcendental number theory. Cambridge Mathematical Library. Cambridge University Press, Cambridge, second edition, 1990.
A. Baker and J. Coates. Integer points on curves of genus 1. Proc. Cambridge Philos. Soc., 67:595–602, 1970.
R. Balasubramanian and N. Koblitz. The improbability that an elliptic curve has subexponential discrete log problem under the Menezes-Okamoto-Vanstone algorithm. J. Cryptology, 11(2):141–145, 1998.
A. F. Beardon. Iteration of Rational Functions, volume 132 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1991. Complex analytic dynamical systems.
E. Bekyel. The density of elliptic curves having a global minimal Weierstrass equation. J. Number Theory, 109(1):41–58, 2004.
D. Bernstein and T. Lange. Faster addition and doubling on elliptic curves. In Advances in cryptology—ASIACRYPT 2007, volume 4833 of Lecture Notes in Comput. Sci., pages 29–50. Springer, Berlin, 2007.
B. J. Birch. Cyclotomic fields and Kummer extensions. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 85–93. Thompson, Washington, D.C., 1967.
B. J. Birch. How the number of points of an elliptic curve over a fixed prime field varies. J. London Math. Soc., 43:57–60, 1968.
B. J. Birch and W. Kuyk, editors. Modular functions of one variable. IV. Springer-Verlag, Berlin, 1975. Lecture Notes in Mathematics, Vol. 476.
B. J. Birch and H. P. F. Swinnerton-Dyer. Notes on elliptic curves. I. J. Reine Angew. Math., 212:7–25, 1963.
B. J. Birch and H. P. F. Swinnerton-Dyer. Elliptic curves and modular functions. In Modular functions of one variable, IV (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), pages 2–32. Lecture Notes in Math., Vol. 476. Springer, Berlin, 1975.
I. F. Blake, G. Seroussi, and N. P. Smart. Elliptic curves in cryptography, volume 265 of London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge, 2000. Reprint of the 1999 original.
D. Boneh and M. Franklin. Identity-based encryption from the Weil pairing. In Advances in Cryptology—CRYPTO 2001 (Santa Barbara, CA), volume 2139 of Lecture Notes in Comput. Sci., pages 213–229. Springer, Berlin, 2001.
D. Boneh, B. Lynn, and H. Shacham. Short signatures from the Weil pairing. In Advances in cryptology—ASIACRYPT 2001 (Gold Coast), volume 2248 of Lecture Notes in Comput. Sci., pages 514–532. Springer, Berlin, 2001.
A. I. Borevich and I. R. Shafarevich. Number theory. Translated from the Russian by Newcomb Greenleaf. Pure and Applied Mathematics, Vol. 20. Academic Press, New York, 1966.
A. Bremner. On the equation Y 2 = X(X 2 + p). In Number theory and applications (Banff, AB, 1988), volume 265 of NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., pages 3–22. Kluwer Acad. Publ., Dordrecht, 1989.
A. Bremner and J. W. S. Cassels. On the equation Y 2 = X(X 2 + p). Math. Comp., 42(165):257–264, 1984.
C. Breuil, B. Conrad, F. Diamond, and R. Taylor. On the modularity of elliptic curves over Q: wild 3-adic exercises. J. Amer. Math. Soc., 14(4):843–939 (electronic), 2001.
F. Brezing and A. Weng. Elliptic curves suitable for pairing based cryptography. Des. Codes Cryptogr., 37(1):133–141, 2005.
M. L. Brown. Note on supersingular primes of elliptic curves over Q. Bull. London Math. Soc., 20(4):293–296, 1988.
W. D. Brownawell and D. W. Masser. Vanishing sums in function fields. Math. Proc. Cambridge Philos. Soc., 100(3):427–434, 1986.
Y. Bugeaud. Bounds for the solutions of superelliptic equations. Compositio Math., 107(2):187–219, 1997.
J. P. Buhler, B. H. Gross, and D. B. Zagier. On the conjecture of Birch and Swinnerton-Dyer for an elliptic curve of rank 3. Math. Comp., 44(170):473–481, 1985.
E. R. Canfield, P. Erdős, and C. Pomerance. On a problem of Oppenheim concerning “factorisatio numerorum.” J. Number Theory, 17(1):1–28, 1983.
H. Carayol. Sur les représentations galoisiennes modulo l attachées aux formes modulaires. Duke Math. J., 59(3):785–801, 1989.
J. W. S. Cassels. A note on the division values of ℘(u). Proc. Cambridge Philos. Soc., 45:167–172, 1949.
J. W. S. Cassels. Arithmetic on curves of genus 1. III. The Tate-Šafarevič and Selmer groups. Proc. London Math. Soc. (3), 12:259–296, 1962.
J. W. S. Cassels. Arithmetic on curves of genus 1. IV. Proof of the Hauptvermutung. J. Reine Angew. Math., 211:95–112, 1962.
J. W. S. Cassels. Arithmetic on curves of genus 1. V. Two counterexamples. J. London Math. Soc., 38:244–248, 1963.
J. W. S. Cassels. Arithmetic on curves of genus 1. VIII. On conjectures of Birch and Swinnerton-Dyer. J. Reine Angew. Math., 217:180–199, 1965.
J. W. S. Cassels. Diophantine equations with special reference to elliptic curves. J. London Math. Soc., 41:193–291, 1966.
J. W. S. Cassels. Global fields. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 42–84. Thompson, Washington, D.C., 1967.
J. W. S. Cassels. Lectures on elliptic curves, volume 24 of London Mathematical Society Student Texts. Cambridge University Press, Cambridge, 1991.
T. Chinburg. An introduction to Arakelov intersection theory. In Arithmetic geometry (Storrs, Conn., 1984), pages 289–307. Springer, New York, 1986.
D. V. Chudnovsky and G. V. Chudnovsky. Padé approximations and Diophantine geometry. Proc. Nat. Acad. Sci. U.S.A., 82(8):2212–2216, 1985.
C. H. Clemens. A scrapbook of complex curve theory, volume 55 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, second edition, 2003.
L. Clozel, M. Harris, and R. Taylor. Automorphy for some l-adic lifts of automorphic mod l representations. 2007. IHES Publ. Math., submitted.
J. Coates. Construction of rational functions on a curve. Proc. Cambridge Philos. Soc., 68:105–123, 1970.
J. Coates and A. Wiles. On the conjecture of Birch and Swinnerton-Dyer. Invent. Math., 39(3):223–251, 1977.
H. Cohen. A Course in Computational Algebraic Number Theory, volume 138 of Graduate Texts in Mathematics. Springer-Verlag, Berlin, 1993.
H. Cohen, G. Frey, R. Avanzi, C. Doche, T. Lange, K. Nguyen, and F. Vercauteren, editors. Handbook of Elliptic and Hyperelliptic Curve Cryptography. Discrete Mathematics and Its Applications (Boca Raton). Chapman & Hall/CRC, Boca Raton, FL, 2006.
D. A. Cox. The arithmetic-geometric mean of Gauss. Enseign. Math. (2), 30(3-4):275–330, 1984.
J. Cremona. Elliptic Curve Data. http://sage.math.washington. edu/cremona/index.html , http://www.math.utexas.edu/users/ tornaria/cnt/cremona.html .
J. E. Cremona. Algorithms for modular elliptic curves. Cambridge University Press, Cambridge, second edition, 1997. available free online at www.warwick.ac.uk/ staff/J.E.Cremona/book/fulltext/index.html .
J. E. Cremona, M. Prickett, and S. Siksek. Height difference bounds for elliptic curves over number fields. J. Number Theory, 116(1):42–68, 2006.
L. V. Danilov. The Diophantine equation x 3 − y 2 = k and a conjecture of M. Hall. Mat. Zametki, 32(3):273–275, 425, 1982. English translation: Math. Notes Acad. Sci. USSR 32 (1982), no. 3–4, 617–618 (1983).
H. Davenport. On f 3 (t) − g 2 (t). Norske Vid. Selsk. Forh. (Trondheim), 38:86–87, 1965.
S. David. Minorations de formes linéaires de logarithmes elliptiques. Mém. Soc. Math. France (N.S.), (62):iv+143, 1995.
B. M. M. de Weger. Algorithms for Diophantine equations, volume 65 of CWI Tract. Stichting Mathematisch Centrum Centrum voor Wiskunde en Informatica, Amsterdam, 1989.
M. Deuring. Die Typen der Multiplikatorenringe elliptischer Funktionenkörper. Abh. Math. Sem. Hansischen Univ., 14:197–272, 1941.
M. Deuring. Die Zetafunktion einer algebraischen Kurve vom Geschlechte Eins. Nachr. Akad. Wiss. Göttingen. Math.-Phys. Kl. Math.-Phys.-Chem. Abt., 1953:85–94, 1953.
M. Deuring. Die Zetafunktion einer algebraischen Kurve vom Geschlechte Eins. II. Nachr. Akad. Wiss. Göttingen. Math.-Phys. Kl. IIa., 1955:13–42, 1955.
M. Deuring. Die Zetafunktion einer algebraischen Kurve vom Geschlechte Eins. III. Nachr. Akad. Wiss. Göttingen. Math.-Phys. Kl. IIa., 1956:37–76, 1956.
M. Deuring. Die Zetafunktion einer algebraischen Kurve vom Geschlechte Eins. IV. Nachr. Akad. Wiss. Göttingen. Math.-Phys. Kl. IIa., 1957:55–80, 1957.
W. Diffie and M. E. Hellman. New directions in cryptography. IEEE Trans. Information Theory, IT-22(6):644–654, 1976.
L. Dirichlet. Über den biquadratischen Charakter der Zahl “Zwei.” J. Reine Angew. Math., 57:187–188, 1860.
Z. Djabri, E. F. Schaefer, and N. P. Smart. Computing the p-Selmer group of an elliptic curve. Trans. Amer. Math. Soc., 352(12):5583–5597, 2000.
D. S. Dummit and R. M. Foote. Abstract algebra. John Wiley & Sons Inc., Hoboken, NJ, third edition, 2004.
R. Dupont, A. Enge, and F. Morain. Building curves with arbitrary small MOV degree over finite prime fields. J. Cryptology, 18(2):79–89, 2005.
B. Dwork. On the rationality of the zeta function of an algebraic variety. Amer. J. Math., 82:631–648, 1960.
H. M. Edwards. A normal form for elliptic curves. Bull. Amer. Math. Soc. (N.S.), 44(3):393–422 (electronic), 2007.
M. Eichler. Quaternäre quadratische Formen und die Riemannsche Vermutung für die Kongruenzzetafunktion. Arch. Math., 5:355–366, 1954.
D. Eisenbud. Commutative algebra, volume 150 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1995. With a view toward algebraic geometry.
T. ElGamal. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inform. Theory, 31(4):469–472, 1985.
N. Elkies. List of integers x, y with \(x < 10^{18}\), \(0 < \vert x^{3} - y^{2}\vert < x^{1/2}\). www.math.harvard.edu/~elkies/hall.html.
N. Elkies. \(\mathbb{Z}^{28}\) in \(E(\mathbb{Q})\). Number Theory Listserver, May 2006.
N. D. Elkies. The existence of infinitely many supersingular primes for every elliptic curve over \(\mathbb{Q}\). Invent. Math., 89(3):561–567, 1987.
N. D. Elkies. Distribution of supersingular primes. Astérisque, (198-200):127–132 (1992), 1991. Journées Arithmétiques, 1989 (Luminy, 1989).
N. D. Elkies. Elliptic and modular curves over finite fields and related computational issues. In Computational perspectives on number theory (Chicago, IL, 1995), volume 7 of AMS/IP Stud. Adv. Math., pages 21–76. Amer. Math. Soc., Providence, RI, 1998.
J.-H. Evertse. On equations in S-units and the Thue-Mahler equation. Invent. Math., 75(3):561–584, 1984.
J.-H. Evertse and J. H. Silverman. Uniform bounds for the number of solutions to Y n = f(X). Math. Proc. Cambridge Philos. Soc., 100(2):237–248, 1986.
G. Faltings. Endlichkeitssätze für abelsche Varietäten über Zahlkörpern. Invent. Math., 73(3):349–366, 1983.
G. Faltings. Calculus on arithmetic surfaces. Ann. of Math. (2), 119(2):387–424, 1984.
G. Faltings. Finiteness theorems for abelian varieties over number fields. In Arithmetic geometry (Storrs, Conn., 1984), pages 9–27. Springer, New York, 1986. Translated from the German original [Invent. Math. 73 (1983), no. 3, 349–366; ibid. 75 (1984), no. 2, 381; MR 85g:11026ab] by Edward Shipz.
S. Fermigier. Une courbe elliptique définie sur Q de rang ≥ 22. Acta Arith., 82(4):359–363, 1997.
E. V. Flynn and C. Grattoni. Descent via isogeny on elliptic curves with large rational torsion subgroups. J. Symbolic Comput., 43(4):293–303, 2008.
D. Freeman. Constructing pairing-friendly elliptic curves with embedding degree 10. In Algorithmic number theory, volume 4076 of Lecture Notes in Comput. Sci., pages 452–465. Springer, Berlin, 2006.
G. Frey. Links between stable elliptic curves and certain Diophantine equations. Ann. Univ. Sarav. Ser. Math., 1(1):iv+40, 1986.
G. Frey. Elliptic curves and solutions of A − B = C. In Séminaire de Théorie des Nombres, Paris 1985–86, volume 71 of Progr. Math., pages 39–51. Birkhäuser Boston, Boston, MA, 1987.
G. Frey. Links between solutions of A − B = C and elliptic curves. In Number theory (Ulm, 1987), volume 1380 of Lecture Notes in Math., pages 31–62. Springer, New York, 1989.
G. Frey and H.-G. Rück. A remark concerning m-divisibility and the discrete logarithm problem in the divisor class group of curves. Math. Comp., 62:865–874, 1994.
A. Fröhlich. Local fields. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 1–41. Thompson, Washington, D.C., 1967.
A. Fröhlich. Formal groups. Lecture Notes in Mathematics, No. 74. Springer-Verlag, Berlin, 1968.
R. Fueter. Ueber kubische diophantische Gleichungen. Comment. Math. Helv., 2(1):69–89, 1930.
W. Fulton. Algebraic curves. Advanced Book Classics. Addison-Wesley Publishing Company Advanced Book Program, Redwood City, CA, 1989. An introduction to algebraic geometry, Notes written with the collaboration of Richard Weiss, Reprint of 1969 original.
J. Gebel, A. Pethő, and H. G. Zimmer. Computing integral points on elliptic curves. Acta Arith., 68(2):171–192, 1994.
S. Goldwasser and J. Kilian. Almost all primes can be quickly certified. In STOC ’86: Proceedings of the eighteenth annual ACM symposium on Theory of computing, pages 316–329, New York, 1986. ACM.
R. Greenberg. On the Birch and Swinnerton-Dyer conjecture. Invent. Math., 72(2):241–265, 1983.
P. Griffiths and J. Harris. Principles of algebraic geometry. Wiley Classics Library. John Wiley & Sons Inc., New York, 1994. Reprint of the 1978 original.
B. Gross, W. Kohnen, and D. Zagier. Heegner points and derivatives of L-series. II. Math. Ann., 278(1-4):497–562, 1987.
B. Gross and D. Zagier. Points de Heegner et dérivées de fonctions L. C. R. Acad. Sci. Paris Sér. I Math., 297(2):85–87, 1983.
B. H. Gross and D. B. Zagier. Heegner points and derivatives of L-series. Invent. Math., 84(2):225–320, 1986.
R. Gross. A note on Roth’s theorem. J. Number Theory, 36:127–132, 1990.
R. Gross and J. Silverman. S-integer points on elliptic curves. Pacific J. Math., 167(2):263–288, 1995.
K. Gruenberg. Profinite groups. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 116–127. Thompson, Washington, D.C., 1967.
M. Hall, Jr. The Diophantine equation x 3 − y 2 = k. In Computers in number theory (Proc. Sci. Res. Council Atlas Sympos. No. 2, Oxford, 1969), pages 173–198. Academic Press, London, 1971.
D. Hankerson, A. Menezes, and S. Vanstone. Guide to elliptic curve cryptography. Springer Professional Computing. Springer-Verlag, New York, 2004.
G. H. Hardy and E. M. Wright. An introduction to the theory of numbers. The Clarendon Press Oxford University Press, New York, fifth edition, 1979.
J. Harris. Algebraic geometry, volume 133 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1992. A first course.
M. Harris, N. Shepherd-Barron, and R. Taylor. A family of Calabi-Yau varieties and potential automorphy. Ann. of Math. (2). to appear.
R. Hartshorne. Algebraic geometry. Springer-Verlag, New York, 1977. Graduate Texts in Mathematics, No. 52.
M. Hazewinkel. Formal groups and applications, volume 78 of Pure and Applied Mathematics. Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York, 1978.
M. Hindry and J. H. Silverman. The canonical height and integral points on elliptic curves. Invent. Math., 93(2):419–450, 1988.
M. Hindry and J. H. Silverman. Diophantine geometry, volume 201 of Graduate Texts in Mathematics. Springer-Verlag, New York, 2000. An introduction.
G. Hochschild and J.-P. Serre. Cohomology of group extensions. Trans. Amer. Math. Soc., 74:110–134, 1953.
J. Hoffstein, J. Pipher, and J. H. Silverman. An introduction to mathematical cryptography. Undergraduate Texts in Mathematics. Springer-Verlag, New York, 2008.
A. Hurwitz. Über ternäre diophantische Gleichungen dritten Grades. Vierteljahrschrift d. Naturf. Ges. Zürich, 62:207–229, 1917.
D. Husemöller. Elliptic curves, volume 111 of Graduate Texts in Mathematics. Springer-Verlag, New York, second edition, 2004. With appendices by Otto Forster, Ruth Lawrence and Stefan Theisen.
J.-I. Igusa. Class number of a definite quaternion with prime discriminant. Proc. Nat. Acad. Sci. U.S.A., 44:312–314, 1958.
A. Joux. A one round protocol for tripartite Diffie-Hellman. In Algorithmic number theory (Leiden, 2000), volume 1838 of Lecture Notes in Comput. Sci., pages 385–393. Springer, Berlin, 2000.
S. Kamienny. Torsion points on elliptic curves and q-coefficients of modular forms. Invent. Math., 109(2):221–229, 1992.
S. Kamienny and B. Mazur. Rational torsion of prime order in elliptic curves over number fields. Astérisque, (228):3, 81–100, 1995. With an appendix by A. Granville, Columbia University Number Theory Seminar (New York, 1992).
N. M. Katz. An overview of Deligne’s proof of the Riemann hypothesis for varieties over finite fields. In Mathematical developments arising from Hilbert problems (Proc. Sympos. Pure Math., Vol. XXVIII, Northern Illinois Univ., De Kalb, Ill., 1974), pages 275–305. Amer. Math. Soc., Providence, R.I., 1976.
N. M. Katz and B. Mazur. Arithmetic moduli of elliptic curves, volume 108 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 1985.
M. A. Kenku. On the number of Q-isomorphism classes of elliptic curves in each Q-isogeny class. J. Number Theory, 15(2):199–202, 1982.
J.-H. Kim, R. Montenegro, Y. Peres, and P. Tetali. A birthday paradox for Markov chains, with an optimal bound for collision in Pollard rho for discrete logarithm. In Algorithmic number theory, volume 5011 of Lecture Notes in Comput. Sci., pages 402–415. Springer, Berlin, 2008.
A. W. Knapp. Elliptic curves, volume 40 of Mathematical Notes. Princeton University Press, Princeton, NJ, 1992.
N. Koblitz. Elliptic curve cryptosystems. Math. Comp., 48(177):203–209, 1987.
N. Koblitz. Introduction to elliptic curves and modular forms, volume 97 of Graduate Texts in Mathematics. Springer-Verlag, New York, second edition, 1993.
V. A. Kolyvagin. Finiteness of \(E(\mathbb{Q})\) and \((E, \mathbb{Q})\) for a subclass of Weil curves. Izv. Akad. Nauk SSSR Ser. Mat., 52(3):522–540, 670–671, 1988.
S. V. Kotov and L. A. Trelina. S-ganze Punkte auf elliptischen Kurven. J. Reine Angew. Math., 306:28–41, 1979.
D. S. Kubert. Universal bounds on the torsion of elliptic curves. Proc. London Math. Soc. (3), 33(2):193–237, 1976.
E. Kunz. Introduction to plane algebraic curves. Birkhäuser Boston Inc., Boston, MA, 2005. Translated from the 1991 German edition by Richard G. Belshoff.
M. Lal, M. F. Jones, and W. J. Blundon. Numerical solutions of the Diophantine equation y 3 − x 2 = k. Math. Comp., 20:322–325, 1966.
S. Lang. Elliptic curves: Diophantine analysis, volume 231 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, 1978.
S. Lang. Introduction to algebraic and abelian functions, volume 89 of Graduate Texts in Mathematics. Springer-Verlag, New York, second edition, 1982.
S. Lang. Complex multiplication, volume 255 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, New York, 1983.
S. Lang. Conjectured Diophantine estimates on elliptic curves. In Arithmetic and geometry, Vol. I, volume 35 of Progr. Math., pages 155–171. Birkhäuser Boston, Boston, MA, 1983.
S. Lang. Fundamentals of Diophantine geometry. Springer-Verlag, New York, 1983.
S. Lang. Elliptic functions, volume 112 of Graduate Texts in Mathematics. Springer-Verlag, New York, second edition, 1987. With an appendix by J. Tate.
S. Lang. Number theory III, volume 60 of Encyclopedia of Mathematical Sciences. Springer-Verlag, Berlin, 1991.
S. Lang. Algebraic number theory, volume 110 of Graduate Texts in Mathematics. Springer-Verlag, New York, second edition, 1994.
S. Lang. Algebra, volume 211 of Graduate Texts in Mathematics. Springer-Verlag, New York, third edition, 2002.
S. Lang and J. Tate. Principal homogeneous spaces over abelian varieties. Amer. J. Math., 80:659–684, 1958.
S. Lang and H. Trotter. Frobenius distributions in \(\mathop{\mathrm{GL}}\nolimits _{2}\) -extensions. Springer-Verlag, Berlin, 1976. Distribution of Frobenius automorphisms in \(\mathop{\mathrm{GL}}\nolimits _{2}\)-extensions of the rational numbers, Lecture Notes in Mathematics, Vol. 504.
M. Laska. An algorithm for finding a minimal Weierstrass equation for an elliptic curve. Math. Comp., 38(157):257–260, 1982.
M. Laska. Elliptic curves over number fields with prescribed reduction type. Aspects of Mathematics, E4. Friedr. Vieweg & Sohn, Braunschweig, 1983.
D. J. Lewis and K. Mahler. On the representation of integers by binary forms. Acta Arith., 6:333–363, 1960/1961.
S. Lichtenbaum. The period-index problem for elliptic curves. Amer. J. Math., 90:1209–1223, 1968.
C.-E. Lind. Untersuchungen über die rationalen Punkte der ebenen kubischen Kurven vom Geschlecht Eins. Thesis, University of Uppsala,, 1940:97, 1940.
J. Liouville. Sur des classes très-étendues de quantités dont la irrationalles algébriques. C. R. Acad. Paris, 18:883–885 and 910–911, 1844.
E. Lutz. Sur l’equation y 2 = x 3 − ax − b dans les corps p-adic. J. Reine Angew. Math., 177:237–247, 1937.
K. Mahler. On the lattice points on curves of genus 1. Proc. London Math. Soc. (3), 39:431–466, 1935.
J. I. Manin. The Hasse-Witt matrix of an algebraic curve. Izv. Akad. Nauk SSSR Ser. Mat., 25:153–172, 1961.
J. I. Manin. The p-torsion of elliptic curves is uniformly bounded. Izv. Akad. Nauk SSSR Ser. Mat., 33:459–465, 1969.
J. I. Manin. Cyclotomic fields and modular curves. Uspehi Mat. Nauk, 26(6(162)):7–71, 1971. English translation: Russian Math. Surveys 26 (1971), no. 6, 7–78.
R. C. Mason. The hyperelliptic equation over function fields. Math. Proc. Cambridge Philos. Soc., 93(2):219–230, 1983.
R. C. Mason. Norm form equations. I. J. Number Theory, 22(2):190–207, 1986.
D. Masser. Elliptic functions and transcendence. Springer-Verlag, Berlin, 1975. Lecture Notes in Mathematics, Vol. 437.
D. Masser and G. Wüstholz. Isogeny estimates for abelian varieties, and finiteness theorems. Ann. of Math. (2), 137(3):459–472, 1993.
D. W. Masser. Specializations of finitely generated subgroups of abelian varieties. Trans. Amer. Math. Soc., 311(1):413–424, 1989.
D. W. Masser and G. Wüstholz. Fields of large transcendence degree generated by values of elliptic functions. Invent. Math., 72(3):407–464, 1983.
D. W. Masser and G. Wüstholz. Estimating isogenies on elliptic curves. Invent. Math., 100(1):1–24, 1990.
H. Matsumura. Commutative algebra, volume 56 of Mathematics Lecture Note Series. Benjamin/Cummings Publishing Co., Inc., Reading, Mass., second edition, 1980.
B. Mazur. Modular curves and the Eisenstein ideal. Inst. Hautes Études Sci. Publ. Math., (47):33–186 (1978), 1977.
B. Mazur. Rational isogenies of prime degree (with an appendix by D. Goldfeld). Invent. Math., 44(2):129–162, 1978.
H. McKean and V. Moll. Elliptic curves. Cambridge University Press, Cambridge, 1997. Function theory, geometry, arithmetic.
A. J. Menezes, T. Okamoto, and S. A. Vanstone. Reducing elliptic curve logarithms to logarithms in a finite field. IEEE Trans. Inform. Theory, 39(5):1639–1646, 1993.
A. J. Menezes, P. C. van Oorschot, and S. A. Vanstone. Handbook of Applied Cryptography. CRC Press Series on Discrete Mathematics and Its Applications. CRC Press, Boca Raton, FL, 1997.
L. Merel. Bornes pour la torsion des courbes elliptiques sur les corps de nombres. Invent. Math., 124(1-3):437–449, 1996.
J.-F. Mestre. Construction d’une courbe elliptique de rang ≥ 12. C. R. Acad. Sci. Paris Sér. I Math., 295(12):643–644, 1982.
J.-F. Mestre. Courbes elliptiques et formules explicites. In Seminar on number theory, Paris 1981–82 (Paris, 1981/1982), volume 38 of Progr. Math., pages 179–187. Birkhäuser Boston, Boston, MA, 1983.
M. Mignotte. Quelques remarques sur l’approximation rationnelle des nombres algébriques. J. Reine Angew. Math., 268/269:341–347, 1974. Collection of articles dedicated to Helmut Hasse on his seventy-fifth birthday, II.
S. D. Miller and R. Venkatesan. Spectral analysis of Pollard rho collisions. In Algorithmic number theory, volume 4076 of Lecture Notes in Comput. Sci., pages 573–581. Springer, Berlin, 2006.
S. D. Miller and R. Venkatesan. Non-degeneracy of Pollard rho collisions, 2008. arXiv:0808.0469.
V. S. Miller. Use of elliptic curves in cryptography. In Advances in Cryptology—CRYPTO ’85 (Santa Barbara, Calif., 1985), volume 218 of Lecture Notes in Comput. Sci., pages 417–426. Springer, Berlin, 1986.
J. S. Milne. Arithmetic duality theorems, volume 1 of Perspectives in Mathematics. Academic Press Inc., Boston, MA, 1986.
J. S. Milne. Elliptic curves. BookSurge Publishers, Charleston, SC, 2006.
J. Milnor. On Lattès maps. ArXiv:math.DS/0402147, Stony Brook IMS Preprint #2004/01.
R. Miranda. Algebraic curves and Riemann surfaces, volume 5 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 1995.
A. Miyaji, M. Nakabayashi, and S. Takano. Characterization of elliptic curve traces under FR-reduction. In Information security and cryptology—ICISC 2000 (Seoul), volume 2015 of Lecture Notes in Comput. Sci., pages 90–108. Springer, Berlin, 2001.
P. Monsky. Three constructions of rational points on Y 2 = X 3 ± NX. Math. Z., 209(3):445–462, 1992.
F. Morain. Building cyclic elliptic curves modulo large primes. In Advances in cryptology—EUROCRYPT ’91 (Brighton, 1991), volume 547 of Lecture Notes in Comput. Sci., pages 328–336. Springer, Berlin, 1991.
L. J. Mordell. The diophantine equation x 4 + my 4 = z 2. . Quart. J. Math. Oxford Ser. (2), 18:1–6, 1967.
L. J. Mordell. Diophantine equations. Pure and Applied Mathematics, Vol. 30. Academic Press, London, 1969.
D. Mumford. Abelian varieties. Tata Institute of Fundamental Research Studies in Mathematics, No. 5. Published for the Tata Institute of Fundamental Research, Bombay, 1970.
D. Mumford, J. Fogarty, and F. Kirwan. Geometric invariant theory, volume 34 of Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)]. Springer-Verlag, Berlin, third edition, 1994.
K.-I. Nagao. Construction of high-rank elliptic curves. Kobe J. Math., 11(2):211–219, 1994.
K.-I. Nagao. \(\mathbb{Q}(T)\)-rank of elliptic curves and certain limit coming from the local points. Manuscripta Math., 92(1):13–32, 1997. With an appendix by Nobuhiko Ishida, Tsuneo Ishikawa and the author.
T. Nagell. Solution de quelque problèmes dans la théorie arithmétique des cubiques planes du premier genre. Wid. Akad. Skrifter Oslo I, 1935. Nr. 1.
NBS–DSS. Digital Signature Standard (DSS). FIPS Publication 186-2, National Bureau of Standards, 2000. http://csrc.nist.gov/publications/ PubsFIPS.html .
A. Néron. Problèmes arithmétiques et géométriques rattachés à la notion de rang d’une courbe algébrique dans un corps. Bull. Soc. Math. France, 80:101–166, 1952.
A. Néron. Modèles minimaux des variétés abéliennes sur les corps locaux et globaux. Inst. Hautes Études Sci. Publ.Math. No., 21:128, 1964.
A. Néron. Quasi-fonctions et hauteurs sur les variétés abéliennes. Ann. of Math. (2), 82:249–331, 1965.
O. Neumann. Elliptische Kurven mit vorgeschriebenem Reduktionsverhalten. I. Math. Nachr., 49:107–123, 1971.
J. Oesterlé. Nouvelles approches du “théorème” de Fermat. Astérisque, (161-162):Exp. No. 694, 4, 165–186 (1989), 1988. Séminaire Bourbaki, Vol. 1987/88.
A. Ogg. Modular forms and Dirichlet series. W. A. Benjamin, Inc., New York-Amsterdam, 1969.
A. P. Ogg. Abelian curves of 2-power conductor. Proc. Cambridge Philos. Soc., 62:143–148, 1966.
A. P. Ogg. Abelian curves of small conductor. J. Reine Angew. Math., 226:204–215, 1967.
A. P. Ogg. Elliptic curves and wild ramification. Amer. J. Math., 89:1–21, 1967.
L. D. Olson. Torsion points on elliptic curves with given j-invariant. Manuscripta Math., 16(2):145–150, 1975.
PARI/GP, 2005. http://pari.math.u-bordeaux.fr/.
A. N. Paršin. Algebraic curves over function fields. I. Izv. Akad. Nauk SSSR Ser. Mat., 32:1191–1219, 1968.
R. G. E. Pinch. Elliptic curves with good reduction away from 2. Math. Proc. Cambridge Philos. Soc., 96(1):25–38, 1984.
S. C. Pohlig and M. E. Hellman. An improved algorithm for computing logarithms over \(\mathop{\mathrm{GF}}\nolimits (p)\) and its cryptographic significance. IEEE Trans. Information Theory, IT-24(1):106–110, 1978.
J. M. Pollard. Monte Carlo methods for index computation \((\mathop{\mathrm{mod}}\nolimits \ p)\). Math. Comp., 32(143):918–924, 1978.
H. Reichardt. Einige im Kleinen überall lösbare, im Grossen unlösbare diophantische Gleichungen. J. Reine Angew. Math., 184:12–18, 1942.
K. A. Ribet. On modular representations of \(\mathop{\mathrm{Gal}}\nolimits (\overline{\mathbf{Q}}/\mathbf{Q})\) arising from modular forms. Invent. Math., 100(2):431–476, 1990.
R. L. Rivest, A. Shamir, and L. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Comm. ACM, 21(2):120–126, 1978.
A. Robert. Elliptic curves. Springer-Verlag, Berlin, 1973. Notes from postgraduate lectures given in Lausanne 1971/72, Lecture Notes in Mathematics, Vol. 326.
D. E. Rohrlich. On L-functions of elliptic curves and anticyclotomic towers. Invent. Math., 75(3):383–408, 1984.
P. Roquette. Analytic theory of elliptic functions over local fields. Hamburger Mathematische Einzelschriften (N.F.), Heft 1. Vandenhoeck & Ruprecht, Göttingen, 1970.
M. Rosen and J. H. Silverman. On the rank of an elliptic surface. Invent. Math., 133(1):43–67, 1998.
K. Rubin. Elliptic curves with complex multiplication and the conjecture of Birch and Swinnerton-Dyer. Invent. Math., 64(3):455–470, 1981.
K. Rubin. Tate-Shafarevich groups and L-functions of elliptic curves with complex multiplication. Invent. Math., 89(3):527–559, 1987.
K. Rubin. The “main conjectures” of Iwasawa theory for imaginary quadratic fields. Invent. Math., 103(1):25–68, 1991.
T. Saito. Conductor, discriminant, and the Noether formula of arithmetic surfaces. Duke Math. J., 57(1):151–173, 1988.
T. Satoh and K. Araki. Fermat quotients and the polynomial time discrete log algorithm for anomalous elliptic curves. Comment. Math. Univ. St. Paul., 47(1):81–92, 1998.
E. F. Schaefer and M. Stoll. How to do a p-descent on an elliptic curve. Trans. Amer. Math. Soc., 356(3):1209–1231 (electronic), 2004.
S. H. Schanuel. Heights in number fields. Bull. Soc. Math. France, 107(4):433–449, 1979.
W. M. Schmidt. Diophantine approximation, volume 785 of Lecture Notes in Mathematics. Springer, Berlin, 1980.
S. Schmitt and H. G. Zimmer. Elliptic curves, volume 31 of de Gruyter Studies in Mathematics. Walter de Gruyter & Co., Berlin, 2003. A computational approach, With an appendix by Attila Pethő.
R. Schoof. Elliptic curves over finite fields and the computation of square roots mod p. Math. Comp., 44(170):483–494, 1985.
R. Schoof. Counting points on elliptic curves over finite fields. J. Théor. Nombres Bordeaux, 7(1):219–254, 1995. Les Dix-huitièmes Journées Arithmétiques (Bordeaux, 1993).
E. S. Selmer. The Diophantine equation ax 3 + by 3 + cz 3 = 0. Acta Math., 85:203–362 (1 plate), 1951.
E. S. Selmer. A conjecture concerning rational points on cubic curves. Math. Scand., 2:49–54, 1954.
E. S. Selmer. The diophantine equation ax 3 + by 3 + cz 3 = 0. Completion of the tables. Acta Math., 92:191–197, 1954.
I. A. Semaev. Evaluation of discrete logarithms in a group of p-torsion points of an elliptic curve in characteristic p. Math. Comp., 67(221):353–356, 1998.
J.-P. Serre. Géométrie algébrique et géométrie analytique. Ann. Inst. Fourier, Grenoble, 6:1–42, 1955–1956.
J.-P. Serre. Complex multiplication. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 292–296. Thompson, Washington, D.C., 1967.
J.-P. Serre. Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent. Math., 15(4):259–331, 1972.
J.-P. Serre. A course in arithmetic. Springer-Verlag, New York, 1973. Translated from the French, Graduate Texts in Mathematics, No. 7.
J.-P. Serre. Local fields, volume 67 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1979. Translated from the French by Marvin Jay Greenberg.
J.-P. Serre. Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math., (54):323–401, 1981.
J.-P. Serre. Sur les représentations modulaires de degré 2 de \(\mathop{\mathrm{Gal}}\nolimits (\overline{\mathbf{Q}}/\mathbf{Q})\). Duke Math. J., 54(1):179–230, 1987.
J.-P. Serre. Lectures on the Mordell-Weil theorem. Aspects of Mathematics. Friedr. Vieweg & Sohn, Braunschweig, third edition, 1997. Translated from the French and edited by Martin Brown from notes by Michel Waldschmidt, With a foreword by Brown and Serre.
J.-P. Serre. Abelian l-adic representations and elliptic curves, volume 7 of Research Notes in Mathematics. A K Peters Ltd., Wellesley, MA, 1998. With the collaboration of Willem Kuyk and John Labute, Revised reprint of the 1968 original.
J.-P. Serre. Galois cohomology. Springer Monographs in Mathematics. Springer-Verlag, Berlin, english edition, 2002. Translated from the French by Patrick Ion and revised by the author.
J.-P. Serre and J. Tate. Good reduction of abelian varieties. Ann. of Math. (2), 88:492–517, 1968.
B. Setzer. Elliptic curves of prime conductor. J. London Math. Soc. (2), 10:367–378, 1975.
B. Setzer. Elliptic curves over complex quadratic fields. Pacific J. Math., 74(1):235–250, 1978.
I. R. Shafarevich. Algebraic number fields. In Proc. Int. Cong. (Stockholm 1962), pages 25–39. American Mathematical Society, Providence, R.I., 1963. Amer. Math. Soc. Transl., Series 2, Vol. 31.
I. R. Shafarevich. Basic algebraic geometry. Springer-Verlag, Berlin, study edition, 1977. Translated from the Russian by K. A. Hirsch, Revised printing of Grundlehren der mathematischen Wissenschaften, Vol. 213, 1974.
I. R. Shafarevich and J. Tate. The rank of elliptic curves. In Amer. Math. Soc. Transl., volume 8, pages 917–920. Amer. Math. Soc., 1967.
A. Shamir. Identity-based cryptosystems and signature schemes. In Advances in Cryptology (Santa Barbara, Calif., 1984), volume 196 of Lecture Notes in Comput. Sci., pages 47–53. Springer, Berlin, 1985.
G. Shimura. Correspondances modulaires et les fonctions ζ de courbes algébriques. J. Math. Soc. Japan, 10:1–28, 1958.
G. Shimura. On elliptic curves with complex multiplication as factors of the Jacobians of modular function fields. Nagoya Math. J., 43:199–208, 1971.
G. Shimura. On the zeta-function of an abelian variety with complex multiplication. Ann. of Math. (2), 94:504–533, 1971.
G. Shimura. Introduction to the arithmetic theory of automorphic functions, volume 11 of Publications of the Mathematical Society of Japan. Princeton University Press, Princeton, NJ, 1994. Reprint of the 1971 original, Kano Memorial Lectures, 1.
G. Shimura and Y. Taniyama. Complex multiplication of abelian varieties and its applications to number theory, volume 6 of Publications of the Mathematical Society of Japan. The Mathematical Society of Japan, Tokyo, 1961.
T. Shioda. An explicit algorithm for computing the Picard number of certain algebraic surfaces. Amer. J. Math., 108(2):415–432, 1986.
R. Shipsey. Elliptic divisibility sequences. PhD thesis, Goldsmith’s College (University of London), 2000.
V. Shoup. Lower bounds for discrete logarithms and related problems. In Advances in cryptology—EUROCRYPT ’97 (Konstanz), volume 1233 of Lecture Notes in Comput. Sci., pages 256–266. Springer, Berlin, 1997. updated version at www.shoup.net/papers/dlbounds1.pdf.
J. H. Silverman. Lower bound for the canonical height on elliptic curves. Duke Math. J., 48(3):633–648, 1981.
J. H. Silverman. The Néron–Tate height on elliptic curves. PhD thesis, Harvard University, 1981.
J. H. Silverman. Heights and the specialization map for families of abelian varieties. J. Reine Angew. Math., 342:197–211, 1983.
J. H. Silverman. Integer points on curves of genus 1. J. London Math. Soc. (2), 28(1):1–7, 1983.
J. H. Silverman. The S-unit equation over function fields. Math. Proc. Cambridge Philos. Soc., 95(1):3–4, 1984.
J. H. Silverman. Weierstrass equations and the minimal discriminant of an elliptic curve. Mathematika, 31(2):245–251 (1985), 1984.
J. H. Silverman. Divisibility of the specialization map for families of elliptic curves. Amer. J. Math., 107(3):555–565, 1985.
J. H. Silverman. Arithmetic distance functions and height functions in Diophantine geometry. Math. Ann., 279(2):193–216, 1987.
J. H. Silverman. A quantitative version of Siegel’s theorem: integral points on elliptic curves and Catalan curves. J. Reine Angew. Math., 378:60–100, 1987.
J. H. Silverman. Computing heights on elliptic curves. Math. Comp., 51(183):339–358, 1988.
J. H. Silverman. Wieferich’s criterion and the abc-conjecture. J. Number Theory, 30(2):226–237, 1988.
J. H. Silverman. The difference between the Weil height and the canonical height on elliptic curves. Math. Comp., 55(192):723–743, 1990.
J. H. Silverman. Advanced topics in the arithmetic of elliptic curves, volume 151 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1994.
J. H. Silverman. The arithmetic of dynamical systems, volume 241 of Graduate Texts in Mathematics. Springer, New York, 2007.
N. P. Smart. S-integral points on elliptic curves. Math. Proc. Cambridge Philos. Soc., 116(3):391–399, 1994.
N. P. Smart. The discrete logarithm problem on elliptic curves of trace one. J. Cryptology, 12(3):193–196, 1999.
K. Stange. The Tate pairing via elliptic nets. In Pairing Based Cryptography, Lecture Notes in Comput. Sci. Springer, 2007.
K. Stange. Elliptic Nets and Elliptic Curves. PhD thesis, Brown University, 2008.
K. Stange. Elliptic nets and elliptic curves, 2008. arXiv:0710.1316v2.
H. M. Stark. Effective estimates of solutions of some Diophantine equations. Acta Arith., 24:251–259, 1973.
W. Stein. The Modular Forms Database. http://modular.fas.harvard. edu/Tables .
W. Stein. Sage Mathematics Software, 2007. http://www.sagemath.org.
N. M. Stephens. The Diophantine equation X 3 + Y 3 = DZ 3 and the conjectures of Birch and Swinnerton-Dyer. J. Reine Angew. Math., 231:121–162, 1968.
D. R. Stinson. Cryptography: Theory and Practice. CRC Press Series on Discrete Mathematics and Its Applications. Chapman & Hall/CRC, Boca Raton, FL, 2002.
W. W. Stothers. Polynomial identities and Hauptmoduln. Quart. J. Math. Oxford Ser. (2), 32(127):349–370, 1981.
R. J. Stroeker and N. Tzanakis. Solving elliptic Diophantine equations by estimating linear forms in elliptic logarithms. Acta Arith., 67(2):177–196, 1994.
J. Tate. Letter to J.-P. Serre, 1968.
J. Tate. Duality theorems in Galois cohomology over number fields. In Proc. Internat. Congr. Mathematicians (Stockholm, 1962), pages 288–295. Inst. Mittag-Leffler, Djursholm, 1963.
J. Tate. Endomorphisms of abelian varieties over finite fields. Invent. Math., 2:134–144, 1966.
J. Tate. Algorithm for determining the type of a singular fiber in an elliptic pencil. In Modular functions of one variable, IV (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), pages 33–52. Lecture Notes in Math., Vol. 476. Springer, Berlin, 1975.
J. Tate. Variation of the canonical height of a point depending on a parameter. Amer. J. Math., 105(1):287–294, 1983.
J. Tate. A review of non-Archimedean elliptic functions. In Elliptic curves, modular forms, & Fermat’s last theorem (Hong Kong, 1993), Ser. Number Theory, I, pages 162–184. Int. Press, Cambridge, MA, 1995.
J. Tate. WC-groups over \(\mathfrak{p}\)-adic fields. In Séminaire Bourbaki, Vol. 4 (1957/58), pages Exp. No. 156, 265–277. Soc. Math. France, Paris, 1995.
J. T. Tate. Algebraic cycles and poles of zeta functions. In Arithmetical Algebraic Geometry (Proc. Conf. Purdue Univ., 1963), pages 93–110. Harper & Row, New York, 1965.
J. T. Tate. Global class field theory. In Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pages 162–203. Thompson, Washington, D.C., 1967.
J. T. Tate. The arithmetic of elliptic curves. Invent. Math., 23:179–206, 1974.
R. Taylor. Automorphy for some l-adic lifts of automorphic mod l representations. II. Inst. Hautes Études Sci. Publ. Math. submitted.
R. Taylor and A. Wiles. Ring-theoretic properties of certain Hecke algebras. Ann. of Math. (2), 141(3):553–572, 1995.
E. Teske. A space efficient algorithm for group structure computation. Math. Comp., 67(224):1637–1663, 1998.
E. Teske. Speeding up Pollard’s rho method for computing discrete logarithms. In Algorithmic Number Theory (Portland, OR, 1998), volume 1423 of Lecture Notes in Comput. Sci., pages 541–554. Springer, Berlin, 1998.
E. Teske. Square-root algorithms for the discrete logarithm problem (a survey). In Public-Key Cryptography and Computational Number Theory (Warsaw, 2000), pages 283–301. de Gruyter, Berlin, 2001.
D. Ulmer. Elliptic curves with large rank over function fields. Ann. of Math. (2), 155(1):295–315, 2002.
B. L. van der Waerden. Algebra. Vols. I and II. Springer-Verlag, New York, 1991. Based in part on lectures by E. Artin and E. Noether, Translated from the seventh German edition by Fred Blum and John R. Schulenberger.
J. Vélu. Isogénies entre courbes elliptiques. C. R. Acad. Sci. Paris Sér. A-B, 273:A238–A241, 1971.
P. Vojta. A higher-dimensional Mordell conjecture. In Arithmetic geometry (Storrs, Conn., 1984), pages 341–353. Springer, New York, 1986.
P. Vojta. Siegel’s theorem in the compact case. Ann. of Math. (2), 133(3):509–548, 1991.
J. F. Voloch. Diagonal equations over function fields. Bol. Soc. Brasil. Mat., 16(2):29–39, 1985.
P. M. Voutier. An upper bound for the size of integral solutions to Y m = f(X). J. Number Theory, 53(2):247–271, 1995.
R. J. Walker. Algebraic curves. Springer-Verlag, New York, 1978. Reprint of the 1950 edition.
M. Ward. Memoir on elliptic divisibility sequences. Amer. J. Math., 70:31–74, 1948.
L. C. Washington. Elliptic curves. Discrete Mathematics and Its Applications (Boca Raton). Chapman & Hall/CRC, Boca Raton, FL, second edition, 2008. Number theory and cryptography.
A. Weil. Numbers of solutions of equations in finite fields. Bull. Amer. Math. Soc., 55:497–508, 1949.
A. Weil. Jacobi sums as “Grössencharaktere.” Trans. Amer. Math. Soc., 73:487–495, 1952.
A. Weil. On algebraic groups and homogeneous spaces. Amer. J. Math., 77:493–512, 1955.
A. Weil. Über die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen. Math. Ann., 168:149–156, 1967.
A. Weil. Dirichlet Series and Automorphic Forms, volume 189 of Lecture Notes in Mathematics. Springer-Verlag, 1971.
E. T. Whittaker and G. N. Watson. A course of modern analysis. Cambridge Mathematical Library. Cambridge University Press, Cambridge, 1996. Reprint of the fourth (1927) edition.
A. Wiles. Modular elliptic curves and Fermat’s last theorem. Ann. of Math. (2), 141(3):443–551, 1995.
A. Wiles. The Birch and Swinnerton-Dyer conjecture. In The millennium prize problems, pages 31–41. Clay Math. Inst., Cambridge, MA, 2006.
G. Wüstholz. Recent progress in transcendence theory. In Number theory, Noordwijkerhout 1983 (Noordwijkerhout, 1983), volume 1068 of Lecture Notes in Math., pages 280–296. Springer, Berlin, 1984.
G. Wüstholz. Multiplicity estimates on group varieties. Ann. of Math. (2), 129(3):471–500, 1989.
D. Zagier. Large integral points on elliptic curves. Math. Comp., 48(177):425–436, 1987.
H. G. Zimmer. On the difference of the Weil height and the Néron-Tate height. Math. Z., 147(1):35–51, 1976.
K. Zsigmondy. Zur Theorie der Potenzreste. Monatsh. Math., 3:265–284, 1892.
P. Deligne. La conjecture de Weil. I. Inst. Hautes Études Sci. Publ. Math., (43):273–307, 1977.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2009 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Silverman, J.H. (2009). Computing the Mordell–Weil Group. In: The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics, vol 106. Springer, New York, NY. https://doi.org/10.1007/978-0-387-09494-6_10
Download citation
DOI: https://doi.org/10.1007/978-0-387-09494-6_10
Publisher Name: Springer, New York, NY
Print ISBN: 978-0-387-09493-9
Online ISBN: 978-0-387-09494-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




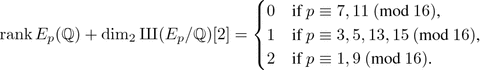

 ,
then the period and the index are equal. (Hint. Use (a), (b), (c), and Exercise
,
then the period and the index are equal. (Hint. Use (a), (b), (c), and Exercise 
