Mathematical Modelling of Cell Adhesion in Tissue Engineering using Continuum Models

Abstract

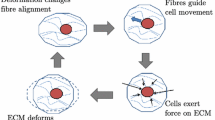
Key factors in the formation of cell aggregates in tissue engineering and other fields are the cell–cell and cell–matrix interactions. Other important factors are culture conditions such as nutrient and oxygen supply and the characteristics of the environment (medium versus hydrogel). As mathematical models are increasingly used to investigate biological phenomena, it is important that processes such as cell adhesion are adequately described in the models. Recently a technique was developed to incorporate cell–cell and cell–matrix adhesion in continuum models through the use of non-local terms. In this study we apply this technique to model adhesion in a cell-in-gel culture set-up often found in tissue engineering applications. We briefly describe the biological issues underlying this study and the various modelling techniques used to capture adhesive behaviour. We furthermore elaborate on the numerical techniques that were developed in the course of this study. Finally, we consider a tissue engineering model that describes the spatiotemporal evolution of the concentration of cells, matrix, hydrogel, matrix degrading enzymes and oxygen/nutrients in a cell-in-gel culture system. Sensitivity analyses indicate a clear influence of the different adhesive processes on the final cell and collagen density and distribution, demonstrating the significance of cell adhesion in tissue engineering and the potential of the proposed mathematical technique.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

How cells organize into structured tissues has been a long-standing question in the field of developmental biology. Recently a new paradigm was proposed in the tissue engineering field that states that in order to obtain successful tissue engineering products, these developmental processes should be recapitulated in vitro, using cell aggregates as building blocks [19]. Crucial factors in the formation of these aggregates are cell–cell and cell–matrix interactions. When mathematical modelling aims to actively contribute to the unraveling and control of tissue engineering processes, it needs to be able to describe these adhesion processes.

In this study we apply a recently developed technique to model cell adhesion on a continuum level. This chapter starts by a brief presentation of the importance of cell adhesion in tissue engineering. It continues by describing the modelling techniques that have been proposed in the literature, both on a discrete and continuum level, to model cellular adhesion, followed by a detailed description of the use of non-local terms to model cell adhesion on a continuum level. A mathematical model describing a number of biological processes in a generic cell-in-gel culture system is presented and the necessary numerical tools for its implementation are elaborated on. Simulations of the mathematical model demonstrate the potential of the applied non-local technique in capturing cell adhesive behaviour.

1.1 Cell Adhesion in Tissue Engineering

Stem cell characteristics are determined by the cell’s microenvironment as schematically represented in Fig. 1 [26]. Current research is focussing intensely on controlling stem cell differentiation by influencing the microenvironment through the use of growth factors, cytokines, hormones, mechanical stimuli, culture conditions (e.g. O₂ and nutrients) and various types of (3D) biomaterials with their specific chemical and physical characteristics. A plethora of studies is available in the literature describing the construction of cell-biomaterial constructs that are able to deliver desired behaviour in vitro or in vivo (such as the production of mineralised collagen in the case of bone tissue engineering) by manipulating one or more of these microenvironmental factors.

Fig. 1

Microenvironmental factors affecting cell behaviour (adapted from [26])

However, a functional cell-biomaterial construct does not automatically equal a piece of functional tissue. A major challenge will be to establish the appropriate topological interactions and spatial organization of cells leading to specific morphological patterns [17, 18]. The concept of developmental engineering states that in order to arrive at high quality cell-derived tissue products, developmental processes (including morphogenetic patterning) need to be recapitulated in vitro [19]. As described in [14] and references cited therein, cell adhesive processes (including cell–cell and cell–matrix adhesion) are a major driving force behind the spatial organization in the developing embryo [3]. As cell adhesion is a critical factor in determining tissue integrity and function, elucidation of the cellular and molecular mechanisms that regulate cell adhesion as well as the influence from the previously mentioned microenvironmental factors on these mechanisms, is fundamentally important for the tissue engineering field.

1.2 Discrete and Continuum Models for Adhesion

The approaches most often followed for the modelling of the behaviour of a cluster of cells are the use of cellular automata and agent-based modelling in which individual cells are simulated and followed based upon a set of biophysical rules (for comprehensive reviews we refer the reader to [1, 2, 7] and [21]. These methods are particularly useful for studying the interactions of individual cells with each other and with their microenvironment. Since these methods are based on a series of rules for each cell, it is straightforward to translate biological processes into model rules. However, these models can be difficult to study analytically and the computational cost increases rapidly with the number of cells modelled. With the number of cells needed for bone tissue engineering applications (10⁶ cells or more), these methods can quickly become unwieldy [20].

For such larger-scale applications, continuum methods provide a good modelling alternative. Much research into the use of ordinary and partial differential equations (PDEs) for the modelling of cell aggregates has been carried out over the past decade, especially in the field of tumour growth, as reviewed by [20]. Various mechanisms have been implemented in these models to account for cell migration. Most models describe cell movement based on chemotactic and/or haptotactic cues (as in the authors’ previous work on bone fracture healing [8]). However, other cues from the microenvironment such as the presence of other cells and extracellular matrix will also direct cell motion. A number of models incorporate cell–cell adhesion in the form of a surface tension force on the tumour surface which then controls the evolution of the tumour shape during growth [20, 5, 6]. Other groups use mesoscopic models to study cell invasion in the extracellular matrix [15, 22]. Recently a continuum description of cell motility due to cell–cell and cell–matrix adhesion has been introduced [4, 13] which is achieved by the inclusion of a non-local interaction term to account for adhesion in the PDE model.

1.3 Non-local Model for Cell Adhesion

In this section we will review and extend the derivation for an integro-partial differential equation model for cell–cell and cell–matrix adhesion first developed in [4]. The principle of conservation of mass for an adhesive cell population, with time- and space-dependent density c(t, x), leads to the conservation equation

$$ {\frac{\partial c(t,{{\mathbf{x}}})}{\partial t}} = -\nabla\cdot {{\mathbf{J}}}(t,{{\mathbf{x}}}) + P(t,{{\mathbf{x}}}) \quad\hbox{for}\quad {{\mathbf{x}}}\in\Omega , t>0 . $$

Here, P describes the production or loss of cells and J is the cell flux within Ω. We assume that the cell flux J is the cumulative effect of cell random motility goverened by

$$ {{\mathbf{J}}}_{{\rm random}}(t,{{\mathbf{x}}}) = -D_c \nabla c(t,{{\mathbf{x}}}) $$

with cell random motility coefficient D _c  > 0 and a flux J _adhesion(t, x) due to adhesion, to be specified below, i.e.

$$ {{\mathbf{J}}}(t,{{\mathbf{x}}}) = {{\mathbf{J}}}_{{\rm random}}(t,{{\mathbf{x}}}) + {{\mathbf{J}}}_{{\rm adhesion}} (t,{{\mathbf{x}}}). $$

We do not include a cell flux due to chemotactic or haptotactic cell migration.

The generic expression for the adhesive flux is J _adhesion(t, x) = v(t, x) c(t, x) where v denotes the velocity field generated through cell adhesion. Consider a spherical particle of radius $\hat{R}$ moving through a fluid having (dynamic) viscosity η and let v denote the relative velocity between particle and fluid (far away from the particle). Then Stokes’ formula states that the force F exerted by the fluid on the particle is given by ${{\mathbf{F}}} = 6\pi\eta \hat{R}{{\mathbf{v}}}.$ Under the assumption that cells can be regarded as spherical particles in such a flow, we can thus express the adhesive flux as

$$ {{\mathbf{J}}}_{{\rm adhesion}}(t,{{\mathbf{x}}}) = {\frac{c(t,{{\mathbf{x}}})}{6\pi\eta\hat{R}}}{{\mathbf{F}}}(t,{{\mathbf{x}}}), $$

where F(t, x) denotes the force exerted on cells at x at time t which is generated by cell adhesion. Defining $\Phi:={\frac{1}{6\pi\eta}}$ results in the expression for the adhesive flux

$$ {{\mathbf{J}}}_{{\rm adhesion}}(t,{{\mathbf{x}}}) = {\frac{\Phi c(t,{{\mathbf{x}}})}{\hat{R}}}{{\mathbf{F}}}(t,{{\mathbf{x}}}), $$

as defined first in [4] and later used in, for instance [13] and [14].

The force F(t, x) is assumed to be the result of non-local adhesive interactions of the cells at x with cells or the extracellular matrix in its vicinity, i.e. at x + r. Here r ranges over a finite region $V\subset{\mathbb{R}}^{{n}}$, the so-called sensing region, which is for our purposes assumed independent of x. Let m(t, x) denote the density of the extracellular matrix. We first express the force exerted on cells at x through cells or matrix at x + r by

$$ f(t,{{\mathbf{x}}},{{\mathbf{r}}}):={\frac{{{\mathbf{r}}}} {|{{\mathbf{r}}}|}} g(c(t,{{\mathbf{x}}}+{{\mathbf{r}}}), m(t,{{\mathbf{x}}}+{{\mathbf{r}}})) \Omega(|{{\mathbf{r}}}|). $$

Here, the first factor defines the force direction from x towards x + r, the second factor describes through the function g how cells and matrix present at x + r contribute to the force, and the final factor accounts through the function Ω for the potential effect that the distance |r| between the two locations under consideration has on the force ¹. We require Ω(|r|) ≥ 0. Specific functional forms for g and Ω will be given below and in the model specification in  Sect. 2. The force F(t, x) is now the accumulated effect of all forces f(t, x, r), i.e.

$$ {{\mathbf{F}}}(t,{{\mathbf{x}}}) = \int_V f(t,{{\mathbf{x}}},{{\mathbf{r}}}) \hbox{d}{{\mathbf{r}}}. $$

We would like to emphasise that the size of the sensing region V is at least the size of an individual cell but typically considerable larger due to cell protrusions (lamellipodia, filopodia). This creates the non-local character of cellular adhesion.

The basic assumption that the more cells or matrix are at a place x + r the more adhesive interaction can take place between cells at x and cells or matrix at x + r is reflected in the dependence of g on c and m at x + r and by requiring that g ≥ 0. The most simple, linear form of g is given by

$$ g(c(t,{{\mathbf{x}}}), m(t,{{\mathbf{x}}})) = S_{cc} c(t,{{\mathbf{x}}}) + S_{cm} m(t,{{\mathbf{x}}}). $$

Here S _cc  ≥ 0 is the self-adhesion coefficient quantifying the strength of adhesive interaction of the cells with other cells and S _cm  ≥ 0 is the cross-adhesion coefficient quantifying the strength of adhesive interaction of the cells with the matrix. Whereas this form is able to account for adhesive aggregation of cells it may at the same time lead to a too strong aggregation, an unrealistic overcrowding in space, see [4] and [14]. In order to avoid, or at least mitigate, this effect, the adhesive interaction should be reduced in crowded regions. Let us assume that c and m are scaled such that they correspond to the volume fractions occupied by cells and matrix, respectively. Then the desired effect can be achieved with the following functional form

$$ g(c(t,{{\mathbf{x}}}), m(t,{{\mathbf{x}}})) = (S_{cc} c(t,{{\mathbf{x}}}) + S_{cm} m(t,{{\mathbf{x}}})) (1-c(t,{{\mathbf{x}}})- m(t,{{\mathbf{x}}}))^+, $$

where (·)⁺ = max{0,·}. The boundedness of solutions of particular models of cell aggregation and cancer invasion using this functional form is analysed in [23]. We will also make use of this form of g in our model.

The nonnegative function Ω(·) is defined for nonnegative arguments and may be utilised to describe that the adhesive interaction over longer distances is weaker than over shorter distances. In this case Ω(|r|) should decrease with increasing |r|. If such an effect is not present or is not intended to be modelled, then Ω(|r|) may be chosen constant. We follow this line in our model, see below Gerisch & Chaplain [13] give a sensible normalisation condition for the function Ω.

We now turn to the spatially one-dimensional situation which is of interest for the work presented here. In this case consider the sensing region V: = (−R, R) with the sensing radius R > 0. Clearly, we should have $R>\hat{R}$, i.e. the sensing radius is larger than the radius of a single cell, but we also assume that 2R is less than the diameter of the spatial domain Ω. We extend the function Ω(·) as an odd function to the real line. Then we can rewrite the adhesive flux as (dropping the bold face in the notation since all quantities are scalar now)

$${\mathbf J}_{{\rm adhesion}}(t,x) = c(t,x) v(t,x), $$

(1)

$$ v(t,x) = {\frac{\Phi}{\hat{R}}} \int \limits _{- R}^ R g(c(t,x+r), m(t,x+r)) \Omega(r)\hbox{d}r. $$

(2)

In order to emphasize the non-local character, we denote the velocity also in the form

$$ v(t,x)= A \{{{\mathbf{u}}}(t,\cdot)\}(x)={\frac{\phi} {\hat{R}}}\int \limits _{- R}^{ R}g({{\mathbf{u}}}(t,x+r))\Omega(r)dr, $$

(3)

where we have assumed that c and m are components of a vector-valued function u(t, x). In this work we consider the case that

$$ \Omega(r):=\left\{\begin{array}{ll} \hbox{sign}(r){\frac{1}{2R}} & r\in[-R,R]\\ 0 & \hbox{otherwise},\\ \end{array}\right. $$

(4)

i.e., it is a (piecewise) constant function.

Systems of partial differential equations must be supplemented with boundary conditions in order to guarantee a unique solution. The choice of boundary condition has a significant effect on the definition of the non-local force F(t, x) for points x near the boundary of the spatial domain Ω. We discuss some options in the spatially one-dimensional setting below.

1.3.1 Periodic Boundary Conditions

Here one assumes that c(t, ·) and m(t, ·) as well as all terms depending on x are extended periodically outside of the domain Ω to the whole of ${\mathbb{R}}.$ In this case we can simply exploit that periodicity and v(t, x) is well defined for all x ∈ Ω. Considering g(c(t, x), m(t, x)) as a function of t and x, also denoted g(t, x), this means that we extend g(t, x) periodically outside of Ω.

1.3.2 Zero-flux Boundary Conditions

These typically model the case of an isolated domain Ω, e.g. representing a Petri dish, and neither cells nor matrix can cross the boundary. For the cells this means that the normal component of the cell flux must vanish on ∂Ω. In the one-dimensional setting this implies that the flux J(t, x) = 0 for all x ∈ ∂Ω. A difficulty arises here for the evaluation of v(t, x) when x ∈ Ω is closer than R to ∂Ω. In this case, g(c(t, x + r), m(t, x + r)) is not defined for some r ∈ V since c and m are not defined outside of Ω. However, the case of an isolated domain also means that cells cannot reach outside of Ω for adhesive interaction and consequently it is appropriate to define g(c(t, x), m(t, x)): = 0 for all $x\not\in\Upomega$, i.e. we extend function g(t, x) by zero outside of Ω. It is important to note that this extension of g(t, x) is a modelling issue and part of the model specification. In particular, we here assume for simplicity that the cells have no adhesive interaction with the boundary of Ω itself. If this would however be the case, for example because the Petri dish is coated with a substance which cells like to adhere to, then zero-flux boundary conditions for the cells are still appropriate but g(t, x) must be extended to reflect this additional adhesive interaction.

1.3.3 Symmetry Boundary Conditions

Symmetries in the PDE problem often allow to reduce the size of the spatial domain Ω and are therefore of computational interest. In one-dimensional space, if the solution is symmetric around x _s  = 0 then Ω = (−L, L) can be reduced to Ω: = (0, L) and at x _s  = 0 symmetry boundary conditions apply. Let x _s  ∈ ∂Ω be a boundary point where symmetry boundary conditions apply. Then it follows that there can be no cell flux through that boundary point as this would violate the symmetry. Therefore, a zero-flux boundary condition applies for the cell density c at x = x _s , i.e. J(t, x _s ) = 0 and, as in the zero-flux boundary condition case above, for x ∈ Ω with |x − x _s | < R the velocity v(t, x) is not defined. Again, as above, we have to extend function g(t, x) across x _s  ∈ ∂Ω for $x\not\in\Omega.$ However, in this case and in contrast to the zero-flux boundary condition case, we do not extend g by zero but must do so by symmetry around x _s . This is because here cells can reach outside of Ω across the symmetry boundary for adhesive interaction because this boundary is not physical but only a theoretical construct to reduce the problem to a smaller domain. Also in contrast to the zero-flux boundary condition case, this extension of g(t, x) is not a modelling issue but follows strictly from the assumed symmetry.

1.3.4 Dirichlet Boundary Conditions

If at some point x _D  ∈ ∂Ω Dirichlet boundary conditions are prescribed for c or m then again information is missing to evaluate the non-local term at x ∈ Ω with |x − x _D | < R and again function g(x, t) must be extended appropriately. A sensible extension is again part of the modelling process in this case. Since in the sequel we do not consider problems with Dirichlet boundary conditions for any of the variables involved in the non-local term we do not discuss this case any further.

Of course, symmetry and zero-flux boundary conditions for the cell density c(t, x) can also be combined. Below in our model we consider the case of a symmetry boundary condition at x = 0 and a zero-flux boundary condition for c(t, x) at x = L. We emphasise that both conditions look the same at the level of the PDE but they differ in the way how the non-local term is evaluated near the boundaries.

2 Modelling Adhesion in Cell Aggregate Behavior

To illustrate the potential of modelling cell–cell and cell–matrix adhesion on a continuum level, we use a model that represents a generic cell-in-gel 3D culture situation. The model encompasses five variables: cell density (c), hydrogel density (w), matrix degrading enzyme density (e), collagen (extracellular matrix) density (m) and oxygen/nutrient density (n). Let u: = (c, w, e, m, n) be the vector of the five variables. The spatiotemporal evolution of these five variables is described by a system of partial differential equations (PDEs) in which the various terms describe the migration of cells (random migration and cell–cell and cell–matrix adhesion), enzymes (diffusion) and nutrients (diffusion), cell proliferation and death (influenced by spatial and nutrient constraints), hydrogel degradation (by matrix-degrading enzymes), enzyme production (by cells) and degradation (half-life), collagen production (influenced by spatial constraints) and oxygen/nutrient consumption (by cells). Each of the five PDE equations will be briefly described below.

The motion of the cells is assumed to be governed by random motility and by adhesion to other cells and the matrix (both the hydrogel and the collagen). Furthermore, the cells are assumed to proliferate, modelled by a logistic growth law, which takes into account the space occupied not only by cells (which would lead to a simple logistic growth law μ₁ c(1 − c)) but also by the hydrogel as well as the produced matrix to avoid overcrowding as explained above. The proliferation of cells is only possible when sufficient oxygen/nutrients are present, which is modelled by introducing a mask function $M_1=n^6(K_p^6+n^6)^{-1}$. Finally cell death occurs under very poor oxygen/nutrient conditions $(M_2=1-n^6(K_d^6+n^6)^{-1})$. This leads to the following equation:

$$ {\frac{\partial c}{\partial t}}=\nabla \cdot\left[D_c \nabla c - cA \{{{\mathbf{u}}}(t,\cdot)\}\right] + \mu_1c(1-c-w-m)M_1-\mu_2M_2c. $$

(5)

The non-local term A{u(t, ·)}, also referred to as the adhesion velocity, is a function of x and for a one-dimensional spatial domain takes the form see Eq. (3):

$$ A \{{{\mathbf{u}}}(t,\cdot)\}(x)={\frac{\phi} {\hat{R}}}\int\limits_{- R}^{ R}g({{\mathbf{u}}}(t,x+r))\Omega(r)dr, $$

(6)

as described in detail in  Sect. 1.3. In this study the weight of all the points in the sensing region is assumed to be equal and so Ω(r) is given by Eq. (4). The following form for g is used: g(c, w, m) = (S _cc c + S _cw w + S _cm m)(1 − c − w − m)⁺. S _cc is the cell–cell adhesion coefficient, S _cw is the cell–hydrogel adhesion coefficient and S _cm is the cell–extracellular matrix adhesion coefficient. Similarly to the logistic growth term, the factor (1 − c − w − m)⁺ ensures that a space point which is already densely filled (or even overcrowded) with cells and/or matrix does not attract more cells via adhesive interaction. In this way unbounded aggregation is avoided.

The hydrogel is considered to be non-motile matter and changes in its distribution are due solely to its local degradation by matrix degrading enzymes at a rate γ.

$$ {\frac{\partial w}{\partial t}}=-\gamma w e $$

(7)

Matrix-degrading enzymes are produced by active cells (when sufficient oxygen/nutrients are present, M ₁) at a constant rate α, are removed from the system at rate λ and are assumed to diffuse freely in the spatial domain.

$$ {\frac{\partial e}{\partial t}}=\nabla \cdot\left[D_e \nabla e\right]+ \alpha M_1 c - \lambda e $$

(8)

The extracellular matrix is produced by the cells at rate β under favourable nutrient/oxygen conditions (M ₁) within the physical limitations of space (factor (1 − c − w − m))

$$ {\frac{\partial m}{\partial t}}=\beta c(1-c-w-m)M_1. $$

(9)

Oxygen and nutrients, which are modelled as a single variable for simplicity reasons, are assumed to diffuse freely in the spatial domain and are consumed by the cells at a constant rate α _s .

$$ {\frac{\partial n}{\partial t}}=\nabla \cdot \left[D_n \nabla n\right] - \alpha_s cn $$

(10)

Equations (5–10) have been obtained after the original variables u have been scaled with respect to time and space using a characteristic time of 1,000 s and a characteristic length of 0.1 cm. They have furthermore been scaled with respect to u ₀ containing characteristic densities/concentrations and are hence in non-dimensionalised form. The following set of non-dimensionalised parameters is used in this study.

$$ \begin{array}{llllll} D_c=0.1 , & S_{cc} = 0.1 , & S_{cw} = 0.5,& S_{cm} = 0.25 , &\mu_1 = 0.1 , & \mu_2 = 1 ,\\ K_p = 0.5 , & K_d = 0.1 , & \gamma= 1,& D_e=10^{-2}, & \alpha = 0.1, &\\ \lambda = 0.5 , & \beta= 0.1 , & D_n=10^{-4} , & \alpha_s = 0.1, & \Phi = 1.\\ \end{array} $$

(11)

The (dimensional) cell radius was set at 5 μm, giving a non-dimensional $\hat{R}=5\times10^{-3}$, the sensing radius was fixed at five cell diameters, i.e. R = 50 × 10⁻³. As the main purpose of this study is to illustrate the potential of modelling cell–cell and cell–matrix adhesion at a continuum level, no further attempts were made to experimentally determine the value of the parameters for a specific cell-in-gel culture set-up.

As mentioned in the previous section, the 1D domain used in this study is derived from a cell-in-gel set-up as represented in Fig. 2. The hydrogel is surrounded by medium in a Petri dish. For symmetry reasons only one half of the domain is used in the calculations. This leads to symmetry boundary conditions on the left boundary, x = 0, for all variables. Apart from the oxygen/nutrients, which can diffuse from the medium into the hydrogel, all other variables are assumed to be restricted to the hydrogel. Therefore, we apply zero-flux boundary conditions on the right edge of the domain, x  =  L = 4, for the cell density and the matrix degrading enzyme concentration. The hydrogel and collagen density is zero for x  > L = 4 (no boundry condition is prescribed since the equations for w  and m involve no transport, but the zero-values are used in the non-local term evalution). For the oxygen/nutrient variable, a Dirichlet boundary conditions is applied as we assume the medium surrounding the hydrogel gets sufficiently often refreshed to maintain a constant level of oxygen and nutrients. At the onset of the simulations, we assume a low concentration of cells, homogeneously distributed throughout the (low-density) hydrogel. Collagen and matrix-degrading enzymes are not present at the onset of the simulations. An initial oxygen/nutrient profile is assumed, representing the diffusional limitations of oxygen into the hydrogel and the resulting hypoxic condition in the centre of the gel [9].

Fig. 2

Derivation of modelling domain. Left cells are homogeneously encapsulated in a hydrogel that is placed in a Petri dish and surrounded by medium. Right the 1D domain used in this study is a horizontal cross-section of the hydrogel. We assume there is no variation in the vertical direction

3 Numerical Technique

The Method of Lines (MOL) is applied for the numerical solution of the model equations in this chapter. In the MOL the discretisation of spatial and temporal derivatives is separated. We apply the so-called vertical MOL here, in which the spatial derivatives are discretised first, followed by temporal discretisation.

For the model considered in this work, we discretise the spatial derivatives on a uniform spatial grid with N grid cells covering the one-dimensional spatial domain Ω = (0, L). Each grid cell, or finite volume, is an interval of length h: = L/N. ² We employ a Finite Volume Method (FVM) of order two on this grid, see, e.g. [12], or more general the book by Hundsdorfer & Verwer [16]. The result of this discretisation in space is a large and in general stiff initial value problem (IVP) for a system of ordinary differential equations (ODEs), the MOL-ODE system,

$$ {\frac{\hbox{d}{{\mathbf{U}}}(t)}{\hbox{d}{t}}} = {{\fancyscript{F}}}(t,{{\mathbf{U}}}(t)),\quad {{\mathbf{U}}}(0)= {{\mathbf{U}}}_{{\mathbf{0}}}. $$

(12)

The MOL-ODE together with the initial data U ₀ represents the PDE model on the spatial grid. As is customary when using the FVM, the components of the MOL-ODE system are approximations to the averages of the PDE solution in each grid cell. Since the model (5–10) has five equations, the MOL-ODE has dimension 5N.

The numerical solution of the IVP (12) constitutes the second step of the MOL and an appropriate time integration scheme must be selected. Implicit time integration schemes can deal efficiently with the inherent stiffness of the MOL-ODE. We favour the fourth order linearly-implicit Runge-Kutta method ROWMAP [25]. The multiple Arnoldi process used within this method for the solution of the linear equation systems in each time step makes this scheme particularly suited for the large ODE system at hand. Furthermore, the method does not require any computation of the Jacobian of the MOL-ODE by the user; the required Jacobian-times-vector products are computed automatically by a suitable finite difference approximation using the right-hand side ${{\fancyscript{F}}}$ of the MOL-ODE.

The FVM described in [12] has been applied to taxis-diffusion-reaction systems. There difficulties arise in regions of strong variation of the solution of the PDE, e.g. near moving fronts. These are due to the taxis term of the model and special attention was given to ensure that the discretisation of that term does not introduce oscillations or negative solution values in the solution of the MOL-ODE. This goal can be achieved, while maintaining the order two of the FVM as much as possible, using a second-order upwind discretisation together with a nonlinear limiter function. The model of this chapter has a non-local adhesion term which is similar to the taxis terms in [12]. So we apply the same discretisation to that term, with the added difficulty of the approximation of the integral defining the adhesive velocity. This is explained in more detail in the following with particular emphasis on the incorporation of boundary conditions.

Recall that the adhesive velocity takes, in the one-dimensional setting, the form, cf. Eq. (2),

$$ v(t,x) = {\frac{\Phi}{\hat{R}}}\int \limits _{-R}^R g(c(t,x+r), m(t,x+r)) \Omega(r)\hbox{d}r, $$

where function g and Ω and the parameters R, $\hat{R}$, and Φ are user-specified. The adhesive velocity v(t, x), and consequently the integral must be approximated on each grid cell interface x = jh, j = 0, 1, ..., N, of the spatial grid for each evaluation of the right-hand side ${{\fancyscript{F}}}$ of the MOL-ODE. This task constitutes the computational bottleneck of the whole numerical solution process. In [10] an approximation procedure for the adhesion velocity is described which yields

$$ v(t,\;jh)\approx v_j(t) := {\frac{\Phi R} {\hat{R}}}\sum_{l=-l^-}^{l^+} w_l G_{j+l}(t)\quad\hbox{with}\quad G_j(t):=g(C_{j}(t), M_{j}(t)), $$

(13)

where C _j (t) and M _j (t) are components of vector U(t) of the MOL-ODE system and approximate the averages of cell density and matrix density in the jth grid cell, that is in [(j − 1)h, jh], respectively. The weights w _l , l =  − l ⁻, ..., l ⁺, define the integration formula and l ⁻ and l ⁺ are related to the sensing region and are roughly equal to R/h, for details see [10]. The factor $\Phi R/\hat{R}$ compensates for the fact that [10] considers the special case $\hat{R}=R$ and Φ = 1. It is important to stress that the weights w _l depend on the function Ω(r), on the spatial grid width h, and on the sensing radius R but on nothing else. In particular, they are independent of the function g and of the cell and matrix densities. This implies that the weights can be computed once Ω(r), R, and h are fixed, i.e. before a simulation run is started.

We first briefly outline how periodic boundary conditions are employed in the evaluation of the adhesion velocity. This is the case considered in [10] and it sets the stage for the zero-flux and symmetry boundary conditions which are of interest for the model considered in this work. As discussed in  Sect. 1.3, in the case of periodic boundary conditions function g, as a function of x, is extended periodically. This implies that G _j (t) is defined for all integers j and that it is N-periodic in j. With this, v _j (t) is well-defined for all j = 1, ..., N according to (13) and v _j (t) also becomes N-periodic in j, in particular v ₀(t) = v _N (t). Furthermore, (13) can be written as the matrix–vector product

$$ {{\mathbf{v}}}(t) = {\frac{\Phi R}{\hat{R}}}A^{({\rm p})} {{\mathbf{G}}}(t), $$

(14)

where

$$ {{\mathbf{v}}}(t):=[v_1(t) , v_2(t) ,\ldots ,v_N(t)]^{{{\mathsf{T}}}} \quad\hbox{and}\quad {{\mathbf{G}}}(t):=[G_1(t), G_2(t),\ldots,G_N(t)]^{{{\mathsf{T}}}}. $$

(15)

Here, $A^{({\rm p})}\in{\mathbb{R}}^{{N,N}}$ is a circulant matrix defined by the weights w _l of the integration formula, consequently A ^(p) is known before a simulation run starts. The superscript (p) is used to refer to the case of periodic boundary conditions. Circulant matrices enjoy favourable properties [24]: any circulant matrix A is (i) defined by its first column a and (ii) diagonalised by the discrete Fourier transform matrix with eigenvalues given by the discrete Fourier transform of a. Property (1) allows for a memory-efficient storage of A and (2) facilitates the efficient computation of matrix–vector products using the fast Fourier transform (FFT) and its inverse (iFFT) through

$$ A{{\mathbf{G}}} = \hbox{iFFT}(\hbox{FFT}({{\mathbf{a}}})\otimes \hbox{FFT}({{\mathbf{G}}})), $$

where $\otimes$ denotes the element-wise product of two vectors.

The first column of matrix A ^(p) is given by

$$ {{\mathbf{a}}}^{({\rm p})}:=\left[w_0 , w_{-1} ,\ldots ,w_{-l^-}, 0,\ldots,0 , w_{l^+}, w_{l^+-1} ,\ldots ,w_{1}\right]^{{{\mathsf{T}}}} \in{\mathbb{R}}^{N}. $$

(16)

Even though matrix A ^(p) has many zero entries due to its banded structure of width characterised by l ⁻ and l ⁺, it pays off computationally, in matrix–vector products, not to exploit this fact but rather the circulant structure of the matrix by using the FFT. This is because refining the spatial grid leads to an increase in the dimension of matrix A ^(p) but also to an increase of its bandwidth. As a result, the fraction of non-zero elements in A ^(p) remains constant for h → 0 and exploiting the zeros would, in consequence, lead to a matrix–vector product of complexity ${{\fancyscript{O}}}({{N^2}})$. The FFT approach, in contrast, requires only ${{\fancyscript{O}}}({{N\log N}})$ complexity and is thus overall more efficient. We note that the growth of the bandwidth of A ^(p) with decreasing h and the associated constant fraction of non-zero entries is a characterising feature of the non-local term in the PDE model and distinguishes it from, for instance, a diffusion term. A matrix representation of the latter involves a matrix where the fraction of non-zero entries tends to zero for h → 0.

If we depart from periodic boundary conditions then the circulant structure is lost, at least on first sight but can be recovered. We will consider two cases: (A) zero flux boundary conditions on both ends of the domain Ω and (B) a symmetry boundary condition at the left end and a zero-flux boundary condition on the right end of Ω. The second scenario applies in the simulations for this chapter. In both cases we compute N + 1 adhesion velocities

$$ {{\mathbf{v}}}(t):=\left[v_0(t), v_1(t),\ldots, v_N(t)\right]^{{{\mathsf{T}}}}\in{\mathbb{R}}^{{N+1}}. $$

In case (A), recall from  Sect. 1.3 that function g is extended by zero outside of the domain Ω. Hence, v(t) can be computed from a matrix–vector product

$$ {{\mathbf{v}}}(t) = {\frac{\Phi R}{\hat{R}}}A^{({\rm zz})} {{\mathbf{G}}}(t), $$

where ${{\mathbf{G}}}(t)\in{\mathbb{R}}^{{N}}$ is given as in the case of periodic boundary conditions. The matrix $A^{({\rm zz})}\in{\mathbb{R}}^{{N+1,N}}$ is now rectangular and has a Toeplitz structure. The superscript (zz) refers to the case that function g has been extended by zeros to the left and right of the domain Ω. A Toeplitz matrix is defined by specifying its first row and column. For A ^(zz) these are given by

$$ \left[w_1 , w_2 ,\ldots ,w_{l^+} , 0 ,\ldots\right]\in{\mathbb{R}}^{{N}} \quad\hbox{and}\quad [w_1 , w_0 ,\ldots ,w_{-l^-}, 0,\ldots]^{{{\mathsf{T}}}}\in{\mathbb{R}}^{{N+1}}, $$

respectively, in particular, $A^{({\rm zz})}\in{\mathbb{R}}^{{N+1,N}}$ is a banded Toeplitz matrix with upper bandwidth l ⁺ − 1 and lower bandwidth l ⁻ + 1.

In case (B), recall from  Sect. 1.3 that function g is extended by symmetry to the left of Ω and by zeros to the right of Ω. Again, v(t) can be computed from a matrix–vector product

$$ {{\mathbf{v}}}(t) = {\frac{\Phi R}{\hat{R}}}A^{({\rm vz})} {{\mathbf{G}}}(t), $$

where now G(t) is given by

$$ {{\mathbf{G}}}(t):=\left[G_{l^-+1}, G_{l^-},\ldots,G_1, G_1, G_2,\ldots,G_N\right]^{{{\mathsf{T}}}}\in{\mathbb{R}}^{{N+l^-+1}}, $$

where the first l ⁻ + 1 entries represent the extension by symmetry on the left. Matrix $A^{({\rm vz})}\in{\mathbb{R}}^{{N+1,N+l^-+1}}$ is a rectangular Toeplitz matrix with first row and column given by

$$ \left[w_{-l^-}, w_{-l^-+1},\ldots ,w_{l^+}, 0 ,\ldots\right]\in{\mathbb{R}}^{{N+l^-+1}} \quad\hbox{and}\quad \left[w_{-l^-}, 0,\ldots\right]^{{{\mathsf{T}}}}\in{\mathbb{R}}^{{N+1}}, $$

respectively. In particular, the lower bandwidth of A ^(vz) is zero and the upper bandwidth is l ⁻ + l ⁺. The superscript (vz) refers to the case that function g has been extended by some “values” to the left of Ω and zeros to the right of Ω. The “values” are in our case defined by symmetry but they could be any other values, e.g. representing some sort of Dirichlet boundary.

Matrix–vector products with Toeplitz matrices cannot be handled directly by FFT techniques. However, rectangular Toeplitz matrices can be embedded in square circulant matrices of often just slightly larger size and then the matrix vector product can again be computed as in the case of periodic boundary conditions [11]. To this end let $T\in{\mathbb{R}}^{{N_1,N_2}}$ be a banded Toeplitz matrix with lower bandwidth 0 ≤ l ⁻ < N ₁ and upper bandwidth 0 ≤ l ⁺ < N ₂ and first row and column given by

$$ \left[t_0, t_1,\ldots ,t_{{l^+}}, 0,\ldots\right]\in{\mathbb{R}}^{{N_2}}\quad\hbox{and}\quad [t_0 , t_{-1} ,\ldots ,t_{-{l^-}} ,0\ldots]^{{{\mathsf{T}}}} \in{\mathbb{R}}^{{N_1}}, $$

respectively. Assume that $t_{-{l^-}}\ne0$ and $t_{l^{+}}\ne0$. Then the following holds.

• (a) The matrix T can be embedded in the circulant matrix $C\in{\mathbb{R}}^{{{\ell},{\ell}}}$, defined by its first column c given by

  $$ {{\mathbf{c}}} = (t_0,t_{-1},\ldots,t_{-{l^-}},0\ldots,0,t_{l^+},t_{{l^+} -1}\ldots,t_1)^{{{\mathsf{T}}}} \in{\mathbb{R}}^{{\ell}}, $$

  where C is 2 × 2 block-structured with (1,1) block equal to T, i.e.

  $$ C = \left(\begin{array}{ll} T & M_{12}\\ M_{21} & M_{22}\\ \end{array}\right), $$

  and ℓ is minimal and given by ℓ = max{N ₁ + l ⁺, N ₂ + l ⁻}.

• (b) It holds ℓ < N ₁ + N ₂.

• (c) Let ${{\mathbf{G}}}\in{\mathbb{R}}^{{N_2}}$. The Toeplitz matrix–vector product $T{{\mathbf{G}}}$ can be computed using a circulant matrix–vector product by

  $$ T{{\mathbf{G}}} = \left[C {\tilde{{\mathbf{G}}}}\right]_{1,\ldots,N_2}, $$

  where $\tilde {{\mathbf{G}}} := ({\bf G}\,{\bf 0})^{{{\mathsf{T}}}} \in{\mathbb{R}}^{{{\ell}}}$ and C is the circulant matrix from (a).

The application of this embedding result to the two Toeplitz matrices $A^{({\rm zz})}\in{\mathbb{R}}^{{N+1,N}}$ and $A^{({\rm vz})}\in{\mathbb{R}}^{{N+1,N+l^-+1}}$ corresponding to the boundary condition cases (A) and (B), respectively, yields that a matrix–vector product with these matrices can be accomplished by computing an FFT-based matrix–vector product with a circulant matrix C of dimension ℓ = N + max{l ⁺, l ⁻ + 1} in case (A) and of dimension ℓ = N + l ⁻ + l ⁺ + 1 in case (B).

4 Results and Discussion

Simulations performed with the model given by Eqs. (5–10) using the parameter set (11) for an initially homogeneously distributed cell population show an increased cell density in the periphery of the gel (right hand side of the domain) and a stagnation of cell density in the centre of the gel (left hand side of the domain) under the influence of the local oxygen/nutrient conditions (Fig. 3). As already at the start of the simulations the oxygen/nutrient concentration is low in the centre of the gel, cells are not able to degrade the hydrogel or produce collagen. Towards the periphery of the gel where oxygen/nutrient conditions are more favourable, cells are able to degrade the surrounding hydrogel, proliferate and produce collagen. The peak in collagen density at the right edge is due to the locally high concentration of nutrients/oxygen. The initial increase in cell density increases the consumption of oxygen limiting the increase in cellular density beyond what is shown in Fig. 3. With the values of the adhesion parameters used in this simulation, the influence of any of the adhesive processes on the simulation result is minimal with the exception of the drop in cell density at the outer edge of the gel (right boundary of the domain). This drop is a modelling effect (zero-flux boundary condition) since cells are only pulled from the left at/near the right boundary (no cells are present outside the gel).

Fig. 3

Simulation results for the model given by Eqs. (5–10). Shown are the (non-dimensional) cell density (cell), the hydrogel density (hydr), the matrix degrading enzyme concentration (enzy), the collagen density (coll) and the oxygen/nutrient concentration (nutr) over the simulated domain (x-axis in cm). Dashed lines indicate the initial conditions (the matrix degrading enzyme concentration and the collagen density are initially zero in the entire domain), full lines correspond to the time point t = 50 (1 week of culture)

Increasing the parameter values related to each of the cell adhesive processes encapsulated in the model (cell–cell, cell–hydrogel and cell–collagen adhesion) clearly shows the effect of these processes on the density and distribution of cells and the produced collagen (Fig. 4).

Fig. 4

Simulation results for the model given by Eqs. (5–10) for increased values of the adhesion parameters. Shown in each subfigure are the (non-dimensional) cell density (full line), the hydrogel density (dashed line) and the collagen density (dotted line) at time point t = 50 over the simulated domain (x-axis in cm). a Results using the basic parameter value set (11). b Cell–cell adhesion increased by factor 10. c Cell–hydrogel adhesion increased by factor 10. d Cell–collagen adhesion increased by factor 10

A tenfold increase of the cell–cell adhesion parameter (S _cc ) causes clustering of the cells in small aggregates throughout the gel. As oxygen/nutrient consumption causes hypoxic conditions in the centre of each aggregate, the collagen production is highest at the edges of each aggregate.

A tenfold increase of the cell–hydrogel adhesion parameter (S _cw ) leads to the accumulation of cells in the centre of the gel. This accumulation is due to a continuous migration of cells from the periphery of the gel towards the centre. Once they arrive at the centre of the gel they will become inactive (no proliferation, hydrogel degradation or collagen production) due to the low concentration of oxygen/nutrients present there. In the periphery of the gel, cells do proliferate, produce collagen and degrade the hydrogel. This maintains the adhesive velocity being directed towards the centre of the gel.

Finally, a tenfold increase of the cell–collagen adhesion parameter (S _cm ) leads to an almost complete depletion of cells in the centre of the gel. As collagen can only be produced in the periphery of the gel where the nutritional conditions allow so, the adhesive velocity will be directed away from the centre towards the periphery of the gel. Due to the accumulation of the cells, nutritional conditions will deteriorate in the periphery of the gel as well causing a halt in the increase in cell density and collagen density.

For the simulation results shown above, the cell sensing radius was chosen to be five cell diameters. Increasing the sensing radius by a factor 10 initially leads to the formation of less aggregates but bigger ones (Fig. 5). These bigger aggregates provide less favourable conditions to the cells inside the aggregate which results in overall less cell proliferation and collagen production at the end of the simulation period when compared to the simulations with a smaller sensing radius.

Fig. 5

Simulation results for the model given by Eqs. (5–10) for different cell sensing radii. Shown in each subfigure are the (non-dimensional) cell density (full line), the hydrogel density (dashed line) and the collagen density (dotted line) over the simulated domain (x-axis in cm). Parameter set (11) was used with the cell–cell adhesion (S _cc ) increased by a factor 10. Simulation results are shown for simulation times t = 5 (a,c) and t = 50 (b,d), using a cell sensing radius of five cell diameters (a,b) or 50 cell diameters (c,d)

We remark that the total density (cell + hydrogel + collagen) always remains below the maximal available space due to the use of the physical space restriction factor that was used in the terms describing cellular proliferation, cellular adhesion and collagen production. As stated above, this prevents the occurrence of nonphysical unlimited growth and aggregation in the model.

The way in which the zero-flux boundary conditions are currently implemented assumes that cells have no particular adhesive interaction with the boundary of the domain itself. When studying situations where this is the case, such as a cell culture in a Petri dish which has been coated with an adhesive substance, the function describing how cells and matrix at a particular location contribute to the adhesive force needs to be elaborated compared to its formulation used in the current study.

Apart from the determination of the parameter values for a specific cell-in-gel culture set-up, other model extension can be considered in the future. One example is the right edge boundary condition on the matrix degrading enzymes which now considers the enzymes to be trapped inside the gel, while more likely they can freely leave the gel and enter the medium similar to the oxygen/nutrient variable. Furthermore in this study adhesion is assumed to generate forces resulting in cell migration whereas the signalling that is initiated through cell–cell and cell–matrix binding also has an influence on many other facets of cell behaviour, including proliferation and apoptosis. Including these phenomena in the model will further enhance its relevance to understanding the role of adhesion in the biological processes under scrutiny.

5 Conclusions

In this chapter we discussed the critical role played by cellular adhesion in tissue engineering processes. A brief review of existing models, discrete and continuous, has demonstrated that for larger-scale applications, continuum models using the recently introduced non-local technique are very well suited to model these adhesive processes. Here we expanded the derivation of this model with respect to previous works [4] and [14] to allow for its application in finite non-periodic spatial domains with various boundary conditions. A generic cell-in-gel culture model was presented to illustrate the technique, showing a clear influence of the different adhesive processes on the final cell and collagen density and distribution. Both the theoretical discussion and the modelling example provided in this chapter show the feasibility of using the non-local technique to capture cell adhesive behaviour in continuum models.