Order and Disorder in Liquid-Crystalline Elastomers

Abstract

Order and frustration play an important role in liquid-crystalline polymer networks (elastomers). The first part of this review is concerned with elastomers in the nematic state and starts with a discussion of nematic polymers, the properties of which are strongly determined by the anisotropy of the polymer backbone. Neutron scattering and X-ray measurements provide the basis for a description of their conformation and chain anisotropy. In nematic elastomers, the macroscopic shape is determined by the anisotropy of the polymer backbone in combination with the elastic response of elastomer network. The second part of the review concentrates on smectic liquid-crystalline systems that show quasi-long-range order of the smectic layers (positional correlations that decay algebraically). In smectic elastomers, the smectic layers cannot move easily across the crosslinking points where the polymer backbone is attached. Consequently, layer displacement fluctuations are suppressed, which effectively stabilizes the one-dimensional periodic layer structure and under certain circumstances can reinstate true long-range order. On the other hand, the crosslinks provide a random network of defects that could destroy the smectic order. Thus, in smectic elastomers there exist two opposing tendencies: the suppression of layer displacement fluctuations that enhances translational order, and the effect of random disorder that leads to a highly frustrated equilibrium state. These effects can be investigated with high-resolution X-ray diffraction and are discussed in some detail for smectic elastomers of different topology.

An erratum to this chapter can be found at http://dx.doi.org/10.1007/12_2011_158

An erratum to this chapter can be found at http://dx.doi.org/10.1007/12_2011_158

1 Introduction

Conventional low-molecular-mass liquid crystals (LC) are anisotropic fluids composed of relatively stiff rod-like molecules. The nematic phase is characterized by long-range orientational order in a preferred direction, given by the director n. Nematic LC are well known for their remarkable electro-optical properties, and are now featured in numerous applications as, for example, flat panel color displays. LC order and polymer properties can be combined by linking mesogenic fragments with polymer chains, thus forming LC polymers. The backbone polymer, in turn, can be weakly crosslinked to form a LC elastomer. For the chemical aspects of this process we refer to Kramer et al. [1]. The macroscopic rubber elasticity introduced via such a percolating network interacts with the LC ordering field. This provides a strong shape response when electric, optical, or mechanical fields are applied. An important feature of nematic LC elastomers is that the overall molecular shape varies parallel to the degree and direction of the orientational order.

At the beginning of the nematic polymer age, De Gennes [2] considered nematic elastomer networks as the most promising way to couple the orientational order to overall molecular shape. Nowadays this promise seems to be fulfilled, both experimentally and theoretically. Over the last two decades, a wealth of LC elastomers have been synthesized and characterized, including nematic, diverse smectic, and discotic phases. We refer to Brand and Finkelmann [3] for a review of work up to about 1997 and to the revised edition of the monograph of Warner and Terentjev [4] for more recent information. The potential applications of nematic elastomers include low frequency, large amplitude actuators and transducers driven by weak electric and optical fields, and components of artificial muscles (biomimetic sensors). A recent overview of LC elastomers as actuators and sensors has been published by Ohm et al. [5]. It is clear that the most attractive applications would involve a strong response to a low electric field. This has led to intense investigations of LC elastomers swollen with low-molecular-mass nematic materials. In the course of these studies, large volume changes and volume transitions have been found, as well as quite significant electromechanical effects in moderate electric fields. These aspects are discussed by Urayama [6].

Prior to discussing LC elastomers, we will consider in Sect. 2 in some detail the conformations and chain anisotropy of their polymer counterparts because the polymer backbone generates the shape anisotropy and elastic response of the elastomer network. In this context, note that two different classes of thermotropic LC polymers exist: main-chain and side-chain (comb-like), as depicted in Fig. 1). In side-chain LC polymers, the pendant mesogenic groups are linked to a linear polymer backbone by an (often flexible) spacer. Main-chain LC polymers are built up by combining rod-like mesogenic fragments and flexible moieties in alternating succession. In a somewhat more modern terminology, one can divide each case into “end-on” and “side-on” LC polymers, which differ in the way the rod-like mesogenic fragment is attached to the spacer. The properties of the nematic phase formed by these two types of polymer appear to be very different. In Sect. 3, these results are extended to the properties and anisotropic shapes of nematic elastomers.

Fig. 1

Various possibilities for connecting a mesogenic side group to a polymer chain: main-chain (a, b) and side-chain (c, d)

Monomer and polymer smectic LC phases are discussed in Sects. 4 and 5. Smectic systems consist of stacks of liquid layers in which thermally excited fluctuations cause the mean-squared layer displacements to diverge logarithmically with the system size (Landau–Peierls instability). As a result, the positional correlations decay algebraically as r ^−η (η being small and positive) and the discrete Bragg peaks change into singular diffuse scattering with an asymptotic power-law form (see Sect. 4.1). In Sect. 4.2, some background information is summarized about random fields, the presence of which can lead to disorder. For smectic elastomers, the layers cannot move easily across the crosslinking points where the polymer backbone is attached. Consequently, layer displacement fluctuations are suppressed, which under certain assumptions has been predicted to effectively stabilize the one-dimensional (1D) periodic layer structure. On the other hand, crosslinks provide a random network of defects that could destroy the smectic order. Thus, in smectic elastomers two opposing tendencies exist: suppression of layer displacement fluctuations that enhances the translational order, and random quenched disorder that leads to a highly frustrated equilibrium state. These two aspects are discussed in Sect. 4.3. The signature of (dis)order is found in the lineshape of the X-ray peaks corresponding to the smectic layer structure. For experimental aspects of the high-resolution X-ray methods involved we refer to Obraztsov et al. [7]. The experimental situation regarding order/disorder due to crosslinking smectic elastomers is reviewed in Sect. 5.1 for end-on side-chain smectic polymers and includes a discussion of the nematic–smectic transition. In Sect. 5.2, the discussion is extended to main-chain smectic elastomers and to a particular side-on side-chain system in Sect. 5.4. Finally, in Sect. 6 some conclusions and an outlook are given.

2 Liquid-Crystalline Polymers

2.1 Conformation and Structure

When LC fragments are covalently linked to a polymer chain, the material acquires the properties of a mesogenic polymer. Such polymeric liquid crystals have an intrinsic conflict between the drive of the backbone to adopt a random coil conformation and the tendency to LC order associated with the mesogenic units. Flexibility of the backbone chain as well as of the connecting spacer is essential to give the mesogenic cores enough freedom to self-assemble into LC phases [8–10]. Ordinary polymers as well as LC polymers in the isotropic phase adopt an overall spherical shape, i.e., their gyration volume is a sphere. By contrast, small angle neutron scattering (SANS) measurements of LC polymers in their mesomorphic state indicate that the backbone conformation deviates from a three-dimensional (3D) Gaussian random coil into a prolate or oblate shape [11–13]. The anisometric shape formed by the backbone can be expressed by the main components R _g// and R _g⊥ of the radii of gyration tensor with respect to the nematic director n (see Fig. 2).

Fig. 2

Various shapes of the gyration tensor spheroid with main components R _g// and R _g⊥. The nematic director is indicated by n. Side groups are omitted for clarity (after [4])

Nematic polymers are qualitatively identical to their simple low-molar-mass counterparts. At elevated temperatures, highly fractioned LC polymers display a first-order transition from the nematic to the isotropic phase. In both types of system there is a jump in the scalar orientational order parameter. The orientational order of the rod-like mesogenic fragments of the polymers is rather similar as for classical nematics. It can be directly measured using nuclear magnetic resonance (NMR) spectroscopy, infrared dichroism of selective absorption bands, optical birefringence and some others methods [14]. At lower temperatures a nematic–smectic-A phase transition may take place. The smectic-A order parameter is a 1D density wave that is parallel to layer normal (director n). The features of smectic ordering can be revealed by high resolution X-ray diffraction, as discussed in Sect. 5.

The main tool for determining the actual conformation of the polymer backbone is SANS of selectively deuterated samples [15, 16]. Upon decreasing the temperature it is possible to align the nematic phase by an external magnetic field or by mechanical stretching. Subsequently, the shape of the polymer chain and its anisotropy can be determined from the two-dimensional (2D) SANS patterns. The contrast of SANS is determined by proper deuterization of the sample, while the intensity decay with the scattering vector q reflects the coil anisotropy and the effective rigidity of the constituting fragments. Generally, for long enough chains described by Gaussian statistics, the mean square end-to-end vector can be written as:

$$ \left\langle {{R_i}{R_j}} \right\rangle = \frac{1}{3}{l_{ij}}L, $$

(1)

where l _ij is the effective step lengths tensor and L the contour length of the chain. For conventional nematic or smectic LC polymers of uniaxial symmetry this expression reduces to the main components of the radii of gyration and step lengths tensor with respect to n: R _g//, R _g⊥ and l _//, l _⊥, respectively. The average value of the contour length of the chain is given by L = Na, in which N is the average number of monomers in the chain and a the monomer size. Knowing these values, the main components of the step length tensor l _// and l _⊥ can be determined. In main-chain polymers, the measured anisotropy l _///l _⊥ = (R _g///R _g⊥)² is generally very large. The anisotropy induced in the backbones of side-chain polymers is much smaller and often is oblate, l _///l _⊥ < 1. Many macroscopic properties, for example the optical and dielectric anisotropy, follow the order of the mesogenic rods. However, for polymer networks the backbone anisotropy is of primary importance because it causes the dramatic elastic response. In the next section, we give a brief overview of the essential results obtained so far for chain anisotropies of the various classes of LC polymers.

2.2 Chain Conformation of “End-On” Side-Chain Polymers

For “end-on” side-chain LC polymers, the coupling of the backbones with the ordering field of the mesogenic rod-like fragments varies over a wide range depending on the flexibility of the backbone, the spacer, and the rod–rod interactions. Possibly this explains why these mesogenic polymers exhibit practically the same wealth of LC polymorphism as their low-molar-mass counterparts, including smectic, hexatic, and crystalline phases [10, 17–19].

SANS results on several nematic polyacrylates indicate that the backbone preferably adopts a weakly prolate shape with R _g///R _g⊥ approximately equal to 1.2–1.5, i.e., the average direction of the backbone is parallel to n [10, 20] and is imposed by the alignment of the mesogenic side groups (Fig. 3a). These observations have been confirmed by NMR studies of LC polyacrylates [23]. This type of prolate conformation of the backbone is also typical for nematic polysiloxane-based end-on polymers, especially when the spacer is relatively short. However, less flexible LC polymethacrylates with the same side-chain and spacer length tend to coil up in the nematic phase in a subtle oblate configuration (side-chains preferably perpendicular to the backbone) [11, 12]. In the smectic phase, both acrylates and methacrylates have an oblate configuration and the anisotropy becomes even more pronounced: R _g///R _g⊥ is approximately 0.3–0.5 [12, 24] (Fig. 3b). The backbones are to some extent confined in 2D between the smectic sublayers of the mesogenic cores [22]. Furthermore, the backbone statistics differ in the directions parallel and perpendicular to the director. In the perpendicular direction, the mean square of the radius of gyration $\left\langle {R_{{\text{g}} \bot }^2} \right\rangle$ is proportional to the degree of polymerization, indicating a trend towards a Gaussian walk in the plane of layers. Parallel to the director, the chains show a rod-like behavior, which corresponds to crossing defects, i.e., backbones hopping from one layer to another [24] (Fig. 3b). Such a behavior has already been examined theoretically [25–27]. According to these models, a confined backbone can cross a mesogenic sublayer, creating a local distortion of the smectic layers. A typical distance between two adjacent side groups along a backbone (say 0.5 nm) is factor of six smaller than a typical layer spacing. This implies that for an oblate configuration about six side-chains do not fit into the smectic lamellae at each crossing event. Hence, a sufficiently large density of crossing defects would induce a stressed state of the smectic layers.

Fig. 3

Side-chain LC polymer with (a) prolate nematic conformation and (b) oblate smectic conformation. (c) Representation of two hairpin defects confined to a long, thin cylinder (after [21, 22])

A special case of inversion of the backbone anisotropy was reported for LC polyacrylate with cyano-terminated side groups possessing a low-temperature re-entrant nematic phase [13]. The phase sequence with decreasing the temperature is: nematic–smectic-A_d–re-entrant nematic. In the smectic-A_d phase with partial overlap of antiparallel mesogenic cores, the packing in the area of the terminal chains will be less dense than in a conventional monolayer smectic-A phase. SANS results indicate an oblate backbone conformation in both the nematic and the smectic-A_d phase, which transforms to prolate in the re-entrant nematic phase. X-ray measurements indicate that the change in backbone conformation takes place in a small pretransitional smectic-A_d region in the re-entrant nematic phase [28]. Similar behavior has been observed for highly fractioned polyacrylates with phenyl benzoate side groups possessing a low-temperature re-entrant nematic phase [29]. Though distinct from the above-mentioned cyano-terminated polyacrylates, whose phase behavior is determined by dipolar frustrations [30–32], the same type of the changeover of the backbone conformation occurs. Thus, an end-on LC polymer can possess in the nematic phase opposite types of backbone anisotropy (oblate and prolate) with varying temperature or phase sequence. Evidently, for a specific LC polymer the backbone conformations are very sensitive to the steric confinement introduced by the mesogenic rod–rod interactions.

2.3 Chain Conformation of Main-Chain Polymers

During the last two decades, main-chain LC polymers have been intensively studied by means of SANS, in particular materials based on polyesters and polyethers [21] with relatively long flexible spacers (8–11 carbon atoms). SANS measurements in the isotropic phase of a series of polyesters of different molecular mass [33] indicate $\langle R_{\text{g}}^2\rangle$ to be proportional to the degree of polymerization. This provides proof of the Gaussian character of the main chain in the isotropic phase, with a persistence length, l, of 1.6 nm, which is close to that of well-known flexible polymers (0.8–1 nm). In spite of the large fraction of rod-like mesogenic fragments, the main chain remains rather flexible.

In the nematic phase, SANS patterns of oriented samples show extremely anisotropic chain conformations, the chain size parallel to n being about an order of magnitude larger than in the perpendicular direction [34–36]. For example, D’Allest et al. [34] report a ratio of gyration radii as large as R _g///R _g⊥ ≈ 8, giving for the ratio of step lengths, l _///l _⊥ ≈ 60. Under these conditions, whole chains are forced into an elongated shape: short chains unfold and become nearly rod-like while longer chains can show rapid reversals of chain direction – so-called hairpin defects (Fig. 3c). The formation of hairpins recovers part of the entropy initially lost during the chains straightening, due to their random placements along the chain contour length. Upon decreasing the temperature, hairpin defects become exponentially unlikely and their increasing separation causes the effective step length l _// to grow with the nematic order [35, 37, 38].

The number of hairpins in a nematic main-chain polymer is given by L/2H, where L is the average contour length of the chain and 2H its dimension parallel to n. SANS of both polyesters [35] and polyethers [21] gives similar results: the polymer chains are confined in very long (2H ≈ 20–35 nm), thin (R ≈ 0.8–1.8 nm) and well-oriented (order parameter P ₂ ≈ 0.8–0.9) cylinders (see Fig. 3c). The number of hairpins for such a cylinder varies from one to two. We conclude that, in contrast to the situation in the isotropic phase, in the nematic phase the chain organization of main-chain polymers is very different from that of conventional flexible polymers. The chain conformation appears to be effectively fully extended.

Apart from hairpins, other types of defect can be present in main-chain polymers (see Fig. 4). First, we note that chain ends represent a source of the local distortion of the director field [39]. Furthermore, a certain number of hairpins could become entangled. In contrast to standard hairpins, these kinds of defect cannot be removed by applying mechanical stress. Such entangled hairpins can easily suppress chain reptation and thus represent a source of (physical) crosslinking in the polymer matrix. Although not being quenched, as crosslinks in elastomer networks they introduce local sources of random orientational disorder in the director field.

Fig. 4

Cartoons of a main-chain smectic polymer: (a) standard picture, (b) end defect, (c) hairpin, and (d) entangled hairpin

Main-chain polymers seem to have little tendency to smectic phases. Only relative recently has the synthesis been reported of some main-chain systems with a direct transition from the isotropic to either a smectic-A [40, 41] or a smectic-C phase [42, 43]. X-ray study of these polymers and elastomers will be discussed in Sect. 5.2. In smectic main-chain polymer systems the chains connect neighboring smectic layers. As a result, any defects of the polymer chain directly translate into layer distortions, in contrast to the situation described in Fig. 3b for side-chain polymers.

2.4 Chain Conformation of “Side-On” Side-Chain Polymers

Linking mesogenic rods “side-on” via a spacer to side-chain polymers clearly promotes extension of the backbone along n. The symmetry is similar to main-chain systems [44]. However, quantitatively this effect is influenced by the nature of the spacer (see Fig. 1b). For side-on nematic polymers, a short spacer group (four to six carbon atoms in the alkyl chain) leads to considerable stretching of the polymer backbone to give a “jacketed nematic structure” [45] with a strongly prolate backbone conformation [16, 46]. The ratio of gyration radii can reach values R _g///R _g⊥ ≈ 4–5, i.e., close to that of main-chain LC polymers. Increasing the spacer length up to about 12 carbon atoms practically uncouples the mesogens from the backbone [47], and the orienting effect of the side groups on the polymer backbone is much weaker. Another way to modify the interaction between the flexible polymer chain and mesogenic rods is to decrease the relative number of mesogenic groups attached to the backbone. For such a “diluted” polymer, SANS measurements demonstrate a dramatic diminishing of the prolate anisotropy with decreasing density of mesogenic groups. The anisotropy of backbone conformation can be reduced from R _g///R _g⊥ ≈ 2.7 for mesogenic groups fixed to 55% of the available backbone positions to R _g///R _g⊥ ≈ 1.1 for 30%.

Side-on LC polymers with longer spacers in principle allow for smectic phases, but very few examples have been reported so far [48–50]. For the above-mentioned siloxane polymer with 55% mesogenic groups and a spacer length of ten carbon atoms, SANS indicated a reversible inversion of the backbone anisotropy at the phase transition from nematic to smectic-C. In the high temperature nematic phase, a weak prolate anisotropy, R _g///R _g⊥ ≈ 1.2, was measured. At the phase transition from nematic to smectic-C, the backbone anisotropy continuously changes from weakly prolate to spherical (isotropic) and then to strongly oblate: R _g///R _g⊥ ≈ 0.5. Intuitively for a side-on type of linking it seems difficult to impose smectic layering and to confine the backbone in between these layers. In fact, neutron diffraction measurements of these polymers show the polymer backbone to be partly distributed in the middle of the mesogenic layers [51]. The observed inversion of the backbone anisotropy in the side-on smectic system can be related to the high flexibility of the polysiloxane chain and the long spacer. The intrinsically conflicting preferred orientations of mesogenic cores, backbones, and aliphatic spacers in these polymer molecules leads to strongly disordered smectic layering.

3 Shape Anisotropy and Orientational Order in Nematic Elastomers

3.1 Structure and Diversity

LC polymers can be covalently crosslinked to form a 3D network leading to a LC elastomer (Fig. 5). Since the synthesis of the first LC elastomer based on a polysiloxane backbone by Finkelmann et al. [52], a number of different types of elastomers have been reported. These include elastomers containing polyacrylates and polymethacrylates with a number of mesogenic pendant groups [53–55]. The concept has been extended to crosslinked main-chain as well as combined main-chain and side-chain materials [53, 54]. The early development of the field is described in various review articles [56–58]; for more recent developments we refer to Kramer et al. [1]. The macroscopic rubber elasticity introduced via the percolating rubbery network interacts with the LC ordering field, which is the basis for the specific properties of LC elastomers. For a low crosslink density, the conformation of the chain segments is not affected and the mesogenic moieties have enough freedom to orient along n. Crosslinking between chains prevents their translational motion (flow) and the polymer melt becomes an elastic solid – a rubber or polymer gel. As a consequence, LC elastomers exhibit resistance to the shape changes under external mechanical stress.

Fig. 5

Representation of an end-on side-chain smectic LC elastomer

Network formation can be induced chemically by copolymerization of polymer chains with a given proportion of reaction positions and bi-, tri-, or multifunctional crosslinking units added to the system. Alternatively, polymerization can be accomplished by addition of a photoinitiator to the system and subsequent exposure to UV light. The size of the crosslinking moieties might be comparable or larger than the constitute mesogenic groups, whereas the linkage can be either stiff (rod-like) or flexible (lengthy terminal alkyl chains). The flexibility of the crosslinker was reported to affect the layer stability in certain side-chain smectic elastomers [7]. Polyacrylate elastomers have low backbone anisotropy and a high glass transition temperature. Methacrylate chains are less flexible, and thus not so sensitive to network formation. The most flexible polysiloxanes form networks with a high elastic response due to the large chain anisotropy, whereas they remain liquid crystalline at room temperature. This explains why the majority of side-chain elastomers synthesized to date utilize siloxane backbones. For main-chain networks, siloxane ring molecules with multifunctional crosslinking positions have been used systematically (see Kramer et al. [1]). However, it is not evident that for such a type of crosslinker all reactive positions are activated. Weak crosslinking of mesogenic polymers appears to have little effect on the range of stability of nematic and smectic phases. However, the elastic properties of the network and the character of long-wavelength excitations of the ordering field depend crucially on whether the LC order was established before or after crosslinking. For example, monodomain nematic elastomers crosslinked in the nematic phase are transparent, indicating suppressed director fluctuations, in contrast to the milky appearance of conventional nematics.

A fundamental question is how many crosslinks are required to transform a polymer melt into a full polymer network (gel) that behaves under external action as a uniform structure. Gelation is a type of connectivity transition that can be described by bond percolation models [59, 60]. Slightly below the transition (gel point c ₀), the system consists of a mixture of polydisperse branched polymers. Slightly beyond the gel point, the situation is still approximately the same, but at least one chain percolates through the entire system. Simultaneously, the system, as a whole, acquires a nonzero static shear modulus (response) [61]. The fully developed network exists far above the percolation threshold c ₀. For a system of long linear precursor chains with a degree of polymerization N ≫ 1 (so-called vulcanization universality class), the mean-field gelation theory predicts c ₀ = 1/(f − 1), where f denotes the functionality of the constituting monomers. The effective functionality of a long chain with N crosslinkable monomers is very large, f ≅ N. Hence, at the threshold value c ₀ = 1/(f − 1) ≅ 1/N ≪ 1 we have on average one crosslink per chain. The end of the gelation regime corresponds to an average of two crosslinks per chain [59, 62]. Moreover, for long precursor chains the number of other chains within their pervaded volume varies, ~N ^1/2, thus guaranteeing sufficient overlap for most of the crosslinking reaction. For LC elastomers, polymer chains with N of 10²–10³ are quite usual, leading to a small threshold density of crosslinks c ₀ ≪ 1. This result is hardly surprising, as, for example, a simple cubic lattice of bonds is known to have a percolation threshold c ₀ ≅ 1–4. For long chains filling space, the majority of bonds are already linked in polymer chains, reducing the crosslinking bonds to minimal numbers. Experimentally, a volume (molar) fraction of mesogenic-like crosslinks of about 4–5% is sufficient to make a mechanically stable LC elastomer sample (see Finkelmann and Kramer [1]).

3.2 Nematic Rubber Elasticity

Let us consider in more detail the elasticity of nematic rubbers, which is at the heart of understanding their specific properties. Consider a weakly crosslinked network with junction points sufficiently well spaced to ensure that the conformational freedom of each chain section is not restricted. We recall that for a conventional isotropic network the stress–strain relation for simple stretching (compression) of a unit cube of material can be derived as [62, 63]:

$$ \sigma = {n_{\text{s}}}{k_{\text{B}}}T\left( {\lambda - \frac{{1}}{{{\lambda^2}}}} \right) = \mu \left( {\lambda - \frac{{1}}{{{\lambda^2}}}} \right){,} $$

(2)

where σ is the mechanical stress, n _s is the average number of individual chain segments (strands) between successive crosslinks per unit volume, k _B is the Boltzmann constant, k _B T is the thermal energy, μ is the rubber modulus, and λ is the extension ratio. Furthermore, μ = n _s k _B T, which is approximately 10⁵–10⁶ N/m². Equation (2) is derived under the assumption that the chain segments obey Gaussian statistics, i.e., the deformations have an affine character and the material is essentially incompressible. The latter condition is satisfied because the energy scale of rubber elastic energies is determined by the characteristic rubber modulus μ, which is about 10⁻⁴ times the bulk compressional modulus (10⁹–10¹⁰ N/m² for polymeric melts). Thus, the entropic effects of rubber elasticity are insignificant compared with the energies required for a volume change, and rubber deformations occur at constant volume. The average density of crosslinks, c, is proportional to the number of chain segments, n _s, and inversely proportional to the functionality of the crosslink f (the number of chains emanating from a junction point) such that c ≅ n _s/f.

An important consequence of (2) is that for σ = constant > 0, as the temperature increases, the magnitude of λ diminishes, i.e., the rubber is compressed upon heating and expands upon cooling (opposite to gas behavior). This is a direct consequence of the entropic origin of the elasticity of the polymer networks. The effects of changing external conditions (in the above example, temperature) have been systematically studied for classical isotropic elastomers. As we shall see, even more dramatic effects from a heating–cooling cycle or photo-actuation are emerging for nematic elastomers.

The difference between nematic and isotropic elastomers is simply the molecular shape anisotropy induced by the LC order, as discussed in Sect. 2. The simplest approach to nematic rubber elasticity is an extension of classical molecular rubber elasticity using the so-called neo-classical Gaussian chain model [64]; see also Warner and Terentjev [4] for a detailed presentation. Imagine an elastomer formed in the isotropic phase and characterized by a scalar step length l ₀. After cooling down to a monodomain nematic state, the chains obtain an anisotropic shape described by the step lengths tensor l _ij . For this case the stress–strain relation can be written as:

$$ \sigma = \mu \left( {\lambda \frac{{{l_0}}}{{{l_{/\!\!/}}}} - \frac{1}{{{\lambda^2}}}\frac{{{l_0}}}{{{l_\bot }}}} \right). $$

(3)

Equation (3) is close to the expression for a classical elastomer undergoing uniaxial extension. However, instead of an overall pre-factor accounting for the change in chain size, separate factors l ₀/l _// and l ₀/l _⊥ occur for the parallel and perpendicular directions, respectively. Now in the absence of external stress, σ = 0, the system will show spontaneous extension [4, 65]:

$$ {\lambda_{\text{m}}} = {({l_{/\!\!/}}/{l_\bot })^{{1}/{3}}}. $$

(4)

We conclude that upon cooling from the isotropic to the nematic phase, there must be a spontaneous uniaxial elongation λ _m providing possibilities for temperature-controlled actuation. The overall distortion must be volume preserving. In this example we assumed the chain conformation to be prolate. If, by contrast, the chain backbone was flattened in the nematic phase to an oblate shape, l _///l _⊥ < 1, then upon entering the nematic phase a contraction would be observed, λ _m < 1. The spontaneous distortion λ _m = (l _///l _⊥)^1/3 at the isotropic to nematic transition is the most essential result of neo-classical rubber elasticity. For Gaussian chains it provides a direct measure of backbone anisotropy at the given conditions. The step length ratio can be deduced from thermal expansion experiments, ${l_{/\!/}}/{l_\bot } = \lambda_{\text{m}}^3$, and compared with data from SANS measurements of selectively deuterated chains.

As an example, we consider oriented samples of side-chain polysiloxane nematic elastomers [66] that show spontaneous elongations up to λ _m = 1.6 upon cooling through the clearing point (Fig. 6). This corresponds to a rather large step length anisotropy l _///l _⊥ = (R _g///R _g⊥)² = λ ³_m of about 4. The shape change occurs not just at transition but continues to lower temperatures as the orientational order parameter S(T) gets larger and the backbone anisotropy increases. One can simultaneously measure the thermal distortion along the nematic director n and the variation of the orientational order parameter, which show a close correspondence [66, 67]. The step length anisotropy is in general a function of S(T), satisfying the linear limit (l _///l _⊥) − 1 ≅ αS at small S [4]. In main-chain elastomers, the orientational order corresponds directly to the backbone; α ≅ 3 for a model of freely joint chains. However, for the side-chain elastomers of the end-on type, the values of α are much smaller (α ≤ 0.5) and can even take small negative values.

Fig. 6

Spontaneous distortion, λ, and optical anisotropy, Δn, of an elastomer as a function of temperature at a fixed external stress of 4 mN/mm² [66]

Not surprisingly, oriented samples of nematic elastomers composed fully or partly of main-chain polymers show the strongest shape anisotropy [68] of up to 400%. From λ _m = 4 = (l _///l _⊥)^1/3, we arrive at a ratio of the radii of gyration R _g///R _g⊥ = (l _///l _⊥)^1/2 = λ ^3/2_m of about 8. This number is consistent with the characteristic values quoted above for main-chain polymers (Sect. 2.3). Such materials are a prime candidate for use as artificial muscles or mechanical actuators. These examples correspond to a prolate backbone anisotropy, which translates into a spontaneous elongation along n. The case of an oblate structure is much less common but has been observed in some side-chain nematic elastomers [53, 54, 69, 70].

To summarize this section, we note that the orientational order in nematic elastomers induces a chain anisotropy, which in turn determines the macroscopic shape of the sample. The manipulation of these shape spheroids by temperature and by electrical, mechanical, and optical fields is at the origin of many of the effects observed in these materials. Obviously this requires oriented monodomain samples, which will now be discussed in some detail.

3.3 Monodomain “Single Crystal” Nematic Elastomers

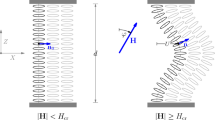
Without special precautions, nematic elastomers form nonuniform polydomain textures during fabrication. As a result, such a sample is opaque due to strong light scattering by disoriented domains. Over the years many attempts, stimulated by the analogy with the conventional liquid crystals, have been made to align polydomain nematic elastomers with magnetic or electric fields. These attempts proved to be unsuccessful, leading to the conclusion that the fields are too weak to cause any significant re-alignment. Under these conditions, mechanical stretching is the only remaining appropriate external field. Alignment of a polydomain elastomer by stretching is readily observed with the naked eye: after a certain degree of extension the initially opaque sample becomes clear and fully transparent [52]. The threshold stress, σ _c, is small, of the order of 10⁴ N/m². The optical transparency of monodomain elastomer samples is rather perfect, in contrast to aligned samples of low-molecular-mass nematics that are still turbid due to thermal director fluctuations. However, for elastomers, n is anchored to the rubbery matrix and the director fluctuations are suppressed. This observation gives a hint as to why application of electric or magnetic fields is insufficient to orient nematic elastomers. The field acts on the highly polarizable mesogenic cores and its influence is amplified by the cooperative nature of the long-range orientational order. However, in elastomers the nematic cooperative factor is limited by the net size (4–5 nm) and, compared to low-molecular-mass nematics, much larger electric (magnetic) fields are needed to align the director. In a typical rubber, the average distance between crosslinks is small. Using the characteristic value of the rubber modulus μ = n _s k _B T ≅ 10⁵ N/m² at room temperature (k _B T ≅ 4 × 10⁻²¹ J), the average separation is n ^−1/3_s  ≅ 4 nm. Mechanical fields act directly on the polymer network as a whole, and thus the reorientation of the mesogenic cores linked to the backbones is much easier than by electric or magnetic fields.

A small mechanical strain, ε = λ − 1 ≅ 10%, acting directly on the polymer backbones, is enough to align the mesogenic cores. These then can be crosslinked to create a highly ordered elastomer monodomain. A very successful procedure along these lines is the two-step crosslinking process by Kupfer and Finkelmann [71, 72], who developed an important yet simple technique for making so-called liquid single crystal elastomers (LSCE). Chains are first lightly crosslinked in the isotropic swollen state. These are then stretched in a uniaxial fashion and the solvent is slowly removed while a second crosslinking proceeds in the aligned nematic state. After this reaction is complete, the stress is removed and the system becomes a clear monodomain. Its stability is remarkable, even after heating to the isotropic phase and cooling back down to the nematic state. Hence, the overall director orientation is “imprinted” by the second crosslinking step, which provides the required memory. Depending on whether the final crosslinking is done in the isotropic or the nematic phase, the material emerging has different properties. In particular, when the crosslinking is done in the nematic phase, this information is fixed in the vicinity of the crosslinking points leading to “frozen-in” orientational order. Some variants of preparing monodomain nematic elastomers combining crosslinking with the mechanical stretching have also been reported [73].

An alternative strategy for producing well-oriented nematic elastomer samples makes use of polymeric liquid crystals containing a photo-initiator. First, a uniform nematic orientation is obtained using standard means like an aligned polyimide substrate or a magnetic field, which is subsequently fixed by photocrosslinking using UV radiation. An overview of these methods is given by Ohm et al. [5]. Recent measurements of the complex shear modulus of aligned samples prepared by photocrosslinking indicate that the polymer strands possess Gaussian statistics [74]. By contrast, elastomer samples prepared by the two-step crosslinking process are more stretched. In the latter case, the chain segments show deviations from a Gaussian distribution. Though these results need further confirmation, they do question the applicability of linear nematic rubber elasticity (based on Gaussian statistics) to elastomer samples prepared by stretching in the nematic phase.

The equilibrium elastic properties of monodomain nematic rubbers have been well studied, both theoretically and experimentally [4, 75, 76]. Of fundamental interest is the relative rotation of the two subsystems, the mesogenic parts and the network [77], which plays a crucial role in understanding the response of nematic elastomers to external fields. In low-molecular-mass nematics, the internal orientational degrees of freedom are determined by the director field n(r). Any distortion of the director field is energetically unfavorable and is penalized by the Frank elastic energy density, K(▽n)². In nematic networks, the antisymmetric part of the strain is also present, expressed by the local rotation vector of the network Ω(r). It contributes to the total elastic energy F when Ω deviates from the director rotation vector ω = [n × δ n], leading to ΔF ~ D ₁[n × (Ω − ω)]². Model expressions for elastomer elastic constants show, apart from the rubber elastic energy μ = n _s k _B T, a dependence on the backbone step lengths anisotropy D ₁ ~ μ(l _///l _⊥ − 1)². Quite naturally, the effects of the relative network rotations become insignificant if the elastomer anisotropy diminishes. Thus, a deviation of Ω from ω costs energy, and this relative rotation is at the origin of a number of unique orientational effects in nematic elastomers.

Director reorientation in monodomain nematic elastomers by an external stress perpendicular to n leads to an extraordinary phenomenon [71, 72, 78]. For intermediate strain values, a shape change costs very little energy. In the stress–strain diagram a plateau region is observed with a very small slope close to zero. Qualitatively the system behaves as if the deformation energy is compensated by the anisotropic reshaping of the backbone coil. This phenomenon has been interpreted as “soft” or “semi-soft” elasticity [79–81]. Consider a nematic network with its director initially oriented along the z-axis. The sample is first subjected to large stretching in the perpendicular x-direction, and then to a slight xz-shear. Using symmetry arguments, coupling of director rotation to the strain leads to zeros in the shear modulus when the large initial stretching takes the elastomer to the onset or end of director rotation. Recent dynamic light-scattering experiments indeed demonstrate that the onset of the semi-soft plateau is associated with a dynamic soft mode [82]. With increasing strain perpendicular to the director, the relaxation rate of the nematic director fluctuations decreases to a very small value at the onset of the soft elastic response. At this point the director becomes unstable and starts to rotate. An alternative explanation of the above phenomenon has been given on the basis of the macroscopic dynamics of nematic elastomers in the nonlinear regime [76, 83].

3.4 Nematic–Isotropic Transition

Phase transitions in liquid crystals have long been attractive for the general physics community because of the wealth of symmetry-breaking scenarios enabling tests of modern theories of phase transition (see [84] and references therein). The presence of a polymer network in nematic elastomers brings truly new aspects to this seemingly well-known area. First, there is a large spontaneous shape change associated with the nematic–isotropic (N–I) transition in monodomain LC elastomers. Second, the N–I transition no longer exists in the LSCEs prepared according to the two-step crosslinking process (Sect. 3.3) once the concentration of crosslinks exceeds a certain number. According to the experiments of Cordoyiannis et al. [85], this number corresponds to a fraction of about 12% of active groups of the polymer backbone. In analogy to the usual gas–liquid critical point, the N–I transition in such a LSCE is “beyond the critical point”, i.e., in the supercritical region where no difference between nematic and isotropic phases exists. In low-molecular-mass liquid crystals and in LC polymers, this transition is first order with a jump of the orientational order parameter S(T) and the entropy Σ(T) at the clearing temperature T _NI. During the last two decades, experiments on various types of LC elastomers showed that both S(T) and the spontaneous strain change smoothly at N–I transition, with no visible first-order discontinuity [86, 87]. Such a behavior could be due either to a strong degree of spatial heterogeneity in the system [88] or to a supercritical character of the N–I transition [89]. Only recently have precise NMR and specific heat measurements revealed a small latent heat and a subtle discontinuity at N–I transition in side-chain LSCEs with a small crosslink density [85]. On increasing the crosslink density, the predominantly first-order N–I transition transforms into a supercritical transition. These data suggest that the critical properties of the N–I transition in LSCEs can be modified by varying the concentration of the crosslinks (Fig. 7). Recently, deuteron NMR and AC calorimetry have been used to also characterize both the orientational dynamics and the N–I transition in main-chain nematic elastomers [90]. Similarly to side-chain LC networks, the N–I transition in main-chain monodomain nematic elastomers shifts from first order to the critical and even to the supercritical regime on increasing the crosslinking density.

Fig. 7

Orientational order parameter of a nematic main-chain elastomer from D-NMR around the N–I transition for different crosslink concentrations x [90]

The origin of the observed behavior is quite clear: internal stress (independently of its origin) shifts the first-order N–I transition towards the critical point and further into the supercritical regime, characterized by zero latent heat and a continuous S(T) profile. The necessary condition is a linear coupling of the nematic order parameter S with a conjugate field σ that adds a term ~–σS to the free-energy expansion in the vicinity of the phase transition point [91]. The transition to a supercritical domain occurs whenever σ exceeds the critical value σ _c. In nematic elastomers, σ is the mechanical stress that may be associated with the monodomain state, imprinted internally in the system through the pattern of crosslinks. It could also come from an external field applied to the sample. Another important source of the nonuniform stress in the sample is due to random quenched disorder. In practice, crosslinking agents are always anisotropic and frequently made of fragments that are mesogenic themselves. Thus, one can always identify the direction of anisotropy, which is quenched because the crosslinks are not totally free to rotate under thermal motion [92, 93]. As a result, there is a local preferred direction of orientational and spatial order that acts as a random orienting (and pinning) field. For a more quantitative discussion of the N–I transition we refer to Lebar et al. [94].

From the discussion so far, the natural question arises whether it is possible to create an ideal nematic network without internal stress, in which the orientational order relaxes to zero at high temperatures in the isotropic phase. The actual answer is no, because in any case the random quenched disorder, introduced by crosslinks, is expected to affect the transition. Although the crosslinks are on average randomly functionalized into the polymer backbone, local variations in their density and orientation lead to quenched randomness. This will manifest itself macroscopically as a mechanical random field that induces smearing of the phase transition. Theory predicts different regimes of the N–I transition affected by quenched disorder [93]. The scalar order parameter S is predicted to be homogeneous in space, whereas the director n follows equilibrium randomly quenched texture with a characteristic size typical for elastomer domains. Depending on the strength of the disorder, one may still see the first-order transition or a continuous-like transition with no phase coexistence. In this situation the thermomechanical history of the samples will be of crucial importance. The same is true for smectic elastomers, in which the phase of the density wave can be locked-in by the random field of crosslinks. These latter effects of a random field on phase transitions are considered in more detail in Secs. 4.2 and 5.

4 Order and Disorder in Smectic Systems

4.1 Landau–Peierls Instability

In a 3D crystal, the molecules vibrate around well-defined lattice positions with an amplitude that is small compared to the lattice spacing. As the dimensionality is decreased, fluctuations become increasingly important. Landau and Peierls [95, 96] were the first to show that translational order is destroyed in 1D and 2D systems by thermal fluctuations (see also, for example, [84]). In 3D space, similar arguments can be applied to systems of stacked fluid monolayers such as smectic-A monomeric or polymeric liquid crystals, surfactant membranes, and lamellar block copolymers. In such structures translation of a layer along the z-axis represents a 1D periodicity in a 3D medium with a typical period of 2–3 nm for thermotropic smectics. Elastic deformations in smectics are governed by the Landau–De Gennes free energy that involves two elastic modes: undulation and compression of the layers (see, for example, [97]). The first mode is characterized by the splay elastic modulus K (typically 10⁻¹¹ N). The second constant B (typically 10⁷ N/m²) involves compression/dilatation of the layers. Fluctuations of the layers are described by the displacement field u(r) = u _z(r _⊥, z), which characterizes the layer displacements along the layer normal in dependence of the in-plane position r _⊥. It is noteworthy that a conventional smectic with liquid layers has no resistance to shear, and a term [▽_⊥ u(r)]² is not allowed in the deformation energy. In the full spectrum of the layer displacement modes, from long wavelengths to molecular sizes, the long-wavelength fluctuations dominate. This can be understood from the observation that a uniform rotation of the layers (corresponding to infinite wavelength) does not require any energy. In the harmonic approximation, the equipartition theorem gives for each mode of the layer displacement u(q) the mean square value:

$$ \left\langle {{u^2}({\mathbf{q}})} \right\rangle = \frac{{{k_{\text{B}}}T}}{{Bq_z^2 + Kq_\bot^4}}. $$

(5)

Integrating over the full spectrum of displacement modes leads to a mean square layer displacement $\left\langle {{u^2}(r)} \right\rangle$ given by (see, for example, [14]):

$$ \left\langle {{u^2}(r)} \right\rangle = \frac{{{k_{\text{B}}}T}}{{8 \pi }}\sqrt {{KB}}\ln \left( {\frac{L}{d}} \right). $$

(6)

The weak logarithmic divergence with the sample size L is known as the Landau–Peierls instability. As a result, for sufficiently large L the fluctuations become of the order of the layer spacing, which means that the layer structure would be wiped out. However, for samples in the millimolar range and typical values of the elastic moduli K ≈ 10⁻¹¹ N and B ≈ 10⁷ N/m², the layer displacement amplitude $\sigma = \sqrt {{\left\langle {{u^2}} \right\rangle }}$ does not exceed 0.5–0.7 nm. For a typical smectic period d ≈ 3 nm this gives relative displacements σ/d ≈ 0.2; the smectic layers are still well defined. Nevertheless, the displacements are large compared to those of a typical 3D crystal for which:

$$ \left\langle {{u^2}(r)} \right\rangle = \frac{{{k_{\text{B}}}T}}{{{{\pi }}aC}}. $$

(7)

For a typical value of the elastic modulus C = 10¹⁰ N/m² and a lattice size a = 0.5 nm, this leads to σ ≈ 0.02 nm and σ/d ≈ 0.04.

The pair density correlation function – the quantity essentially measured in an X-ray experiment – is defined as:

$$ G({\mathbf{r}}) = \left\langle {\rho ({\mathbf{r}})\rho (0)} \right\rangle - \left\langle {\rho ({\mathbf{r}})} \right\rangle \left\langle {\rho (0)} \right\rangle, $$

(8)

where the brackets indicate an average. As a result of the Landau–Peierls instability the correlation function shows a slow algebraic decay G(r) ~ r ^−η. Writing q ₀ = 2π/d, the exponent η is given by:

$$ \eta = \frac{{q_0^2{k_{\text{B}}}T}}{{8{{\pi }}\sqrt {{KB}} }}. $$

(9)

The resulting order is referred to as quasi-long-range order. It provides a marginal case between true long-range positional order and short-range order. These various types of order are illustrated in Fig. 8.

Fig. 8

Representation of correlation function, G(r), and X-ray intensity, I(q), for long-range order, algebraically decaying quasi-long-range order, and short-range order

The scattered intensity I(q) is proportional to the structure factor S(q), the Fourier transform of the correlation function G(r), and thus reflects the nature of the correlations in the system. In the case of long-range order, the correlation function G(r) remains constant as r→∞. As a result, the Bragg reflections are nominally delta functions, S(q) ~ δ(q − q _n ) at each reciprocal lattice vector q _n , accompanied by weak tails of thermal diffuse scattering ~(q − q _n )^–2 (Fig. 8, upper graphs). In practice, the central part of the X-ray peak takes the form of a Gaussian due to the finite size of the ordered domains (grains) and/or the resolution of the setup. Short-range order is represented by an exponentially decaying function G(r) ~ exp(−r/ξ), in which ξ is the correlation length. The resulting lineshape is a Lorentzian (Fig. 8, lower graphs).

Algebraically decaying order in smectics can be revealed by X-ray diffraction (Fig. 8, middle graphs). The scattering from the smectic density modulation produces X-ray peaks in reciprocal space along the layer normal at a scattering vector q _n  = nq ₀, n being an integer. As shown by Caillé [98, 99], the algebraic decay of the positional correlations transforms the discrete set of Bragg peaks into the power-law singularities of the form:

$$ S({q_\bot } = 0,{q_z}) \propto {({q_z} - {q_n})^{ - 2 + {\eta_n}}}, $$

(10a)

$$ S({q_\bot },{q_z} = {q_n}) \propto q_\bot^{ - 4 + 2{\eta_n}}, $$

(10b)

in which;

$$ {\eta_n} = {n^2}\eta, $$

(11)

with η given by (11). This type of lineshape was first reported for low-molecular-mass smectics by Als-Nielsen et al. [100] and then confirmed for various thermotropic [101, 102] and lyotropic lamellar phases [103–105], smectic polymers [106], and lamellar block copolymers [107]. There are a finite number of power-law peaks of the type of (10a): when η _n  > 2 the exponent changes sign and the singularities are replaced by cusp-like peaks. For thermotropic low-molecular-mass smectics, η is small and positive, typically 0.05–0.1 deep in the smectic-A phase. Equation (9) indicates that for less-compressible materials (B large), such as lyotropic smectics and some polymers, η can be even smaller. On the other hand, close to a smectic–nematic transition B can decrease strongly and η might be an order of magnitude larger. When several higher harmonics are present, the quasi-long-range order can be established unambiguously from the scaling relation η _n  = n ² η.

Algebraic decaying order is demonstrated in Fig. 9 for a typical smectic elastomer. In a double-logarithmic plot with q _z − q _n still on the x-axis, the characteristic features are a central plateau-like region at small deviations from q _n due to the finite size of the smectic domains, and a power-law behavior in the tails. The latter regions fulfill the scaling law η _n /n ² = η = 0.16 ± 0.02, providing a rigorous proof of algebraic decay.

Fig. 9

Three orders of lineshape for the elastomer depicted in Fig. 11 with 10% crosslinks. The wings of the peaks (shown logarithmically for emphasis on the right) indicate algebraic decay following ${(q - {q_n})^{ - (2 - {\eta_n})}}$ (straight lines) [7]

The various contributions to the X-ray intensity distribution in the vicinity of the Bragg position in smectics have been outlined by Kaganer et al. [102]. Additionally to the finite size of the system, the effects of the mosaic distribution (distribution of the layer normals within the illuminated area) have to be taken into account. At large deviations from q _n we can find the power-law due to the algebraic decay of positional correlations leading to ${({q_z} - {q_n})^{ - 2 + {\eta_n}}}$. At smaller distances from q _n the effect of the mosaic distribution gradually takes over, approximating finally to behavior like ${({q_z} - {q_n})^{ - 1 + {\eta_n}}}$. The central part, including the full-width-at-half-maximum (FWHM), is determined by the residual Bragg peak due to finite-size domains of the sample [99, 108]. The intensity measured in the X-ray experiment can be represented by the convolution of the various factors mentioned [102]:

$$ I({\mathbf{q}}) = S({\mathbf{q}}) \otimes F({\mathbf{q}}) \otimes H({\mathbf{q}}) \otimes R({\mathbf{q}}). $$

(12)

F(q) and H(q) stand for the broadening due to the mosaic distribution and due the finite size, respectively, while R(q) describes the resolution function of the setup. Deconvolution of the experimental data provides the required determination of the structure factor S(q).

4.2 Random Disorder

In condensed matter physics, the effects of disorder, defects, and impurities are relevant for many materials properties; hence their understanding is of utmost importance. The effects of randomness and disorder can be dramatic and have been investigated for a variety of systems covering a wide field of complex phenomena [109]. Examples include the pinning of an Abrikosov flux vortex lattice by impurities in superconductors [110], disorder in Ising magnets [111], superfluid transitions of He³ in a porous medium [112], and phase transitions in randomly confined smectic liquid crystals [113, 114].

Liquid crystals provide beautiful possibilities to study the structural and dynamic effects of quenched disorder. Their algebraic decay of positional correlations gives an interesting starting point, they are experimentally easily accessible, and can be confined within appropriate random porous media. Liquid crystals have been incorporated into the connected void space of an aerogel, which is a highly porous (up to 98% void) fractal-like network of multiply connected filaments of aggregated 3–5-nm diameter silica spheres. Alternatively, quenched disorder can be introduced in a liquid crystal by dispersing a hydrophilic aerosil (nanosize silica particles forming a hydrogen-bonded thiotropic gel). Both methods allow the study of the effects of weak random point forces and torques on the LC order, an idealized disordering mechanism that affects molecular location and orientation in random ways but occupies little physical space. Even at very low density of aerogel or aerosil (about 1–3%), the 1D smectic order is destroyed, in agreement with general theoretical predictions that generic quenched disorder should do so, no matter how weak [115, 116]. More precisely, if the nematic–smectic phase transition is approached from above, the smectic correlation length does not diverge any more as observed normally, but instead reaches a finite value. Upon cooling through the smectic phase this value saturates at a length scale of the order of 100 nm providing “extended short-range order” [113, 114, 117–119] (see Fig. 10). Note that the correlation length is not limited by some sort of effective “pore size” as if the system has simply been broken up in small pieces. It is rather a result of competition between the randomizing effect of the confinement and the smectic elasticity.

Fig. 10

X-ray correlation length, ξ, for the smectic layer order around the nematic–smectic-A transition (solid vertical line) for liquid crystal 8CB confined in 10% aerogels (after [120])

Ordering effects and phase transitions in imperfect crystals are strongly influenced by the types of defects and their mobility (see, for example, [121]). If point defects have a high enough mobility to adjust (rearrange) to changing long-range order, their presence has no qualitative effect on the large-scale properties of the medium. Such weak “annealed disorder” causes only a finite renormalization of the effective parameters of the ordered state, and the phase transition to a less-ordered state remains sharp. In the case of “quenched disorder” the positions of the impurities are fixed in space and time and they produce a much stronger effect. Their effective field is linearly related to the order parameter and violates the symmetry of the ordered state. Under these conditions, defects can destroy the long-range-order in a 3D crystal, leading to a disordered state. Even weak quenched disorder destroys translational order below four dimensions, resulting in exponentially decaying positional correlations [122]. Under certain conditions a continuous transition can occur to a state with the peculiar property of being a glass with many metastable states and at the same time showing Bragg peaks as in conventional crystals – a so-called Bragg glass [123].

Radzihovsky and Toner [115, 116] studied smectic LC in a random environment, e.g., aerogels, in the framework of the classical Landau–De Gennes model. They introduced additional terms describing a linear coupling of random potentials g(r) and V(r), with the nematic director n(r) and smectic order parameter ψ(r), respectively. Analysis of this model identifies two sources of disorder: layer displacement disorder, which represents the tendency of the aerogel to force the smectic layers to particular positions, and orientational (or tilt) disorder, reflecting the inclination of the aerogel to promote particular orientations of the director (and thus of smectic layers). The disorder leads to short-range smectic correlations that fall off exponentially in the direction of the layer normal: $\left\langle {\psi (0)\psi (r)} \right\rangle \propto \exp (r/\xi )$. This should happen even for arbitrarily weak quenched disorder (i.e., arbitrarily low aerogel or aerosil density), in agreement with the diffuse character of the X-ray scattering from the smectic layers in these dispersions [113, 114, 117, 118, 124] (see also Fig. 10). Another theoretical prediction is that a disordered smectic should possess an anomalous length-scale dependence of the elastic moduli. Furthermore, for weak disorder and a certain range of renormalized elastic constants, a sharp phase transition can occur to an orientationally ordered (but elastically distorted) smectic Bragg glass phase. Experimentally, for smectics confined in aerogels the glass-like dynamics and anomalous elasticity observed upon decreasing temperature suggest the presence of such a smectic Bragg glass [113]. However, somewhat surprisingly, such a behavior was not found in aerosils [114], which impose a more gentle distortion of the smectic than aerogels.

In the framework presented so far, the structure factor for X-ray scattering in a randomly disordered system can be written as:

$$ S(q) \propto \frac{{{B_{\text{thermal}}}}}{{{1} + \xi_{/\!/}^2({q_z} - {q_0}) + \xi_\bot^2q_\bot^2}} + \frac{{{C_{\text{disorder}}}}}{{{{{[1} + \xi_{/\!/}^2({q_z} - {q_0}) + \xi_\bot^2q_\bot^2]}^2}}}. $$

(13)

Here, the Lorentzian term represents the (dynamic) thermal layer fluctuations, and the square Lorentzian the (static) variations in the smectic order due to quenched random field. The correlation lengths ξ _⇓ and ξ _⊥ describe the extent of local smectic order parallel and perpendicular to n, respectively. Equation (13) arrives naturally from the theory of Radzihovsky and Toner [116] but also describes the short-range correlations induced by the quenched disorder in random field Ising magnets [111]. For smectics confined to aerogels, the smectic quasi-long-range order is clearly suppressed by the presence of the last term, which becomes dominant at lower temperatures. However, the situation is less clear for the aerosil networks that are gentler in introducing disorder due to their weaker hydrogen bonding. The latter property could lead to some compliance of an aerosil gel to the smectic elasticity, resulting in partial annealing of the disorder [125, 126]. In the disordered smectic phase, recent studies of smectics confined in an aligned colloidal aerosil gel reveal finite-size domains and power-law tails of diffuse scattering at low temperatures [119]. This situation bridges the gap between smectics confined in aerosils and smectic elastomer networks in which the quasi-long-range translational order survives up to certain concentration of crosslinks [7, 127].

4.3 Fluctuations and Disorder in Smectic Elastomers

In Fig. 1 we summarized the various ways in which LC order and polymer properties can be combined by attaching mesogenic molecules to, or incorporating in, a polymer backbone. Once the backbone polymer is weakly crosslinked to form an elastomer, the resulting macroscopic rubber elasticity interacts with the LC ordering field [4]. In smectic LC elastomers the layers cannot move easily across the crosslinking points where the polymer backbone is attached. Consequently, layer displacement fluctuations are suppressed, which effectively stabilizes the 1D periodic layer structure and could under certain assumptions reinstate true long-range order [128, 129]. On the other hand, the crosslinks provide a random network of defects that could destroy the smectic order [130–132]. Thus, in smectic-A elastomers two opposing tendencies exist: the suppression of layer displacement fluctuations that enhances translational order, and the effect of random disorder that leads to a highly frustrated equilibrium state.

Let us look at the physical origin of the predicted behavior in some more detail. On the continuum level, the coupling between the layer fluctuations and the elastic matrix can be considered as layer pinning by crosslinks, which constitutes a penalty for local relative displacements. This coupling is additive to the ordinary smectic elastic energy of deformations and to the elastic energy of anisotropic rubber network as a whole. The latter contains essentially the five terms expected for a uniaxial solid on the basis of its symmetry. This includes the deformation energy related to the shear elastic moduli perpendicular and parallel to n, C ₄ and C ₅ respectively, that do not come into play for the liquid smectic layers. This is essentially the physical reason for a possible solid-like elastic response in weakly crosslinked smectic elastomers. The rubber elastic constants are renormalized by the smectic fluctuations and acquire effective values for two bulk (compression) and three shear moduli. The renormalization is determined solely by the rubber elastic parameters: shear modulus and coupling constants. This leads to a combination of four small and one large elastic constant (C _i/C ₃ ≪ 1, i = 1, 2, 4, 5), which is very different from conventional solids in which all elastic moduli have about the same large magnitude. A similar situation occurs in the crystal-B phase of liquid crystals (highly anisotropic molecular crystal) in which the Landau–Peierls instability is eliminated due to the presence of a term ${C_4}q_\bot^2$ in the elastic energy. Nevertheless, large layer fluctuations are still found because of the small value of this elastic modulus compared to the other modulii [133, 134].

The expression for the free energy of a smectic elastomer as a function of layer displacements is rather complicated. However, it is relatively easy to study its implications for the two limiting cases, q _z →0 and q _⊥→0, leading to the following dispersion law for the elastomer phonon modes [129]:

$$ {\left\langle {{u^2}({\mathbf{q}})} \right\rangle_\bot } = \frac{{{k_{\text{B}}}T}}{{{B^* }q_z^2 + 2C_5^* q_\bot^2 + 2C_5^{{\text{ef}}f}(q_z^4/q_\bot^2)}}, $$

(14)

in which ${B^* }$ and $C_5^*$ are renormalized bulk compression and shear moduli, respectively. The elastic modes now feature a solid-like elastic energy proportional to an overall squared power of q. Consequently, in smectic-A elastomers, long-range positional order in the direction along layer normal could be reestablished due to the coupling of the smectic order to the rubbery network. This should result in Bragg-type diffraction peaks. Though layer displacement fluctuations are suppressed, they are strong enough to contribute to the thermal diffuse scattering in the vicinity of the Bragg peaks, ~(q − q _n )^–2. The difference from algebraic decay is that the Caillé exponent η now attains the limit η→0. Because η is typically quite small, this makes the discrimination between Caillé lineshapes and thermal diffuse scattering of a true crystal difficult. The best way to discriminate between these two cases is to look at whether the scaling relation of (11) holds for various harmonics of the smectic layer diffraction, like in Fig. 9.

So far, we have assumed that the crosslinks pin the smectic layers at a number of points but do not disturb the smectic density wave. However, a sufficient large density of crosslinks might lead to layer distortions that could destroy the quasi-long-range order of 1D lamellar lattices [130, 131]. The crosslinks are randomly functionalized into the polymer backbone, and local density variations lead to quenched random disorder. This manifests itself as a mechanical random field that disturbs local layer positions and orientations. The effect of crosslinks on the smectic layer structure can be introduced via a corrugated potential that penalizes deviations of crosslinks from the local layer positions [4, 132]:

$$ {F_{\text{random \ field}}} = \gamma \int {c({\mathbf{r}})\psi ({\mathbf{r}})} \cos \{ {q_0}[z - u({\mathbf{r}}) + {v_z}({\mathbf{r}})]\} {\text{d}}{\mathbf{r}}. $$

(15)

In this equation, γ is the interaction strength, c(r) the crosslink concentration, ψ(r) the smectic order parameter, and v _z(r) the relative displacement of the rubber matrix. Witkowski and Terentjev [132] evaluated (15) for $\left| {\psi ({\mathbf{r}})} \right| = 1$, which is valid deep in the smectic phase, i.e., far below the smectic–nematic transition. Using the so-called replica trick, they integrated out the rubbery matrix fluctuations and obtained an effective free-energy density that depends only on the layer displacements u(r). Under the restriction that wave vector components along the layer normal dominate over in-layer components, q _⊥ ≪ q _z, and considering only long-wavelength fluctuations, the authors obtained an expression for the mean-square amplitude of the displacement modes that contains a Lorentzian term and a square Lorentzian term like in (13). Though different coefficients come into play, again the first term corresponds to ordinary thermal fluctuations, modified by the coupling of smectic layering to the rubbery matrix, whereas the second term represents the effect of the random field of crosslinks. However, now the induced short-range order is characterized by a correlation length ξ = (B/2Λ)^1/2, where Λ is a coupling constant determined by the strength of interaction between smectic ordering and rubbery matrix. As Λ depends linearly on the volume density of crosslinks c, the relation between correlation length and crosslink density becomes: ξ ~ c ^−1/2. However, in order to use this proportionality, we have to take the percolation limit of an elastomer into account, i.e., the minimum density of crosslinks, c ₀, needed to form a continuous rubbery network (see also Sect. 3.1). The elastic properties of the material should depend on the excess of crosslinks over this minimum, leading to the proportionality ξ ~ (c − c ₀)^−1/2.

In conclusion, in analogy to the general theory for quenched disordered systems we can expect a transition to disorder in smectic-A elastomers for high-enough crosslink concentrations. However, this analogy might fail because in smectic elastomers the crosslinks are not rigidly “frozen” defects, but consist of flexible chains embedded in the slowly fluctuating elastomer gel. This could make the situation different from, for example, smectics confined to aerogel (or aerosil) networks, though the “softer” aerosil analogy might still be appropriate. Evidently, predictions from general theories of quenched disorder, when applied to LC elastomers, have to be treated with severe care. In the absence of theory for random crosslinks embedded in a fluctuating layered system, no definite predictions for the nature of these disordering effects in an elastomer network can be made.

5 Smectic Elastomers

5.1 “Single Crystal” Smectic Elastomers

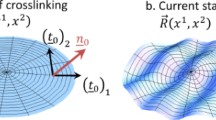
In this section we will review high-resolution X-ray studies of well-aligned smectic elastomer samples. Recently, siloxane samples [7, 127, 135] were studied, prepared by a two-stage process similar to that described in Sect. 3.3 for nematic LSCEs [136, 137]. In the first step, the sample is slightly crosslinked in the isotropic phase while solvent still abundantly present. Subsequently, the solvent is slowly removed with the sample being kept under a uniaxial load. During this process the isotropic sample is thought to pass through a nematic phase and subsequently becomes smectic. In the transient nematic phase, the director is oriented in the direction of the uniaxial stress, which determines the long direction of the sample (smectic layer normal). This orientation is fixed by the second crosslinking step in the smectic phase.

Thermoelastic measurements on such samples reveal a spontaneous elongation along n at the transition to the smectic phase, indicating a prolate polymer backbone conformation in the smectic elastomer [137]. On another hand, SANS results for end-on side-chain polymers in the smectic phase indicate an oblate chain conformation, with the backbone preferentially confined in the plane of the layers (Sect. 2.2). Thus, the chain distribution and macroscopic shape of the smectic elastomer change their sign if crosslinking is made under uniaxial mechanical stress in the isotropic and/or nematic phase. This result is remarkable and indicates that the oblate chain conformation of a smectic end-on polymer can be easily turned into prolate by a low uniaxial extension during solvent evaporation.

When analyzing experimental results, it is important to consider how the smectic elastomer sample was prepared. If the smectic layers are aligned by a surface or an external field and then crosslinked, we can expect the crosslinks to be in registry with the smectic layers and to stabilize the lamellar structure against layer displacement fluctuations. This situation will facilitate the theoretical prediction [128, 129] that translational order can be enhanced and even become a truly long-range order. If the crosslinking is first made in nematic or isotropic phase, then uniaxially alignment is accomplished to form a monodomain nematic elastomer, and only after that cooled down to the smectic phase, the result will be opposite. Though the sample will preserve uniaxial alignment, the layer positions will be frustrated due to random crosslink positioning. In this case, crosslinks provide a random network of defects that could destroy the smectic order [130–132]. The final thermodynamic state of the sample will depend on the relative impact of crosslinking at the first stage and at the final stage when the network is fixed.

Earlier experiments by Wong et al. [138] used a polyacrylate-based side-chain smectic elastomer samples with about 5 mol% crosslinks. In this case, the elastomer sample was prepared via reaction with a crosslinking agent in toluene. Alignment was achieved in situ by stretching by 25% the freely suspended sample in the nematic phase and subsequently cooling into an aligned smectic phase. This situation differs strongly from the method described in the previous paragraph.

There are several other possible ways to prepare well-aligned smectic elastomer samples crosslinked directly in the smectic phase. Low-molecular-weight mesogens are easily aligned by surface forces. Driven by the tendency to minimize the surface energy, smectic membranes (freely suspended smectic films) with a perfect homeotropic alignment are easily formed [134]. Smectic polymer materials are much more viscous than their low-molecular-weight counterparts. Still uniform smectic membranes can be made close to the clearing temperature to the isotropic phase or even above it. After cooling down into the smectic phase, the films can be crosslinked by UV irradiation. Such methods have been used to produce planar films [139–144] and even curved elastomer films in the shape of inflated balloons [145, 146]. However, no high-resolution X-ray work has been performed with these types of sample.

The elastic properties of monodomain smectic elastomers are different from those of nematic elastomers [147]. The stress–strain diagram shows a considerable anisotropy of the elastic moduli. Stretching along the layer normal is associated with a large modulus of ~10⁷ N/m², comparable to the smectic compressional modulus B in low-molecular-mass and polymer smectics. This value is about two orders larger than the modulus in the plane of the layers, which is comparable to the shear modulus μ ~ 10⁵ N/m² characteristic of the isotropic state. These observations indicate that the crosslinks are strongly pinned by smectic layers. As a result, when stretching along the layer normal the crosslinks cannot glide through the layers. The associated modulus is therefore associated with deformation energy of the smectic layers and is not rubbery. The physical reason for the large anisotropy in smectic networks is clear: stretching along the layer normal attempts to change the layer spacing, which is resisted by the smectic ordering. The mechanical field acts on the mesogenic in the smectic layers rather than on the crosslinks responsible for rubber elasticity. Such high elastic anisotropy is unprecedented even in strongly ordered nematic networks. In the latter case, both elastic moduli (parallel and perpendicular to the director) are of the same magnitude [4].

Upon stretching along the layer normal, at relatively small strain on a rubbery scale of about 5–7%, smectic elastomers may break up into stripes leading macroscopically to a cloudy appearance [148]. The striped texture corresponds to a local layer inclination (rotation) relative the average direction of the layer normal. The system prefers the layers to rotate in order to relieve any layer extension deformation in favor of lower-cost rubber distortions at constant layer spacing. This reaction is the rubbery equivalent of the classical instability to avoid layer dilation in low-molecular-mass smectics, described in [149]. However, this type of behavior is not universal because other samples show isotropic rubber behavior [142, 144, 145].

5.2 “End-On” Side-Chain Elastomers

5.2.1 Order at Small Crosslink Concentration

The structure of a series of end-on side-chain polysiloxanes is given in Fig. 11a. This is the only series known at present for which an extensive variation of crosslink concentration c has been realized (c = 5–20%). In addition, the nature of the crosslink has been varied using the flexible crosslink unit V1 and the stiffer V8 (for structures see Fig. 11a). Oriented elastomer samples were obtained through the two-step crosslinking process (Sect. 5.1). The elastomers and polymers were studied in the smectic-A phase at room temperature, well below their smectic–isotropic transition at around 65–75°C (depending on c). The smectic-A phase was identified through a set of sharp (00n) quasi-Bragg peaks along the layer normal at a wave vector q _n and a broad liquid-like peak from the in-plane short-range order (Fig. 11b). The X-ray scattering profiles of the first-order peak are displayed in Fig. 12a for the homopolymer and the elastomer at low c, and in Fig. 12b for higher crosslink concentrations. The FWHM of the quasi-Bragg peaks is not resolution limited, and the central part can be well described by a Gaussian. For the first-order peak of the homopolymer this indicates smectic domains with a finite size along the layer normal, L ≈ 0.6–0.7 μm. Away from the center of the peak, algebraic decay is observed with an exponent η _n /n ² = η = 0.15 ± 0.02, similar to that reported for other smectic polymers [106]. For the elastomer with c = 10%, three harmonics are displayed in Fig. 9. Interestingly, the peak width Δq _z increases approximately linearly with the harmonic number n. In the tails of the peak, algebraic decay is nicely preserved and no evidence of true long-range order is found.

Fig. 11

(a) Structure of the side-chain polymer with two different mesogenic groups (X, Y)=(R1, R2). The corresponding elastomer is obtained by crosslinking with R3, which can be either V1 (flexible) or V8 (rigid). (b) 2D X-ray picture of the non-oriented elastomer

Fig. 12

Comparison of the first-order X-ray peaks of the elastomer of Fig. 11 for (a) low crosslink concentrations and (b) higher crosslink concentrations (after [7, 127])

At small crosslink concentration, the peak width Δq _z of these systems (Fig. 12a) shows a remarkable trend. For c = 5%, the finite size L = 2π/Δq _z of the smectic domains is about five times larger than that of the corresponding homopolymer. At c = 10%, the domain size has decreased somewhat, but is still two times larger than for the homopolymer. Only at 15% is the domain size back at about the homopolymer value. Evidently, the elastomer network initially enhances the stability of the smectic layer structure in the sense that the smectic order extends over larger domains than for the homopolymer. However, no evidence of true long-range order is found, as might follow from theory (Sect. 4.3). There are limited other data with which these results for small or moderate crosslink concentrations can be compared. We investigated a rather different siloxane with fluorinated end groups at the end-on mesogens and 9% crosslink V1. Scaling of η _n over five harmonics provided a rigorous proof of algebraic decay. Variation of the crosslink density led to a trend in the domain size that was qualitatively similar to that described above: the FWHM of the first-order peak changed from about 15 (homopolymer) via 11 (for c = 9%) to 26 millidegrees (for c = 12.5%). The situation in main-chain elastomers will be described in the next section.

Finally, an earlier report by Wong et al. [138] concerned a polyacrylate-based side-chain liquid-crystalline polymer that was about 2–5 mol% crosslinked. Alignment was achieved as described above in Sect. 5.2. They found at the tails of the smectic peaks convincingly had different slopes for the homopolymer (1.85 ± 0.10) and the elastomer (2.40 ± 0.10), as shown in Fig. 13. As algebraic decay leads necessarily to a slope <2, the larger slope for the elastomer was taken as evidence that long-range order was restored. Unfortunately, no higher orders could be measured. Several possibilities can be considered to explain why this behavior is rather different to that just discussed. One could assume that the Caillé limit and the correct exponent had not been reached yet and would turn up at larger offsets in q − q ₀. However, the range of normalized intensity and offset from the center of the peak was very similar to those in Fig. 9, for which algebraic decay was confirmed by the appropriate scaling relation. Nevertheless, we note that for the first-order peak of Fig. 9 the necessary dynamic range was only just reached: for slightly smaller values of q − q ₀, still comparable to those in [138], no correct value of η would have been obtained. Alternatively, one could imagine that the processing of the elastomer influences the resulting order. The uniform siloxane samples discussed above were made via the two-stage crosslink process, the present acrylate system that behaves differently through in situ stretching in the nematic phase. According to the discussion in Sect. 5.1, this should not make a major difference. Finally we mention the possibility that in this case the situation of a topologically ordered XY Bragg glass has been reached (compare [119]). In this case an exponent of 2.45, independent of temperature, has been predicted theoretically and is in good agreement with the present experiment. However, no further details are available to confirm this hypothesis.

Fig. 13

(a) Structure of the polyacrylate-based side-chain LC compound. (b) Comparison of the asymptotic diffraction intensity tails from the crosslinked elastomer (circles; slope –2.40) and the corresponding uncrosslinked homopolymer (triangles; slope –1.85) [138]

5.2.2 Road to Disorder

We return to the siloxane elastomer of Fig. 11 and consider the situation for higher crosslink concentrations (Fig. 12b). For c = 15% crosslink, the domain size is already considerable smaller than for the homopolymer, indicating the end of the range of increased domain sizes due to crosslinking. With increasing c, the transparency of the samples decreases, which is also expressed by a larger mosaic distribution and fewer higher harmonics. Whereas for c = 10% three harmonics are observed (Fig. 9b), for c = 15% only two orders of diffraction occur. Algebraic decay of the positional correlations is still preserved with η ≃ 0.15 ± 0.01 but is partly masked by a substantial broadening of the peak along q _z and by the increased mosaic spread. In Fig. 12b, the remaining first harmonic for c = 20% is compared with those at other crosslink densities. It is strongly broadened both along q _z (domain size about 100 nm) and along q _x (mosaic distribution of the smectic layer normal). In this figure, an additional result is included for 15% of the stiff crosslink V8, which behaves as anticipated for a concentration of the flexible crosslink V1 appreciably larger than 20%. The results for various concentrations of both types of crosslink are summarized in Fig. 14. With increasing concentration of crosslinks above 10%, the disorder gradually takes over, as indicated by (i) broadening of the X-ray peak along the layer normal (Δq _z) and (ii) a crossover of the lineshape from Gaussian to Lorentzian. Though this behavior is consistent with the general predictions for random quenched disorder, it is remarkable that the algebraic decay survives up to rather large crosslink densities of 15%.

Fig. 14

Central part of the first-order diffraction of the elastomer of Fig. 11 for different crosslink concentrations. Dashed line Lorentzian fit (β = 0.5); dotted line Gaussian fit (β = 1); solid line best fit to (16) with β-values of 0.96, 0.66, 0.59, 0.51, 0.44 (from left to right). Note the different horizontal scales [7]

To become more quantitative, we note that various factors contribute to the structure factor in smectics. These include in particular the finite size of the sample and the effects of the mosaic distribution [see (12) in Sect. 4.1]. For the present discussion we shall simplify things somewhat and emphasize (a) the broadening of the central part of the X-ray peak due to the finite size, H(q), and (b) the possible power-law behavior in the tails of the peak. Let us start with the finite-size term. As discussed in some detail by Obraztsov et al. [7], a suitable distribution function to describe the central part of the X-ray peaks is given by:

$$ H(z) = \exp \left[ { - \frac{{{{({\sigma_\beta }z)}^{2\beta }}}}{{2\beta }}} \right]. $$

(16)

This expression gives a Gaussian function for β = 1 and a simple exponential for β = 0.5, leading to a Gaussian and a Lorentzian lineshape, respectively. Equation (16) allows a smooth transition between these cases. The situation 0.5 < β < 1 can be described as a stretched Gaussian or equivalently as a compressed exponential; β < 0.5 corresponds to a stretched exponential. The variation of the central part of the observed lineshapes is illustrated in Fig. 14. In fitting these data, the various lineshapes are constrained to reproduce the correct FWHM. Going from c = 10% via 15% to 20% of crosslink V1, the lineshape changes from approximately Gaussian to close to Lorentzian. This is nicely expressed by the value of the exponent of (13) that varies from β = 0.96 ≈ 1 (pure Gaussian) for c = 10% to close to 0.5 for c = 20%. Most importantly, this trend is continued by the results for the stiff crosslink V8 (Fig. 14). The result for c = 10% of the stiff crosslink V8 is close to the situation for c = 20% of the flexible crosslink V1: a fit with variable β can hardly be distinguished from a pure Lorentzian (β = 0.5). Upon increasing the concentration of V8, the exponent β decreases further down to β = 0.44 for c = 15%, corresponding to a stretched exponential correlation function. At this stage we cannot give a precise interpretation, but we note that a stretched exponential can be related to an average over dimensions varying over a broad range. A compressed exponential (or equivalently a stretched Gaussian) is often in a loose way associated with cooperative behavior (see, for example, [150, 151]). Summarizing, we encounter a gradual transition from well-distinguishable finite-size domains (flexible crosslinks; Gaussian) to an average over a broad range of sizes that leads first to a Lorentzian (large density of flexible crosslinks; medium density of rigid crosslinks) and subsequently to a stretched Lorentzian (large density of rigid crosslinks).

The signature of disorder is, according to the theories of random disorder discussed in Sect. 4.3, a shape of the diffraction profile corresponding to a stretched Gaussian with β ≅ 0.7. This value corresponds approximately to a square Lorentzian [last term of (13)]. For the flexible crosslinker V1, this point is reached for a crosslink concentration of about 15%, which is definitely much larger than predicted theoretically. The stiff crosslinker V8 shows a crossover to disorder at smaller concentrations than V1, providing a better connectivity with theory. Taking the onset of disorder for V8 at 7–8% and a percolation threshold c ₀ ≅ 4%, we arrive at c − c ₀ being approximately equal to 3–4%, in reasonable correspondence with theories of random disorder. Thus, the properties of smectic elastomers with a rigid crosslinker and low-molecular-mass smectics confined within aerosils are rather close to each other. Nevertheless, the quantitative interpretation of the behavior of smectic networks constitutes a major theoretical challenge.

The description of crosslinking in smectic elastomers involves effects arising from internal nonuniform strain. In smectic elastomers prepared according to the two-step crosslinking process, mechanical strain is imprinted in the system during the uniaxial alignment. In smectic networks, crosslinks can generate various types of defect with the associated elastic fields leading to additional stress. Strain-induced broadening of X-ray peaks is well known in various fields, for example, in metals subjected to cold work and in certain semiconductors [121, 152, 153]. Generally, two effects contribute to X-ray peak broadening: the finite size of the crystalline or smectic domains (as discussed above) and nonuniform strain. The strain broadening of a diffraction peak leads approximately to a linear increase of Δq _z with harmonic number n, whereas the size effect does not depend on it. Hence, the measured FWHM can be written as in [154], dropping for convenience the index z:

$$ \Delta q_{\exp }^2 = \Delta q_{\text{size}}^2 + {n^2}\Delta q_\varepsilon^2, $$

(17)

in which Δq _ε is the strain-induced contribution and the instrumental resolution has been disregarded for convenience. Experimentally, the width of the quasi-Bragg peaks along q _z increases about linearly with n in agreement with (17). In a simple harmonic description, the width of the smectic peaks would be the same for all different orders of diffraction. We can in principle separate the two contributions using (17) and obtain an average domain size. However, to obtain a good accuracy several harmonics are needed that are not available for the present elastomers. For that reason, we have attributed the full width of the first-order peaks to finite-size effects, which is only approximately correct.

5.2.3 Smectic-A–Nematic Transition

An interesting extension of the above results is obtained if, in the siloxane system of Fig. 11, the side group R1 is replaced by a nematogenic side group M3. The resulting phase diagram, sketched in Fig. 15, indicates that this provides access to a smectic-A–nematic (SmA–N) phase transition. We have studied the elastomers E70/30 and E60/40 with 30% and 40% of the nematogenic group M3, respectively, and two crosslink concentrations, 5% and 10%. Note that the fully smectic compounds discussed in the previous section would be indicated in this terminology as E100/0. The elastomer E70/30 5% has a stronger smectic tendency than E60/40 5%, as follows from the smaller nematic range, and twice as large a compression modulus B. Both samples with 5% crosslink show a clear SmA–N transition that can be determined precisely from a lineshape analysis as illustrated in Fig. 16a, b for E60/40 5%. In the nematic phase the lineshape is nicely Lorentzian, indicating short-range order characterized by correlation length ξ = 2/Δq _z of the order of 10–100 nm (Fig. 16c). In agreement with the paranematic nature of the stretched monodomain sample (Sect. 3.4), no indication of the phase transition to the isotropic phase is found. In the smectic phase, deviations from a Lorentzian lineshape occur similar to the situation described above for E100/0 at low crosslink concentration. Approximating the central part of the peak by a Gaussian, an average domain size L ≅ 2π/Δq _z of about 500–800 nm is found. Second-order peaks have been observed at room temperature in the smectic phase of both elastomers with 5% crosslinks. These peaks are broadened by a factor of two relative to the first-order peaks, indicating strain-induced broadening as discussed in Sect. 5.2.2. The intensity profile shows power-law behavior at large q – q _n while scaling is nicely obeyed, with a value η = 0.22 ± 0.02 for E60/40 5%.

Fig. 15

Schematic phase diagram for mixing the nematogenic side group M3 into the system of Fig. 11 with X=Y=R2. The two compositions investigated are indicated by vertical lines and designated as E70/30 and E60/40, respectively, where the numbers give the percentage R2/M3. In the same terminology E100/0 stands for the fully smectic elastomer

Fig. 16

Smectic–nematic transition in E60/40 5% as studied with high-resolution X-ray diffraction. Lineshape (a) just below and (b) just above the transition temperature, T _NA, of 52°C. The solid lines are fits to a Lorentzian. (c) Domain size L below T _NA and correlation length ξ from a Lorentzian fit above T _NA. Vertical lines indicate T _NA and T _IN

X-ray results for polymer networks containing 10% crosslinks are shown in Fig. 17. In a wide temperature range around the former SmA–N transition, all lineshapes can be well described by a simple Lorentzian corresponding to a disordered state. For E70/30, the correlation length ξ increases with decreasing temperature continuously from 5 nm to about 50 nm, and then saturates. The latter value corresponds to correlation over about 18 smectic layers. The temperature dependence of ξ as displayed in Fig. 17a shows an inflection point at 61°C. At this point we observed the subtle asymmetry in the X-ray profile, which is related to a small shift of the maximum of the mosaic spread in the sample. We assume that below the singular point E70/30 forms a randomly disordered smectic-like state, with some memory of the distribution of layer normals, that transforms to a nematic state with thermal layer fluctuations only.

Fig. 17

Correlation length vs. temperature from Lorentzian fits to the lineshape of the smectic peak at various temperatures for the samples E70/30 and E60/40 for 10% crosslinks. Vertical lines indicate the original SmA–N and N–I transition temperatures of the corresponding 5% samples

For the more nematogenic compound E60/40 with 10% crosslinks, no inflection point is observed in the curve of ξ(T) (Fig. 17b). Moreover, the saturated value of ξ at low temperatures is about half that for E70/30. ξ(T) behaves as if we are in a “para-smectic” regime of a first-order smectic–isotropic transition and reflects mainly changes associated in S(T) and ψ(T), the orientational and translational order parameters, respectively. Note that in the purely smectic elastomer E100/0, disordering effects of similar strength occurred only at a crosslink concentration of about 20% (Sect. 5.2.2). The smaller value observed in E60/40 can be attributed to its rather soft layer system, due to the wide nematic range and the reduced value of the elastic modulus B. Obviously E70/30, with a larger smectogenic component, represents an intermediate case between E60/40 and the purely smectic elastomer E100/0.

Interpretation of the above results is not straightforward. The overall results of Fig. 17 are reminiscent of the extended short-range layer correlations found in low-molecular-mass smectics confined in random silica aerogels or aerosils (see Sect 4.2 and Fig. 10). In the latter case, the lineshape has been fitted to a combination of a Lorentzian (describing the thermal layer fluctuations) and a squared Lorentzian (describing the effect of random fields), the latter becoming dominant at lower temperatures. It is clear from Fig. 16a that the present smectic elastomer lineshapes could be represented by such a combination of terms. As discussed in Sect. 4.3, short-range order induced by the random crosslinks can be characterized by the correlation length ξ = (B/2Λ)^1/2 ~ [B/2(c − c ₀)]^1/2. Using the data from Fig. 16 and B-values derived from stretching experiments, we can make some estimates. First, at the same crosslink density of 10%, the compression modulus B of E60/40 is about a third of that for E70/30. If the value ξ ≅ 50 nm, characteristic of the low temperature state of E70/30, is divided by √3 we arrive at ξ ≅ 29 nm, which is close to the saturated correlation length ξ ≅ 27 nm of E60/40. Second, a reasonable value of the percolation limit of the present elastomers is c ₀ ≅ 0.04. Then, neglecting a possible temperature dependence of the modulus B, the ratio ξ _5%/ξ _10% should be (6)^1/2 ≅ 2.4. Considering first E70/30, taking ξ _5% ≅ 150 nm (at the transition point to nematic phase) and ξ _10% ≅ 50 nm at low temperatures, we arrive at a ratio ξ _5%/ξ _10% = 3, close to our estimate. However, for E60/40 we find a ratio ξ _5%/ξ _10% ≅ 6, which is too large. This discrepancy could indicate that for E70/30 10% the distortion of the smectic layers at low temperatures is due to random fields, whereas for the more nematogenic E60/40 10% the contribution from thermal disorder is still appreciable.

From the discussion so far we conclude that the available theories of random disorder can describe some important details of the disorder in fully smectic elastomers. The results around the SmA–N transition in elastomers indicate the complex interplay of thermal and random disorder mechanisms. Currently, there is no consistent theory to describe disorder in the SmA–N phase transition region, which constitutes a major theoretical challenge. Upon increasing the crosslink density, the fully smectic compound E100/0 showed a wide lineshape variation from Gaussian via stretched Gaussian to Lorentzian. A stretched Gaussian with β ≅ 0.7 corresponds approximately to a square Lorentzian and thus could indicate the onset of disorder, in agreement with theory. The further evolution might be attributed to increasing dominance of the thermal disorder component.

5.3 “End-On” Main-Chain Elastomers

As mentioned earlier, for end-on main-chain smectic polymers the polymer chains connect the smectic layers. As a result, polymer defects are expected to be directly translated into layer distortions (Fig. 4b–d). This probably offsets any possible influence of damping of the layer fluctuations (potentially leading to increased order) because of the connectivity of the layer structure via the chains. As mentioned already in Sect. 2.3, main-chain polymers and elastomers have little tendency to form a smectic phase. They have been less thoroughly investigated than their side-chain counterparts. X-ray structural information of several main-chain elastomers with about 10% of approximately the same cyclic multifunctional crosslink have been compared with their homopolymer counterparts by De Jeu et al. [155]. As no results are available for other crosslink concentrations, little can be said about the specific contribution of the crosslinks to disorder.

As a typical example, we shall discuss the polymer and elastomer MeHQ, depicted in Fig. 18a. In this system, the rigid mesogenic groups are not only connected by an alkyl chain but also with a short siloxane fragment (chain extender). An overall X-ray view of the elastomer is shown in Fig. 18b and indicates a smectic-C structure with tilted layers. Let us first consider the polymer (MeHQ-pol) in some detail. The high-resolution data shown in Fig. 19a, b for its two harmonics indicate rather broad peaks. In fact, Δq _z varies little for the first and second harmonics. For both harmonics, fitting the wings in the double-logarithmic plot leads to a straight line compatible with η _n /n ² = η = 0.06 ± 0.01. In combination with other examples, we can conclude that for end-on main-chain smectic polymers algebraic decay is maintained within the smectic domains [155]. However, rather unusually for smectic polymers, the overall lineshape can be reasonably well fitted by a Lorentzian with a correlation length ξ that is of the same order for both harmonics. A straightforward interpretation of this Lorentzian as indicating short-range order can be excluded for two reasons. First, the correlation lengths and/or domain sizes are large, of the order of hundreds of nm. More importantly, for short-range order higher harmonics are hardly expected because the width Δq of the successive harmonics increases as n ². This leaves as the most plausible explanation that the Lorentzian lineshape is due to a broad exponential-like distribution of domain sizes in the sample. Such situations have been well documented in powder diffraction (see, for example, [156]). The specific nature of the distribution (as compared to other smectic systems) could arise from the direct coupling between polymer defects and smectic layer correlations typical for main-chain systems only. The first candidates for such defects are hairpins (Fig. 4c) [37, 157, 158]. However, stress–strain experiments on nematic main-chain networks indicate that during the formation of a monodomain sample simple hairpins are probably removed by the mechanical strain and might play only a minor role [68]. On the other hand, this argument does not hold for entangled hairpins as depicted in Fig. 4d. The presence of such defects would be compatible with a plateau in the stress–strain curve. Additionally, chain ends may play a role. Analogous to the situation described for the nematic phase [39], these could also lead to local distortion of the smectic layers (Fig. 4b). In main-chain systems, the polymer chains themselves contribute to the building of the smectic layers. Due to dispersion of the polymer chain length, the layered structure in the direction along layer normal cannot be terminated at any arbitrary place, thus leading to finite-size dispersion. Inside the domains/grains leading to the Lorentzian average, algebraic decaying smectic order still appears to be present.

Fig. 18

(a) Molecular structure of the main-chain smectic polymer MeHQ and the cyclic crosslinker used. (b) X-ray picture of the elastomers MeHQ indicating a smectic-C phase

Fig. 19

First- and second-order peaks of MeHQ-pol (a, b) and MeHQ-el (c, d). Dashed lines Lorentzian fit, solid lines best fit to (15) giving β = 0.61, 0.65, 071 (for a, b, c, respectively) [155]

Next, we come to the corresponding elastomer sample MeHQ-el (Fig. 19c, d). In this case, the domain sizes as measured (tens of nanometers) are appreciably smaller than for the corresponding polymer. The broadening of the smectic peaks with increasing harmonic number n is very similar to that observed for the end-on side-chain elastomer systems discussed in Sect. 3.3. In the latter situation, the broadening was attributed to the internal stress due to the aligning memory of the samples, random disordering effects, and other types of defects generated by the presence of crosslinks. Applying (17) to the present data one finds Δq _size ≈ 0.024 nm^–1, leading to intrinsic average domain size L = 2π/Δq _size ≅ 260 nm, close to the value for the corresponding polymer. Similar results were obtained for the related compound, MC11-el, with an average domain size L ≅ 150 nm. We conclude that main-chain elastomers at a crosslink concentration of about 10% differ from the corresponding polymers, mainly by an excess amount of strain.

Regarding the wings of the elastomer peaks, the situation is somewhat complicated. For MeHQ-el reasonable scaling was found with η = 0.17 from the first harmonic (Fig. 19c) and η = 0.20 from the second-order peak. However, for MC11-el no scaling relation could be established [155]. This does not allow strong conclusions because practical experimental considerations are probably involved at the limit of what could be measured. The intrinsic domain sizes being as small as 200 nm, the question arises whether algebraic decay can survive over such small distances. We speculate that in these small-size domains the internal strain is strong enough to modify the Caillé correlation function. Then, the latter will be multiplied by another correlation function describing correlations of displacements induced by the above-mentioned factors. The resulting power-law asymptotes could very well be different from that predicted by the Caillé function only, and rather ambiguous results could be anticipated from analysis of the wings of the elastomer peaks.

Summarizing, we note that in these main-chain elastomers we did not reach a disordered state as for the siloxane end-on side-chain (Sect. 5.2.2). Although we considered chemically very different mesogenic polymers, all systems involved a rather similar cyclic multifunctional crosslinker at a single concentration of about 10%. We expect from the topology that a point-like multifunctional cyclic crosslinker connecting main-chains would induce less disorder in the smectic polymer matrix than the stiff anisotropic mesogenic-like bifunctional crosslinks used for side-chain elastomers. Evidently there is a need for further study of the role of the crosslink topology, stiffness, and variation of crosslink density to improve our understanding of the disordering processes in main-chain polymer networks.

5.4 “Side-On” Elastomers

Finally, we come to side-on systems (see Fig. 1b, d) in which the preferred direction of the mesogenic groups changes orientation compared to the end-on systems of Fig. 1a, c. Information on these systems is so far very limited. Let us first consider side-on side-chain smectic polymers (Fig. 1b) in which the polymer chains are on average oriented parallel to the smectic layer normal, thus connecting the layers similarly as in main-chain systems. We shall consider the material depicted in Fig. 20a, which has partly fluorinated end groups attached to the mesogenic central core. Figure 20b gives an X-ray overview of the oriented elastomer. Axially, we see two orders of diffraction from smectic layering and equatorially, at wide angles, we see diffuse crescents corresponding to the smectic-A liquid in-plane structure. At angles somewhat smaller than those corresponding to the smectic layers, a full diffuse ring is observed with weak maxima along the equator. This diffuse scattering is also observed for the homopolymer and survives in the isotropic phase. It has been attributed to poorly correlated short-range structures from local concentrations of the fluorinated end groups of the mesogens that “nanosegregate” from the hydrocarbon surroundings. As a result, “pre-existing” disorder is present in this system, which might make it not very typical for the class of side-on side-chain systems. The first-order smectic layer peak can be well described by a Lorentzian with a large correlation length, indicating order of about 20 smectic layers [135]. The width of the second-order peak is between two and three times larger than the first-order peak width, violating the quadratic increase with harmonic number that is expected for simple short-range order. This behavior is very similar to that described above for main-chain systems and is again attributed to a broad exponential-like distribution of domain sizes.

Fig. 20

(a) Molecular structure of the smectic side-chain elastomer with 96% side-on group R1 and 4% crosslinker R2. (b) 2D X-ray picture of the elastomer with the smectic layer peaks visible axially [135]

The described fluorinated compound shows interesting elastic properties [159]. The sample remains fully transparent when stretched either parallel or perpendicular to the director (Sect. 5.1). These results have been correlated with high-resolution X-ray scattering [135]. An increase in the FWHM of the smectic peak found during stretching corresponds to a decrease of the average domain size from the original 180 nm down to about 45 nm at the threshold to plastic deformation. At this level, at which the sample still remains transparent, a transition to a highly disordered nematic-like state occurs. At the highest strain, the X-ray peak reveals a correlation length ξ ≈ 10 nm corresponding to only four smectic layers.

Finally, we come to an example corresponding to the symmetry of Fig. 1d: the side-on main-chain system. Again only one case has been studied in some detail [155, 160]. The structure of this compound (abbreviated as TR5-el) is shown in Fig. 21a. No X-ray data are available for the homopolymer. The X-ray picture of a stretched elastomer sample shows a smectic-A phase with an appreciable number of harmonics (Fig. 21b). However, the combination of the rigid pentaphenyl rod and the flexible siloxane main-chain leads to packing constraints that make the siloxane chains align parallel to the rods (see Fig. 21c). As a result, the appropriate scheme corresponding Fig. 1d (polymer chain perpendicular to smectic layer normal) does not apply. In agreement with the model of Fig. 21c, the high-resolution X-ray lineshape data fit into the general trends described earlier in this section for end-on main-chain elastomer systems.

Fig. 21

(a) Molecular structure of the main-chain smectic system TR5 with pentaphenyl transverse rods. (b) X-ray picture of the smectic-A structure of the elastomer stretched at room temperature. (c) Structural model of the elastomer [160]

6 Conclusions and Outlook

In this review we have discussed ordering and frustration in LC polymer networks. In the first part, we treated the dominant role of the polymer backbone anisotropy in shaping the specific properties of nematic polymers and elastomers. Using results of neutron and X-ray measurements and applying some theoretical models, we have demonstrated how orientational order induces chain anisotropy in nematic polymers, which, in turn, determines their macroscopic shape. In spite of these results there is still need for more extensive information on the anisotropic shape of LC polymers. Such results could provide clues for the application of a greater variety of polymers for crosslinking. Up to now, most elastomer systems use flexible siloxanes as the polymer backbone.

In the second part, we discussed smectic liquid-crystalline systems that show quasi-long-range order of the smectic layers (positional correlations decaying algebraically). In smectic elastomers, the smectic layers cannot move easily across the crosslinking points where the polymer backbone is attached. Consequently, layer displacement fluctuations are suppressed, which can stabilize the periodic layer structure. On the other hand, the crosslinks manifest themselves as a mechanical random field that disturbs local layer positions and orientations. The presence of crosslinks radically alters the positional and orientational order in smectics at large distances. Analysis of the X-ray lineshape of the quasi-Bragg peaks associated with the smectic layering indicates a transition from algebraic decaying order to disorder upon increasing the crosslink density. The broadening of higher harmonics of the X-ray peak points to strong nonuniform strain within the elastomer samples. Also in the case of a smectic–nematic phase transition, the smectic layer order disappears with increasing crosslink density and the transition can no longer be distinguished.

Theoretical studies of a smectic LC in a random environment identify, on short length scales, layer displacement disorder, i.e., the tendency of the random field to force the smectic layers to particular positions. This should provoke disorder of the smectic state even for arbitrarily weak quenched disorder, which has been confirmed in several classical systems. In smectic LC elastomers, the road to disorder seems to be rather universal: algebraically decaying order survives up to high crosslink density, in dependence of the nature of the crosslinks (somewhat stiff or more flexible). This leaves little space for classical quenched random disorder theories. Evidently, crosslinks are not rigidly “frozen” defects, but consist of flexible chains embedded in the slowly fluctuating elastomer gel. The challenge for further theoretical study would be to include flexibility of crosslinks and general conformational freedom of the network.

Most experiments on LC elastomers have so far used “single crystal” elastomers made via the two-step crosslinking process, which involves stretching in the LC state. There is increasing evidence that this situation represents a special thermodynamic state – smectic elastomers made in such a way are well aligned but their layer positions are frustrated due to the random crosslink distribution. Evidently, there is room for experiments on nematic and smectic elastomer samples oriented in different ways, for example by photo-crosslinking. In such a way, any memory of the aligning procedure imprinted in the samples will be avoided (at least partially) and new features of phases and phase transitions could be revealed.