Piecewise Linearity and Spectroscopic Properties from Koopmans-Compliant Functionals

Abstract

Density-functional theory is an extremely powerful and widely used tool for quantum simulations. It reformulates the electronic-structure problem into a functional minimization with respect to the charge density of interacting electrons in an external potential. While exact in principle, it is approximate in practice, and even in its exact form it is meant to reproduce correctly only the total energy and its derivatives, such as forces, phonons, or dielectric properties. Quasiparticle levels are outside the scope of the theory, with the exception of the highest occupied state, since this is given by the derivative of the energy with respect to the number of electrons. A fundamental property of the exact energy functional is that of piecewise linearity at fractional occupations in between integer fillings, but common approximations do not follow such piecewise behavior, leading to a discrepancy between total and partial electron removal energies. Since the former are typically well described, and the latter provide, via Janak’s theorem, orbital energies, this discrepancy leads to a poor comparison between predicted and measured spectroscopic properties. We illustrate here the powerful consequences that arise from imposing the constraint of piecewise linearity to the total energy functional, leading to the emergence of orbital-density-dependent functionals that (1) closely satisfy a generalized Koopmans condition and (2) are able to describe with great accuracy spectroscopic properties.

Graphical Abstract

1 Introduction

Optimizing the performance of materials involves understanding their properties as a function of structure and composition [1]. At the experimental level, some of the most powerful approaches are provided by spectroscopic techniques of increasing time and space resolution. However, as spectroscopy experiments become more detailed, the data they provide become more difficult to interpret. Therefore, computational methods that deliver insight into complex spectroscopic data become critical to characterize complex or novel materials. A number of electronic-structure methods [2] have been developed to address spectroscopic properties. These methods rely on solving the equations of quantum mechanics to capture the interactions of electrons with electromagnetic fields, but, due to the complexity of the many-electron Schrödinger problem, these equations must first be simplified before they can be solved computationally.

To break down this complexity, one general approach aims to map the total energy, in principle an expectation value over the very cumbersome N-electron wave function Ψ(r ₁,r ₂, …,r _N ), onto simpler reduced variables, which encode the properties that are relevant to the physical phenomenon at hand. For instance, if one’s goal is to capture the energy of an electronic system, one can choose the reduced variable to be the ground-state electron density ρ(r). Then there exists a functional whose minimization with respect to ρ(r) yields the exact ground-state density and total energy of the system as a function of the atomic positions. This approach is referred to as density-functional theory (DFT); its proof was first established by Hohenberg and Kohn [3] and then extended to degenerate ground states and open systems using Legendre transform analysis [4, 5]. In addition to the energy, variations of the DFT energy functional with respect to any external variable are also reproduced correctly. As an example, the first derivatives of the DFT energy with respect to atomic coordinates provide atomic forces from which one can extract equilibrium geometries, and its second derivatives provide interatomic force constants, from which one can derive dynamical properties and vibrational spectra. In quantitative terms, existing local and semilocal approximations to density-functional theory enable one to predict vibrational spectra with a typical accuracy of 1–2%, for systems containing hundreds of atoms. Density-functional calculations and related perturbation methods are reviewed in [6, 7].

DFT can also describe changes in energy with respect to the number of particles, and thus provides orbital levels either exactly [8] or accurately for the frontier valence shells [9]. In particular, exact Kohn–Sham (KS) DFT calculations yield the exact highest occupied orbital energies of many-electron systems and provide reasonable approximations to single-electron energies for the other valence states (for a discussion of the subtleties connected to the interpretation of Kohn–Sham eigenvalues see, e.g., [9, 10]). Approximate DFT calculations usually make matters worse, and in general are only poor predictors of electronic spectra, notwithstanding their very good performance in describing the thermodynamic and kinetic properties of molecular systems. For instance, local and semilocal KS-DFT overestimate occupied electron levels and underestimate unoccupied levels, causing band gaps¹ to be systematically underestimated, and thus providing a poor description of charged excitations, where an electron is removed or added to the system, as happens in photoemission experiments. Conversely, time-dependent extensions to DFT (TDDFT) [11, 12] have the power to describe correctly the optical response of materials (i.e., neutral excitations). However, TDDFT calculations based upon adiabatic local and semilocal approximations exhibit severe limitations in describing the optical response of extended systems [13] and in capturing charge-transfer excitations, whereby the absorption of a photon is accompanied by a significant displacement of the excited electrons [14–17].

To overcome these limitations, one approach consists of selecting reduced variables that encode more spectral information. In this vein, methods that rely on the Green’s function G(r,r′,ω) as the central variable (as the quasiparticle GW approximation) have been very successful in predicting electronic spectra [18–23], and their extensions (such as the Bethe–Salpeter equation) have provided reliable optical spectra [13, 24–27]. Likewise, electronic-structure approaches that rely on the one-body density matrix γ(r,r′) (the reduced density matrix functional theory) have shown great promise [28–31]. Nevertheless, due to the simplicity of DFT and the extensive experience gained over decades in building more predictive density functionals, the DFT approach remains conceptually and computationally appealing [32]. Hence, it is of interest to develop better approximations beyond conventional local and semilocal methods. To this end, successful hybrid DFT functionals, which include a fraction of Hartree–Fock exchange in a simple linear-admixture or more sophisticated range-separated fashion, have been developed [33, 34]. The state-of-the-art of these methods is reviewed in [35] and other extensions have recently been proposed [36, 37].

In this work we review another route towards more accurate and efficient DFT or beyond-DFT methods. These functionals are obtained by imposing the condition of piecewise linearity for the energy into existing local and semilocal functionals, generalizing earlier suggestions for determining the strength of Hubbard corrections to DFT [38, 39] and correcting for self-interaction in DFT [40] beyond the case of localized d and f manifolds. The resulting functionals become orbital-density-dependent, but retain the conceptual simplicity of conventional DFT approximations while restoring important conditions connected to the description of electronic spectra, namely, the Koopmans compliance of orbital energies. The review is organized as follows. We first recall the essential features of DFT. We then explain the construction of Koopmans-compliant orbital-density-dependent (ODD) functionals and discuss their practical minimization. Finally, we present spectral predictions for a range of molecular systems to establish the predictive potential of Koopmans-compliant methods.

2 Methods

2.1 Functionals of the Total Density

Before presenting ODD Koopmans-compliant functionals, we outline in this section the main features of conventional DFT. In particular, we place emphasis on the analytical interpretation of calculated electronic spectra. To this end, we work within the independent-electron mapping of Kohn and Sham [41] generalized to fractional orbital occupations.

It is important to note that fractional orbital occupations are beyond the scope of the original Kohn–Sham framework. The introduction of fractional orbital occupations is generally attributed to Janak who first interpreted orbital energies as derivatives of the total energy with respect to these new electronic variables [42]. In the literature, the generalization of the Kohn–Sham functional to fractional occupations is termed the extended Kohn–Sham model [43]. Beyond its central importance to interpret orbital energies, the extended Kohn–Sham model is a powerful framework to construct robust energy minimization schemes. Examples of such algorithms are provided by the ensemble-DFT algorithm [44] and relaxed-constraint algorithm [45] that both rely on exploring fractionally occupied states to reduce the nonconvexity of the Kohn–Sham electronic-structure problem. Paradoxically, fractional orbital occupations appeared in the DFT literature even before fractional electron numbers were discussed physically by Perdew et al. [8] in terms of grand-canonical mixtures of pure states (and then by Yang et al. [46] in terms of pure states), and formalized mathematically by Lieb [5] using convex-envelope analysis. The theory of fractional orbital occupations and that of fractional electron numbers are nonetheless closely related (the Aufbau principle), and are both critical to understanding the failure of conventional Kohn–Sham DFT approximations in predicting electronic spectra. Therefore, both of these theories are central to the subsequent discussion.

To begin our discussion, let us recall that, within the Kohn–Sham theory, the ground-state energy E(N) of the N-electron system can be obtained by minimizing the energy functional [41]

$$ {E}_{\mathrm{KS}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]={\displaystyle \sum_{i=1}^{+\infty }{f}_i{\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)+{E}_{\mathrm{Hxc}}\left[\rho \right]}}, $$

(1)

which includes the nonlinear electron-interaction term E _Hxc[ρ] that depends on the total electron density

$$ \rho \left(\mathbf{r}\right)={\displaystyle \sum_{i=1}^{+\infty }{f}_i\left|{\varphi}_i\right|{}^2\left(\mathbf{r}\right)}, $$

(2)

where the f _i 's and φ _i 's denote the fractional occupations and wave functions of the fictitious independent-electron system, respectively (for simplicity, the spin index is omitted throughout). The linear part in (1) involves the Hamiltonian operator

$$ {\widehat{h}}_0=-\frac{1}{2}{\nabla}_{\mathbf{r}}^2+v\left(\mathbf{r}\right) $$

that is the sum of the one-electron kinetic operator and potential v(r) generated by the atomic nuclei and external contributions.

The total energy E(N) of the system in its ground state is obtained by performing the minimization

$$ E(N)=\underset{{\displaystyle \overset{\int {\varphi}_i^{\ast }{\varphi}_j={\delta}_{ij}}{{\displaystyle {\sum}_{i=1}^{+\infty }}{f}_i=N, 0\le {f}_i\le 1}}}{min}{\displaystyle \sum_{i=1}^{+\infty} {f}_i{\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)+{E}_{\mathrm{Hxc}}\left[{\displaystyle \sum_{i=1}^{+\infty} {f}_i\left|{\varphi}_i\right|{}^2}\right]}}, $$

(3)

where the occupations f _i of the orthonormal Kohn–Sham orbitals φ _i must add up to N and must obey the constraints 0 ≤ f _i  ≤ 1.

To perform this minimization, we first focus on the orbital degrees of freedom (the minimization with respect the occupations will be examined in a second step). We thus introduce the Lagrange functional

$$ \begin{array}{lll}{\mathcal{L}}_{\mathrm{KS}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & =\hfill & {\displaystyle \sum_{i=1}^{+\infty }{f}_i{\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)+{E}_{\mathrm{Hxc}}\left[{\displaystyle \sum_{i=1}^{+\infty }{f}_i\left|{\varphi}_i\right|{}^2}\right]}}\hfill \\ {}\hfill & \hfill & -{\displaystyle \sum_{i,j=1}^{+\infty }{\Lambda}_{ij}\left({\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right){\varphi}_j\left(\mathbf{r}\right)-{\delta}_{ij}}\right)}\hfill \end{array}. $$

(4)

Variations of ℒ_KS with respect to the orbitals φ _i and their complex conjugates φ ^∗ _i yield a set of coupled one-electron equations:

$$ {f}_i\left({\displaystyle {\widehat{h}}_0}{\varphi}_i\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc}}\left(\mathbf{r}\right){\varphi}_i\left(\mathbf{r}\right)\right)={\displaystyle \sum_{j=1}^{+\infty }{\Lambda}_{ij}{\varphi}_j\left(\mathbf{r}\right)}, $$

(5)

$$ {f}_i\left({\displaystyle {\widehat{h}}_0}{\varphi}_i\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc}}\left(\mathbf{r}\right){\varphi}_i\left(\mathbf{r}\right)\right)={\displaystyle \sum_{j=1}^{+\infty }{\Lambda}_{ji}^{\ast }{\varphi}_j\left(\mathbf{r}\right)}, $$

(6)

where ${v}_{\mathrm{Hxc}}\left(\mathbf{r}\right)=\frac{\updelta {E}_{\mathrm{Hxc}}\left[\rho \right]}{\updelta \rho \left(\mathbf{r}\right)}$ stands for the effective single-electron potential, which includes a classical electrostatic contribution (the Hartree potential) and quantum exchange-correlation interactions. Note that these equations must be solved self-consistently as v _Hxc(r) is a functional of ρ(r) that itself depends on the solution of the Kohn–Sham problem. Using orthonormality relations, it can be shown that the matrix of Lagrange multipliers fulfills the conditions

$$ {\Lambda}_{ij}={\Lambda}_{ji}=0, $$

(7)

whenever the state φ _i is not occupied (f _i  = 0). Additionally, the Lagrange matrix is Hermitian:

$$ {\Lambda}_{ij}={\Lambda}_{ji}^{\ast }. $$

(8)

It should also be noted that the Λ _ij 's can only couple orbitals φ _i and φ _j that have the same occupations (f _i  = f _j ). This condition can be derived from the relation

$$ \left({f}_i-{f}_j\right){\Lambda}_{ij}=0, $$

(9)

which implies that Λ _ij vanishes whenever f _i differs from f _j . As a result, the Λ _ij 's form a block-diagonal matrix in which each block corresponds to orbitals that have the same occupations.

Now, bearing in mind that v _Hxc(r) is a functional of the density ρ(r) and invoking the invariance of ρ(r) with respect to block-diagonal unitary transformations, we can recast the self-consistent equations into

$$ {f}_i\left({\displaystyle {\widehat{h}}_0}{\psi}_i\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc}}\left(\mathbf{r}\right){\psi}_i\left(\mathbf{r}\right)\right)={\lambda}_i{\psi}_i\left(\mathbf{r}\right), $$

(10)

where the coefficients λ _i are the eigenvalues of the Lagrange matrix and the orbitals ψ _i are related to the initial orbitals φ _i through the block-diagonal rotation U that diagonalizes the Lagrange matrix Λ of the same block-diagonal form:

$$ {\psi}_i\left(\mathbf{r}\right)={\displaystyle \sum_{j=1}^{N_{\mathrm{occ}}}{U}_{ji}^{\ast }{\varphi}_j\left(\mathbf{r}\right)}, $$

(11)

$$ {\Lambda}_{ij}={\displaystyle \sum_{k=1}^{N_{\mathrm{occ}}}{U}_{ik}{\lambda}_k{U}_{jk}^{\ast }}, $$

(12)

with ${\displaystyle {\sum}_{k=1}^{N_{\mathrm{occ}}}}{U}_{ki}{U}_{kj}^{\ast }={\displaystyle {\sum}_{k=1}^{N_{\mathrm{occ}}}}{U}_{ik}^{\ast }{U}_{jk}={\delta}_{ij}$ and (f _i  − f _j )U _ij  = 0. For the moment, all the summations are restricted to the N _occ occupied states (the extension to unoccupied states is described below). We can then rewrite (10) in the canonical form

$$ {\displaystyle {\widehat{h}}_0}{\psi}_i\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc}}\left(\mathbf{r}\right){\psi}_i\left(\mathbf{r}\right)={\varepsilon}_i{\psi}_i\left(\mathbf{r}\right), $$

(13)

where the eigenvalues of the self-consistent Kohn–Sham Hamiltonian ${\displaystyle {\widehat{h}}_{\mathrm{KS}}}={\displaystyle {\widehat{h}}_0}+{v}_{\mathrm{Hxc}}\left(\mathbf{r}\right)$ and of the Lagrange matrix Λ are related through ε _i  = λ _i /f _i .

We are now in a position to define the occupation-dependent energy

$$ E\left({f}_1,{f}_2,\dots \right)={E}_{\mathrm{KS}}\left[{f}_1,{f}_2,\dots, {\psi}_1,{\psi}_2,\dots \right], $$

(14)

where the ψ _i 's stand for the canonical Kohn–Sham orbitals at self-consistency (13) ordered in ascending order of their eigenenergies, that is, ε ₁ ≤ ε ₂ ≤ …. The definition E(f ₁, f ₂, …) allows us to rewrite the ground-state energy in terms of a constrained minimization over the occupation numbers:

$$ E(N)=\underset{\begin{array}{l}{\displaystyle {\sum}_{i=1}^{+\infty }}{f}_i=N\\ {}0\le {f}_i\le 1\end{array}}{min}E\left({f}_1,{f}_2,\dots \right). $$

(15)

From this definition, one can interpret the Kohn–Sham eigenvalues as the derivatives of the occupation-dependent energy including self-consistent orbital relaxation:

$$ \frac{\partial E\left({f}_1,{f}_2,\dots \right)}{\partial {f}_i}={\varepsilon}_i, $$

(16)

where use has been made of the relation

$$ {\displaystyle \int {d}^3\mathbf{r}\left(\updelta {\psi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\displaystyle {\widehat{h}}_{\mathrm{KS}}}{\psi}_j\left(\mathbf{r}\right)+{\psi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\displaystyle {\widehat{h}}_{\mathrm{KS}}}\updelta {\psi}_j\left(\mathbf{r}\right)\right)=0}, $$

(17)

that results from Kohn–Sham stationarity and orthonormality conditions. In the literature, (16) is referred to as Janak’s theorem [42]. The theorem stands true for unoccupied states upon extending the diagonalization of ${\displaystyle {\widehat{h}}_{\mathrm{KS}}}$ to empty orbitals instead of only considering the N _occ occupied states. This straightforward extension does not affect the occupation-dependent energy while enabling us to define energy derivatives at f _i  = 0⁺ and offering an analytical interpretation for the eigenenergies of the empty states.

A central consequence of Janak’s theorem is the Aufbau principle, which has been alluded to at the beginning of this section. In fact, from Janak’s theorem, one can infer that the system remains unstable as long as a state that has an energy ε _i strictly lower than the energy ε _ℋ of the highest occupied orbital is not entirely filled.² The Aufbau principle can also be extended to the case where the highest occupied level is degenerate, as expressed by the relation

$$ E(N)=E\left(1,1,\dots, 1,{f}_1^{\mathrm{\mathcal{H}}},\dots, {f}_d^{\mathrm{\mathcal{H}}},0,0,\dots \right). $$

(18)

Equation (18) indicates that the ground state of the N-electron system can be constructed by simply filling the Kohn–Sham levels in ascending order until reaching the highest occupied levels of degeneracy d and of fractional occupations f ^ℋ₁ , …, f ^ℋ _d . Finally, using the Aufbau principle, it can be shown that

$$ \frac{\mathrm{d}E(N)}{\mathrm{d}N}=\frac{\partial E(N)}{\partial {f}_i^{\mathrm{\mathcal{H}}}}={\varepsilon}_{\mathrm{\mathcal{H}}}, $$

(19)

which reflects the fact that changes in the total electron number N can only occur through changes in the occupation numbers at the highest occupied level ε _ℋ. These important relations provide an analytical interpretation for the Kohn–Sham eigenenergies. They are exploited in the next section to construct ODD functionals beyond conventional DFT approximations.

2.2 Functionals of the Orbital Densities

2.2.1 Charged Excitations

Spectroscopy experiments in the X-ray and ultraviolet wavelength ranges involve excitations whose energies are sufficiently high to modify the charge of the sample through the removal (or addition) of an electron. The description of charged excitations requires us to predict correctly the energy of the system as a function of a reaction coordinate that parametrizes the excitation process, e.g., the occupation of the ionized state. In particular, if one is interested in capturing the onset of ultraviolet photoemission, one must correctly describe the dependence of the energy on the occupations of the highest occupied orbitals f ^ℋ _i or, equivalently, as a function of the electron number N (see (19) and the related discussion). Beyond charged excitations, correctly predicting the analytical behavior of the energy is important to describe lower-energy neutral excitations. Indeed, the accuracy of adiabatic TDDFT approximations in predicting neutral excitations and related optical resonances depends in particular on the ability of the underlying DFT approximations to describe orbital energies, that is, the derivatives of the energy with respect to the occupation numbers [17].

However, conventional Kohn–Sham DFT approximations do not correctly describe charged excitations; typically, the energy E(N) exhibits a strong nonlinear dependence within local, semilocal, and hybrid approximations, whereas the exact behavior of E(N) is known to be a connection of straight line segments between integer electron numbers. In fact, at fractional electron number, the ground state can be expressed as a statistical mixture of at most two pure states and its total energy verifies the linearity relation

$$ E(N)=\left(1-\omega \right)E(M)+\omega E\left(M+1\right), $$

(20)

where M and ω are the integer and fractional parts of N, respectively.

The piecewise linearity of the total energy was first established by Perdew et al. [8] and is critical to describe a range of orbital properties. It was then suggested by Cococcioni and de Gironcoli that it could be used to determine the strength U of Hubbard corrections to DFT [38, 39]. The connection between self-interaction and the lack of piecewise linearity was first made by Kulik et al. [40], arguing that Hubbard corrections reduce the hybridization and delocalization of d or f orbitals, and thus improve self-interaction errors rather than correlations, and by Mori-Sánchez et al. [47], who introduced the related concept of many-electron self-interaction. In addition to the inaccurate prediction of orbital energy levels, the lack of piecewise linearity of conventional DFT approximations results in an incorrect description of orbital densities [48]; functionals for which the dependence of E(N) on N is convex tend to delocalize the orbital densities, whereas functionals for which E(N) is concave lead to overlocalization [49, 50].³ Equivalently, imposing the piecewise linearity condition amounts, by definition, to cancelling many-electron self-interaction errors [51, 52] taking into account self-consistent electronic relaxation. In other words, the energy of the highest occupied orbital should not change as a function of its fractional occupations, that is, the orbital should not interact with itself:

$$ \frac{\partial {\varepsilon}_{\mathrm{\mathcal{H}}}}{\partial {f}_i^{\mathrm{\mathcal{H}}}}=0. $$

(21)

In the language of quantum chemistry, this condition is equivalent to the (generalized) Koopmans theorem,⁴ whereby the energy of the highest occupied state equals the energy of the ionization from the (M + 1)-electron to M-electron ground state, including full orbital relaxation:

$$ {\varepsilon}_{\mathrm{\mathcal{H}}}(N)=E\left(M+1\right)-E(M). $$

(22)

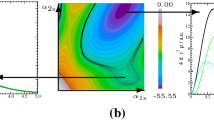
At this stage, it is important to mention that different definitions of self-interaction correction exist in the literature (Fig. 1). The term self-interaction may refer to one-electron self-interaction or many-electron self-interaction, and the latter may correspond either to the frozen picture where orbitals are kept unchanged upon varying f ^ℋ _i (the frozen-orbital many-electron self-interaction) or to the opposite situation where electrons are allowed to relax self-consistently (the relaxed-orbital many-electron self-interaction). We note in passing that there is no distinction between frozen-orbital self-interaction and relaxed-orbital self-interaction for one-electron systems as the two concepts are equivalent in that case. Identical hierarchies exist for piecewise linearity and Koopmans compliance (see the correspondences summarized in Fig. 1).

Fig. 1

Distinctions and equivalences between the different levels of self-interaction correction, piecewise linearity, and Koopmans compliance

To make the different definitions clear, let us first recall that DFT functionals are said to be one-electron self-interaction-free when the nonlinear electron–electron contributions satisfy

$$ {E}_{\mathrm{Hxc}}\left[\rho \right]=0 $$

(23)

for any one-electron density ρ(r) = f ₁|φ ₁|²(r), whether the orbital is allowed to relax or not. Equation (23) is not fulfilled by conventional DFT approximations. For instance, the local (spin) density approximation (LDA) exhibits a strong nonlinear behavior with a well-known singularity in $\frac{\mathrm{d}{\varepsilon}_1}{\mathrm{d}{f}_1}$ at f ₁ = 0 that is due to the Slater exchange contribution to E _Hxc[ρ] [53]. A simple correction to one-electron self-interaction errors in approximate DFT functionals was first proposed by Fermi and Amaldi in the context of the Thomas–Fermi–Dirac theory [53]; for KS-DFT, the Fermi–Amaldi one-electron self-interaction correction reads

$$ {E}_{\mathrm{FA}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]={E}_{\mathrm{KS}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]-N{E}_{\mathrm{Hxc}}\left[\frac{\rho }{N}\right]. $$

(24)

This functional satisfies (23) for one-electron systems (N = 1) but it exhibits important errors when more electrons are present. In particular, it does not preserve the size-consistency of the underlying DFT functional and lessens the precision of total energy predictions in general [54, 55]. The one-electron self-interaction correction of Perdew and Zunger improves upon the Fermi–Amaldi correction by subtracting individual electron-interaction contributions to the total energy functional:

$$ \begin{array}{ll}{E}_{\mathrm{PZ}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={E}_{\mathrm{KS}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill \\ {}\hfill & -{\displaystyle \sum_{i=1}^{+\infty }{E}_{\mathrm{Hxc}}\left[{f}_i\left|{\varphi}_i\right|{}^2\right].}\hfill \end{array} $$

(25)

The Perdew–Zunger self-interaction-corrected functional fulfills (23) by construction while preserving size-consistency. However, in its simplest form, the predictive accuracy and practical usefulness of the Perdew–Zunger method is restricted to one-electron systems and isolated atoms; its precision deteriorates rapidly with the number of atoms in the system and it exhibits important many-electron self-interaction errors in both the frozen-orbital and relaxed-orbital approximations [51].

A more balanced correction of one-electron and frozen-orbital many-electron self-interaction errors is instead achieved by Hartree–Fock (HF) theory. In fact, it is well known that in the expression for the Hartree–Fock energy functional

$$ \begin{array}{ll}{E}_{\mathrm{HF}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={\displaystyle \sum_{i=1}^{+\infty }{f}_i{\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)}}\hfill \\ {}\hfill & +\frac{1}{2}{\displaystyle \sum_{i=1}^{+\infty }{\displaystyle \sum_{j=1}^{+\infty }{f}_i{f}_j{\displaystyle \int {d}^3\mathbf{r}{d}^3{\mathbf{r}}^{\mathbf{\prime}}\frac{\left|{\varphi}_i\left|{}^2\left(\mathbf{r}\right)\right|{\varphi}_j\left|{}^2\right({\mathbf{r}}^{\mathbf{\prime}}\right)}{\left|\mathbf{r}-{\mathbf{r}}^{\mathbf{\prime}}\right|}}}}\hfill \\ {}\hfill & -\frac{1}{2}{\displaystyle \sum_{i=1}^{+\infty }{\displaystyle \sum_{j=1}^{+\infty }{f}_i{f}_j{\displaystyle \int {d}^3\mathbf{r}{d}^3{\mathbf{r}}^{\mathbf{\prime}}\frac{\varphi_i^{\ast}\left(\mathbf{r}\right){\varphi}_j\left(\mathbf{r}\right){\varphi}_j^{\ast}\left({\mathbf{r}}^{\mathbf{\prime}}\right){\varphi}_i\left({\mathbf{r}}^{\mathbf{\prime}}\right)}{\left|\mathbf{r}-{\mathbf{r}}^{\mathbf{\prime}}\right|}}}}{\delta}_{\sigma_i{\sigma}_j,}\hfill \end{array} $$

(26)

the self-Hartree and self-exchange terms (that is, the terms corresponding to i = j in the double sums) cancel out. (In (26), σ _i denotes the spin of φ _i .) Consequently, the HF functional is one-electron self-interaction-free. Furthermore, due to the cancellation between Hartree and Fock contributions, it is quite straightforward to show that HF verifies (21) within the frozen-orbital approximation for many-electron systems. In other words, the HF method fulfills the restricted (original) Koopmans theorem (Fig. 2) in addition to one-electron Koopmans compliance (Fig. 3). The situation is completely different for relaxed orbitals. In fact, as illustrated in Fig. 4, all the approximations mentioned above, namely, the LDA, HF, and PZ formulations, predict the energy of the highest occupied state ε _ℋ to vary as a function of the occupation number f ^ℋ, meaning that the energy of the ground state E(N) is not linear. In specific terms, the LDA ground-state energy is strongly convex since ${\varepsilon}_{\mathrm{\mathcal{H}}}=\frac{\mathrm{d}E}{\mathrm{d}N}$ increases rapidly upon raising f ^ℋ or N. The HF energy exhibits the opposite trend, whereas the PZ energy is seen to be mostly convex.

Fig. 2

Frozen-orbital many-electron self-interaction (the restricted Koopmans theorem). Dependence of the highest orbital energy as a function of its occupation for carbon within the frozen-electron approximation. It can be seen that the HF method is frozen-orbital many-electron self-interaction-free, meaning that it verifies the restricted Koopmans theorem at variance with the LDA, PZ, and Koopmans-compliant (K) methods (Sect. 2.2.2). We emphasize that the restricted Koopmans theorem is also not fulfilled by exact DFT

Fig. 3

One-electron self-interaction (the one-electron Koopmans theorem). Dependence of the highest orbital energy as a function of its occupation for hydrogen including full self-consistency. It is readily apparent that the local (spin) density approximation (LDA) does not fulfill (21) and is therefore not self-interaction-free for one-electron systems (23). In contrast, the Hartree–Fock (HF) and Perdew–Zunger (PZ) methods are exact and one-electron self-interaction-free by construction. Likewise, the Koopmans-compliant (K) correction (Sect. 2.2.2) to LDA fulfills (21) exactly and (23) very accurately

Fig. 4

Relaxed-orbital many-electron self-interaction (the generalized Koopmans theorem). Dependence of the highest orbital energy as a function of its occupation for carbon including full self-consistency. It can be seen that only the K method verifies the generalized Koopmans theorem within very good approximation in accordance with exact DFT and at variance with the LDA, HF, and PZ methods

The lack of generalized Koopmans compliance of conventional quantum approximations reverberates negatively on the electronic-structure description of physical systems and on the accuracy of spectroscopic predictions. The importance of the generalized Koopmans theorem lies in the fact that, if one could impose generalized Koopmans compliance, that is, self-consistent piecewise linearity, while preserving the precision of DFT energy predictions, one would automatically obtain accurate highest occupied levels (see (22)). Furthermore, in practice, imposing the generalized Koopmans theorem to the full electronic spectra would enable one to inherit from the established accuracy of finite-difference DFT energy predictions (the ΔSCF method) [56] in describing low- and high-energy charged excitations without requiring repeated calculations for the non-Aufbau ionized states.

Therefore, imposing generalized Koopmans compliance (that is, restoring self-consistent piecewise linearity and correcting relaxed-orbital many-electron self-interaction) is fundamental to the accuracy of calculated charged-excitation spectra. The importance of the generalized Koopmans theorem has been highlighted in a number of theoretical and computational studies [8, 35, 36, 49, 51, 52, 57–61]. In the next section, we present the Koopmans-compliant method [62–64] specifically devised to correct relaxed-orbital many-electron self-interaction errors and to restore the generalized Koopmans theorem for DFT approximations (Fig. 4).

2.2.2 Generalized Koopmans Compliance

To impose generalized Koopmans compliance in DFT calculations, the first important step is to provide a precise definition of the lack of piecewise linearity. A quantitative definition of deviations from Koopmans compliance is provided by the non-Koopmans energy first introduced by Perdew and Zunger. It is simply obtained by comparing the correct linear behavior imposed by Koopmans’ theorem and the incorrect nonlinear behavior of the approximate ground-state energy. Explicitly, the non-Koopmans energy can be expressed as

$$ {\Pi}_{\mathrm{\mathcal{H}}}\left(N;{\omega}_{\mathrm{ref}}\right)={\displaystyle {\int}_0^{\omega}\mathrm{d}{\omega}^{\prime}\left(\frac{\mathrm{d}E}{\mathrm{d}N}\left(M+{\omega}_{\mathrm{ref}}\right)-\frac{\mathrm{d}E}{\mathrm{d}N}\left(M+{\omega}^{\prime}\right)\right)} $$

(27)

$$ =E(M)-E\left(M+\omega \right)+\omega \frac{\mathrm{d}E}{\mathrm{d}N}\left(M+{\omega}_{\mathrm{ref}}\right), $$

(28)

where the reference fractional number ω _ref denotes the value of ω at which

$$ \frac{\mathrm{d}E}{\mathrm{d}N}\left(M+{\omega}_{\mathrm{ref}}\right)=E\left(M+1\right)-E(M). $$

(29)

In other words, Π_ℋ(N;ω _ref) can be written as

$$ {\Pi}_{\mathrm{\mathcal{H}}}\left(N;{\omega}_{\mathrm{ref}}\right)=E(M)-E\left(M+\omega \right)+\omega \left(E\left(M+1\right)-E(M)\right). $$

(30)

Then, making use of the fact that E(N) can be accurately approximated by a parabola between M and M + 1 in most practical situations, we can obtain a very close approximation to the non-Koopmans energy by setting ${\omega}_{\mathrm{ref}}=\frac{1}{2}$ (the Slater one-half approximation) [48]:

$$ {\tilde{\Pi}}_{\mathrm{\mathcal{H}}}(N)={\Pi}_{\mathrm{\mathcal{H}}}\left(N;\frac{1}{2}\right)=E(M)-E\left(M+\omega \right)+\omega \frac{\mathrm{d}E}{\mathrm{d}N}\left(M+\frac{1}{2}\right). $$

(31)

Now we can rely on (31) to construct a correction to the lack of Koopmans compliance.⁵ To this end, we must express the non-Koopmans energy as a functional of the φ _i 's and f _i 's. As a first attempt to write ${\tilde{\Pi}}_{\mathrm{\mathcal{H}}}(N)$ explicitly, let us perform a Taylor series expansion. We assume for simplicity that the highest occupied state ψ _M + 1 is not degenerate, that is, ω ≡ f _M + 1 and ℋ ≡ M + 1. Hence, to second order around ω = 0, the expansion⁶ reads

$$ \begin{array}{ll}{\tilde{\Pi}}_{M+1}(N)\hfill & =\frac{1}{2}{f}_{M+1}\left(1-{f}_{M+1}\right)\hfill \\ {}\hfill & \times {\displaystyle \int {d}^3\mathbf{r}{d}^3{\mathbf{r}}^{\mathbf{\prime}}{d}^3{\mathbf{r}}^{\mathbf{{\prime\prime}}}\left|{\psi}_{M+1}\right|{}^2\left(\mathbf{r}\right){\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right){f}_{\mathrm{Hxc}}\left({\mathbf{r}}^{\mathbf{\prime}},{\mathbf{r}}^{\mathbf{{\prime\prime}}}\right)\left|{\psi}_{M+1}\right|{}^2\left({\mathbf{r}}^{\mathbf{{\prime\prime}}}\right)+\cdots,}\hfill \end{array} $$

(32)

where ${f}_{\mathrm{Hxc}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)}=\frac{\updelta {v}_{\mathrm{Hxc}}\left(\mathbf{r}\right)}{\updelta \rho \left({\mathbf{r}}^{\mathbf{\prime}}\right)}$ stands for the exchange-correlation kernel and ${\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)=\delta \left(\mathbf{r}-{\mathbf{r}}^{\mathbf{\prime}}\right)+\frac{\updelta {v}_{\mathrm{Hxc}}\left(\mathbf{r}\right)}{\updelta v\left({\mathbf{r}}^{\mathbf{\prime}}\right)}$ denotes a screening function of the Kohn–Sham system. Equation (32) underscores the main difficulties that arise in expressing the non-Koopmans energy explicitly; the computational challenge here is to evaluate the Kohn–Sham nonlocal dielectric function ${\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)$, which captures the complex self-consistent response of the electrons to an external perturbation.

Nonetheless, (32) suggests us that the expression of the non-Koopmans energy would be greatly simplified if self-consistent electronic relaxation were not present. This observation leads us to consider first the simpler case in which orbitals are frozen. Explicitly, we work within the approximation

$$ \updelta {\psi}_i=0,\kern2em \updelta {v}_{\mathrm{Hxc}}\left(\mathbf{r}\right)=0,\kern2em {\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)=\delta \left(\mathbf{r}-{\mathbf{r}}^{\mathbf{\prime}}\right). $$

(33)

In this frozen orbital picture, expressing the non-Koopmans energy becomes straightforward; by evaluating each term in (31) for the fixed ψ _i 's, we obtain

$$ \begin{array}{ll}{\tilde{\Pi}}_{M+1}^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\psi}_1,{\psi}_2,\dots \right]\hfill & ={E}_{\mathrm{Hxc}}\left[{\displaystyle \sum_{i=1}^M{f}_i\left|{\psi}_i\right|{}^2}\right]-{E}_{\mathrm{Hxc}}\left[{\displaystyle \sum_{i=1}^{M+1}{f}_i\left|{\psi}_i\right|{}^2}\right]\hfill \\ {}\hfill & +{f}_{M+1}{\displaystyle \int {d}^3\mathbf{r}\;{v}_{\mathrm{Hxc}}\left(\mathbf{r};\left[{\displaystyle \sum_{i=1}^M{f}_i\left|{\psi}_i\right|{}^2+{\scriptscriptstyle \frac{1}{2}}\left|{\psi}_{M+1}\right|{}^2}\right]\right){\left|{\psi}_{M+1}\right|}^2\left(\mathbf{r}\right),}\hfill \end{array} $$

(34)

where the superscript {⋅}^u indicates that orbitals are kept unrelaxed during the fictitious ionization process. We note in passing that all the linear contributions related to ${\widehat{h}}_0$ vanish in the frozen orbital picture.

With the explicit expression of the non-Koopmans contributions in hand, it is now possible to impose Koopmans compliance for frozen orbitals by defining

$$ \begin{array}{ll}{E}_{\mathrm{K}}^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={E}_{\mathrm{K}\mathrm{S}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill \\ {}\hfill & +{\tilde{\Pi}}_{M+1}^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right].\hfill \end{array} $$

(35)

Indeed, one can verify that the new functional ${E}_{{}_{\mathrm{K}}}^{\mathrm{u}}$ is exactly linear in the absence of relaxation due to the fact that

$$ \frac{\partial^2{\tilde{\Pi}}_{M+1}^{\mathrm{u}}}{\partial {f}_{M+1}^2}=-\frac{\partial^2{E}_{\mathrm{KS}}}{\partial {f}_{M+1}^2}, $$

(36)

while not altering the energy E(N) at integer occupations since the unrelaxed non-Koopmans energy

$$ \begin{array}{ll}{\tilde{\Pi}}_{M+1}^{\mathrm{u}}\hfill & =\frac{1}{2}{f}_{M+1}\left(1-{f}_{M+1}\right)\hfill \\ {}\hfill & \times {\displaystyle \int {d}^3\mathbf{r}{d}^3{\mathbf{r}}^{\mathbf{\prime}}{\left|{\varphi}_{M+1}\right|}^2}\left(\mathbf{r}\right){f}_{\mathrm{Hxc}}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right){\left|{\varphi}_{M+1}\right|}^2\left({\mathbf{r}}^{\mathbf{\prime}}\right)+\cdots, \hfill \end{array} $$

(37)

is nearly zero when φ _M + 1 is completely empty or filled.

Having imposed Koopmans compliance for frozen orbitals, it remains to include the effect of self-consistent orbital relaxation. To address this problem, let us use the expression of E ^u_K as a first approximation and monitor the analytical behavior of the ground-state energy. From these calculations, one can observe that the energy E(N), which is exactly linear in the frozen orbital approximation, becomes downward convex when orbitals relax self-consistently. This observation is in line with the intuition that neglecting screening contributions leads to an overestimation of the correction. In fact, it can be rigorously shown that any functional that fulfills the restricted Koopmans theorem leads to a downward convex dependence of the energy E(N) when relaxation is taken into account. A perfect illustration of this result is provided by the HF theory whose ground-state energy is piecewise linear for frozen orbitals (that is, the HF theory fulfills the restricted Koopmans theorem) and becomes piecewise concave for relaxed orbitals.

Since including self-consistent relaxation through the nonlocal electronic dielectric function ${\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)$ would be prohibitively expensive, we resort here to a much simpler correction, which consists of making the zeroth-order approximation

$$ {\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)={\alpha}_{M+1}+\cdots, $$

(38)

to capture the self-consistent relaxation effects that take place upon ionizing φ _M + 1. Substituting (38) into (32) and comparing with the expansion of ${\tilde{\Pi}}^{\mathrm{u}}$, we infer

$$ {\tilde{\Pi}}_{M+1}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]={\alpha}_{M+1}{\tilde{\Pi}}_{M+1}^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]+\cdots . $$

(39)

Hence, we arrive at the Koopmans-compliant functional

$$ \begin{array}{ll}{E}_{\mathrm{K}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={E}_{\mathrm{K}\mathrm{S}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill \\ {}\hfill & +{\alpha}_{M+1}{\tilde{\Pi}}_{M+1}^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right],\hfill \end{array} $$

(40)

which generalizes (35) by taking into account orbital screening through the uniform dielectric constant α _M + 1.⁷

In principle, the dielectric coefficient α _M + 1 should be calculated by averaging the nonlocal permittivity in some suitable system-dependent and orbital-dependent fashion.⁸ However, it can also be obtained in a more pragmatic and efficient manner by directly imposing Koopmans compliance (22), thereby avoiding complex averaging procedures. In our calculations, we obtain α _M + 1 through the necessary condition:

$$ {\varepsilon}_{M+1}\left({M}^{+}\right)={\varepsilon}_{M+1}\left(M+{1}^{-}\right), $$

(41)

which reflects the fact that the electron affinity of the M-electron system ${\mathcal{A}}_M=-{\varepsilon}_{M+1}\left({M}^{+}\right)$ should be equal to the ionization potential of the (M + 1)-electron system ${\mathcal{I}}_{M+1}=-{\varepsilon}_{M+1}\left(M+{1}^{-}\right)$. Admittedly, (41) is not a sufficient condition for complete Koopmans compliance. However, it provides a very accurate correction of the lack of piecewise linearity of local and semilocal DFT approximations. In practice, the calculation of the dielectric screening coefficient can be performed using the secant-method recursion:

$$ \begin{array}{ll}{\alpha}_{M+1}^{\left(n+2\right)}\hfill & ={\alpha}_{M+1}^{(n)}\hfill \\ {}\hfill & +\frac{\left({\alpha}_{M+1}^{\left(n+1\right)}-{\alpha}_{M+1}^{(n)}\right)\left({\varepsilon}_{M+1}^{(n)}\left({M}^{+}\right)-{\varepsilon}_{M+1}^{(n)}\left(M+{1}^{-}\right)\right)}{\left({\varepsilon}_{M+1}^{(n)}\left({M}^{+}\right)-{\varepsilon}_{M+1}^{(n)}\left(M+{1}^{-}\right)\left)-\right({\varepsilon}_{M+1}^{\left(n+1\right)}\left({M}^{+}\right)-{\varepsilon}_{M+1}^{\left(n+1\right)}\left(M+{1}^{-}\right)\right)}.\hfill \end{array} $$

(42)

Note that, due to the almost linear behavior of the orbital-energy difference ε _M + 1(M ⁺) − ε _M + 1(M + 1⁻) as a function of α _M + 1, two recursions of (42) are most of the time sufficient in our experience to converge α _M + 1 and impose Koopmans’ condition [63].

Finally, we emphasize that the correction described above restores the generalized Koopmans theorem for the highest occupied orbital but leaves the energies of the other states unchanged. However, imposing Koopmans’ theorem on the other states would clearly improve the description of the electronic spectrum by equating orbital energies with the accurate total energy differences [15, 56]. Although applying the correction to both the occupied and unoccupied manifolds is guided by practical considerations,⁹ it will be shown that this extension provides accurate ionization potentials and electron affinities, often comparable to many-body predictions.

We thus define the non-Koopmans energy ${\tilde{\Pi}}_i^{\mathrm{u}}$ associated with the removal or addition of φ _i using a straightforward generalization of (34):

$$ \begin{array}{ll}{\tilde{\Pi}}_i^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={E}_{\mathrm{Hxc}}\left[{\displaystyle \sum_{\begin{array}{c}j=1\\{}j\ne {\mathrm{i}}\end{array}}^{+\infty }{f}_j\left|{\varphi}_j\right|{}^2}\right]-{E}_{\mathrm{Hxc}}\left[{\displaystyle \sum_{j=1}^{+\infty }{f}_j\left|{\varphi}_j\right|{}^2}\right]\hfill \\ {}\hfill & +{f}_i{\displaystyle \int {d}^3\mathbf{r}\;{v}_{\mathrm{Hxc}}\left(\mathbf{r};\left[{\displaystyle \sum_{\begin{array}{c}j=1\\{}j\ne {\mathrm{i}}\end{array}}^{+\infty }{f}_j\left|{\varphi}_j\right|{}^2+{\scriptscriptstyle \frac{1}{2}}\left|{\varphi}_i\right|{}^2}\right]\right)\left|{\varphi}_i\right|{}^2\left(\mathbf{r}\right).}\hfill \end{array} $$

(43)

This definition allows us to define a Koopmans-compliant functional extended to the full spectrum:

$$ \begin{array}{ll}{E}_{\mathrm{K}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={E}_{\mathrm{K}\mathrm{S}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill \\ {}\hfill & +{\displaystyle \sum_{i=1}^{+\infty }{\alpha}_i{\tilde{\Pi}}_i^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right],}\hfill \end{array} $$

(44)

where a different dielectric screening constant α _i is introduced for each of the orbitals. However, in practical simulations, evaluating the α _i 's would require a different calculation to impose Koopmans’ condition on each of the electronic states, thereby considerably increasing the computational burden. Fortunately, it is observed in practice that the α _i 's vary in a narrow range of values so that approximating the α _i 's to be all equal to a unique α that depends only on the system does not significantly alter the accuracy of electronic level predictions in most practical cases.¹⁰ In explicit terms, the functional that we employ in our simulations reads

$$ \begin{array}{ll}{E}_{\mathrm{K}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={E}_{\mathrm{K}\mathrm{S}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill \\ {}\hfill & +\alpha {\displaystyle \sum_{i=1}^{+\infty }{\tilde{\Pi}}_i^{\mathrm{u}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right].}\hfill \end{array} $$

(45)

This completes the presentation of the Koopmans-compliant functional. In summary, imposing Koopmans compliance leads us to considering the ionization of individual Kohn–Sham orbitals, thereby defining a functional of the general ODD form

$$ \begin{array}{ll}{E}_{\mathrm{ODD}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]\hfill & ={\displaystyle \sum_{i=1}^{+\infty }{f}_i{\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)}}\hfill \\ {}\hfill & +{E}_{\mathrm{Hxc}}\left[{f}_1{\left|{\varphi}_1\right|}^2,{f}_2{\left|{\varphi}_2\right|}^2,\dots \right].\hfill \end{array} $$

(46)

Although other definitions of the non-Koopmans error could be envisioned, the procedure outlined above would always provide functionals of this form, i.e., with an exchange-correlation term E _Hxc[f ₁|φ ₁|², f ₂|φ ₂|², …] that depends on the individual orbital densities instead of E _Hxc[∑ _i = 1 ^+ ∞ f _i |φ _i |²] that depends on the total density. It is important to note that ODD functionals can still be regarded as implicit DFT functionals [65], yet defined in a non-Kohn–Sham framework, unless ad hoc optimized effective potential (OEP) techniques [66, 67] are adopted. Alternatively, a beyond-DFT perspective on ODD methods, based upon the local and frequency-dependent spectral-density potential introduced by Gatti et al. [68], is discussed elsewhere [69].

To close the presentation of orbital-dependent corrections, it should be said that orbital-independent methods have been proposed to reduce many-electron self-interaction errors in DFT approximations [64, 70]. These DFT approaches improve energy predictions for systems with fractional electron numbers. Nevertheless, they are not meant to improve the description of spectroscopic properties and charged excitations, except for the highest occupied orbital of the system. The advantage of the ODD approach in that regard will be discussed extensively in Sect. 4.

2.2.3 Energy Minimization

The minimization of ODD energy functionals deserves particular attention, and important aspects of it are presented in this section.

To minimize the ODD energy, we first write the Lagrange functional related to the orthonormality constraints on the orbitals:

$$ {\mathrm{\mathcal{L}}}_{\mathrm{ODD}}={E}_{\mathrm{ODD}}\left[{f}_1,{f}_2,\dots, {\varphi}_1,{\varphi}_2,\dots \right]-{\displaystyle \sum_{i,j=1}^{+\infty }{\Lambda}_{ij}\left({\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right){\varphi}_j\left(\mathbf{r}\right)-{\delta}_{ij}}\right)}. $$

(47)

The corresponding stationary conditions can be written as

$$ \frac{\updelta {\mathrm{\mathcal{L}}}_{\mathrm{ODD}}}{\updelta {\varphi}_i\left(\mathbf{r}\right)}=0,\kern1em \frac{\updelta {\mathrm{\mathcal{L}}}_{\mathrm{ODD}}}{\updelta {\varphi}_i^{\ast}\left(\mathbf{r}\right)}=0. $$

(48)

This leads to a set coupled self-consistent equations

$$ {f}_i\left({\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc},i}\left(\mathbf{r}\right){\varphi}_i\left(\mathbf{r}\right)\right)={\displaystyle \sum_{j=1}^{+\infty }{\Lambda}_{ij}{\varphi}_j\left(\mathbf{r}\right)}={\displaystyle \sum_{j=1}^{+\infty }{\Lambda}_{ji}^{\ast }{\varphi}_j\left(\mathbf{r}\right)}, $$

(49)

in which the unique Kohn–Sham potential v _Hxc(r) of conventional DFT is replaced by a collection of potentials corresponding to the different orbitals of the system:

$$ {v}_{\mathrm{Hxc},i}\left(\mathbf{r}\right)=\frac{\updelta {E}_{\mathrm{Hxc}}\left[{\rho}_1,{\rho}_2,\dots \right]}{\updelta {\rho}_i\left(\mathbf{r}\right)},{\rho}_i\left(\mathbf{r}\right)={f}_i{\left|{\varphi}_i\right|}^2\left(\mathbf{r}\right). $$

(50)

Similarly to the original Kohn–Sham, the Λ _ij 's form a Hermitian matrix:

$$ \begin{array}{ll}{\Lambda}_{ij}\hfill & ={f}_i{\displaystyle \int {d}^3\mathbf{r}{\varphi}_j^{\ast}\left(\mathbf{r}\right)\left({\widehat{h}}_0{\varphi}_i\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc},i}\left(\mathbf{r}\right){\varphi}_i\left(\mathbf{r}\right)\right)}\hfill \\ {}\hfill & ={f}_j{\displaystyle {\left({\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\left({\displaystyle {\widehat{h}}_0}{\varphi}_j\left(\mathbf{r}\right)+{v}_{\mathrm{Hxc},j}\left(\mathbf{r}\right){\varphi}_j\left(\mathbf{r}\right)\right)}\right)}^{\ast }}={\Lambda}_{ji}^{\ast },\hfill \end{array} $$

(51)

which can be rewritten as

$$ {\displaystyle \int {d}^3\mathbf{r}{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot \left({f}_i{\widehat{h}}_i-{f}_j{\widehat{h}}_j\right){\varphi}_j\left(\mathbf{r}\right)=0}, $$

(52)

with

$$ {\widehat{h}}_i={\widehat{h}}_0+{v}_{\mathrm{Hxc},i}. $$

(53)

Equation (52) is the ODD counterpart of (9) and is also known as the Pederson condition [71]. It highlights an important feature of ODD functionals; since those are not in general invariant under a unitary transformation U of the orbitals, the gradient of the ODD energy with respect to U is usually not zero. As shown in [72], the expression of such gradient is proportional to the left-hand side of (52) for f _i  = f _j  = 1. At the minimum, the Pederson condition determines the specific unitary rotation of the orbitals that makes the energy stationary. For certain ODD functionals, such as PZ, the minimizing orbitals are usually localized (and often similar to Wannier functions [73, 74]), so the Pederson condition can also be regarded as a localization condition; for Koopmans-compliant functionals, the driving force to localization changes depending on the functional chosen, but it is always present in the functionals described here.

In general, when dealing with ODD functionals it is customary to consider two set of orbitals, namely the minimizing orbitals discussed above and the so-called canonical orbitals, corresponding to the eigenvectors of the Λ matrix [69, 75]. This second set is introduced to define orbital ionization energies by identifying the Λ _ij 's as being proportional to the coefficients of an effective Hamiltonian (see the following discussion for details). It is important to stress here that while the diagonalization of Λ is fully supported by Janak’s theorem in the KS-DFT framework (providing an interpretation to the eigenvalues of Λ), this is not the case for ODD, as stressed by Vydrov et al. [76]. In fact, when dealing with ODD methods, we have

$$ \frac{\partial {E}_{\mathrm{ODD}}}{\partial {f}_i}={\displaystyle \int {d}^3\mathbf{r}\;{\varphi}_i^{\ast}\left(\mathbf{r}\right)\cdot {\widehat{h}}_i{\varphi}_i\left(\mathbf{r}\right)=\frac{\Lambda_{ii}}{f_i}}. $$

(54)

Bearing in mind that the minimizing orbitals are typically localized, it is clear that the ODD Janak’s theorem (54) does not provide a physical definition of orbital energies. On the other hand, canonical orbitals are physical but not protected by a Janak-like theorem. This issue, still a very important open problem in the field, has been thoroughly discussed by Stengel and Spaldin [72]. In [72] the authors stressed the fact that the breakdown of a Janak-definition for orbital energies in ODD methods has to be found in the extension of ODD functionals to fractional occupations, suggesting that an alternative extension providing also a proper Janak’s theorem would be very desirable and a major advancement.

Because of these issues in defining ODD functionals for fractional numbers of electrons, in the following we will consider only the case where we have two subspaces, the valence and the conduction manifold, separated by a gap and with occupations 1 and η respectively, where the limit η → 0 has to be taken. This construction allows one to define an effective Hamiltonian for both occupied and empty states. Within these definitions, at the minimum we obtain

$$ {\Lambda}_{ij}={\Lambda}_{ji}^{\ast}\sim \eta \to 0\kern1em \left(1\le i\le {N}_{\mathrm{occ}}\ \mathrm{and}\ {N}_{\mathrm{occ}}<j\right). $$

(55)

This leads us to the following set of equations:

$$ {\widehat{h}}_i{\varphi}_i\left(\mathbf{r}\right)={\displaystyle \sum_{j=1}^{N_{\mathrm{occ}}}{\Lambda}_{ij}{\varphi}_j\left(\mathbf{r}\right)}\kern1em \left(1\le i\le {N}_{\mathrm{occ}}\right), $$

(56)

$$ {\widehat{h}}_i{\varphi}_i\left(\mathbf{r}\right)={\displaystyle \sum_{j={N}_{\mathrm{occ}}+1}^{+\infty }{\tilde{\Lambda}}_{ij}{\varphi}_j\left(\mathbf{r}\right)}+{\displaystyle \sum_{j=1}^{N_{\mathrm{occ}}}{\tilde{\Lambda}}_{ij}{\varphi}_j\left(\mathbf{r}\right)}\kern1em \left({N}_{\mathrm{occ}}<i\right), $$

(57)

with

$$ {\tilde{\Lambda}}_{ij}=\frac{1}{\eta }{\Lambda}_{ij}. $$

(58)

While the equation for occupied orbitals (56) does not couple them to the empty manifold, the equation for the empty states (57) involves the occupied ones because of the orbital orthogonality constraint.

It is then useful to introduce projectors onto the occupied and empty manifolds and define projected Hamiltonians as

$$ {\displaystyle {\widehat{P}}_i}{\varphi}_j\left(\mathbf{r}\right)={\varphi}_i\left(\mathbf{r}\right){\displaystyle \int {d}^3{\mathbf{r}}^{\mathbf{\prime}}{\varphi}_i^{\ast}\left({\mathbf{r}}^{\mathbf{\prime}}\right){\varphi}_j\left({\mathbf{r}}^{\mathbf{\prime}}\right)}, $$

(59)

$$ \widehat{P}={\displaystyle \sum_{i=1}^{Nocc}{\widehat{P}}_i}, $$

(60)

$$ \widehat{Q}=\widehat{I}-\widehat{P}, $$

(61)

$$ {\widehat{H}}_{\mathrm{V}}={\displaystyle \sum_{i=1}^{N_{\mathrm{occ}}}{\widehat{h}}_i{\widehat{P}}_i}, $$

(62)

$$ {\widehat{H}}_{\mathrm{C}}={\displaystyle \sum_{i={N}_{\mathrm{occ}}+1}^{+\infty }{\widehat{h}}_i{\widehat{P}}_i}. $$

(63)

By operating $\widehat{P}$ and $\widehat{Q}$ on both sides of (56) and (57) and using the above definitions, we obtain

$$ \widehat{P}{\widehat{H}}_{\mathrm{V}}\widehat{P}{\varphi}_i\left(\mathbf{r}\right)={\displaystyle \sum_{j=1}^{N_{\mathrm{occ}}}{\Lambda}_{ij}{\varphi}_j\left(\mathbf{r}\right)}\kern1em \left(1\le i\le {N}_{\mathrm{occ}}\right), $$

(64)

$$ \widehat{Q}{\widehat{H}}_{\mathrm{C}}\widehat{Q}{\varphi}_i\left(\mathbf{r}\right)={\displaystyle \sum_{j={N}_{\mathrm{occ}}+1}^{+\infty }{\tilde{\Lambda}}_{ij}{\varphi}_j\left(\mathbf{r}\right)}\kern1em \left({N}_{\mathrm{occ}}<i\right). $$

(65)

These expressions have the important merit of explicitly decoupling the valence and the conduction manifolds, thus suggesting us to use

$$ \widehat{H}=\widehat{P}{\widehat{H}}_{\mathrm{V}}\widehat{P}+\widehat{Q}{\widehat{H}}_{\mathrm{C}}\widehat{Q}, $$

(66)

as an effective (Hermitian) Hamiltonian for the system (which is equivalent to considering the canonical orbitals and the Λ eigenvalues to define the electronic structure of the system). The construction above is routinely used in interpreting eigenvalues of the Λ matrix provided by self-interaction corrections, and it is argued for in [69]. The practical performance of this approach is highlighted in the next section.

Before closing this section, it is worth discussing the extension of the above ODD approaches to the solid limit. While this still represents an open problem, the localization properties of the minimizing orbitals may be exploited. As an example, let us focus first on the PZ case. The behavior of E _Hxc[ρ _i ] as a function of the spread of ρ _i (modeled as a Gaussian distribution) has been studied recently [77]; it has been confirmed that the PZ-ODD corrections would vanish for fully delocalized orbitals. Focusing now on the K functional, a similar problem appears, since the ${\tilde{\Pi}}_i^{\mathrm{u}}$ terms of (45) would become identically zero for extended orbitals (for the same reason the ΔSCF method fails for solids [78]). The role of localized minimizing orbitals appears then to be pivotal for the use of ODD methods on extended systems, since it would yield a non-zero orbital-dependent correction. A detailed analysis of the localization properties of the orbitals for PZ-ODD is given in [77]. Further numerical investigation along these lines is required, especially concerning the K functional, and will be the subject of a future publication.

3 Numerical Approach

In this section we present the analytical expressions of the Hamiltonians resulting from Koopmans-compliant functionals together with the implementation of the method. Full computational details are also provided.

3.1 Koopmans-Compliant Contributions

According to (49), (56), and (57), we need to evaluate the quantities

$$ {\widehat{h}}_i=\frac{\updelta {E}_{\mathrm{ODD}}}{\updelta {\rho}_i\left(\mathbf{r}\right)}={\widehat{h}}_0+\frac{\updelta {E}_{\mathrm{Hxc}}}{\updelta {\rho}_i\left(\mathbf{r}\right)}, $$

(67)

focusing on the case of the Koopmans-compliant functional E _ODD = E _K, as defined in (45). To this end, we have to compute the derivatives $\frac{{\updelta \tilde{\Pi}}_j^{\mathrm{u}}}{\rho_i\left(\mathbf{r}\right)}$. As a first step, we evaluate the term corresponding to i = j:

$$ \frac{{\updelta \tilde{\Pi}}_j^{\mathrm{u}}}{\updelta {\rho}_i\left(\mathbf{r}\right)}={v}_{\mathrm{Hxc}}\left(\mathbf{r};\left[{\rho}_i^{\mathrm{ref}}\right]\right)-{v}_{\mathrm{Hxc}}\left(\mathbf{r};\left[\rho \right]\right)+{w}_i^{\mathrm{ref}}\left(\mathbf{r}\right), $$

(68)

$$ \begin{array}{ll}{w}_i^{\mathrm{ref}}\left(\mathbf{r}\right)\hfill & =\frac{1}{2}{\displaystyle \int {d}^3{\mathbf{r}}^{\mathbf{\prime}}{f}_{\mathrm{Hxc}}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}};\left[{\rho}_i^{\mathrm{ref}}\right]\right){n}_i\left({\mathbf{r}}^{\mathbf{\prime}}\right)}\hfill \\ {}\hfill & -\frac{1}{2}{\displaystyle \int {d}^3{\mathbf{r}}^{\mathbf{\prime}}{d}^3{\mathbf{r}}^{\mathbf{{\prime\prime}}}{f}_{\mathrm{Hxc}}\left({\mathbf{r}}^{\mathbf{\prime}},{\mathbf{r}}^{\mathbf{{\prime\prime}}};\left[{\rho}_i^{\mathrm{ref}}\right]\right){n}_i\left({\mathbf{r}}^{\mathbf{\prime}}\right){n}_i\left({\mathbf{r}}^{\mathbf{{\prime\prime}}}\right)}\hfill \end{array}, $$

(69)

where we have introduced the compact notations

$$ {n}_i\left(\mathbf{r}\right)=\left|{\varphi}_i\right|{}^2\left(\mathbf{r}\right), $$

(70)

$$ {\rho}_i\left(\mathbf{r}\right)={f}_i{n}_i\left(\mathbf{r}\right), $$

(71)

$$ {\rho}_i^{\mathrm{ref}}=\rho \left(\mathbf{r}\right)-{\rho}_i\left(\mathbf{r}\right)+\frac{1}{2}{n}_i\left(\mathbf{r}\right). $$

(72)

Next, for i ≠ j, we have the following derivative expression:

$$ \frac{{\updelta \tilde{\Pi}}_j^{\mathrm{u}}}{\updelta {\rho}_i\left(\mathbf{r}\right)}={v}_{\mathrm{xc}}\left(\mathbf{r};\left[\rho -{\rho}_j\right]\right)-{v}_{\mathrm{xc}}\left(\mathbf{r};\left[\rho \right]\right)+{\displaystyle \int {d}^3{\mathbf{r}}^{\mathbf{\prime}}{f}_{\mathrm{xc}}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}};\left[{\rho}_j^{\mathrm{ref}}\right]\right){n}_j\left({\mathbf{r}}^{\mathbf{\prime}}\right)}. $$

(73)

Collecting the above contributions, the Koopmans-compliant Hamiltonian reads

$$ {\widehat{h}}_i=\widehat{h}\left[{\rho}_i^{\mathrm{ref}}\right]+{w}_i^{\mathrm{ref}}\left(\mathbf{r}\right)+{w}_i^{\mathrm{xd}}\left(\mathbf{r}\right), $$

(74)

where we have defined the cross-derivative (xd) term as

$$ {w}_i^{\mathrm{xd}}\left(\mathbf{r}\right)={\displaystyle \sum_{j\ne i}\frac{{\updelta \tilde{\Pi}}_j^{\mathrm{u}}}{\updelta {\rho}_i\left(\mathbf{r}\right)}}. $$

(75)

In a nutshell, the leading term of the Koopmans-compliant Hamiltonian in (74) is the original KS Hamiltonian evaluated at the reference density ρ ^ref _i , that is, the density where the occupation of the ith orbital has been replaced by $\frac{1}{2}$ in the Slater transition-state spirit. Additionally, we have two variational terms, w ^ref _i and w ^xd _i . The latter comes from the interdependence of the corrective terms corresponding to different orbitals; those can be shown analytically and numerically to have little influence on ODD spectral predictions. In fact, by expanding f _xc in Taylor series, one can see that w ^xd _i does not contribute up to the second order (e.g., no Hartree term shows up) and its leading contribution comes from the third derivative of E _xc with respect to the density. Instead, the reference potential w ^ref _i comes from the dependence of ρ ^ref _i on the ith orbital density.

We note that this term preserves the expectation value of the orbital-dependent Hamiltonian ${\widehat{h}}_i$ since ∫ d ³ r w ^ref _i (r)n _i (r) = 0. Nevertheless, w ^ref _i cancels long-range contributions (arising from the Hartree term) to the Hamiltonian and tends to reduce the localization of the orbitals. Thus, this term has to be considered as an unwanted by-product of variationality. Neglecting w ^ref _i means that the reference density is not updated during the minimization but only at the end of the calculation; the minimization is then repeated at fixed w ^ref _i until full self-consistency is reached. This approach (where the potential w ^xd _i is also omitted for simplicity) is termed the K ₀ method. Most of the results shown in the following have been produced by this version of the functional. We have checked numerically that K and K ₀ electronic-structure predictions do not differ significantly, except for quantities that are very sensitive to charge localization (such as polarizabilities).

In fact, while corrections to orbital energies of the K and K ₀ functionals are usually rather similar, the K functional has a weak tendency to localization (i.e., it does not fully exploit the corrections to orbital energies to improve on the localization of the charge density). Ultimately this results in the K charge density being very similar to that of the LDA functional (at variance with K ₀ where strong Perdew–Zunger like localization occurs), such that also the potential energy surfaces (PES) obtained by K are only slightly changed with respect to the LDA ones. This happens because the Koopmans correction is first and foremost an approach that addresses particle exchanges with an external path, hence charged excitations and photoemission. As such, it does not automatically improve on the total energies and the interplay between corrected orbital energies and charge density localization are key to current efforts to further develop the functionals. To this end, different flavors of the Koopmans-compliant functionals have been introduced (e.g., building K on top of PZ); these approximations will be discussed elsewhere.

3.2 Computational Details

Atomic calculations have been performed using a modified version of the ld1 code from the QUANTUM-ESPRESSO distribution [79]. For each angular momentum channel, the orbital occupations are averaged among the m quantum numbers, leading to a spherically symmetric contribution to the charge density. The ODD energy functionals (either PZ or K) are minimized by optimizing the radial distribution of each orbital at fixed angular momentum. Orbitals with the same l quantum numbers but corresponding to different n are then not automatically orthogonal. The validity of this approximation is carefully discussed in [65]. The MOLPRO code has been employed for the atomic HF calculations using the def2-QZVPP basis set.

With the exception of atoms, all calculations have been performed via a modified version of the CP code of QUANTUM-ESPRESSO. This implementation exploits plane-wave basis sets and pseudopotentials. Periodic boundary conditions are implicitly assumed because of the basis set, and a Coulomb cutoff technique (based upon auxiliary regularization functions of the Coulomb kernel [80]) is adopted to compute the electrostatic contributions. The energy minimization is carried out by using either a fictitious damped dynamics on the electronic degrees of freedom or conjugate gradient steps. The convergence threshold in minimizing the energy is 10⁻⁷ Ha. In the following we have used real wave functions expanded into plane waves up to a kinetic energy cutoff of 60 Ry (reduced to 40 Ry for acenes and fullerenes which contain just C and H atoms). DFT calculations have been performed within the local density approximation (LDA) [65]. Unless otherwise specified, all Koopmans-compliant calculations are carried out with the K ₀[LDA] scheme where the same dielectric screening coefficient α is used for all the orbitals (see (45)) and computed by requiring the ionization potential at N electrons to be equal to the electron affinity at N − 1 electrons (within a tolerance of 0.01 eV) (41).

4 Results

In this section, we review spectroscopic data for atoms and molecules, computed through standard KS-DFT, Hartree–Fock (HF), and orbital-density dependent (ODD) functionals, such as the Perdew–Zunger (PZ) and Koopmans-compliant methods. Theoretical estimates are compared with experimental data, when available. We mostly focus on ionization potentials (IPs), electron affinities (EAs), and energy levels (as obtained from photoemission experiments, for instance). In the case of molecules, all the energy transitions studied (including ionizations) have to be considered vertical, meaning that atomic relaxation is not allowed after the excitation.

4.1 Atoms

In Table 1 we report the ionization potentials for isolated atoms ranging from H to Kr computed at different levels of theory (LDA, HF, PZ, K[LDA], K ₀[LDA]) as (the opposite of) the topmost valence eigenvalue. In agreement with previous literature [65], the LDA HOMO (highest occupied molecular orbital) levels are not particularly accurate with an average error of 4.40 eV, and up to 9 eV for He. This reflects the intrinsic inaccuracy of LDA; in fact, exact DFT would provide exact ionization potentials for finite systems [81, 82]. It is interesting to note that the LDA functional systematically underestimates the IPs (HOMO levels are not sufficiently bound). Since the exponential decay of the total charge density [82] in the vacuum region is related to the IP I _N through

Table 1 Ionization potential of atoms

$$ \rho \left(\mathbf{r}\right)\sim {\mathrm{e}}^{-2\kappa \left|\mathbf{r}\right|}\kern2em \kappa =\sqrt{2{I}_N}, $$

(76)

underestimating the IP also leads to an overestimated delocalization of the charge density.

In contrast, despite its simplicity, the HF method gives rather accurate estimates for atomic IPs with an average error of 0.4 eV. A similar behavior is also shown by the ODD methods (PZ, K[LDA], K ₀[LDA]) with mean absolute deviations (MADs) ranging from 0.35 to 0.50 eV. However, this accuracy is not retained by all the functionals in predicting electron affinities, as discussed below. This fact is particularly apparent for PZ, which leaves the LDA empty states unaffected up to changes arising from the orthogonalization with respect to the occupied manifold (in the specific case of atoms where orthogonality is not imposed, PZ and LDA energy levels for empty states are identical by construction).

Before turning to molecules, we also analyze the performance of the above functionals in describing the deeper valence energy levels of atoms and compare the theoretical estimates with X-ray photoemission (XPS) results (Table 2). In agreement with previous data, LDA energy levels are the least accurate with a mean relative error of about 27%. Nevertheless, it has to be stressed that, at variance with the IP case, this error is not totally due to the LDA approximation but, as is well known, it is also inherent in the Kohn–Sham scheme itself [9, 13, 82]. For a detailed discussion of the accuracy of the KS-DFT scheme to describe charged excitations, we refer the reader to [9, 10]. The HF method (that can be formally viewed as the simplest approximation to a self-energy) works appreciably better (MAD of 6.6%) than LDA. In this context, the ODD methods provide the best accuracy with an average error of about 3.5%. The lowest MAD (ca. 3.3%) is found for K ₀[LDA]. Along with HF, these ODD methods do not fit into the standard KS scheme (where exchange and correlation effects are not described by a simple local potential) but go beyond it, having a more general structure with local but orbital-specific potentials. The properties of these theoretical schemes are discussed in more detail in [69] with particular emphasis on the description of energy levels and spectroscopic information.

Table 2 LDA, HF, PZ, K[LDA], and K ₀[LDA] orbital energies of He, Be, Ne, Mg, Ar, and Ca compared with experimental photoemission energies

4.2 Molecules

We now turn to assessing the predictive performance of ODD functionals for molecules.

4.2.1 Ionization Potentials

We have used four different sets of molecules in our benchmark. The first set includes 17 small molecules (H₂ to C₂H₄) from the G2 set. Computed and experimental ionization potentials are reported in Fig. 5a. The second set is taken from [83] and contains larger aromatic molecules (such as PTCDA, porphyrins, and phthalocyanines). Results are shown in Fig. 5b. The third and fourth sets are molecules from the acene (benzene to hexacene) and fullerene (C₂₀ to C₈₀) families (Fig. 5c). In all graphs, LDA (black), HF or GW (blue), PZ (orange), and K ₀[LDA] (red), results are compared with experimental ionization potentials (green). Vertical IPs are considered when available.

Fig. 5

Ionization potentials (IPs) of selected molecules. (a) Molecules from the G2 set [90]. (b) Molecules from the set in [83]. (c) Acenes (benzene to hexacene) and fullerenes from [84]. LDA, PZ, GW, K ₀[LDA] computed IPs are compared with experimental data where available. HF data are shown in (a) instead of GW. Reference (exp) data from: (a) [91]; (b) [83]; (c) [83, 85, 92, 93] for acenes and [84] for fullerenes

Confirming the trends observed for atoms, LDA IPs exhibit the largest error (25–35% depending on the molecular set) and systematically underestimate molecular IPs. On the other hand, unscaled PZ results show the opposite behavior, all the time resulting in IPs appreciably larger than the reference data with a relative error in the range 13–18%. As for atoms, the K approach performs extremely well (with an error of 1.7–2.5%) and its accuracy is comparable to high-level GW calculations. This level of accuracy is remarkable considering the reduced computational load of K relative to GW. Moreover, the predictive precision of K ₀[LDA] remains more or less constant through a large variety of systems, ranging from atoms to small and more extended molecules.

Concerning the GW method, we note that several practical schemes have been proposed in the literature to include partial or full self-consistency or to go beyond the random phase approximation (RPA) to screening. For each molecular set, we have chosen the most accurate GW results. This may explain the fluctuating accuracy of the GW calculations reported in Fig. 5. For instance, GW reference data [83] (Fig. 5b) have been obtained by starting from LDA eigenvalues and eigenvectors and performing a GW calculation with self-consistency on eigenvalues. On the other hand, GW data for fullerenes [84] come from a fully self-consistent GW calculation where the adiabatic TDDFT kernel based upon LDA is used in the calculation of W to improve upon the RPA polarizability. GW calculations for acenes are instead performed at the G₀W₀ (LDA) level. Benzene, naphthalene, and anthracene data are from [85], while results for tetracene and pentacene are from [83] (taken at the G₀W₀ (LDA) level for consistency).

4.2.2 Electron Affinities

Table 3 reports electron affinities (EAs) for the same molecule sets. Data computed at the LDA, PZ, and K ₀[LDA] levels of theory are compared to GW results from the literature and experiments. As expected, the LDA EAs are systematically too large (LUMO levels excessively bound). This is due to both the intrinsic inaccuracy of the LDA approximation and to the missing derivative discontinuity required by the KS scheme. As for atoms, the PZ scheme is not correcting the empty states because both the energy contributions and the potential corrections are zero for those levels. K ₀[LDA] instead shows a clear trend of systematic correction of the LDA results, with a residual error of about 0.5 eV in the most problematic cases (as compared to experimental data when available or GW otherwise). The accuracy of the K[LDA] results tends to improve when strong acceptors are considered, as is the case for fullerenes. While it is clear from the theoretical description of the K functionals that the accuracy of the method is connected to that of the ΔSCF approach [56], the ability to compute empty states using the K method highlights its important advantages over ΔSCF. In fact, it is known that the LDA functional (as well as other approximate DFT functionals) would not be able to bind the extra electron for most anions. Instead, the K formulation overcomes this difficulty and leads to a quantitatively reliable description of EAs.

Table 3 Electron affinities (EAs) for selected molecules

4.2.3 Energy Levels

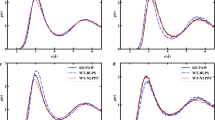
After we have carefully analyzed the accuracy of the K[LDA] method in predicting IPs and EAs, we now study full electronic spectra using ultraviolet photoemission spectroscopy (UPS) data as references. The peaks in these spectra correspond to the charged excitations of the system and are usually described in terms of main peaks (more or less sharp features with a finite width bearing most of the spectral weight) and satellites (shallow structures). For a full discussion see, e.g., [13, 86, 87]. In the present treatment, we will consider only the main peak structures, which we will refer to as orbital energies. Moreover, we will mostly compare the computed density of states (DOS) with the UPS spectra without including any transition matrix elements. Therefore, our analysis will not address UPS intensities, but only peak positions.

We report a detailed analysis for the case of four molecules, namely furan, pyrrole, anthracene, and tetracene. Data for the first two molecules are shown in Fig. 6 while data for the acenes are given in Fig. 7. In each panel we report the computed LDA, HF, PZ, and K ₀[LDA] DOS together with the UPS intensities at the top. A Gaussian broadening of 0.2 eV has been included in the DOS as a guide for the eye while the theoretical orbital energies (eigenvalues) are reported as vertical bars. We have also highlighted the most evident experimental features by dashed vertical lines. The energy scale corresponds to negative binding energies, the zero being the vacuum level. The spectral features at the highest energy (the smallest binding energy) correspond to the HOMO levels (negative ionization potentials) already described in the previous paragraphs. LUMO (lowest unoccupied molecular orbital) levels are not shown (when bound, out of the graphs at higher frequencies).

Fig. 6

Experimental UPS data (from [94]) are compared with the DOS computed at different levels of theory: LDA, HF, PZ, and K ₀[LDA]. Data for furan and pyrrole molecules are reported in the left and right panels, respectively

Fig. 7

Experimental UPS data (from [95]) are compared with the DOS computed at different levels of theory: LDA, HF, PZ, and K ₀[LDA]. Data for anthracene and tetracene molecules are reported in the left and right panels, respectively

In the case of furan and pyrrole, the electronic structure spectra are rather simple and orbital energy patterns can be easily followed, moving across different theoretical methods. In both cases, the LDA DOS shows systematic errors in predicting the HOMO position (about 3–4 eV above the experimental peak). The spectrum thus appears overall shifted to higher energies. The same holds for anthracene and tetracene, though the energy error on the HOMO position is smaller. As we have already discussed, this error can be totally attributed to the quality of the functional approximation. Moreover, by examining deeper energy levels, one can also note a slight shrinking of the energy scale with respect to experiment. This feature can also be perceived in the case of acenes. Besides the quality of the functional, here the use of a KS-DFT Hamiltonian (denoted by a local potential instead of a nonlocal and dynamical self-energy) is also expected to contribute to the error. For further details, see [69].

The onsets of photoemission in the HF spectra (the LUMO levels) are definitely more accurate than their LDA counterparts, showing remarkable an agreement for furan and pyrrole (with an error of 0.3 eV), as well as acenes (with an error of 0.4 eV). Despite the accuracy of the HOMO levels, deeper valence states are strongly over-bound, the spectrum being overall stretched towards negative energies. This behavior can be ascribed to missing correlation contributions in the HF method. Comparing with the GW theory [20, 88], one can show that correlation contributions would show up at first as static and dynamical screening effects. The systematic over-binding of HF can then be considered to be related to the absence of screening contributions.

The spectra obtained through the PZ method display an even more bound position of the HOMO levels, showing appreciable errors with respect to experiment (1.5–2 eV). At variance with the HF method, where the valence band width is strongly enhanced, PZ band widths are slightly more extended than the LDA ones, as shown in Table 4. This can be understood in terms of the correction to the potential provided by PZ. Assuming that the ODD minimizing orbitals are localized (as is typically the case with closed shell covalently bound systems), the representation of the Hamiltonian on this basis can be read in a tight-binding picture. Neglecting self-consistency effects, the PZ correction on LDA acts only on on-site matrix elements of the Hamiltonian, providing no correction for the off-diagonal (hopping) elements, which govern the band widths. When including self-consistency, PZ tends to provide a decoupling force that reduces the hybridization of the orbital. Such a conclusion is also supported by noting that the patterns of the PZ energy levels for acenes are rather different from that corresponding to the other methods and experiment. This observation does not extend to HF, which tends to increase the band width of covalent systems relative to LDA because the nonlocality of the exchange potential leads to larger hopping [89].

Table 4 Highest occupied orbital energy ε _ℋ and valence band width Δε of furan, pyrrole, anthracene, and tetracene computed at the LDA, HF, PZ, and K ₀ levels of theory

Finally, K ₀[LDA] spectra are in remarkable agreement with experimental data in terms of orbital energies over a wide energy range. We stress that no semiempirical shift or ad hoc alignment has been performed here. For furan and pyrrole, where deep valence states are very evident in the experimental data, the agreement with theory holds for states as deep as 25 eV. Even if the experimental data do not cover the full valence energy range, this comparison confirms that K ₀[LDA] band widths are very accurate and can be taken as a reference in assessing the accuracy of other theoretical methods (Table 4).

These results establish the precision of Koopmans-compliant methods in describing full electronic structures for representative families of systems, ranging from isolated atoms to large π-conjugated molecules. Extending this accuracy to the solid limit will be the subject of separate work.

5 Conclusions

In summary, we argued that the generalized Koopmans condition, i.e., the piecewise linearity of the self-consistent ground-state energy E(N) as a function of the electron number N, is critical to describe charged excitations in molecular systems and related spectroscopic properties. We have shown that imposing the generalized Koopmans theorem is equivalent to canceling relaxed-orbital many-electron self-interaction. We have also emphasized the distinction between the generalized Koopmans theorem, which is fulfilled by exact KS-DFT, and the restricted (original) Koopmans theorem, which is satisfied by the HF method (owing to the known cancellation of the self-Hartree and self-exchange terms) but not by exact DFT. To impose Koopmans compliance, we have constructed an ODD functional working first in the frozen-orbital approximation where self-consistent orbital relaxation and dielectric screening are neglected. Within this approximation, deviations from Koopmans compliance can be precisely quantified in terms of a non-Koopmans energy ${\tilde{\Pi}}_i$. This definition has then been extended to relaxed orbitals by approximating the nonlocal dielectric function ${\tilde{\varepsilon}}^{-1}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)$ as an orbital-independent uniform coefficient α that can be determined in a fully nonempirical fashion. The accuracy of the method has been demonstrated by computing the ionization potentials, electron affinities, and the full electronic structures of a wide range of atomic and molecular systems. Quantitative results from the Koopmans-compliant method have been shown to be comparable to those of high-level many-body perturbation theory methods such as GW at a fraction of the computational cost.

In introducing the ODD Koopmans-compliant functional, we have discussed one definition, based on the Slater one-half construction [63]. We have also developed alternative definitions of the non-Koopmans energy, leading to different flavors of Koopmans-compliant functionals and subtle differences in performance that will be discussed elsewhere. In addition, the uniform screening approximation that we have employed in constructing the functional could be refined by restoring the orbital dependence or non-locality of the dielectric function. Refinements in the description of electronic spectra through the prediction of photoemission amplitudes are underway. The study of extended systems and the prediction of optical spectra represent other exciting lines of development. A systematic and critical assessment of the accuracy of thermodynamic and kinetic properties within the different Koopmans-compliant functionals is also important; essentially, Koopmans-compliant functionals restore the correct energy levels, and can provide the foundations for other strategies aimed at reducing the delocalization tendency of common functionals. In fact, one of the most notable features of Koopmans-compliant methods is the fact that they can lead to spontaneous localization of the minimizing orbitals, suggesting that they would be ideally suited to basis-set reduction and linear-scaling techniques for the study of large-scale systems. These directions represent promising opportunities to extend the scope of current quantum simulations.