Anti-rollover Artificial Potential Field Motion Planning Method of an Autonomous Heavy Truck Optimised by Game Theory

Abstract

Anti-rollover is a critical factor to consider when planning the motion of autonomous heavy trucks. This paper proposed a method for autonomous heavy trucks to generate a path that avoids collisions and minimizes rollover risk. The corresponding rollover index is deduced from a 5-DOF heavy truck dynamic model that includes longitudinal motion, lateral motion, yaw motion, sprung mass roll motion, unsprung mass roll motion, and an anti-rollover artificial potential field (APF) is proposed based on this. The motion planning method, which is based on model predictive control (MPC), combines trajectory tracking, anti-rollover APF, and the improved obstacle avoidance APF and considers the truck dynamics constraints, obstacle avoidance, and anti-rollover. Furthermore, by using game theory, the coefficients of the two APF functions are optimised, and an optimal path is planned. The effectiveness of the optimised motion planning method is demonstrated in a variety of scenarios. The results demonstrate that the optimised motion planning method can effectively and efficiently avoid collisions and prevent rollover.

1 Introduction

1.1 Motivation

The autonomous vehicle is a significant technological advancement that has the potential to alleviate traffic congestion, reduce energy consumption, and enhance road safety. The advancement of artificial intelligence algorithms, communication technology, navigation technology, sensor technology, and other technologies has resulted in the advancement of autonomous vehicle technology [1, 2]. Vehicle motion planning is a critical component of self-driving vehicle technology. Its objective is to determine the safest and collision-free optimal path for vehicles to reach the target location as quickly as possible, given the change in the environmental state [3]. While most relevant research to date has concentrated on avoiding obstacles during vehicle motion planning, serious rollover accidents are more likely to occur with heavy trucks due to their structural characteristics of large unsprung mass and a high centre of mass. According to the National Highway Safety Administration's 2020 survey report, there were more than 12 million traffic accidents in the United States in 2019, with only about 1.8% being caused by vehicle rollover. However, 15.8% of fatal crashes were caused by vehicle rollover, with heavy trucks accounting for 12.1% of fatal accident models [4]. As a result, it is critical to investigate the motion planning method for heavy trucks that incorporates obstacle avoidance and anti-rollover.

1.2 Related Research

Many methods have been applied to vehicle motion planning to date. The planning of vehicle motion begins with planning the robot's path. It primarily constructs the environment map as a discrete grid in the early stage. It generates the shortest path using grid graph search algorithms such as the A* algorithm [5], and the improved A* algorithm [6, 7]. However, the algorithm based on the vehicle motion graph does not easily reflect production characteristics. Scholars have focused their attention on motion planning methods based on curve interpolation, sampling, machine learning, and numerical optimisation in recent years. Polynomial curves [8] and the Bezier curve [9] are two methods for interpolating curves that can generate a continuous and smooth driving path. However, this method describes the path using a specific curve function, which does not fully exploit the vehicle's movement capabilities. Random sampling and fixed sampling are both methods of sampling. We can determine the sequence of sample points with the desired connectivity in state space by generating sample points in configuration space. Typical sampling methods include the probabilistic road map (PRM) algorithm [10] and the fast search random tree (RRT) algorithm [11]. They are, however, unsuitable for complex conditions due to the blind nature of random sampling. Machine learning techniques such as neural networks [12], reinforcement learning [13], and depth learning [14] all rely on many training samples to solve the actual planning problem. It is suitable for complex scenes, but requires many training samples, and the quality of the training also influences the decision-making level. The artificial potential field (APF) method [15], the genetic algorithm [16], and the model predictive control (MPC) algorithm [17] are all examples of numerical optimisation methods. By establishing differential equations, necessary constraints and vehicle driving performance indicators are added to create an optimisation problem, which has evolved into the most advanced method for vehicle motion planning in recent years. Additionally, there are some specialized methods for planning vehicle motion. Smirnov et al. [18], for instance, employed game theory to forecast the behaviour of traffic vehicles. Additionally, there are some motion planning methods for specialized work environments, such as parallel parking of passenger cars, vehicle warehousing, and parking of vehicles in multiple conditions [19,20,21]. To summarise, most existing motion planning methods address the problem of vehicles avoiding obstacles while in motion, but few of them focus on rollover prevention. This paper is primarily concerned with this issue.

The rollover index of the vehicle at any point in time is used as the evaluation index to describe and judge whether the vehicle rolls over. Lateral load transfer rate (LTR) applies to a wide variety of vehicle models and is frequently used as a vehicle rollover evaluation index [22, 23]. However, because the vertical load on the wheel is difficult to measure, scholars have studied and proposed many rollover indicators that can measure vehicle parameters. Zhu et al. [24] proposed an early warning algorithm based on time to rollover (TTR) for determining the rollover state of the vehicle. Jin et al. [25] proposed a new rollover index with measurable parameters for predicting a vehicle's rollover risk under various conditions. Currently, some scholars have taken lateral stability into account when designing autonomous vehicles' decision-making and executive levels. For example, Li et al. [26] proposed a new local path planning method for off-road autonomous driving on various road profiles, combining it with a rollover warning time, and provided a predefined global path. Gwayi eta al. [27] proposed a nonlinear model predictive control-based roll control algorithm for autonomous vehicles (MMPC). By adjusting the steering angle and braking the front wheels, the vehicle followed the prescribed path at the optimal speed while also observing roll angle, yaw rate, and physical constraints to maintain vehicle stability. Cheng et al. [28] proposed a lateral stability-coordinated collision avoidance control system (LSCACS). LSCACS obtains reference values for yaw angle and yaw angle via a linear two-degree-of-freedom vehicle model, determines the system’s operating mode using time to collision (TTC), and finally calculates the corresponding tire force using MPC. Jin et al. [29] considered tracking error and anti-rollover constraints when designing the MPC strategy and planned a safe path without rollover for autonomous vehicles.

1.3 Contributions

This paper proposes a method for planning the motion of an autonomous heavy truck using MPC, anti-rollover APF, obstacle avoidance APF, and game theory. The main contributions of this paper are as follows:

• 1. A novel obstacle avoidance APF technique is proposed. Consider vehicles and obstacles as rectangles and create ellipses around them. To obtain a more accurate obstacle avoidance APF function, the minimum distance between ellipses is used as the factor of the APF function.

• 2. The concept of anti-rollover APF is proposed and applied to vehicle motion planning using the 5-degrees-of-freedom (DOF) autonomous heavy truck model, rollover index, and APF principle.

• 3. Game theory is used to optimise the MPC motion planning algorithm, which combines obstacle avoidance and anti-rollover APF, to obtain a safe path from obstacles and stability from rollover.

1.4 Paper Organization

The remainder of this paper is organized as follows. Section 2 establishes a 5-DOF vehicle rollover model that takes longitudinal motion, lateral motion, yaw motion, sprung mass roll motion, and unsprung mass roll motion into account. Additionally, the rollover index of a large truck is calculated and verified. Section 3 defines and illustrates the obstacle avoidance and anti-rollover APF functions. In Section 4, the MPC strategy is designed and optimised using game theory in conjunction with anti-rollover APF and obstacle avoidance APF. Section 5 simulates and analyses the motion planning algorithm under two conditions. Finally, Section 6 summarises the conclusions.

2 Rollover Dynamics of the Autonomous Heavy Truck

In general, vehicle dynamics modelling takes longitudinal motion, lateral motion, and yaw motion into account. However, compared to other models, the primary characteristic of heavy trucks is their high unsprung mass, which makes them more prone to rollover accidents. As a result, this section extends the traditional 3-DOF vehicle dynamics model by including the roll motion of the heavy truck's sprung and unsprung mass, establishing a 5-DOF heavy truck dynamics model, validating it, and deducing the rollover index suitable for the autonomous heavy truck.

2.1 Vehicle Model

The autonomous heavy truck has a high centre of gravity, large unsprung mass, and a relatively large aspect ratio, so interaction and coupling of yaw motion, lateral motion, and roll motion need to be considered in vehicle modelling. However, some factors that have little influence on vehicle rollover are ignored, such as pitch motion, vertical motion, and lateral wind. Thus, a 5-DOF heavy truck dynamic model is built, as shown in Figure 1, which includes longitudinal, lateral, yaw, sprung mass roll, and unsprung mass roll motions.

Figure 1

Dynamics model of the heavy truck

Newton's second law and D'Alembert's principle allow us to obtain the motion equations for each degree of freedom in the entire vehicle model as follows.

Longitudinal motion equation of vehicle:

$$ma_{{\text{x}}} = 2F_{{{\text{xf}}}} \cos \delta_{{\text{f}}} - 2F_{{{\text{yf}}}} \sin \delta_{{\text{f}}} + 2F_{{{\text{xr}}}} .$$

(1)

Lateral motion equation of the whole vehicle coupled with the roll motion of the sprung mass:

$$ma_{{\text{y}}} - m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )\ddot{\varphi }_{{\text{s}}} = 2F_{{{\text{yf}}}} \cos \delta_{{\text{f}}} + 2F_{{{\text{xf}}}} \sin \delta_{{\text{f}}} + 2F_{{{\text{yr}}}} .$$

(2)

Vehicle yaw motion equation coupled with lateral motion:

$$I_{{\text{Z}}} \dot{r}\,{ = 2}a(F_{{{\text{yf}}}} \cos \delta_{{\text{f}}} + F_{{{\text{xf}}}} \sin \delta_{{\text{f}}} ) - 2bF_{{{\text{yr}}}} .$$

(3)

Roll motion equation of sprung mass:

$$\begin{aligned} & \left[I_{\text{Xs}} + m_{\text{s}}\;(h_{\text{s}}-h_{\text{rc}})^{2}\right]{\ddot{\varphi}}_{\text{s}}-m_{\text{s}} a_{\text{y}} \left(h_{\text{s}}-h_{\text{rc}}\right) \\ & = m_{\text{s}}g \left(h_{\text{s}}-h_{\text{rc}}\right){\varphi}_{\text{s}} - K_{\text{s}} \left({\varphi}_{\text{s}}-\varphi_{\text{u}}\right) - C_{\text{s}} \left({\dot{\varphi}}_{\text{s}} - {\dot{\varphi}}_{\text{u}}\right). \end{aligned}$$

(4)

Roll motion equation of unsprung mass:

$$\begin{aligned} I_{{{\text{Xu}}}} \ddot{\varphi }_{{\text{u}}} = \, & k_{{\text{s}}} (\varphi _{{\text{s}}} - \varphi _{{\text{u}}} ) + c_{{\text{s}}} (\dot{\varphi }_{{\text{s}}} - \dot{\varphi }_{{\text{u}}} ) \\ & + 2F_{{\text{y}}} h_{{\text{u}}} + \frac{{T_{{\text{w}}} }}{2}(F_{{{\text{zL}}}} - F_{{{\text{zR}}}} ), \\ \end{aligned}$$

(5)

where F_y is the lateral force, and its equation can be obtained as follows:

$$F_{{\text{y}}} = F_{{{\text{yf}}}} \cos \delta_{{\text{f}}} + F_{{{\text{xf}}}} \sin \delta_{{\text{f}}} + F_{{{\text{yr}}}} .$$

(6)

The longitudinal and lateral accelerations at the mass centre are expressed as follows:

$$a_{{\text{x}}} = \dot{u} - vr,$$

(7)

$$a_{{\text{y}}} = \dot{v} + ur,$$

(8)

where m, m_s and m_u denote the total mass, sprung mass and unsprung mass of the heavy truck, respectively, a_x and a_y denote the longitudinal and lateral accelerations of the vehicle, respectively, h_s, h_u and h_rc denote the height of the sprung mass centroid, unsprung mass centroid and roll centre, respectively, a and b denote the distance from the front and rear axles to the centroid, respectively, T_w denotes the width of the wheelbase of heavy truck, $\ddot{\varphi}_{\text{s}}$ and $\ddot{\varphi}_{\text{u}}$ denote the roll angle of sprung mass and unsprung mass, respectively, δ_f denotes the front wheel angle, F_xf and F_xr denote the longitudinal force of the front and rear axle tires, respectively, F_yf and F_yr are the lateral deflection force of the front and rear axle tires, respectively, F_zL and F_zR are the vertical force of the left and right tires, respectively, F_y denotes the lateral force on the vehicle, u and v are the longitudinal speed and lateral speed of the vehicle, respectively, r denotes the yaw angular speed, g denotes the gravitational acceleration, I_Z denotes the yaw moment of inertia of the vehicle, I_Xs and I_Xu denote the roll moment of inertia of sprung mass and unsprung mass around their respective centroids, k_s denotes the equivalent roll stiffness of the suspension, c_s denotes the equivalent roll damping of the suspension.

Tires generate most of the vehicle's motion force, classified as longitudinal force and lateral force. The longitudinal force is the primary source of force required to propel and brake the vehicle. The lateral force provides the necessary force for steering the vehicle, which is also a critical factor in determining the vehicle's safety and handling stability. The angle of side deflection of the heavy truck's front and rear wheels can be expressed as follows:

$$\beta_{{\text{f}}} = \arctan \left( {\frac{v + ar}{u}} \right) - \delta_{{\text{f}}} ,$$

(9)

$$\beta_{{\text{r}}} = \arctan \left( {\frac{v - br}{u}} \right).$$

(10)

To simplify theoretical research on the dynamic rollover characteristics of heavy trucks, Pacejka's brush tire model is used to calculate the tire lateral force as follows [30]:

$$F_{{\text{yf,r}}} = \left\{ \begin{gathered} \left( \begin{gathered} \frac{{k_{{\text{f,r}}}^{2} \tan \beta_{{\text{f,r}}} }}{{3\mu F_{{\text{zf,r}}} }}\left| {\tan \beta_{{\text{f,r}}} } \right| \hfill \\ - k_{{\text{f,r}}} \tan \beta_{{\text{f,r}}} \hfill \\ - \frac{{k_{{\text{f,r}}}^{3} }}{{27\mu^{2} F_{{\text{zf,r}}}^{2} }}\tan^{3} \beta_{{\text{f,r}}} \hfill \\ \end{gathered} \right), \, \left| {\beta_{{\text{f,r}}} } \right| < \arctan \left( {\frac{{3\mu F_{{\text{zf,r}}} }}{{k_{{\text{f,r}}} }}} \right), \hfill \\ - \mu F_{{\text{zf,r}}}\, {\text{sgn}} \beta_{{\text{f,r}}} , \quad \left| {\beta_{{\text{f,r}}} } \right| \ge \arctan \left( {\frac{{3\mu F_{{\text{zf,r}}} }}{{k_{{\text{f,r}}} }}} \right). \hfill \\ \end{gathered} \right.$$

(11)

Among them, β_f and β_r denote the sideslip angle of the front and rear tire, k_f and k_r represent the cornering stiffness of the front and rear tire, μ denotes the road adhesion coefficient, F_zf and F_zr denote the vertical load of the front and rear tire.

2.2 Rollover Index

LTR is the ratio of the vertical loads on the vehicle's left and right wheels to the total vertical load. Because it applies to a wide variety of models, it has become the most frequently used rollover evaluation index. However, it is difficult to directly measure the vertical load on the left and right wheels during the actual driving of heavy trucks. As a result, the applicable rollover index for heavy trucks must be determined.

According to the force balance and moment balance equations in Figure 1, the vertical loads F_zL and F_zR on the heavy vehicle's left and right wheels satisfy the following relationship:

$$F_{{{\text{zL}}}} + F_{{{\text{zR}}}} = mg,$$

(12)

$$\begin{aligned} \frac{{T_{{\text{w}}} }}{2}\left( {F_{{{\text{zL}}}} - F_{{{\text{zR}}}} } \right) = \, & I_{{{\text{Xu}}}} \ddot{\varphi }_{{\text{u}}} - k_{{\text{s}}} (\varphi _{{\text{s}}} - \varphi _{{\text{u}}} ) \\ & - c_{{\text{s}}} (\dot{\varphi }_{{\text{s}}} - \dot{\varphi }_{{\text{u}}} ) - 2F_{{\text{y}}} h_{{\text{u}}} . \\ \end{aligned}$$

(13)

By incorporating Eq. (2) and Eq. (4) into Eq. (13), the following result is obtained:

$$\begin{aligned} F_{{{\text{zL}}}} - F_{{{\text{zR}}}} = \, & \frac{2}{{T_{{\text{w}}} }}\{ I_{{{\text{Xu}}}} \ddot{\varphi }_{{\text{u}}} + I_{{{\text{Xs}}}} \ddot{\varphi }_{{\text{s}}} - ma_{{\text{y}}} h_{{\text{u}}} \\ & + m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[(h_{{\text{s}}} - h_{{{\text{rc}}}} + h_{{\text{u}}} )\ddot{\varphi }_{{\text{s}}} - g\varphi _{{\text{s}}} - a_{{\text{y}}} ]\} . \\ \end{aligned}$$

(14)

According to the principle of LTR, the rollover index (RI) can be obtained from Eqs. (12) and (14):

$$\begin{aligned} RI = \, & \frac{2}{{mgT_{{\text{w}}} }}\{ I_{{{\text{Xu}}}} \ddot{\varphi }_{{\text{u}}} + I_{{{\text{Xs}}}} \ddot{\varphi }_{{\text{s}}} - ma_{{\text{y}}} h_{{\text{u}}} \\ & + m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[(h_{{\text{s}}} - h_{{{\text{rc}}}} + h_{{\text{u}}} )\ddot{\varphi }_{{\text{s}}} - g\varphi _{{\text{s}}} - a_{{\text{y}}} ]\} . \\ \end{aligned}$$

(15)

The vertical load of the vehicle's left and right vehicles can be converted to more easily measurable state variables via Eq. (15), such as roll angle, roll angle acceleration, lateral acceleration. This rollover index is more appropriate for the model of heavy truck dynamics developed in this paper.

2.3 Validation of Vehicle Model and Rollover Index

To verify the validity and accuracy of the heavy-duty truck dynamics model and rollover index established in this paper, the simulation vehicle model in TruckSim software, which is closer to the actual vehicle, is compared to the established model and index. Table 1 summarises the simulation model parameters that were chosen.

Table 1 Heavy truck model parameters

When the simulation condition is set to J-Turn, the vehicle travels at a speed of 60 km/h, and the front wheel has a step angle of 3.5°. Execution of the simulation and theoretical models, respectively. The dynamic response of the vehicle is depicted in Figure 2.

Figure 2

Dynamic response of the heavy truck: (a) Yaw rate, (b) Roll angle

As illustrated in Figure 2, the established theoretical model for heavy trucks is very similar to the yaw rate and roll angle response curves of the simulation model under J-Turn conditions. In Figure 2 (a), the steady-state values of the yaw rate calculated by the simulation model and theoretical model are 8.55°/s and 8.41°/s, respectively, with an error of about 1.6%; in Figure 2 (b), the steady-state values of roll angle calculated by the simulation model and theoretical model are 0.42° and 0.407° respectively, with an error of about 3.1%. The yaw rate and roll angle errors are both less than 5%, which is within the allowable range. This paper establishes an accurate and effective theoretical model of the heavy truck.

Figure 3 shows the dynamic performances of the triaxle bus rollover. The solid lines are the results simulated by TruckSim model, and the dotted lines are calculated by the theoretical model.

Figure 3

Rollover index of the heavy truck

Similarly, the rollover index derived from the established heavy truck dynamic model is verified and compared to LTR under this operating condition. Figure 3 illustrates the results. LTR and RI have steady-state values of −0.285 and −0.288, respectively, with an error of approximately 1.5%. As a result, the rollover index can be considered effective and feasible to measure heavy truck rollover stability.

3 Artificial Potential Field of the Autonomous Heavy Truck Motion Planning

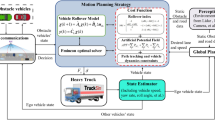
Figure 4 depicts the framework for the motion planning system of an autonomous heavy truck, which includes a perception module, a global path planning module, an MPC motion planning module optimised using game theory, and a controlled autonomous heavy truck. The perception module can obtain road data, obstacle location, and the location and speed of surrounding vehicles via lidar, radar, camera, and V2V communication, which are then output to the global path planning module and the motion planning module. The module for global path planning determines an appropriate global path based on-road data. The motion planning module, based on MPC and game theory, combines received environment information with the state of the self-vehicle, calculates and optimises the optimal longitudinal force and steering angle, and outputs them to the controlled heavy truck. The nonlinear solver is used to predict iteratively the nonlinear vehicle model derived from the heavy truck anti-rollover model. The cost function is enhanced with the obstacle avoidance APF and anti-rollover APF functions, and their coefficients are optimised using game theory. Additionally, vehicle dynamics constraints are considered.

Figure 4

Block diagram of the autonomous heavy truck motion planning system

Khatib proposed the concept of an APF as a virtual force field [17]. Its fundamental idea is that by designing specific functions, one can abstract the environment of moving objects into an APF. This section proposes a new method for calculating obstacle avoidance APF and the concept of anti-rollover APF, both of which are combined to produce a new APF function.

3.1 Obstacle Avoidance APF

The basic idea of obstacle avoidance APF is to control the motion of the controlled object by utilizing the gravitational potential field of the target point on the controlled object and the repulsive potential field of the obstacle on the controlled object. The tracking term in the MPC cost function is used in this paper to track the controlled heavy truck's desired global trajectory. Therefore, only the repulsive potential field function for avoiding obstacles is considered, rather than the gravitational potential field.

In the traditional APF, the change rate of the repulsion potential field function increases rapidly as the distance between the controlled object and the obstacle decreases and approaches infinity, preventing the controlled object from colliding with the obstacle. In general, the controlled object and all other moving objects and obstacles are considered particles or a circle [15], and the potential field force is calculated by calculating the distance between them. It is, however, inapplicable to heavy trucks, as their longitudinal safety distance should be greater, and their transverse safety distance should be relatively smaller.

Moving vehicles and obstacles are treated as rectangles in this paper. They are represented as circumscribed ellipses whose long axis direction is the same as the rectangle's longest side, as illustrated in Figure 5. Additionally, as a factor of the obstacle avoidance APF function, the minimum distance between two circumscribed ellipses (D) is calculated. When the object is treated as an ellipse, we can obtain a greater longitudinal safety distance and a smaller transverse safety distance between the controlled vehicle and other objects. As a result, a more accurate and reliable APF function for obstacle avoidance is obtained.

Figure 5

The shortest distance between the vehicle and the obstacle

By the position point C_E (x_c, y_c), length (L_E), width (W_E), and heading angle of vehicle or obstacle (ψ). The external ellipse that can be used as the vehicle or obstacle is expressed as:

$$\begin{gathered} \frac{{2[(x - x_{{\text{c}}} )\cos \psi + (y - y_{{\text{c}}} )\sin \psi ]^{2} }}{{L_{{\text{E}}}^{2} }} \hfill \\ + \frac{{2[(y - y_{{\text{c}}} )\cos \psi - (x - x_{{\text{c}}} )\sin \psi ]^{2} }}{{W_{{\text{E}}}^{2} }} = 1. \hfill \\ \end{gathered}$$

(16)

Assume that (x₁, y₁) and (x₂, y₂) are points on the circumscribed ellipses of the vehicle and the obstacle, respectively. The shortest distance between two circumscribed ellipses (D_NC) is denoted as follows:

$$D_{{NC}} = \min \left[ {\sqrt {(x_{1} - x_{2} )^{2} + (y_{1} - y_{2} )^{2} } } \right].$$

(17)

Suppose (x₃, y₃) is the point on the pit circumscribed ellipse. The minimum distance between vehicle circumscribed ellipse and pit circumscribed ellipse (D_C) is expressed as:

$$D_{\text{C}} = \min \left[\sqrt {(x_{1} - x_{3} )^{2} + (y_{1} - y_{3} )^{2} } \right].$$

(18)

Suppose (x₄, y₄) is the point on the road boundary. The minimum distance between vehicle circumscribed ellipse and road boundary (D_R) is expressed as:

$$D_{\text{R}} = \min \left[\sqrt {(x_{1} - x_{4} )^{2} + (y_{1} - y_{4} )^{2} } \right].$$

(19)

The obstacle avoidance APF function includes the potential field function of non-crossing obstacles (U_NC), the potential field function of crossing obstacles (U_C), and the potential field function of road boundary (U_R), as shown in Eq. (20):

$$oaAPF = \sum\limits_{i} {U_{{{\text{NC}}_{i} }} } + \sum\limits_{j} {U_{{{\text{C}}_{j} }} } + \sum\limits_{q} {U_{{{\text{R}}_{q} }} } ,$$

(20)

where i, j, and q are the indices of the uncrossable obstacle, crossable obstacle, and road's boundary, respectively.

Fixed obstacles, other vehicles, and pedestrians are all examples of non-crossing obstacles. They are obstacles that heavy trucks must avoid when planning their route. Otherwise, they will cause significant damage to vehicles and their occupants. As an example of a potential field function for non-crossing obstacles, consider the followings:

$$U_{{\text{NC}}} \left( {D_{{\text{NC}}} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}k_{{\text{NC}}} \left( {\frac{1}{{D_{{\text{NC}}} }} - \frac{1}{{D_{NC0} }}} \right)^{2} ,} & {D_{{\text{NC}}} \le D_{{{\text{NC0}}}} ,} \\ {0,} & {D_{{\text{NC}}} > D_{{{\text{NC0}}}} ,} \\ \end{array} } \right.$$

(21)

where k_NC denotes the repulsion field constant of the non-crossing obstacle greater than zero, D_NC denotes the shortest distance between the current position of the vehicle and the respective external ellipse of the non-crossing obstacle, and D_NC0 denotes the maximum influence range of the point repulsion potential field at the position of the non-crossing obstacle. When D_NC > D_NC0, the repulsive potential field of the obstacle location point has no effect.

The obstacles that can be crossed include speed bumps, uneven roads, and others that will affect the vehicle's movement when it passes but are not necessary to avoid. Avoiding contact with them can help reduce the risk of vehicle instability, such as rollover, caused by a change in the vehicle's motion state. The exponential function is used to design the potential field of crossing obstacles. Because its change rate is larger, the potential field value increases rapidly when the distance between the vehicle and the crossing obstacles is close, but the potential field value is smaller than that of the non-crossing obstacles [17]. Assume the following function represents the possible field function of the obstacle that can be crossed:

$$U_{\text{C}} \left( {D_{\text{C}} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}k_{\text{C}} \left( {\frac{1}{{e^{{2D_{\text{C}} }} }} - \frac{1}{{e^{{2D_{C0} }} }}} \right),} & {D_{\text{C}} \le D_{C0} ,} \\ {0,} & {D_{\text{C}} > D_{{{\text{C}} 0}} ,} \\ \end{array} } \right.$$

(22)

where k_C denotes the crossing obstacle's repulsion field constant greater than zero, D_C denotes the shortest distance between the vehicle's current position and the crossing obstacle's external ellipse, and D_C0 denotes the crossing obstacle's repulsion potential field's maximum influence range. When D_C > D_C0, the repulsive potential field of the obstacle position point has no effect.

The road boundary can be used to restrict the driving path of vehicles and thus reduce the likelihood of collisions with other vehicles or obstacles. Consider the following function as the road boundary's potential field function:

$$U_{\text{R}} (D_{\text{R}} ) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}k_{\text{R}} \left( {\frac{1}{{D_{\text{R}} }} - \frac{1}{{D_{R0} }}} \right)^{2} ,} & {D_{\text{R}} \le D_{R0} ,} \\ {0,} & {D_{\text{R}} > D_{R0} ,} \\ \end{array} } \right.$$

(23)

where k_R denotes the road boundary's repulsion field constant greater than zero, D_R denotes the shortest distance between the external ellipse at the vehicle's current position and the road boundary, and D_R0 denotes the road boundary's minimum allowable distance.

The distribution of the repulsion potential field generated by the non-crossable obstacle (20,0), the crossable obstacle (20,0), and the two-lane boundary is shown in Figure 6. The figure shows that the potential field value generated around the non-crossing obstacle is extremely large. The closer the self-vehicle is to the obstacle, the faster the potential field value increases and the stronger the "repulsion" generated to the self-vehicle, allowing it to avoid the obstacle. The potential field value generated around a crossing obstacle is negligible compared to the value generated around a non-crossing obstacle. The potential field value increases slowly as it approaches the obstacle. The two-lane road boundary generates a large potential field value. In contrast, the centre line of each lane generates the smallest potential field value, which increases slightly on the two-lane boundary. It demonstrates that the road boundary potential field function encourages vehicles to travel along the lane centreline and away from the road boundary, but they are permitted to cross it.

Figure 6

Potential field value: (a) Non-crossing obstacles at (20,0), (b) Crossing obstacles at (20,0), (c) Two-lane boundary

3.2 Anti-Rollover APF

Heavy truck rollovers result in vehicle instability, which in severe cases results in traffic accidents, significant financial losses, and even jeopardises human life safety. The dynamic rollover problem is considered in this paper when planning the motion of a heavy truck. The concept of anti-rollover APF is proposed in conjunction with the application of traditional APF. Assuming the vehicle driving path and the heavy truck itself have a virtual anti-rollover potential field (U_R1 and U_R2), the anti-rollover APF function is defined as follows:

$$arAPF = U_{{{\text{R1}}}} + U_{{{\text{R2}}}} .$$

(24)

In general, the road design meets the safety curvature required by heavy truck steering. When the steering of heavy trucks is excessively large, the path curvature during actual driving is excessive, significantly increasing the risk of rollover. If the target path induces a gravitational force on the heavy truck to align the curvature of its planned path with the target path curvature, the gravitational potential field function generated by the target path curvature on the heavy truck (U_R1) is defined as follows:

$$U_{{{\text{R1}}}} = \frac{1}{2}k_{{\uprho }} (\rho - \rho_{{\text{g}}} )^{2} ,$$

(25)

where k_ρ denotes the anti-rollover gravitational field constant greater than zero, ρ denotes the actual path curvature of a heavy vehicle, and ρ_g denotes the curvature of the target path.

Depending on the circumstances, the vehicle may be required to deviate from the road's curvature while driving. To avoid rolling over, it is assumed that the vehicle generates an anti-rollover potential field on its own. When the rollover index of a heavy truck increases in absolute value, the vehicle generates gravity to reduce the rollover index and prevent rollover accidents. Assign the following definition to the anti-rollover gravitational potential field function generated by the heavy vehicle:

$$U_{{{\text{R2}}}} = \frac{1}{2}k_{{\text{R}}} RI^{2} ,$$

(26)

where k_R denotes the anti-rollover gravitational field constant greater than zero and RI denotes the rollover index of a heavy vehicle.

It can be obtained from Eq. (26) and Eq. (15):

$$U_{{{\text{R2}}}} = \frac{{2k_{{\text{R}}} }}{{m^{2} g^{2} T_{{\text{w}}}^{2} }}\left\{ {I_{{{\text{Xu}}}} \ddot{\varphi }_{{\text{u}}} + I_{{{\text{Xs}}}} \ddot{\varphi }_{{\text{s}}} - ma_{{\text{y}}} h_{{\text{u}}} + m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )\left[ {(h_{{\text{s}}} - h_{{{\text{rc}}}} + h_{{\text{u}}} )\ddot{\varphi }_{{\text{s}}} - g\varphi _{{\text{s}}} - a_{{\text{y}}} } \right]} \right\}^{2} .$$

(27)

The distribution of the gravitational potential field generated by the curvature of the road's target path with a radius of curvature of 10 m in the natural coordinate system and the anti-rollover gravitational potential field generated by the vehicle are depicted in Figure 7.

Figure 7

Potential field value: (a) Road curvature, (b) Vehicle itself

When the vehicle travels along the road and the curvature at each time is consistent with the curvature of the target path, that is, the turning radius of the vehicle is equal to the half diameter of the curvature of the target road, the value of the gravitational potential field generated by the road to the vehicle is zero; when the vehicle's curvature changes, the target path generates attraction for the vehicle, allowing the vehicle's curvature to remain as close to the target path's curvature as possible. The greater the vehicle's curvature change, the greater the gravitational potential field generated by the target path to the vehicle, and thus the greater the attraction. When the vehicle's rollover index is close to zero, that is, when the vehicle does not roll, the ant-rollover potential field value generated by the vehicle tends to zero; when the vehicle turns, it rolls, changing the rollover index. At this point, the vehicle will generate a large anti-rollover gravity to cause the vehicle's movement state to change, thereby reducing the change in rollover index and preventing the vehicle from rolling over.

4 MPC Motion Planner of the Autonomous Heavy Truck

The MPC algorithm is used in this paper to control the motion of a driverless heavy vehicle. It possesses favourable control properties, a rapid response time, and high robustness, and is capable of effectively resolving multivariable and multi-constraint problems. Taking the 5-DOF heavy vehicle dynamic model established earlier and combined with the kinematic model as the prediction model, the future motion state of the heavy vehicle is predicted. The cost function is iteratively optimised through a nonlinear solver according to the error value between the set front wheel angle reference value, roll angle reference value, and yaw rate expected value and the actual front wheel angle, roll angle, and yaw rate, the optimal control sequence of the front wheel angle and longitudinal force is obtained, so as to realise the motion planning of driverless heavy truck. Additionally, the MPC controller continuously collects the current state parameters of the heavy truck for correction during driving, including front-wheel angle, roll angle, and yaw rate.

4.1 Prediction Model of the Autonomous Heavy Truck

Kinematics must be considered first when planning the motion of heavy trucks. The kinematics equation for a large truck in an inertial coordinate system is as follows:

$$\left\{ \begin{gathered} \dot{X} = u\cos \psi - v\sin \psi , \hfill \\ \dot{Y} = u\sin \psi + v\cos \psi , \hfill \\ \end{gathered} \right.$$

(28)

where X and Y respectively represent the displacement of the vehicle in the X direction and Y direction in the natural coordinate system.

Combined with the kinematics model of heavy trucks and the 5-DOF dynamic model established above, it is used as the MPC. Let the state quantity $\xi = \left[ {u \, v \, r \, \dot{\varphi }_{{\text{s}}} \, \dot{\varphi }_{{\text{u}}} \, X \, Y \, \psi \, \varphi_{{\text{s}}} \, \varphi_{{\text{u}}} } \right]^{{\text{T}}}$, control quantity $\eta = \left[ {\delta_{{\text{f}}} \, F_{{{\text{xf}}}} \, F_{{{\text{xr}}}} } \right]^{{\text{T}}}$. Linearizing the tire model, it can be obtained from Eqs. (1)−(11) and Eq. (28):

$$\dot{\xi } = f(\xi ,\eta ),$$

(29)

where,

$$f_{1} (\xi ,\eta ) = \frac{{2u(F_{{{\text{xf}}}} + F_{{{\text{xr}}}} - k_{{\text{f}}} \delta_{{\text{f}}}^{2} ) + 2k_{{\text{f}}} \delta_{{\text{f}}} (v + ar)}}{mu} + vr,$$

$$f_{2} (\xi ,\eta ) = \frac{{\left\{ \begin{gathered} 2u\delta_{{\text{f}}} (F_{{{\text{xf}}}} { + }k_{{\text{f}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ] \hfill \\ + um_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )g\varphi_{{\text{s}}} - k_{{\text{s}}} (\varphi_{{\text{s}}} - \varphi_{{\text{u}}} ) \hfill \\ - c_{{\text{s}}} (\dot{\varphi }_{{\text{s}}} - \dot{\varphi }_{{\text{u}}} )] - 2[(k_{{\text{f}}} + k_{{\text{r}}} )v{ + }r(ak_{{\text{f}}} \hfill \\ - bk_{{\text{r}}} )][I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ] \hfill \\ \end{gathered} \right\}}}{{u[mI_{{{\text{Xs}}}} + m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}} - ur,$$

$$f_{3} (\xi ,\eta ) = \frac{{{2}au(F_{{{\text{xf}}}} + k_{{\text{f}}} )\delta_{{\text{f}}} - 2(ak_{{\text{f}}} - bk_{{\text{r}}} )v - 2(a^{2} k_{{\text{f}}} + b^{2} k_{{\text{r}}} )r}}{{I_{{\text{Z}}} u}},$$

$$f_{4} (\xi ,\eta ) = \frac{{\left\{ \begin{gathered} um_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[2\delta_{{\text{f}}} (F_{{{\text{xf}}}} + k_{{\text{f}}} ) + mg\varphi_{{\text{s}}} ] \hfill \\ - um[k_{{\text{s}}} (\varphi_{{\text{s}}} - \varphi_{{\text{u}}} ) + c_{{\text{s}}} (\dot{\varphi }_{{\text{s}}} - \dot{\varphi }_{{\text{u}}} )] \hfill \\ - 2m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[(k_{{\text{f}}} + k_{{\text{r}}} )v + (ak_{{\text{f}}} - bk_{{\text{r}}} )r] \hfill \\ \end{gathered} \right\}}}{{u[mI_{{{\text{Xs}}}} + m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$\begin{gathered} f_{5} (\xi ,\eta ) = \frac{{k_{{\text{s}}} (\varphi_{{\text{s}}} - \varphi_{{\text{u}}} ) + c_{{\text{s}}} (\dot{\varphi }_{{\text{s}}} - \dot{\varphi }_{{\text{u}}} ) - m_{{\text{s}}} g(h_{{\text{s}}} - h_{{{\text{rc}}}} )\varphi_{{\text{s}}} }}{{I_{{{\text{Xu}}}} }} \hfill \\ \, - \frac{{\left\{ \begin{gathered} 2m_{{\text{s}}} u\delta_{{\text{f}}} (F_{{{\text{xf}}}} { + }k_{{\text{f}}} )(h_{{\text{s}}} - h_{{\text{u}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ] \hfill \\ + um_{{\text{s}}}^{2} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(h_{{\text{s}}} - h_{{\text{u}}} )[m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )g\varphi_{{\text{s}}} \hfill \\ - k_{{\text{s}}} (\varphi_{{\text{s}}} - \varphi_{{\text{u}}} ) - c_{{\text{s}}} (\dot{\varphi }_{{\text{s}}} - \dot{\varphi }_{{\text{u}}} )] - 2m_{{\text{s}}} (h_{{\text{s}}} - h_{{\text{u}}} )[(k_{{\text{f}}} \hfill \\ + k_{{\text{r}}} )v + (ak_{{\text{f}}} - bk_{{\text{r}}} )r][I_{{{\text{Xs}}}} + m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ] \hfill \\ \end{gathered} \right\}}}{{u[mI_{{{\text{Xs}}}} + m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}, \hfill \\ \end{gathered}$$

$f_{6} (\xi ,\eta ) = u\cos \psi - v\sin \psi$,$f_{7} (\xi ,\eta ) = u\sin \psi + v\cos \psi$,$f_{8} (\xi ,\eta ) = r$,$f_{9} (\xi ,\eta ) = \dot{\varphi }_{s}$,$f_{10} (\xi ,\eta ) = \dot{\varphi }_{u}$.

The vehicle dynamics model is a nonlinear system, and predictive control of a linear model performs better in real-time and is easier to analyse and calculate than predictive control of a nonlinear model. As a result, the nonlinear vehicle dynamics model must be linearised. The points on a given reference trajectory satisfy the above dynamic equation.

$$\dot{\xi }_{{\text{r}}} = f(\xi_{{\text{r}}} ,\eta_{{\text{r}}} ).$$

(30)

The Taylor series expansion of Eq. (30) at the reference track point is obtained:

$$\dot{\xi } = f(\xi_{{\text{r}}} ,\eta_{{\text{r}}} ){ + }\frac{\partial f}{{\partial \xi }}\left| {_{{\xi_{{\text{r}}} ,\eta_{{\text{r}}} }} } \right.(\xi - \xi_{{\text{r}}} ){ + }\frac{\partial f}{{\partial \eta }}\left| {_{{\xi_{{\text{r}}} ,\eta_{{\text{r}}} }} } \right.(\eta - \eta_{{\text{r}}} ){ + }o.$$

(31)

Ignoring the higher-order term o and making a difference with Eq. (31), we can obtain:

$$\tilde{\dot{\xi }} = {\varvec{A}}\tilde{\xi } + {\varvec{B}}\tilde{\eta },$$

(32)

where $\tilde{\xi }$ and $\tilde{\eta }$ denote state quantity error and control quantity error, respectively,

$${\varvec{A}} = \frac{\partial f}{{\partial \xi }}{ = }\left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {a_{21} } & {a_{22} } & {a_{23} } & {a_{24} } & {a_{25} } & 0 & 0 & 0 & {a_{29} } & {a_{210} } \\ {a_{31} } & {a_{32} } & {a_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {a_{41} } & {a_{42} } & {a_{43} } & {a_{44} } & {a_{45} } & 0 & 0 & 0 & {a_{49} } & {a_{410} } \\ {a_{51} } & {a_{52} } & {a_{53} } & {a_{54} } & {a_{55} } & 0 & 0 & 0 & {a_{59} } & {a_{510} } \\ {\cos \psi } & { - \sin \psi } & 0 & 0 & 0 & 0 & 0 & { - u\sin \psi - v\cos \psi } & 0 & 0 \\ {\sin \psi } & {\cos \psi } & 0 & 0 & 0 & 0 & 0 & {u\cos \psi - v\sin \psi } & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],$$

$${\varvec{B}} = \frac{\partial f}{{\partial \eta }} = \left[ {\begin{array}{*{20}c} {b_{11} } & \frac{2}{m} & \frac{2}{m} \\ {b_{21} } & {b_{22} } & 0 \\ {\frac{{2a(F_{{{\text{xf}}}} + k_{{\text{f}}} )}}{{I_{{\text{Z}}} }}} & {\frac{{2a\delta_{{\text{f}}} }}{{I_{Z} }}} & 0 \\ {b_{41} } & {b_{42} } & 0 \\ {b_{51} } & {b_{52} } & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],$$

$$a_{11} = - \frac{{2k_{{\text{f}}} \delta_{{\text{f}}} (v + ar)}}{{mu^{2} }},\,\,a_{12} = \frac{{2k_{{\text{f}}} \delta_{{\text{f}}} }}{mu} + r,\,a_{13} = \frac{{2ak_{{\text{f}}} \delta_{{\text{f}}} }}{mu} + v,$$

$$a_{21} = \frac{{2[(k_{{\text{f}}} { + }k_{{\text{r}}} )v{ + }(ak_{{\text{f}}} - bk_{{\text{r}}} )r][I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{u^{2} [mI_{{{\text{Xs}}}} + m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}} - r,$$

$$a_{22} = \frac{{ - 2(k_{{\text{f}}} + k_{{\text{r}}} )[I_{{{\text{Xs}}}} + m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{u[mI_{{{\text{Xs}}}} + m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{23} = \frac{{ - 2(ak_{{\text{f}}} - bk_{{\text{r}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{u[mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}} - u,$$

$$a_{24} = \frac{{ - m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )c_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{25} = \frac{{m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )c_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{29} = \frac{{m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )g - k_{{\text{s}}} ]}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{210} = \frac{{m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )k_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{31} = \frac{{2(ak_{{\text{f}}} - bk_{{\text{r}}} )v{ + }2(a^{2} k_{{\text{f}}} { + }b^{2} k_{{\text{r}}} )r}}{{I_{{\text{Z}}} u^{2} }},$$

$$a_{32} = \frac{{ - 2(ak_{{\text{f}}} - bk_{{\text{r}}} )}}{{I_{{\text{Z}}} u}},$$

$$a_{33} = \frac{{ - 2(a^{2} k_{{\text{f}}} { + }b^{2} k_{{\text{r}}} )}}{{I_{{\text{Z}}} u}},$$

$$a_{41} = \frac{{2m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )[(k_{{\text{f}}} { + }k_{{\text{r}}} )v{ + }(ak_{{\text{f}}} - bk_{{\text{r}}} )r]}}{{u^{2} [mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{42} = \frac{{ - 2m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(k_{{\text{f}}} { + }k_{{\text{r}}} )}}{{u[mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{43} = \frac{{ - 2m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(ak_{{\text{f}}} - bk_{{\text{r}}} )}}{{u[mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{44} = \frac{{ - mc_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{45} = \frac{{mc_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{49} = \frac{{mm_{{\text{s}}} g(h_{{\text{s}}} - h_{{{\text{rc}}}} ) - mk_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{410} = \frac{{mk_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{51} = \frac{{\left\{ \begin{gathered} - 2m_{{\text{s}}} (h_{{\text{s}}} - h_{{\text{u}}} )[(k_{{\text{f}}} + k_{{\text{r}}} )v \hfill \\ + (ak_{{\text{f}}} - bk_{{\text{r}}} )r][I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ] \hfill \\ \end{gathered} \right\}}}{{u^{2} [mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{52} = \frac{{2m_{{\text{s}}} (h_{{\text{s}}} - h_{{\text{u}}} )(k_{{\text{f}}} { + }k_{{\text{r}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{u[mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{53} = \frac{{2m_{{\text{s}}} (h_{{\text{s}}} - h_{{\text{u}}} )(ak_{{\text{f}}} - bk_{{\text{r}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{u[mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}},$$

$$a_{54} = \frac{{c_{{\text{s}}} }}{{I_{{{\text{Xu}}}} }}{ + }\frac{{m_{{\text{s}}}^{2} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(h_{{\text{s}}} - h_{{\text{u}}} )c_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{55} = \frac{{ - c_{{\text{s}}} }}{{I_{{{\text{Xu}}}} }} - \frac{{m_{{\text{s}}}^{2} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(h_{{\text{s}}} - h_{{\text{u}}} )c_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{59} = \frac{{k_{{\text{s}}} - m_{{\text{s}}} g(h_{{\text{s}}} - h_{{{\text{rc}}}} )}}{{I_{{{\text{Xu}}}} }} - \frac{{m_{{\text{s}}}^{2} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(h_{{\text{s}}} - h_{{\text{u}}} )[m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )g - k_{s} ]}}{{mI_{{{\text{Xs}}}} + m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$a_{510} = \frac{{ - k_{{\text{s}}} }}{{I_{{{\text{Xu}}}} }} - \frac{{m_{{\text{s}}}^{2} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(h_{{\text{s}}} - h_{{\text{u}}} )k_{{\text{s}}} }}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$b_{11} = \frac{{2k_{{\text{f}}} (v + ar - 2u\delta_{{\text{f}}} )}}{mu},$$

$$b_{21} = \frac{{2(F_{{{\text{xf}}}} { + }k_{{\text{f}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$b_{22} = \frac{{2\delta_{{\text{f}}} [I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$b_{41} = \frac{{2m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )(F_{{{\text{xf}}}} { + }k_{{\text{f}}} )}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$b_{51} = \frac{{ - 2m_{{\text{s}}} (F_{{{\text{xf}}}} { + }k_{{\text{f}}} )(h_{{\text{s}}} - h_{{\text{u}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$b_{42} = \frac{{2m_{{\text{s}}} \delta_{{\text{f}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }},$$

$$b_{52} = \frac{{ - 2m_{{\text{s}}} \delta_{{\text{f}}} F_{{{\text{xf}}}} (h_{{\text{s}}} - h_{{\text{u}}} )[I_{{{\text{Xs}}}} { + }m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} ]}}{{mI_{{{\text{Xs}}}} { + }m_{{\text{u}}} m_{{\text{s}}} (h_{{\text{s}}} - h_{{{\text{rc}}}} )^{2} }}.$$

MPC is well suited for variable control in the discrete-time domain, which means that the vehicle dynamics model must be discretized. The discrete state-space equation can be expressed as follows using the first-order differential method:

$$\tilde{\xi }(k + 1) = ({\varvec{I}} + {\varvec{A}}t_{{\text{s}}} )\tilde{\xi }(k) + {\varvec{B}}t_{{\text{s}}} \tilde{\eta }(k),$$

(33)

where I denotes the unit matrix with the same order as matrix A, and t_s denotes the discrete sampling time (t_s = 0.001 s).

Transform Eq. (33) as follows:

$$\chi (k) = \left[ \begin{gathered} \, \tilde{\xi }(k) \hfill \\ \tilde{\eta }(k - 1) \hfill \\ \end{gathered} \right].$$

(34)

The discrete state space can be transformed into:

$$\left\{ \begin{gathered} \chi (k{ + }1) = \tilde{\user2{A}}\chi (k) + \tilde{\user2{B}}\Delta {\varvec{H}}(k), \hfill \\ \lambda (k) = \tilde{\user2{C}}\chi (k), \hfill \\ \end{gathered} \right.$$

(35)

where,

$$\tilde{\user2{A}} = \left[ {\begin{array}{*{20}c} {{\varvec{I}} + {\varvec{A}}t_{{\text{s}}} } & {{\varvec{B}}t_{{\text{s}}} } \\ {0_{3 \times 10} } & {{\varvec{I}}_{3 \times 3} } \\ \end{array} } \right],\,\,\tilde{B} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}t_{{\text{s}}} } \\ {{\varvec{I}}_{3 \times 3} } \\ \end{array} } \right],\,\tilde{\user2{C}} = \left[ {\begin{array}{*{20}c} {\varvec{C}} & {0_{2 \times 1} } \\ \end{array} } \right],\,\Delta {\varvec{H}}(k) = \left[ \begin{gathered} \, \tilde{\eta }(k) \hfill \\ \, \tilde{\eta }(k + 1) \hfill \\ \, \vdots \hfill \\ \tilde{\eta }(k + N_{{\text{c}}} ) \hfill \\ \end{gathered} \right].$$

After derivation, the system prediction output equation is:

$$\begin{aligned} \left[ \begin{gathered} \lambda \left( {k{ + }1} \right) \hfill \\ \lambda \left( {k{ + }2} \right) \hfill \\ \, \vdots \hfill \\ \lambda \left( {k{ + }N_{{\text{c}}} } \right) \hfill \\ \, \vdots \hfill \\ \lambda \left( {k{ + }N_{{\text{p}}} } \right) \hfill \\ \end{gathered} \right] = & \tilde{\user2{C}}\left[ \begin{gathered} \, \tilde{\user2{A}} \hfill \\ \tilde{\user2{A}}^{2} \hfill \\ \, \vdots \hfill \\ \tilde{\user2{A}}^{{N_{{\text{c}}} }} \hfill \\ \, \vdots \hfill \\ \tilde{\user2{A}}^{{N_{{\text{p}}} }} \hfill \\ \end{gathered} \right]\chi \left( k \right) \\ & + \user2{\tilde{C}\tilde{B}}\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ {\tilde{\user2{A}}} & 1 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{\user2{A}}^{{N_{{\text{c}}} { - }1}} } & {\tilde{\user2{A}}^{{N_{{\text{c}}} - 2}} } & \cdots & 1 \\ {\tilde{\user2{A}}^{{N_{{\text{c}}} }} } & {\tilde{\user2{A}}^{{N_{{\text{c}}} { - }1}} } & \cdots & {\tilde{\user2{A}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{\user2{A}}^{{N_{{\text{p}}} { - }1}} } & {\tilde{\user2{A}}^{{N_{{\text{p}}} { - }1}} } & \cdots & {\tilde{\user2{A}}^{{N_{{\text{p}}} { - }N_{{\text{c}}} { - }1}} } \\ \end{array} } \right]\Delta {H}(k), \\ \end{aligned}$$

(36)

where N_c is the control time domain, and N_p is the prediction time domain.

4.2 Cost Function Considering Anti-Rollover APF

MPC is based on the design of a cost function and its constraints. The cost function should be capable of ensuring the control quantity required for the vehicle's rapid and stable output, that is, to realise the motion planning of a driverless heavy vehicle while having the least impact on the global motion planning. The anti-rollover and obstacle avoidance APF functions are integrated into the cost function in this section. The cost function is as follows:

$$\begin{aligned} J{\text{ = }} & \sum\limits_{{k = 1}}^{{N_{{\text{p}}} }} {\left( \begin{gathered} \left\| {{\Lambda }(t + k) - {\Lambda }_{{{\text{ref}}}} (t + k)} \right\|_{{\user2{Q}_{{\text{1}}} }}^{2} \hfill \\ {\text{ + }}\left\| {\eta (t + k) - \eta _{{{\text{ref}}}} (t + k)} \right\|_{{\user2{Q}_{{\text{2}}} }}^{2} \hfill \\ + \left\| {oaAPF(t + k)} \right\|_{{\user2{Q}_{{\text{C}}} }}^{2} {\text{ + }}\left\| {arAPF(t + k)} \right\|_{{\user2{Q}_{{\text{R}}} }}^{2} \hfill \\ \end{gathered} \right)} \\ & + \sum\limits_{{k = 1}}^{{N_{{\text{c}}} - 1}} {\left\| {\Delta \user2{{\ H}}(t + k)} \right\|_{{\user2{Q}_{{\text{3}}} }}^{2} + \tau \varepsilon ^{2} } , \\ \end{aligned}$$

(37)

where,

$${\varvec{\varLambda}}(k) = \left[ {\lambda (k{ + }1) \, \lambda (k{ + }2) \, \cdots \, \lambda (k{ + }N_{{\text{c}}} ) \, \cdots \, \lambda (k{ + }N_{{\text{p}}} )} \right]^{{\text{T}}} ,$$

Λ_ref represents the expected value of the state quantity output by the prediction model, η_ref represents the expected value of the control quantity input by the prediction model, oaAPF represents the function value of the obstacle avoidance APF, arAPF represents the function value of the anti-rollover APF, ΔΗ represents the control increment, Q₁ represents the weight matrix of the state quantity, Q₂ represents the weight matrix of the control quantity, Q₃ represents the weight matrix of the control increment, Q_C represents the weight coefficient of the obstacle avoidance APF function, and Q_R represents the weight coefficient of the anti-rollover APF function. Because the system's model changes in real-time, it cannot guarantee that the optimisation goal will always obtain a feasible solution. A relaxation factor is added to the cost function (ε = [ε₁ ε₂]^T), and τ denotes the weight coefficient of the relaxation factor.

4.3 Constraint Condition of the Autonomous Heavy Truck

By including the controlled heavy truck's kinematic and dynamic constraints in the MPC, it is possible to ensure the practical feasibility of the vehicle motion planning results, reduce the range of the state space, and shorten the calculation time. First, the output constraints imposed by MPC control must be considered. Longitudinal force (F_xT) and wheel steering angle (δ_f) shall meet the constraints of vehicle dynamics:

$$\left\{ \begin{gathered} F_{{{\text{xf}}}} + F_{{{\text{xr}}}} \le F_{{{\text{xT\_max}}}} = T_{{{\text{max}}}} /R_{{\text{t}}} , \hfill \\ \left| {\delta_{{\text{f}}} } \right| \le \delta_{{{\text{fmax}}}} , \hfill \\ \left| {\Delta \delta_{{\text{f}}} } \right| \le \Delta \delta_{{{\text{fmax}}}} , \hfill \\ \end{gathered} \right.$$

(38)

where F_{xT_max} represents the maximum longitudinal resultant force of the vehicle, T_max represents the maximum driving torque, R_t represents the tire radius, δ_fmax represents the maximum value of wheel angle, Δδ_fmax represents the maximum steering angle increment.

Additionally, the longitudinal and lateral forces exerted by vehicle tires must meet the constraints imposed by the friction ellipse.

$$\left( {\frac{{F_{{{\text{xT}}}} }}{{F_{{{\text{xT\_max}}}} }}} \right)^{2} + \left( {\frac{{F_{{\text{Y}}} }}{{F_{{{\text{Y\_max}}}} }}} \right)^{2} \le \mu^{2} ,$$

(39)

where F_{Y_max} represents the maximum lateral force of the tire.

4.4 Iterative Solution of MPC Motion Planner

According to Eqs. (37)−(39), when the obstacle avoidance and anti-rollover APF functions are added to the cost function, the cost function becomes nonlinear. The motion planning of an autonomous heavy truck is transformed into the following nonlinear programming problem with constraints. In the control time domain, the nonlinear solver is used to find the optimal solution and a series of control increments.

$$\Delta \user2{\ H}^{ * } (k) = \left[ {\begin{array}{*{20}c} {\tilde{\eta }^{ * } (k)} & {\tilde{\eta }^{ * } (k + 1)} & \cdots & {\tilde{\eta }^{ * } (k + N_{{\text{c}}} )} \\ \end{array} } \right]^{{\text{T}}} .$$

(40)

In MPC, the first element of the control increment sequence is used as the actual control to determine the system's expected control quantity.

$$\eta (k) = \eta (k - 1) + \tilde{\eta }^{ * } (k).$$

(41)

The system continues to execute the control until the next time it is invoked. The control system then forecasts the output of the model's next cycle using the new state quantity, obtains a series of control increments in the next control time domain, and feeds the system the first element as the actual control. This is repeated to complete the MPC of the driverless heavy truck's motion planning. The remotely controlled vehicle can avoid obstacles and avoiding rollover accidents.

4.5 Game Theory Optimisation

When the target path contains obstacles, the obstacle avoidance repulsion force field generates a repulsion force that causes the heavy truck to turn to avoid the obstacles. When the coefficient of the obstacle avoidance APF function is larger in the cost function, the obstacle avoidance repulsion force is greater, and the vehicle's ability to avoid obstacles is improved. However, heavy trucks' roll angles will change significantly due to excessive steering, increasing the risk of rollover accidents. When the coefficient of the anti-rollover APF function is large, the vehicle's rollover stability improves, but the heavy truck is unable to safely avoid obstacles due to insufficient steering.

Consider that the motion planning of a heavy truck should take into account not only the vehicle's ability to safely avoid obstacles, but also the vehicle's rollover stability. This paper introduces the concept of game theory to make heavy truck steering obstacle avoidance and active rollover prevention a game, while also taking into account the obstacle avoidance safety and rollover stability of heavy truck motion planning.

The anti-rollover APF function coefficient and the obstacle avoidance APF function coefficient are chosen as the two sides of the game in the cost function design of the MPC motion planner, and the MPC motion planner is designed using game theory. Figure 8 illustrates the optimisation process.

Figure 8

Flow chart of the game theory optimization

Firstly, the obstacle avoidance APF function coefficient (Q_C) and the anti-rollover APF function weight coefficient (Q_R) are selected as the two sides of the game. There are two players in the game, that is, the player set N = {1,2}, and each player's decision corresponds to a strategy set S.

Then, according to several simulation tests, the ranges of coefficients Q_C and Q_R are [Q_C1 Q_Cm] and [Q_R1 Q_Rn], respectively, and multiple data are selected as the strategy of the coefficient in the corresponding range of the two coefficients. Given that a small number of data reduces the accuracy of the calculation results, and a large number of data increases the calculation time, the number of strategies with two coefficients, m = 20 and n = 20, is chosen here, and the game's strategy set is obtained:

$$\left\{ \begin{gathered} S_{{1}} = \left\{ {Q_{{{\text{C1}}}} ,Q_{{{\text{C2}}}} ,...,Q_{{{\text{C20}}}} } \right\}, \hfill \\ S_{2} = \left\{ {Q_{{{\text{R1}}}} ,Q_{{{\text{R2}}}} ,...,Q_{{{\text{R20}}}} } \right\}. \hfill \\ \end{gathered} \right.$$

(42)

Set the payoffs for the two players under any strategy combination (Q_Ci, Q_Rj) according to simulation experience, which are denoted by P₁(Q_Ci, Q_Rj) and P₂(Q_Ci, Q_Rj), respectively.

Then, matrixes A_G and B_G denote the payoff matrixes of the two players:

$$\left\{ \begin{gathered} {\varvec{A}}_{{\text{G}}} = \left[ {\begin{array}{*{20}c} {P_{1} (Q_{{{\text{C1}}}} ,Q_{{{\text{R1}}}} )} & {P_{1} (Q_{{{\text{C1}}}} ,Q_{{{\text{R2}}}} )} & \cdots & {P_{1} (Q_{{{\text{C1}}}} ,Q_{{{\text{R20}}}} )} \\ {P_{1} (Q_{{{\text{C2}}}} ,Q_{{{\text{R1}}}} )} & {P_{1} (Q_{{{\text{C2}}}} ,Q_{{{\text{R2}}}} )} & \cdots & {P_{1} (Q_{{{\text{C2}}}} ,Q_{{{\text{R20}}}} )} \\ \vdots & \vdots & \ddots & \vdots \\ {P_{1} (Q_{{{\text{C20}}}} ,Q_{{{\text{R1}}}} )} & {P_{1} (Q_{{{\text{C20}}}} ,Q_{{{\text{R2}}}} )} & \cdots & {P_{1} (Q_{{{\text{C20}}}} ,Q_{{{\text{R20}}}} )} \\ \end{array} } \right], \hfill \\ {\varvec{B}}_{{\text{G}}} = \left[ {\begin{array}{*{20}c} {P_{2} (Q_{{{\text{C1}}}} ,Q_{{{\text{R1}}}} )} & {P_{2} (Q_{{{\text{C1}}}} ,Q_{{{\text{R2}}}} )} & \cdots & {P_{2} (Q_{{{\text{C1}}}} ,Q_{{{\text{R20}}}} )} \\ {P_{2} (Q_{{{\text{C2}}}} ,Q_{{{\text{R1}}}} )} & {P_{2} (Q_{{{\text{C2}}}} ,Q_{{{\text{R2}}}} )} & \cdots & {P_{2} (Q_{{{\text{C2}}}} ,Q_{{{\text{R20}}}} )} \\ \vdots & \vdots & \ddots & \vdots \\ {P_{2} (Q_{{{\text{C20}}}} ,Q_{{{\text{R1}}}} )} & {P_{2} (Q_{{{\text{C20}}}} ,Q_{{{\text{R2}}}} )} & \cdots & {P_{2} (Q_{{{\text{C20}}}} ,Q_{{{\text{R20}}}} )} \\ \end{array} } \right]. \hfill \\ \end{gathered} \right.$$

(43)

The payoff matrix of both sides of the game is constructed as follows:

$$\left[ {\begin{array}{*{20}c} {(P_{1} (Q_{{{\text{C1}}}} ,Q_{{{\text{R1}}}} ),P_{2} (Q_{{{\text{C1}}}} ,Q_{{{\text{R1}}}} ))} & {(P_{1} (Q_{{{\text{C1}}}} ,Q_{{{\text{R2}}}} ),P_{2} (Q_{{{\text{C1}}}} ,Q_{{{\text{R2}}}} ))} & \cdots & {(P_{1} (Q_{{{\text{C1}}}} ,Q_{{{\text{R20}}}} ),P_{2} (Q_{{{\text{C1}}}} ,Q_{{{\text{R20}}}} ))} \\ {(P_{1} (Q_{{{\text{C2}}}} ,Q_{{{\text{R1}}}} ),P_{2} (Q_{{{\text{C2}}}} ,Q_{{{\text{R1}}}} ))} & {(P_{1} (Q_{{{\text{C2}}}} ,Q_{{{\text{R2}}}} ),P_{2} (Q_{{{\text{C2}}}} ,Q_{{{\text{R2}}}} ))} & \cdots & {(P_{1} (Q_{{{\text{C2}}}} ,Q_{{{\text{R20}}}} ),P_{2} (Q_{{{\text{C2}}}} ,Q_{{{\text{R20}}}} ))} \\ \vdots & \vdots & \ddots & \vdots \\ {(P_{1} (Q_{{{\text{C20}}}} ,Q_{{{\text{R1}}}} ),P_{2} (Q_{{{\text{C20}}}} ,Q_{{{\text{R1}}}} ))} & {(P_{1} (Q_{{{\text{C20}}}} ,Q_{{{\text{R2}}}} ),P_{2} (Q_{{{\text{C20}}}} ,Q_{{{\text{R2}}}} ))} & \cdots & {(P_{1} (Q_{{{\text{C20}}}} ,Q_{{{\text{R20}}}} ),P_{2} (Q_{{{\text{C20}}}} ,Q_{{{\text{R20}}}} ))} \\ \end{array} } \right].$$

Drawing the payoff area from the payoff matrix and calculate the Nash equilibrium point (Q_Ci', Q_Rj') according to the graph line.

The actual distance D_NC, D_C, D_R, and rollover index RI are obtained by the MPC planner corresponding to the Nash equilibrium point and are compared to the set minimum safety distance D₀ and minimum safety rollover index RI₀. The optimal coefficients Q_C* and Q_R* will be output until meeting the requirements of obstacle avoidance safety and rollover stability. Otherwise, Q_Ci' and Q_Rj' will be adjusted, and the new D_NC, D_C, D_R, and RI will be solved using the MPC planner.

5 Case Studies

Two cases are designed to evaluate the performance of the autonomous heavy truck motion planner developed in this paper. The simulation test and the analysis of its results are as follows.

Case I: As illustrated in Figure 9, the global path is represented by the green dotted line. The heavy truck (controlled vehicle) must drive on Lane 1 along the global path at a target speed of 72 km/h. Lane 1, 60 meters ahead, and Lane 2, 100 meters ahead, are discovered to have an obstruction. The motion planning algorithm must generate an appropriate longitudinal force and steering angle for the front wheel to cause the controlled vehicle to change lanes to Lane 2 and then back to Lane 1. Avoid colliding with obstacles and remaining within the global path. At the same time, it is necessary to avoid the controlled vehicle rolling over due to excessive speed or steering angle when changing lanes.

Figure 9

Road condition in Case I

The path generated by the motion planning of the autonomous heavy truck in Case I is depicted schematically in Figure 10, where the green virtual line represents the global path and the black box, and its circumscribed ellipse represents the size of the obstacle. The virtual red line, blue chain line, and solid purple line represent, respectively, the trajectory generated by the controlled vehicle's motion planning without anti-rollover, with anti-rollover, and after game theory optimisation. The red, blue, and purple boxes, along with their circumscribed dotted ellipses, represent the size of the controlled vehicle at its closest approach to the obstacle. As can be seen, when only obstacle avoidance is considered during motion planning, the controlled vehicle turns and changes lanes to another lane where it can safely avoid obstacles before changing lanes to return to the lane where the global path is located. When anti-rollover is considered during motion planning, the controlled vehicle can also change lanes and avoid obstacles. To avoid the risk of rolling over due to excessive steering, the controlled vehicle turns and changes lanes ahead of time and then returns to the original lane. The entire process is maintained at a low steering angle, but closer to the obstacle. Although the vehicle turning and lane-changing are more radical in the path optimised by game theory, they are still relatively gentle, and the risk of a rollover accident is low. It is worth noting that it has a greater effect on avoiding obstacles, which benefits both the driver and the vehicle by lowering the risk of a rollover accident and allowing for safe obstacle avoidance.

Figure 10

Motion planning path of the vehicle in Case I

In Case I, Figure 11 illustrates the RI value, front-wheel steering angle, longitudinal force, yaw rate, longitudinal speed, and distance between vehicle and obstacle during motion planning.

Figure 11

Vehicle motion parameter in Case I: (a) Rollover index, (b) Distance between vehicle and obstacle, (c) Steering angle of the front wheel, (d) Longitudinal force, (e) Yaw rate, (f) Longitudinal velocity

As can be seen from Figure 11 (a) and (b), the rollover factor value of the vehicle is high when only considering obstacle avoidance. When anti-rollover is considered in addition to obstacle avoidance, the rollover factor value and distance between vehicle and obstacle are reduced. That is, the rollover risk can be effectively controlled but the collision risk will be increased. However, after optimisation using game theory, the safety of obstacle avoidance and rollover prevention can be guaranteed at the same time.

As shown in Figure 11 (c) and (d), compared the method with only considering obstacle avoidance, two other methods considering both rollover prevention and obstacle avoidance can reduce the front wheel angle input, so as to reduce the yaw rate and improve the lateral stability of the vehicle.

Figure 11 (e) and (f) show that methods considering both rollover prevention and obstacle avoidance can reduce the longitudinal velocity fluctuation compared the method with only obstacle avoidance. Thus, a smaller longitudinal control force need input to increase the driving speed, and the vehicle longitudinal stability can be improved.

Case II: As illustrated in Figure 12, the green dotted line indicates the global path. The heavy truck (controlled vehicle) must travel on Lane 1 along the global path at a target speed of 54 km/h. It is discovered that there is an obstruction ahead of the large curve. The controlled vehicle must be capable of avoiding the obstacle without rolling over.

Figure 12

Road condition in Case II

As illustrated in Figure 13, the path diagram generated by the motion planning of the autonomous heavy truck in Case II is shown, with the lines conveying the same meaning as in the preceding text. Additionally, when the controlled vehicle's motion planning is limited to obstacle avoidance, it can achieve lane change obstacle avoidance and follow the global path, with a favourable obstacle avoidance effect. In motion planning with anti-rollover, the controlled vehicle can also change lanes and avoid obstacles, as well as reduce steering, thereby reducing the risk of vehicle rollover, but at the expense of slightly reducing the obstacle avoidance effect. Although the distance between the circumscribed ellipse of the size of the heavy truck and the obstacle is the smallest in the optimal path planned using game theory optimisation, the distance between the circumscribed ellipse and the obstacle is the greatest in the optimal path planned using game theory optimisation. At this point, the vehicle can safely avoid the obstacle, and the rollover risk is minimal when safety is considered. As a result, this path is the most optimal planning path given the circumstances.

Figure 13

Motion planning path of the vehicle in Case II

In Case II, Figure 14 illustrates the RI value, front-wheel steering angle, longitudinal force, yaw rate, longitudinal speed, and distance between vehicle and obstacle during motion planning.

Figure 14

Vehicle motion parameter in Case II: (a) Rollover index, (b) Distance between vehicle and obstacle, (c) Steering angle of the front wheel, (d) Longitudinal force, (e) Yaw rate, (f) Longitudinal velocity

As can be seen from Figure 14 (a) and (b), when only considering obstacle avoidance, the rollover factor value reaches the peak value of 0.98 at 4.8 s, and the vehicle has the danger of rollover. The method considering both rollover and obstacle avoidance can reduce the rollover factor value but the distance between vehicle and obstacle is close to zero at 4.2−4.5 s. That is, the method can avoid vehicle rollover but generate collision risk with the obstacle under extreme condition. However, after optimisation using game theory, it not only ensures the safety of vehicle against rollover, but also safely avoids the obstacle.

Figure 14 (c) and (d) illustrate that methods considering both rollover prevention and obstacle avoidance can reduce the front wheel angle input and the yaw rate compared the method with only considering obstacle avoidance. In addition, Figure 14 (e) and (f) show that, compared the method with only considering obstacle avoidance, they can reduce the longitudinal velocity fluctuation and the longitudinal control force input. Therefore, it can be seen that the effect of improving the lateral and longitudinal stability of vehicle under extreme condition is more obvious after optimisation using game theory.

In conclusion, game theory optimisation MPC motion planning satisfies motion planning requirements, increases obstacle avoidance safety, and decreases rollover risk. The controlled vehicle can pass through this condition safely and stably.

6 Conclusions

To emphasise the importance of anti-rollover in autonomous heavy truck motion planning, we propose an MPC-based motion planning method for autonomous heavy trucks that takes vehicle rollover dynamics into account.

• (1) A novel obstacle avoidance APF technique is proposed, which increases the longitudinal safety distance while decreasing the lateral safety distance between vehicle and obstacle, thereby improving the obstacle avoidance safety of autonomous heavy trucks.

• (2) An anti-rollover APF is proposed and integrated into the motion planning cost function, reducing rollover index and enhancing the roll safety of autonomous heavy trucks.

• (3) The MPC motion planning algorithm, which combines trajectory tracking, anti-rollover APF, and obstacle avoidance APF, is then developed. Additionally, the anti-rollover and obstacle avoidance APF coefficients are optimised using game theory. The proposed motion planning method has a high level of rollover stability and obstacle avoidance safety.