The influence of the structure of atomic systems on the dynamics of electron exchange in ion–ion collision

Abstract

One electron exchange between the Rydberg states of ions is elaborated within the time-symmetrized framework of two-wave-function model. It was observed that in an atomic collision, the population of ionic states by electron exchange, is strongly conditioned by the structure of the subsystem itself, especially at intermediate velocities. This circumstance is particularly pronounced when determining the ion–ion distances at which the charge exchange is most likely. The specificity of the model is reflected in the fact that the determination of the electron capture distance is carried out at fixed initial and final states of the system under consideration. As an illustrative example, XeVIII was used as a target of collision process, i.e. ion Xe$^{8+}$ initially populated in Rydberg state $\nu _B=(n_B=8,l_B=0,m_B=0)$, while argon ions Ar$^{Z_A+}$ were used as projectiles in the core charge range $Z_A\in [3,9]$.

Graphic Abstract

1 Introduction

The exchange of electrons between ions represents one of the basic problems of the physics of the interaction of atomic particles. A fundamental understanding of ionization and neutralization processes is essential for describing elementary processes in plasma. There are numerous theoretical and experimental studies in the field of atomic collision processes: close-coupling calculation of the resonance and near resonance charge exchange in collisions of beryllium with its ion at low and intermediate energies [1], proton–ion collision in a high-temperature low density astrophysical plasma [2], theoretical computational methods for effective cross sections of charge exchange (electron capture) and electron loss (projectile ionization) processes involving heavy many-electron ions colliding with neutral atoms in $E\approx$ 10 keV/u–10 GeV/u energy range [3], charge transfer in ion–atom collision for high-temperature plasma modeling [4], atom–ion collision in an ultracold spin polarized mixture of Sr$^+$-Rb [5], experimental data measured by the crossed beams technique for charge transfer in ion–ion collisions at keV energies [6]. Special attention from the theoretical point of view is devoted to the exchange of only one electron in ion–atom and ion–ion collision processes [7,8,9].

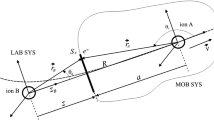
One of the more convenient methods for describing neutralization processes is the time-symmetrized two-wave-function model (TWF) [10]. This model is based on the concept of time-symmetric quantum ensemble, where the instant quantum mechanical state is described by two vectors one of which evolves from a fixed initial state and the other from a fixed final state. Moreover, a specific time-symmetrized quantum mechanics based on the Demkov–Ostrovskii’s formalism [11], originally developed in atomic collision processes on the base of a concept of the mixed flux through the Firsov plane $S_{\textrm{F}}$ [12], belongs to the domain of quantum teleology. Unlike the standard quantum ensemble, the time symmetric quantum ensemble must be defined with two measurements at two different time. For each particle that survives both measurements, we can say that belong to the teleological ensemble. The mentioned Firsov plane $S_{\textrm{F}}$, in the case of the atomic collision processes considered in this paper, separates the ionic subsystems and its position is specified by the variable $a=a(t)$, which represents the distance between the point of intersection of the Firsov plane and the interionic axis and the position of the projectile ion.

The first theoretical study of partial ion neutralization, within the model, was devoted to the consideration of electronic capture in the Rydberg state of highly charged ions moving away from a certain metal surface at intermediate velocities $v\approx 1$ a.u. [13,14,15]. It has been shown that within this approach to the problem, a complete quantum-mechanical picture of the process is obtained. In addition, it was shown [16] that the reionization of a previously populated ionic state can be relevant for individual Rydberg states. The mentioned investigations were primarily focused on the final population probabilities and later the model was adapted to consider intermediate probabilities as well. Until now, several theoretical models have been developed for researching the process of electronic exchange: classical over-barrier model [17], coupled-angular-mode method [18], complex-scaling method [19] or time-depending close-coupling technique [20].

In this paper, the intermediate stages of the process of electron capture are considered within the modified TWF model [10]. The electron transition from target (laboratory system) ion B to the projectile ion A (moving system), during ion–ion interactions, is described by two wave functions in two different scenarios which actually means that we use two different subdynamics at the same time.

Determining the analytical forms for the transition probability and the corresponding rates, enables us to calculate the neutralization distances $R_{ec}$ as one of the important parameters during charge exchange in ion–ion collisions. We point out that the modified TWF model allows taking into account the polarization of the electronic cloud of the ionic cores. Moreover, the charge exchange process at intermediate velocities is nonresonant. The obtained relatively simple analytical forms for population probability represent a convenient circumstance for future comparison with experimental results.

Atomic units ($e^2=\hbar =m_e=1$) will be used throughout the paper unless indicated otherwise.

2 Formulation of the problem

The purpose of this paper is to consider the influence of the structure of atomic particles on the electron capture during ion–ion collisions. As can be seen from Fig. 1, ion A (projectile) moves away from ion B (target) at intermediate velocities $v=dR(t)/dt\approx 1$ a.u., where $R(t)=vt$ is the instantaneous distance between the ions. Since the model is highly asymptotic, the assumption of such a simple dependence between velocity and distance is fully justified. Both, the initial state of the electron at time $t=t_{in}=0$ and the final state of the electron at time $t=t_{\textrm{fin}}\rightarrow \infty$ will be taken into account, i.e. the system that was ”preselected” in the atomic state $|\nu _B\rangle$, and ”postselected” in the atomic state $|\nu _A\rangle$ will be analyzed, where $|\nu \rangle =(n,l,m)$ is the set of spherical quantum numbers.

Fig. 1

Presentation of electron capture in ion–ion collision within the framework of the adapted time-symmetrized two-wave-function model

For the system defined in this way, intermediate transition probabilities and corresponding rates will be calculated. Analytical forms of these functions can be used for a very sensitive estimation of the ion–ion distances $R_{ec}$ at which the electron exchange is most likely. At every moment $t\in [t_{in}, t_{\textrm{fin}}]$, the state of the representative electron is described by a vector of two states $|\Psi _B(\vec {r},t)\rangle \langle \Psi _A(\vec {r},t)|$ which evolves as $|\Psi _B(\vec {r},t)\rangle =\hat{U}_1(t_{in},t)|\nu _B\rangle$ and $|\Psi _A(\vec {r},t)\rangle =\hat{U}_2(t_{\textrm{fin}},t)|\nu _A\rangle$. Evolution operators are determined by the following Hamiltonians: $\hat{H}_{B/A}(R)=-\nabla ^2/2-Z_{B/A}/r_{B/A}+\sum _{l=0}^{\infty }c_{l_{B/A}}\hat{P}_l/r_{B/A}^2+\hat{U}_{B/A,A/B}$, where Simons-Bloch potential, via the projection operator onto the subspace of an orbital quantum number l, is recognized. Since the ion–ion interaction is under consideration, the last term in analytical expressions for Hamiltonians represent the potential energy of the representative (active) electron in the field of polarized ionic core.

The peculiarity of the TWF model is reflected in the fact that it is sufficient to know the wave functions $|\Psi _B(\vec {r},t)\rangle$ and $|\Psi _A(\vec {r},t)\rangle$ only in the vicinity of the Firsov plane $S_{\textrm{F}}$ [15] which is localized enough away from both ions. So, it is clear that the dependence of the model on the shape of the potential in the vicinity of the ion is almost negligible. The interaction of an active electron with a polarized ionic core can be expressed through different model potentials. For very large distances between the active electrons and ions, which in that case can be treated as point charges, the Coulomb interaction is used. For the case when the active electron approaches closer to the electron cloud consisting of electrons that are already in a bound state around the given nucleus of the ion, the mentioned Simons-Bloch potential is used. In this case, the active electron interacts with the ion over the corresponding effective potential. In the case of the ionic interaction considered in this paper, both Hamiltonians possess spherical symmetry with discrete spectrum: $E_B(R)=-\gamma _B^2/2=-\tilde{\gamma }_B^2/2-Z_A/R$ and $E_A(R)=-\gamma _A^2/2=-\tilde{\gamma }_A^2/2-Z_B/R$, where the introduced energy parameters $\tilde{\gamma }_B$ and $\tilde{\gamma }_A$ are directly determined based on spectroscopic measurements.

In order to present the neutralization process in a time-symmetrized way, the neutralization is described by the two-state probability amplitude $A_{\nu _B,\nu _A}(t)=\langle \Psi _B(t)|\hat{P}_{A}(t)|\Psi _A(t)\rangle$, where $\hat{P}_{A}(t)$ is the projector onto the ion A region $V_{A}(t)$ [21]. The two-state probability amplitude satisfies the initial condition $A_{\nu _B,\nu _A}(t_{in})=0$, where $t_{in}$ is the beginning of the neutralization process. Consequently, it follows that the transition probability is given by $T_{\nu _B,\nu _A}(t)=|A_{\nu _B,\nu _A}(t)|^2$. The function $T_{\nu _B,\nu _A}(t)$ represents the probability that the representative electron is localized in the volume $V_{A}(t)$ at time $t\in [t_{in},t_{\textrm{fin}}]$ if it comes from the state corresponding to energy $E_B(R)$. Obviously, in the limiting case $t=t_{\textrm{fin}}\rightarrow \infty$, we have $T_{\nu _B,\nu _A}^{\textrm{fin}}=\lim _ {t\rightarrow t_{\textrm{fin}}}T_{\nu _B,\nu _A}(t)=|A_{\nu _B,\nu _A}(t_{\textrm{fin}})|^2=|\langle \Psi _B(t_{\textrm{fin}})|\hat{P}_{A}(t_{\textrm{fin}})|\Psi _A(t_{\textrm{fin}})\rangle |^2$. Using the two-state probability amplitude $A_{\nu _B,\nu _A}(t)$, we are able to define normalized transition probability $\tilde{T}_{\nu _B,\nu _A}(t)=T_{\nu _B,\nu _A}(t)/T_{\nu _B,\nu _A}^{\textrm{fin}}$ whose time derivative finally gives corresponding normalized neutralization rate $\tilde{\Gamma }_{\nu _B,\nu _A}(t)=d\tilde{T}_{\nu _B,\nu _A}(t)/dt$. Normalized rate, together with the $a=a(t)$, i.e. with the Firsov plane $S_{\textrm{F}}$-ion A distance (see Fig. 1), are directly related to the problem of localization of the neutralization process. Namely, the position of the maxima of normalized rate $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$, determine the neutralization distances $R_{ec}$. We point out here that in cases of small values of angular momentum l (states with a large eccentricities), which are considered in the paper, electron transfers through the Firsov plane $S_{\textrm{F}}$ are dominant. It can be concluded from Fig. 1 that Firsov plane located in a narrow band around the axis passing through both ions, and is an integral part of the total closed surface area that includes the volume $V_A(t)$ in which the ion (A) projectile is located. Transition probability can be presented in integral form via mixed flux $I_{\nu _B,\nu _A}(t)$ as: $T_{\nu _B,\nu _A}(t)=|\int _{t_{in}}^tI_{\nu _B,\nu _A}(t)dt|^2$, where the analytic form of the mixed flux is given by [10]:

$$\begin{aligned} \begin{aligned} I_{\nu _B,\nu _A}(t)&=\frac{i}{2}\text {exp}(iwt)\left[ \tilde{\gamma }_B+\tilde{\gamma }_A+iv\left( 1-2\frac{da}{dR}\right) \right] \\&\quad \times \text {exp}\left( f_B+f_A^*-\frac{2Z_B}{\tilde{\gamma }_B}\frac{R-a}{R}-\frac{2Z_A}{\tilde{\gamma }_A}\frac{a}{R}\right) \\&\quad \times D_B\, D_A\, N_B\, N_A\, 2\pi \delta _{m_B,m_A} \\&\quad \times \frac{\Gamma (2\tilde{l}_B+2)}{\Gamma (\tilde{l}_B+\tilde{n}_B+1)}e^{i\pi (\tilde{n}_B-\tilde{l}_B-1)} \\&\quad \times \frac{\Gamma (2\tilde{l}_A+2)}{\Gamma (\tilde{l}_A+\tilde{n}_A+1)}e^{i\pi (\tilde{n}_A-\tilde{l}_A-1)} \\&\quad \times S_{n_B,l_B}(4n_B)\,S_{n_A,l_A}(4n_A) \\&\quad \times P_{l_B}^{m_B}(1)\,P_{l_A}^{m_A}(-1) \\&\quad \times (2\tilde{\gamma }_B)^{\frac{Z_B}{\tilde{\gamma }_B}}(2\tilde{\gamma }_A)^{\frac{Z_A}{\tilde{\gamma }_A}} \\&\quad \times (R-a)^{\frac{Z_B}{\tilde{\gamma }_B}-1}\tilde{\gamma }_A^{-\frac{Z_A}{\tilde{\gamma }_A}-1}e^{-\tilde{\gamma }_B(R-a)} \\&\quad \times \Gamma \left( \frac{Z_A}{\tilde{\gamma }_A}+1,a\tilde{\gamma }_A\right) , \end{aligned} \end{aligned}$$

(1)

with $w=(\gamma _B^2-\gamma _A^2)/2-v^2(1-2a/R)/2$. Analytical forms of time-space factors $f_B$ and $f_A$, as well as constants $D_M$, $D_A$ and normalization constants of spherical harmonics $N_B$ and $N_A$, are given in Ref. [10]. Also, with $S_{n,l}(x)$ we denoted the following function:

$$\begin{aligned} S_{n,l}=\sum _{k=0}^{n-l-1}\frac{(-1)^k(n+l)!(n-l-1)!x^{-k}}{k!(n+l-k)!(n-l-1-k)!}, \end{aligned}$$

(2)

while $\Gamma (s,x)$ is the upper incomplete gamma function.

3 Results

Taking into account that the specificity of the TWF model is reflected in the description of the active electron with two quantum states $\Psi _B(\vec {r},t)$ and $\Psi _A(\vec {r},t)$ whose evolution is described by two, in the general case, very different Hamiltonians, it is to be expected that two important energy parameters $\tilde{\gamma }_B$ and $\tilde{\gamma }_A$ are always used when determining the analytical forms of normalized transition probabilities $\tilde{T}_{\nu _B,\nu _A}(t)$. The values of the relevant parameters used in this work were obtained by spectroscopic measurements and can be found in the reference [22]. Only those values, corresponding to the ground state of the ionic cores, were considered.

In this work we analyzed intermediate stages of the partial neutralization of the Ar ions. As an important illustrative example, we discussed electron capture, during the ion–ion collision, from XeVIII Rydberg state ($n_B=8, l_B=0$) as a target ion, into the ArIII-ArIX Rydberg state ($n_A=4, l_A=0$) at intermediate velocity $v\approx 1$a.u., i.e. ion–ion collision of forms $\text {Ar}^{Z_A+}+\text {Xe}^{7+}=\text {Ar}^{(Z_A-1)+}+\text {Xe}^{8+}$, Fig. 2. In addition, the values of quantum numbers $m_B\ne 0$ and $m_A\ne 0$ were not considered because their contribution under the stated conditions in charge exchange processes is negligible. Consideration of the intermediate stages of the process is possible precisely by using analytical expressions for normalized transition probability and corresponding normalized rate, obtained on the basis of the modified TWF model.

Fig. 2

Population of the energy level ($n_A=4$ and $l_A=0$) of ArIII–ArIX ions was considered. The observed case refers to the projectile (A ion) velocity $v=1$. In Fig. 2a normalized transition probabilities $\tilde{T}_{\nu _B,\nu _A}(t)$ are presented. Also, the corresponding normalized neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$, scaled by ion velocity, are presented in Fig. 2b

Table 1 Energy levels of ionized argon from ArIII to ArIX

In Fig. 2a, we present normalized transition probabilities $\tilde{T}_{\nu _B,\nu _A}(t)$ for population of the energy level $n_A=4$ and $l_A=0$ of Ar$^{Z_A+}$ with variable values $Z_A$ in the range from 3 to 9. As was to be expected, the values of all functions at final time $t_{\textrm{fin}}$ converge towards unity according to the definition of normalized transition probability $\tilde{T}_{\nu _B,\nu _A}(t)$, which means that the state of Ar ion is populated with certainty. The fact is that the curves have a similar shape and move towards larger distances with decreasing of $Z_A$, but there is also a noticeable violation of the observed regularity in the case of $Z_A=3$. The corresponding normalized neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$, presented scaled by ion velocity, highlight the mentioned anomaly much better Fig. 2b. Moreover, the presented rates clearly indicated that with increasing of the ionic core charge, the value of the neutralization distance $R_{ec}$, i.e. the most likely distance between ions at which electron transfer occurs, decreases. In addition, the specificity of ion–ion collisions is also reflected in the localization of the charge exchange process. Namely, at large values of ionic core charge $Z_A$, the process of electron capture is well localized, while at small values, the localization of the process is disturbed.

For all considered argon ions, values of energy levels, uncertainty of energy levels, electronic configurations, terms, values of total angular momentum as well as energy parameter $\tilde{\gamma }_A$ are given in Table 1. All energy level values of ionized argon, from ArIII to ArIX, are taken from the Ref. [23]. Table 1 also gives the values of the ionization limit for each ionized argon in order to determine the value of the energy parameter $\tilde{\gamma }_A$ that appears in every analytical expressions for normalized transition probability $\tilde{T}_{\nu _B,\nu _A}(t)$ and corresponding normalized neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$.

Fig. 3

Normalized neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$ (scaled by v) of the population of the ArVI ion in state $n_A=3$ and $l_A=2$ and $m_A=0$ escaping from the XeVIII initially populated into Rydberg state $n_B=8$, $l_B=0$ and $m_B=0$ at velocity $v=3$ a.u

It should be noted that, after numerous calculations [10, 16], an exceptional sensitivity of the TWF model was observed by almost all relevant parameters of the considered charge exchange process. Undoubtedly, one of the important parameters in the ion–ion collision process is certainly, aforementioned, the distance between the ions at which the highest probability of charge exchange should be expected. In that context, in Fig. 3 we present normalized neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$ of the population of the ArVI ion ($n_A=3,l_A=2, m_A=0$) escaping, with intermediate velocity $v=3$ a.u., from the XeVIII initially populated into Rydberg state ($n_B=8, l_B=0, m_B=0$). Three energy levels of ArVI were considered: $3s3p(^3\text {P})3d\,\,^4\text {D}$, $3s3p(^3\text {P})3d\,\,^2\text {D}$ and $3s3p(^1\text {P})3d\,\, ^2\text {D}$ with energy values (319905(10) cm$^{-1}$, 328960.4(1.8) cm$^{-1}$ and 395494(3) cm$^{-1}$) and with total angular momentum (7/2, 5/2 and 3/2), respectively [23]. Based on the form of neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$, we are able to recognize neutralization distances $R_{ec}$ via the position of maximal values. From Fig. 3 it can be clearly concluded that the levels $3s3p(^3\text {P})3d\,\, ^4\text {D}$ and $3s3p(^3\text {P})3d\,\, ^2\text {D}$ have an almost identical value of the neutralization distance $R_{ec}$, approximately $R_{ec}=16.44$ a.u., while the value of the neutralization distance of the $3s3p(^1\text {P})3d\,\, ^2\text {D}$ level has been moved to $R_{ec}=18$ a.u. This is a clear indication that the influence of the atomic structure of the projectile ion is dominant in atomic collision processes in which one electron is exchanged. Specifically, in the considered case, the spin multiplicity of ionic core significantly affects the dynamics of charge exchange [10]. The first two energy levels have spin multiplicity 3 (triplet states), while the last one has spin multiplicity equal to unity (singlet state). It should be noted, as in the previous case, a small but noticeable greater delocalization of the electronic capture process with an increase of the neutralization distance $R_{ec}$. The mentioned effect does not depend on the value of the intermediate velocities, which were considered in this paper.

Taking into account considerations of neutralization distances in ion–ion collisions from reference [10], it can be concluded that the influence of the atomic structure of projectile ions, in terms of charge exchange, is even more pronounced with increasing of the orbital angular momentum $l_A$. Consequently, in the analyzed case of electron capture from XeVIII Rydberg state ($n_B=8, l_B=0, m_B=0$) into the ArVI state ($n_A=3, l_A=2, m_A=0$) at $v=3$ a.u., due to the small value of the angular momentum $l_B=0$, i.e. due to the pronounced eccentricity of the XeVIII state along the outgoing part of the projectile trajectory, the appearance of longer neutralization distances is completely understandable.

4 Concluding remarks

In this paper, the process of charge exchange in ion–ion collisions is considered. Multiply charged argon ions were used as projectiles, while the target was a xenon ion XVIII in Rydberg state ($n_B=8, l_B=0, m_B=0$). The dynamics of electronic capture is analyzed for intermediate projectile velocities $v\approx 1$ a.u. and $v\approx 3$ a.u. using an adapted quantum mechanical (teleological) TWF model.

By considering the population of close energy levels of argon ions, a significant influence of the atomic structure on the dynamics of the process was observed. It was shown, by calculating the neutralization distances $R_{ec}$, that the values of the spin and angular momentum of the ionic core significantly affect the localization of the population process of the considered states. On the example of a population of two close energy levels of ArVI ions $3s3p(^3\text {P})3d$ and $3s3p(^1\text {P})3d$, of which the ion core in the first one is in the triplet state and in the second one in the singlet state, a significant difference between the values of the neutralization distance was observed.

Taking into account the derived analytical form of the mixed flux $I_{\nu _B,\nu _A}(t)$, as well as the distribution of the normalized neutralization rates $\tilde{\Gamma }_{\nu _B,\nu _A}(t)$ obtained on the basis of the data for the energy levels given in Table 1, it can be concluded that the localization of the electron capture process in ion–ion collision is very sensitive to the change in the value of $\tilde{\gamma }_A$ (also $\tilde{\gamma }_B$ in first scenario). From an experimental point of view, the stabilization of the collision chamber potential is of crucial importance. Namely, for the collision chamber potential $\varphi$, the energy spectra in the first and second scenarios are $E_B=-\gamma _B^2/2=-\tilde{\gamma }_B^2/2-Z_A/R-\varphi =-\tilde{\gamma }_{B\varphi }^2/2-Z_A/R$ and $E_A=-\gamma _A^2/2=-\tilde{\gamma }_A^2/2-Z_B/R-\varphi =-\tilde{\gamma }_{A\varphi }^2/2-Z_B/R$, which means that all analytical expressions given in the paper are valid with replacement $\tilde{\gamma }_B\rightarrow \tilde{\gamma }_{B\varphi }=\sqrt{\tilde{\gamma }_B^2+2\varphi }$ and $\tilde{\gamma }_A\rightarrow \tilde{\gamma }_{A\varphi }=\sqrt{\tilde{\gamma }_A^2+2\varphi }$ but with uncertainty $\Delta \tilde{\gamma }_{\varphi }=\Delta \varphi /\sqrt{\tilde{\gamma }^2+2\varphi }$ in both TWF model scenarios.

The authors sincerely hope that future experimental measurements of the most probable interionic distances for electron exchange will be based on the working analytical expressions given in this paper.