Introduction

Decadal prediction refers to predictions on annual, multi-year, and decadal time scales. Decadal predictions do not attempt to predict day-to-day weather patterns, but instead predict changes in statistical quantities like annual means or the chance of extremes. Much attention has been focused on improving decadal predictions of temperature, precipitation, hurricane activity, droughts, storm tracks, Arctic sea ice cover, air quality, and the Hadley Circulation. Numerous reviews of decadal prediction exist in the scientific literature, including a chapter in the fifth assessment report of the Intergovernmental Panel on Climate Change [55], books [13], reports from conferences and workshops [66, 92], and peer-reviewed journals [67]. Also, some major scientific projects are focused on decadal prediction [5, 64]. Nevertheless, several interesting developments in decadal prediction of temperature have occurred since the appearance of these reviews. In addition, in the opinion of the author, certain important issues have not received the attention they deserve. The purpose of this paper is to review these more recent or overlooked developments.

Unified Framework for Quantifying Decadal Predictability

This section follows closely a predictability framework that is discussed in more detail in DelSole and Tippett [21]. Decadal predictability can arise from two distinct mechanisms. First, internally generated components of the climate system, especially in the subsurface ocean, evolve naturally on decadal (and longer) time scales and thus are predictable because of their persistence or periodicity [4, 10, 30, 42, 60]. This form of predictability is called Initial Value Predictability. Second, changes in greenhouse gas concentrations, aerosol concentrations, solar insolation, and volcanic activity occur on multi-year time scales and alter the energy balance of the climate system, thereby forcing climate changes on these time scales. This is called Boundary Condition Predictability or Forced Predictability. Both mechanisms operate simultaneously, but separating their roles in observed temperature variations often is challenging [33, 81, 84, 85].

Quantifying predictability requires defining the distribution of a variable under certain conditions. The unconditional distribution of a variable y at time t is called the climatological distribution and denoted p t (y). If the climate system is stationary, then the climatological distribution is independent of time t and describes the frequency of values that would be obtained by sampling the system at random points in time. A more realistic assumption is that the climate system is cyclostationary; that is, the climatological distribution is a periodic function of time, primarily on annual (i.e., 1-year) and diurnal (i.e., 1-day) time scales, reflecting periodicities in solar insolation. In this case, the climatological distribution describes the frequency of values that would be obtained by randomly sampling the system at the same calendar day and time of day. However, as a result of anthropogenic and natural climate change, the climatological distribution varies in additional ways, especially in the form of a shift toward warmer temperatures on centennial time scales. Forced predictability refers to changes in the climatological distribution.

The distribution of a variable changes after observations are taken into account. Let o t denote all observations up to and including time t. The distribution after observations are taken into account is denoted by the conditional distribution p t (y|o t ) and called the analysis distribution, following similar terminology in data assimilation. The analysis distribution differs from the climatological distribution because observations provide information about the system beyond that contained by knowing the calendar day, clock time, and year.

Predictability is concerned with predicting the future value of a variable y at time t + τ, where τ is a positive parameter called lead time. The distribution of the future state given presently known observations is called the forecast distribution and denoted p t + τ (y|o t ). The forecast distribution is related to the analysis distribution through the Markov law

$$ \begin{matrix} p_{t+\tau}(y | o_{t}) & = \displaystyle {\int}_{- \infty}^{\infty} & p_{t+\tau} (y | y_{t}) & & p_{t}(y_{t}| o_{t}) & dy_{t} ,\\ \text{forecast} & & \text{dynamics} & & \text{initial} \end{matrix} $$
(1)

where p t + τ (y|y t ) is the transition kernel between initial and final states. The transition kernel is obtained either from physical laws or from empirical laws inferred from past observations. In addition, the transition kernel is assumed to satisfy the Markov property (i.e., the distribution conditioned on previous states depends only on the most recent state). The integral is a representation of an initial value problem in which the initial distribution p t (y t |o t ) is propagated forward in time according to physical laws embodied in the transition kernel p t + τ (y|y t ). If the physical laws are deterministic, in the sense that a unique future state evolves from a unique initial state, the forecast distribution still is probabilistic because of observational uncertainty that always exist in nature and is expressed through p t (y t |o t ). On the other hand, if the transition kernel is empirical and linear, then the initial condition uncertainty often is neglected and the forecast distribution can be derived from linear regression (also called a linear inverse model, or LIM). A variable is said to have no initial value predictability if its forecast distribution equals the climatological distribution:

$$ p_{t+\tau}\!(y | o_{t}) \,=\, p_{t+\tau}\!(y)\!\! \quad \text{for no initial value predictability}. $$
(2)

The above identity is equivalent to the statement that the future value of a variable is independent of observations available at the current time.

Because predictability depends on changes in distributions, it is natural to quantify predictability by some measure of the difference in distributions. There is no unique measure of a difference in distributions, but an attractive measure is relative entropy, which is a central quantity in information theory and arises naturally in a number of fields, including statistics, communication, and finance [18]. One compelling reason for choosing this measure is that it emerges naturally as a measure of financial gain derived from selected investment or gambling strategies [18]. Additional reasons for choosing this measure will be given shortly. Relative entropy is defined as the average difference in the logarithms of the distributions. Thus, the initial value predictability associated with a particular forecast distribution can be measured by

$$ R_{IV} = {\int}_{- \infty}^{\infty} \left[ \log p_{t+\tau}(y | o_{t}) - \log p_{t+\tau}(y) \right] p_{t+\tau}(y | o_{t}) dy . $$
(3)

Averaging this quantity over all o t yields mutual information [20]:

$$ M_{IV} = {\int}_{- \infty}^{\infty} R_{IV} p(o_{t}) do_{t} . $$
(4)

R I V depends on o t and generally depends on both t and τ, but M I V is an average measure of predictability and depends only on lead time τ. These measures take simple forms for Gaussian distributions [24, 56]. Regardless of distribution, the measure M I V has the following properties [24]:

  • It is non-negative.

  • It vanishes if and only if the two distributions are equal.

  • It is invariant to invertible nonlinear transformations.

  • It generalizes naturally to multivariate systems.

The first two properties convey the notion of a “distance” between two distributions: the measure vanishes when the two distributions are equal and is positive otherwise. The third property implies that predictability is independent of the variable units or the basis set used to represent the data.

It is important to recognize that changes due to external forcing do not automatically contribute to initial value predictability. For instance, if external forcing causes the forecast and climatological distributions to shift equally, then the integrated difference in distributions (3) would not change. To quantify both types of predictability, we need, in addition to a forecast distribution, two climatological distributions: one at time t + τ from which to measure initial value predictability, and one at time t from which to measure forced predictability. In practice, these two distributions would be estimated from two simulations: one with the same forcing at time t applied throughout the integration, and one with time-evolving forcing for t + τ for all τ. These distributions are illustrated in Fig. 1a. In this framework, a natural measure of forced predictability is the average change in the logarithm of climatological distributions between the initial and verification times:

$$ M_{F} = {\int}_{- \infty}^{\infty} {\int}_{- \infty}^{\infty} \left[ \log p_{t+\tau}(y) - \log p_{t}(y) \right] p_{t+\tau}(y| o_{t}) p(o_{t}) dy do_{t} . $$
(5)

This measure of forced predictability was proposed by Branstator and Teng [8]. It is straightforward to show that M F is merely the relative entropy between the two climatological distributions. Adding forced and initial value predictability gives a measure called total climate predictability:

$$ M_T = M_{IV} + M_F . $$
(6)

It can be shown that M T can be expressed equivalently as the difference in logarithms of the forecast and initial climatology:

$$ M_T \,=\,\! {\int}_{- \infty}^{\infty} {\int}_{- \infty}^{\infty} \!\left[ \log p_{t+\tau}(y|o_{t}) \,-\, \log p_{t}(y) \right] \!p_{t+\tau}(y| o_{t}) p(o_{t}) dy do_{t} . $$
(7)
Fig. 1
figure 1

Schematic of the spread of the three distributions relevant to quantifying decadal predictability (a) and the corresponding relative entropies (b). Schematics are based on results from Branstator and Teng [8] for the upper 300-m ocean temperature anomalies in model simulations [8]

Full size image

A schematic of total, forced, and initial value predictability is shown in Fig. 1b. Unlike initial value predictability, total predictability does not always decay monotonically with lead time, because external forcing can cause changes in the climatological distribution that increase with time.

The above framework has been applied to a variety of model simulations of the upper ocean heat content [8,9,10]. These studies suggest that initial value predictability remains statistically significant for roughly a decade in each ocean basin. However, the precise limit of predictability varies widely among models, especially in the North Atlantic, and locations of maximum predictability differ between models. Significant model sensitivity of decadal predictability is characteristic of the current state of the science.

Explaining Past Changes on Multidecadal Time Scales

The above discussion is based on theoretical considerations and evidence from model simulations. Another aspect of decadal predictability is explaining past multidecadal variations. In particular, a satisfying theory of decadal predictability ought to explain the major climate variations and persistent anomalies that have been observed in the past.

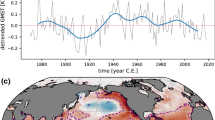
The most prominent variation observed on multidecadal time scales is the ˜ 1∘C increase in global average temperature over the past century (see Fig. 2). There exists strong scientific consensus that this increase is caused by anthropogenic increase in greenhouse gas concentrations [3]. Over northern latitudes, however, observations show that surface temperatures increased from 1900 to 1940, decreased from 1940 to 1970, and increased from 1970 to the present (see Fig. 2a). The cause of these multidecadal fluctuations is very much debated. Climate models from phase 3 of the Coupled Model Intercomparison Project (CMIP3) did not simulate these multidecadal fluctuations, leading many to conclude that these fluctuations were most likely due to internal variability [29, 57, 85]. However, some of the newer generation of models in CMIP5 were found to capture much of the amplitude and phasing of the multidecadal fluctuations [6]. A key point is that most CMIP3 models omitted or only partly represented the indirect aerosol effects on cloud lifetime and reflectivity, whereas some models that included indirect aerosol effects could capture much of the multidecadal fluctuations. Among those models for which sulfate aerosol deposition rates are available, those that most closely reproduced the cooling also have sulfate aerosol deposition rates most consistent with ice-core records [39]. Unfortunately, some inconsistencies always exist in model simulations, and some of these inconsistencies raise serious questions about the extent to which the models give a physically satisfactory explanation of observed anomalies [94]. These debates are still ongoing. In addition, forcing by anthropogenic aerosols is very uncertain, especially during the pre-satellite era, so attributing mid-century cooling to a strong—but highly uncertain— aerosol forcing rests on a shaky foundation.

Fig. 2
figure 2

Annual mean surface temperature anomalies (dots connected by line segments), relative to the 1951–1980 base period, for (a) northern latitudes (24∘ N– 90∘ N) and (b) tropical latitudes (24∘ S– 24∘ N). The smooth solid curve shows a polynomial fit. Data is from the GISS Surface Temperature Analysis (GISTEMP) [45]. The last year plotted is 2015

Full size image

The. main alternative hypothesis for multidecadal variability is that it is caused primarily by internal variability [12, 70, 87]. Consistent with this, the spatial structure of observed multidecadal variability of sea surface temperature is similar to the most predictable component of internal variability in climate models [29]. However, this hypothesis would imply that surface temperature fluctuations on the order of 0.5∘C on multidecadal time scales can arise from internal variability (the number is a typical difference between multi-model CMIP3 simulations and observations; e.g., [6]). Many climate models simulate much less internal variability than this [11, 77, 91]. Whether climate models simulate the correct magnitude of internal variability on multidecadal time scales is an essential question in decadal prediction. Unfortunately, instrumental records are too short to constrain the variability of surface temperature at multidecadal time scales. Proxies of land surface temperature suggest consistency between observations and climate models on continental scales [7]. However, proxies of sea surface temperature suggest much larger variability (one or two orders of magnitude) than that simulated by climate models, especially at low latitudes and long time scales [1, 59]. This result raises serious questions about the ability of climate models to simulate internal variability at multidecadal (and longer) time scales and highlights the need for better observational constraints on the internal variability of sea surface temperature.

Recent Slowdown in Warming (the “Hiatus”)

Theories of decadal predictability also should explain changes on decadal or shorter time scales. The decadal change that has received the most attention in the recent literature is the so-called “hiatus” or “pause.” Although global mean surface temperature has risen by about 0.8∘C since the late nineteenth century [47], the rate of warming began to slow after the turn of this century, even as the concentration of atmospheric greenhouse gases increased [65]. This “hiatus” has been a prominent talking point by climate skeptics and politicians, although it will likely be dropped in the future given the surprisingly large warming in both 2015 and 2016. While the rate of warming has varied considerably over the past century, including periods of cooling during the 1950s–1970s, the recent slowdown is noteworthy because it was significantly slower than that predicted by climate models [38]. The cause of this discrepancy has been plausibly explained as the combined influence of internal decadal variability and external forcing. An updated global surface temperature analysis suggested that global trends remained steady through the turn of this century [53], but the updated warming rate still remained a standard deviation or more slower than that predicted by climate models [38].

In comparing model simulations to observations, one must recognize that most climate models to which observations are compared are not initialized based on observations and therefore the internal variability in these models has no predictive usefulness. A particular component of internal variability that has been associated with other hiatus periods, including the recent one, is the Interdecadal Pacific Oscillation (IPO), which resembles the PDO [19]. The negative phase of the IPO is associated with strengthening of the Pacific trade winds, which enhances heat uptake through increased subduction in shallow overturning cells, and drives cooling in the eastern Pacific through enhanced equatorial upwelling [34, 65]. Prescribing these winds associated with the negative IPO in fully coupled atmosphere-ocean models produces a cooling that can explain a significant fraction of the hiatus [34]. A significant fraction of the hiatus also can be simulated by imposing cooling in the eastern equatorial Pacific in climate models [58], or subsampling model simulations by matching the phase of internal variability to that of observations [68, 75]. These results are consistent with some statistical analyses that decompose northern hemisphere temperatures into forced and internal variability and find that the recent hiatus is associated with a cooling in Pacific-based internal variability [84]. Finally, there is evidence that the hiatus could have been predicted by CMIP5 models if they had been initialized in the 1990s [68].

Although variations in the IPO, and its relative the Pacific Decadal Oscillation (PDO), are widely assumed to be dominated by internal variability, it has been shown that negative phases of the PDO can occur in response to anthropogenic aerosols [80]. Although the multi-model mean of CMIP5 models did not in fact reproduce the observed negative phase of the PDO during the recent hiatus, the response to anthropogenic aerosol forcing has large uncertainties, especially from indirect effects on changing cloud albedo and lifetime, so the role of external human influences by this mechanism is unclear.

The hiatus also has been partly explained by external forcing (both internal and forced variability co-exist simultaneously, so there is no reason to believe the hiatus should be explained by only one of these mechanisms). The particular climate models most often cited in relation to the hiatus are from phase five of the Coupled Model Intercomparison Project (CMIP5), which included observationally-based estimates of external influences only up to 2000 or 2005. Beyond those years, external forcing was extrapolated into the future based on “scenarios” called Representative Concentration Pathways, or RCPs. It turns out that during the recent hiatus period several minor volcanic eruptions occurred, the solar minimum was deeper than anticipated, and aerosol forcing was larger than expected, all of which lead to externally forced cooling that was not included in the RCPs [78, 82]. Taking account of these cooling influences brings the predicted temperatures more in line with observations [54, 78], although some models do not reproduce the slowdown based on updated external forcings alone [43].

Mechanisms of Decadal Predictability

It is well established that the atmospheric system, by itself, is predictable for at most a few weeks. Despite this, some atmospheric components, such as the North Atlantic Oscillation (NAO), can contribute to decadal variability simply because they have large variance and large spatial scales [32]. Nevertheless, significant decadal predictability must arise from the coupling of the atmosphere to slower parts of the climate system, such as the ocean, sea ice, and soil moisture. A widely accepted null hypothesis for predictability beyond a few weeks is that put forth by Hasselman (1976): atmospheric variables are essentially unpredictable on oceanic time scales and thus act as white noise forcing on the oceanic surface layers, which in turn integrates atmospheric heat fluxes to produce slowly varying SST anomalies [48]. In this mechanism, the uppermost ocean layer interacts only thermodynamically with the atmosphere. In the case of a well-mixed layer, energy balance yields the following equation for ocean temperature T:

$$ \rho_{o} c_{p} H \frac{dT}{dt} = - \lambda T + Q , $$
(8)

where Q is the surface heat flux into the ocean, ρ o is the density of seawater (≈ 1000 kg m−3), c p is the specific heat of seawater (≈ 4128 J kg−1 K−1), and H is the depth of the mixed layer. To the extent that surface heat flux Q behaves as white noise forcing, the above equation reduces to a first order stochastically forced differential equation whose solutions are well known [48]. The parameter λ is a feedback factor representing a damping to climatological conditions and has a typical value of 20 W m−2 K−1 [36], which for a mixed layer depth of 50 m, leads to a damping rate of

$$ \frac{\lambda}{\rho_{o} c_{p} H} \approx \left( 4 \text{ months} \right)^{-1} . $$
(9)

However, this time scale is somewhat misleading because the oceanic mixed layer undergoes a large seasonal cycle. For instance, the mixed layer depth during winter routinely exceeds 150 m and 450 m in the North Pacific and North Atlantic, respectively, giving damping rates exceeding 1 year−1 and (3 years)−1, at least locally. Modifications of the above stochastic model to account for seasonal variations in the mixed layer have been proposed and can improve the fit to observations, especially by capturing the “reemergence” phenomenon [31]. Also, it is well known that temperature anomalies tend to be more persistent on longer spatial scales, suggesting that the feedback parameter depends on the spatial scale of the temperature anomaly [35, 74].

The most prominent components of decadal variability tend to be large scale and therefore cannot be explained by a set of spatially independent ocean mixed-layer models. A more realistic model of decadal variability is provided by atmospheric general circulation models coupled to slab ocean mixed layer models, which we call slab models. In slab models, the ocean temperature at each geographic location is governed by an equation of the type (8), but the heat flux forcing Q is determined by an overlying atmospheric general circulation model. The surface heat flux arising in these models tends to fluctuate with characteristic spatial structures and with certain dependencies on the distribution of SSTs, but often still has a white power spectrum.

Slab models can reproduce the observed simultaneous regression between the AMO and SST, sea level pressure, and winds over the North Atlantic [15]. Slab models also can generate variability similar to the PDO [73]. To be sure, not all details of this variability matches observations. For instance, slab models do not clearly produce the tropical expressions of these components [76]. In some locations, the lag-correlation between AMO and surface heat flux in slab models has the wrong sign relative to coupled models and observations [44, 72, 95], which impacts the atmospheric response to the AMO. On the other hand, these surface heat fluxes tend to be in close balance with ocean heat transport convergence on long time scales [16], so it is unclear whether these fluxes play a driving role or are simply a response to AMO variability. Also, the AMO is anti-correlated with subsurface temperatures and surface salinity in the tropical Atlantic [90]. These features cannot be explained by slab models because slab models have a single temperature in a column (due to the well-mixed assumption) and do not contain salinity as a prognostic variable. Again, whether these relations are associated with driving mechanisms or a response to AMO variability is unclear. Attempts to diagnose causality through time-lagged covariances are problematic because the physical relation is presumed to depend on time scale, and isolating certain time scales by temporal filtering can significantly distort the cross correlation between atmospheric and oceanic variables in a way that depends on the choice of filter [37].

Predictability can be explored systematically using methods discussed in “Identifying the Most Predictable Components”. These methods reveal that the most predictable components of fully coupled models are remarkably similar to those of slab models [83], suggesting that the essential physics of many forms of decadal predictability do not involve interactive ocean dynamics. On the other hand, studies show that components like the AMO and PDO can be predicted with more skill than univariate regression models by including additional predictors associated with ocean dynamics (e.g., meridional overturning circulation or ENSO) [71, 86], suggesting that ocean dynamics augments or modulates decadal variability that can occur in the absence of ocean dynamics.

Recently, a very different hypothesis about AMO variability has been proposed: some studies argue that, during the past century and a half, AMO variability has been forced primarily by aerosol emissions and periods of volcanic activity [6]. Again, some aspects of the simulations used in these studies are at odds with observations [94]. In any case, the existence of competing hypotheses for the same observations suggest that the mechanisms of decadal predictability are far from settled science.

Decadal Predictions

Multi-year predictions based on dynamical models have been discussed extensively [55]. Predictions based on empirical models, in contrast, have received much less attention, and thus will be our focus here. Empirical predictions provide a valuable tool in decadal predictability because they are economical to perform, they serve as benchmarks for dynamical model forecasts, their predictability can be diagnosed comprehensively by methods in linear algebra, and they are sufficiently skillful as to be useful in their own right. Energy balance models provide the simplest physically based prediction models for global average temperature [46]. Recently, multivariate regression models that incorporate time lag information in climate forcings and include components of internal variability, such as ENSO, have been developed [62]. These models can account for a significant fraction of multidecadal variability in global average temperature and have some explanatory power. As an example, one such model attributes the rapid rise in global average temperatures from 1992–1998 to the combined influences of anthropogenic global warming, ENSO-induced warming, and the recovery from the Pinatubo eruption in 1991 [61].

Empirical prediction models for internal variability often are of the form

$$ \hat{\mathbf{x}}_{t+\tau} = \mathbf{L}_{\tau} \mathbf{x}_{t} $$
(10)

where x t is the state vector at time t, L τ is a transition matrix, \(\hat {\mathbf {x}}_{t+\tau }\) is the predicted state vector at time t + τ. In most cases, the state space is defined by the leading principal components of the domain being predicted. A linear inverse model (LIM) defines the transition matrix as

$$ \mathbf{L}_{\tau} = \mathbf{L}_{1}^{\tau} , $$
(11)

where L 1 is the least squares prediction operator for a 1-year lag. These models show that for short leads (e.g., a year or two), transient growth mechanisms associated with non-orthogonality of eigenmodes are important. For larger leads, predictability is dominated by the persistence of the least damped modes, which often have a strong projection on the AMO and PDO [69, 93]. The skill of linear inverse models for multi-year leads is comparable to, or even better than, the skill of dynamical model hindcasts [49, 69].

A complementary approach to estimating empirical models from observations is to estimate them from dynamical model simulations. This approach is attractive because the forced and internal components can be analyzed separately, whereas these components are superposed in observations. In addition, the available observational record is relatively short—only 15 decades—whereas dynamical model output is orders of magnitude larger, thereby providing a much larger sample size for estimating empirical models. Of course, dynamical models are imperfect and hence empirical relations derived from them may not be realistic or may miss important physical relations. This deficiency can be mitigated to some extent by a multi-model approach in which many dynamical model simulations are pooled together. Another attractive aspect is that the training sample is completely independent of observations, hence the entire observational record becomes a genuinely independent verification sample. This aspect is especially attractive in light of the fact that cross-validation techniques usually are employed to estimate empirical models from observations. In cross-validation, some portion of the sample (often a decade) is withheld from the training process and the remaining sample used to train the model, then the resulting model is used to predict the withheld sample. Unfortunately, different empirical models are generated in this procedure, thereby complicating the interpretation of predictability. Also, cross validation gives inflated estimates of skill if the data are serially correlated, which is certainly the case when trends or multidecadal variability is present. These issues do not automatically discredit empirical estimation, but they do raise questions that have to be addressed carefully. These questions are avoided completely if the empirical model is derived from dynamical model output.

Individual predictions for forced and internal variability can be added together to produce a climate prediction. By itself, the forced component is independent of lead time, and thus, its skill is independent of lead time. Adding predictions of internal variability to the prediction of the forced component adds skill for 2–5 years, depending on spatial structure [23]. This result demonstrates that initial condition information can improve decadal prediction skill for a few years. This improvement occurs even when the empirical model for internal variability is estimated from dynamical model simulations rather than from observations [23]. In contrast to current decadal predictions based on dynamical models, this type of decadal prediction system avoids initialization shock because the regression model does not require initialization of a full ocean model, and avoids climate drift because the regression model can be estimated from equilibrated control runs. This type of decadal prediction system also is extremely economical relative to AOGCMs.

Identifying the Most Predictable Components

Studies of decadal predictability often focus on the predictability of certain climate indices, such as the AMO or PDO. The AMO is simply a spatial average of the SSTs over the North Atlantic and the PDO is a component in the North Pacific with maximum variance. These indices have proven useful for certain kinds of studies, but they were not defined for the explicit purpose of studying decadal predictability. The question arises as to whether there exists a systematic, optimal method for identifying indices of decadal predictability.

One approach to the above question is to find indices that maximize a measure of predictability. For forced predictability, the appropriate measure is M F (7), which in the case of Gaussian distributions becomes

$$\begin{array}{@{}rcl@{}} M_{F} &=& - \frac{1}{2} \log \frac{| \boldsymbol{\Sigma}_{F} |}{|\boldsymbol{\Sigma}_{U} |} + \frac{1}{2} \text{tr} \left[ \left( \boldsymbol{\Sigma}_{F} - \boldsymbol{\Sigma}_{U} \right) \boldsymbol{\Sigma}_{U}^{-1} \right]\\ &&+\,\frac{1}{2} \left( \boldsymbol\mu_{F} - \boldsymbol\mu_{U} \right)^{T} \boldsymbol{\Sigma}_{U}^{-1} \left( \boldsymbol\mu_{F} - \boldsymbol\mu_{U} \right) , \end{array} $$
(12)

where μ F and μ U are the means, and Σ F and Σ U are covariance matrices, for the forced and unforced systems, respectively (i.e., forced and control simulations). The terms in the top line measure dispersion while terms in the bottom line measure signal [56]. The linear combination of variables that maximize dispersion are found by solving the generalized eigenvalue problem

$$ \boldsymbol{\Sigma}_{F} \mathbf{q} = \lambda \boldsymbol{\Sigma}_{U} \mathbf{q} . $$
(13)

The linear combination of variables that maximize the signal term is found from Fisher’s linear discriminant. Finally, the linear combination of variables that maximize all terms in M F except the log-term are called the most detectable components, because it can be shown that they maximize the average detection statistic in optimal fingerprinting [52].

For initial value predictability, the natural approach is to identify projections that maximize the predictability measure M I V defined in Eq. 4. If the distributions are Gaussian, then this measure reduces to

$$ M_{IV} = - \frac{1}{2} \log \frac{| \boldsymbol{\Sigma}_{E} |}{|\boldsymbol{\Sigma}_{C} |} , $$
(14)

where Σ E and Σ C are the covariance matrices for the forecast and climatological distributions [24]. The linear combination of variables that maximize this measure are found by solving the generalized eigenvalue problem

$$ \boldsymbol{\Sigma}_{E} \mathbf{q} = \lambda \boldsymbol{\Sigma}_{C} \mathbf{q} . $$
(15)

The resulting components are called the most predictable components of the forecast system. In the context of ensemble forecasting, Σ E is estimated from differences between ensemble member and ensemble mean. This technique appears in various guises and under various names, including Signal-to-Noise Maximizing EOFs, Predictable Component Analysis, and Multivariate Analysis of Variance (MANOVA) [28, 79, 89].

It is instructive to consider the most predictable components of a linear regression model, which has the form

$$ \mathbf{x}_{t+\tau} = \mathbf{L}_{\tau} \mathbf{x}_{t} + \boldsymbol\epsilon_{t}. $$
(16)

A standard result in regression theory is that the forecast error covariance matrix is related to the time-lagged covariance matrix as

$$ \boldsymbol{\Sigma}_{E} = \boldsymbol{\Sigma}_{0} - \boldsymbol{\Sigma}_{\tau} \boldsymbol{\Sigma}_{0}^{-1} \boldsymbol{\Sigma}_{\tau}^{T} , $$
(17)

where Σ τ is the time-lagged covariance matrix of x t . Substituting (17) into (15) leads to an eigenvalue problem that is equivalent to Canonical Correlation Analysis (CCA) [24]. Thus, the most predictable components of a linear regression model are precisely the patterns that maximize correlation between initial and final states. These components also can be derived as the singular vectors of the propagator, provided suitable vector norms are used [25].

One shortcoming of maximizing predictability at a single lead is that the results depend on the choice of lead. For instance, the most predictable component at 1 year differs from that at 5 years. However, the space spanned by the most predictable components often is the same over a range of lead times. To derive predictable components in a way that avoids a lead-time dependence, one can maximize the integral of predictability over lead time. Such integrals are called integral time scales and are common in turbulence studies. Unfortunately, integrating M I V leads to a nonlinear optimization problem even for Gaussian distributions. However, integrating the related measure

$$ P = 1 - e^{-2M_{IV}} = 1 - \frac{| \boldsymbol{\Sigma}_{F} |}{|\boldsymbol{\Sigma}_{C} |} , $$
(18)

leads to an optimization problem that can be solved by eigenvector methods [26]. This approach is called Average Predictability Component (APT) Analysis and has been used to clarify the spatial structure of decadal predictability globally, and in distinct ocean basins and continents [29, 50, 51].

A practical limitation of the above methods is that, in most applications, the covariance matrices estimated from data are singular, owing to the fact that the number of grid points far exceeds the sample size. Consequently, solving the above maximization problems requires some sort of regularization procedure. The most common regularization is to project the data onto a reduced dimension subspace, usually the space spanned by the leading empirical orthogonal functions (EOFs) of the data. EOFs can be problematic because they depend on the data and complicate significance testing. An alternative basis set that has several attractive properties are the eigenvectors of the Laplace operator. These eigenvectors can be ordered by a measure of spatial scale, hence they provide an objective basis for reducing the dimension of a data set by filtering out small-scale variability. This approach is attractive given that most mechanisms of decadal predictability involve large-scale spatial patterns. In addition, Laplacian eigenvectors depend only on the geometry of the domain and therefore are independent of the data, a feature that is attractive for small sample sizes. Recently, new algorithms have been discovered for computing Laplacian eigenfunctions over arbitrary domains [27].

A key question in the above approaches is how many basis vectors should be chosen in a particular application. This question is tantamount to model selection question and is an active area of research [96]. For large data sets, a typical approach is to split the data into two parts: one part, called the training set, for deriving the predictable components, and another part, called the verification set, for verifying the predictability of the components.

The above framework applies for Gaussian distributions and analyzes only the first and second moments of random variables. However, the climate system is nonlinear and probably contains predictable variability that cannot be captured by the first two moments. For instance, intermittent patterns arising in turbulent dynamical systems tend to have low variance but play an important role in turbulence. Recently, methods based on Laplacian eigenmaps and diffusion maps have been proposed for representing a high-dimensional data set with a low dimensional description in a way that preserves information about the nonlinear manifold in which the data lies [2, 17, 41]. These methods have proven capable of identifying intermittent structures in climate simulations that would otherwise go undetected with EOF-type methods [41].

Predictability and the Power Spectrum

It is sometimes suggested that the predictability time scale can be identified with the peak of a power spectrum. For instance, the AMO index has an apparent peak around 50–70 years [30]. However, no prediction of AMO has demonstrated skill anywhere close to 50 years. How can a process have a spectral peak around 50 years and yet have predictability much less than that? The answer is that the location of a spectral peak need not have anything to do with predictability. Instead, predictability time scale often is related to the width of a spectral peak [14, 24], as we demonstrate below in the context of an analytically solvable model.

We consider the classical beta-plane model for Rossby waves:

$$ \frac{\partial \zeta}{\partial t} = - U \frac{\partial \zeta}{\partial x} - \beta \frac{\partial \psi}{\partial x}, $$
(19)

where ζ = ∇2 ψ is vorticity, ψ is streamfunction, U is a zonally symmetric background zonal flow, and the other variables have their usual meaning [88]. The beta-plane model is barotropic and hence its solutions have no direct relation to temperature. We use it here merely to illustrate certain basic concepts that hold in any damped linear system that supports wave solutions. Because the system is linear and deterministic, its solutions are predictable for an infinite amount of time. To study a system with finite predictability, we add stochastic forcing and Rayleigh damping:

$$ \frac{\partial \zeta}{\partial t} = - U \frac{\partial \zeta}{\partial x} - \beta \frac{\partial \psi}{\partial x} - r \zeta + \epsilon , $$
(20)

where r is the dissipation rate and 𝜖 is white noise forcing with zero mean. Since the coefficients are constant, the equation supports eigenmode solutions of the form

$$ \psi(x,y,t) = \psi_{k,l} (t) \exp \left[ i (kx + ly) \right] . $$
(21)

Fourier transform methods yield the following equation for wavenumbers k and l:

$$ \frac{\partial \psi_{k,l}}{\partial t} =\lambda \psi_{k,l} + \epsilon_{k,l} , $$
(22)

where λ = λ R + i λ I is the corresponding eigenvalue with

$$ \lambda_{R} = - r \quad \text{ and } \quad \lambda_{I} = - k \left( U - \frac{\beta}{k^{2}+l^{2}} \right) . $$
(23)

Because the coefficients in the beta-plane model are constant, each Fourier mode can be solved independently of the others. Therefore, we focus only on a specific value of k and l, in which case the k,l subscripts can be dropped to yield the simple stochastic differential equation

$$ \frac{\partial \psi}{\partial t} =\lambda \psi + \epsilon , $$
(24)

where 𝜖 is assumed to be a (complex) white noise process with covariance

$$ E[ \epsilon(t) \epsilon^{*}(t^{\prime}) ] = \sigma_{\epsilon}^{2} \delta(t-t^{\prime}) , $$
(25)

where E[⋅] denotes the expectation operator and the asterisk denotes the complex conjugate. Because the forcing term 𝜖 is random, only the statistics of the solution are relevant. Methods for solving these statistics are standard [22, 24, 40]. In the case of a deterministic initial condition, the variance of the ensemble of solutions grows with time as

$$ {\sigma_{t}^{2}} = E \left[ \left| \left( \psi_{t} - E[\psi_{t}] \right) \right|^{2} \right] = \sigma_{\epsilon}^{2} \left( \frac{1- e^{2 \lambda_{R} t} }{- 2 \lambda_{R}} \right) , $$
(26)

the stationary time-lagged covariance is

$$ c_{\tau} \,=\, E \left[ \left( \psi_{t+\tau} \,-\, E[\psi_{t+\tau} ] \right) \left( \psi_{t} \,-\, E[\psi_{t} ] \right)^{*} \right] \,=\, e^{\lambda \tau } \sigma_{\infty}^{2} , \quad \text{ for } \tau \ge 0 , $$
(27)

and the power spectrum is

$$ s(\omega) = \frac{\sigma_{\epsilon}^{2}}{ \left| \lambda - i \omega \right|^{2}} = \frac{\sigma_{\epsilon}^{2}}{ {\lambda_{R}^{2}} + (\omega - \lambda_{I} )^{2}}. $$
(28)

Predictability of this system can be measured by M I V , which for Gaussian distributions reduces to Eq. 14, and for the present scalar system reduces to

$$ M_{IV} = -\frac{1}{2} \log \frac{{\sigma_{t}^{2}}}{\sigma_{\infty}^{2}} = -\frac{1}{2} \log \left( 1- e^{2 \lambda_{R} t} \right) . $$
(29)

This measure decays monotonically with lead time. Stochastic models have limited predictability because random noise in the dynamics renders the future uncertain even with perfect initial conditions. The variance of the ensemble of solutions (26) can be viewed as measuring errors of forecasts starting from the same initial condition. The error variance saturates at \(\sigma _{\infty }^{2}\) at asymptotically long times, as illustrated in Fig. 3a. The limit of predictability τ P usually is defined as the time at which the error variance exceeds some pre-chosen fraction α of the saturation variance [63]. From (26), this time scale is

$$ \tau_{P} = \frac{\log(1-\alpha)}{2 \lambda_{R}} . $$
(30)

This time scale is illustrated in Fig. 3a. Note that the limit of predictability depends only on the real part of the eigenvalue, which in turn depends only on the damping rate in the model. Thus, the limit of predictability in this model is determined by the damping time scale.

Fig. 3
figure 3

Results from a stochastically forced linear differential equation: error growth as a function of lead time (a), power spectrum (b), and autocorrelation function (c). The curves are generated from Eqs. 26–28 for λ R = −1 and λ I = 4.5. The limit of predictability is based on the fraction α = 80%

Full size image

The above definition of predictability limit is of course arbitrary. However, variance depends only on λ R , hence any definition of a predictability time scale derived from variance would depend only on the real part of the eigenvalue.

The power spectrum (28) has a simple interpretation: the spectrum peaks at ω = λ I and decays asymptotically as ω −2 for large frequencies. These features are illustrated in Fig. 3b. Thus, the location of the spectral peak is determined by the imaginary part of the eigenvalue, which is the Rossby frequency. The real part of the eigenvalue turns out to effect the width of the spectral peak. For instance, the width of the spectral peak can be measured by the full width at half-maximum (i.e., the distance between two points on the spectral curve that are at half the maximum amplitude). This width is indicated in Fig. 3b. The two frequencies at half-maximum are ω = λ I ± λ R , hence the width is 2|λ R |, which depends only on the real part of the eigenvalue. These results demonstrate that, in this simple model, the location of the spectral peak is independent of predictability. Instead, predictability is reflected by the width of the spectral peak– narrow peaks correspond to high predictability while broad peaks correspond to low predictability. In the limit of no predictability, the spectrum is flat, corresponding to white noise.

The autocorrelation function provides a complementary perspective of the above concepts. The autocorrelation function is defined as

$$ ACF = \frac{c_{\tau}}{c_{0}} = e^{\lambda \tau} = e^{\lambda_{R} \tau} \left( \cos(\lambda_{I} \tau ) + i \sin(\lambda_{I} \tau ) \right) , $$
(31)

the real part of which is illustrated in Fig. 3c. Note that the autocorrelation function is the product of an exponentially decaying function and a sinusoid. The exponential function defines the envelope of the autocorrelation function while the sinusoid defines the oscillatory part. The envelope decays with an e-folding time − 1/λ R while the oscillatory part has period 2π/λ I . Thus, based on the previous discussion, predictability is reflected by the envelope, while the spectral peak is reflected by the oscillation frequency. This example illustrates how predictability and oscillation frequency characterize different aspects of the autocorrelation function, and in particular how the oscillation frequency can differ from predictability.

Conclusion: Future Prospects

In regards to future prospects, some trends are clear: long standing assumptions about the mechanisms of decadal predictability are currently being questioned intensely [15], so it is likely that further progress will be made in this area. Also, because the effective sample size in decadal predictability is small, comparison between models and observations is challenging and is likely to drive new statistical techniques and new analyses of different kinds of data, especially paleo-records. Research stimulated by the recent slowdown in global surface warming has lead to a better understanding of decadal variability in the ocean and of the role of decadal changes in volcanic forcing and solar variability, which is likely to be exploited in future forecast systems. The importance of improving ocean observations to track ocean heat uptake also has become clear. On the other hand, there are a number of open questions that do not seem to be the focus of any coordinated research. For instance, dynamical models differ considerably in their internal variability [10], revealing a large uncertainty in the physical modeling of decadal variability. Indeed, some analyses suggest that current climate models grossly underestimate variability on multidecadal and longer time scales [1, 59]. These potential inadequacies warrant further research. Some “low-hanging fruit” also can be exploited. For instance, simple energy balance models and empirical models have been shown to give skillful predictions of temperature variations for years. It seems that these models should be used more routinely for decadal predictions.