1 Introduction

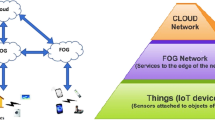
Mesh network is a common topology to be used in deploying Edge/Fog computing for Internet of Things (IoT) system due to several advantages over cloud based or centralized topology. Some of the advantages are robustness for no single point of failure, expandable, and reliable [16, 21].

Unlike centralised topology as seen in Figure 1 where each sensor is connected directly to the cloud [3], gateways are the key roles that connect the mesh network to the cloud infrastructures. In Edge/Fog computing, gateways are devices where local computation powers or local storages are placed [8, 12]. Therefore, it is important to make sure all devices (sensors and routers) in the network can connect to the nearest gateways to minimize network latency [4].

Fig. 1
figure 1

IoT network topology

Full size image

Leaving routers with no alternate gateways will cause major problem in the mesh network since some sensors might not work properly [13]. Providing pre-defined alternate gateways will not only make all routers will automatically switch to another nearest gateways, but also ensure that these gateways have minimum number of hops from the routers. The illustration for routers redirection during a gateway failure can be viewed in Figure 2. In this example, a gateway might have failed and force the routers that are fully depended to this gateway to find alternate routes (dashed green line) to reach another gateway within this network to ensure network traffics are unaffected during gateway failover. The routes to reach the backup gateway will be longer that the original route to the primary gateway, however the main aim in mesh network is to ensure that the failure of a device will not disturb the communication within the network.

Fig. 2
figure 2

Gateway failure

Full size image

To provide backup gateways for the routers, our previous work proposed hops Voronoi diagram expansion to provide primary and secondary nearest gateway for the routers [1]. The trial an error in determining the expansion value will cause some routers have no backup gateway. In this Figure 3, gateways are indicated by large circles while routers without alternate gateways are identified by “X” mark. In the previous experiments, 100% expansion for all Voronoi cells will not guarantee that all routers will have alternate nearest gateway. Furthermore, only one backup gateway is possible by using this method.

Fig. 3
figure 3

Routers with no alternate gateways (X)

Full size image

While providing backup gateways through Voronoi expansions leaves a small portion of the routers without backup gateways, the generalization of Voronoi diagram, named order-k Voronoi diagram provides region segmentation where each region has two nearest facilities. However, since distance-based calculation in Network Voronoi Diagram (NVD) has improper hops distributions, order-k NVD also suffers with the same problem as well.

Motivated by some drawbacks in the previous work, in this paper we propose an order-k hops Voronoi diagram (order-k HVD) to identify k-gateways backup in mesh network where we utilize sink tree algorithm in constructing an order-k HVD. Unlike HVD expansion, our contribution in this paper ensures that no routers are left behind without having backup gateways, as long as the routers are connected to the mesh network. Our experiments show that order-k HVD can provide shorter hops for k-alternate gateways compare to order-k NVD, hence provide shorter hops distribution and offer lower network latency.

The paper is organized as follow: Section 2 presents higher order Voronoi diagram, hops concepts and other related works; Section 3 provides the proposed concept of order-k hops Voronoi diagram. The evaluation and discussion is presented in Sections 4 and 5 concludes our work in this paper.

2 Related works

2.1 Network routing algorithms

Routing algorithm is the algorithm that manages the routing table and make the routing decision. Generally, packets will require multiple hops to reach destination from the source node. To improve the overall network throughput, routing algorithms are aimed to minimise the travel path for the packets or reduce the number of hops a packet must have in the journey.By reducing the distance or number of hops, the network delay and amount of bandwidth needed to transmit the packets can be reduced.

In computer network, there are two different metrics that can be used as distance which are hops and physical distance. Although distance does not always corelate with hops [9], in some cases a physical distance-based shortest path algorithms may lead into higher number of hops, hence reduce network performance.

To preserve the overall network performance and keeping the latency to a minimum, it is important to have a gateway with minimum hops in the network [7, 14].

As illustrated in Figure 4, gateway G1 and G2 are separated by middle line, which means this line is in the middle between G1 and G2. Therefore even though this line divides the segment equally, the number of routers in each area are different. It means, the furthest router r3 in G1 will have to hops 2 times before reaching the gateway G1 while the furthest router r4 for G2 will have to perform 6 hops to reach the gateway G2.

Fig. 4
figure 4

Inequal hops on distance based

Full size image

The optimal routes from a given destination to all possible sources can form a tree where the root is the sole destination. This tree is called a sink tree as illustrated in Figure 5. In this figure, the sink tree is constructed with two different metrics which are hops and physical distance. Figure 5a shows a sink tree where hops is used as distance metric to reach all destination nodes with minimal hops and another sink tree is created with physical distance to reach all nodes with minimum distances as in Figure 5b. The goal of all routing algorithms is to obtain and use sink trees for all possible paths with minimum cost.

Fig. 5
figure 5

Sink tree

Full size image

The most common algorithm to compute the shortest path between two nodes in a network graph is Dijkstra algorithm [2, 23]. This algorithm works by labelling each node with its distance from source point along the shortest known path. Since the aim in this paper is to find the shortest path with minimal hops, the metric distance that will be used in Dijkstra algorithm is hops metric. While Dijkstra algorithm is limited to find an optimum route, Sink Tree on the other hand is aimed to find all optimum routes to reach a destination point from all routes. Therefore, a multi-source Dijkstra can be used to form Sink Tree structure.

In this paper, Sink Tree will be used in conjunction with order-k hops Voronoi diagram to identify alternate k-gateways for mesh network topology.

2.2 Definition of Voronoi diagram

Let S be a fixed axis-parallel rectangle in Euclidean space \(S \subseteq \mathbb {R}^{2}, \) a set of facility points \(P = \{p_{1},p_{2},p_{3},..,p_{m}\}\subseteq S\) and m = ∣P∣. Voronoi diagram can be defined as a method in dividing space into a number of regions where each region will consider a facility point pi as the nearest point. The nearest point is called the generator point [18]. The regions in the Voronoi diagram are called V oronoi cells.

The region for a generator point pi or a Voronoi cell can be defined as an intersection of all halfspace of pi with other generator points H(pi, pj).

Let x be an arbitrary point in S and {x} ∩ S ≠ ∅, the Euclidean distance between x and pi is given by d(x, pi). If pi is the nearest generator point from x, then d(x, pi) ≤ d(x, pj) where i≠j, 1 ≤ i, j ≤ m.

Therefore, the Voronoi cell can also be defined as the region where any point x located in a Voronoi cell R(pi) will consider pi as the nearest generator point.

$$ R(p_{i}) = \{x |~ d(x,p_{i}) \le d(x,p_{j}), i\ne j, 1\le i,j\le m \} $$

Since Voronoi diagram can be used to make space partition with distance-based calculation, this method is commonly used in solving region-based spatial queries [15, 18]. For IoT devices deployment, a Voronoi diagram is utilized to group the sensors to reduce latency [19]. Authors [5] presented Hivory, a model of hierarchical Voronoi range query to support multi-attributes range query in IoT distributed system. In [6, 17], the authors employed a Voronoi cell to indicate the coverage of the sensors during the IoT deployment. Although Voronoi diagram is mainly used to calculate static region, the implementation is not only limited in static spatial queries, but also in a movement environment to obtain nearest objects during movement [22, 23].

In a graph or network problem, Voronoi diagram can be implemented as network Voronoi diagram (NVD) [11], where the Euclidean distance metric is replaced by the physical edge between devices. In a computer network, NVD is commonly used to observe signal coverage [17].

Let O = {o1, o2, o3, ... , ob} be a set of objects that are not generator points, O ∩ P = ϕ, graph network G(E, V ) and E = O + P.

The network Voronoi cell Rn(pi) is defined as all objects o that consider pi as the nearest generator point. A shortest distance function sd(o, pi) is used to indicate the distance between object o and generator point pi. If pi is the nearest generator point from o, then sd(o, pi) ≤ sd(o, pj) where i≠j, 1 ≤ i, j ≤ m.

$$ Rn(p_{i}) = \{o |~ sd(o,p_{i}) \le sd(o,p_{j}), i\ne j, 1\le i,j\le m \} $$

Since computer network uses the graph structure, NVD can also be used to distribute gateways workload evenly in the network [13]. The workload distribution aim is to assign nearest gateway for all available routers in the mesh network [1, 20].

2.3 Definitions of higher order Voronoi diagram

In a higher order Voronoi diagram, the number of generator points for one cell depends on the order of the Voronoi diagram itself. An order-n Voronoi diagram is another form of Voronoi diagram where each cell has n generator point; hence, each Voronoi cell has n-nearest generator points. An order-n Voronoi diagram is also called Higher Order Voronoi diagram (HOVD) [10].

Let D(k) as set of distinct k elements of P. Region in Order-k HOVD R(D(k)[i]) can be considered as a Voronoi cell where this cell has k generator points. As for higher order NVD, an order-k Voronoi cell for D(k) in G(E, V ) can be defined as all objects that have D(k) as their k NN.

$$ Rn(D^{(k)}) = \{o | kNN(o_{i})=D \} $$

The illustration of order-2 Voronoi diagram can be seen in Figure 6. In order-2 VD, each cell will have 2 nearest generators. Generator P1 area is calculate without including P3 and vice versa as in Figure 6a and b. Their area will be intersected as in Figure 6c to form an area that consider both P1 and P3 as the two nearest generators. The complete set of order-2 VD for this example is shown in Figure 6d.

Fig. 6
figure 6

Order-2 Voronoi diagram construction

Full size image

Another implementation of order-k in network Voronoi diagram is also shown in Figure 7. The left figure shows the network Voronoi diagram for city of Melbourne that is partitioned into 12 suburbs where the points represent the estimated centre of the suburbs. The opposite figure is the order-2 NVD to show the coverage of two nearest centres.

Fig. 7
figure 7

City of Melbourne

Full size image

3 Order-k hops Voronoi diagram

3.1 Definition of hops Voronoi diagram

The hops Voronoi diagram (HVD) is based on NVD where all edges share the uniform length, regardless the actual physical distance [1]. A hop represents a segment that connect two adjacent vertices where the length is 1.

The graph structure G(E, V ) in NVD and HVD is remain the same. The shortest distance between o and generator pi is defined as sh(o, pi). The hops Voronoi cell for generator pi hRn(pi) can be defined as

$$ hRn(p_{i}) = \{o |~ sh(o,p_{i}) \le sh(o,p_{j}), i\ne j, 1\le i,j\le m \} $$

The construction of hops Voronoi diagram from G(E, V ) is conducted by using multi-sources Dijkstra algorithm as shown in Figure 8. The algorithm will start from all generator points simultaneously to obtain unclaimed points as indicated by gray points, and it will stop after no more points can be obtained. The final HVD result is shown in Figure 8b.

Fig. 8
figure 8

Multi-sources Dijkstra for HVD construction

Full size image

3.2 Definition of order-k hops Voronoi diagram

Order-k HVD is based on order-k Voronoi diagram where the aim is to find k nearest gateways for each router. Order-k HVD shares similar characteristic with Order-k NVD, however, the physical distance between vertices is substituted with uniform value of 1 to represent a single hop. Unlike NVD that uses multisource Dijkstra algorithm, in our proposed order-k HVD, we utilize multi-step sink tree in constructing the order-k HVD.

figure a

The first step in constructing order-k HVD is creating sink tree structure for each gateway. Once the sink trees have been created, the hop value in each router will be sorted to identify the closeness of a router to all gateways. Once the distance value has been sorted, the k number of gateways will be taken to make order-k HVD structure.

In order to handle multiple sink trees in the graph network, we modify the sink tree structure in each node to store multiple distances along with their gateways. By using this method, we are able to retrieve the order-k structure dynamically for any value of k without having to reconstruct the sink trees. The visual illustration for this structure is shown in Figure 9.

Fig. 9
figure 9

Overlaid sink tree

Full size image

The illustration how order-k HVD is constructed can be observed in Figure 10. In this example, we have 100 routers with 3 gateways where each router will have connection to 4 other nearby routers. Figure 10a–c shows the sink tree for each gateway. Figure 10d shows order-2 HVD from the overlaid sink trees.

Fig. 10
figure 10

Sink tree for order-2 HVD

Full size image

In the next following section, we will perform the experiments over synthetic and real dataset to see whether order-k HVD can be used to identify alternate k-gateways and also the hops reductions compared to native order-k NVD.

4 Evaluation and discussion

In this section, we evaluate the performance between order-k NVD and order-k HVD in terms of providing alternate-k gateways with minimal hops from various dataset. All algorithms are implemented in Java. We conduct experiments on two different dataset, one being synthetic dataset comprising data on 1K, 10K, 20K and 50K routers that are distributed uniformly in an area of 100km x 100km. The synthetic dataset is created in a way to simulate a high density hops network that may consists of 1k to 50k vertices. The distribution graphs is shown in Figure 11. The network structure is constructed with All-kNN queries where k = 4. We keep the service load of each gateway a 1 : 100 ratio, which means the number of gateways is 1% of the number of routers. In addition to the synthetic dataset, we also conduct experiments on real dataset. The first dataset is obtained from AEMO for electrical substation distribution in Eastern AustraliaFootnote 1 that consists of around 1k substations and generators. The second real dataset is flight route database obtained from openflights.orgFootnote 2 which is closely related to the hops problem. As in June 2014, this dataset contains 67,663 routes flights between 3321 airports on 548 airlines. After we disregarded airline ID for all routes, we ended up with 6073 distinct airports and 37,573 distinct routes. The details of the dataset are given in Table 1.

Fig. 11
figure 11

Average points for each facility

Full size image
Table 1 Experiment dataset
Full size table

4.1 Scenario

Since order-k HVD has ensured that all routers will always have alternate k-gateways as the backup routers, we will evaluate the impact of k values to the hops for both order-k NVD and order-k HVD. We will evaluate the number of hops that need to be taken for the furthest router in the network to reach primary and alternate gateways. We also will evaluate the distribution for hops for both order-k NVD and order-k HVD to see the average hops in the network as the indication for the overall network performance.

The baseline for the NVD and HVD statistics can be seen in Tables 2. As we can see in this table, as a baseline, HVD has less hops by 1 hop for all dataset, and the average number of nodes that need to be served for each gateway is similar for both NVD and HVD.

Table 2 Baseline table
Full size table

4.2 Order-k hops Voronoi diagram

The next experiments are aimed to observe the effectiveness of order-k HVD to obtain k alternate gateways with minimum hops for all of the routers. We perform the experiments using both synthetic and real dataset as explained above. For the sake of simplicity, we limit the number of alternate gateways into 5 gateways for each router. The result for our experiment can be seen in Table 3 and we put the result in a visualization chart in Figure 12.

Fig. 12
figure 12

Hops comparison

Full size image
Table 3 Order-k average hops
Full size table

From the experiment result, we can clearly see that order-k HVD outperform order-k NVD in terms of lower number of hops for the whole range value of k. It means that each routers can have k alternate gateways with minimum number of hops to reach its primary or alternate gateways with minimum network latency (Figure 13).

Fig. 13
figure 13

Hops frequency

Full size image

Further investigation on hops frequency for both order-k NVD and order-k HVD shows similar pattern. Both method share similar hops frequency for all value of k, however order-k NVD has several longer hops than order-k HVD as shown in Figure 14.

Fig. 14
figure 14

Average Hops distributions

Full size image

Figure 14 shows the average hops distribution in these experiments. From this figure, we cans see that the maximum hops increase in conjunction with the increment value of k. With an increase in k, the number of hops for the furthest point and the number of most frequent hops increases.

If we look more closely in detail, the differences between average hops for order-k NVD and order-k HVD for all k values are around 1.5 hops. It means that each router in order-k NVD will have 1 until 2 hops more than router in order-k HVD (Figure 15).

Fig. 15
figure 15

Order-k NVD vs order-k HVD hops differences

Full size image

While the average number of hops between order-k NVD and order-k HVD are different, the average number of members in each dataset are exactly the same. This result proofs that both NVD and HVD have the same performance in term of distributing the routers in the network (Figure 16).

Fig. 16
figure 16

Average members for each gateway

Full size image

The verdict of this experiment is clear, where order-k HVD can give alternate k-gateways for the routers to overcome failover problem in Mesh network, and at the same time ensure minimum hops to all k-nearest gateways for all routers. The less hops for the routers means that the overall network throughput.

5 Conclusion

In this paper, we propose an order-k hops Voronoi diagram to assign alternate k-gateways in Mesh IoT network to overcome failover problem. Our experiment shows that order-k HVD not only provide k nearest gateways for all routers, but also ensure the gateways are within minimal hops from the routers, hence minimize network latency to the overall network performance. Our experiments using AEMO and flight data also show that the order-k hops Voronoi diagram also suitable for a condition where physical distance can be set aside in analyzing the graph connectivity.

We are working on evaluating the effectiveness of k backup gateways that are obtained from order-k HVD in handling gateway failover to understand how many backups are sufficient to avoid blackout in multiple gateways failures.