Introduction

Surface nano-patterning of optical materials can provide them antireflective, superhydrophobic, self-cleaning and antifogging properties [1,2,3,4,5,6,7,8], which are very useful in many applications for which moisture and dust are detrimental to the optical performance. Square or hexagonal lattices a few microns high, slightly truncated cones, can be generated by lithography and etching steps at the surface of germanium or silicon wafers. For transparency, the period (p) of the lattice has to be smaller than the wavelength of light, that is, less than one to two microns, since germanium is used in the longwave infrared domain, and silicon in the midwave infrared domain. This implies a cone aspect ratio between 3 and 6, which makes it vulnerable to compression-induced buckling, as a result of impacts of raindrops, hail, sand or any projectile debris in defense applications. Even if such mechanical instability occurs within the elastic regime (and is thus denoted as elastic buckling), it induces a significant change in shape of the cones and thus bending stresses likely to lead to fracture. The resistance to buckling is thus a central aspect of any slender structures like the nanocones [9]. Besides, optical windows also have to pass normalized abrasion tests—during which a tool applied on the window with a given pressure moves to-and-fro with a given displacement range and number of cycles—without losing too much of their optical performance. During such tests, the cones are thus submitted to steady compression and reversed bending stresses. To protect the cones, hard coatings (Al2O3 [10], diamond [11], diamond-like carbon [12], C:H:SiOx [13], and others…). thin enough not to compromise light transmission, can be deposited by various processes, like atomic layer deposition (ALD) or microwave plasma enhanced chemical vapor deposition (MPECVD) [10]. Many studies concerning the optimal deposition process, to obtain the best optical and mechanical properties (mostly hardness, toughness and adhesion, which control their resistance to scratching, wear, cracking and delamination), have been performed on such coatings laid on smooth substrates, but their efficiency in protecting surfaces patterned with slender nanostructures has not been investigated so much.

Besides, optical windows may be subjected to a temperature and/or a pressure differential between both sides, inducing biaxial bending, potentially leading to fracture. Bending fracture of brittle materials is—to a large extent—controlled by surface roughness and surface defects that constitute stress concentration sites, as illustrated for Ge by Craig et al. [14] and for Si by Barnat [15] and McLaughlin & Willoughbly [16]. Surface patterning might thus have a detrimental effect, which should be evaluated.

However, very few studies investigated the mechanical resistance of surface-patterned optical windows. An experimental study of sand or water erosion of sapphire, Alon or diamond windows patterned with truncated nanocones was reported by Hobbs [3]. Infante et al. [4] performed wipe tests on surface-patterned glass. Park et al. [2] used an analytical approach to design truncated silicon oxide cones against elastic buckling or bending fracture due to the dynamic pressure induced by the impact or raindrops.

In this work, the compressive resistance of Si or Ge nanocones, and the protection efficiency of alumina or diamond coatings are investigated by numerical simulations and nano-compression tests. The latter show that the problem cannot be analyzed just in terms of elastic buckling, and that plasticity or even viscoplasticity play an important role.

The impact of surface patterning on the fracture resistance of the substrate is also investigated by finite element simulations and biaxial bending tests.

Of course, concerning multifunctional optical windows, design optimization should be based primarily on optical and microfluidic properties, before considering the mechanical resistance and durability and in some cases, the resistance to corrosive environments [7]. The problem thus includes many aspects (developed in [1,2,3,4,5,6,7,8]) that fall outside the scope of this paper, devoted only to the mechanical robustness.

Numerical study

Elastic buckling of bare or coated truncated cones

For an elastic isotropic truncated cone, an analytical assessment of the resistance to buckling can be made [2]. However, a numerical approach is better suited to capture the effect of elastic anisotropy/crystal orientation, and that of a thin coating. To compute the buckling resistance of a bare or coated truncated cone, taking the elastic anisotropy of Si or Ge single crystals (C11 = 165,6 GPa, C12 = 63,9 GPa, C44 = 79,5 GPa for the former, and C11 = 127 GPa, C12 = 48 GPa, C44 = 67 GPa for the latter [17]) and the (001) or (111) orientation of the wafer into account, a parametric 3D finite element model was developed, using the Cast3M code (Fig. 1).

Figure 1 
figure 1

Finite element model to analyze compression-induced elastic buckling of a bare a or coated b cone. a–d 2D sections to specify the geometry and notations a–b, boundary conditions c–d, crystal orientations (001) c or (111) d, and e 3D model generated by rotation

Full size image

The nominal height of the cone, the height at which it is truncated, and its width at the base are denoted by h, htrunc and w, respectively. An elastic isotropic behavior, with a Young’s modulus, E = 202 GPa and a Poisson’s ratio, ν = 0.26 is assumed for the 100 nm thick alumina coating. The reduced elastic modulus \(Er=\frac{E}{(1-{\upsilon }^{2})}\) was first estimated, using Oliver and Pharr’s method [18], from the load–displacement nanoindentation curves on an alumina coating deposited by ALD on a smooth Si wafer, at Thales Research & Technology, and subsequently annealed 1 h at 1000 °C, which, according to X-ray diffraction measurements, leads to a partial crystallization in the monoclinic form. To minimize the influence of the substrate, the indentation depth was smaller than 15% of the coating thickness. The Young’s modulus, E, was then deduced, assuming ν = 0.26 [19].

The normal displacement of the bottom face of the substrate was blocked. Two types of boundary conditions on the top surface of the cone were enforced to simulate buckling: either a uniform compressive load distribution, which allows rotation, as it can occur in case of raindrop or sand impact, or a uniform normal displacement, which keeps the top surface horizontal. The latter condition mimics compression by a rigid tool, as in the nano-compression experiments described below, or as during the abrasion tests that the optical windows have to pass. The smallest buckling load, corresponding to the first buckling mode, was computed for various sets of geometrical parameters and simply denoted as « the buckling load». Figure 2a shows an example of deformed mesh for this mode, when the rotation of the summit is allowed.

Figure 2 
figure 2

Buckling of 2-μm-high bare silicon cones when the rotation of the summit is allowed a deformed mesh for the first mode, b buckling load versus the degree of cone truncation htrunc/h for various nominal aspect ratios, h/w

Full size image

Figure 2b shows the buckling load of 2 μm-high bare silicon cones with various nominal aspect ratios, h/w (or in other words, various cone opening angles: ArcTan (h/w)), versus the degree of cone truncation htrunc/h. As expected, the higher the nominal cone aspect ratio, and/or the sharper the cone (that is the closer htrunc is to h), the lower the buckling load. It is interesting to note that a significant truncation can compensate a high nominal aspect ratio.

Figure 3a illustrates the influence of the boundary conditions for a 5 μm high, 1 μm wide bare germanium cone on a (111) wafer. As expected, buckling is easier when the rotation of the summit is allowed. Figure 3b illustrates, for the same cone geometry, the influence of the material and elastic anisotropy. For the same (001) wafer orientation, the Si cone has a better resistance to buckling than the Ge cone, because Si is stiffer.

Figure 3
figure 3

Buckling load of a 5-μm-high, 1-μm-wide cone. a Influence of the boundary conditions for a (111) germanium cone and b influence of the material and wafer orientation, with free rotation

Full size image

Figure 4 illustrates the effect of a 100-nm-thick alumina coating for a 2 μm-high, 1 μm-wide bare Si cone on a (001) wafer. The coating is predicted to increase very substantially the buckling load, especially for the sharpest cones.

Figure 4 
figure 4

Effect of a 100 nm thick alumina coating on the buckling load of a 2 μm-high, 1 μm-wide bare Si cone on a (001) wafer

Full size image

These simulations provide guidelines for the design of robust surface-patterned optical windows: (111) wafers should be preferred. The risk of elastic buckling, which rises with the nominal cone aspect ratio, can be mitigated by truncation, but above all, by the deposition of a thin coating. The nanocompression tests described below will, however, reveal the limitation of this analysis, not only because the specimens geometry often deviate from the assumed truncated cone, but also because the assumptions of a fully elastic behavior of Si and Ge nanocones and infinitesimal strain proved wrong.

II.2 Stress concentration induced by surface patterning

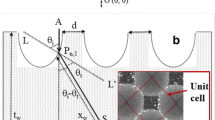
To investigate the effect of surface patterning on the resistance of the substrate to fracture in biaxial bending, the stress concentration at the foot of the cones when the wafer is in equibiaxial tension (the stress state that prevails on the side from which fracture initiates) was estimated for a square or hexagonal lattice, using one of the finite element models shown in Fig. 5.

Figure 5
figure 5

Finite element models used to compute the stress concentration at the bottom of a cone in a a square lattice and b a hexagonal lattice

Full size image

For the square lattice, uniform normal displacements were imposed on two lateral sides, while the normal displacement was blocked on the opposite side. For the hexagonal lattice, the normal displacements imposed on each of the six side surfaces, labeled A sto F, were such that:

$$ u_{i} \left( {x_{A} } \right) - u_{i} \left( {x_{B} } \right) = E_{ij} .(x_{j}^{A} { - }x_{j}^{B} ) $$
(1a)
$$ u_{i} \left( {x_{C} } \right) - u_{i} \left( {x_{D} } \right) = E_{ij} .(x_{j}^{C} { - }x_{j}^{D} ) $$
(1b)
$$ u_{i} \left( {x_{E} } \right) - u_{i} \left( {x_{F} } \right) = E_{ij} .(x_{j}^{E} { - }x_{j}^{F} ) $$
(1c)

where E denotes the strain tensor corresponding to equibiaxial stretching:

$$ E = \left( {\begin{array}{*{20}c} {\varepsilon_{11} } & 0 & 0 \\ 0 & {\varepsilon_{11} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right) $$
(2)

In this part of the study, elastic anisotropy was neglected.

Figure 6a shows the profile of the first principal stress along the two red lines superimposed in Fig. 5a. The two peaks correspond to the foot of the cone. The stress concentration factor is computed as the ratio between the peak stress and the stress away from this concentration area. Similar profiles were obtained along the lines joining opposite faces for the hexagonal lattice. Figure 6b shows the stress concentration factor versus p/w, for both lattice types. The smaller p/w (or the smaller the gap between neighboring cones, p-w), the higher the stress concentration factor. Besides, the stress concentration at the bottom of the cones is more severe in square than in hexagonal lattice. The presence of a coating does not reduce the stress concentration.

Figure 6 
figure 6

a Profile of the first principal stress along the two red lines superimposed in Fig. 5a and b stress concentration factor versus p/w for both lattice types

Full size image

According to these simulations, a surface patterning-induced reduction of the resistance of the wafers in biaxial bending can be expected, especially for dense, square lattices. The fracture tests described below tend to support this prediction.

Experimental study

Nano-compression tests

Nano-compression tests were run using a circular, flat-ended diamond tool with a diameter of 10.6 μm mounted on a Hysitron Ti950 nanoindentor equipped with a 12-mN load sensor. Load or displacement control was used, following a trapezoidal waveform: loading within 5 s, 5 s dwell time at peak load or displacement, and unloading within 5 s. The data acquisition time-step was 0.5 ms. After the tests, observations of the indented cones were made using a FEI XL40 FEG-SEM. Denoting by S the end surface of the diamond tool, the approximate number of cones that it touches depends on the type and period, p, of the cone lattice:

$$ N = \frac{S}{{p^{2} }}\;{\text{for a square lattice}} $$
(3a)
$$ N = \frac{2S}{{\sqrt 3 p^{2} }}\;{\text{for a hexagonal lattice}} $$
(3b)

This equations show that for a given lattice period, p, an hexagonal lattice is more robust than a square lattice, because the compressive load transmitted by a tool or any projectile is shared between more numerous cones that are thus individually less severely loaded.

Series of nanocompression tests with different peak loads were run on each sample. Those run with a small peak load did leave any visible trace under the SEM, making it impossible to find the imprint, check the number of cones effectively contacted by the tool, and thus to compute the load per contacted cone and the corresponding stress at the top. Since the aim of these tests was to document the geometrical stability of the compressed cones, as well as their damage mechanisms, in relation with the compressive load and stress on each one, only the tests that induced visible damage are reported in the paper.

In those cases, the count of damaged cones on SEM images after the compression tests confirmed these estimates within one to two, in each case. This small variation was expected, since the exact positioning of the tool in relation to the lattice cannot be controlled, due to the low resolution of the optical images provided by the nanoindentor. Each test was thus repeated at least twice, with a minimum distance of 30 μm between the indents.

When a truncated cone is submitted to a compression load F at its summit, the compressive stress at a distance z from its base is:

$$ \sigma \left( z \right) = \frac{F}{S\left( z \right)} = \frac{F}{{\left. {\pi R^{2} (z} \right)}} $$
(4)

Since the radius of the cross section at altitude z is:

$$ \left. {R\left( z \right) = \frac{w}{2}(1 - \frac{z}{h}} \right) $$
(5)

The compressive stress is:

$$ \sigma \left( z \right) = \frac{4F}{{\pi w^{2} \left( {1 - \frac{z}{h}} \right)^{2} }} $$
(6)

In particular, at the top of the truncated cone:

$$ \sigma \left( {h_{trunc} } \right) = \frac{4F}{{\pi w^{2} \left( {1 - \frac{{h_{trunc} }}{h}} \right)^{2} }} $$
(7)

In some of the tested specimens, however, the shape of the nanostructures deviated from that of a truncated cone so that Eq. (7) could not be used. When a kind of « platform» at the summit was observed (as illustrated below), the load per cone was divided by the surface of this platform, measured on a top view in the SEM, and averaged over a few cones.

Two (001) 1-mm-thick Ge wafers structured according to a square lattice of 5 μm high cones, a cone aspect ratio h/w ≈ 3, and a truncation ratio htrunc/h around 0.91 were submitted to load–controlled nanocompression tests, up to 6500 μN. The former was uncoated, the latter had a 100-nm-thick amorphous alumina coating deposited by ALD (Fig. 7, on which no scale is provided for confidentiality reasons). For this lattice geometry, the load applied by the tool is distributed over N = 34 ± 2 cones so that the peak load on each cone is approximately 191 μN.

Figure 7
figure 7

Surface-patterned (001) Ge wafers submitted to nanocompression tests. a No coating, b 100-nm-thick amorphous alumina. No scale is provided for confidentiality reasons

Full size image

Figure 8a shows two load–displacement curves measured in the same conditions on the uncoated specimen. Even though duplicate tests lead to slightly different curves, in both cases, no significant instability was observed until at least 1000 nm displacement, which is nearly 20% of the 5 μm cones height. Then, sudden displacement jumps associated with slight temporary load drops, initially less than 100 nm, but finally reaching 1000–1500 nm were observed. In both cases, during the 5 s dwell period at peak load, a progressive increase in displacement by 67–95 nm was observed (Fig. 8b). The displacement rate decreased progressively. To rule out the possibility of an instrumental artifact, similar compression tests were run on a smooth quartz sample, using the same diamond tool and same loading rate. Within 20 s dwell period at an even higher peak load (10 000 μN), the increase in displacement was less than 3 nm. It seems thus that the much larger increase in compressive strain during the shorter dwell period on Ge cones is not an artifact.

Figure 8
figure 8

Nanocompression duplicate tests on bare Ge cones a load–displacement curves and b displacement–time curves during the 5 s dwell period at peak load

Full size image

Figure 9 (on which no scale is provided for confidentiality reasons) shows SEM images of compressed cones (top view in Fig. 9a, 15° tilt in Fig. 9b). The top view of intact cones outside of the contact area reveals the presence of a pre-existing « platform» at their summit, whose average surface is estimated as 416*416 nm [2]. Dividing the 191 μN peak load per cone by this surface, a peak compressive stress at the top of 1105 MPa is estimated. Most of the cones that were touched by the tool are broken along one or several plane(s) inclined relative to the compression axis. An accurate measurement of their inclination angle was, however, not possible. Broken pieces, up to 1500–2000 nm long can be observed. This length is of the same order of magnitude as the final large displacement jumps on the load–displacement curves, which seem thus related to fracture.

Figure 9 
figure 9

SEM observations of compressed bare Ge nanocones. a Top view, b with 15° tilt. No scale is provided for confidentiality reasons

Full size image

Figure 10a compares the load–displacement curves of bare and alumina-coated Ge. The stiffness of the latter is much higher, there are no displacement jumps, nor any increase in displacement during the dwell period at peak load, and the residual depression is less than 100 nm. Figure 10b (on which no scale is provided for confidentiality reasons) shows SEM images of coated cones compressed under 6500 μN. Since in those samples, the average surface of the top « platform» was 622*622 nm [2], these loads correspond to a stress at the top of the alumina coatings of 494 MPa, less than half the stress at the top of bare Ge cones for the same applied load. Very little damage is observed, which is consistent with the absence of significant instabilities on the load–displacement curves.

Figure 10
figure 10

Nanocompression tests on alumina-coated Ge cones a comparison of load–displacement curves with those of bare Ge cones and b SEM observations after compression. No scale is provided for confidentiality reasons

Full size image

A square lattice of 8 μm-high, Si « cones», with a period ≈ 2.4 μm was submitted to displacement or load-controlled nano-compression tests. As it can be seen in Fig. 11a (on which no scale is provided for confidentiality reasons), the initial shape of the structures is more pyramidal than conical (so that the finite element estimate of the buckling load is not relevant in that case), with a « platform» at the top, whose average surface is approximately 253*253 nm2. For this lattice, the load on the diamond tool is shared by 15 ± 2 cones. Figure 11b shows load–displacement curves for displacement-controlled tests until 75, 105 and 120 nm. Multiple pop-in or pop-out and elbows can be observed, upon loading or unloading in spite of very small loads. SEM observations did not reveal any damage in that case.

Figure 11 
figure 11

Compression tests on bare Si cones. a Initial aspect of the cones, b displacement-controlled tests, c load-controlled tests and d SEM observations after compression at 2000 μN. No scale is provided for confidentiality reasons

Full size image

Figure 11c shows load–displacement curves for load-controlled tests until 2000 μN, which corresponds approximately to 2080 MPa at the top of each cone. A large displacement jump is observed around 1000 μN (1040 MPa). Surprisingly, the SEM observations reveal very little damage as well. Within the 5 s dwell time at peak load, the continuous increase in the displacement was at most 6 nm, much less than in Ge, in spite of a twice higher stress at the top of the cones.

Two (001) Si wafers structured according to an hexagonal lattice of 3.5 μm high cones, with a period p ≈ 1 µm, and a cone aspect ratio h/w ≈ 3.25 were submitted to load-controlled nanocompression tests, up to 2000 μN. The former (see Fig. 12, on which no scale is provided for confidentiality reasons) was uncoated, and the latter had an 80-nm-thick polycrystalline diamond coating deposited by MPECVD, using a Seki AX6500 diamond growth reactor, as described in [11]. For such polycrystalline diamond films, the elastic modulus was shown to increase from approximately 500–1200 GPa, as the grain size rises from 80 to 900 nm [20]. The grain size is not known precisely here, but smaller than 80 nm so that the Young’s modulus of the coating was probably around 500 GPa. For this lattice geometry, the load applied by the tool was distributed over N = 83 ± 2 cones so that the peak load on each cone was approximately 24 μN.

Figure 12 
figure 12

Surface-patterned (001) Si wafers submitted to nanocompression tests. a–b Uncoated, c–d with an 80-nm-thick diamond coating. No scale is provided for confidentiality reasons

Full size image

Figure 13a compares the load–displacement curves of bare and coated cones. While the former exhibit repeated displacement jumps, associated with transient load drops, starting well below the expected elastic buckling load (1300 μN), and 1200–1500 nm residual displacement after unloading, the diamond-coated cones show only one or two displacement jumps, and less than 250 nm residual displacement. However, when the peak load is increased to 12,000 μN, repeated displacement jumps also appear in the latter (Fig. 13b). After compression at 2000 μN, many bare Si cones are broken, and some of the debris seems permanently bent or curved. After compression at 12,000 μN, many diamond-coated Si cone are broken as well. No sign of decohesion of the coating is visible.

Figure 13 
figure 13

Compression tests on bare or diamond-coated Si cones. a Compared load–displacement curves until 2000 μN, b load–displacement curves of diamond-coated cones until 12,000 mN, c SEM observations of bare Si cones after compression at 2000 μN and d SEM observations of diamond-coated Si cones after compression at 12,000 μN. No scale is provided for confidentiality reasons

Full size image

Biaxial bending tests

One-mm-thick (001) Si wafers with a diameter of 50.8 mm were submitted to biaxial bending at a displacement rate of 3 μm. s−1, using a ball-on-ring device (Fig. 14a). The supporting ring was made of porous ceramic and its diameter was 30 mm. A bearing steel ball of 7 mm in diameter was used to bend the wafer. Ten wafers had a polishing of optical quality on both faces (Ra < 0.2 nm). For two samples, the bottom surface was patterned, according to a square lattice of 4 μm high cones, with a period p = 1.6 μm. The load–displacement curves of the smooth wafers, shown in Fig. 14b, are highly nonlinear, which is due to the large deflection of the wafers.

Figure 14
figure 14

Biaxial bending tests on smooth Si wafer. a ball-on-ring testing device and b load–displacement curves

Full size image

Figure 15 shows a non-patterned broken wafer. Radial cracks developed in two orthogonal directions, corresponding to the trace of {111} cleavage planes.

Figure 15 
figure 15

Broken (001) Si wafer

Full size image

Axisymmetric elastic finite element simulations taking these large displacements into account were run to deduce the fracture stress (σrr = σtt at the center of the bottom face) from the measured fracture load. The model (illustrated in Fig. 16) takes into account a frictionless contact with the support ring and the steel ball, as well as the elastic properties of corresponding materials. The simulated load–displacement curve superimposed in Fig. 11b reproduces well the nonlinearity of the experimental curves. Table 1 gathers the fracture loads and stresses of the ten smooth Si wafers (the number of data points is not sufficient for a Weibull plot). The fracture load ranges from 715 to 2297 N, and the fracture stress ranges from 2070 to 5856 MPa, with a mean value of 4122 MPa. These values are consistent with those obtained by Barnat et al. [15] with a ball on ring device for Si wafers with a comparable surface condition.

Figure 16 
figure 16

Finite element simulation of biaxial bending tests. a Deformed mesh, b radial stress contour and c radial profiles of the radial and hoop stress on the bottom side

Full size image
Table 1 Fracture load and fracture stress of smooth Si wafers in biaxial bending
Full size table

As expected, the load–displacement curves of the two surface-patterned Si wafers did not deviate from those of the smooth wafers (Fig. 17a), since the structured layer has a negligible thickness compared to that of the wafer, but failure occurred much earlier, at 296 and 418 N respectively, that is, 850 and 1222 MPa. These values are compatible with the stress concentration factor of 3.3 computed for this geometry. Unfortunately, the limited availability of surface-patterned wafers did not allow to repeat such tests. However, these results and SEM observations (Fig. 17b) of cracks passing right at the foot of the cones, where stress peaks were predicted by the simulations, suggest that the stress concentration induced by surface-patterning reduces the fracture resistance of the substrate. Increasing the thickness of the substrate to reduce the bending stresses might partly compensate this detrimental effect.

Figure 17 
figure 17

Biaxial bending tests on surface-structured Si wafers. a Comparison of load–displacement curves with those of smooth wafers, b SEM observation of the crack path. No

Full size image

Discussion

During the nanocompression tests run on bare surface-patterned Ge (Fig. 8a), no significant instability was observed until at least 1000 nm displacement, that is, 20% of the 5 μm cones height. Such a huge stable compressive strain can in no case be fully elastic. Starting from Eq. (6), the elastic strain at height z along a truncated cone on a (001) wafer can be deduced as:

$$ \varepsilon \left( z \right) = \frac{\sigma \left( z \right)}{{C_{11} }} = \frac{4F}{{\pi C_{11} w^{2} \left( {1 - \frac{z}{h}} \right)^{2} }} $$
(8)

The total elastic displacement at the top of the cone is thus:

$$ \Delta h_{elas} = \mathop \smallint \limits_{0}^{{h_{trunc} }} \varepsilon \left( z \right).dz $$
(9)

Combining Eqs. 8 and 9, it comes:

$$ \Delta h_{elas} = \frac{{4Fh_{trunc} }}{{\pi C_{11} w^{2} }}\left[ {1 + \frac{1}{3}\left( \frac{htrunc}{h} \right)^{2} - \frac{htrunc}{h}} \right] $$
(10)

For the tests shown in Fig. 8, Eq. (10) yields Δhelas ≈ 2.7 nm, far below the 1000 nm displacement observed before the large instabilities associated with fracture. These Ge cones thus had a fairly ductile behavior. Furthermore, the substantial, progressive, and decelerating rise in displacement during the dwell period at peak load (Fig. 8b) suggests room-temperature creep, which, to the best of our knowledge, had not yet been reported for germanium.

The odd shape of the load–displacement curves of Si nanocones shown in Fig. 11b, with several elbows, pop-in and pop-out upon loading and unloading is evocative of contact-induced phase changes (from Si-I to SI-II, Si-III…. Si-XII, or amorphous Si) well documented in classical nanoindentation, based on micro-Raman spectroscopy and TEM observations below the indents [21, 22]. Nanoindentation-induced phase changes (from Ge-I to Ge-II, Ge-III or Ge-IV) have also been reported for germanium [23]. They noticed that these phase transformations are loading/unloading rate sensitive. In the present study with a fixed loading/unloading time but various peak loads or displacements, this parameter changed substantially from one series of test to the other, making comparisons difficult.

In terms of stress state, the present uniaxial compression tests are, however, closer to the compression tests run by Östlund et al. [24] on single, FIB-machined (001) Si nanopillars, 250–930 nm in diameter. Above a diameter of 300–400 nm, a brittle behavior with discontinuities on the load–displacement curves and formation of a nearly vertical crack were observed, while pillars with a smaller diameter behaved in a ductile way, with smooth curves up to 22% engineering strain, no cracking, but formation of slip bands along {111} planes. The average yield stress of ductile pillars was 5.3 GPa.

The elastic–plastic behavior of 20–65-nm-wide Si nanocubes under uniaxial compression along (001) was investigated by Wagner et al. [25]. They reported a linear elastic behavior until 7 ± 1% true strain, corresponding to a true stress of 7.7 ± 1.1 GPa. Then a progressive deviation from linearity was observed, until an upper yield point at 21 ± 3% true strain, corresponding to a true stress of 11.6 ± 2 GPa. After the yield point, a plateau was observed on the stress–strain curve before strain hardening resumed, and a true strain of 60% was reached before unloading, without any damage. From TEM observations, they concluded that plastic flow at this scale was mediated by partial dislocations gliding on {111} planes.

Equation (6) shows that a stress level of 5–8 GPa is very easily reached at the top of a truncated cone, provided htrunc/h is not too low. Figure 18 shows the compressive stress profile for a 2 μm high, 0.6 μm wide Si cone under a 36 μN compressive load. The stress is higher than 5 GPa for z > 0.8 h and largely sufficient to trigger plastic flow. When a 100-nm-thick coating is present, the compressive stress at the top of the cone is substantially reduced. Simulations performed with various Young’s moduli for the coating show that this reduction is mostly due to the increase in cross section and that the stiffness of the coating has a secondary influence. Alumina or diamond coatings, expected to protect the cones from elastic buckling actually, mostly protect it from plastic yielding.

Figure 18 
figure 18

Compressive stress profile along the axis of an uncoated 3-μm-high, 1.2-μm-wide (001) Si cone truncated at 0.95 h, under a 61 μN load scale is provided for confidentiality reasons

Full size image

The numerical analysis of nanocones buckling assuming an elastic behavior presented in part II.1 thus provides useful guidelines for the design of the cones (influence of their nominal aspect ratio, and degree of truncation), the coating (influence of its thickness and elastic behavior) and the cone lattice geometry (square or hexagonal and filling ratio), but cannot capture the plastic flow and underlying mechanisms (dislocation glide, phase transformations…) that often occur below the expected elastic buckling load. Unfortunately, even though some papers in the literature report compressive stress–strain curves in the plastic regime on silicon or germanium nanopillars or nanoparticles [24, 25], there is yet no sufficient consensus on their yield stress and strain hardening behavior (probably size and stress-state-dependent) to attempt elastic–plastic finite element simulations of nanocones compression and buckling, using either phenomenological constitutive equations, or crystal plasticity (even more demanding in terms of data). As an alternative, molecular dynamics might be envisaged, as in [26, 27], but the number of atoms in a nanocone is so high that computational costs would be prohibitive.

By contrast, the numerical analysis of the stress concentration at the bottom of the cones presented in part II.2 is quite consistent with the experimental results obtained on the fracture of surface patterned wafers in biaxial bending, since the reduction in the fracture resistance was in accordance with its computed value. However, the number of such tests was limited by the availability of such specimens, and it would be useful to run more to allow a statistical comparison between the fracture stress of smooth and patterned wafers.

Conclusions

The slender nanocones formed by lithography and etching steps at the surface of silicon or germanium wafers to produce antireflective superhydrophobic windows are more vulnerable to compression-induced plastic deformation than to elastic buckling. Thin alumina or diamond coatings can, however, provide an effective protection against both phenomena.

A compressive stress of 1.1 GPa induced significant creep in Germanium nanocones at room-temperature, while creep remained negligible in Si nanocones under 2 GPa.

Surface patterning induces stress concentrations at the foot of the cones which are responsible for a reduction of the fracture resistance of the substrate in biaxial bending. Increasing the thickness of the substrate to reduce the bending stresses might partly compensate this detrimental effect, as long as it remains compatible with the desired optical performances.

From a mechanical point of view, for a given nanocone geometry and lattice period, surface patterning according to an hexagonal lattice is better than according to a square lattice, because (1) it reduces the stress concentration at the foot of the cones so that the reduction of the fracture resistance of the substrate in biaxial bending is less important and (2) compressive loads are shared between more numerous cones, each being less severely loaded.