1 Introduction

Gas-microphone photoacoustics is the first and the most widely used of photothermal (PT) methods for the characterization of optical, thermal, electronic and other related properties [1–3]. Shortly after the clarification and the development of the PA response model [1], a transmission variant of this particular method was developed, in which the so-called minimum volume cell is applied, with the microphone cavity itself acting as the PA cell chamber [4, 5]. For this configuration, the classic theory predicts monotonic amplitude and phase-frequency characteristics and a greater impact of the thermoelastic (TE) component at high frequencies (for the majority of materials these frequencies are around 1 kHz, while for the samples of thickness of around and under 80 \(\upmu \)m, the theory predicts the TE component dominance even at lower modulation frequencies) [5]. In a number of papers, high-frequency-range measurements, 3 kHz to 5 kHz, and even above 10 kHz, are presented [6–9]. Resonant peaks, which appear in this frequency range, are not much discussed in the literature—they are attributed to the influence of the measuring system; however, these resonant peaks occur at frequencies lower than those expected due to the influence of the instrumental response. On the other hand, generalized theory of PA response predicts resonances caused by finite heat propagation speed in approximately the same frequency range for low-order materials [10], which is the reason why we think high-frequency resonances should be explored in more detail.

It was observed that a microphone exhibits the behavior of the acoustic filter (Helmholtz resonator), since it has a form of an acoustical chamber, open on one end. The transfer function of the cell regarded as an acoustic filter is derived with the use of electro-acoustic analogy. However, the chamber wall opposing the aperture is the diaphragm that vibrates in a nonlinear manner. This nonlinearity, in the first approximation, is linearized in such a way that the vibrations are regarded as the convolution of the two limiting cases: first—the maximum displacement of the diaphragm, increasing the resonant cavity volume, and second—the minimum diaphragm displacement, with negligible influence on the resonant cavity volume. This way, the transfer function of the cell, in the frequency domain, can be regarded as a product of these two cases. A generalized model of photoacoustic response is derived in a way that the previous theoretical model is multiplied by the transfer characteristics of the photoacoustic cell.

Our measurements, performed on a number of samples (Al plate [9], polymer thin films [11], and laser-sintered polyamide PA12) predict the appearance of the resonances in the frequency range above 10 kHz. They are explained in this paper using the generalized model which includes the impact of the cell as an acoustic filter.

2 Theory

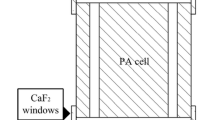
In this paper, a transmission PA configuration, schematically presented in Fig. 1, is considered. An optically opaque solid sample, of thickness \(l_{s}\), surrounded by air, which is considered a thermal insulator, is exposed to the radiation of an optical beam passing through a layer air of the length \(l_{a}\). Since the heating of the sample surface is considered uniform over the entire heated area, the temperature can be assumed uniform over the all cross sections of the sample, and its variation is evaluated along the direction of the incident light beam only (x-axis in Fig. 1). Hence, the heat transfer may be considered one-dimensional [12].

Fig. 1
figure 1

Geometry of the problem

Full size image

Based upon previous works related to the generalized PA response (thermal and mechanical piston-like), which include the thermal memory of the sample [13, 14], the expression for the total pressure of the PA response (the sum of the thermoconducting, \(\tilde{p}_{th} \) and thermoelastic, \(\tilde{p}_{ac} \) components [5]) is given as:

$$\begin{aligned} \tilde{p}= & {} \tilde{p}_{th} +\tilde{p}_{ac} \end{aligned}$$
(1)
$$\begin{aligned} \tilde{p}_{th}= & {} \frac{\gamma P_0 S_0 }{l_g T_0 }\frac{\tilde{z}_{cs} }{\tilde{\sigma }_g }\frac{1}{sh(\tilde{\sigma }_s l_s )} \end{aligned}$$
(2)
$$\begin{aligned} \tilde{p}_{ac}= & {} \frac{3\gamma P_0 }{V_0 }\pi a_T \frac{R^{4}}{l_s^3 }\;\frac{I_0 \tilde{z}_{cs} }{\tilde{\sigma }_s^2 sh (\tilde{\sigma }_s l_s )}\left[ {ch(\tilde{\sigma }_s l_s )-\frac{\tilde{\sigma }_s l_s }{2}sh(\tilde{\sigma }_s l_s )-1} \right] \nonumber \\= & {} \frac{3\gamma P_0 a_T R^{4}I_0 }{R_c^2 l_g k_s } \frac{1+j\omega \tau _s }{(\tilde{\sigma }_s l_s )^{3}} \;\frac{ch{(\tilde{\sigma }_s l_s )-1-\frac{\tilde{\sigma }_s l_s }{2}sh(\tilde{\sigma }_s l_s )}}{sh (\tilde{\sigma }_s l_s )}\nonumber \\= & {} \frac{3\gamma P_0 a_T R^{4}I_0 }{R_c^2 l_g k_s } \frac{1+j\omega \tau _s }{(\tilde{\sigma }_s l_s )^{3}}\left[ {th\left( {\frac{\tilde{\sigma }_s l_s }{2}} \right) -\frac{\tilde{\sigma }_s l_s }{2}} \right] \end{aligned}$$
(3)

where \(\gamma \) represents the ratio of the specific heats, \(P_{0}\) [Pa] is the ambient pressure, \(T_{0}\) [K] is the ambient temperature, \(S_{0} [\hbox {W}\,\hbox {m}^{-3}]\) represents volumetric heat generation rate which equals to half the intensity of the incident light beam \(I_{0} [\hbox {W}\,\hbox {m}^{-2}]\), \(a_{T}\) is the linear thermal expansion coefficient of the sample, lg [m] is the distance from the source to the sample, R [m] represents the radius of the sample, \( R_{c}\) [m] is the radius of the cell, \(k_{s}\, [\hbox {W}\,\hbox {m}^{-1} \hbox {K}^{-1} ]\) represents the heat conductivity of the sample, \(D_{Ti} \, [\hbox {m}^{2}\,\mathrm{s}^{-1}]\) represents the thermal diffusivity, and \(\tau _{i}\) represents the thermal relaxation time of the medium i (a—air layer, s—the sample), \(\omega \,[\hbox {s}^{-1}]\) represents the angular frequency (\(\omega =2 \pi \hbox {f}\)), \(l_{s}\) is the sample thickness, and \(\tilde{\sigma }_s \ [\hbox {m}^{-1}]\) and \(\tilde{z}_{cs} \) represent the complex coefficient of thermal wave propagation and thermal impedance, respectively, defined by the following expressions [10]:

$$\begin{aligned} \tilde{\sigma }_i= & {} \sqrt{\frac{j\omega (1+j\omega \tau _i )}{D_{Ti} }}\nonumber \\ \tilde{z}_{ci}= & {} \frac{\sqrt{D_{Ti} }}{k_i }\cdot \sqrt{\frac{1+j\omega \tau _i }{j\omega }}=\frac{1+j\omega \tau _i }{k_i \tilde{\sigma }_i } \end{aligned}$$
(4)

Putting \(\tau _{s}=0\) (in that case a generalized theory of heat conduction becomes equal to the classical one), these expressions from Eq. 3 become equal to expression reported by Perondi and Miranda Eq. 8 in paper [4].

Fig. 2
figure 2

Experimental setup

Full size image

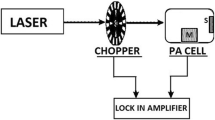
In the experimental setup [15], shown in Fig. 2, the minimum volume PA cell was used, meaning that the sample is placed on the top of detection system itself like as in paper [4]. In this case the detector is an electret microphone, consisting of a chamber, an electrets diaphragm and a metal backplate separated from the diaphragm by an air gap. Sound enters through the round hole on the front side of the microphone into the air chamber closed by the diaphragm, which actually plays the role of the PA chamber.

Fig. 3
figure 3

Electric model of microphone as PA Helmholtz resonator

Full size image
Fig. 4
figure 4

Microphone chamber as the Helmholtz resonator of minimal and maximal volume

Full size image
Fig. 5
figure 5

Model capacitor scheme

Full size image

Microphone chamber (i.e., the PA cell) is regarded as a Helmholtz resonator. Based on papers [16–22] and Molton lectures [23], an electro-acoustic analogy of the PA response is made (Fig. 3), where the resistor and the inductor simulate acoustic properties of the duct on the front side of the microphone and the capacitor simulates the microphone cavity. There are at least six models describing electrical components of circuits analogous to the acoustic system [16, 18]. One model suggests the description of electrical components like as in Eqs. 5–8. The wall of the cavity is not considered to be solid, but rather a diaphragm which exhibits nonlinear properties. The nonlinear behavior of the diaphragm is linearized in a way that the microphone is modeled through its two extreme cases: when its chamber has minimum and maximum volumes (Fig. 4). The capacitor model of such a cavity can be obtained as the circuit consisting of two capacitors in parallel (Fig. 5) with the capacitances:

$$\begin{aligned} C_i= & {} \frac{V_i }{\rho v^{2}} i=V,\varepsilon \end{aligned}$$
(5)
$$\begin{aligned} V_V= & {} r_1^2 \pi l_1 \end{aligned}$$
(6)
$$\begin{aligned} V_\varepsilon= & {} r_1^2 \pi ( l_1 +\Delta \varepsilon ) \end{aligned}$$
(7)

and the duct inductance is given by the expression:

$$\begin{aligned} L=\frac{\rho l}{S} S=r^{2}\pi \end{aligned}$$
(8)

where v is the speed of sound in air, \(\rho \) represents the mass density of the air, l is the length of the microphone orifice, S is the cross-sectional area, r is the radius of the duct, \(r_{1 }\) and \(l_{1}\) are radius and length of the microphone chamber, \(\Delta \varepsilon \) is the maximum displacement of the diaphragm, and \(V_{i }\) is the minimum (\(i=V\)) and the maximum (\(i= \varepsilon \)) volume of the microphone chamber. The signal obtained from the microphone is given by the expression:

$$\begin{aligned} \tilde{p}_{mic} (j\omega )={\frac{1}{s^{2} LC_{ekv} (\omega )+sRC_{ekv} (\omega )+1}}{\tilde{p}}_{in} , \end{aligned}$$
(9)

Based on the electrical analogies, two serial connected low-pass filters were obtained. The main cavity resonance parameters are the resonance frequency (\(f_{i})\) and the quality factor (\(Q_{i})\). The transfer characteristics are second-order functions and have the same appearance in both cases (expression 10), but the resonance frequencies of the systems are different.

$$\begin{aligned} \tilde{H}_i (j\omega )= & {} \frac{\omega _i^2 }{\omega _i^2 -\omega ^{2}+j\omega \frac{\omega _i }{Q_i }},\quad \left[ {\begin{array}{l} i=V,\varepsilon \\ \omega =2\pi f \\ \omega _i =2\pi f_i \\ \end{array}} \right] \end{aligned}$$
(10)
$$\begin{aligned} \omega _i= & {} v\sqrt{\frac{S}{lV_i }} \end{aligned}$$
(11)

Entering the above-described transfer characteristics (expression 10) into the previously derived theoretical model [expressions (1)–(3)], the final theoretical model is obtained:

$$\begin{aligned} \tilde{p}_u (j\omega )=\tilde{p}(j\omega )\cdot \tilde{H}_V (j\omega )\cdot \tilde{H}_\varepsilon (j\omega ) \end{aligned}$$
(12)

3 Results and Discussion

The amplitude A(f) and the phase F(f) of the experimentally obtained PA response of laser-sintered PA12 are presented in Fig. 4 as the function of the modulation frequency f, for two thickness values (640 \(\upmu \hbox {m}\) and 1030 \(\upmu \hbox {m}\)). Alongside, the theoretical model with as well as without the obtained acoustic resonators (Theory 1 and Theory 2, respectively) is shown. Table values of the PA12 thermal characteristics are given in Table 1 [24], while the suggested values of thermal relaxation times are \(\tau _g =2\cdot 10^{-10}s\) and \(\tau _s =10^{-4}s\) [10]. The microphone chamber dimensions are \(r=1\,\hbox {mm}, l=200\,\upmu \hbox {m}, r_{1}=5\,\hbox {mm}\) and \( l_{1}=3\,\hbox {mm}\), and the obtained values of the acoustic resonator parameters are shown in Table 2. The value of the resonance frequency \(f_{V}\) is calculated from the expression (11) and the values of the resonance frequency \(f_{\varepsilon }\) and quality factors \(Q_{V}\) and \(Q_{\varepsilon }\) are fitted from the experimental curves.

Table 1 Thermal properties for polyamide (PA12)
Full size table
Table 2 Properties of acoustic resonators
Full size table
Fig. 6
figure 6

Experimental and theoretical results for PA12: (a) amplitude spectrum for a sample of thickness \(640\,\upmu \hbox {m}\), (b) phase spectrum for a sample of thickness \(640\,\upmu \hbox {m}\), (c) amplitude spectrum for a sample of thickness \(1030\,\upmu \hbox {m}\), (d) phase spectrum for a sample of thickness \(1030\,\upmu \hbox {m}\)

Full size image

From Fig. 6 it can be seen that the obtained results at high frequencies do not coincide with the previously developed generalized theoretical model including thermal memory, neither in amplitude nor in phase characteristics. In the amplitude, resonance peaks occur, while in the phase, the decline is experimentally observed, which is not predicted by the theoretical model [13, 14]. On the other hand, the extended theoretical model shows significant agreement with the experimental data. The peaks’ position in acoustic resonances and their shape as well as height depend on the geometric characteristics of the cell (measuring microphone cavity, wall thickness, the cross-sectional area and the length of the microphone orifice, characteristic of microphone diaphragm). The analytical solution for the acoustic resistance is very complex, but its value is indirectly available from the experimental measurements as follows:

$$\begin{aligned} R=\frac{1}{Q}\sqrt{\frac{\rho ^{2}vl}{SV}} \end{aligned}$$
(13)

The displacement of the microphone diaphragm can also be obtained from the experimental data:

$$\begin{aligned} \Delta \varepsilon =\frac{v^{2}}{4\pi ^{2}lf_\varepsilon ^2 } \frac{r^{2}}{r_1^2 }-l_1 \end{aligned}$$
(14)

and for the used microphone \(\Delta \varepsilon =30\,\upmu \hbox {m}\) was calculated.

4 Conclusion

The considered resonances extend the application of photoacoustics in characterization of microphone properties and its acoustic resistance, which have not been experimentally evaluated until now by means of PA measurements. Besides, the software elimination of these resonances may expand a measurement range, contributing to a better material characterization in the high-frequency range on this way.

Finally, from the presented results and from the fact that observed resonant peaks occur in PA measurements of other materials it can be concluded that this model can be considered as a valuable explanation of the phenomenon, as well as the improvement of the interpretation of future PA results.