Improving the core resilience of real-world hypergraphs

Abstract

Interactions that involve a group of people or objects are omnipresent in practice. Some examples include the list of recipients of an email, the group of co-authors of a publication, and the users participating in online discussion threads. These interactions are modeled as hypergraphs in which each hyperedge is a set of nodes constituting an interaction. In a hypergraph, the k-core is the sub-hypergraph within which the degree of each node is at least k. Investigating the k-core structures is valuable in revealing some properties of the hypergraph, one of which is the network behavior when facing attacks. Networks in practice are often prone to attacks by which the attacker removes a portion of the nodes or hyperedges to weaken some properties of the networks. The resilience of the k-cores is an indicator of the robustness of the network against such attacks. In this work, we investigate the core resilience of real-world hypergraphs against deletion attacks. How robust are the core structures of real-world hypergraphs in these attack scenarios? Given the complexity of a real-world hypergraph, how should we supplement the hypergraph with augmented hyperedges to enhance its core resilience? In light of several empirical observations regarding core resilience, we present a two-step method that preserves and strengthens the core structures of the hypergraphs.

1 Introduction

Graphs are employed to represent social networks in which people and objects are connected. Such modeling allows for an investigation of social networks in a convenient manner. The progressive studies on the properties of graphs offer not only interesting insights into how social beings interact but also several practical applications, such as marketing influence maximization (Lei et al. 2015), fraud detection (Akoglu and Faloutsos 2013), and product recommendation (Huang et al. 2002).

Some of the most important properties of graphs revolve around the concept of k-core (Seidman 1983). The k-core of a graph is the maximal sub-graph in which the degree of each node is at least k. The core number of a node v is the maximum integer k such that v is in the k-core. The core number has demonstrated effectiveness in indicating the centrality of nodes in a network, especially in the problems of finding influential nodes (Kitsak et al. 2010; Shin et al. 2016) and graph clustering (Mei et al. 2021).

Real-world graphs often face attacks that remove or render several parts of the network impaired (Freitas et al. 2022), and a line of work has investigated the resilience of the core structure against such attacks (Linghu et al. 2020; Medya et al. 2020; Zhu et al. 2018). That is, in these works, resilience is characterized by the ability of the core structure of a graph to maintain one or several properties after a portion of the network has been removed. These works focus on how the size of the k-core decreases or how the ranking of core numbers is altered as the consequence of removing several nodes or edges from the network. One may devise strategies to delete some nodes or edges to minimize the k-core size (Medya et al. 2020; Zhu et al. 2018; Chen et al. 2021) or supplement the network with augmented edges to consolidate the core structure (Laishram et al. 2018; Zhou et al. 2019; Linghu et al. 2020).

Despite extensive studies on the properties and robustness of graphs, much is left undiscovered for hypergraphs. Hypergraphs, which are the extension of pair-wise graphs allowing multiple nodes to be in the same hyperedge rather than just two, naturally represent group interactions that are omnipresent in practice (Benson et al. 2018a; Yin et al. 2017; Do et al. 2020; Lee et al. 2021, 2020). For example, each hyperedge may represent a publication whose co-authors are nodes in the hypergraph, an email involving several email addresses as nodes, or a discussion thread consisting of several participants. Hypergraphs have been applied in the domain of image processing (Liu et al. 2011), social networks (Tan et al. 2014; Yang et al. 2019), contagion models (Iacopini et al. 2019; de Arruda et al. 2020), electronic commerce (Zhu et al. 2016), and circuit design (Ouyang et al. 2002).

Real-world hypergraphs may also face attacks that involve removing a portion of the network (Peng et al. 2022; Ma et al. 2018) for the same reasons as graphs. Hypergraphs are abstract structures representing several types of higher-order interactions and are stored in databases for mining purposes. For instance, coauthorship data are stored in academic databases (Sinha et al. 2015), emails are saved in storage systems (Klimt and Yang 2004), and discussion threads are stored in online forums.¹ Attackers may intrude on those systems to remove several nodes or hyperedges to weaken several properties of the networks, which corresponds to deletion attacks on hypergraphs.

The concept of k-core has been proven useful also in hypergraphs, and thus attackers may aim to impair the core structure in hypergraphs. Similarly to pair-wise graphs, the k-core of a hypergraph (Sun et al. 2020) is construed as the maximal sub-hypergraph within which the degree of each node is at least k. In hypergraphs, the concept of k-cores demonstrates applications in identifying dense regions (Gabert et al. 2021b) or monitoring epidemics (Gabert et al. 2021a), and as shown in Sect. 4, hypergraph cores are also useful in several other practical applications, such as identifying seed nodes for influence maximization or detecting abnormally dense sub-networks. Invaders, hoping to degrade the performances in those tasks, may be incentivized to attack the networks via the deletions of nodes or hyperedges, for the same motivations that attackers aim to impair the core structures in graphs (Linghu et al. 2020; Medya et al. 2020; Zhu et al. 2018).

In this work, we focus on the core resilience of real-world hypergraphs. Motivated by the applications of hypergraph k-cores and the possibilities of attacks on hypergraphs, we formulate CREAM (Core-conserving REsilience mAxiMization), the problem of improving the core resilience of the hypergraphs against deletion attacks through the means of augmenting hyperedges while conserving the original core structure. We first explore the relevant patterns of core resilience of real-world hypergraphs when a portion of the node set or the hyperedge set has been removed. Based on these, we consider supplementing each hypergraph with augmented hyperedges that strengthen the core resilience of the hypergraph while preserving all core numbers. Note that supplementing hyperedges to those hypergraphs constitutes adding “virtual” hyperedge records into the respective databases to strengthen those networks. These virtual hyperedges should be constructed carefully so that they preserve the network properties. Moreover, while remaining indistinguishable from real hypergraphs to attackers, these supplemented hyperedges can be removed by database administrators whenever necessary, thus staying harmless to the network’s applications.

However, there is a major challenge in augmenting hypergraphs through the addition of hyperedges, which is due to the complexity of hypergraphs. In hypergraphs, each hyperedge may contain an arbitrary number of nodes, and thus the number of all possible node combinations, which may form augmented hyperedges, is insurmountable. As a result, the cost of iterating through each possible combination of nodes and checking whether it is desirable to add the combination would be prohibitive.

To address the challenge, we introduce COREA, a fast, effective, and theoretically sound method that augments hyperedges to preserve the core structure and improve the core resilience of the hypergraphs. Inspired by several observations related to core resilience, COREA constructs a pool of candidate hyperedges, which are guaranteed to conserve all core numbers, and selects the best candidates to augment to the hypergraph. Our experiments show that COREA is up to $1.7\times$ more effective than several baseline approaches while providing a better time-performance trade-off.

In short, our contributions in this research are three-fold:

• Problem definition We propose and tackle CREAM (Core-conserving REsilience mAxiMization), the problem of core resilience improvement in real-world hypergraphs, for the first time, to the best of our knowledge.

• Key concepts and empirical observations We propose relevant concepts and present the key observations regarding the core resilience of real-world hypergraphs that motivate the design of our method.

• Method We propose COREA, a fast, effective, and theoretically sound method for enhancing the core resilience of hypergraphs. Our extensive experiments demonstrate the consistent superiority of COREA over several baseline approaches across ten real-world hypergraphs.

For reproducibility, the code and datasets are available at https://github.com/manhtuando97/CoReA.

The remaining sections of this paper are as follows: In section 2, we review some related work. We introduce some preliminaries and problem formulation in Sect. 3. We then present some applications of core numbers in hypergraphs in Sect. 4 to motivate our work. The key observations are summarized in Sect. 5. We propose our method in Sect. 6. We evaluate our method in Sect. 7, where we also investigate how our proposed method helps support the applications of hypergraph core numbers in the tasks outlined in Sect. 4 under various attack scenarios. Lastly, we conclude our work in Sect. 8.

2 Related work

Hypergraphs: Hypergraphs represent high-order interactions in various fields (Benson et al. 2018a; Yin et al. 2017; Do et al. 2020). There have been numerous studies on the structures and properties of real-world hypergraphs regarding transitivity (Kim et al. 2023), reciprocity (Kim et al. 2022), simplicial closures (Benson et al. 2018a), motifs (Lee et al. 2020), evolution patterns (Kook et al. 2020; Benson et al. 2018b), and realistic generative models (Do et al. 2020; Lee et al. 2021; Kim et al. 2023, 2022; Giroire et al. 2022; Benson et al. 2018b). Meanwhile, some others tackle several learning problems on hypergraphs, such as clustering (Rota Bulò and Pelillo 2013; Li and Milenkovic 2017; Amburg et al. 2020), link prediction (Kumar et al. 2020; Yadati et al. 2020; Hwang et al. 2022), and node classification (Feng et al. 2019; Yadati et al. 2019; Chien et al. 2022).

$\textit{k-Core in graphs and hypergraphs}:$ The concept of k-core plays an integral role in the graph mining domain. It is used to detect dense subgraphs and influential nodes in (Shin et al. 2016), whereas Giatsidis et al. (2011) employ this concept to evaluate the cooperation within a community in social networks. Some other problems on k-cores include scalable core decomposition (Li et al. 2013; Aridhi et al. 2016), its maintenance on dynamic graphs (Lin et al. 2021), and core decomposition on uncertain graphs (Peng et al. 2018). On the other hand, little attention has been paid to the k-cores of hypergraphs. Some preliminary work focus on scalable maintenance of k-cores in dynamic hypergraphs (Gabert et al. 2021a; Sun et al. 2020) or how the concept of k-core in hypergraphs is applied in discovering dense components in social networks (Gabert et al. 2021b).

Core resilience: Medya et al. (2020) define the resilience of a k-core as its ability to maintain its nodes. After many edges are deleted, several nodes can lose their core numbers, and the size of the k-core can be reduced. Several studies attempt to minimize the number of remaining nodes in the k-core by deleting edges (Medya et al. 2020; Zhu et al. 2018) or removing nodes (Zhang et al. 2017). In contrast, some others enhance the resilience of the k-core against such attacks by anchoring nodes, i.e considering some nodes as having an infinite degree (Bhawalkar et al. 2015; Laishram et al. 2020; Linghu et al. 2020). Following a different approach, Laishram et al. (2018) define core resilience as the rank correlation of nodes in core numbers after several nodes or edges have been deleted. The authors correlate this statistic with several node-level measurements and design an algorithm to enhance the core resilience via adding edges.

In this work, we tackle the problem of improving the core resilience in hypergraphs. We adopt the same notion of hypergraph k-cores in (Leng et al. 2013) and core resilience in (Laishram et al. 2018. To this end, we extend the existing concepts of core strength and core influence in this work from graphs to hypergraphs, introduce new relevant concepts, and design an algorithm for the core resilience improvement problem. In this problem, we face new challenges unique to the complexity of hypergraphs, outlined in Sect. 3.2, and propose our method to address these challenges. The details for our technical contributions are presented in Sects. 5 and 6.

3 Preliminaries and problem definition

3.1 Basic concepts

We introduce some basic concepts. The key notations are in Table. 1.

Hypergraphs: A hypergraph is defined as $\textbf{G}=(\textbf{V},\textbf{E})$, where $\textbf{V}$ is the set of nodes, and $\textbf{E}\subseteq 2^{\textbf{V}}$ is the set of hyperedges. Each hyperedge $e \subseteq V$ is a set of $|e |$ ($\ge 2$) nodes.² For each node v, we define the set $\textbf{E}_{\textbf{G}}(v)$ of hyperedges incident to v as $\textbf{E}_{\textbf{G}}(v)=\{e \in \textbf{E}\mid v \in e \}$. The degree $d_{\textbf{G}}(v)$ of v is defined as the number of hyperedges incident to v, i.e., $d_{\textbf{G}}(v) = |\textbf{E}_{\textbf{G}}(v) |$. A node having degree 0 is an isolated node. A sub-hypergraph $\tilde{\textbf{G}}=(\tilde{\textbf{V}}, \tilde{\textbf{E}})$ of $\textbf{G}$ is a hypergraph (i.e., $\tilde{\textbf{E}} \subseteq 2^{\tilde{\textbf{V}}}$) where $\tilde{\textbf{V}} \subseteq \textbf{V}$, and $\tilde{\textbf{E}} \subseteq \textbf{E}$.

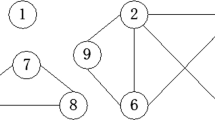
Clique expansion: The clique expansion of hypergraph $\textbf{G}=(\textbf{V}, \textbf{E})$ is a graph $\textbf{G}_{(1)}=(\textbf{V}, \textbf{E}_{(1)})$ where $\textbf{E}_{(1)} = \{\{u,v\} \mid u, v \in \textbf{V}, \exists e \in \textbf{E}, \{u,v\} \subseteq e \}$. That is, $\textbf{G}_{(1)}$ is a graph in which two nodes $u,v \in \textbf{V}$ are adjacent if and only if there exists a hyperedge e in $\textbf{E}$ containing both u and v. A hyperedge $e \in \textbf{E}$ results in a clique of $|e|$ nodes in $\textbf{G}_{(1)}$. The clique expansion is a representation of the hypergraph in the form of a pair-wise graph. However, this representation incurs information loss as the original hypergraph $\textbf{G}$ cannot be reconstructed from $\textbf{G}_{(1)}$ and two different hypergraphs may result in the same clique expansion, as depicted in Fig. 1.

Fig. 1

The clique expansion of a hypergraph is a pair-wise graph in which two nodes are adjacent if and only if there exists at least one hyperedge of the original hypergraph containing them. This representation is lossy, as the original hypergraphs cannot be reconstructed from the clique expansion and different hypergraphs may have the same clique expansion

Table 1 Frequently used symbols

k-Core and core numbers: The k-core of $\textbf{G}$, denoted by $\textbf{C}(k,\textbf{G})$, is the sub-hypergraph of $\textbf{G}$ within which the degree of every node is at least k (Leng et al. 2013). The core number $N_{\textbf{G}}(v)$ of node v in hypergraph $\textbf{G}$ is the maximum integer k such that v is in $\textbf{C}(k,\textbf{G})$. The degeneracy $N_{\textbf{G}}^{*}$ of hypergraph $\textbf{G}$ is the highest core number of a node $v \in \textbf{V}$. The degeneracy core of $\textbf{G}$ is the $N_{\textbf{G}}^{*}$-core of $\textbf{G}$, denoted by $\textbf{C}(N_{\textbf{G}}^{*}, \textbf{G})$.

Core decomposition: Core decomposition is the process of obtaining the k-cores and core numbers of nodes in a hypergraph $\textbf{G}$ (Algorithm 3 in Appendix 1). After removing all isolated nodes, the remaining hypergraph is the 1-core. For each $k \ge 1$, to obtain the $(k+1)$-core, a pruning process starts from the k-core and repeatedly removes the nodes of degrees lower than $(k+1)$ until no such removal is possible. The nodes removed in this pruning process are assigned core number k.

Node and hyperedge deletions: Attackers often seek to weaken the structure of $\textbf{G}$ by deleting several nodes or hyperedges (Peng et al. 2022; Ma et al. 2018). We denote a deletion attack as $\textsf{A}^{\textbf{V}}(r, s)$ that deletes $r\%$ of the nodes in $\textbf{V}$ by a strategy s. Similarly, $\textsf{A}^{\textbf{E}}(r, s')$ is an attack that deletes $r\%$ of the hyperedges in $\textbf{E}$ by a strategy $s'$. We introduce several potential attack strategies that attackers may employ in Sect. 5.2.

Spearman’s rank correlation: Spearman’s rank correlation is a measurement of rank correlation between two variables. Let $X = [x_1,...,x_n]$ and $Y=[y_1,...,y_n]$ be two variables. Let $R(X)=[\tau _X(x_1),...,\tau _X(x_n)]$ be the rank variable of X in which $\tau _X(x_i)$, for $i=1,...,n$, is the relative ranking position of $x_i$ when the values in $\{x_1,...,x_n\}$ are sorted in the descending order³. Simiarly, let $R(Y)=[\tau _Y(y_1),...,\tau _Y(y_n)]$ be the rank variable of Y. The Spearman’s rank correlation between X and Y, denoted as $\rho (R(X), R(Y))$, equals to the Pearson correlation coefficient of R(X) and R(Y), i.e.,

$$\begin{aligned} \rho (R(X), R(Y))=\frac{\text {cov}(R(X), R(Y))}{\sigma _{R(X)}\sigma _{R(Y)}}, \end{aligned}$$

(1)

where $\text {cov}(R(X), R(Y))$ is the covariance of R(X) and R(Y); $\sigma _{R(X)}$ and $\sigma _{R(Y)}$ are the standard deviations of R(X) and R(Y), respectively. We have $-1 \le \rho (R(X), R(Y)) \le 1$, with $\rho (R(X), R(Y))=1$ when R(X) and R(Y) are identical and $\rho (R(X), R(Y))=-1$ when R(X) and R(Y) are fully opposed.

Core resilience: The core resilience ${\mathcal {R}}^{\textbf{V}}_{\textbf{G}}(r, s)$ against node deletions of a hypergraph $\textbf{G}$ is defined as the Spearman’s rank correlation coefficient of the core numbers of the nodes before and after $r \%$ of the nodes have been deleted from $\textbf{V}$ by attack $\textsf{A}^{\textbf{V}}(r, s)$. After several nodes are deleted alongside their incident hyperedges, there remains a sub-hypergraph $\tilde{\textbf{G}}=(\tilde{\textbf{V}}, \tilde{\textbf{E}})$ in which some of the remaining nodes may lose their original core numbers, potentially distorting the ranking of core numbers. Denote the original and post-attack core numbers of the remaining nodes $\tilde{V}=\{v_{i_1},...,v_{i_m}\}$ as $N_{\textbf{G}}= [N_{\textbf{G}}(v_{i_1}),...,N_{\textbf{G}}(v_{i_m})]$ and $N_{\tilde{\textbf{G}}} = [N_{\tilde{\textbf{G}}}(v_{i_1}),...,N_{\tilde{\textbf{G}}}(v_{i_m})]$⁴, respectively. The core resilience ${\mathcal {R}}^{\textbf{V}}_{\textbf{G}}(r,s)$ is defined as the Spearman’s rank correlation between $N_{\textbf{G}}$ and $N_{\tilde{\textbf{G}}}$, which is equal to $\rho (R(N_{\textbf{G}}), R(N_{\tilde{\textbf{G}}}))$. Similarly, the core resilience ${\mathcal {R}}^{\textbf{E}}_{\textbf{G}}(r, s')$ against hyperedge deletions of a hypergraph $\textbf{G}$ is defined as the Spearman’s rank correlation coefficient of the core numbers of the nodes before and after $r \%$ of the hyperedges have been deleted from $\textbf{E}$ by attack $\textsf{A}^{\textbf{E}}(r, s')$.

These definitions of core resilience against node deletions and hyperedge deletions are adopted from (Laishram et al. 2018) and extended to hypergraphs. The core number serves as a measure of node centrality (Shin et al. 2016; Laishram et al. 2018), and core resilience measures the tendency of central (or peripheral) nodes to remain central (or peripheral) after the network faces node/hyperedge deletions.

3.2 Problem definition

In this section, we aim to establish a clear understanding of the problem at hand. First, we present a formal definition of the problem. Then, we discuss its objective and constraints. Lastly, we discuss the challenges associated with this problem and discuss its relevance to existing problems.

Problem 1

(CREAM: Core-conserving REsilience mAxiMization)

• Input: a hypergraph $\textbf{G}=(\textbf{V},\textbf{E})$ with the hyperedge size distribution D and a budget B,

• Find: b hyperedges: $\overline{\textbf{E}} = \{e_1,...,e_b\}$ where $\overline{\textbf{E}} \subseteq 2^{\textbf{V}}$ and $\overline{\textbf{E}} \cap \textbf{E}= \emptyset$ to augment to $\textbf{G}$ to form $\textbf{G}'=(\textbf{V}, \textbf{E}')$ with $\textbf{E}'=\textbf{E}\cup \overline{\textbf{E}}$,

• to Maximize: the core resilience ${\mathcal {R}}_{\textbf{G}'}^{\textbf{T}}(r,s)$ of $\textbf{G}'$ in a case of attack $\textsf{A}^{\textbf{T}}(r, s)$, whose target $\textbf{T}$, degree r and strategy s are unknown in advance ($\textbf{T}$ is either $\textbf{V}$, for a node deletion attack, or $\textbf{E}'$, for a hyperedge deletion attack)

• Subject to constraints

  • all core numbers of nodes are conserved, i.e., $N_{\textbf{G}}(v) = N_{\textbf{G}'}(v)$,

  • the hyperedges are augmented within the budget, i.e., $b \le B$,

  • the size distribution of the hyperedges in $\overline{\textbf{E}}$ follows D.

Objective: As shown later in Sect. 4, the ranking of core numbers is useful in several applications. Such ranking may be distorted once several nodes or hyperedges are deleted from the hypergraph. Thus, we wish to preserve such ranking under deletion attacks by improving the core resilience.

Constraints on cores numbers: The goal is to consolidate the resilience of the core structure, so it is essential to avoid distorting the core structure, to begin with. Also, we augment hyperedges as a pre-caution measure without any prior knowledge of the attack, so the augmented hyperedges should preserve the core structure even in the case that the attack would not occur. These justify the constraint of preserving the core numbers.

Constraints on the number of augmented hyperedges: While Problem 1 allows a maximum budget of B, in order to satisfy the requirement of preserving all core numbers, the actual number b of hyperedges that any method can augment to $\textbf{G}$ can be smaller than B.

Constraints on the size of augmented hyperedges: In addition, since the augmented hyperedges should not be easily distinguishable from the real hyperedges or harmful to the network properties, the original hyperedge size distribution should be preserved. Moreover, if the size distribution of the augmented hyperedges deviates significantly from the real distribution, they become easily noticeable to the attackers, which may enable them to deliberately ignore all the augmented hyperedges that they deem unrealistic prior to any attacks, which renders the augmentation unavailing.

Related problems and unique challenges: A similar problem in graphs is defined in (Laishram et al. 2018), where the authors propose a method named MRKC. Among all pairs of non-adjacent nodes, MRKC retains those guaranteed to preserve all core numbers when they are added to the network while discarding the others. MRKC then ranks all the retained pairs by a certain metric and greedily selects the one with the highest score to be added to the network. A naive extension of MRKC to hypergraphs is to check all combinations of nodes that are not actual hyperedges and select only those that preserve all core numbers, However, the number of the combinations is in the order of $\mathcal {O}(2^{|\textbf{V}|})$, which is huge in practice. Therefore, the cost of checking all possible node combinations is prohibitive and renders this approach impractical. This proves the challenge of Problem 1. We address this challenge by our method, COREA, in Sect. 6.

4 Motivating applications

In this section, we present two applications of the concept of k-core on hypergraphs, in the identification of influential nodes and anomaly detection, to motivate our studies on the core resilience of hypergraphs. Due to the importance of k-cores, attackers are often incentivized to impair the core structures of pair-wise graphs (Linghu et al. 2020; Medya et al. 2020; Zhu et al. 2018). Similarly, hypergraph core structures, proving useful in these applications, are vulnerable to deletion attacks. As subsequently shown in Sect. 7.6, the usefulness of hypergraph cores in those tasks is degraded when the networks face deletion attacks, and our proposed method helps mitigate such degradation.

4.1 Identification of influential nodes

The concept of core number in graphs has proven useful in finding influential nodes in social networks (Kitsak et al. 2010; Shin et al. 2016). We generalize the SIR model in (Kitsak et al. 2010) to hypergraphs (see Algorihm 4 in Appendix 2). In each dataset, we start with one seed node (initially infected), simulate the SIR process, and measure the number of ever-infected nodes (i.e., recovered nodes) as the influence of the seed node.

In Table 2, we report the Spearman’s rank correlation coefficient between the node influences and each of the following node-level statistics:

• Core: the core numbers in the original hypergraph.

• Degree: the degrees in the original hypergraph.

• Clique-C: the core numbers in the clique expansion of the hypergraph.

• Clique-D: the degrees in the clique expansion of the hypergraph.

Among them, the core number in hypergraph is the most correlated with the individual nodes’ influences, demonstrating the usefulness of hypergraph core number ranking in finding influential nodes in real-world hypergraphs.

Table 2 The Spearman’s rank correlation coefficient between the nodes’ influences and the statistics

4.2 Anomaly detection

Shin et al. (2016) introduce an effective scoring function to detect abnormally dense subgraphs. The scoring function employed to measure the abnormality of node v is the difference in the rankings of v in core number and degree, specifically, $s(v) = |\log (rank_c(v)) - \log (rank_d(v))|$.

In each hypergraph, we select k nodes uniformly at random as abnormal nodes and inject $\left\lceil\left\lceil {\frac{k(k-1)}{m}}\right\rceil\right\rceil$ hyperedges of size m in which each of the abnormal nodes is incident to $(k-1)$ hyperedges, with m is the maximum hyperedge size of the hypergraph. Each abnormal node now has core number and degree at least $(k-1)$. We use the score s(v) to estimate how abnormal each node v is in the two settings:

• Core: $rank_c(v)$ and $rank_d(v)$ are the rankings of v in core number and degree in the hypergraph, respectively.

• Clique-C: $rank_c(v)$ and $rank_d(v)$ are the rankings of v in core number and degree in the clique expansion of the hypergraph, respectively.

The AUC-PR of predicting which nodes are the abnormal nodes based on the score s(v) in the two settings Core and Clique-C is reported in Fig. 2. Using core numbers in hypergraphs yields better prediction than using the core numbers in the clique expansion, showing the usefulness of the concept of hypergraph core numbers, particularly the ranking of core numbers.

Fig. 2

The AUC-PR of predicting the abnormal nodes. Employing core numbers in hypergraphs results in a more accurate prediction than core numbers in the clique expansions

5 Proposed concepts and observations

The objective of Problem 1, core resilience, is a hypergraph-level measurement, and it is difficult to optimize directly for two major reasons. Firstly, measuring the core resilience is computationally expensive as we need to conduct core decomposition on the original hypergraph, apply a deletion attack, and administer core decomposition again on the attacked networks. Furthermore, due to the unpredictable nature of attacks, it is impossible to anticipate their magnitude and strategy accurately. This lack of foresight hinders the precise computation of core resilience for our network. Thus, we define several node-level and hyperedge-level measurements to characterize the core resilience so that we can improve the core resilience indirectly via these measurements. In this section, we introduce such measurements and show that they are effective indicators of the core resilience of real-world hypergraphs via several empirical observations.

5.1 Proposed concepts

We introduce a number of concepts that are related to core resilience. These concepts serve as the foundation for the observations made in Sect. 5 and our proposed method presented in Sect. 6.

5.1.1 Hyperedge core number and anchor

As we wish to augment the hyperedges that preserve the core numbers, we seek to unravel how hyperedges contribute to the core numbers of nodes. While a node relies on having enough incident hyperedges for its core number, by definition, the existence of a hyperedge may not contribute to the core numbers of all of its incident nodes. In the core decomposition process, when a node v of core number k is removed, its incident hyperedges are also removed. If e is one of those hyperedges, e is not incident to any nodes of core numbers smaller than k; otherwise, e would have been removed before v. Moreover, e cannot contribute to the core numbers of the incident nodes whose core numbers are higher than k as e is not present in the core levels higher than k. In other words, e only helps contribute to the core numbers of the incident nodes whose core numbers are equal to k, and we refer to them as the anchors of e.

Core number of a hyperedge e: It is the maximum integer k such that e is in $\textbf{C}(k,\textbf{G})$ and denoted by $\overline{N_{\textbf{G}}}(e)$. In the pruning process to obtain the $(k+1)$-core from the k-core, a node is removed along its incident hyperedges. Therefore, $\overline{N_{\textbf{G}}}(e)$ is equal to the lowest core number of a node included in e: $\overline{N_{\textbf{G}}}(e) = \min _{v \in e} N_{\textbf{G}}(v)$.

Anchor(s) of a hyperedge e: They are the nodes involved in e having core number equal to $\overline{N_{\textbf{G}}}(e)$. The set of anchors of e is denoted by $\textbf{A}_{\textbf{G}}(e)$. For each $v \in \textbf{A}_{\textbf{G}}(e)$, e is said to be anchored at v. The anchors are critical to the core number of the hyperedge as the hyperedge loses its core number once an anchor loses its core number.

Each hyperedge incident to a node v has a core number that is either equal to or lower than that of v. We denote the sets of such hyperedges as $\textbf{E}_{\textbf{G}}^=(v)=\{e \in \textbf{E}_{\textbf{G}}(v) \mid \overline{N_{\textbf{G}}}(e) = N_{\textbf{G}}(v) \}$ and $\textbf{E}_{\textbf{G}}^<(v)=\{e \in \textbf{E}_{\textbf{G}}(v) \mid \overline{N_{\textbf{G}}}(e) < N_{\textbf{G}}(v) \}$, respectively.

5.1.2 Core strength and core influence

Before exploring the core resilience of the hypergraph as a whole, which is difficult to compute exactly, we characterize what constitutes the resilience of nodes in keeping their core numbers, how nodes benefit from the connections with other nodes for their core numbers, and in turn how nodes contribute to the core numbers of other nodes. As described, a node v of core number k relies entirely on the incident hyperedges whose core numbers are also k for its core number, i.e., the incident hyperedges consisting of only nodes having core numbers at least k. If v is incident to many hyperedges of such kind, even when some are removed, v may still have enough incident hyperedges, at least k, to maintain its core numbers k. In those hyperedges, the nodes having core numbers greater than k help contribute to the core number of v via the incident hyperedges. We extend the concepts of core strength and core influence in graphs (Laishram et al. 2018) to hypergraphs to quantify how resilient a node is in keeping its core number and how much a node contributes to the connected nodes of lower core numbers, respectively, in a hypergraph.

Core strength of a node v: It is the minimum number of hyperedges to delete to certainly reduce $N_{\textbf{G}}(v)$, denoted by $\mathcal{C}\mathcal{S}_{\textbf{G}}(v)$. The node v depends on its incident hyperedges in $\textbf{E}_{\textbf{G}}^=(v)$ to obtain its core number because all hyperedges in $\textbf{E}_{\textbf{G}}^<(v)$ are deleted before the core decomposition process reaches the $N_{\textbf{G}}(v)$-core. $|\textbf{E}_{\textbf{G}}^=(v) |- N_{\textbf{G}}(v)$ is the number of “extra” hyperedges incident to v in the $N_{\textbf{G}}(v)$-core, beyond its minimum requirement of $N_{\textbf{G}}(v)$ incident hyperedges, so after merely removing $\mid \textbf{E}_{\textbf{G}}^=(v) \mid - N_{\textbf{G}}(v)$ incident to v, v is not guaranteed to lose its core number k. Thus, $\mathcal{C}\mathcal{S}_{\textbf{G}}(v) = \mid \textbf{E}_{\textbf{G}}^=(v) \mid - N_{\textbf{G}}(v) + 1$. A node with a higher core strength has higher resilience to maintain its core number against deletion attacks. In order to improve a node’s resilience, we add hyperedges to improve its core strength.

Core strength of a hyperedge e: It is the minimum number of hyperedges to delete to certainly reduce $\overline{N_{\textbf{G}}}(e)$. Since $\overline{N_{\textbf{G}}}(e)$ certainly decreases once the core number of at least 1 anchor of e decreases, $\overline{N_{\textbf{G}}}(e)$ is equal to the lowest core strength among those of its anchor(s). We denote the core strength of e by $\overline{\mathcal{C}\mathcal{S}_{\textbf{G}}}(e)=\min _{x \in \textbf{A}_{\textbf{G}}(e)} \mathcal{C}\mathcal{S}_{\textbf{G}}(v)$. A hyperedge with a higher core strength has higher resilience to maintain its core number against deletion attacks.

Core influence of a node v: It is a number measuring v’s contribution to the core numbers of the anchors of the hyperedges in $\textbf{E}_{\textbf{G}}^<(v)$, denoted by $\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$. As a node relies on its incident hyperedges consisting of nodes having equal or higher core numbers to maintain its own core number, a node can contribute to the core numbers of lower-core nodes via such incident hyperedges. Particularly, the anchors of these hyperedges benefit from such contribution. $\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$ measures such contribution and is defined as:

$$\begin{aligned} \mathcal{C}\mathcal{I}_{\textbf{G}}(v) = 1 + \sum _{e \in \textbf{E}_{\textbf{G}}^<(v)}(1 + \frac{\Delta }{N_{\textbf{G}}(v) - 1})\max _{t \in \textbf{A}_{\textbf{G}}(e)}\left[ (1 - \frac{\mathcal{C}\mathcal{S}_{\textbf{G}}(t)-1}{\mid \textbf{E}_{\textbf{G}}^=(t) \mid })\mathcal{C}\mathcal{I}_{\textbf{G}}(t)\right] , \end{aligned}$$

where $\Delta = N_{\textbf{G}}(v) - \overline{N_{\textbf{G}}}(e)$ indicates the gap in the core numbers between v and e, and $\frac{\Delta }{N_{\textbf{G}}(v) - 1}$ is the gap normalized by the highest possible gap ($N_{\textbf{G}}(v) - 1$). Among the nodes in $e \setminus \textbf{A}_{\textbf{G}}(e)$, the term $1 + \frac{\Delta }{N_{\textbf{G}}(v) - 1}$ gives a higher value to a node with a higher core number. For each anchor $t \in \textbf{A}_{\textbf{G}}(e)$, t has $(\mathcal{C}\mathcal{S}_{\textbf{G}}(t)-1)$ “extra hyperedges” (deleting them does not change the core number of t). The term $1 - \frac{\mathcal{C}\mathcal{S}_{\textbf{G}}(t)-1}{\mid \textbf{E}_{\textbf{G}}^=(t) \mid }$ reflects the idea that the more extra hyperedges t has, the less dependent t is on e. Among the anchors of e, the node with the greatest dependence on v is selected, explaining the $\max$ aggregation. To compute the core influences, we first initialize the core influence of each node to 1 We start computing the core ìnluences of the nodes having the minimum core number and continue up until the nodes in the degeneracy core. The core influence of each node only depends on the nodes with lower core numbers, so we only need to iterate through each hyperedge once. A node that has a high core influence is important to the core numbers of many nodes, so if this node disappears or loses its core numbers, numerous nodes are affected. As a result, to preserve the core structure of the network, we wish to enhance the resilience in maintaining core numbers of the nodes having high core influences.

5.1.3 Core influence-strength and degeneracy centralized index of a hypergraph

Having described the resilience to maintain core numbers at the node and hyperedge levels, we aggregate the relevant measures to the hypergraph level to characterize the hypergraph’s core resilience. These characterizations involve core strengths, core influences, and the degeneracy core.

Core influence-strength of G: It is the average of $\mathcal{C}\mathcal{I}_{\textbf{G}}\times \mathcal{C}\mathcal{S}_{\textbf{G}}$ over the nodes in $\textbf{V}$, denoted by $\mathcal {CIS}(\textbf{G})$: $\mathcal {CIS}(\textbf{G})=\frac{1}{|\textbf{V}|}\sum _{v \in \textbf{V}}\mathcal{C}\mathcal{I}_{\textbf{G}}(v)\mathcal{C}\mathcal{S}_{\textbf{G}}(v)$. If nodes of high core influences have high core strengths, they are resilient in keeping their core numbers, and as a result, many nodes benefit from the contribution of the high-influence nodes in keeping their core numbers, making the core structure more resilient. Thus, we hypothesize that the $\mathcal {CIS}(\textbf{G})$ is a good indicator of core resilience of $\textbf{G}$, which is confirmed in Observation 4 in Sect. 5.3.

Degeneracy centralized index of G: It is a value from 0 to 1 measuring how centralized $\textbf{G}$ is around its degeneracy core. An index of 0 means that in every hyperedge, every node has the same core number. An index of 1 indicates that every hyperedge is incident to at least one node in the degeneracy core. The degeneracy centralized index of a hypergraph $\textbf{G}$ is defined as: $i(\textbf{G}) = \frac{1}{ |\textbf{E}|}\sum _{e \in \textbf{E}}\frac{k^*(e) - \overline{N_{\textbf{G}}}(e)}{N_{\textbf{G}}^{*}- \overline{N_{\textbf{G}}}(e)}$, where $k^*(e)$ denotes the highest $N_{\textbf{G}}(v)$ among all nodes $v \in e$. We extend a similar measurement for graphs in (Laishram 2020), which is theoretically proven to be positively correlated with the core resilience of a random graph, to hypergraphs.

5.2 Attack strategies

In this section, we introduce several attack strategies that attackers may exploit to weaken a hypergraph $\textbf{G}=(\textbf{V}, \textbf{E})$. Each strategy reflects the preferences of the attackers to delete particular nodes/hyperedges, which they may deem more vital to the core structure of the network. By simulating these attacks, we measure the core resilience of each hypergraph against each attack strategy and confirm the usefulness of the concepts proposed in Sect. 5.1.

Node deletions: We introduce different strategies s for an attack $\textsf{A}^{\textbf{V}}(r,s)$ that deletes $r \%$ of nodes.

• If s is Random Attack: $r\%$ of the nodes, together with their incident hyperedges, are chosen uniformly at random and deleted by $\textsf{A}^{\textbf{V}}(r,s)$.

• If s is Degree Attack: The high-degree nodes are targeted, and the chance for a node v to be deleted by $\textsf{A}^{\textbf{V}}(r,s)$, alongside its incident hyperedges, is proportional to its degree $d_{\textbf{G}}(v)$.

• If s is Core Number Attack: The nodes having high core numbers are targeted, and the chance for a node v to be deleted by $\textsf{A}^{\textbf{V}}(r,s)$, with its incident hyperedges, is proportional to its core number $N_{\textbf{G}}(v)$.

• If s is Core Strength Attack: The nodes of low core strengths are targeted, and the chance for a node v to be deleted by $\textsf{A}^{\textbf{V}}(r,s)$ is proportional to $\frac{1}{\overline{\mathcal{C}\mathcal{S}_{\textbf{G}}}(v)}$.

Hyperedge deletions: We introduce different strategies s for an attack $\textsf{A}^{\textbf{E}}(r,s)$ that deletes $r \%$ of hyperedges.

• If s is Random Attack: $r\%$ of the hyperedges are chosen uniformly at random and deleted by $\textsf{A}^{\textbf{E}}(r,s)$.

• If s is Cardinality Attack: The large-cardinality hyperedges are targeted, and the chance for a hyperedge e to be deleted by $\textsf{A}^{\textbf{E}}(r,s)$ is proportional to its cardinality $|e |$.

• If s is Degree Attack: The hyperedges incident to high-degree nodes are targeted, and the chance for a hyperedge e to be deleted by $\textsf{A}^{\textbf{E}}(r,s)$ is proportional to the degree of its highest-degree constituent node.

• If s is Core Strength Attack: The hyperedges of low core strengths are targeted, and the chance for a hyperedge e to be deleted by $\textsf{A}^{\textbf{E}}(r,s)$ is proportional to $\frac{1}{\overline{\mathcal{C}\mathcal{S}_{\textbf{G}}}(e)}$.

5.3 Observations in real-world hypergraphs

Fig. 3

The core resilience of real-world hypergraphs against hyperedge-deletion attacks varies among the attack strategies and across deletion ratios. The x-axis shows the deletion ratio, and the y-axis indicates Spearman’s rank correlation coefficient between the original and the post-attack core number distributions. Core strength attack is consistently the most destructive to the core resilience, while random attack is the least destructive

We present several patterns of core resilience of 10 real-world hypergraphs (Benson et al. 2018a) to validate the usefulness of the concepts proposed in Sect. 5.1. More details on the datasets are in Appendix 1. In this section, we present the results of hyperedge deletions only. The figures highlighting the results of node deletions are in Appendix 3.

Observation 1

Core strength attack is the most destructive to the core resilience of real-world hypergraphs for both node-deletion and hyperedge-deletion attacks.

Figure 3 shows the core resilience of real-world hypergraphs against hyperedge-deletion attack strategies, random, degree, cardinality, and core strength, across deletion ratios. The figure illustrates how the Spearman’s rank correlation, between the original and the post-attack core number distributions, changes depending on the ratio of the hyperedges that are deleted. Core strength attack results in the lowest core resilience per deletion ratio, while random attack results in the highest core resilience.

Fig. 4

The distribution of core strengths of nodes in each dataset, visualized on a log-log scale, is positively skewed. This indicates that a majority of nodes have relatively low core strengths, indicating the potential for improvement through the augmentation of hyperedges

Fig. 5

The skewness of the distribution of core strengths is negatively correlated with the core resilience. “CorrCoef” indicates Spearman’s rank correlation coefficient. It is worth noting that datasets within the same domain exhibit similarities in terms of both skewness and core resilience

Observation 2

The node core-strength distribution in each dataset is positively skewed.

The core strength distribution of nodes for each dataset is illustrated in Fig. 4. In each dataset, the distribution of core strengths is positively skewed, i.e., most nodes have low core strengths, and they are more prone to losing core numbers due to hyperedge deletions. Augmenting hyperedges to enhance their core strengths can make them more robust against deletion attacks.

Observation 3

A hypergraph of high core resilience tends to possess a low skewness of the core-strength distribution and vice versa. Hypergraph datasets within the same domain exhibit similarities in terms of both skewness and core resilience.

The relationship between the skewness of core-strength distribution and core resilience, when $50\%$ of hyperedges are deleted, is depicted in Fig. 5. A high skewness indicates a tendency for the distribution to have a heavy tail to the right, indicating more nodes of low core strengths. This tendency is negatively correlated with core resilience. The two datasets in each domain (“co-authorship”, “contact”, “email”, “NDC”, and “threads”) exhibit similarities in terms of both core resilience and the skewness of core strength distribution.

Observation 4

A hypergraph of high core resilience tends to possess a high core influence-strength and vice versa.

Fig. 6

The core influence-strength is positively correlated with the core resilience. “CorrCoef” indicates Spearman’s rank correlation coefficient

Fig. 7

The degeneracy centralized index is positively correlated with core resilience. “CorrCoef” indicates Spearman’s rank correlation coefficient

Observation 5

A hypergraph of high core resilience tends to possess a high degeneracy centralized index, and vice versa.

For each hypergraph $\textbf{G}$, we measure the core influence-strength, $\mathcal {CIS}(\textbf{G})$, and the degeneracy centralized index $i(\textbf{G})$. The positive correlations between the core resilience, when $50\%$ of hyperedges are deleted, with $\mathcal {CIS}(\textbf{G})$ and $i(\textbf{G})$ are shown in Figs. 6 and 7, respectively. The results imply two indicators for high core resilience. The first indicator is that the nodes of high core influences have high resilience against deletion attacks, i.e., high core strengths. The second indicator is that many hyperedges are incident to the nodes in the degeneracy core.

The core resilience, a hypergraph-level measurement, is difficult to optimize directly as core resilience is computationally expensive to measure exactly and the deletion strategies and degree of attacks that attackers employ are unknown. Therefore, we seek to optimize the correlated measurements that are presented in this section. The details of our proposed method, COREA, are described in Sect. 6. Apart from basing on the observations, COREA also has several theoretical merits, outlined in Sect. 6.4.

6 Proposed method: COREA

In this section, we introduce our proposed method, COREA (COre REsilience Improvement by Hyperedge Augmentation), for addressing Problem 1. We begin by providing an overview of the approach, followed by a detailed description of each step. Lastly, we present its theoretical merits.

6.1 Overview

We present an overview of our two-step method, COREA, whose pseudocode is given in Algorithm 1. The inputs of Problem 1, which are defined regardless of specific solutions, are a hypergraph $\textbf{G}$ with the hyperedge size distribution D and a budget B. Given these problem input parameters, COREA is tasked to find at most B hyperedges to augment to $\textbf{G}$ such that these hyperedges have a size distribution following D and conserve all core numbers of the nodes in $\textbf{G}$.

• Step 1: Construct a pool P of candidate hyperedges that are guaranteed to conserve all core numbers. Firstly, COREA follows the core decomposition process (see Algorithm 2), i.e., a node-deletion process, to determine $\mathcal {C}$, the maximum number of hyperedges to augment to $\textbf{G}$ while conserving all core numbers. We introduce a tie-breaking scheme $\textsf{T}$ to determine the order by which nodes are deleted in this process. Once the number $\mathcal {C}$ is determined, we introduce a sampling scheme $\textsf{S}$ to construct $\mathcal {C}$ candidate hyperedges.

• Step 2: Theorem 3 shows that there is a maximum number $\mathcal {M}$ of hyperedges that can be augmented to $\textbf{G}$ while preserving all core numbers and $\mathcal {C} = \mathcal {M}$. Therefore, the maximum number b of hyperedges COREA can augment is $b=\text {min}\{B, \mathcal {C}\}$, subject to the constraints of Problem 1. As our budget is limited and $|P |$ might be greater than b, we need to select a few of the candidate hyperedges, constructed in Step 1, from P to add to $\textbf{G}$. The core resilience is a hypergraph-level objective that is hard to maximize directly due to computational cost and attack unpredictability. Therefore, we use the improvement to the core influence-strength of $\textbf{G}$, demonstrated to correlate with the core resilience in Observation 4, as the ranking metric. At each step, c candidate hyperedges with the highest scores are chosen to augment to $\textbf{G}$, with c as the batch size of each step, an input parameter of COREA.

Apart from the input parameters given by Problem 1, COREA also employs 3 other algorithm input parameters: the tie-breaking scheme $\textsf{T}$ in Step 1-1, the sampling scheme $\textsf{S}$ in Step 1-2, and the batch size c in Step 2, as described above. These algorithm input parameters are the exclusive hyperparameters of our method, which may not be used for other algorithms. In section 7.3, we present our ablation study to investigate the importance of these algorithm input parameters.

6.2 Step 1: construct candidate hyperedges

As discussed, it is infeasible to check all possible node combinations and select those guaranteed to change no core numbers. As a workaround, we instead answer this question: for each node v of core number k, how many hyperedges anchored at v can be augmented without changing the core number of v?

Suppose a candidate hyperedge e is formed by grouping v with other nodes having core numbers higher than or equal to k. If we can guarantee the augmentation of e preserves the core number k of its anchor(s) including v, e will be deleted in process of obtaining the $(k+1)$-core from the k-core. Therefore, the core numbers of all the nodes in e are unchanged. Because each hyperedge only contributes to the core number of its anchor(s), e does not affect any nodes of core numbers lower than k. As a result, augmenting e into $\textbf{G}$ changes no core numbers. In Step 1, COREA forms a pool P of such candidate hyperedges like e. We further divide Step 1 into two parts.

6.2.1 Step 1-1: compute anchor availabilities

This step is outlined in Algorithm 2 Following the core decomposition process, for each node $v \in \textbf{E}$, Algorithm 2 computes the number of hyperedges anchored at v that can be augmented while preserving $N_{\textbf{G}}(v)$.

In the pruning process of obtaining the $(k+1)$-core from the k-core, when node v, $N_{\textbf{G}}(v) = k$, is about to be deleted, its degree is lower than $(k+1)$, i.e., $d_{\textbf{G}}(v) \le k$, and let $a\ge 0$ be the value satisfying $d_{\textbf{G}}(v) = k -a$. If we augment $a = k - (k-a)$ hyperedges anchored at v, its degree becomes $k - a + a = k$, which still qualifies v for removal. Prior to removing v, Algorithm 2 computes the number $c(v) = a$, referred to as the anchor availability of v. c(v) is the number of hyperedges anchored at v that can be augmented while preserving $N_{\textbf{G}}(v)$. The total number $\mathcal {C}$ of hyperedges that can be augmented by COREA, subject to preserving all core numbers, is the sum of all anchor availabilities of the nodes: $\mathcal {C}=\sum _{v \in \textbf{V}}c(v)$.

Fig. 8

An illustration of Algorithm 2 with two different valid orders of node removals in the core decomposition of hypergraph $\textbf{G}$. Incorporating the core decomposition process, the method computes the anchor availability c(v) before removing node v of core number $N_{\textbf{G}}(v)$. While different orders lead to different individual anchor availabilities, the sum of anchor availabilities is always 0 for the one node of core number 1, 1 for the nodes of core number 2, 5 for the nodes of core number 3, and 6 for total

At any point during the pruning process of obtaining the $(k+1)$-core from the k-core, several nodes may have degree $\le k$, and the order by which those nodes are removed may affect their respective anchor availabilities. In particular, when both u and v have degree $\le k$. If we delete u first, the hyperedges anchored in both u and v are removed along u, which further reduces the degree of v. As a result, Algorithm 2 will afford a higher anchor availability for v. The tie-breaking scheme $\textsf{T}$ that decides which node to remove first impacts the anchor availabilities of the nodes. While COREA does not assume a specific tie-breaking scheme, we set $\textsf{T}$ to select v to delete first with the chance proportional to $\mathcal{C}\mathcal{S}_{\textbf{G}}(v)/\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$. By this, we defer the removals of the nodes having high $\mathcal{C}\mathcal{I}_{\textbf{G}}/\mathcal{C}\mathcal{S}_{\textbf{G}}$ values to potentially afford them higher anchor availabilitiles. Our experiment results in Sects. 7.2 and 7.3 justify this choice for the tie-breaking scheme $\textsf{T}$.

An example in Fig. 8 illustrates the process of computing the anchor availabilities of Algorithm 2 in two different deletion orders. In the two different deletion orders, the anchor availabilities of a node may be different, but the total anchor availabilities is always zero for the one node of core number 1, one for the nodes of core number 2, five for the nodes of core number 3, and six for total.

Note that our method does not always afford the maximum anchor availabilities for all nodes. Different deletion orders, governed by the tie-breaking scheme $\textsf{T}$, may result in different anchor availabilities for the same node v, and not every order guarantees the maximum availability for v. In Appendix 5, we conduct additional analysis regarding the reasons why achieving the maximum anchor availabilities for all nodes is not always guaranteed. As presented in Sect. 6.4, Theorem 2 shows that the sum $\mathcal {C}$ of anchor availabilities, where the anchor availabilities of some nodes might be sub-optimal, is always constant with respect to $\textbf{G}$. More importantly, however, Theorem 3 shows that $\mathcal {C}$ is actually the maximum number of hyperedges any method can augment to $\textbf{G}$, subject to conserving all core numbers of $\textbf{G}$. That is, any method that augments more than $\mathcal {C}$ hyperedges, attempting to provide more anchor availabilities than COREA, certainly violates the core-conserving constraint of Problem 1.

Given $\textbf{G}$ and the tie-breaking scheme $\textsf{T}$, the first output of Step 1-1 (Algorithm 2) is the anchor availabilities of the nodes in $\textbf{V}$, which are the number of hyperedges anchored at the respective nodes that can be augmented while conserving all core numbers. The anchor availabilities are exclusive to COREA. Other output results include the core numbers of the nodes in $\textbf{V}$, the deletion order $\mathbb {O}$ of the nodes in $\textbf{V}$ in the core decomposition process, and the degeneracy of $\textbf{G}$, which are the output of a core decomposition process.

6.2.2 Step 1-2: build a pool P of candidate hyperedges

Given the results of Step 1-1, Step 1-2 constructs a pool P of $\mathcal {C}$ candidate hyperedges guaranteed to conserved all core numbers if augmented to $\textbf{G}$.

For each v, COREA constructs c(v) candidate hyperedges anchored at v to add to the pool P of candidates. To conserve the size distribution D of the hyperedges in $\textbf{E}$, the size s of each candidate hyperedge e is drawn from D. e includes v, and the other $(s-1)$ nodes have the core numbers $\ge N_{\textbf{G}}(v)$.

As shown in Line 11 of Algorithm 1, those $(s-1)$ nodes are chosen from $\mathbb {O}[i+1:]$ by the sampling scheme $\textsf{S}$, which are the nodes removed after v in the core decomposition process. As stated in Theorem 1, it is guaranteed that augmenting e into $\textbf{G}$ does not alter any core numbers. While our method does not assume a particular sampling scheme $\textsf{S}$, we set $\textsf{S}$ to choose each node u with a chance proportional to $\mathcal{C}\mathcal{I}_{\textbf{G}}(u)/\mathcal{C}\mathcal{S}_{\textbf{G}}(u)$, giving the nodes of high core influences and relatively low core strengths more incident hyperedges, and include at least one node in the degeneracy core. In Sect. 5.3, we show that the core influence-strength and degeneracy centralized index are positively correlated with the core resilience (see Observations 4 and 5). The nodes of high $\mathcal{C}\mathcal{I}_{\textbf{G}}/\mathcal{C}\mathcal{S}_{\textbf{G}}$ values are favored with higher anchor availabilities (due to the tie-breaking scheme $\textsf{T}$ described in Sect. 6.2.1) and in turn higher core strenghts in the augmented hypergraph, making them more robust in keeping core numbers and indirectly improve the core influence-strength of $\textbf{G}$. Therefore, the anchors of e can potentially benefit from the connections with such nodes. Moreoever, to maximize the degeneracy centralized index of the augmented hyperedges, each hyperedge of core number lower than $N_{\textbf{G}}^{*}$, the degenracy of $\textbf{G}$, needs to include at least one of in the degeneracy. The choices for $\textsf{S}$ reflect the results of Observations 4 and 5 and prove helpful in the empirical performance of COREA in Sects. 7.2 and 7.3.

6.3 Step 2: select the best hyperedges from the pool

As shown in Theorem 3, there is a maximum number $\mathcal {M}$ of hyperedges that can be augmented to $\textbf{G}$ while preserving all core numbers, and the total anchor availabilities $\mathcal {C} = \sum _{v \in \textbf{V}}c(v)$ is equal to $\mathcal {M}$. As a result, in order to satisfy all constraints of Problem 1, the maximum number b of hyperedges that COREA can augment to $\textbf{G}$ is not only $\le B$ but also $\le \mathcal {C}$. In other words, $b = \text {min}\{B, \mathcal {C}\}$. In the case $|P |> b$, which is usually true as the budget B is usually tight in practice, COREA needs to select b hyperedges from P to augment to $\textbf{G}$.

Given the pool P of candidate hyperedges from Step 1, COREA ranks each candidate e in P by the increase in the core influence-strength of the hypergraph. At each iteration, let the current hypergraph snapshot be $\textbf{G}_{\text {cur}}=(\textbf{V}, \textbf{E}_{\text {cur}})$, where COREA has augmented q hyperedges from P to $\textbf{E}$ to form $\textbf{E}_{\text {cur}}$ ($q=0$ at the beginning of Step 2). For each $e \in P$, COREA computes a score $s(e) = \mathcal {CIS}(\textbf{G}_{\text {new}}) - \mathcal {CIS}(\textbf{G}_{\text {cur}})$, with $\textbf{G}_{\text {new}}=(\textbf{V}, \textbf{E}_{\text {new}}), \textbf{E}_{\text {new}}=\textbf{E}_{\text {cur}} \cup \{e\}$.

COREA keeps greedily selecting c candidate hyperedges with the highest scores, augmenting them to $\textbf{G}$, and updating the scores of the remaining hyperedges in P until b hyperedges have been augmented to $\textbf{G}$.

This scoring method is based on Observation 4 in which a higher core influence-strength implies a higher core resilience. Since the core resilience is difficult to optimize directly for the computational challenges and unpredictable behavior of attackers, we employ a surrogate objective that is the improvement to the core influence-strength of $\textbf{G}$ in Step 2 This surrogate objective reflects the goal of maximizing the core influence-strength of $\textbf{G}$, which is positively correlated with core resilience, and is more convenient to maximize.

6.4 Theoretical analysis

In this section, we present several theoretical results regarding COREA. All proofs can be found in "Appendix 4".

Theorem 1

(Feasibility of COREA) Step 1 of COREA guarantees to construct a pool P of candidate hyperedges that do not change the core number of any node when they are added together to $\textbf{G}$.

Theorem 2

(Invariance of COREA) The total number of anchor availabilities $\mathcal {C} = \sum _{v \in \textbf{V}}c(v)$ realized by COREA is always constant with respect to $\textbf{G}$.

Theorem 3

(Exhaustivenessof COREA) There is a maximum number $\mathcal {M}$ of hyperedges that can be augmented to $\textbf{G}$ while conserving all core numbers, and the total number of anchor availabilities $\mathcal {C}$ realized by COREA is equal to $\mathcal {M}$.

Theorems 1 and 2 state that COREA always satisfies the constraint of preserving all core numbers in Problem 1 and returns the same total number $\mathcal {C}$ of anchor availabilities regardless of the tie-breaking scheme $\textsf{T}$ in Step 1. According to Theorem 3, $\mathcal {C}$, is equal to $\mathcal {M}$, which is the maximum possible number of hyperedges that can be augmented without altering any core numbers. That is, in a case where the budget B exceeds $\mathcal {M}$, COREA is guaranteed to augment the maximum number $\mathcal {M}$ of hyperedges while ensuring the preservation of all core numbers. In general, COREA always augments $b=\text {min}\{B, \mathcal {M}\}$ hyperedges, which is the maximum number of hyperedges that can be augmented subject to all constraints.

Theorem 4

(Time Complexity of COREA) Given the hypergraph $\textbf{G}=(\textbf{V}, \textbf{E})$ with maximum hyperedge cardinality m, the budget B, the total number of anchor availabilities $\mathcal {C}$ of all nodes (constant with respect to each dataset), and the batch size c by which COREA augments c hyperedges at a time in Step 2, the time complexity of COREA is $\mathcal {O}\left[ |\textbf{V}|\text {log}|\textbf{V}|+ \mathcal {C}m \log |\textbf{V}|+ (|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ \mathcal {C}m^2)\frac{b}{c}\right]$, where $b = \text {min}\{B, \mathcal {C}\}$.

7 Empirical evaluation of COREA

In this section, we answer the following questions:

• Q1. Time and performance how are different methods compared in terms of the running time and improvement of the core resilience in real-world hypergraphs?

• Q2. Ablation study how do different variants of each component of COREA affect the performance and running time?

• Q3. Effect of hyperedge size distribution what is the effect of the size distribution of the augmented hyperedges on the performance?

• Q4. Further insights what are interesting characteristics of the hyperedges returned by COREA?

• Q5. Applications to what extent do the hyperedges augmented by COREA contribute to the applications of core numbers discussed in Sect. 4?

7.1 Experiment settings

Datasets: We used 10 real-world hypergraphs across several domains. The basic statistics of the datasets are provided in Appendix 1.

Proposed method: For COREA, the tie-breaking scheme $\textsf{T}$ in Step 1-1 selects v to delete first with the chance proportional to $\mathcal{C}\mathcal{S}_{\textbf{G}}(v)/\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$ among several nodes up for removals. This defers removing nodes having high $\mathcal{C}\mathcal{I}_{\textbf{G}}/\mathcal{C}\mathcal{S}_{\textbf{G}}$ to potentially afford them higher anchor availabilities. The sampling scheme $\textsf{S}$ in Step 1-2 selects v with the chance proportional to $\mathcal{C}\mathcal{I}_{\textbf{G}}(v)/\mathcal{C}\mathcal{S}_{\textbf{G}}(v)$ and ensures each candidate hyperedge has at least one node in the degeneracy core. These options stem from Observations 4 and 5. Including one node in the degeneracy core maximizes the degeneracy centralized index after augmentation. To improve the core strengths of the nodes having high core influences, COREA prioritizes nodes of high $\mathcal{C}\mathcal{I}_{\textbf{G}}/\mathcal{C}\mathcal{S}_{\textbf{G}}$ with higher anchor availabilities and more incident hyperedges. COREA is implemented in Java.

Baselines: We consider the following baseline methods:

• MRKC-G: we apply the method MRKC in (Laishram et al. 2018) to generate the augmented edges for the clique expansion. We augment the edges (i.e., size-2 hyperedges) that satisfy the constraints of Problem 1 to the hypergraph.

• MRKC-D: we construct the decomposed pairwise graphs from the original hypergraph, as in (Do et al. 2020), and then apply MRKC  (Laishram et al. 2018) to each decomposed graph to generate edges. After that, we construct the hyperedges from those edges (each edge in a decomposed graph corresponds to a hyperedge), select those that satisfy the constraints of Problem 1, and augment them to $\textbf{G}$.

• MRKC-H: we generate the hyperedges of size 2 only in Step 2 of COREA and use the same scoring function as MRKC in (Laishram et al. 2018).

• Random: We replace the tie-breaking scheme $\textsf{T}$ in Step 1-1 and the sampling scheme $\textsf{S}$ in Step 1-2 of COREA by uniform random selection. The selection of candidate hyperedges in Step 2 from the pool P is also uniform at random.

MRKC-G and MRKC-D are extentions of the core-resilience improvement method for pair-wise graph (Laishram et al. 2018) with proper adjustments to hypergraphs, and we use the implementation provided by the authors for these two baselines. We implement MRKC-H as a variant of COREA that constructs size-2 hyperedges only. Random is a simplified variant of COREA with randomization at each step outlined in Sects. 6.2 and 6.3.

Experimental details: We evaluate the performance of each method in terms of the improvement of core resilience: ${\mathcal {R}}_{\textbf{G}'}^{\textbf{E}'}(r,s) - {\mathcal {R}}^{\textbf{E}}_{\textbf{G}}(r, s)$ with $\textbf{G}'$ obtained by augmenting the hyperedges selected by each method to $\textbf{G}$. The budget B is fixed to $5\% \times |\textbf{E}|$. For hyperedge-deletion attacks, $r\% \times |\textbf{E}|$ ($r=10,20, 30, 40, 50$) hyperedges are deleted. For node-deletion attacks, $r\% \times |\textbf{V}|$ ($r=5,10, 15, 20, 25$) nodes are deleted along their incident hyperedges. For each method and each dataset, we report the average running time and performance over 10 trials.

In this section, we present the results of hyperedge-deletion attacks when s is Core Strength Attack only. The results for node-deletion attacks when s is Core Strength Attack are in Appendix 3. The results for all other attack strategies are in the supplementary material. In all cases, we draw similar conclusions regarding the superior performance of COREA compared with the baselines and the roles each component of COREA plays in the performance.

7.2 Q1. Time and performance

Performance: The comparison of different methods in core resilience improvement across deletion ratios is in Fig. 9. The x-axis indicates the deletion ratios, the y-axis shows the performance, and the vertical bars indicate the standard deviations. COREA consistently outperforms the others in all datasets. In each dataset, the performance by COREA is $5\%-35\%$ better than that of the best-performing baseline and up to $70\%$ superior to the performance of Random. While Random is consistently the worst-performing baseline, for the three baselines MRKC-G, MRKC-D, and MRKC-H, they all perform slightly better than Random, and no method surpasses the other two consistently in all datasets.

Time and performance trade-off: The time-performance tradeoff of the methods is illustrated in Fig. 10. The x-axis indicates the running time, the y-axis shows the performance when the deletion ratio $r=50\%$, and the vertical bars indicate the standard deviations. COREA significantly outperforms other methods in all datasets, while the running time of COREA is relatively close to the fastest baseline Random, which is the worst-performing method.

In addition to Figs. 9 and 10, for each dataset, we test the difference in the performance of our method with that of the best-performing baseline using an one-tailed Student’s t-test as follows:

• $H_0$: the mean performance of COREA is lower than or equal to the mean performance of the baseline.

• $H_a$: the mean performance of COREA is greater than the mean performance of the baseline.

At $95\%$ confidence when $\alpha = 0.05$, the test rejects $H_0$ in favor of $H_a$ (p-value $<0.05$), confirming that COREA is significantly superior to all the baselines.

Fig. 9

The comparison of different methods in terms of performance. The x-axis shows the deletion ratios, and the y-axis shows the core resilience improvement of the methods. The vertical bars indicate the standard deviations. COREA consistently brings better improvement of core resilience than the others in all datasets regardless of deletion ratios

Fig. 10

The trade-off of the methods in terms of time and performance. The x-axis shows the running time, and the y-axis shows the core resilience improvement of each variant when the deletion ratio $r=50\%$. The vertical bars indicate the standard deviations. COREA consistently provides a better time-performance trade-off than the other methods in all datasets regardless of deletion ratios

Fig. 11

The comparison of different variants in terms of performance. The x-axis shows the deletion ratios, and the y-axis shows the core resilience improvement of each variant. The vertical bars indicate the standard deviations. The full-fledged version of COREA consistently outperforms the other variants in all datasets regardless of deletion ratios

Fig. 12

The trade-off of different variants in terms of time and performance. The x-axis shows the running time, and the y-axis shows the core resilience improvement of each variant when the deletion ratio $r=50\%$. The vertical bars indicate the standard deviations. The full-fledged version of COREA consistently provides a better time-performance trade-off than the other variants in all datasets regardless of deletion ratios

7.3 Q2. Ablation study

We investigate the role of each component of COREA in improving the core resilience of the hypergraphs. Similar to Sect. 7.2, in each section of the ablation study, apart from highlighting the results in Figs. 11, 12, 13, and 14, we also employ an one-tailed Student’s t-test, at $95\%$ confidence, to verify that our full-fledged method significantly outperforms all the other variants. In all cases, the p-value is smaller than 0.05, so the test rejects $H_0$ in favor of $H_a$ that the full-fledged variant of COREA is superior to the best-performing simplified variant.

Simplified variants of COREA: We compare the full-fledged version of COREA, as described in Sect. 7.1, with the following five simplified variants in terms of running time and performance:

• CoReA-CI: obtained by modifying the scoring function s(.) in Step 2 of COREA to the sum of the core influences of the anchor. The score for each candidate hyperedge e is: $s'(e) = \sum _{v \in \textbf{A}_{\textbf{G}}(e)}\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$. This scoring function gives high priority to hyperedges anchored at high-influence nodes, those contributing to the core numbers of other nodes.

• RB1: obtained by replacing the tie-breaking scheme $\textsf{T}$ in Step 1-1 of COREA by selecting a node uniformly at random.

• RB2: obtained by replacing the sampling scheme $\textsf{S}$ in Step 1-2 of COREA by selecting nodes from $\mathbb {O}[i+1:]$ uniformly at random.

• RB3: in Step 2 of COREA, choose candidate hyperedges uniformly at random.

• Random: the same as method Random in Sects. 7.1 and 7.2.

For each method, if we increase the batch size c while keeping other components unchanged, the running time decreases as there are fewer iterations of the loops in lines 16-22 of Algorithm 1. However, the performance declines as the method augments more hyperedges at 1 iteration and undertakes fewer updates on the scores of the candidate hyperedges in Step 2 of Algorithm 1. For the full-fledged version, we set the batch size c equal to the budget b and record the running time as t. For the competitors, we set the batch size $c'$ to afford them sufficient time and update iterations for potentially better performance. Specifically, for each competitor, we set $c' = \min \{10, b\}$ if the running time is at least as long as t, and otherwise, we set $c'=1$ to give it the most possible time. We compare the performance across deletion ratios in Fig. 11 and the time-performance trade-off of all methods when deletion ratio $r=50\%$ in Fig. 12. It is clear that the full-fledged version of COREA consistently yields a better time-performance trade-off and outperforms the others regardless of deletion ratios.

Fig. 13

The performance of COREA when the degeneracy requirement is enforced and waived. The x-axis shows the deletion ratios, and the y-axis shows the core resilience improvement of each variant. The vertical bars show the standard deviations. Enforcing the degeneracy requirement of having at least one node in the degeneracy core in each candidate hyperedge is helpful to the performance

Fig. 14

The performance of COREA with different tie-breaking schemes in Step 1-1. The x-axis shows the deletion ratios, and the y-axis shows the core resilience improvement of each variant. The vertical bars show the standard deviations. The tie-breaking scheme $\mathcal{C}\mathcal{S}_{\textbf{G}}/\mathcal{C}\mathcal{I}_{\textbf{G}}$, leads to the highest improvement of core resilience among the three schemes

Fig. 15

The distribution of hyperedge sizes in each dataset, visualized on a log-log scale, is positively skewed. In each distribution, only a small fraction of hyperedges have large sizes, while the majority of hyperedges are of small sizes

Fig. 16

The performances of COREA when following the original and uniform hyperedge size distributions, respectively. The x-axis shows the deletion ratios, and the y-axis shows the core resilience improvement. The vertical bars indicate the standard deviations. For the uniform distribution, COREA augments larger-size hyperedges, potentially helping more nodes with the augmentation, and results in a better performance

Degeneracy core: We examine the effectiveness of the idea of including at least one node in the degeneracy core in each candidate hyperedge, as proposed in Sect. 6.2.2. Figure 13 highlights the performance of COREA in two scenarios: when the requirement of including at least one node in the degeneracy core in each candidate hyperedge is enforced in Step 1-2 of COREA, and when the requirement is waived. A better performance is achieved when this requirement is enforced, indicating that it is necessary to meet this requirement in our method.

Tie-breaking scheme: We also examine how different tie-breaking schemes $\textsf{T}$ in Step 1-1 of COREA, which is discussed in Sect. 6.2.1, leads to different performances. Recall that a tie-breaking scheme $\textsf{T}$ governs the order nodes are deleted in the core decomposition process and in turn determines the anchor availabilities of nodes. We compare three schemes of selecting which node to delete first when facing multiple nodes qualified for removal in Algorithm 2:

• $\mathcal{C}\mathcal{S}_{\textbf{G}}/\mathcal{C}\mathcal{I}_{\textbf{G}}$: the chance of selecting a node v is proportional to $\mathcal{C}\mathcal{S}_{\textbf{G}}(v)/\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$ as of COREA described in Sect. 7.1.

• $1/\mathcal{C}\mathcal{I}_{\textbf{G}}$: the chance to select a node v, to delete first among several nodes up for removal in the core decomposition process, is proportional to $1/\mathcal{C}\mathcal{I}_{\textbf{G}}(v)$. This defers removing nodes of high $\mathcal{C}\mathcal{I}_{\textbf{G}}$ values to potentially afford them higher anchor availabilities.

• Random: a node is selected uniformly at random. This is method RB1 in Sect. 7.3.

Figure 14 shows that the scheme $\mathcal{C}\mathcal{S}_{\textbf{G}}/\mathcal{C}\mathcal{I}_{\textbf{G}}$ consistently leads to better performance than the other two.

7.4 Q3. Effect of hyperedge size distribution

The distributions of hyperedge sizes in real-world hypergraphs are known to be positively skewed (Kook et al. 2020), where most hyperedges have small sizes while only a small fraction of hyperedges have large sizes (see Fig. 15). To examine the effect of the size distribution, for each dataset, we reconfigure COREA to augment the hyperedges whose size distribution follows the uniform distribution. In other words, we replace the original hyperedge size distribution D of $\textbf{G}$ in Algorithm 1 by the uniform distribution. The results are highlighted in Fig. 16. In the case of uniform distribution, as COREA creates and augments more hyperedges of larger sizes, due to switching from a heavy-tailed to the uniform distribution, the augmented hyperedges potentially help more nodes to maintain their core numbers, resulting in a better performance of core resilience improvement. However, it would be unrealistic to assume such uniform distribution as we are constrained to preserve the original skewed hyperedge size distributions in order to prevent attackers from deliberately ignoring our augmented hyperedges, as discussed in Sect. 3.2.

7.5 Q4. Further insights

We present three interesting characteristics of the hyperedges returned by COREA.

Insight 1

The augmentation by COREA is more helpful to the nodes of with medium to high original core numbers.

For each dataset, we group the nodes into three groups based on core numbers: low, medium, and high (each accounts for one-third of the range of core numbers) and measure the decrease in core numbers in each group after $50\%$ of the hyperedges are removed by the Core Strength Attack, with or without the augmentation by COREA. As Fig. 17 shows, COREA mitigates such decrease more clearly in the medium and high groups.

Fig. 17

Hyperedges augmented by COREA are more helpful in mitigating the core number degree, due to core strength attack, of the nodes of medium and high core numbers

Insight 2

A hypergraph of higher core resilience tends to possess less availability for augmentation and vice versa.

For each dataset, we define the ratio of availability as the average of anchor availabilities of nodes, found by COREA, normalized by their respective core numbers: $r(\textbf{G}) = \frac{1}{|\textbf{V}|}\sum _{k=2}^{N_{\textbf{G}}^{*}}\sum _{v \in \textbf{V}_k}\frac{c(v)}{k} = \frac{1}{|\textbf{V}|}\sum _{k=2}^{N_{\textbf{G}}^{*}}\frac{\sum _{v \in \textbf{V}_k}c(v)}{k}$ ($V_k = \{v \in \textbf{V}\mid N_{\textbf{G}}(v)=k\}$). For each $v \in \textbf{V}_k$, $0 \le c(v) \le k$. A dataset with high $r(\textbf{G})$ implies more availability for augmentation, and this statistic is negatively correlated with core resilience, as shown in Fig. 18 (left). Intuitively, if we can augment more, i.e., a high value of $r(\textbf{G})$, the core structure of the hypergraph is “less complete”, resulting in weak core resilience against deletion attacks.

Fig. 18

(Left) The ratio of availability is negatively correlated with core resilience. (Right) the set of actual hyperedges and the set of candidate hyperedges, constructed by COREA, have positively correlated distribution skewness of core numbers. “CorrCoef” indicates Spearman’s rank correlation coefficient

Insight 3

The skewness of the distributions of the core numbers of hyperedges in $\textbf{E}$ is positively correlated with that of the hyperedges constructed by COREA.

This positive correlation is shown in Fig. 18 (right). For example, in threads-ask-ubuntu, the skewness of the core number distribution of hyperedges in $\textbf{E}$ is positive, indicating more hyperedges of low core numbers but fewer hyperedges of high core numbers, and this tendency is also found in the pool of hyperedges P returned by COREA. By contrast, such skewness for the set $\textbf{E}$ in contact-primary-school is negative, implying more hyperedges of high core numbers, and this is also true for the hyperedges in P from the dataset.

7.6 Q5. Applications

In this section, we demonstrate that the hyperedges augmented by COREA support the applicability of hypergraph core numbers, introduced in Sect. 4, when the networks face deletion attacks.

Identification of influential nodes: Table 3 reports the Spearman’s rank correlation coefficient between the nodes’ influences in the original hypergraph with: the original core numbers (Before Attack), the core numbers of the hypergraph after $50\%$ of hyperedges have been deleted (No Augmentation), and the core numbers of the hypergraph after several hyperedges are augmented by COREA and then $50\%$ of hyperedges are deleted (COREA). After the deletion attack, the ranking of core number is less correlated to the ranking of node influences, i.e., core numbers become less useful in characterizing influential nodes. However, the hyperedges augmented by COREA help alleviate that decrease in the usefulness of core numbers.

Anomaly detection: Fig. 19 highlights the AUC-PR of predicting abnormal nodes of the method Core with the settings detailed in Sect. 4.2 before (Original) and after $50\%$ of hyperedges have been deleted (COREA and No Augmentation). COREA and No Augmentation indicate the cases where hyperedges are augmented by COREA before the attack and no augmentation is undertaken, respectively. After an attack, the ranking of core numbers is less useful in detecting anomalies, but this decline of usefulness is mitigated with the hyperedges augmented by COREA.

Table 3 Spearman’s rank correlation coefficients between the node’s influences and the core numbers before an attack, after an attack, and after an attack with augmentation by COREA. COREA helps preserve the usefulness of core numbers in finding influential nodes after the networks are attacked

Fig. 19

The AUC-PR of predicting abnormal nodes by the method Core, which is based on the ranking of core numbers and outlined in Sect. 4, before (Original) and after deletion attack with (COREA) and without (No Augmentation) the hyperedges augmented by COREA. After the attack, the ranking of core numbers is less useful in predicting anomalies, but the augmentation by COREA helps reduce such drop in usefulness

8 Conclusion

In this work, we formulate and study the problem of enhancing the core resilience of real-world hypergraphs. We discuss the challenges of the problem, introduce the relevant concepts, and present the key patterns regarding the core resilience of the hypergraphs

Based on these, we develop a two-step method, COREA, to consolidate the core structure of hypergraphs by augmenting hyperedges within a given budget. COREA is fast, theoretically sound, and empirically effective in improving the core resilience of the hypergraphs. The hyperedges augmented by COREA not only preserve the core structure of the hypergraphs but also enhance its resilience. Through our extensive experiments in ten real-world hypergraphs, we demonstrate the superiority of COREA over the baseline approaches, investigate the characteristics of the augmentation by COREA, and examine the role each component plays in the performance of COREA. In addition, we show that COREA helps support the applications of hypergraph core numbers when the hypergraphs face deletion attacks. The code and datasets are available at https://github.com/manhtuando97/CoReA.

Appendices

Appendix A: Datasets

Throughout the paper, we use 10 real-world hypergraph datasets (Benson et al. 2018a). The basic statistics are provided in Table 4. Their domains are:

• Co-authorship (coauth-MAG-Geology and coauth-MAG-History): each node is an author, and each hyperedge is the list of coauthors in a publication.

• Contact (contact-high-school and contact-primary-school): each node is an individual, and each hyperedge is a group of people in contact at a high/primary school.

• Email (email-Enron and email-Eu): each node is an email address, and each hyperedge consists of the sender and recipients of an email.

• Drugs (NDC-classes and NDC-substances): each node represents a drug class/substance, and each hyperedge represents a set of classifications/substances of a drug.

• Threads (threads-ask-ubuntu and threads-math): each node is a user in an online forum, and each hyperedge is the list of users in a question thread.

Table 4 Basic statistics of real-world hypergraphs

Appendix B: Core decomposition algorithm

The Core Decomposition process is outlined in Algorithm 3.

Appendix C: Algorithm for SIR on hypergraphs

The SIR model generalized to the hypergraph setting is outlined in Algorithm 4.

For the results reported in Sects. 4 and 7.6, we set $r = 1$ and $t=0.025$ in all datasets. Similar conclusions regarding the applicability of hypergraph core numbers (Sect. 4) and how the hyperedges augmented by COREA help support the applications of core numbers (Sect. 7.6) are drawn with different values of t in $\{0.05, 0.025, 0.01, 0.005\}$.

Appendix D: Results on node-deletion attacks

We present the results of node-deletion attacks. The five observations, similar to those in Sect. 5.3, are reported for all attack strategies in Figs. 20, 21, 22, and 23. The results in Figs. 21, 22, and 23 are of the cases where $25 \%$ of nodes are deleted.

The method evaluation results reported in Figs. 24, 25, 26, 27, 28, 29 and 30 are of Core Strength Attack. Similarly to Sect. 7, we also report the mean of 10 trials together with the standard deviations indicated by the vertical bars. Overall, our full-fledged method COREA significantly outperforms and provides a better time-performance trade-off than the baselines and simplified variants. The statistical significance of the gap is also verified by the one-tailed Student’s t-test, as in Sect. 7.2, at $95 \%$ confidence (p-values $< 0.05$ in all cases).

For all other attack strategies, we draw the same conclusion about the superiority in performance and time-performance trade-off of the full-fledged version of COREA compared to the baselines and simplified variants. Due to the large number of figures, we present the results of all other attack strategies in the supplementary material.

When switching from the real hyperedge size distribution, heavy-tailed, to the uniform distribution, COREA achieves a better performance as more larger-size hyperedges are augmented. However, assuming a uniform hyperedge distribution is both unrealistic and violative of the constraints of Problem 1.

Fig. 20

The core resilience of real-world hypergraphs against node-deletion attacks varies among the attack strategies and across deletion ratios. The x-axis shows the deletion ratio, and the y-axis indicates Spearman’s rank correlation coefficient between the original and the post-attack core number distributions. Core Strength Attack is consistently the most destructive to the core resilience, while Random Attack is the least destructive

Fig. 21

The skewness of the distribution of core strengths is negatively correlated with the core resilience against node-deletion attacks. “CorrCoef” indicates Spearman’s rank correlation coefficient. It is worth noting that datasets within the same domain exhibit similarities in terms of both skewness and core resilience

Fig. 22

The core influence-strength is positively correlated with the core resilience, against node-deletion attacks. “CorrCoef” indicates Spearman’s rank correlation coefficient

Fig. 23

The degeneracy centralized index is positively correlated with core resilience, against node-deletion attacks. “CorrCoef” indicates Spearman’s rank correlation coefficient

Fig. 24

The comparison of different methods in terms of performance against node-deletion attacks. The x-axis shows the node deletion ratios, and the y-axis shows the core resilience improvement of the methods. The vertical bars indicate the standard deviations. COREA consistently brings better improvement of core resilience than the others in all datasets regardless of deletion ratios

Fig. 25

The trade-off of the methods in terms of time and performance against node-deletion attacks. The x-axis shows the running time, and the y-axis shows the core resilience improvement of each variant when the node deletion ratio $r=25\%$. The vertical bars indicate the standard deviations. COREA consistently provides a better time-performance trade-off than the other methods in all datasets regardless of deletion ratios

Fig. 26

The comparison of different variants in terms of performance against node-deletion attacks. The x-axis shows the node deletion ratios, and the y-axis shows the core resilience improvement of each variant. The vertical bars indicate the standard deviations. The full-fledged version of COREA consistently outperforms the other variants in all datasets regardless of deletion ratios

Fig. 27

The trade-off of different variants in terms of time and performance against node-deletion attacks. The x-axis shows the running time, and the y-axis shows the core resilience improvement of each variant when the node deletion ratio $r=25\%$. The vertical bars indicate the standard deviations. The full-fledged version of COREA consistently provides a better time-performance trade-off than the other variants in all datasets regardless of deletion ratios

Fig. 28

The performance of COREA when the degeneracy requirement is enforced and waived. The x-axis shows the node deletion ratios and the y-axis shows the core resilience improvement of each variant. The vertical bars show the standard deviations. Enforcing the degeneracy requirement of having at least one node in the degeneracy core in each candidate hyperedge is helpful to the performance

Fig. 29

The performance of COREA against node-deletion attacks with different tie-breaking schemes in Step 1–1. The x-axis shows the node deletion ratios, and the y-axis shows the core resilience improvement of each variant. The vertical bars show the standard deviations. The tie-breaking scheme $\mathcal{C}\mathcal{S}_{\textbf{G}}/\mathcal{C}\mathcal{I}_{\textbf{G}}$, leads to the highest improvement of core resilience among the three schemes

Fig. 30

The performances of COREA against node-deletion attacks when following the original and uniform hyperedge size distributions, respectively. The x-axis shows the node deletion ratios, and the y-axis shows the core resilience improvement. The vertical bars indicate the standard deviations. For the uniform distribution, COREA augments larger-size hyperedges, potentially helping more nodes with the augmentation, and results in a better performance

Appendix E: Theoretical results and proofs

In this section, we present detailed theoretical results with the accompanying proofs to support the soundness of COREA.

We first define a valid deletion order in a hypergraph $\textbf{G}= (\textbf{V}, \textbf{G})$ as a particular permutation $\mathbb {O}= [v_{i_1}, v_{i_2},...,v_{i_n}]$ of the nodes in $\textbf{V}= \{v_1,...,v_n\}$ such that the nodes in $\textbf{V}$ are removed exactly in the order of $\mathbb {O}$ in an execution of the core decomposition process. Different tie-breaking schemes $\textsf{T}$, described in Sect. 6.2.1 determine differently which node to delete first when several nodes are up for removal, resulting in different executions of the core decomposition process of $\textbf{G}$ and in turn different valid deletion orders. In addition, we refer to any augmentation method that augments several hyperedges of its choice to hypergraph $\textbf{G}$ while preserving all core numbers of $\textbf{G}$ as a feasible augmentation of $\textbf{G}$.

1.1 E.1: Feasibility of COREA

In this section, we prove that COREA is a feasible augmentation method, i.e., the hyperedges augmented by COREA to $\textbf{G}$ are guaranteed to preserve all core numbers of $\textbf{G}$.

Lemma 1

Assuming that after applying F, a feasible augmentation of $\textbf{G}$, a subsequence of a valid deletion order in the core decomposition process for the nodes having core number k is: $S_k = [a_1,...,a_q]$. Without F, $S_k$ is still a subsequence of a valid deletion order for the nodes having core number k in the pruning process of obtaining the $(k+1)$-core in the original hypergraph $\textbf{G}$.

Proof

Let $\textbf{G}'$ denote the result of applying F to $\textbf{G}$. For $i=1,...,q$, let $\textbf{E}_F(a_i)$ be the set of hyperedges augmented by F, each of which has $\{a_i\} \cup s$, with $s \subseteq \{a_{i+1},...,a_q\}$ (s may be an empty set) as the set of anchors. Let $F(a_i) = |\textbf{E}_{F}(a_i)|$. Following the core decomposition process, all the hyperedges in $\textbf{E}_F(a_i)$ are removed when $a_i$ is removed.

For $a_1$, as $a_1$ can be removed first in the process of obtaining the $(k+1)$-core from the k-core of $\textbf{G}'$, its degree at the k-core of $\textbf{G}'$ is $d_{\textbf{G}'}^k(a_1) \le k$. As the degree of $a_1$ in the k-core of $\textbf{G}$ is equal to $d_{\textbf{G}}^k(a_1) = d_{\textbf{G}'}^k(a_1) - F(a_1) \le k$, $a_1$ can also the first node of core number k to be deleted in the core decomposition process of $\textbf{G}$.

For any $a_i, i>1$, during the pruning process of obtaining the $(k+1)$-core, after nodes $a_1,...,a_{i-1}$ have been removed along with their incident hyperedges, the degree of $a_i$ in $\textbf{G}'$ must be lower than or equal to k. In other words, the degree of $a_i$ at this point is equal to $k - g(a_i) \le k$ with $g(a_i) \ge 0$. This value is equal to $F(a_i)$ plus the degree of $a_i$ in a sub-hypergraph of $\textbf{G}$, obtained by removing $a_1,...,a_{i-1}$ along with their incident hyperedges. If the order $S_k$ is followed in the core decomposition process of the original hypergraph $\textbf{G}$ (without the augmentation F), the degree of $a_i$ at this point, after nodes $a_1,...,a_{i-1}$ have been removed along with their incident hyperedges, would be: $k - g(a_i) - F(a_i) \le k$, which also qualifies $a_i$ for deletion.

Therefore, without the hyperedges augmented by F, $S_k$ is still a subsequence of a valid deletion order for the nodes having core number k in the pruning process of obtaining the $(k+1)$-core in the original hypergraph $\textbf{G}$.

Theorem 1

(Feasibility of COREA) Step 1 of COREA guarantees to construct a pool P of candidate hyperedges that do not change the core number of any node when they are added together to $\textbf{G}$.

Proof

We show that after COREA augments all the candidate hyperedges in P, the pool of candidate hyperedges constructed in Step 1 of COREA (Sect. 6.2), to $\textbf{G}=(\textbf{V}, \textbf{E})$ to form $\textbf{G}'=(\textbf{V}, \textbf{E}')$, the original deletion order $\mathbb {O}=[v_{i_1}, v_{i_2},...,v_{i_n}]$ of an execution of the core decomposition process on $\textbf{G}$ in Algorithm 2 is still a valid deletion order in $\textbf{G}'$ and returns the original core numbers.

We prove by induction on the elements $v_{i_1},...,v_{i_n}$ in $\mathbb {O}$ that in $\textbf{G}'$, $\mathbb {O}$ is still a valid deletion order and $N_{\textbf{G}}(v_{i_j}) = N_{\textbf{G}'}(v_{i_j}), j = 1,...,n$.

- Base case: As $v_{i_1}$ is the first node deleted in $\textbf{G}$, immediately prior to the removal of $v_{i_1}$, $d_{\textbf{G}}(v_{i_1})<N_{\textbf{G}}(v_{i_1}) + 1$, and $d_{\textbf{G}}(v_{i_1})\ge N_{\textbf{G}}(v_{i_1})$ (no hyperedges have been removed at this point and the degree of $v_{i_1}$ must be sufficient for the core number of $v_{i_1}$). Therefore, $d_{\textbf{G}}(v_{i_1}) = N_{\textbf{G}}(v_{i_1})$, so the anchor availability $c(v_{i_1})$ realized for $v_{i_1}$ is $c(v) = N_{\textbf{G}}(v_{i_1}) - d_{\textbf{G}}(v_{i_1}) = 0$. As a result, in $\textbf{G}'$, $d_{\textbf{G}'}(v_{i_1})=d_{\textbf{G}}(v_{i_1})$, so $v_{i_1}$ can also be the first node deleted in the core decomposition process in $\textbf{G}'$ and $N_{\textbf{G}}(v_{i_1}) = N_{\textbf{G}'}(v_{i_1})$.

- Inductive hypothesis: Assume that in an execution of the core decomposition process on $\textbf{G}'$, the nodes $v_{i_1},...,v_{i_{h-1}}$ have been deleted exactly in this order (same order as in $\textbf{G}$) and $N_{\textbf{G}}(v_{i_j}) = N_{\textbf{G}'}(v_{i_j}), j = 1,...,h-1$. We need to show that $v_{i_h}$ can now also be deleted and $N_{\textbf{G}}(v_{i_h}) = N_{\textbf{G}'}(v_{i_h})$. Indeed, suppose $N_{\textbf{G}}(v_{i_h})=k$ and $c(v_{i_h})$ is the anchor availability realized for $v_{i_h}$ by COREA. COREA constructs $c(v_{i_h})$ hyperedges, formed by grouping $v_{i_h}$ with other nodes from $\{v_{i_{h+1}},...,v_{i_{n}}\}$ (Line 11 of Algorithm 1) and augments those $c(v_{i_h})$ hyperedges to $\textbf{G}$.

Firstly, these $c(v_{i_h})$ hyperedges do not affect the core numbers of the nodes that have been deleted before v in $\mathbb {O}$, which are $v_{i_1},...,v_{i_{h-1}}$.

In addition, as $\textbf{E}\subseteq \textbf{E}'$, $N_{\textbf{G}'}(v_{i_j}) \ge N_{\textbf{G}}(v_{i_j})$ for $j = h,...,n$. Moreover, after $v_{i_1},...,v_{i_{h-1}}$ have been removed in the core decomposition process of $\textbf{G}'$, the degree of $v_{i_j}$ in $\textbf{G}'$ is no less than the degree of $v_{i_j}$ in $\textbf{G}$ after $v_{i_1},...,v_{i_{h-1}}$ have been removed in the core decomposition process of $\textbf{G}$, for $j = h,...,n$.

Following the removal order $\mathbb {O}$ in the pruning process of obtaining the $(k+1)$-core from the k-core in $\textbf{G}$, after the nodes $v_{i_1},...,v_{i_{h-1}}$ have been removed, the degree of $v_{i_h}$ in $\textbf{G}$ immediately prior to its removal is $k - c(v_{i_h})$. Therefore, in $\textbf{G}'$, at this point of the core decomposition process when $v_{i_1},...,v_{i_{h-1}}$ along with their incident hyperedges have been deleted, the degree of $v_{i_h}$ is $d_{\textbf{G}'}(v_{i_h}) = k - c(v_{i_h}) + c(v_{i_h}) = k < k+1$, so $N_{\textbf{G}'}(v_{i_h}) \le k$. Therefore, $N_{\textbf{G}'}(v_{i_h}) = k = N_{\textbf{G}}(v_{i_h})$, and the degree of $v_{i_h}$ at this point is equal to k. Thus, in $\textbf{G}'$, $v_{i_h}$ can be removed immediately after $v_{i_1},...,v_{i_{h-1}}$ have been removed. Such removal deletes $v_{i_h}$ and all of its incident hyperedges, including the newly augmented $c(v_{i_h})$ hyperedges, thus having no impacts on $v_{i_{h+1}},...,v_{i_n}$.

By the principle of mathematical induction, in $\textbf{G}'$, $\mathbb {O}$ is still a valid deletion order and $N_{\textbf{G}}(v_{i_j}) = N_{\textbf{G}'}(v_{i_j}), j = 1,...,n$. Thus, Step 1 of COREA guarantees to construct a pool P of candidate hyperedges that do not change the core number of any node when they are added together to $\textbf{G}$.

When the given budget B is tight, which is usually true in practice, only a subset of P is chosen to augment to $\textbf{G}$ in Step 2 of COREA  6.3. Whether all hyperedges in P are augmented or only a subset of P is augmented to $\textbf{G}$, in all cases, the hyperedges augmented by COREA are guaranteed to preserve all the original core numbers.

1.2 E2: Invariance of COREA

Lemma 2

Let $\mathbb {S}= \{a_1,...,a_n\}$ be a set of n elements, $\mathcal {F}(\mathbb {S})$ be the set of all subsets of S, and $t:\mathcal {F}(\mathbb {S}) \mapsto \mathbb {N}$ be a function that maps each subset of $\mathbb {S}$ to a natural number. Denote $S^{(i)} \in \mathcal {F}(\mathbb {S})$ as the set of all subsets of $\mathbb {S}$ contaning the element $a_i$. Then, the following equality holds:

$$\begin{aligned} \sum _{i=2}^{n} \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s)= \sum _{s \subseteq \mathbb {S}, |s |\ge 2}(|s |-1)t(s). \end{aligned}$$

(2)

Proof

It suffices to show the sum on the left-hand side of Equation (2) only involves the subsets of $\mathbb {S}$ whose cardinalities are no less than 2 and that each term t(s) for each $s \subseteq \mathbb {S}, |s |\ge 2$, appears exactly $(|s |-1)$ times in this sum.

Indeed, the set $\bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})$ is the set of all subsets of $\mathbb {S}$ that contain $a_i$ and at least 1 element among $a_1,..., a_{i-1}$. In addition, on the left-hand side of Equation (2), the sum only involves all subsets of $\mathbb {S}$ having at least 2 elements. It is because each subset needs to involve at least 2 distinct elements and for any subset $s' \subseteq \mathbb {S}$ such that $|s' |\ge 2$, take 2 elements $a_p, a_q \in s', p<q$, then $s' \in \bigcup \limits _{j=1}^{q-1} (S^{(q)} \cap S^{(j)})$.

Let $s = \{a_{k_1},...,a_{k_m}\}$ with $k_1<...<k_m$ and $|s |=m \ge 2$ be a subset of $\mathbb {S}$. For each $i = k_2,...,k_m$, s appears exactly once in $\bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})$ because for each of those $i=k_2,...,k_m$, the set s is a subset of $\mathbb {S}$ that contains $a_i$ and $a_{k_1} (k_1 < i)$.

For each $i \in \mathbb {S} \setminus \{k_2,...,k_m\}$, s does not appear in $\bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})$ as s fails to contain both $a_i$ and an element $a_j (j<i)$.

Therefore, the term t(s) corresponding each set s, $s \subseteq \mathbb {S}, |s |\ge 2$, appears exactly $(|s |-1)$ times on the left-hand side of Eq. (2). Since both sides of Eq. (2) involve exactly all the subsets of $\mathbb {S}$ whose cardinalities are greater than or equal to 2, the two sides of Equation (2) are equal to each other.

Lemma 3

(Invariance of COREA in each k-core) For $k=k_0,...,N_{\textbf{G}}^{*}$, with $k_0$ as the minimum core number of a node in $\textbf{G}$, the total number of anchor availabilities of nodes having core number k, realized by COREA, remains unchanged regardless of the order of nodes removed in the core decomposition.

Proof

Without loss of generality, assume a particular order in which the nodes are deleted in the pruning process of obtaining the $(k+1)$-core from the k-core is $[a_1,..., a_q]$, and their respective anchor availabilities realized by COREA are $c(a_1),..., c(a_q)$. Note that $\mathbb {S} = \{a_1,...,a_q\}$ is the set of all nodes having core number k. Denote $S^{(i)}$ as the set of all subsets of $\mathbb {S}$ containing $a_i$. For each subset $s \subseteq \mathbb {S}$, $|s |\ge 1$, let t(s) be the number of hyperedges that have s as the set of anchors: $t(s) = |\{e \in \textbf{E}\mid \textbf{A}_{\textbf{G}}(e) = s \}|$. Denote the set of all subsets of $\mathbb {S}$ that contain $a_i$ as $S^{(i)}$. The set of subsets of $\mathbb {S}$ that contain $a_i$ and at least one element among $a_1,...,a_{i-1}$ is $\bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})$.

At the k-core, the degree $d_{\textbf{G}}(v_{i_1})$ of node $a_i\in \mathbb {S}$ is $k + R(a_i)$ with $R(a_i) \ge 0$ since the degree of each node among $\{a_1,...,a_q\}$ has to be at least k. It should be noticed that $R(a_i)=d_{\textbf{G}}(v_{i_1})-k$ is independent of the order of node deletions.

Assuming that Algorithm 2 is now at the k-core and undertakes the pruning process to obtain the $(k+1)$-core while simultaneously obtaining the anchor availability for each node that has core number k. As node $a_1$ is the first node to delete, its degree is $\le k$. However, since no hyperedges at the k-core have been deleted yet, the degree of $a_1$ at this point is $k + R(a_1) \le k$. Therefore, $R(a_1) = 0$, and according to COREA, the anchor availability realized for $a_1$ is $c(a_1)=0$.

For each $i=2,...,q$, after nodes $a_1,..., a_{i-1}$ have been removed, all of the hyperedges anchored at any of those nodes have also been removed from the network. Among those hyperedges, the ones that affect the degree of $a_i$ are the ones co-anchored by $a_i$ and at least 1 among $a_1,..., a_{i-1}$. The number of such hyperedges is: $\sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s)$. Due to the removals of these hyperedges, the degree of $a_i$ immediately prior to its deletion is $k + R(a_i) - \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s)$. To qualify for deletion, the degree of $a_i$ must be lower than $(k+1)$. In other words, $k + R(a_i) - \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s) \le k$, or $- R(a_i) + \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s) \ge 0$. The anchor availability realized for node $a_i$ by COREA is then equal to: $c(a_i) = - R(a_i) + \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s)$.

The sum of anchor availabilities realized by COREA for all nodes in the k-core is: $c_k = \sum _{i=1}^q c(a_i) = -\sum _{j=1}^{n}R(a_j) + \sum _{i=2}^{q} \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s)$. Lemma 2 implies the following equality:

$$\begin{aligned} \sum _{i=2}^{q} \sum _{s \in \bigcup \limits _{j=1}^{i-1} (S^{(i)} \cap S^{(j)})} t(s) = \sum _{s \subset \mathbb {S}, |s |\ge 2}(|s |-1)t(s). \end{aligned}$$

(3)

Thus, $c(k) = -\sum _{j=1}^{q}R(a_j) + \sum _{s \subset \mathbb {S}, |s |\ge 2}(|s |-1)t(s)$. This value is symmetric with respect to each of $a_1,...,a_q$, which is independent of any particular ordering of $\mathbb {S} = \{a_1,...,a_q\}$.

Therefore, the total number of anchor availabilities realized by COREA for the nodes in the k-core is constant regardless of the order of deletions.

Lemma 4

For each $k=k_0,...,N_{\textbf{G}}^{*}$, with $k_0$ as the minimum core number of a node in $\textbf{G}$, in the pruning process of obtaining the $(k+1)$-core from the k-core, assume that in two different valid deletion orders $\mathbb {O}$ and $\mathbb {O}'$, $a_p$ is the p-th node having core number k deleted and $a_1,...,a_{p-1}$ are the $(p-1)$ nodes of core number k deleted before $a_p$ (with different orders). The anchor availability realized for $a_p$ is the same in both $\mathbb {O}$ and $\mathbb {O}'$.

Proof

We employ all the notations as in Lemma 3. According to the proof of Lemma 3, the anchor availability realized for $a_p$ in either $\mathbb {O}$ or $\mathbb {O}'$ is $- R(a_p) + \sum _{s \in \bigcup \limits _{j=1}^{p-1} (S^{(p-1)} \cap S^{(j)})} t(s)$, which is symmetric with respect to $a_1,...,a_{p-1}$ and does not depend on any particular ordering or $a_1,...,a_{p-1}$. This demonstrates that the anchor availability realized for each node is only dependent on the set of nodes deleted before it and independent of the deletion order by which those nodes are deleted.

Theorem 2

(Invariance of COREA) The total number of anchor availabilities $\mathcal {C} = \sum _{v \in \textbf{V}}c(v)$ realized by COREA is always constant with respect to $\textbf{G}$.

Proof

According to Lemma 3, for each $k=k_0,...,N_{\textbf{G}}^{*}$, with $k_0$ as the minimum core number of a node in $\textbf{G}$, the total anchor availabilities realized by COREA for the nodes having core number k is the same regardless of the order $\mathbb {O}$ of deletion ($\mathbb {O}$ is a valid deletion order).

Since the total anchor availabilities realized by Algorithm 1 can be obtained by summing up all anchor availabilities realized at each core level, the total number of anchor availabilities realized by COREA is constant regardless of the order of deletions.

1.3 E3: Exhaustiveness of COREA

Lemma 5

(Exhaustiveness of COREA in each k-core) For $k=k_0,...,N_{\textbf{G}}^{*}$, with $k_0$ as the minimum core number of a node in $\textbf{G}$, the total anchor availabilities for the nodes having core number k realized by COREA always is the maximum number of hyperedges anchored at the nodes of core number k that can be augmented, subject to the constraint of preserving the core number k of those nodes.

Proof

According to Lemma 3, the total anchor availabilities realized by Algorithm 1 for the nodes having core number k, is always the same regardless of the order of node deletions, and let $T_k$ be such total number.

Assume the contradiction that $T_k$ is not the maximum number of hyperedges anchored at the nodes of core number k that can be augmented to $\textbf{G}$ while conserving all core numbers. As a result, there is a feasible augmentation method I that augments $I_k$ hyperedges anchored at the nodes having core number k-core that preserve all core numbers with $I_k \ge T_k + 1$. Without loss of generality, assume that with I, in a valid deletion order of the core decomposition process, all nodes having core number k are deleted in the order $[a_1,...,a_q]$ in the pruning process to obtain the $(k+1)$-core from the k-core. Immediately before the deletion of $a_i$, its degree is $k - x(a_i) \le k$, with $x(a_i) \ge 0$. Denote $I_k^{(i)}$ as the number of hyperedges augmented by I whose anchors involve $a_i$ and a subset s of $\{a_{i+1},...,a_q\}$ (s maybe an empty subset). We then have $\sum _{i=1}^{q}I_k^{(i)}= I_k$

By Lemma 1, we know that without I, $[a_1,...,a_q]$ is still a subsequence, involving all the nodes having core number k, of a valid deletion order in the core decomposition of the original hypergraph $\textbf{G}$. That is, without I, in the original hypergraph $\textbf{G}$, the pruning process can still delete nodes $a_1,...,a_q$ in this particular order to obtain the $(k+1)$-core from the k-core. The degree of $a_i$ immediately prior to its deletion is $k - x(a_i) - I_k^{(i)}$. As a result, COREA realizes the anchor availability $c(a_i) = x(a_i) + I_k^{(i)}$ for node $a_i$. Lemma 3 proves that the value of $T_k$ is always equal to: $T_k = \sum _{i=1}^{q}c(a_i) = \sum _{i=1}^{q} [x(a_i) + I_k^{(i)}] = \sum _{i=1}^{q}I_k^{(i)} + \sum _{i=1}^{q} x(a_i) = I_k + \sum _{i=1}^{q} x(a_i) \ge I_k \ge T_k + 1$, which is a contradiction.

Therefore, the initial assumption is false, which proves that COREA returns the maximum number of hyperedges anchored at the nodes having core number k, subject to the constraint of preserving all core numbers.

Theorem 3

(Exhaustiveness of COREA) There is a maximum number $\mathcal {M}$ of hyperedges that can be augmented to $\textbf{G}$ while conserving all core numbers, and the total number of anchor availabilities $\mathcal {C}$ realized by COREA is equal to $\mathcal {M}$.

Proof

Lemma 5 shows that COREA always returns the maximum total number of anchor availabilities $T_k$ of nodes having core number k for $k=k_0,...,N_{\textbf{G}}^{*}$, with $k_0$ as the minimum number of core number of a node in $\textbf{G}$. According to Theorem 2, the total anchor availabilities realized by COREA is always $\mathcal {C} = \sum _{v \in \textbf{V}}c(v)= \sum _{k=k_0}^{N_{\textbf{G}}^{*}}T_k$. Below, we prove that $\mathcal {C}$ is actually the maximum number of hyperedges that can be augmented to $\textbf{G}$ while conserving all core numbers.

Indeed, assume that a feasible augmentation method F augments $I_k$ hyperedges, anchored at the nodes having core number k, for each $k=k_0,...,N_{\textbf{G}}^{*}$, without changing any core numbers of the nodes in $\textbf{G}$. The total anchor availability realized by F is $I = \sum _{k=1}^{N_{\textbf{G}}^{*}}I_k$. According to Lemma 5, $I_k \le T_k$, so: $I = \sum _{k=k_0}^{D}I_k \le \sum _{k=k_0}^{N_{\textbf{G}}^{*}}T_k = \mathcal {C}$. In other words, the total number of hyperedges augmented by F is $\le \mathcal {C}$.

Thus, the total anchor availabilities $\mathcal {C}$ found by COREA is the maximum number of hyperedges that any feasible augmentation method can add to $\textbf{G}$, subject to the constraint of preserving all core numbers. Theorem 2 states that $\mathcal {C}$ is always constant with respect to $\textbf{G}$, indicating that $\mathcal {C}$ is the maximum number $\mathcal {M}$ of hyperedges that can be augmented to $\textbf{G}$ while conserving all core numbers, and $\mathcal {M}=\mathcal {C}$.

1.4 E4: Time complexity of COREA

Theorem 4

(Time Complexity of COREA) Given the hypergraph $\textbf{G}=(\textbf{V}, \textbf{E})$ with maximum hyperedge cardinality m, the budget B, the total number of anchor availabilities $\mathcal {C}$ of all nodes (constant with respect to each dataset), and the batch size c by which COREA augments c hyperedges at a time in Step 2, the time complexity of COREA is $\mathcal {O}\left[ |\textbf{V}|\text {log}|\textbf{V}|+ \mathcal {C}m \log |\textbf{V}|+ (|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ \mathcal {C}m^2)\frac{b}{c}\right]$, where $b = \text {min}\{B, \mathcal {C}\}$.

Proof

As described in Sect. 5.1, computing the core influences of all nodes requires initializing the value 1 for each node and iterating through each node in each hyperedge once, so the time complexity of computing core influences is $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |)$.

Step 1–1 of COREA, presented in Algorithm 1, undertakes the core decomposition process and computes the anchor availability of each node. The core decomposition process requires iterating through each node v for its removal and each hyperedge e for its removal and updating the degrees of its constituent nodes. The total time complexity for these operations is $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |)$. Computing the anchor availability of each node v, $N_{\textbf{G}}(v) = k$, requires some primitive operations (subtracting the degree immediately prior to the removal from k), so the time complexity of removing nodes, along with their incident hyperedges, and computing anchor availabilities for all nodes is $\mathcal {O}(|\textbf{V}|)$, which is dominated by $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |)$.

If the tie-breaking scheme $\textsf{T}$ is being proportional to $\mathcal{C}\mathcal{S}_{\textbf{G}}/\mathcal{C}\mathcal{I}_{\textbf{G}}$ (or $1/\mathcal{C}\mathcal{I}_{\textbf{G}}$), the core strength and core influence of each node v can be computed when v becomes qualified for removal in the core decomposition process. The reason is that the core influences of all the nodes in the k-core can be computed by the time Algorithm 2 completes finding the $(k-1)$-core (the core influence of v only depends on the hyperedges incident to v having lower core numbers than that of v). Also, when a node v becomes qualified for removal in Algorithm 2, its core strength can be updated with constant time (based on its degree at the beginning of the k-core and its core number, which is determined to be k at this point already). Therefore, computing core strengths and core influences of all nodes for the scheme $\textsf{T}$ does not affect the time complexity. For each $k=k_0,...,N_{\textbf{G}}^{*}$, with $k_0$ as the minimum core number of a node in $\textbf{G}$, denote $N_k$ as the number of nodes in $\textbf{G}$ that have core number k. For each k, in the pruning process of obtaining the $(k+1)$-core from the k-core, at each step, among the nodes in $\mathbb{T}\mathbb{D}$ (Line 5 in Algorithm 2) that are the nodes qualified for removal, the tie-breaking scheme $\textsf{T}$ needs to conduct weighted sampling to select a node to delete first. For each node v among $N_k$ nodes of core number k, according to Vitter (1987), adding v to $\mathbb{T}\mathbb{D}$ takes $\mathcal {O}(1)$ time, sampling v from $\mathbb{T}\mathbb{D}$ takes $\mathcal {O}(\text {log}|\mathbb{T}\mathbb{D}|)$ time, and removing v after sampling from $\mathbb{T}\mathbb{D}$ takes $\mathcal {O}(\text {log}|\mathbb{T}\mathbb{D}|)$ time. Since $|\mathbb{T}\mathbb{D}|\le N_k$, the total time complexity the tie-breaking scheme $\textsf{T}$ to decide the order of nodes to delete in the k-core is $\mathcal {O}(N_k \text {log}N_k)$. Therefore, the total time complexity for $\textsf{T}$ to decide the deletion order $\mathbb {O}$ for $\textbf{G}$ is $\sum _{k=k_0}^{N_{\textbf{G}}^{*}}\mathcal {O}(N_k \text {log}N_k)$. We have: $\sum _{k=k_0}^{N_{\textbf{G}}^{*}}N_k \log N_k \le \sum _{k=k_0}^{N_{\textbf{G}}^{*}}N_k \log |\textbf{V}|= |\textbf{V}|\log |\textbf{V}|$. Therefore, $\sum _{k=k_0}^{N_{\textbf{G}}^{*}}\mathcal {O}(N_k \text {log}N_k) = \mathcal {O}(|\textbf{V}|\text {log}|\textbf{V}|)$.

As a result, the total time complexity of Step 1–1 of COREA is $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |) + \mathcal {O}(|\textbf{V}|\text {log}|\textbf{V}|) = \mathcal {O}(|\textbf{V}|\text {log}|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |)$.

In Step 1-2 of COREA, for each node v, we need to construct c(v) hyperedges anchored at v. For each hyperedge e among those c(v) hyperedges, this requires sampling a hyperedge size (constant time) and sampling other nodes from $\mathbb {O}[i+1:]$ (as shown in Line 11 of Algorithm 1). For the sampling scheme $\textsf{S}$ described in Sect. 6.2.2, the sampling step of other nodes to fill up e takes $\mathcal {O}(m\log |\textbf{V}|)$ time, according to Vitter (1987). Therefore, the total time complexity of Step 1-2 is $\mathcal {O}(\sum _{v \in \textbf{V}}c(v)m\log |\textbf{V}|) = \mathcal {O}(\mathcal {C}m \log |\textbf{V}|)$.

In Step 2, we go through b/c iterations, and in each iteration, we add c hyperedges to $\textbf{G}_{\text {cur}}$. At each iteration, before choosing the hyperedges to augment to $\textbf{G}_{\text {cur}}$, for each candidate hyperedge e in the pool P, COREA needs to evaluate how much augmenting e improves the term $f(\textbf{G}_{\text {cur}}) = \sum _{v \in \textbf{V}}\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(v)\mathcal{C}\mathcal{S}_{\textbf{G}_{\text {cur}}}(v)$, with $\textbf{G}_{\text {cur}}$ as the current hypergraph snapshot. To do this, we maintain a measurement g(v) for each node v, quantifying how much $f(\textbf{G}_{\text {cur}})$ increases if $\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(v)$ is incremented by 1 unit. Particularly, if $\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(v)$ increases by 1 unit, $f(\textbf{G}_{\text {cur}})$ increases by g(v). In order to achieve this, we reverse the process of calculating all core influences. In the formula of core influence in Sect. 5.1, suppose $\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(v) = 1 + \sum _{e \in \textbf{E}_{\textbf{G}_{\text {cur}}}^<(v)}(1 + \frac{\Delta }{N_{\textbf{G}_{\text {cur}}}(v) - 1})\left[ (1 - \frac{\mathcal{C}\mathcal{S}_{\textbf{G}_{\text {cur}}}(t)-1}{|\textbf{E}_{\textbf{G}_{\text {cur}}}^=(t) |})\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(t)\right]$, for each $e \in \textbf{E}_{\textbf{G}_{\text {cur}}}^<(v)$, if $\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(t)$ increases by 1 unit, $\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(v)$ increases by $(1 + \frac{\Delta }{N_{\textbf{G}_{\text {cur}}}(v) - 1})\left[ (1 - \frac{\mathcal{C}\mathcal{S}_{\textbf{G}_{\text {cur}}}(t)-1}{|\textbf{E}_{\textbf{G}_{\text {cur}}}^=(t) |})\right]$ units. As a result, g(t) needs to increase by $(1 + \frac{\Delta }{N_{\textbf{G}_{\text {cur}}}(v) - 1})\left[ (1 - \frac{\mathcal{C}\mathcal{S}_{\textbf{G}_{\text {cur}}}(t)-1}{|\textbf{E}_{\textbf{G}_{\text {cur}}}^=(t) |})\right] g(v)$ units. To compute such value g(v) for each node v, we first initialize $g(v) = \mathcal{C}\mathcal{S}_{\textbf{G}_{\text {cur}}}(v)$, start from the nodes with the highest core number, update the values g(.) until reaching the nodes with the lowest core number. The whole process requires iterating through each node once and each node in each hyperedge once, accounting for the total time complexity of $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}_{\text {cur}}}|e |)$.

Once the values g(.) are up-to-date, for each candidate hyperedge e anchored at $\{v_1,...,v_a\}$, and the other nodes in e that are not anchors of e are $\{u_1,...,u_b\}$. Suppose adding e increases the core influences of $u_1,...,u_b$ by $\beta _1,...,\beta _b$, respectively, which can be calculated in $\mathcal {O}(|e |^2)$ time that is upper-bounded by $\mathcal {O}(m^2)$. The contribution of e into $f(\textbf{G}_{\text {cur}})$ if augmented is then: $\sum _{i=1}^{a}\mathcal{C}\mathcal{I}_{\textbf{G}_{\text {cur}}}(v_i) + \sum _{j=1}^{b}\beta _j \times g(u_j)$, which can be calculated in $\mathcal {O}(m)$ time. Assume that we are at iteration t, for $t=1,...,b/c$, when $(t-1)c$ candidate hyperedges have been added to $\textbf{G}$, there are $\mathcal {C} - (t-1)c$ hyperedges remaining in P. The time complexity of calculating the scores for the candidate hyperedges and choosing c hyperedges with the highest scores is then $\mathcal {O}([\mathcal {C} - (t-1)c]m^2)$.

At each iteration t, for $t=1,...,b/c$, of Step 2, after calculating the g(.) values and the score of each candidate hyperedge in P, we add c candidate hyperedges with the highest scores to the hypergraph. Once we augment c more hyperedges into $\textbf{G}_{\text {cur}}$, we need to update all core strengths, core influences, and the values g(.), whose complexity is $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}_{\text {cur}}}|e |)$.

At each iteration t, since tc hyperedges have been added to $\textbf{G}$, $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}_{\text {cur}}}|e |)=\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ tcm)$ holds. Thus, the total time complexity of iteration t, for $t=1,...,b/c$, of Step 2 is: $\mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ tcm)+\mathcal {O}([\mathcal {C} - (t-1)c]m^2) + \mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ tcm) = \mathcal {O}(|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ [\mathcal {C} - (t-1)c]m^2 + tcm)$.

Summing over all iterations $t=1,...,b/c$, the total time complexity of Step 2 of COREA is: $\sum _{t=1}^{b/c}\mathcal {O}\left[ |\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ [\mathcal {C} - (t-1)c]m^2 + tcm \right] = \mathcal {O}\left[ (|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ \mathcal {C}m^2)\frac{b}{c}\right]$.

Summing up the time complexities of Steps 1-1, 1-2, and 2, the total time complexity of COREA is $\mathcal {O}\left[ |\textbf{V}|\text {log}|\textbf{V}|+ \mathcal {C}m \log |\textbf{V}|+ (|\textbf{V}|+ \sum _{e \in \textbf{E}}|e |+ \mathcal {C}m^2)\frac{b}{c}\right]$.

1.5 E5: Maximum anchor availability of a node

In this section, we discuss the cases when COREA cannot guarantee to afford maximum anchor availabilities for all nodes and the sufficient conditions to achieve the maximum anchor availability of a particular node v. While Theorem 2 shows that the sum of anchor availabilities of all nodes, realized by COREA, is always constant with respect to $\textbf{G}$, different deletion orders in Step 1 of COREA, governed by the tie-breaking scheme $\textsf{T}$ in Line 6 of Algorithm 2, may result in different anchor availabilities for each node.

In the pruning process of obtaining the $(k+1)$-core form the k-core, at any point, there might be several nodes qualified for removal, i.e., they all have degrees $\le k$. We first show that, deferring the removal of v, while choosing another node to delete first, potentially helps afford a higher anchor availability for v, as stated in Lemma 6.

Lemma 6

In the pruning process of obtaining the $(k+1)$-core from the k-core, assume that both u and v are up for removal, and a valid deletion order $\mathbb {O}$ chooses to remove v immediately before u. If we obtain a valid deletion order $\mathbb {O}'$ by switching the positions of nodes v and u in $\mathbb {O}$, the anchor availability realized by COREA for v remains the same or increases.

Proof

Assume that by the ordering of $\mathbb {O}$, immediately prior to the deletion of v, the degrees of u and v are d(u) and d(v), respectively, with $d(u), d(v) \le k$. Also assume that there remain $t(\{u,v\}) \ge 0$ hyperedges anchored by both u and v. In $\mathbb {O}$, we remove v then u and the deletion of v will remove all of its incident hyperedges, along with those $t(\{u,v\})$ hyperedges anchored by u and v, so the respective degrees of v and u immediately prior to removals are d(v) and $d(u) - t(\{u,v\})$. As a result, COREA realizes the respective anchor availabilities for v and u as $c(v) = k - d(v)$ and $c(u) = k - d(u) + t(\{u,v\})$, respectively.

Switching the positions of v and u in $\mathbb {O}$, we obtain another valid deletion order $\mathbb {O}'$. In $\mathbb {O}'$, the deletion of u will remove all of its incident hyperedges, along with those $t(\{u,v\})$ hyperedges anchored by u and v, so the respective degrees prior to removals of u and v are d(u) and $d(v) - t(\{u,v\})$. As a result, the afforded anchor availabilities of u and v become $c'(u) = k - d_{\textbf{G}}(u)$ and $c'(v) = k - d(v) + t(\{u,v\})$.

As $t(\{u,v\}) \ge 0$, $c'(v) \ge c(v)$. Therefore, if we switch the positions of nodes v and u to obtain another valid deletion order, the anchor availability realized by COREA for v remains the same or increases.

In the proof for Lemma 6, in the case that $t(\{u,v\}) > 0$, if we swap from a valid deletion order, deleting v first then deleting u, to obtain another valid deletion order, deleting u first then deleting v, the anchor availability for u decreases and that of v increases. Since COREA needs to remove one node at a time, it is clear that if u is deleted before v, u is certainly not afforded its maximum anchor availability, and the same holds for v in the case when v is removed before u. Therefore, if there are several nodes up for deletion and there are hyperedges co-anchored by them, those nodes cannot be afforded their respective maximum anchor availabilities simultaneously.

Lemma 7

In the pruning process of obtaining the $(k+1)$-core from the k-core, in 2 different valid deletion orders $\mathbb {O}$ and $\mathbb {O}'$ where the removal of node v is deferred until a point when v is the only node up for removal, the anchor availabilities of v realized by Algorithm 2 in both $\mathbb {O}$ and $\mathbb {O}'$ are the same.

Proof

For each $x \in \textbf{V}$ and $N_{\textbf{G}}(x)=k$, refer to the degree of x at the beginning of the pruning process to obtain the $(k+1)$-core from the k-core, when no nodes of core number k have been deleted, as the core degree of x, denoted as d(x). Denote $S_{\mathbb {O}}(x)$ and $S_{\mathbb {O}'}(x)$ as the sets of nodes that have core number k and get removed before x in $\mathbb {O}$ and $\mathbb {O}'$, respectively.

We first show that in both $\mathbb {O}$ and $\mathbb {O}'$, the sets of nodes deleted before v, denoted as $S_{\mathbb {O}}(v)$ and $S_{\mathbb {O}'}(v)$ respectively, are the same.

If $S_{\mathbb {O}}(v) = \emptyset$, starting at the k-core, $\mathbb {O}$ has to begin with v in the pruning process of obtaining the $(k+1)$-core from the k-core. It implies that among the nodes of core number k, v is the only node whose core degree is equal to k. As a result, in $\mathbb {O}'$, v also has to be the first node of core number k to delete, i.e., $S_{\mathbb {O}'}(v) = \emptyset$. Therefore, $S_{\mathbb {O}}(v) = S_{\mathbb {O}'}(v)$. A similar argument is made for the case in which $S_{\mathbb {O}'}(v) = \emptyset$.

Assume the case that both $S_{\mathbb {O}}(v)$ and $S_{\mathbb {O}'}(v)$ are non-empty sets. Note that starting at the k-core, both $\mathbb {O}$ and $\mathbb {O}'$ need to begin with a node, other than v, whose core degree is exactly equal to k. Furthermore, all of the nodes, of core number k and other than v, whose core degrees are exactly equal to k must belong to both $S_{\mathbb {O}}(v)$ and $S_{\mathbb {O}'}(v)$ as these nodes are always qualified for removal at the beginning of the pruning process. It implies that $S_{\mathbb {O}}(v) \cap S_{\mathbb {O}'}(v) \ne \emptyset$.

Assume by contradiction that there exists $u \in S_{\mathbb {O}}(v)$ such that $u \notin S_{\mathbb {O}'}(v)$. In other words, in $\mathbb {O}'$, u is deleted after v, so $d(u) > k$. For u to be deleted before v in $\mathbb {O}$, the necessary and sufficient condition is that the removals of the nodes in $S_{\mathbb {O}}(u)$, along with their incident hyperedges, result in the degree of u dropping lower than $k+1$. We have $S_{\mathbb {O}}(u) \subset S_{\mathbb {O}}(v)$. In $\mathbb {O}'$, as we defer removing v to the point when v is the only node up for removal and u is deleted after v, the degree of u never drops lower than $k+1$ before v is removed. If all nodes in $S_{\mathbb {O}}(u)$ are also in $S_{\mathbb {O}'}(v)$, u can be qualified for removal before v is removed in $\mathbb {O}'$. Therefore, $\exists t \in S_{\mathbb {O}}(u)$ and $t \notin S_{\mathbb {O}'}(v)$, which also implies that $t \in S_{\mathbb {O}}(v)$ and $d(t)>k$. t is removed before u in $\mathbb {O}$, $t \ne u, t \in S_{\mathbb {O}}(v)$, and $t \notin S_{\mathbb {O}'}(v)$. We now repeat the argument for u on t to derive that $\exists y \in S_{\mathbb {O}}(v)$, y is removed before t in $\mathbb {O}$, $d(y)>k$, $y \ne u, y \ne t$, and $y \notin S_{\mathbb {O}'}(v)$. Applying the same argument on y and so on, we can repeat it infinitely many times. However, that is impossible because $S_{\mathbb {O}}(v)$ has a finite number of elements. Therefore, the assumption that $u \notin S_{\mathbb {O}'}(v)$ is false, i.e., $u \in S_{\mathbb {O}'}(v)$.

Thus $S_{\mathbb {O}}(v) \subseteq S_{\mathbb {O}'}(v)$. Similarly, we can also show $S_{\mathbb {O}'}(v) \subseteq S_{\mathbb {O}}(v)$. It implies that $S_{\mathbb {O}}(v) = S_{\mathbb {O}'}(v)$

According to Lemma 4, even though the orders of the nodes preceding v are different in $\mathbb {O}$ and $\mathbb {O}'$, since they are the same set of nodes, the anchor availabilities of v in both $\mathbb {O}$ and $\mathbb {O}'$, are the same.

Theorem 5

5 [Maximum anchor availability of a node] If the tie-breaking scheme $\textsf{T}$ in Algorithm 2 always defers the removal of node v, $N_{\textbf{G}}(v)=k$, until the point when v is the only node qualified for removal during the pruning process to obtain the $(k+1)$-core, COREA achieves the maximum anchor availability $c^*(v)$ for v. For all tie-breaking schemes, the anchor availability c(v) realized for v, in Algorithm 2, is always $\le c^*(v)$.

Proof

Denote $S_1$ as a valid deletion order resulting from a tie-breaking scheme $\textsf{T}$ that always defers the removal of v, $N_{\textbf{G}}(v) = k$, in the core decomposition process until the point when v is the only node qualified for removal.

According to lemma 7, in all valid deletion orders that defer removing v to the point when v is the only node qualified for removal, the anchor availability realized for v by COREA is always the same, and equal to $c_{S_1}(v)$, the anchor availability realized by following $S_1$. If there exists a valid deletion order $\mathbb {O}_0$ such that when v and at least another node are qualified for removal, v is chosen to be deleted first and afforded anchor availability $c_{\mathbb {O}_o}(v)$, we can always form another valid deletion order by deferring the removal of v and deleting the other node first until v is the only node qualified for removal. According to Lemma 6, each time we do so, the new anchor availability for v is higher than or equal to the previous value, so $c_{\mathbb {O}_o}(v) \le c_{S_1}(v)$. Therefore, $c_{S_1}(v)$ is the maximum anchor availability for v that can be realized by COREA in any valid deletion order.

Thus, if the tie-breaking scheme $\textsf{T}$ in Algorithm 2 always defers the removal of v until the point when v is the only node qualified for removal, COREA achieves the maximum anchor availability for $c^*(v)$ for v.

Given a particular valid deletion order $\mathbb {O}$ of nodes in the core decomposition, governed by the tie-breaking scheme $\textsf{T}$, the anchor availability for each node is either the maximum possible or sub-optimal. While not guaranteeing to afford the maximum anchor availabilities for all nodes, in Theorem 5, we provide sufficient conditions to achieve the maximum anchor availability for a particular node v. That is, in the core decomposition process, COREA needs to always defer the deletion of v until the point when v is the only node qualified for removal.

However, as previously mentioned, it is important to note that, regardless of whether the availability for each node is sub-optimal, the sum $\mathcal {C}$ of all anchor availabilities realized by COREA is always constant with respect to each hypergraph (Theorem 2) and equal to the maximum number of hyperedges any method can augment to the hypergraph without altering any core numbers (Theorem 3). Therefore, given the constraint of preserving all core numbers, no feasible augmentation method can augment more than $\mathcal {C}$ hyperedges.