1 Introduction

As a difference with well-studied Newtonian fluids, the rheological behaviour of complex fluids is often non-Newtonian and, with stresses no longer proportional to the instantaneous value of the shear rate, remarkable new physics emerge (Morrison 2001). Well-studied examples of complex fluids include polymers solutions (Doi and Edwards 1988), polymer melts (Larson 1988), colloidal suspensions (Gast and Russel 1998), gels (Larson 1999) and liquid crystals (Prost 1995). The mathematical modelling of the behaviour of complex fluids involves the combination of kinetic theory describing the microscopic thermodynamics of individual constituents in the solvent (Bird et al. 1987; Larson 1999) along with the new fluid mechanics which results from it (Bird 1976; Bird et al. 1987; Tanner 1988; Bird and Wiest 1995).

After many years of research on the physics of complex fluids, recent efforts have focused on their impact in biological systems and in particular on the locomotion of small organisms (Spagnolie 2015). For example, spermatozoa have to swim in cervical mucus, a complex fluid with a relaxation time on the order of seconds (Katz and Berger 1980), much larger than the typical oscillation time scale of a spermatozoon and its flagellum (Gaffney et al. 2011). As a result, the flagellar waveforms of spermatozoa are impacted by non-Newtonian stresses and they differ significantly from those observed in Newtonian fluids (Ishijima et al. 1986). Theoretical efforts in the context of elastic fluids have allowed to compute leading-order hydrodynamic forces on beating flagella (Fulford et al. 1998), their impact on the beating waveforms (Fu et al. 2008) and on cell locomotion (Lauga 2007; Fu et al. 2009; Teran et al. 2010). Later work showed that the coupling between the flexibility of the swimmer and the stresses in the fluid could lead to both hindered and enhanced locomotion (Riley and Lauga 2014; Thomases and Guy 2014). Collective effects are also affected and interactions of spermatozoa in mucus lead to long-lived clusters (Tung et al. 2017). Even in the absence of elastic stresses, shear-thinning rheology impacts waving locomotion (Vélez-Cordero and Lauga 2013).

Although spermatozoa have received the biggest share of research, other small swimming organisms have been shown to be affected by complex fluids. Nematodes (Shen and Arratia 2011; Gagnon et al. 2013), algae (Qin et al. 2015) and bacteria (Patteson et al. 2015; Liu et al. 2011; Spagnolie et al. 2013) exhibit a different behaviour when swimming in polymeric fluids. Some changes in the swimming motion can be in part explained by the ability of the cells to push against the microstructure (Berg and Turner 1979; Magariyama and Kudo 2002; Leshansky 2009) and by the presence of length scales in the fluid comparable to, or larger than, the cell size (Martinez et al. 2014). A boost in locomotion is also possible due to polymer depletion near the swimmer and resulting apparent fluid slip (Man and Lauga 2015; Zöttl and Yeomans 2017). A commonly used model for microorganism locomotion is the spherical squirmer (Zhu et al. 2011) whose swimming has been shown to be significantly affected by viscoelasticity (Zhu et al. 2012; De Corato et al. 2015). More broadly, suspensions of swimmers behave as complex fluids themselves as shown experimentally for bacteria (Sokolov and Aranson 2009; Ryan et al. 2011) and algae (Rafai et al. 2010; Mussler et al. 2013), and rationalised theoretically (Hatwalne et al. 2004; Saintillan 2018).

Beyond their impact on the biological world, complex fluids also affect artificial swimmers. Flexible filaments oscillated externally using magnetic fluids can swim faster in Boger fluids (Espinosa-Garcia et al. 2013) in a manner which depends on the kinematics of their deformation (Godinez et al. 2015). More importantly, the nonlinearities offered by non-Newtonian flows can be exploited to induce novel propulsion modes and design new types of swimmers (Lauga 2014). Rigid helices rotated externally and unable to move in water can swim efficiently in a gel (Schamel et al. 2014). The time-reversibility constraints of Stoke flows can be bypassed and shear-dependent viscosity used to generate net forces from time-reversible forcing (Qiu et al. 2014). Propulsive forces can also result from the secondary flows induced by non-Newtonian normal stress differences (Normand and Lauga 2008; Pak et al. 2010, 2012; Keim et al. 2012). Secondary flows have been long recognized as an important feature of viscoelatic flows (Bird et al. 1987); however, they have only been studied for a few canonical cases.

In this work we report on experiments demonstrating the use of normal stress differences for propulsion following the theoretical proposal of Pak et al. (2012). We use rigid dumbbells rotated by an external magnetic field along their axis of symmetry in a Boger fluid. By symmetry, no motion is induced for symmetric dumbbells but when the shape of the dumbbell is asymmetric (snowman geometry), non-Newtonian normal stress differences lead to net propulsion. The use of a simple model allows to rationalise the experimental results and to predict the dependence of the snowman swimming speed as a function of the size ratio between the two spheres (Pak et al. 2012). Note that a similar configuration was studied in Rogowski et al. (2018); however, in their case, the dumbbell was composed of two equal-sized spheres and the propulsion resulted from heterogeneities of the media.

The paper is organised as follows. In Sect. 2 we introduce the experimental setup, the dumbbells used for the locomotion, and characterise the rheological properties of the fluids used. We present our experimental results in Sect. 3 and compared them with the model of Pak et al. (2012) in Sect. 4. A conclusion and perspectives are offered in Sect. 5.

Fig. 1
figure 1

Schematic view of the configuration studied experimentally. A neutrally buoyant dumbbell made up of two attached spherical particles of diameters \(D_{\text {L}}\) and \(D_{\text {S}}\le D_{\text {L}}\) is rotated with angular velocity \(\omega\) along its symmetry axis in a viscoelastic fluid

Full size image

2 Experimental setup and test fluids

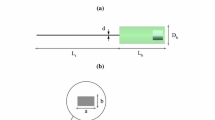
Following the theoretical proposal put forward by Pak et al. (2012), we conduct experiments consisting in rotating a neutrally buoyant sphere–sphere magnetic dumbbell immersed in a viscoelastic fluid. The experiment is schematically represented in Fig. 1. The large sphere in the dumbbell has diameter \(D_{\text {L}}\) and the smaller one \(D_{\text {S}}\) and the whole dumbbell rotates with angular velocity \(\omega\) along its symmetry axis.

We use the magnetic setup developed in Godinez et al. (2012), which is a device capable of producing a magnetic field of uniform strength 6 mT and rotated mechanically. The dumbbells were placed inside a rectangular tank (\(160 \, {\text {mm}} \times 100\,{\text {mm}} \times 100\,{\text {mm}}\)) that fit into the region of uniform magnetic field inside the coils of approximately \((100 \, {\text {mm}})^3\) in size where the test fluids were contained. In this configuration, the ratio of the large sphere to the containing walls was 0.09; the wall effects are therefore small but finite.

The spheres in the dumbbells were made out of plastic and we inserted inside them a permanent magnet (Magcraft, models NSN0658). In all cases, the angular frequency of the rotating coils was below the step-out frequency (Godinez et al. 2012) and the dumbbells rotate at the same rate as the external magnetic field. The swimmers were nearly neutrally buoyant; the effective density was adjusted by filling up the cavity (where the permanent magnet was inserted) with small amounts of the test liquid.

To achieve locomotion in the viscoelastic fluid, the sphere–sphere arrangement had to be made of spheres with unequal sizes (snowman configuration). Five dumbbells were considered, varying the diameter ratio \(D^*=D_{\text {S}}/D_{\text {L}}\) from 0 to 1. The dimensions for each dumbbell are shown in Table 1. The motion of the dumbbell was filmed and its position was tracked in time.

Table 1 Sizes of the spheres in the five dumbbells used in this investigation (colour figure online)
Full size table
Fig. 2
figure 2

Circles: shear viscosity (in Pa s) as a function of shear rate (1/s) for the Boger (B, black circle) and Newtonian (N, \(\circ\)) liquids. The dashed dotted line shows a fit to a power-law viscosity fit with \(m=0.97 \, {{\text {Pa s}}}^n\) and \(n=0.94\), (Eq. 1) for \({\dot{\gamma }}<20 \, {\text {s}}^{-1}\). Squares: first normal stress difference, \(N_1\), (blue square), as a function of shear rate. The dashed blue line shows the fit to an Oldroyd-B model (Eq. 2). The two vertical lines show the window of shear rates within which the experiments were conducted (\(5.5 \, {\text {s}}^{-1} <\omega <31.0 \, {\text {s}}^{-1}\)) (colour figure online)

Full size image

Two types of fluids were fabricated, tested and used. One was Newtonian (N) and used as a reference fluid while the other was a Boger-type fluid (B) with a nearly constant shear viscosity and viscoelastic properties (Boger 1977). The B fluid was fabricated by dissolving polyacrylamide (PAA, molecular weight \(5 \times 10 ^{6} \, {\text {g/mol}}\)) in non-ionic water at a slow mixing rate for 24 h. Afterwards, the solution was added to glucose and slowly mixed for four days. The proportions (by weight) of the mixture were 84.9% glucose, 15% water and 0.1% PAA. The liquid was left in repose for 2 weeks previous to testing.

The rheological properties were determined in an Anton Paar rheometer (stress controlled and cone-plate geometry). All physical and rheological properties of both fluids are summarised in Table 2. Steady shear tests were conducted, within the range of shear rates within \(1\, {\text {s}}^{-1}< {{\dot{\gamma }}} < 100 \, {\text {s}}^{-1}\), to determine the shear viscosity and the first normal stress difference. All tests were conducted at \(T=23\,^\circ {\text {C}}\). The results of the rheological tests are shown in Fig. 2 (filled symbols). After the shear viscosity of the B fluid was determined, the N fluid was prepared by adding water to glucose until the viscosity was matched to that of the B fluid. The N fluid was left standing for 24 h prior to testing. The shear viscosity of the N fluid is also shown in Fig. 2 (empty circles).

The viscosity measurements show that the B fluid has a nearly constant viscosity, \(\eta\), for shear rates \({{\dot{\gamma }}} < 30 \, {\text {s}}^{-1}\). Fitting the data to a power-law model as

$$\begin{aligned} \eta =m {{{\dot{\gamma }}}}^{n-1}, \end{aligned}$$
(1)

leads to \(m=0.97 \, {{\text {Pa s}}}^n\) and \(n=0.94\). Hence, shear-tinning effects are almost negligible. At higher shear rates, the fluid displayed a slight shear-thickening behaviour. The range of shear rates attainable during the experiments (shown by the two vertical lines in the figure) is within the nearly-constant viscosity region.

Table 2 Physical and rheological properties of the fluids used in this investigation
Full size table

To characterise the viscoelastic nature of the B fluid, we fitted the measurement of the first normal stress difference, \(N_1\), to an Oldroyd-B model as (Oldroyd 1950)

$$\begin{aligned} N_1=2\eta _{\text {o}} (1-\beta ) \lambda {{{\dot{\gamma }}}}^2, \end{aligned}$$
(2)

where \(\eta _{\text {o}}=\eta _{\text {p}}+\eta _{\text {s}}\) is the total viscosity (where \(\eta _{\text {p}}\) and \(\eta _{\text {s}}\) are the polymer and solvent viscosities, respectively), \(\beta =\eta _{\text {s}}/\eta _{\text {o}}\) is the ratio of solvent-to-total viscosities and \(\lambda\) is the relaxation time. Since the rheological measurements agreed well with the \({{{\dot{\gamma }}}}^2\)-dependence of \(N_1\), we estimate the relaxation time, \(\lambda\), from fitting the data to Eq. (2). We obtain \(\lambda \approx 0.5102 \, {\text {s}}\) with \(\eta _{\text {o}}\approx 0.84 \, {\text {Pa s}}\), \(\eta _{\text {s}}\approx 0.19 \, {\text {Pa s}}\) and \(\beta \approx 0.2252\). The resulting fit is shown in Fig. 2. With the determination of the relaxation we can define the Deborah number \({\rm De}\) as

$$\begin{aligned} {\rm De}=\omega \lambda , \end{aligned}$$
(3)

where \(\omega\) is the rotational speed of the swimmer. For the experiments reported here the maximum \({\rm De}\) number was 15. The Reynolds number, defined as

$$\begin{aligned} {\rm Re}=\frac{UD_{\text {L}}\rho }{\eta _{\text {o}}}, \end{aligned}$$
(4)

had a maximum value of 0.11. For this range of values of Re and \({\rm De}\) we can assert that the elastic effects dominate, \({\rm De}/{\rm Re}>5\). Note that, since the flow is induced by rotation, a rotational Reynolds number can also be considered

$$\begin{aligned} {{\rm Re}_\omega }=\frac{\omega D_{\text {L}}^2\rho }{\eta _{\text {o}}}. \end{aligned}$$
(5)

For the range of parameters tested in this study, \({{\rm Re}}_\omega <4.5\), for which the inertial forces are no longer negligible. However, the ratio \({\rm De}/{{\rm Re}}_\omega =3.5\) (independent of \(\omega\)) which indicates that the elastic effects remain dominant. For the case of particles in a viscoelastic fluid, flowing a tube, work in Trofa et al. (2015) and Del Guidice et al. (2015) has shown that for \({\rm De}/{{\rm Re}}>1\) the flow is dominated by elastic effects even with finite inertia. Since this is the limit we are in, the results we obtain are primarily due to fluid elasticity.

Fig. 3
figure 3

Swimming speed of dumbbells, U (mm/s), as a function angular velocity, \(\omega\) (1/s). The different symbols for each experiment correspond to the symbol shapes shown in Table 1. Empty and filled symbols correspond to the data for the Newtonian fluid (N) and Boger viscoelastic fluid (B), respectively

Full size image

3 Experimental results

The velocities of the dumbbells were measured in both fluids for the range of rotational speeds indicated above. The results are shown in Fig. 3 with empty symbols used for the data in the Newtonian fluid (N) and the solid symbols for the Boger viscoelastic fluid (B). First, we tested the limiting case \(D^*=0\), corresponding to the limit where the dumbbell is in fact a single sphere. By symmetry a single rotating sphere is not expected to swim in either fluid, as confirmed experimentally (circular symbols). Similarly, the dumbbell with \(D^*=1\) (formed by two equal spheres) should not self-propel in any fluid because, again, it is symmetric. This is also confirmed by our measurements (square symbols)

For the other three dumbbells in a snowman configuration (\(D^*= 0.27\), 0.64 and 0.82), the swimming speed was confirmed to be zero for the case of the Newtonian fluid, as shown in Fig. 3 (empty symbols). The absence of swimming is a result of the time-reversibility of the Stokes equations and the small experimental deviations from zero in the figure result from uncertainties in our measurements.

The most important result, which confirms the fundamental idea of this paper, is the non-zero swimming speed measured for case of dumbbells in an asymmetric snowman configuration when immersed in the Boger fluid. In the three cases, the swimming speed is found to monotonically increase with the angular velocity (Fig. 3, filled symbols). The direction of motion is always in the direction from the largest to the smaller sphere, as expected from the difference in viscoelastic force between large and small spheres explained below. We next plot in Fig. 4 the normalized swimming speed, \(U^*=2U/(\omega D_{\text {L}})\), as a function of the Deborah number, \({\rm De}\) (for clarity we only display the case for \(D^*= 0.64\), the others being similar). This dimensionless swimming speed increases with Deborah number, reaches a maximum value after which it decreases, in qualitative agreement with Pak et al. (2012). It is notable that the swimming speeds in both the experiments and the model have (described below in Sect. 4) a maximum for a certain value of the Deborah number, despite the fact that the model is expected to be valid only for small De. We also note that for small values of De  the swimming speed increases linearly with De, in agreement with the analytical calculation in Pak et al. (2012). The dashed line in the plot shows the trend \(U^* \sim {\rm De}\), showing the good agreement.

Fig. 4
figure 4

Normalized swimming speed, \(2U/(\omega D_{\text {L}})\), as a function of Deborah number, \({\rm De}\). For clarity, we display only the results for the size ratio \(D^*= 0.64\). Filled and empty symbols show the normalized swimming speed for the Boger (N) and Newtonian (N) fluids, respectively. The dashed line in the plot shows the trend \(U^* \sim {\rm De}\), proposed by Pak et al. (2012)

Full size image

As was demonstrated by Pak et al. (2012), the swimming speed of snowmen is maximized for a specific ratio of sphere sizes (\(D^*\approx 0.5\) in that work). The existence of an optimum is a simple consequence of the fact that no swimming is obtained in the limits \(D^*= 0\) or 1 and therefore maximum swimming is obtained at some intermediate value of \(D^*\). To demonstrate the existence of an optimal size ratio in our experiments, we plot in Fig. 5 our results of the normalized swimming speed as a function of size ratio, \(D^*\), for the value \({\rm De}=10\) at which the speed was maximum. Although only five data points are available, the existence of an optimal size ratio is clear. Among our experiments, the snowman with \(D^*=0.64\) has the largest dimensionless speed.

Fig. 5
figure 5

Normalized swimming speed, \(2U/(\omega D_{\text {L}})\), as a function of size ratio, \(D^*\), for Deborah number \({\rm De}=10\). Error bars are ± one standard deviation and symbols refer to the swimmer geometries in Table 1. The solid lines shows the analytical model from Pak et al. (2012) with no fitting parameters (Eq. 6 below, which is Eq. 51 in their original study). The dashed line shows the same theoretical prediction but for a value of \({\rm De}=1\) below which the analytical model would normally be expected to be valid

Full size image

4 Modelling

In their original paper, Pak et al. (2012) proposed a physical mechanism to explain the swimming of the snowman based on our understanding of the non-Newtonian flows induced by the rotation of spheres in elastic fluids. When an isolated sphere is rotated in a viscoelastic liquid, a secondary flow is induced away from the sphere along the axis of rotation and towards it in the perpendicular direction (Bird et al. 1987). Since the streamlines are curved, hoop stresses appear which stretch the polymer molecules giving rise to an additional tension along the close stream lines. This tension leads to an inward contraction which results in this secondary flow. Considering a dumbbell made up of two widely-separated spheres, the secondary flows created by the rotation each sphere would tend to push the two spheres apart. However, since the flow strength depends on the sphere size, an unequal sphere pair will result in a net elastic force directed from the large to the small sphere.

This physical argument was verified using the numerical simulations and theory by Pak et al. in their original article, and the current study allows to confirm these results experimentally. We can compare our measurements to the mathematical model derived by Pak et al. (2012). Balancing the net viscoelastic force resulting from the difference between the secondary flows induced by the two spheres (evaluated analytically in the small-\({\rm De}\) limit) with the viscous drag on the dumbbell leads to a prediction for the swimming speed U as

$$\begin{aligned} \frac{2U}{\omega D_{\text {L}}} = {\rm De}(1-\beta )\frac{2(D^*)^3(1-D^*)}{(1+D^*)^6}, \end{aligned}$$
(6)

where \({\rm De}\) is de Deborah number (defined in Eq. 3) and \(\beta\) is the ratio of solvent-to-total viscosities (see Table 2).

In Fig. 5 the prediction from Eq. (6) is shown, for \({\rm De}=10\) and using the value \(\beta =0.1149\) from Table 2, along with the experimental measurements. Given that the model has no fitting parameters, and although it is valid only in the limit \({\rm De}\ll 1\), the agreement with the experimental measurements is very good.

5 Conclusions

Motivated by a recent theoretical proposal, we carried out experiments demonstrating the use of normal stress differences for propulsion. Rigid dumbbells were rotated by an external magnetic field along their axis of symmetry in a constant-viscosity viscoelastic fluid. When the shape of the dumbbell is asymmetric (snowman geometry), normal stress differences lead to a net propulsion in the direction of the smaller sphere. The use of a simple mathematical model developed in the limit of widely-separates spheres allows to the rationalize the experimental results by predicting the dependence of the snowman swimming speed on the size ratio between the two spheres. Although the model is only valid for asymptotically small values of the Deborah number, the good agreement obtained between experiments and theory indicates that it is able to capture the relevant physics, namely propulsion induced by secondary elastic flows. Of course, it is well known that many mathematical models derived in a specific asymptotic limit continue to be semi-quantitatively correct outside their domains of validity. The good agreement demonstrates that the model is robust and its use and validity should be explored further.

The results in this paper are valuable because they confirm experimentally an important idea: the viscoelastic nature of a complex fluid can be exploited in a useful manner. In general, the elastic flow effects are considered a negative feature since their implications are often unclear and detrimental. In this case, however, elasticity leads to a clear, measurable and well characterized effect: net propulsion resulting from geometrical asymmetry. Such an effect can give rise to micro-swimmers that can propel themselves in biological fluids (most of which are viscoelastic) for biomedical applications, without complex actuation mechanisms. Other similar attempts with equal-sized-sphere dimers were observed to swim in heterogenous viscoelastic media (Rogowski et al. 2018), but their maneuverability could not be fully controlled. In contrast, for the snowman configuration proposed here, the displacement will always occur in a known direction. Furthermore, as original hypothesised by Pak et al. (2012), the measurement of rheological properties of viscoelastic liquids, which remains a technical challenge, could be determined directly from the speed of asymmetric swimmers since there is a direct link between rheology and propulsion characteristics. Finally, the asymmetries of flow configurations could also be used to induce elastic effects in a controlled fashion, for fundamental fluid mechanic studies. We plan to pursue some of these ideas in the future.

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 682754 to EL). RZ acknowledges the Isaac Newton Institute, Cambridge, for granting a Simons Fellowship; this work was finalised during a stay supported by the fellowship.