Numerical simulations on the dynamics of a particle pair in a viscoelastic fluid in a microchannel: effect of rheology, particle shape, and confinement

Abstract

The dynamics of two particles suspended in a viscoelastic fluid and aligned on the centerline of a microfluidic channel is investigated by direct numerical simulations. The shear-thinning elastic fluid is modeled by the Giesekus constitutive equation. The relative particle velocity is studied by varying the interparticle distance, the Deborah number, fluid shear thinning, confinement ratio, and particle shape. Concerning the latter aspect, spherical and spheroidal particles with different aspect ratios are considered. The regimes of particle attraction and repulsion as well as the equilibrium configurations are identified and correlated with the fluid rheological properties and particle shape. The observed dynamics is related to the distribution of the viscoelastic normal stresses in the fluid between the particles. The results reported here provide useful insights into design efficient microfluidics devices to achieve particle ordering, i.e., the formation of equally spaced particle structures.

1 Introduction

The focusing of particles at the centerline of a microfluidic channel induced by fluid viscoelasticity has been of great interest over the last years (D’Avino et al. 2017; Lu et al. 2017). As compared to other similar techniques (Xuan et al. 2010), particle alignment in a viscoelastic medium can be achieved in a simple straight microchannel avoiding extra components and/or complex designs of the device. Several theoretical, experimental and numerical works have elucidated the mechanism behind the focusing phenomenon as well as the role of fluid rheology, flow intensity, and geometry (shape of the channel cross section and confinement ratio, i.e., the ratio between the particle size and the characteristic dimension of the channel) on the alignment efficiency (Leshansky et al. 2007; Yang et al. 2011; D’Avino et al. 2012; Lee et al. 2013; Kang et al. 2013; Del Giudice et al. 2013; Lim et al. 2014; Seo et al. 2014; Del Giudice et al. 2015; Yang et al. 2017; Yuan et al. 2018; Li and Xuan 2018; Xiang et al. 2019). In brief, a particle suspended in a viscoelastic medium experiences a motion transversal to the main flow direction, firstly observed by Mason and co-workers (Karnis and Mason 1966; Gauthier et al. 1971), induced by the fluid normal stresses (D’Avino and Maffettone 2015; D’Avino et al. 2017; Lu et al. 2017). Since the ‘migration velocity’ is 2–3 orders of magnitude lower than the main flow velocity, very long channels (compared to the cross-section characteristic dimension) are required to achieve highly efficient alignment. Microfluidics is, then, a very well-suited framework to exploit the migration phenomenon, as demonstrated for the first time by Leshansky et al. (2007). To date, 3D particle focusing induced by fluid viscoelasticity is a well established, finely controllable technique to manipulate trajectories of particles with spherical shape. Studies on non-spherical particle suspensions recently appeared (Lu et al. 2015; Lu and Xuan 2015; D’Avino et al. 2019). Specifically, numerical simulations have reported that the migration mechanism occurs for non-spherical particles as well and that, after reaching the axis channel, they slowly orient with their major axis along the main flow direction (D’Avino et al. 2019).

A step forward in particle focusing is the ordering of the aligned particles, i.e., the capability of forming a train of equally spaced particles. Very recent experiments and simulations have shown that viscoelasticity is able to rearrange the microstructure and promote ordering (Del Giudice et al. 2018). More specifically, the formation of a train of particles at approximately equal distances has been observed in a shear-thinning viscoelastic fluid, while no ordering has been reported for constant viscosity fluids. The ordering mechanism has been confirmed by numerical simulations carried out in the same conditions explored in the experiments. A simple qualitative argument on the particle train stability able to explain the observed train dynamics has been also derived. A remarkable result of the proposed argument is that, although the evolution of the microstructure is due to complex hydrodynamic interactions of a multi-particle system, many features of the final particle arrangement can be predicted by simply analyzing the dynamics of only two particles.

The problem of the dynamics of a pair of spherical particles suspended in a viscoelastic fluid and aligned at the centerline of a cylindrical microchannel has been tackled by direct numerical simulations (D’Avino et al. 2013). The results can be summarized as follows: (i) the particles can reduce or increase their distance while traveling along the channel depending on the initial distance and the Deborah number (defined as the ratio between the fluid and flow characteristic time); (ii) a critical Deborah number $De_\text {cr}$ is identified such that, for $De<De_\text {cr}$, two particles attract or repel depending on whether their initial distance is lower or higher than a critical distance; (iii) if $De>De_\text {cr}$ only repulsion dynamics occurs. These results, however, were obtained for a single fluid rheology. The effect of shear thinning was investigated by fixing the Deborah number, making difficult to draw general conclusions. Furthermore, all the simulations were limited to relatively small interparticle distances, whereas it has been shown that behavior at large distance is crucial in determining the final microstructure (Del Giudice et al. 2018).

In this work, we re-visit and extend the pair particle problem to a wide and fully combined parametric space of Deborah number, fluid shear thinning, confinement ratio, and interparticle distance. We anticipate that new regimes of the pair dynamics appear in ranges of the investigated parameters that were not explored before. Furthermore, motivated by the recent results on focusing of non-spherical particles mentioned above, we consider the completely new problem of the dynamics of two aligned spheroidal particles.

The study is carried out by direct numerical simulations whereby the macroscopic governing equations, together with a viscoelastic constitutive equation, are solved. State diagrams reporting the relative particle velocity as a function of the investigated parameters are shown, giving a complete overview of the pair particle dynamics problem.

2 Governing equations and numerical method

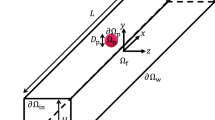
The system investigated in this work is reported in Fig. 1a. A viscoelastic suspension of two spherical or spheroidal particles flows in a straight cylindrical microchannel. The centers of volume of the particles lie on the channel centerline and, in case of non-spherical shape, the particles are oriented along the axis channel. As previously reported, this is, indeed, the stable equilibrium configuration of spheroidal particles in a viscoelastic fluid (D’Avino et al. 2019). We denote by a and b the particle semi-major and semi-minor axes, and with $\mathrm{AR}=a/b$ the aspect ratio. For a sphere, $a=b$ and $\mathrm{AR}=1$. The channel diameter is denoted by D and the length by L. A Cartesian reference frame is selected with origin at the center of the channel inlet with z denoting the flow direction. Because of the symmetry, the particles remain on the axis channel aligned along the flow direction. Their positions and velocities are $z_1$ and $z_2$, and $U_1$ and $U_2$, respectively, where ‘1’ and ‘2’ denote the trailing (left in Fig. 1) and leading (right in Fig. 1) particles. The distance between the surfaces of the two particles is d.

Fig. 1

Schematic representation of the investigated system (a) and the corresponding computational domain (b)

The channel wall is $\partial \varOmega _{\text {w}}$, the inflow and outflow channel sections are $\partial \varOmega _{\text {in}}$ and $\partial \varOmega _{\text {out}}$, respectively, and the boundaries of the particles are $\partial P_1$ and $\partial P_2$. Since the particles are aligned on the centerline, we can reduce the 3D domain to a 2D axisymmetric one, shown in Fig. 1b. The boundary $\partial \varOmega _\text {sym}=\partial \varOmega _\text {sym1} \cup \partial \varOmega _\text {sym2} \cup \partial \varOmega _\text {sym3}$ is the axis of symmetry.

We assume incompressibility and negligible inertia for both solid and fluid. The governing equations are the mass and momentum balance equations:

$$\begin{aligned} \nabla \cdot {\varvec{u}}= 0, \end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot \varvec{\sigma }= {\varvec{0}}, \end{aligned}$$

(2)

where ${\varvec{u}}$ is the fluid velocity and $\varvec{\sigma }$ is the total stress tensor, expressed as:

$$\begin{aligned} \varvec{\sigma }=-p{\varvec{I}} + 2\eta _\text {s}{\varvec{D}}+\varvec{\tau }. \end{aligned}$$

(3)

In Eq. (3), p, ${\varvec{I}}$, $\eta _\text {s}$ and ${\varvec{D}}=(\nabla {\varvec{u}}+(\nabla {\varvec{u}})^{T})/2$ are the pressure, the unity tensor, the viscosity of a Newtonian ‘solvent’ and the rate-of-deformation tensor, respectively. As in D’Avino et al. (2013), the Giesekus model is chosen as constitutive equation (Larson 1988):

$$\begin{aligned} \lambda {\mathop {\varvec{\tau }}\limits ^{\nabla }}+\frac{\alpha \lambda }{\eta }\varvec{\tau }\cdot \varvec{\tau }+ \varvec{\tau }=2\eta _\text {p}{\varvec{D}}, \end{aligned}$$

(4)

where $\eta _\text {p}$ is the polymer viscosity, $\lambda$ is the fluid relaxation time, the symbol $(^{\nabla })$ denotes the upper-convected time derivative:

$$\begin{aligned} {\mathop {\varvec{\tau }}\limits ^{\nabla }}\equiv \frac{\partial \varvec{\tau }}{\partial t}+{\varvec{u}}\cdot \nabla \varvec{\tau }-(\nabla {\varvec{u}})^{T}\cdot \varvec{\tau }-\varvec{\tau }\cdot \nabla {\varvec{u}}, \end{aligned}$$

(5)

and $\alpha$ is a constitutive parameter. We recall that, in shear flow, the Giesekus model predicts a non-zero first normal stress difference and, for $\alpha >0$, a shear-thinning viscosity and a non-zero second normal stress difference. The zero-shear viscosity is defined as $\eta _0=\eta _\text {s}+\eta _\text {p}$.

Regarding the boundary conditions, no-slip is imposed at the channel wall:

$$\begin{aligned} {\varvec{u}}={\varvec{0}}\quad \text {on}~\partial \varOmega _{\text {w}}, \end{aligned}$$

(6)

and the rigid-body motion is imposed at the particle surfaces:

$$\begin{aligned} {\varvec{u}}=(0,U_{i})\quad \text {on}~\partial P_{i}(t), \end{aligned}$$

(7)

with i the particle number.

Axial symmetry is applied on the boundaries representing the axis of symmetry:

$$\begin{aligned} {\varvec{u}}\cdot {\varvec{i}}= 0\quad \text {on}~\partial \varOmega _{\text {sym}}, \end{aligned}$$

(8)

$$\begin{aligned} \left( \varvec{\sigma }\cdot {\varvec{i}}\right) |_{z}= 0\quad \text {on}~\partial \varOmega _{\text {sym}}, \end{aligned}$$

(9)

where ${\varvec{i}}$ is the unit vector along the x-direction.

Periodic boundary conditions are prescribed between the inflow and outflow sections, together with a flow rate in inflow:

$$\begin{aligned} {\varvec{u}}|_{\partial \varOmega _{\text {in}}}= {\varvec{u}}|_{\partial \varOmega _{\text {out}}}, \end{aligned}$$

(10)

$$\begin{aligned} \left( \varvec{\sigma }\cdot {\varvec{k}}\right) |_{\partial \varOmega _{\text {in}}}= \left( \varvec{\sigma }\cdot {\varvec{k}}\right) |_{\partial \varOmega _{\text {out}}}-\varDelta p\,{\varvec{k}}, \end{aligned}$$

(11)

$$\begin{aligned} \int _{\partial \varOmega _{\text {in}}}{\varvec{u}}\cdot {\varvec{k}}\,\mathrm{d}S= & Q, \end{aligned}$$

(12)

where ${\varvec{k}}$ is the unit vector along the z-direction and $\varDelta p$ is the pressure drop along the channel between $\partial \varOmega _\text {in}$ and $\partial \varOmega _\text {out}$. The flow rate Q is imposed through a constraint where the associated Lagrange multiplier is identified as the unknown pressure difference $\varDelta p$ (Bogaerds et al. 2004). Due to the periodicity along the z-direction, the domain length L must be chosen much larger than the channel diameter to avoid that the particles hydrodynamically interact with their images.

As inertia is neglected, no initial condition for the velocity field needs to be specified. On the other hand, since the time-derivative of the viscoelastic stress tensor appears in the constitutive equation, an initial condition for $\varvec{\tau }$ is required. We assumed a stress-free initial condition, i.e., that the stress is zero everywhere in the fluid at the initial time:

$$\begin{aligned} \varvec{\tau }|_{t=0}={\varvec{0}}. \end{aligned}$$

(13)

Finally, the hydrodynamic force acting on the particles needs to be specified. Under the assumptions of the absence of particle inertia, and of no ‘external’ forces (force-free particle), the z-component of the total forces $F_{i}$ on the particle surfaces must be zero:

$$\begin{aligned} F_{i}=\int _{\partial P_{i}(t)}(\varvec{\sigma }\cdot {\varvec{n}})|_{z}\,\mathrm{d}S=0, \end{aligned}$$

(14)

where ${\varvec{n}}$ is the outwardly directed unit normal vector on $\partial P_{i}$.

At each time step, the particle positions are updated by integrating the kinematic equations:

$$\begin{aligned} \frac{\mathrm{d} z_{i}}{\mathrm{d}t}=U_{i} \end{aligned}$$

(15)

with initial conditions $z_{i}|_{t=0}=z^{0}_{i}$.

Fig. 2

Relative particle velocity as a function of the interparticle distance for a pair of spherical particles aligned along the centerline of a cylindrical channel and suspended in a Giesekus fluid at $De=0.5$, $\alpha =0.05$, $\beta =0.4$. The values of the distances corresponding to the minima, the maximum and the zeros of the function are highlighted in red. On the top of the figure, a schematic representation of the pair dynamics for the different regimes is shown (color figure online)

The governing equations are solved by the finite element method. To achieve convergent results at relatively high Deborah numbers, the DEVSS-G/SUPG formulation combined with a log representation for the conformation tensor is implemented (Guénette and Fortin 1995; Bogaerds et al. 2002; Brooks and Hughes 1982; Fattal and Kupferman 2004; Hulsen et al. 2005). A boundary-fitted mesh with triangular elements is used with an adequate number of triangles between the particle surfaces where larger gradients of the flow fields are expected. The mesh is generated by the Gmsh software (Geuzaine and Remacle 2009). The arbitrary Lagrangian–Eulerian (ALE) technique is employed to handle the particle motion (Hu et al. 2001). Further details on the numerical method used as well as mesh and time convergence tests can be found elsewhere (D’Avino et al. 2013).

We made the equations dimensionless by choosing the channel diameter D as characteristic length, the average velocity ${\bar{u}}=4Q/(\pi D^2)$ as characteristic velocity, and $\eta _0 {\bar{u}}/D$ as characteristic stress. The dimensionless parameters governing the problem are: the Deborah number $De=\lambda {\bar{u}}/D$ that is the ratio between the fluid and flow characteristic time, the aspect ratio, $\mathrm{AR}=a/b$, the confinement ratio $\beta = 2b/D$, the viscosity ratio $\eta _{\mathrm{r}}=\eta _\text {s}/\eta _0$, the constitutive parameter $\alpha$, and the initial particle distance $d_0/D$.

In this work, we set the viscosity ratio to $\eta _{\mathrm{r}}=0.091$. In what follows, all the symbols refer to dimensionless quantities.

3 Results and discussion

Previous numerical simulations on the dynamics of two spheres aligned on the channel centerline and suspended in a viscoelastic fluid reported that the interparticle distance decreases or increases depending on the initial distance and the Deborah number (D’Avino et al. 2013). The effect of the parameter $\alpha$ was investigated for a single value of De and no qualitative change of the pair dynamics was found by increasing or reducing this constitutive parameter. Furthermore, the simulations were limited to relatively small interparticle distances.

As previously remarked D’Avino et al. (2013), beyond an initial start-up due to the stress development, the trends of the relative particle velocity $\varDelta U=U_2-U_1$ collapse on a single master curve when plotted as a function of the current interparticle distance d. We can then directly consider the master trend obtained by running several simulations for different initial distances $d_0$ and take the relative velocity after the transient. Hence, all the curves showing the relative velocity as a function of the interparticle distance are obtained by interpolating a set of data (d, $\varDelta U$) taken after the start-up and corresponding to a specific $d_0$. Although the current interparticle distance d used to construct the master curves is not exactly equal to $d_0$, the two values are very similar because the stress development characteristic time (which is of the same order of magnitude of the fluid relaxation time) is much lower than the characteristic time to have appreciable variations of the relative particle positions.

Fig. 3

Relative particle velocity as a function of the interparticle distance for a pair of spherical particles aligned along the centerline of a cylindrical channel and suspended in a Giesekus fluid at $De=0.5$, $\alpha =0.2$, $\beta =0.4$. The values of the distances corresponding to the minimum, the maximum and the zero of the function are highlighted in red. On the top of the figure, a schematic representation of the pair dynamics for the different regimes is shown (color figure online)

To fully characterize the dynamics of the system under investigation, we carry out direct numerical simulations by covering the parametric space (d, De, $\alpha$, $\beta$) with ranges chosen in the following way. The interparticle distance interval corresponds to initial distances $d_0$ selected between $[d_\text {0,min},d_\text {0,max}]=[0.01,3]$. The value of $d_\text {0,min}=0.01$ corresponds to an interparticle distance of $5\%$ of the particle radius, i.e., the particles are almost in contact. Lower values are not feasible due to numerical instabilities and problems related to the meshing procedure. The maximum value $d_\text {0,max}=3$ is sufficiently large so that the particles do not interact anymore and behave like isolated objects. The range of distances is discretized by choosing a step of 0.02 up to a distance of 0.15. The step is then increased to 0.05 up to a distance of 0.4. Finally, the step is further increased to 0.1 up to $d_\text {0,max}$. The Deborah number interval is set to $[De_\text {min},De_\text {max}]=[0.5,3]$. The lowest value corresponds to weak viscoelastic effects able, however, to produce a relative particle motion appreciable in real microfluidic devices (D’Avino et al. 2013). The maximum value denotes a system characterized by significant elasticity. In this range, we consider two intermediate Deborah numbers, $De=1$ and $De=2$, for a total of four values. Regarding the role of the constitutive parameter $\alpha$, we recall that, for the model used in the present work, non-zero values of $\alpha$ produce both shear thinning and a second normal stress difference. To elucidate the importance of these two fluid properties on the pair particle dynamics, we have performed few simulations with a different constitutive equation (Phan–Thien Tanner model (Larson 1988)) that only predicts the first normal stress difference and shear thinning. Since the results are qualitatively similar to those obtained for the Giesekus model, we conclude that shear thinning plays the most relevant role in determining the pair particle dynamics. Hence, in what follows, different values of the constitutive parameter $\alpha$ will be connected to variations of the fluid shear-thinning degree. The range of $\alpha$ is chosen as $[\alpha _\text {min},\alpha _\text {max}]=[0.05,0.4]$ where the lowest value corresponds to a fluid with a constant viscosity over a wide range of shear rates, whereas the highest one is characteristic of a strong shear-thinning medium. Together with the extrema, two intermediate values in this interval are considered, i.e., $\alpha =0.1$ and $\alpha =0.2$. Finally, two values of the confinement ratio are selected, $\beta =0.2$ and $\beta =0.4$, that identify the range of confinement ratios typically used in viscoelastic microfluidics. Indeed, lower values would require extremely long channels to achieve particle focusing [the migration velocity scales as the third power of $\beta$ (D’Avino et al. 2012)], whereas higher values could lead to channel clogging.

Fig. 4

Relative particle velocity as a function of the interparticle distance for a pair of spherical particles aligned along the centerline of a cylindrical channel and suspended in a Giesekus fluid at $De=3$, $\alpha =0.2$, $\beta =0.4$. The value of the distances corresponding to the maximum of the function is highlighted in red. On the top of the figure, a schematic representation of the pair dynamics is shown (color figure online)

Before presenting the results of the pair dynamics by varying these four parameters, it is useful to illustrate the possible regimes experienced by the pair. In Fig. 2, the relative particle velocity $\varDelta U$ is reported as a function of the interparticle distance d. The parameters are $De=0.5$, $\alpha =0.05$, $\beta =0.4$. We started with this specific case since the resulting pair particle dynamics shows the most complex behavior. As visible in Fig. 2, depending on the interparticle distance d, the relative velocity can be negative or positive corresponding to particle attraction or repulsion, respectively. Specifically, by increasing d, the particles first attract, then repel, and finally attract again. These three behaviors, highlighted by different colors and sketched on the top part of the diagram, are delimited by the zeros of the black solid curve that correspond to equilibrium solutions. The first zero is the case at $d=0$, i.e., the two spheres are in contact. (The very first trend of this and the following curves are obtained by extrapolating the data points due to the aforementioned problems in simulating distances lower than 0.01.) This solution is stable as, by slightly increasing the interparticle distance, the relative velocity is negative and d decreases again.

On the contrary, the distance denoted by $d_\text {z1}$ corresponds to an unstable equilibrium condition as small perturbations lead the system to move away from such configuration. The third zero denoted by $d_\text {z2}$ is stable again. Hence, depending on the interparticle distance, at long times, the two particles can travel in contact (if $d < d_\text {z1}$) or at a fixed distance $d_\text {z2}$ (if $d > d_\text {z1}$). It is worthwhile to mention that the stable solution at $d=d_\text {z2}$ was not found in previous numerical simulations (D’Avino et al. 2013) due to the aforementioned limited set of investigated parameters.

An important piece information reported in Fig. 2 is the magnitude of the relative velocity that is related to the time scale over which a stable configuration is attained. For distances lower than $d_\text {z2}$ (blue and red regions), $\varDelta U$ is about three orders of magnitude lower than the main flow average velocity ${\bar{u}}$. Since the migration velocity (responsible for particle focusing) for similar parameters is approximately three orders of magnitude lower than ${\bar{u}}$ as well (Villone et al. 2011), we conclude that a focusing length, generally corresponding to few centimeters, is sufficient to observe a significant change of the distance between two particles. On the contrary, the relative velocity in the green region is extremely low. This is not surprising as the very large distances lead to weak hydrodynamic interactions slowing down the pair particle dynamics. Hence, two particles initially positioned at $d>d_\text {z2}$ travel at a nearly constant speed and significant variations of their distance are hardly detectable in standard microfluidic channels.

Fig. 5

Contours of the relative particle velocity as a function of the interparticle distance and the Deborah number for a pair of spherical particles ($\mathrm{AR}=1$) for different values of $\alpha$ and for $\beta =0.4$. The blue, red and black lines correspond to the maximum, minimum and zero values of the relative particle velocity, respectively. The roman numbers denote the different pair dynamics: (I) attraction for $d<d_\text {min1}$; (II) attraction for $d>d_\text {min1}$; (III) repulsion for $d<d_\text {max}$; (IV) repulsion for $d>d_\text {max}$; (V) attraction for $d<d_\text {min2}$; (VI) attraction for $d>d_\text {min2}$ (color figure online)

Fig. 6

Contours of the relative particle velocity as a function of the interparticle distance and the Deborah number for a pair of spherical particles ($\mathrm{AR}=1$) for different values of $\alpha$ and for $\beta =0.2$. The blue, red and black lines correspond to the maximum, minimum and zero values of the relative particle velocity, respectively. The roman numbers denote the different pair dynamics: (I) attraction for $d<d_\text {min1}$; (II) attraction for $d>d_\text {min1}$; (III) repulsion for $d<d_\text {max}$; (IV) repulsion for $d>d_\text {max}$ (color figure online)

Fig. 7

Contours of the relative particle velocity as a function of the interparticle distance and the Deborah number for a pair of spheroidal particles with $\mathrm{AR}=2$ for different values of $\alpha$ and for $\beta =0.4$. The blue, red and black lines correspond to the maximum, minimum and zero values of the relative particle velocity, respectively. The roman numbers denote the different pair dynamics: (I) attraction for $d<d_\text {min1}$; (II) attraction for $d>d_\text {min1}$; (III) repulsion for $d<d_\text {max}$; (IV) repulsion for $d>d_\text {max}$; (V) attraction for $d<d_\text {min2}$; (VI) attraction for $d>d_\text {min2}$ (color figure online)

Fig. 8

Contours of the relative particle velocity as a function of the interparticle distance and the Deborah number for a pair of spheroidal particles with $\mathrm{AR}=2$ for different values of $\alpha$ and for $\beta =0.2$. The blue, red and black lines correspond to the maximum, minimum and zero values of the relative particle velocity, respectively. The roman numbers denote the different pair dynamics: (I) attraction for $d<d_\text {min1}$; (II) attraction for $d>d_\text {min1}$; (III) repulsion for $d<d_\text {max}$; (IV) repulsion for $d>d_\text {max}$ (color figure online)

Fig. 9

Contours of the relative particle velocity as a function of the interparticle distance and the Deborah number for a pair of spheroidal particles with $\mathrm{AR}=4$ for different values of $\alpha$ and for $\beta =0.4$. The blue, red and black lines correspond to the maximum, minimum and zero values of the relative particle velocity, respectively. The roman numbers denote the different pair dynamics: (III) repulsion for $d<d_\text {max}$; (IV) repulsion for $d>d_\text {max}$; (V) attraction for $d<d_\text {min2}$; (VI) attraction for $d>d_\text {min2}$ (color figure online)

Fig. 10

Difference between the zz-component of the viscoelastic stress tensor $\tau _\text {zz}$ and the same component of the unperturbed fluid $\tau _{\text {zz},\infty }$ for a $\mathrm{AR}=1$, $d=0.1$, b $\mathrm{AR}=1$, $d=0.4$, c $\mathrm{AR}=4$, $d=0.1$. d The single particle case is shown. The other parameters are $De=1$, $\alpha =0.2$, $\beta =0.4$

As discussed above, the distances corresponding to $\varDelta U=0$ are equilibrium configurations for the pair dynamics. However, when dealing with a multiparticle system, the extrema of the curve (in the case of Fig. 2 two minima and one maximum) can give useful information on the final microstructure. Indeed, as discussed in a recent work on particle ordering (Del Giudice et al. 2018), the position of the equilibrium distance $d_\text {eq}$ with respect to the extrema of the relative velocity curve gives insight into the stability of an equally spaced train of particles. (The equilibrium distance is defined as the distance between equally spaced particles; it is related to the volume fraction by a geometrical relationship.) Just as an example, let us assume that a train of equally spaced particles with distance $d_\text {eq}$ has been formed, and only one particle is slightly displaced from the equilibrium position. Let us also assume that $d_\text {eq}$ falls in the red region and that it is greater than the distance $d_\text {max}$ corresponding to the maximum. Since the slope of the relative velocity curve is negative, two particles attract or repel depending on whether the interparticle distance is higher or lower than $d_\text {eq}$, respectively. In both cases, the displaced particle attains the equilibrium distance and ordering is restored. An opposite scenario occurs if $d_\text {eq}$ corresponds to a point of the curve in Fig. 2 where the slope is positive (e.g., for a value in the red region lower than $d_\text {max}$. In this case, the particle displaced from the equally spaced configuration tends to approach the closest particle and form a doublet (Del Giudice et al. 2018).

A second scenario is represented in Fig. 3. The parameters are $De=0.5$ (as in the previous case), $\alpha =0.2$, and $\beta =0.4$. As compared to the state diagram in Fig. 2, we observe that: (i) the zero at $d_\text {z2}$ and the minimum at $d_\text {min2}$ disappear and the curve asymptotically tends to the horizontal axis from positive values; (ii) as a consequence of the previous point, only two dynamics are possible, i.e., pair attraction for $d<d_\text {z1}$ (blue region) or repulsion for $d>d_\text {z1}$ (red region), corresponding, at long times, to doublet formation or two isolated particles, respectively; (iii) the magnitude of the relative velocity is lower than the previous case both in case of particle attraction and repulsion, requiring longer channels to observe significant changes of the interparticle distance.

Finally, the last possible scenario is depicted in Fig. 4 where the parameters are $De=3$, $\alpha =0.2$, and $\beta =0.4$. In this case, also the zero at $d=d_\text {z1}$ and the minimum at $d=d_\text {min1}$ disappear and the relative velocity is positive for any interparticle distance. The dynamics is, then, repulsive, leading to the formation of isolated spheres at a distance such that the hydrodynamic interactions have a negligible effect on the relative particle motion.

3.1 State diagrams for spherical particles

The particle pair dynamics shown in Figs. 3 and 4 were also reported in D’Avino et al. (2013). However, the change from one behavior to the other was associated with a variation of the Deborah number only (a ‘critical Deborah number’ was introduced) as shear thinning did not produce any qualitative change of the relative velocity curve for the fixed value of the Deborah number considered ($De=1$). This is clearly not true if one compares Figs. 2 and 3 corresponding to the same value of De and two different $\alpha$. To clarify this aspect, we now present the complete particle pair dynamics by varying d, De and $\alpha$ in the whole parametric space for two values of the confinement ratio, highlighting how the magnitude of $\varDelta U$, the zeros, and the extrema of the relative velocity curve are affected.

In Fig. 5, the contour plots of the relative particle velocity $\varDelta U$ as a function of the interparticle distance d and the Deborah number De for four values of the parameter $\alpha$ are reported. The confinement ratio is $\beta =0.4$. The black, red and blue lines are the curves corresponding to the zero, minimum and maximum values of the relative velocity. The magnitude of $\varDelta U$ is given by the colors: the positive values increase from light to dark orange and the negative values increase from light to dark yellow. In these plots, the pair particle dynamics for any combination of the investigated parameters can be readily identified. For instance, the curve in Fig. 2 is obtained by ‘intersecting’ the upper-left plot of Fig. 5 with a vertical line at $De=0.5$. From these plots, the following general conclusions on the dynamics of two aligned spheres can be drawn: (i) the number of equilibrium points and, consequently, the long-time regimes depend on both the Deborah number and the fluid shear thinning; (ii) for Deborah numbers lower than a critical value, the particles attract at small distances regardless of fluid shear thinning; such critical Deborah number, however, reduces with increasing $\alpha$; (iii) at small De-values, and for low or moderate shear-thinning fluids, a stable equilibrium regime appears at large distances (black line on the upper-left part of the plots); for sufficiently high $\alpha$ values, this regime is not present; the relative particle velocity near this equilibrium point is, however, very low, leading to extremely slow changes of the particle relative motion; (iv) the magnitude of the relative particle velocity is an increasing function of the Deborah number and a decreasing function of the parameter $\alpha$; hence, the fastest variation of the particle microstructure is obtained for highly elastic and nearly constant viscosity fluids; (v) the maximum relative velocity [which is related to the train stability (Del Giudice et al. 2018)] is nearly insensitive to both the Deborah number and fluid shear thinning and its value is $d_\text {max}\approx 0.5$.

From Fig. 5, it can be also noticed that the dynamics at low Deborah numbers ‘translates’ to the left for increasing values of $\alpha$ (for instance, the black and red lines on the top-left part of the state diagram for $\alpha =0.05$ move at smaller De for $\alpha =0.1$, and then disappear for higher $\alpha$). Indeed, even at high $\alpha$-values, a plateau of viscosity exists at low Deborah numbers.

Hence, the pair dynamics observed for $\alpha =0.05$ can be considered as the typical behavior of two particles in viscoelastic fluids at small Deborah numbers (where the viscosity is constant). As such, the regions denoted by (V) and (VI) in Fig. 5 might be observed at higher $\alpha$ values as well but at Deborah numbers smaller than the one investigated in this work ($De_\text {min}=0.5$).

In Fig. 6, the contours of the relative particle velocity are shown for a lower confinement ratio $\beta =0.2$. In agreement with previous results (D’Avino et al. 2013), the relative particle velocity is about one order of magnitude lower than the case at $\beta =0.4$ (compare the scales between Figs. 5, 6), resulting in a slower re-arrangement of the microstructure. Furthermore, the attraction region at large distances is not present for any of the $\alpha$ values investigated. Finally, the attraction region at small distances is observed for almost all the $\alpha$ and De values. Only at $De=3$ and for a strong shear-thinning fluid such region disappears.

3.2 State diagrams for non-spherical particles

All the results presented so far refer to particles with spherical shape. As recently reported D’Avino et al. (2019), spheroidal particles immersed in a viscoelastic fluid undergo a focusing dynamics similar to spheres, attaining a final equilibrium orientation with major axis along the main flow direction. We, then, investigated the dynamics of a pair of spheroids with center of volume on the microchannel centerline and aligned along the cylinder axis, as depicted in Fig. 1. We start with the confinement ratio $\beta =0.4$. The particle aspect ratio is set to $\mathrm{AR}=2$. Notice that, fixing the confinement ratio implies that non-spherical particles ($\mathrm{AR}>1$) have a volume larger than spheres ($\mathrm{AR}=1$). Figure 7 reports the contours of the relative particle velocity as a function of the other parameters. A behavior very similar to that found for spherical particles is observed. The most relevant quantitative difference concerns the attraction region at small distances (the black and red lines in the lower part of the plots): for spheroids, the critical Deborah number is slightly lower and, more importantly, the black and red lines are closer to the x-axis, i.e., the attraction region is narrower than the spherical particle case. A behavior similar to spherical particles is also observed when the confinement ratio is reduced to $\beta =0.2$, as shown in Fig. 8. The attraction region at large distances is never observed whereas attraction at small distances is always present except for high values of $\alpha$ and De.

In Fig. 9, the contours of the relative particle velocity for spheroids with $\mathrm{AR}=4$ and $\beta =0.4$ are shown. Notice that, for the confinement ratio and aspect ratio chosen, the particles are not free to perform full rotations through the gap. In this sense, such configuration is a bit artificial and might be unreliable due, for instance, to clogging issues. On the other hand, one could think of a microchannel with a contraction geometry where focusing is achieved in a large channel followed by a smaller one where the particles enter already aligned. In the present context, however, we consider this configuration to evaluate the effect of an elongated particle shape on the pair dynamics.

As compared to the previous cases, a relevant qualitative difference is readily observed: the attraction region at small distances is not present for any value of the parameter $\alpha$ in the investigated range, i.e., the relative particle velocity is always positive at small interparticle distances. Hence, regardless of the Deborah number and the fluid shear thinning, two close spheroids always repel and reach an equilibrium distance given by the black line, if present, or a sufficiently large distance such that hydrodynamic interactions become negligible. Notice also that the maximum relative velocity is still relatively insensitive to the Deborah number and fluid shear thinning. However, its value ($d_\text {max}\approx 0.3$) is lower than the previous cases.

3.3 Local stress distribution

A possible explanation for the attraction/repulsion dynamics at small distances can be based on the local stress field in the fluid domain around the particles reported in Fig. 10. The colors refer to the quantity $\tau _\text {zz}-\tau _{\text {zz,}\infty }$ where $\tau _\text {zz}$ is the zz-component of the viscoelastic stress tensor $\varvec{\tau }$ (see Eq. (4)) and $\tau _{\text {zz,}\infty }$ is the same component of the fluid without particles. Hence, the plotted quantity gives the perturbation of the axial viscoelastic normal stress due to the presence of the particles. In analogy with the particle migration mechanism where the viscoelastic normal stress along the migration direction causes the transversal particle motion, the zz-component might be responsible for the relative particle motion along the flow direction.

We examine three cases: (a) spherical particles at a distance $d=0.1$, (b) spherical particles at a distance $d=0.4$, (c) spheroidal particles with $\mathrm{AR}=4$ at $d=0.1$. The other parameters are $De=1$, $\alpha =0.2$, and $\beta =0.4$. For the sake of comparison, the stress field around a single particle are plotted in panel (d). In the first case, the particles attract, whereas they repel for the other two cases. First of all, we observe from Fig. 10a, b that the stress fields on the left of the trailing particle and on the right of the leading one do not depend on the distance. This is somewhat expected since both particles are ‘isolated’ in one direction and the stress field in these regions is equal to that around a single particle reported in Fig. 10d. A similarity is also observed for spheroidal particles where the fields are just more ‘stretched’ due to the elongated shape. A significant difference is, instead, observed in the fluid between the particles. In Fig. 10b, the stress field between the two spheres is qualitatively similar to the one expected for an isolated particle. Indeed, a high stress region (red) appears on the right of the trailing particle (similar to the red region on the right of the leading particle) and a low stress zone (blue) can be observed on the left of the leading particle (similar to the blue region on the left of the trailing particle). The stress distribution is, of course, quantitatively different from the isolated case because the particles are still relatively close one to each other. On the contrary, in Fig. 10a the interparticle distance is much lower and the normal stress is more uniform in the gap. In this case, indeed, the fluid between the two particles travels at approximately the same velocity of the particles leading to a small velocity gradient that, in turn, produces low viscoelastic stresses. In the former case (Fig. 10b), the normal stress gradient at the internal particle surfaces counteracts the stress around the external part of the particles, giving rise to a net force that pushes the particles away. On the other hand, the weak stress gradient between the particles in the case of Fig. 10a is not able to contrast the external stresses resulting in particles attraction. The local stress field for spheroidal particles shown in Fig. 10c confirms this argument. We recall that, in this case, the two particles repel. By comparing the stress distribution within the gap with Fig. 10a (where the distance between the particle surfaces is the same), a red and cyan region can be observed, i.e., the shear rate (and, in turn, the stress) is not uniform. This is likely due to the particle shape and, more specifically, to the large curvature near the tips of the spheroids. Such effect is similar to what observed for the lateral migration of a spheroid where, around the tip, the normal stresses are larger as compared to spherical particles, leading to wall repulsion even when the spheroid is very close to the wall (D’Avino et al. 2019).

4 Conclusions

In this work, the dynamics of a pair of spherical and spheroidal particles aligned at the centerline of a cylindrical microchannel and suspended in a viscoelastic fluid is studied by numerical simulations. The relative particle velocity is investigated by varying the interparticle distance, the Deborah number, the fluid shear thinning, and the confinement ratio.

At a moderate confinement ratio, spherical and spheroidal particles with small aspect ratio attract at small distances regardless of fluid shear thinning for Deborah numbers lower than a critical value. For small De values, and for low or moderate shear-thinning fluids, a stable equilibrium regime also appears at large distances. Such regime, however, disappears by increasing the fluid shear thinning. The magnitude of the relative particle velocity increases by increasing the Deborah number and by decreasing the shear thinning. Hence, the fastest variation of the particle microstructure is observed for highly elastic and nearly constant viscosity fluids. The maximum relative velocity is nearly insensitive to both the Deborah number and fluid shear thinning. For particles with spheroidal shape and large aspect ratios, the attraction region at small distances is not present, reducing the formation of doublets. Finally, by reducing the confinement ratio, the pair dynamics significantly slows down and the attraction region at short distances is always present. The normal stress field in the fluid region between the particles justifies the observed dynamics.

The simulation results presented in this paper are useful to design and optimize microfluidics devices aimed at ordering particles. Indeed, as recently reported (Del Giudice et al. 2018), the dynamics of two particles gives useful information in terms of train stability and doublet formation. Since the present work explores the detailed pair dynamics in a wide range of the relevant fluid, flow, and geometrical parameters, useful indications in selecting the proper viscoelastic fluid and operating conditions are provided. Of course, the selection of a specific fluid rheology and flow rate must also assure an efficient focusing mechanism, which is the preliminary step to achieve particle ordering.