1 Introduction

The characteristics of wave propagation over varying bathymetry and bottom sediments have been studied for some time. In the nearshore, random ocean waves are significantly altered by nonlinear triad wave-wave interactions (e.g., Phillips 1977), wave breaking, varying bathymetry, and dissipation caused by bottom type. Predictive models which are able to simulate wave transformation in these nearshore areas include phase-averaged models (e.g., Booij et al. 1999), mild-slope equation type models (Berkhoff 1972; Radder 1979; Agnon et al. 1993; Kaihatu and Kirby 1995; Agnon and Sheremet 1997), and Boussinesq-type models (Peregrine 1967; Freilich and Guza 1984; Liu et al. 1985; Madsen et al. 1991; Nwogu 1993; Wei and Kirby 1995), among others. Dissipation caused by wave breaking has been included in both phase-resolving (e.g., Dally et. al. 1985; Zelt (1991) and probabilistic (Battjes and Janssen 1978; Thornton and Guza 1983; Janssen and Battjes 2007) forms. In most cases, nonlinear wave-wave interactions and dissipation by breaking are considered to be the major influences on the characteristics of wave transformation; wave dissipation by bottom friction (and scattering by bottom features) is generally considered to be significant only over long distances as an accumulative effect (Ardhuin et al. 2002; Ardhuin et al. 2003).

While generally true for sandy cohesionless sediments, relatively few of the world’s coastlines can be considered sandy (Holland and Elmore 2008). In particular, large expanses of bottom mud can exact significant damping on incoming waves; Gade (1958) performed laboratory experiments that showed that as much as 80 % of wave energy can be dissipated by mud, while Wells and Coleman (1981) found that 90 % of the incident wave energy can be damped on the mudbanks of Surinam. The mechanism by which waves are damped by bottom mud has been framed by representing the fluid mud layer variously as viscous Newtonian fluid (Gade 1958; Dalrymple and Liu 1978; Ng 2000), Bingham plastic (Mei and Liu 1987), viscoelastic material (Macpherson 1980; Hsiao and Shemdin 1980), or a non-Newtonian fluid (Foda et al. 1993). In addition to direct damping of energy due to interaction with bottom mud, nonlinear processes in the wave field also allow for indirect damping of energy at frequencies which interact with those experiencing significant direct damping. This was seen in field data (Sheremet and Stone 2003), with corresponding numerical model results which point to possible indirect damping mechanisms. For example, (Sheremet et al. 2005) and (Kaihatu et al. 2007) hypothesized that nonlinear subharmonic interactions are draining high-frequency energy, while Mei et al. (2010) and Torres-Freyermuth and Hsu (2010) ascribed high-frequency damping to short wave modulations. Recently, Torres-Freyermuth and Hsu (2014) determined that different regimes of low-frequency energy dissipation could occur, in which the source of low-frequency energy loss could be identified as either due to nonlinear interactions or direct damping by mud.

Models such as those mentioned above are quite skillful, provided there is sufficient certainty in the input parameters. For example, the characterization of mud as a viscous fluid requires knowledge of the fluid’s viscosity, density, and layer thickness (Dalrymple and Liu 1978), each of which are susceptible to errors. In many instances, it is possible to reliably estimate these parameters when comparing to laboratory data (Kaihatu et al. 2007; Kaihatu and Tahvildari 2012). Field estimates of these parameters, however, are far more uncertain (Safak et al. 2013; Sahin et al. 2012). Recent studies have attempted to use observable characteristics of the wave field (typically surface properties such as wave height or free surface elevation) to deduce properties of the viscous mud (Rogers and Holland 2009; Tahvildari and Kaihatu 2011).

In addition to issues regarding the estimation of mud characterization properties, the effect of wave directionality on transformation and damping characteristics in wave-mud interaction is also largely unexplored. It is known (e.g., Kaihatu et. al 2007) that the presence of mud affects the wavelength; for identical frequencies and water depths, waves propagating over mud are shorter than those which undergo no dissipation. This affects how waves refract, leading to differences in the predicted wave height and approach angle relative to those over non-dissipative bottoms. Models which predict the evolution of directional spectra over mudbanks have compared well with field data (Winterwerp et al. 2007; Rogers and Holland 2009), but generally the comparisons have been limited to bulk spectral properties (e.g., significant wave height); changes in directional tendencies due to bottom mud have not been tested.

In this paper, we conduct a sensitivity study to investigate the effect of directionality on the propagation characteristics of waves over a muddy shelf representative of the central chenier plain coast on the western Louisiana (USA) shelf. A nonlinear parabolic numerical model with a mud dissipation mechanism, previously detailed in (Kaihatu et al. 2007), is used to simulate the evolution of random waves over the mud bank. In the immediate absence of directional information on the incident waves, one-dimensional random waves are transformed with various assumed initial approach angles and compared with measurements in order to determine if the incorporation of directionality would improve comparisons. Additionally, we are also interested in the effect that mud has on the nonlinear interaction between waves and the generation of low-frequency components. To this end, we also run a linear version of the parabolic wave-mud interaction model to gauge the effect of wave nonlinearity on the low frequencies. The results of this sensitivity study would serve to motivate more comprehensive comparisons using full directional spectra.

2 Model description

2.1 Parabolic nonlinear wave model

The model used is the parabolic nonlinear phase-resolving wave model of (Kaihatu and Kirby 1995). The model was developed as an extension of the classical mild-slope equation (Berkhoff 1972) with second-order near-resonant (triad) nonlinear interactions included; as a result, both the linear transformation terms and the nonlinear interaction terms are fully dispersive and are thus not limited to shallow water (small kh).

Details of the model development can be seen in (Kaihatu and Kirby 1995); here, we simply outline the derivation. It is assumed that the free surface elevation can be decomposed into a truncated complex amplitude Fourier series:

$$ \eta(x,y,t)=\sum\limits_{n=1}^{N}\frac{A_{n}}{2}e^{i\int k_{n}dx-\omega_{n}t}+c.c. $$
(1)

In (1), A n is the complex amplitude, ω n is the radian frequency, and k n the wave number for the nth component; x and t are the cross-shore dimension and time, respectively. The complex conjugate is denoted by c.c.. Expanding the boundary value problem for water waves to second order in ka (where a is the wave amplitude), deriving the nonlinear extension to the mild slope equation and using the parabolic approximation (Radder 1979), the parabolic nonlinear model is (Kaihatu and Kirby 1995):

$$\begin{array}{@{}rcl@{}} & &2i\left( kCC_{g}\right)_{n}\frac{\partial A_{n}}{\partial x}-2\left( kCC_{g}\right)_{n}\left( \overline{k}_{n}-k_{n}\right)A_{n} +i\frac{\partial\left( kCC_{g}\right)_{n}}{\partial x}A_{n}\\ &+&\frac{\partial}{\partial y}\left( \left[CC_{g}\right]_{n}\frac{\partial A_{n}}{\partial y}\right)\\ &=&\frac{1}{4}\left( {\sum}_{l=1}^{n-1}RA_{l}A_{n-l}e^{i{\Theta}(l,n-l,n)}+2{\sum}_{l=1}^{N-n}SA_{l}^{*}A_{n+l}e^{i{\Theta}(-l,n+l,n)}\right) \end{array} $$
(2)

where the asterisk denotes complex conjugate. Furthermore:

$$\begin{array}{@{}rcl@{}} R&=&\frac{g}{\omega_{l}\omega_{n-l}}\left[\omega_{n}^{2}k_{l}k_{n-l}+\left( k_{l}+k_{n-l}\right)\left( \omega_{n-l}k_{l}+\omega_{l}k_{n-l}\right)\omega_{n}\right]\\ &-&\frac{{\omega_{n}^{2}}}{g}\left( {\omega_{l}^{2}}+\omega_{l}\omega_{n-l}+\omega_{n-l}^{2}\right) \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} S&=&\frac{g}{\omega_{l}\omega_{n+l}}\left[\omega_{n}^{2}k_{l}k_{n+l}+\left( k_{n+l}-k_{l}\right)\left( \omega_{n+l}k_{l}+\omega_{l}k_{n+l}\right)\omega_{n}\right]\\ &-&\frac{{\omega_{n}^{2}}}{g}\left( {\omega_{l}^{2}}-\omega_{l}\omega_{n+l}+\omega_{n+l}^{2}\right) \end{array} $$
(4)

and the phase functions Θ are:

$$\begin{array}{@{}rcl@{}} {\Theta}(l,n-l,n)&=&\int\left( \overline{k}_{l}+\overline{k}_{n-l}-\overline{k}_{n}\right) dx \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} {\Theta}(-l,n+l,n)&=&\int\left( \overline{k}_{n+l}-\overline{k}_{l}-\overline{k}_{n}\right) dx \end{array} $$
(6)

The linear dispersion governing the kinematic properties of the waves is:

$$ {\omega_{n}^{2}}=gk_{n}\tanh k_{n}h $$
(7)

As mentioned previously, a linear model was also run to investigate the nature of nonlinear wave-wave interaction. This linear model results from neglecting the nonlinear summations on the right-hand side of Eq. 2.

2.2 Mud dissipation

The mud dissipation model used here is that of (Ng 2000). This model is an approximation of the model of (Dalrymple and Liu 1978), in that the depth of the mud layer is assumed to be of the same size as the thickness of the mud’s Stokes boundary layer, thus ensuring that the entire viscous mud layer is in shear:

$$ ka\approx kd_{m}\approx k\delta_{m}\ll 1 $$
(8)

where d m is the thickness of the mud layer and \(\delta _{m}=\sqrt {2\nu /\omega }\) is the thickness of the boundary layer of the viscous fluid representing mud; ν is the kinematic viscosity of the fluid. With this scaling, Ng (2000) allowed the mud-induced dissipation to be a second-order effect on wave propagation. Thus, the wavenumber K of a dissipative mode can be written:

$$ K=k_{1}+k_{2} $$
(9)

where

$$ |k_{1}| \gg |k_{2}| $$
(10)

The leading order term k 1 is real and a solution of the linear dispersion relation (7), while k 2 is a complex wavenumber which incorporates the effect of the mud. The imaginary part of k 2, which governs the dissipation D, is:

$$ Im\left( k_{2}\right)=D=-\frac{Im\left( B\right)k_{1}}{\sinh k_{1}h\cosh k_{1}h+k_{1}h} $$
(11)

while the real part of k 2 determines the effect of the mud dissipation on the wavelength:

$$ k=k_{1}+Re\left( k_{2}\right)=k_{1}-\frac{Re\left( B\right)k_{1}}{\sinh k_{1}h\cosh k_{1}h+k_{1}h} $$
(12)

In both (11) and (12), B is a complex coefficient:

$$ B=\frac{k_{1}\delta_{m}}{2B_{3}}\left[\left( B_{1}-B_{2}\right)+i\left( B_{1}+B_{2}\right)\right]+\gamma k_{1}d_{m} $$
(13)

where:

$$\begin{array}{@{}rcl@{}} B_{1}&=&\gamma(-2\gamma^{2}+2\gamma-1-\zeta^{2})\sinh{\tilde d}\,\cosh{\tilde d} - \gamma^{2}\zeta\\ &&\qquad\qquad\qquad\qquad\times\left( \cosh^{2}{\tilde d}+\sinh^{2}{\tilde d}\right)\\ &-&(\gamma-1)^{2}\zeta\left( \cosh^{2}{\tilde d}\,\cos^{2}{\tilde d}+ \sinh^{2}{\tilde d}\sin^{2}{\tilde d}\right)\\ &-&2\gamma\left( 1-\gamma\right)\left( \zeta\cosh{\tilde d}+\gamma\sinh{\tilde d} \right)\cos{\tilde d}, \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} B_{2}&=&\gamma\left( -2\gamma^{2}+2\gamma-1+\zeta^{2}\right)\sin{\tilde d}\cos{\tilde d} -2\gamma\left( 1-\gamma\right)\\ &&\qquad\qquad\qquad\qquad\times\left( \zeta\sinh{\tilde d}+\gamma\cosh{\tilde d} \right)\times\sin{\tilde d}, \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} B_{3}&\,=\,&\left( \zeta\cosh{\tilde d}+\gamma\sinh{\tilde d}\right)^{2}\cos^{2} {\tilde d}\,+\,\left( \zeta\sinh{\tilde d}+\gamma\cosh{\tilde d}\right)^{2} \sin^{2}{\tilde d}. \end{array} $$
(16)

Furthermore, there is a dependence on dimensionless quantities:

$$ \gamma=\frac{\rho_{w}}{\rho_{m}} $$
(17)
$$ \zeta=\sqrt{\frac{\nu_{m}}{\nu_{w}}} $$
(18)
$$ {\tilde{d}}=\frac{d}{\delta_{m}} $$
(19)

where the subscripts m and w refer to mud and water, respectively. The advantage of the dissipation model of Ng (2000) in a modeling framework is the explicit nature of the calculation for dissipation D, as it is dependent on mud parameters and the nondissipative wavenumber k 1 only. In contrast, more comprehensive dissipation models (Dalrymple and Liu 1978; Macpherson 1980; Hsiao and Shemdin 1980) require iterative solution for the complex wavenumber K, which can lead to multiple roots in the complex plane (Mendez and Losada 2004; Ng and Chiu 2009).

2.3 Nonlinear parabolic model with mud dissipation

The dissipation D in (11) can be incorporated into the nonlinear parabolic model (Kaihatu et al. 2007):

$$\begin{array}{@{}rcl@{}} & &2i\left( kCC_{g}\right)_{n}\frac{\partial A_{n}}{\partial x}+2i\left( kCC_{g}\right)_{n}D_{n}A_{n}-2\left( kCC_{g}\right)_{n}\left( \overline{k}_{n}-k_{n}\right)A_{n}\\ &+&i\frac{\partial\left( kCC_{g}\right)_{n}}{\partial x}A_{n}+\frac{\partial}{\partial y}\left( \left[CC_{g}\right]_{n}\frac{\partial A_{n}}{\partial y}\right)\\ &=&\frac{1}{4}\left( {\sum}_{l=1}^{n-1}RA_{l}A_{n-l}e^{i{\Theta}(l,n-l,n)}+2{\sum}_{l=1}^{N-n}SA_{l}^{*}A_{n+l}e^{i{\Theta}(-l,n+l,n)}\right) \end{array} $$
(20)

where D n denotes the mud-induced dissipation for the nth component of the wavefield. Kaihatu et al. (2007) used the model (20) to investigate the behavior of a unidirectional train of cnoidal-type waves over isolated mud patches of various sizes. The model was able to simulate both the damping of the waves over the mud and the diffraction of wave energy into the area of reduced wave energy on the downwave side of the mud patch.

While it is not anticipated that nonlinearity will have a significant effect on bulk properties such as wave heights, wave-wave energy exchange will definitely alter the free surface elevation spectra. As a point of comparison, a linear version of (20) is also used to simulate wave propagation over the same domain. Comparison of the two models with data will suggest the importance of nonlinear processes, particularly on the low-frequency wave attenuation (Torres-Freyermuth and Hsu 2014).

2.4 Effect of mud on refraction and shoaling

The mud dissipation model of (Ng 2000) yields two components: the dissipation D and the modified wavenumber k. While this dissipation is the most observable aspect of the effect of mud, the effect of mud on the wavenumber implies an influence on the refraction characteristics as well (Tables 1 and 2).

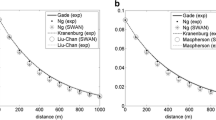
As an illustration, a refraction calculation was performed for waves of periods T = 10 s, 5 s, and 3 s. These waves were assumed to approach the shoreline at an angle of 30 ∘ from shore normal at a water depth h = 4 m. The nearshore wave angle was calculated at a nearshore depth of h = 2 m; both depths were representative of the overall domain used for the model simulations, as described below. The following mud parameters were specified: γ=0.9, \({\tilde d}=1\), and 0≤ζ≤100. Figure 1 shows the refracted wave angle 𝜃, normalized by the refracted angle in the absence of mud 𝜃 n m . At the nearshore location, the wave angle relative to shore normal is smaller when waves propagate over mud than when they propagate over an impermeable, solid bottom; the presence of mud thus increases refraction. It is also clear that the effect of mud on refraction appears to be more evident for longer periods, though in general the effect is not drastic. It is not clear, however, what the accumulated effect would be on refracting wave spectra of reasonable spectral width. Furthermore, despite the small magnitude, it is a potential and cumulative source of error, and would be notable over a long propagation distance.

Fig. 1
figure 1

Effect of viscous mud on refraction angle; this is shown as percentage difference relative to no mud (𝜃/𝜃 N M ). Refracting waves are traversing from h = 4 m to h = 2 m

Full size image

The effect of a mud bottom on the resulting wave height modification for both pure shoaling and combined shoaling / refraction is shown in Fig. 2. Here, using a wave period T = 10 s and the mud parameter as discussed above, both effects are demonstrated with and without the presence of mud. It is apparent that the dissipative effect of mud overcomes any wave height amplification due to shoaling. Additionally, for wave propagation over mud, the added refraction does not greatly alter the shoaled waveheight. This implies that the overall effect of mud on the wavenumber (and associated processes) is small with the mud dissipation formulation used here. This was also shown for a similar scenario by Kaihatu et al. (2007).

Fig. 2
figure 2

Effect of viscous mud on relative wave height, for both shore normal and refracting waves

Full size image

3 Site characteristics and data

3.1 Study site

The study area is located off the muddy chenier-plain coast near western Louisiana, USA, along the northern coast of the Gulf of Mexico, offshore of Vermilion Parish (Fig. 3 and Table 1). The site is near the western edge of the subaqueous delta comprised of Atchafalaya River sediment (Draut et al. 2005). The shelf in the area is very flat, with a slope of around 0.13 % (Safak et al. 2013). Figure 3 also shows the bottom slope and instrument locations.

Fig. 3
figure 3

Atchafalaya and vicinity, Louisiana, USA (top) and depth profile and location of sensors (bottom)

Full size image
Table 1 Sensors
Full size table

A field experiment was held during February and March of 2008, a period during which the local wave environment was highly energetic and the discharge from the Atchafalaya River was near its peak. A transect of four acoustic Doppler velocimeters (ADVs) and an acoustic current profiler were deployed during this time, sampling pressure and three-dimensional velocities. The surface wave, current, and near-bed observations show evidence of fluid mud layers of thickness exceeding 10-cm under strong long wave action (1-m significant height and 7-s peak period at 4-m depth) between 28 February 2008 and 02 March 2008. Field observations, inverse modeling of spectral wave transformation to estimate kinematic viscosity of the mud layer (≈10−4−10−3 m 2/s), and muddy bottom boundary layer modeling were performed for the site. The results indicate that mud-induced dissipation is highest when a fluid mud layer with sediment concentrations exceeding 10 g/L is formed, and that this formation is due to decreasing bottom turbulence and resulting settling of wave-induced resuspension of sediment (Safak et al. 2013).

3.2 Estimates of mud characteristics

The mud layer thickness d m was deduced from acoustic backscatter return from a current profiler near the bed. (Safak et al. 2013) shows the vertical location of the maximum acoustic return in the fluid bed; this is taken to be the lutocline and thus the limit of the mud layer. This depth varied between 0.03 and 0.12 m over the time span of interest. The kinematic viscosity ν m in the mud formulation of Ng (2000) was replaced by a so-called “effective” viscosity (Sheremet et al. 2011), which was dependent only on the mud density ρ m , thereby reducing calibration to that of only one parameter. Sheremet et al. (2011) used a nonlinear stochastic wave model (Agnon and Sheremet 1997) in conjunction with the mud model of (Ng 2000) and an optimization algorithm to determine the effective viscosity which best matches the Fourier components of energy flux. A direct relationship between viscosity and mud density was derived from laboratory experiments on wave forcing of Atchafalaya mud by Robillard (2009), and was used to obtain mud density estimates. Further details concerning the optimization of the effective viscosity and the deduction of ancillary characteristics can be found in Sheremet et al. (2011). Table 2 shows the mud density, effective viscosities, and mud layer depths used in the simulations.

Table 2 Mud parameters
Full size table

3.3 Wave data

Measurements of pressure from the ADVs were sampled at 2 Hz and converted to free surface elevation using standard conversion techniques (e.g., Dean and Dalrymple 1991). Data were taken in bursts of 6144 time series points apiece, thus spanning a time frame of around 51 min per burst. The time period represented in each burst of data is also shown in Table 2.

Data from the offshore sensor (Sensor ADV #1 as shown in Fig. 4) are used to provide the initial condition to the model. The time series are divided into 24 realizations of 256 points apiece, resulting in 48 degrees of freedom. Each realization is input into a fast Fourier transform (FFT), which results in the complex Fourier amplitudes of the free surface input to the model. These initial spectra are truncated at f = 0.3 Hz, as motion at higher frequencies would likely have been attenuated through the water column. This truncation resulted in a total of 39 frequency components per realization put into the model. All realizations of the initial condition corresponding to each burst were run with the model over the mud domain, and were Bartlett-averaged to smooth the spectral estimates.

Fig. 4
figure 4

Model domain for small (top) and wide (bottom) approach angle simulations. Locations of the measurements and the mud patch are shown

Full size image

3.4 Domain and model input

Our primary intent is to investigate the effect of directionality on wave propagation over bottom mud. The most straightforward method for evaluating this effect would be to allow waves to refract over a plane sloping bottom and evaluate the difference between this and one-dimensional propagation.

The depth profile measured along the transect of the instruments (Safak et al. 2013) was thus projected in the longshore direction to create a planar slope. The offshore extent of the modeled domain is a subset of the overall distance to the shoreline; it encompasses the measurement area but does not extend to the shoreline. The modeled domain covers a cross-shore distance of 936 m and spans a range of water depths from 4.16 m offshore to 2.89 m at the nearshore side.

The model input consists of one-dimensional wave spectra measured at the offshore end of the grid. In order to incorporate an approach angle (as defined with respect to the shore normal), the complex Fourier amplitudes from the random time series comprising the spectrum are phase-lagged as follows:

$$ A_{n}(x=0,y) = A_{n}(x=0,y=0)e^{\int ik(\omega_{n},h) \sin\left( \theta\right)dy} $$
(21)

This has the effect of altering the phase of the complex amplitude in a manner representative of a wave propagating at an angle to the x-axis. Because the phase-lagging operation originates at (x=0,y=0; the model origin), directional symmetry about shore normal is not maintained. The free surface wave field for 𝜃 = 30 ∘, for example, does not mirror that for 𝜃 = −30 ∘, since the phase specification would not be symmetric. (For symmetry to be maintained, the origin of the phase lagging operation in Eq. 21 would need to be at the point y = Y/2, where Y is the overall width of the domain.) For linear models, this asymmetry is not reflected in the wave spectra from the model, since there is no correlation between wave phases. However, for nonlinear models, the wave phases are correlated due to the nonlinear interaction terms in the model, and thus the resulting wave spectra appear different between these symmetric directions. This will have an impact on comparisons to data, as will be shown in a later section. The model is run using assumed initial angles of 0∘, ±15∘ (both considered “small” angles) and ±30∘ (considered a “large” angle) with respect to shore normal, in accord with the lack of directional information.

The wave angle affects the longshore extent of the domain. The lateral boundaries of the model are assumed to be fully reflective, which can cause errors to propagate into the area of interest at oblique angles of incidence. To ameliorate this problem without incorporating an open lateral boundary condition, the longshore extent of the domain was extended for high incidence angles. The entire set of parameters used to describe the domain and the model resolution are shown in Table 3. Figure 4 shows the grid configuration for small and wide incident wave angles. A patch of mud is specified, aligned along the central axis of the domain. It was noted by Dalrymple et al. (1984) that diffraction effects would occur near the edges of the dissipation region, possibly affecting the results. From inspection of plots of amplitudes from the model (not shown here), we note that there were no diffraction lobes evident in the results at the gage locations even at the steepest initial approach angles.

Table 3 Domain parameters
Full size table

4 Results and discussion

As mentioned earlier, several previous studies have shown the effect of nonlinear wave-wave interaction on wave processes. However, given that the average peak period is near the short wave range, and that the evolution distance is less than 1 km, it is not clear how prevalent nonlinear processes are in this situation. Simulations using a linearized version of the model (Eq. 2) were also performed, and the results analyzed similarly.

Our first set of comparisons are of the significant waveheight H s from the model to those from the measurements. This comparison does not strictly test the nonlinear energy transfer characteristics of the model against those seen in the data, as it is only a lumped parameter resulting from integration over the entire spectrum, but it does show whether the results are degraded with incident wave angle. Figure 5 shows the results for all bursts, as well as a best fit line, for waves at different initial approach angles. The effect of the asymmetry of the initial condition mentioned above is also evident in these comparisons of bulk statistics, likely due to the limited number of degrees of freedom and the resultant insufficient averaging of phase correlations inherent in the nonlinearity. Overall, it is clear that the approach angle imparted to the incoming wave does not have a deleterious effect on the comparisons with data.

Fig. 5
figure 5

Significant waveheight H s comparisons at sensor ADV #4—modeled vs. measured. Presumed initial approach angle noted in figure panes

Full size image

Figure 6 shows the wave spectral density measured at ADV#4 (the sensor at the shallowest location in the domain) as a function of frequency and burst number. It is evident that the peak frequency of the spectra begins near f p ∼ 0.2 Hz at the beginning of the measurement period, then increases in energy and decreases in peak frequency (to f p ∼ 0.15 Hz) between bursts 8 and 10, then generally reduces in energy toward the end of the measurement period. Interestingly, the low-frequency portion of the spectra seems largely devoid of significant energy, beginning from burst 20 and continuing to the end of the experiment. In addition to the data at ADV#4, results from both the linear (second row of Fig. 6) and nonlinear (bottom row of Fig. 6) models, for all approach angles, are shown. Qualitative comparisons between the measured and modeled spectral densities do not reveal significant differences between either linear or nonlinear model and data, with the exception of the low frequencies (f≤ 0.10 Hz).

Fig. 6
figure 6

Color maps of log of spectral density S(f) as a function of burst number at sensor ADV # 4. Top figure is the observation. Linear and nonlinear model results are shown in the middle and bottom rows, respectively. Incident wave angles are shown below the columns of figures

Full size image

As described earlier, it is apparent that the presence of mud has an effect on the refraction properties of waves. However, this may not be demonstrated particularly well in the significant waveheight comparisons, as refraction characteristics are dependent on (among other things) wave frequency. Instead, the spectral wave energy is summed over a range of frequencies and the comparisons to data made. The spectra are divided into three bands, each of which is believed to have a distinct response to the water depth and the presence of mud:

$$ f_{low}\leq \frac{f_{p}}{2}\leq f_{mid}\leq \frac{3f_{p}}{2}\leq f_{high} $$
(22)

where f p is the peak frequency of the spectrum at the offshore boundary. The average peak frequency for all bursts is f p ≈0.15 Hz, which sets the average \(\frac {f_{p}}{2}\approx \)0.075 Hz and the average \(\frac {3f_{p}}{2}\approx \)0.225 Hz. Figure 7 shows comparisons of the nonlinear model results to data at ADV #4, separated into the various frequency bands, while Fig. 8 shows the same for the linear model. In general, there is an indication that the model has estimable skill. However, close inspection of the correlation coefficients reveals some of the effects of directionality, for both linear and nonlinear runs. While no single approach angle fits best across all comparisons, it is clear that the case of normal incidence does not demonstrate the most skill in any of the comparisons, a possible indication that waves were not shore normal at the offshore boundary, and that the effect of directionality is detectable.

Fig. 7
figure 7

Comparisons of modeled variance in low-, mid-, and high-frequency bands to data at sensor ADV #4: nonlinear wave model. Presumed initial approach angle noted in figure panes

Full size image
Fig. 8
figure 8

Comparisons of modeled variance in low-, mid-, and high-frequency bands to data at sensor ADV #4: linear wave model. Presumed initial approach angle noted in figure panes

Full size image

Comparisons between linear and nonlinear model results are also informative. While the correlation coefficients are a useful overall statistic, strict reliance can be misleading. For each modeled direction, the correlation coefficients are quite similar between linear and nonlinear results for all frequency bands, with slightly higher skill at low-frequency prediction shown by the nonlinear model. However, this similarity should not be taken to mean that nonlinear processes are unimportant; both Torres-Freyermuth and Hsu (2010) and Torres-Freyermuth and Hsu (2014) demonstrate the importance of low-frequency motion generation in wave-mud interaction. Figure 9 shows a comparison of both linear and nonlinear models to data at all sensors for Burst 13, which occurred after the peak energy was measured at ADV # 4 and appears to be representative of conditions with a relatively low peak frequency (f p e a k ≈ 0.13 Hz). It is apparent that there are substantial differences between the linear and nonlinear model results at all sensors and over the entire modeled frequency range. Wave spectra from the linear model show very little change in shape during the transformation process, while those from the nonlinear model show as much variability across all frequencies as the data. A statistical correlation measure would only detect differences between the models and data, which may be relatively low if the model shows no variation and (conversely) relatively high if the variations do not match well.

Fig. 9
figure 9

Comparison of modeled spectra with data for burst 13 and a presumed approach angle normal to shore. Offshore sensor (ADV # 1) is at x = 802 m and was used for initializing the model. Sensor closest to shore (ADV # 4) is at x = 1738 m. Solid line: model. Dotted line: measurements

Full size image

5 Directional spectra

As mentioned previously, the wave conditions simulated here are unidirectional waves with different initial angles, and represent an initial investigation of the directional effects of waves propagating over a muddy bed. While illuminating, a more complete investigation would involve use of the full directional spectrum as input. Figure 10 shows the directional spectrum for 29 February 2008, 0800 (Burst #11), in log scale; this burst was the only one for which sufficient data were available to discern the directional characteristics of the incident waves. There is a distinct peak at f = 0.3 Hz, a harmonic of the peak frequency f = 0.15 Hz which is likely present due to nonlinear wave-wave interactions. Additionally, the peak itself appears to be split between two different directions (8 and 15 ∘ with respect to shore normal; the waves are generally arriving from the south or south-southwest). It is not clear if this is the result of two different wave systems or if some degree of spectral broadening is taking place. (We note here that the direction of one of the peaks—15 ∘—is the same as one of the assumed angles in the directionality sensitivity study, an indication that these angles are reasonable assumptions for the area.)

Fig. 10
figure 10

Directional spectrum measured at sensor ADV#1 for 29 February 2008, 0800 (Burst # 11)

Full size image

The inclusion of directional spectra into a linear parabolic model is straightforward (Chawla et al. 1998). In nonlinear parabolic models, however, it is less so. While the nonlinear interaction terms in (2) are not explicitly dependent on direction, angular spread is still represented as phase differences in the complex amplitudes via Eq. (21). The reduction of wave-wave interactions to frequencies which satisfy the resonance condition (Kaihatu and Kirby 1995) greatly reduces the number of wave components involved in the nonlinear summations on the right hand side of Eq. (2). However, there is no corresponding condition among angles; nonlinear interactions would thus occur explicitly among all waves traveling in different directions but with frequencies matching the triad condition, and would require accommodation in the nonlinear terms of the model. For wave fields with broad directionality, the resulting increase in computational effort would be substantial. (We note here that the use of an angular spectrum (Agnon and Sheremet 1997), with the corresponding resonant conditions assumed among longshore wavenumber modes, would provide the necessary reduction of directional wave interactions; however, while useful for the present study, these models could not be used for nonuniform longshore conditions in their present form.)

There is precedent for treatment of directional spectra within nonlinear parabolic models; this was performed by Freilich et al. (1990), who used a parabolic, weakly-nonlinear, weakly-dispersive Boussinesq frequency domain model to propagate directional waves over sloping bathymetry. The assumption of weak dispersion in the model used by Freilich et al. (1990) is better suited for long swell waves than they would be for the shorter waves present at the western Louisiana site. Furthermore, the weakly-dispersive assumption greatly expedites the computation relative to the fully-dispersive nonlinear model used in this study (Kaihatu and Kirby 1997). Investigation into efficient implementation of this capability into the dispersive parabolic model is a basis for future work.

6 Conclusions

The sensitivity of the characteristics of wave-mud interaction on directionality and nonlinearity was studied. A two-dimensional parabolic nonlinear wave model, supplemented with a thin-layer mud dissipation mechanism, was tested with data from an experiment conducted in 2008 along the central chenier plain coast of western Louisiana, USA. Mud parameters were optimized using a one-dimensional model (Safak et al. 2013). The refraction properties of waves affected by mud were studied analytically using the approximate bathymetry of the site and Snell’s Law; it was shown that mud would exert a relatively small effect on the nearshore wave angle relative to the absence of mud.

The parabolic model was initialized with measured non-directional wave spectra at the offshore boundary of the domain shown in Fig. 4. To study the effect of the approach angle, the initialization was performed by phase-lagging the Fourier amplitudes of the wave spectrum at ±15 and ±30 ∘, in addition to shore normal. Comparisons of wave spectra and significant wave heights show that the model has estimable skill. However, comparisons of total variance in low frequency, swell, and wind sea bands show that the zero degree approach angle case does not show the best comparison to data at the low and swell frequencies (those assumed to be the most affected by the bottom bathymetry and mud). Thus, it can be inferred that directionality does play a role in the transformation process over bottom mud. Furthermore, comparison of wave spectra from the linear and nonlinear models to the measurements reveals that the variability of the spectral shape seen in the measurements is represented in the nonlinear model results and not in the linear model spectra. This indicates that, despite the favorable skill shown by the statistics, the linear model does not entirely capture the wave dynamics apparent even over a short transformation distance and in a highly damped environment.

Directional information will be available at the measurement locations for future work. This information can be used to initialize and validate the model.