Introduction

For many years, research into numerical processing was dedicated mainly to the study of single-digit numbers. This focus on single-digit processing had the consequence of emphasizing some research areas and overlooking others (see Nuerk, Moeller, Klein, Willmes, & Fischer, 2011, for a critical review on this topic). Among those understudied areas is the processing of multi-digit numbers (i.e., numbers composed of more than one digit) and, within this, place-value coding. The Arabic numerical system employs two dimensions to create multi-digit numbers: digits symbols and place-value (Zhang & Norman, 1995). The position of each digit within the string is used to code different quantities, hence “2” means two units, but in “24” it means two-tens, and in “247” it means two-hundreds. This implies that, in multi-digit numbers, coding the place-value is at least as relevant in number processing as coding the identity of each digit.

The present research is concerned with how place-value is coded in four-digit numbers (e.g., 2795); specifically, we explore to what extent this process is automatic (i.e., whether this process is carried out quickly, effortlessly, and without intention; see Logan 1988). Considering automaticity as a continuum (e.g., MacLeod & Dunbar, 1988), we explored whether the automatic processing of the place value is modulated by the characteristics of the string of digits.

In multi-digit research, the automaticity of place-value has been examined only indirectly. Some of these studies have used the compatibility effect (Nuerk, Weger, & Willmes, 2001), which shows slower reaction times (RTs) when comparing two double-digit numbers in which the unit digit is larger for the smaller number (e.g., 47, 92) compared to a pair in which the unit digit is larger for the larger number (e.g., 42, 87). This effect has also been reported with three-digit numbers (see Korvorst & Damian, 2008), supporting the hypothesis that participants compare units against units, decades against decades, and hundreds against hundreds in parallel. More recent research has shown that, whereas parallel processing is found in two-digit numbers, a combination of parallel and sequential processes arose in four- (not showing compatibility effects) and six-digit numbers (see Meyerhoff, Moeller, Debus, & Nuerk, 2012). These results are relevant because they clearly show that place-value and single-digit magnitude information are taken into account simultaneously. The problem with these lines of evidence is that they have been obtained in explicit comparison tasks; as place-value processing was processed intentionally, these data do not provide a proper test of automaticity (see Tzelgov, 1997).

To the best of our knowledge, only one study has directly assessed the automaticity of place-value coding in multi-digit numbers, using a task where the place-value was not relevant. In this latter study, Kallai and Tzelgov (2012, Experiment 2) found support for the automatic processing of the place-value in four-digit numbers.Footnote 1 They presented two four-digit numbers that differed from each other with regards to their actual physical size (i.e., different font sizes) and asked participants to decide which was physically bigger. Numbers were composed of zeros, and the place value of a non-zero digit was varied within the string (e.g., 0040 vs. 0400). In this way, they simulated different place-values that were irrelevant to the task at hand, but that may conflict (or not) with the physical size of the number strings. Three congruency conditions were included: congruent (e.g., 0040 vs. 0400), incongruent (e.g., 0400 vs. 0040) and neutral (0400 vs. 0400). Additionally, they controlled for the distance, in power of tens, between the numbers, i.e., 0004 has a “decimal distance” of one with 0040, a decimal distance of two with 0400, and a decimal distance of three with 4000. A size-congruency effect (i.e., a worse performance in incongruent as opposed to congruent trials; see also Henik & Tzelgov, 1982) was evident both in RTs and errors. Moreover, the analysis of the decimal distance also confirmed the automatic processing of place value as larger congruency effects were seen with increasing distance. An extended view of these effects, usually found with single digits, is that the congruency effect might be caused by the automatic activation of a quantity representation that would categorize the digits as “small” or “large”, whereas the existence of an interaction between congruency and distance would provide evidence of access to a more refined numerical representation (e.g., the numbers would be placed on a mental number line; see Tzelgov, Meyer & Henik, 1992; see also, Girelli, Lucangeli, & Butterworth, 2000; Szücs & Soltész, 2007; Tang, Critchley, Glaser, Dolan, & Butterworth, 2006; White, Szücs, & Soltész, 2012). In the light of their results, Kallai & Tzelgov (2012) concluded that place-value should be considered a “primitive” unit of our cognitive system. It would be, in addition to single digits, one of those long-term memory representations that are automatically retrieved and are not affected by strategic procedures. Place-value would constitute one of the building blocks of numerical representations (Kallai & Tzelgov, 2012, see also Nuerk, Moeller and Willmes, 2015; Tzelgov, Ganor-Stern, Kallai & Pinhas, 2015).

In the present study, we questioned whether the findings of Kallai and Tzelgov (2012) can be generalized to more complex and life-like digit strings (e.g., 3124), and, hence, whether place-value can be considered a primitive. Compare the following pair of stimuli: 0040 vs. 0400 and 3142 vs. 3412. Despite the fact that they were subjected to the same manipulation (two digits are transposed whereas the other two remain the same), it seems easier to process place-value in the condition with repeated zeros than in the condition in which all the digits are different. The sequences employed by Kallai & Tzelgov (2012) provide clear clues to localize the position of the non-zero number in the string. Perceptually, it is easier to code the position of a different number within a sequence of similar numbers (e.g., García-Orza & Perea, 2011). Additionally, it might be easier to assign place-value to numerically less complex numerals (we will expand on these arguments in the Discussion). Hence, it is possible that the strong activation of place-value that was found when using several zeros reduces or even disappears when more complex stimuli are employed, thus supporting that place-value coding is only partially automatic (e.g., MacLeod & Dunbar, 1988). This distinction between partial and fully automatic process is relevant as it implies that different conditions may perturb the processing of place-value. For instance, being able to process place-value in an automatic way is fundamental to the understanding of the numerical value of multi-digits, and will allow freeing of resources that can be exploited in subsequent tasks involving those multi-digits (e.g., Ho & Cheng, 1997). Moreover, some children experience great difficulties in acquiring this concept, and previous research suggests it is a good predictor of future arithmetical skills (Hanich, Jordan, Kaplan & Dick, 2001). Finally, the automatization of this knowledge is a fundamental step in children’s numerical development.

To test whether the automatic processing of place-value is affected by the characteristics of the numbers, we presented participants with a physical comparison task in which they were requested to decide which of the two displayed numbers was physically bigger. In the ‘simple’ condition, which replicates Kallai and Tzelgov’s (2012, Experiment 2), stimuli were pairs of four-digit numbers composed of a non-zero digit and three zeros (e.g., 0040 vs. 0400). In the ‘complex’ condition, the four-digit numbers were composed of different integers (e.g., 3142 vs. 3412). The place-value of two digits (the non-zero digit and one zero in the simple condition, and two different digits in the complex condition) was varied within the string, keeping decimal and single-digit distances controlled overall. According to their numerical value and physical size, the pair of stimuli presented could be congruent (i.e., the number shown in a bigger font size is also numerically bigger) or incongruent (i.e., the number shown in a bigger font size is numerically smaller). From a strong automatic view of place-value coding, larger congruency effects are expected in larger distances. Importantly, this interaction should be equivalent in the simple and the complex condition. From a weak automatic view, interaction effects are expected to arise in the simple condition, being smaller (or even absent) in the more complex condition.

Methods

Participants

Twenty-five undergraduates (aged between 20 and 33 years; average age = 23.6 years; 20 women) participated voluntarily in this experiment. All had normal or corrected-to-normal vision, and were naive regarding the purpose of the study. Seven additional participants were excluded from the analyses for misunderstanding the task (despite having read the instructions, they decided to press the side of the numerically larger number) or employing inappropriate response keys. In their experiment, Kallai and Tzelgov (2012) obtained congruency effect sizes that corresponded roughly to an f = .73. An a priori power analysis using G*Power 3.1 (Faul et al. 2007) revealed that a sample size of 25 should be sufficient to detect a similar congruency effect in our experiment (95% power, α = .05).

Stimuli

The stimuli were pairs of four-digit strings (see Table 1 for an example, and see Appendix for a complete list of the stimuli used). In one condition, following Kallai and Tzelgov (2012), the numbers to be compared were composed of three zeros and a digit from 1 to 9 (e.g., 0040 vs. 0400). We will term this the “zero-condition”. In the other condition, the stimuli were composed by strings of four different digits (e.g., 2487–2478); we termed this “all-different condition”, as the integers in each string were never repeated. Nine pairs of four-digit numbers in both conditions were created in such a way that digits in each number pair were exactly the same, with two digits (we termed them “reference digits”) exchanging their position between numbers (e.g., 1000–0001; 8247–7248); in the case of the zero-condition, one of the reference digits was always the non-zero digit and the other was a zero. The numerical distance between the reference digits was maintained the same in the zero and the all-different conditions (e.g., the distance in 1000-0001and in 8247–7248, is 1, respectively: 1–0 and 8–7), and it ranges from 1 to 9.Footnote 2 Similarly, the overall distance between the numbers to be compared was exactly the same in both conditions (e.g., in the previous example the distance is 999 for both pairs). Once this number pairs were created, then the position of the reference digits was moved to create six combinations of number pairs where the reference digits occupied all positions (unit-decade, unit-hundred, unit-thousand, decade-hundred, decade-thousand, hundred-thousand); in contrast to Kallai and Tzelgov (2012), we do not include the four identical conditions (e.g., unit-unit, decade-decade) as we decided not to include neutral pairs (0400–0400). Displacing two reference numbers along the four-digit strings to create different decimal distances allowed us to avoid differences in compatibility between the zero and the all-different condition when the numbers in each pair are compared: two digits are the same, and in one position there is a smaller number and in the other position a bigger number; hence, all the pairs were incompatible in one position. The 54 pairs created in each condition (9 number pairs × 6 position combinations) were presented four times to each participant, with the numerically bigger number in the right or in the left, and with the physically bigger number in the right or in the left, to give a total of 216 trials in each condition. The combination of physical and numerical size determined the congruent (the numerically bigger number appeared in bigger font size) and the incongruent (the numerically bigger number appeared in smaller font size) conditions. The font used for small and big numbers was, respectively, 20 or 21 MS serif font that subtended approximately 6 mm × 12.5 mm and 5 mm × 11.5 mm numbers.

Table 1 An example of experimental stimuli employed in the Experiment. In each number pair, two digits are presented, they share two digits in the same position and two digits in different positions. In this example, all the stimuli are incongruent, as those in bigger physical size are numerically smaller
Full size table

Procedure

Participants were tested in small groups in a quiet room. Stimuli were presented on a 19-inch color monitor. Presentation of the stimuli and recording of response times were controlled by a Windows-based computer using E-prime 2.0 software (Psychology Software Tools, Pittsburgh, PA). Each trial began with a fixation point centered in the screen for a varied time of 200-500 ms. Pairs of strings stayed on the screen until either a response had been given, or 1500 ms had passed. The interval between trials was 800 ms. RTs were measured from target onset to the participant’s response.

Participants were requested to press, as rapidly and as accurately as possible, the right or left button on the keyboard (M or Z, respectively), the one corresponding to the side of the numeral in larger font size.

Each participant received a different (randomized) order of trials. A short break was included every 100 trials. Participants performed a total of 432 trials. The whole experimental session lasted approximately 25 min.

Results

ANOVAs, with the within-subjects factors congruency (congruent, incongruent), string type (zero, all-different) and decimal distance (1, 2, 3), were conducted on median correct RTs and the proportion of errors. As errors were not normally distributed, they were arcsin transformed before the analyses. In the analyses when the condition of sphericity was not met, the Greenhouse-Geisser correction was applied to degrees of freedom. In addition, when planned comparisons were conducted, α values were corrected using the Bonferroni adjustment. Partial eta-square (ηp 2) values were reported as measure of effect size. Finally, following Pinhas, Tzelgov and Ganor-Stern (2012; see also Kallai & Tzelgov, 2012), linear trend analyses were calculated to estimate the existence of decimal distance effects and its interactions.

For the RTs, the three-way ANOVA yielded main effects of congruency [F(1, 24) = 43.02; P < .001; ηp 2 = .64] and string type [F(1, 24) = 22.89; P < .001; ηp 2 = .49]. These main effects were qualified by the two-way interactions between congruency and string type [F(1, 24) = 24.72; P < .001; ηp 2 = .51] and congruency and distance [F(1, 24) = 13.61; P < .001; ηp 2 = .36], and the three way interaction between congruency, string type and distance [F(1, 24) = 4.7; P = .04; ηp 2 = .16]. No other effect or interaction was significant (all Fs < 1). The analysis of errors produced, as in the RT analysis, main effects of congruency [F(1, 24) = 85.09; P < .001; ηp 2 = .78], and two-way interactions between congruency and string type [F(1, 24) = 11.5; P = .002; ηp 2 = .32], and congruency and distance [F(1, 24) = 21; P < .001; ηp 2 = .47]. However, the interaction between the three factors was not significant [F(1, 24) = 1.79; P = .19; ηp 2 = .07]. Not any other effect or interaction were significant (all Fs < 1.5).

To explore the pattern of congruency and distance in each type of string, separate ANOVAs were conducted for the zero and the all-different conditions both over RTs and errors.

For the zero-condition, the ANOVA on the RTs showed a main effect of congruency [F(1, 24) = 45.89; P < .001; ηp 2 = .65] and, more importantly, an interaction between congruency and distance [F(1, 24) = 17.29; P < .001; ηp 2 = .42]. The congruency effect, which was present in all distances (all Ps < .008), increased progressively with decimal distance, so it was about 30 ms at distance 1, about 68 ms at distance 2, and about 127 at distance 3. A similar pattern was found in the error analyses, a congruency effect [F(1, 24) = 74; P < .001; ηp 2 = .75] and an interaction between distance and congruency [F(1, 24) = 20.52; P < .001; ηp 2 = .46]. The congruency effect was present at all distances (all ps < .001), and this effect increased linearly with decimal distance (distance 1: 5%; distance 2: 9%, distance 3: 14%).

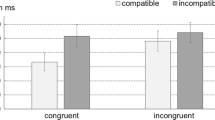
For the all-different condition, the ANOVA on the RTs showed effects neither of distance nor interaction between distance and congruency (both Fs < 1). A main effect of congruency [F(1, 24) = 9.53; P < .01; ηp 2 = .28] arose, i.e., participants responded around 20 ms faster to congruent than to incongruent pairs. An analysis of the errors showed a main effect of congruency [F(1, 24) = 30.42; P < .001; ηp 2 = .56] and, more importantly, an interaction between congruency and decimal distance [F(1, 24) = 5.79; P = .02; ηp 2 = .19]. The congruency effect arose at all three distances (all ps < .03); however, its increase with distance was somewhat smaller in magnitude (distance 1: 3%; distance 2: 6%, distance 3: 8%) compared to that found in the zero-condition (see Fig. 1).

Fig. 1
figure 1

Mean response time (RT) and percentage of errors in each decimal distance for congruent and incongruent pairs in the zero and the all-different conditions. Error bars Standard error

Full size image

Discussion

Place-value is an inherent dimension of the Arabic numerical system, and its understanding is fundamental to managing multi-digit numbers. Understanding of place-value has even emerged as a good predictor of mathematical skills (e.g., Hanich et al., 2001; Ho & Cheng, 1997); additionally, there is wide evidence showing that some people struggle with this concept. The automatization of place-value coding, which allows freeing of resources involved in tasks with multi-digit numbers, has been the focus of recent research. Kallai & Tzelgov (2012) reported automatic access to place-value in four-digit numbers composed of three zeros and a non-zero digit (e.g., 0090), and this was taken as supporting the view that place-value is a primitive of our cognitive system. From this viewpoint, it is considered that the syntactic roles of the digits within a numerical string are retrieved automatically as an “instance” from memory (e.g., Kallai & Tzelgov, 2012; Nuerk et al., 2015).

In the present research, we explored whether the evidence of automatic processing of place-value found by Kallai and Tzelgov (2012) was also observed when more complex numbers (e.g., 2795) were employed. In the zero-condition, we found larger congruency effects in more distant pairs, thus replicating Kallai and Tzelgov’s results pattern. This interaction indicated the access to refined numerical representations (see Tzelgov 1997; see also, Girelli et al., 2000; Szücs & Soltész, 2007; Tang et al., 2006; White et al., 2012), both in RTs and errors when the stimuli employed by Kallai and Tzelgov (2012) were employed. Interestingly, with more complex numbers, carefully matched in different metrics to those used by Kallai and Tzelgov, a similar interaction was found in the error responses, but it does not appear in the RT analysis. These results indicate smaller activation of place-value when multi-digit numbers composed of four different digits were presented (see Fig. 1).

The present findings, while supporting the idea of an automatic access to place-value, at the same time pose some limits on the view of place-value activation as a fully automatic process. As the access to place-value is modulated by the properties of the stimuli to be processed, our results support a partially automatic view (e.g., Kahneman & Treisman, 1984; MacLeod & Dunbar, 1988) of place-value processing. In the processing of four-digit numbers, adding complexity to the sequence of numbers reduces (but does not cancel) the availability of place-value information.

In the following, we shall comment on these findings, but before doing so it is worth clarifying the similarities and differences between our stimuli and those of Kallai and Tzelgov (2012). The pairs of four-digit numbers were built in the same way in both conditions: two digits swapped their positions whereas the other two remain in the same position (see Methods and Table 1). In this way only the order (place-value) was manipulated within the numbers in the pairs. This manipulation also controlled differences in compatibility effects (see Nuerk et al., 2001). Additionally, global distances (i.e., distances considering the overall quantity represented in the four-digit numbers) remained the same in both conditions; even the distances between the reference digits in the four digit numbers were the same (e.g., distance 4: 0400–0040 vs 2735–2375). Thus, a critical difference exists only between the all-different and the zero-condition: this latter condition always had three repeated digits, the zeros, whereas no digits were repeated in the all-different condition. We claim that this difference may affect the early visual processing and place-value assignment that should be carried out for each number, and this precedes the process of numeric comparison that takes place later and causes the distance by congruency interaction. We will sustain our account in the following, but we will first frame the discussion in a broader context, describing a model of place-value processing.

Recently, Nuerk and colleagues (2015) proposed that understanding multi-digit numbers implies creating a structural representation of place-value, and this involves three steps: place identification, place-value activation, and place-value computation. Place identification would be a perceptual process, and would not involve activation of the numerical value of the located digits (e.g., see García-Orza & Perea, 2010). In a second step, once the perceptual process provides us with a spatially distributed sequence of digits, the values associated with these positions are activated (e.g., Nuerk, et al., 2001). A third step, place-value computation, would take place in some circumstances (i.e., it is not automatic), for instance, when computations across place-values are demanded; hence, this step is not relevant for the question in hand for this research. From our standpoint, stimuli complexity (e.g., 0400–0040 vs 2735–2375) would affect the processing of both place identification and place-value activation. The processing of repeated numbers (e.g., 0040) would simplify the perceptual process by facilitating both digit identity processing (only the digits 0 and 4 have to be identified, whereas four digits have to be identified when all different numbers are employed, 2-7-3-5) and place identification. Indirect support may be drawn from priming studies. Using a masked-priming same-different task, García-Orza and colleagues found that two or four digit numbers composed of the same numbers, but in different positions (e.g., 18–81; 3479–3749) primed each other more than unrelated numbers (e.g., 79–18; 3659–3749) (Garcia-Orza et al., 2010; García-Orza & Perea, 2011). Consequently, the visual processes that support place identification are more demanding in all-different numbers than in numbers with three zeros. Similarly, the place-value activation step also seems easier with strings including many zeros. In the zero-condition, most of the numbers included zeros to the left of the non-zero digit (e.g., 0040); in this case, there is no need to code place-value beyond the non-zero digit (e.g., 40). Moreover, it also seems reasonable to think that zeros to the right of a non-zero digit define an empty category (e.g., no-units in the above example), which should also be simpler to process than filling in that category with a real value (see Kallai & Tzelgov, Experiment 1). Thus, there are clear reasons and evidence to consider that processing the place-value of four-digit numbers composed of different digits is more difficult, and hence time consuming, than processing four-digit strings with three zeros. In the case of numbers with three zeros, there is time to compare the numbers, and to reach, as indexed by the interaction between decimal distance and congruency, a refined representation of the difference between the digits. In this case, this would take place before participants respond to the physical task, and hence the numerical information affects the physical task (see Schwarz & Ischebeck, 2003, for a race-based account of the numerical stroop effect). In the all-different condition, the place-value computation is more time consuming and, although a computation of the differences takes place, the effect on the physical task is reduced; in our case it appears only in the errors.

To conclude, the current study was aimed at identifying whether place-value is processed automatically under different conditions. Our results show different levels of automaticity depending on the characteristics of the numbers. It seems that the complexity of the string of digits increases the perceptual load at the identification and position coding processes, and taxes the activation of place-value and its comparison with another number. Automaticity is considered a continuum (e.g., MacLeod & Dunbar, 1988), and our results show that stimuli complexity modulates the capability of the system to process place value. This research supports the view that, in studying automaticity, the focus should be not only whether specific processes are automatic but also under which circumstances more or less automaticity is met.