It is widely agreed that individuals have arithmetic facts represented in long-term memory (e.g., Ashcraft, 1992; Campbell & Graham, 1985; Siegler & Shrager, 1984), which are automatically retrieved when an arithmetic problem is presented (although, see Barrouillet & Thevenot, 2013; Fayol & Thevenot, 2012, for a suggestion that simple additions are resolved through procedures). To illustrate, when a simple addition problem appears (i.e., 2 + 4), due to the principle of spreading activation, there is activation of the correct answer (i.e., 6) and other results related to the operands such as the result of multiplying them (i.e., 8; Winkelman & Schmidt, 1974; Zbrodoff & Logan, 1986) or subtracting them (i.e., 2; Ashcraft & Battaglia, 1978). There is empirical evidence supporting the coactivation of several arithmetic facts when people resolve arithmetic problems (Winkelman & Schmidt, 1974; Zbrodoff & Logan, 1986): When participants perform an arithmetic verification task where they have to decided whether the result of an addition is correct or not, they show higher response latencies for false problems when the stated result is correct for the multiplication operation (i.e., 2 + 4 = 8) compared to when it is not (2 + 4 = 10). This effect was named confusion-product effect, and it seems to indicate that participants coactivate the results associated to the addition and the multiplication problem. Furthermore, Lemaire, Fayol, and Adbi (1991) showed that this confusion-product effect was automatic because the multiplication answer was activated unintentionally after presenting the operands of the addition problem. Importantly, this effect disappeared when there was a 300 ms delay between the operands and the result, suggesting that people had time to resolve the competition among the correct addition result and the irrelevant multiplication result.

It has been proposed that the resolution of conflict after the coactivation of several arithmetic responses is resolved by an inhibitory mechanism (Campbell & Dowd, 2012; Campbell & Thompson, 2012; although, see Censabella & Noël, 2004, for an alternative explanation). Campbell et al. (Campbell & Dowd, 2012; Campbell & Thompson, 2012) used an adaptation of the retrieval practice paradigm. This paradigm is typically employed to demonstrate the inhibition of irrelevant information that competes for selection (Anderson, 2003; Anderson, Bjork & Bjork, 1994). Participants performed a practice phase with simple multiplication problems (i.e., 2 × 3 = ?; 4 × 6 = ?) and, afterward, the same operands were used in a second test phase with simple addition problems (i.e., 2 + 3 = ?; 4 + 6 = ?). The overall finding was that practicing the multiplication problems slowed down the response times to resolve additions whose operands were presented in the practice phase, relative to additions problems whose operands did not appear before. This retrieval induced forgetting effect was interpreted in terms of inhibitory processes. When participants resolved the multiplication problems in the practice phase, the addition problems that competed with the multiplications needed to be inhibited. Therefore, participants took more time to reactivate the additions when they were presented in the test phase.

In addition, recent evidence suggests that individuals apply this inhibitory mechanism in a continuous manner when competition between arithmetic facts takes place during the course of an arithmetic task (Megías, Macizo, & Herrera, 2014). Megías et al. designed an adaptation of the negative priming paradigm (Macizo, Bajo, & Matín, 2010; Tipper & Driver, 1988) in which additions were presented and participants decided whether they were correct or incorrect. The task structure comprised blocks of two trials. In the first trial, participants took more time to respond to an incorrect addition whose result was that of multiplying the operands (i.e., 2 + 4 = 8) relative to a control condition with an unrelated result (i.e., 2 + 4 = 10). This interference effect corroborated that participants activated multiplication facts when they verified addition problems. Moreover, participants took more time to respond in a subsequent trial when a correct addition was presented and its result was that of multiplying the operands of the previous trial (i.e., 2 + 6 = 8) relative to a control condition with an unrelated result (i.e., 4 + 6 = 10). This interference effect obtained in the second trial was the consequence of inhibiting the irrelevant multiplication result in the first trial. Hence, participants needed additional time to reactivate it when it was presented again and became relevant to perform the task.

The main goal of the current study was to evaluate if the coactivation of arithmetic facts and this inhibitory mechanism depended on the numerical surface format with which arithmetic problems were presented. To address this point, we compared the processing of arithmetic problems presented in different numerical formats.

FormalPara The role of the numerical format in mathematical cognition

There is no consensus on whether the representation of number magnitude, which is needed to decide, for instance, the larger of two numbers, is format dependent. Similarly, there is no agreement on whether the representation of arithmetic facts used to resolve simple mathematical operations depends on the format in which they are presented (Cohen Kadosh, Henik, & Rubinsten, 2008).

Some models of mathematical cognition have proposed that magnitude information and arithmetic facts are abstract representations that do not depend on the format of the problem (i.e., the abstract-modular model; McCloskey, 1992; see also, Blankenberger & Vorberg, 1997). These models assume that, regardless of the format, the processing of a numerical input involves the transcoding to an amodal representation. Hence, any difference observed between numerical formats would be located at the encoding stage of processing. For example, individuals take more time to resolve problems in the word format relative to problems in the digit format (Blankenberger & Vorberg, 1997; Campbell & Fugelsang, 2001). The amodal perspective would explain this difference as due to the additional time needed to encode the operands presented in the word format relative to the digit format.

Moreover, this amodal perspective would predict that an effect directly related to the representation of magnitude information or arithmetic facts in long-term memory would not depend on the format in which the problems are presented (i.e., McCloskey, Macaruso, & Whetstone, 1992). However, empirical data do not support this claim. To illustrate, the problem-size effect, which consists in longer reaction times and more errors when individuals resolve operations with large problem size relative to problems with small problem size (Ashcraft, 1992; Groen & Parkman, 1972) seems to depend on the numerical format of the problem (Campbell & Clark, 1988). In fact, the problem-size effect is larger with operations presented in the word format relative to the same operations presented with Arabic digits. This pattern of evidence is easy to accommodate within models suggesting that the representation of arithmetic facts indeed depends on the format of the problem, for instance, the encoding-complex model (Campbell, 1992; Campbell & Clark, 1988), in which it is assumed that the processing and representation of number magnitude and arithmetic facts is format dependent.

Therefore, although there are studies suggesting the existence of an abstract representation of numbers at the behavioral level (e.g., Dehaene & Akhavein, 1995; Naccache & Dehaene 2001b; Schwarz & Ischebeck, 2003) and at the neuronal level (Dehaene 1996; Libertus, Woldrorff, & Brannon, 2007; Naccache & Dehaene, 2001a); many recent studies support the format-dependent representation of number magnitude and arithmetic facts (Bernardo, 2001; Blankenberger & Vorberg, 1997; Campbell & Alberts, 2009; Campbell & Clark, 1992; Jackson & Coney, 2007; McNeil & Warrington, 1994; although see Cohen & Dehaene, 1994; Noël & Seron, 1992; for evidence of format-independent arithmetic processing). For instance, Jackson and Coney used a priming procedure to evaluate format-dependent differences in the resolution of simple arithmetic problems. Participants had to name numbers (e.g., 5) that were preceded by congruent operations (e.g., 2 + 3 = 5), incongruent operations (9 + 7 = 5), or neutral operations (X + Y = 5). The overall priming effect (congruent vs. incongruent condition) was greater when the primes were presented with digit operands than with word operands.

In short, there is previous research demonstrating reliable format-dependent effects in mathematical cognition (e.g., number magnitude and arithmetic facts). Therefore, the question to be addressed is what is the reason for the differences observed in the resolution of mathematical operations depending on the numerical surface format of the problems. We address this point in the following section.

FormalPara Format effects and automaticity

The constant and continued practice on a specific task allows cognitive operations to be automatic (Posner & Snyder, 1975). Automaticity can be considered a relatively low-effort cognitive process that leads to faster and more stable responding (Shiffrin & Schneider, 1977). In the field of mathematical cognition, it has been proposed that the resolution of problems presented in the digit format might be more automatic than problems presented in the word format due to the continuous practice of individuals with Arabic digits (Campbell & Epp, 2004, 2005). For example, as we commented in the previous section, the problem-size effect is larger for problems written in word format relative to problems with Arabic digits (Campbell, 1994; Campbell & Alberts, 2009; Noël, Fias & Brysbaert, 1997). The usual interpretation of this format-dependent effect is that small problems are encountered more frequently in the digit format than in the word format, so they are more likely to have high memory strength and to be retrieved more automatically relative to large problems.

FormalPara The current study

Given that previous research has provided evidence of the role of surface format on the processing of numerical information and the resolution of arithmetic facts (Campbell, 1994; Campbell & Alberts, 2009; Lemaire & Reder, 1999; Noël et al., 1997; Schunn & Reder, 2001; Siegler & Shipley, 1995), the main goal of the current study was to evaluate whether the coactivation of arithmetic facts and the inhibitory mechanism that seems to be responsible to select the correct answer (Campbell & Dowd, 2012; Campbell & Thompson, 2012; Megías et al., 2014) depend on the format of the problem.

In the current study, we manipulated variables to index two processing stages during the resolution of arithmetic problems. The numerical format in which equations were presented directly tapped an encoding stage of processing, while the relationship between additions and multiplications was intended to evaluate two processes at a central level (the coactivation and the inhibition of nodes in the associative network of arithmetic facts). We expected that the activation and the selection of arithmetic facts through an inhibitory mechanism would depend on the format in which simple arithmetic problems were presented. This interaction would support the idea that encoding processes (the type of format in which the problems are presented) determine a central stage of processing (the spread of activation in the associative network represented in long-term memory). To evaluate whether the format of problems determined the coactivation and selection of arithmetic facts, we used the paradigm developed by Megías et al. (2014) and extended it to the case of arithmetic equations presented with words. The participants verified the correctness of additions presented in the digit format (i.e., 2 + 6 = 8) and the word format (i.e., two + six = eight). The first trial was intended to evaluate the automatic coactivation of multiplication facts. We expected to find longer response latency to verify incorrect additions whose result was that of multiplying the operands (2 + 4 = 8) relative to a control condition with unrelated results (2 + 4 = 10). More importantly, if we assume that the automaticity in the resolution of simple arithmetic depends on the format of the problem, this effect would be observed with problems presented in the digit format but not with problems in the word format. These results would support the idea that the coactivation of arithmetic facts depends on the format in which the operations are presented. In addition, participants would inhibit the coactivated result in the digit format so they would take additional time to verify a correct addition whose result was that of multiplying the operands of the previous trials. Again, this effect would interact with the format of the problem so that it might be only observed in the digit format condition but not in the word format condition, indicating that inhibition is applied when competition between coactivated arithmetic facts takes place.

Experiment 1

In Experiment 1, we evaluated the coactivation and selection of arithmetic facts with problems presented in digit format and word format. Evidence for the coactivation of arithmetic facts with the adaptation of the negative priming paradigm was reported in Megías et al. (2014). Since the results reported by the authors with problems in the digit format were innovative, we wanted to replicate them here. Importantly, this condition was directly compared to a new condition where problems were presented using word format for numbers. This was done in order to explore the role played by presentation format in the retrieval of arithmetic facts. If the retrieval of arithmetic facts is less automatic in the case of operations presented with words relative to problems with digit operands, the coactivation of arithmetic facts would be weaker in the written word format relative to the Arabic digit format.

Method

Participants

Twenty-six students from the University of Granada took part in this study. Thirteen participants (12 women and 1 man) were assigned randomly to the group of digit format. Their mean age was 20 years (SD = 2.22). All participants of the digit-format condition were right-handed. Similarly, 13 participants (12 women and 1 man) were assigned randomly to the group of word format. Their mean age was 21 years (SD = 1.99). As in the digit-format group, all participants were right-handed. All the participants gave informed consent to participate in the study at the beginning of the experimental session, and their participation was remunerated with academic credits. The participants completed a questionnaire to determine their use of simple arithmetic (Colomé, Bafalluy, & Noël, 2011) before performing the experimental task (see Table 1). All the participants made simple calculations on a daily basis, at least once daily. Furthermore, t test analyses did not show differences between the participants of the digit-format group and the participants of the word-format group in the scores of this questionnaire, so they had the same knowledge of simple arithmetic (see Table 1). The percentage of calculation of additions on a daily basis was similar in both groups, t(24) = 0.07, p = .94 (43.46 % for the digit-format group and 43.08 % for the word-format group). Similarly, most of the participants in both groups learned the multiplication tables orally (75.38 % for the digit-format group and 83.08 % for the word-format group), t(24) = 0.77, p = .45.

Table 1 Use of simple arithmetic of participants in Experiment 1
Full size table

To evaluate the participants’ knowledge about multiplication tables, they performed a multiplication task in which the operands used in the main experiment were presented (i.e., 2 × 4 = ?) and they had to say aloud the correct result (i.e., 8). The mean correct responses in the multiplication task was similar in both groups (94.65 % for the digit format group and 92.31 % for the word format group), t(24) = 1.08, p = .29. Response times in the multiplication task were also similar in the digit and word format groups (1,062 ms and 1,306 ms, respectively), t(24) = 2.02, p > .05.

Design and materials

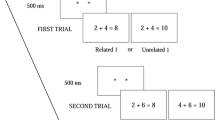
We used a verification task in which participants received additions, and they decided whether they were correct or incorrect. The format of problems, digit format (2 + 4 = 8) and word format (two + four = eight), was manipulated between participants. The additions were presented in blocks of two trials. In the first trial, two conditions were manipulated within participant. The Related 1 condition included incorrect additions whose result was that of multiplying the operands (i.e., 2 + 4 = 8). The Unrelated 1 condition contained incorrect additions whose result was not that of multiplying the operands (i.e., 2 + 4 = 10). In the second trial, two conditions were also manipulated within participant. The Related 2 condition contained correct additions whose result was that of multiplying the previous trial (i.e., 2 + 6 = 8). The Unrelated 2 condition included correct additions with a result that was not that of multiplying the previous trial (4 + 6 = 10). An example of trials in each experimental condition is shown in Table 2.

Table 2 Example of trials used in the experiments
Full size table

To create the experimental blocks of trials, 20 false additions were selected in the first trial (10 Related 1 additions and 10 Unrelated 1 additions), and 20 correct additions were selected in the second trial (10 Related 2 additions and 10 Unrelated 2 additions).Across participants, each addition in each condition of Trial 1 (Related 1 and Unrelated 1) was presented half of the times, followed by a Related 2 addition, and in the other half it was followed by an Unrelated 2 addition. Therefore, the Related 2 and Unrelated 2 additions were preceded an equal number of times by Related 1 trials and Unrelated 1 trials. Each participant received the experimental block of trials twice. Hence, for each participant, there was a total number of 40 observations in each condition of Trial 1 (Related 1 and Unrelated 1) and each condition of Trial 2 (Related 2 and Unrelated 2 condition). The complete set of stimuli used in the experiment is reported in Appendix Table 6.

The additions used in the experimental task were carefully selected to equate them in several factors that might determine possible differences between the conditions in the first and second trial of the experiment. All additions were composed of single-digit operands. The two operands of each problem were presented in ascending order (i.e., 2 + 6) and never in descending order (i.e., 6 + 2 was not used). The parity (even and odd digits) of operands and results was equally distributed across the conditions of the first and second trial of the experimental blocks. In each trial, the solution corresponded to multiplication tables from 1 to 4, and it was never one of the two operands presented in the addition (i.e., 2 + 1 = 2 was not presented).

In the first trial, the Related 1 condition and the Unrelated 1 condition were equated in problem size (the sum of the two operands in both conditions was exactly the same: M = 7.40). The size of the incorrect results presented in the Related 1 condition and the Unrelated 1 condition was also similar (M = 11.80 and M = 11.60, respectively), t(18) = 0.12, p = .90. Also, the distance between the incorrect and the correct result in Trial 1 was exactly the same (M = 4.40). In the second trial, the problem size was equated in the Related 2 condition (M = 11.80) and the Unrelated 2 condition (M = 11.60), t(18) = 0.12, p = .90. In order to maintain the same problem size in the two conditions of Trial 2, one addition problem in the Related 2 condition (7 + 9 = 16) and one problem in the Unrelated 2 condition (4 + 6 = 10) were repeated. The selection of these problems to maintain this criterion was random.

Moreover, we controlled for the degree of similarity between the additions presented in the first trial and those corresponding to the Related 2 condition and the Unrelated 2 condition of the second trialFootnote 1. The numerical distance between the incorrect result presented in the first and second trial was the same in the Related 2 condition and the Unrelated 2 condition (M = 1.40). The difference between the problem size in the first and second trial was the same in the Related 2 condition and the Unrelated 2 condition (M = 4.40). The number of repetitions between the digits presented in the first and second trial (i.e., 2 was repeated in the block composed of the first trial 2 + 3 = 6 followed by 2 + 4 = 6) was the same in the Related 2 condition and the Unrelated 2 condition (8 repetitions). Furthermore, we controlled for the length of the written number words when the additions were presented in word format. In the first trial, the Related 1 condition and the Unrelated 1 condition were equated in the number of letters of the first operand (M = 3.6 in both conditions), the number of letters of the second operand (M = 4.9 in both conditions), and the number of letters of the result presented to the participant (M = 5.6 and M = 5.4, respectively), t(18) = .23, p = .82. In the second trial, the length of the written number words was similar in the Related 2 condition and the Unrelated 2 condition for the first operand (M = 4.4 and M = 4.7, respectively), t(18) = .25, p = .49, the second operand (M = 4.6 and M = 4.7, respectively), t(18) = .32, p = .75, and the result of the addition problem (M = 5.6 and M = 5.4, respectively), t(18) = .23, p = .82.

In order to check that there were no differences in response latency and accuracy when individuals answered to the additions problems used in the Related 2 and Unrelated 2 condition without any manipulation, we performed a pilot study. We evaluated 35 students from the same population as those participating in the main experiment. The participants performed a production task that contained the addition problems presented in the Related 2 and Unrelated 2 conditions. In this task, the order of presentation of additions was pseudorandom, so we controlled that the result of one addition was different from the operands and the result of the preceding addition. We analyzed error percentages, mean RT, and median RT on correct responses with Relation 2 (Related 2 or Unrelated 2) as a within-participant factor. There were no differences in the percentage of errors associated to Related 2 additions (13.53 %) and Unrelated 2 additions (11.59 %), F < 1. Furthermore, the results on the mean RT did not show significant differences between the Related 2 (990 ms) and the Unrelated 2 conditions (984 ms), F < 1. Similarly, the median RT was equated in the Related 2 condition (970 ms) and the Unrelated 2 condition (946 ms), F < 1.

To prevent the participants from noticing the structure of the experimental blocks (a sequence of an incorrect operation in the first trial and a correct operation in the second trial), each list of experimental blocks was randomly intermixed with 10 filler blocks of trials that were repeated four times. The correct responses in the first and second trial of these blocks were yes–yes, no–no, and yes–no, respectively. Therefore, the sequence of responses within each block of two trials was unpredictable through the experiment. The filler blocks included six addition problems and four multiplication problems (see Appendix Table 7). These filler blocks were presented as Arabic digits or as written number words in the digit condition and the word condition, respectively.

Before starting the verification task, the participants performed four blocks of practice trials (two pairs of additions and two pairs of multiplications) with problems that were not used in the main experiment.

Procedure

The experiment was designed and controlled by E-Prime experimental software, 1.1 version (Schneider, Eschman, & Zuccolotto, 2002). The stimuli were always presented in the middle of the screen in black color (Arial font, 30-point size) on a white background. Participants were tested individually and were seated at approximately 60 cm from the computer screen.

The experimental task was a verification of arithmetic problems presented in blocks of two trials. All the problems were presented with Arabic digits (digit condition) or written number words in Spanish (word condition). Participants had to decide if the result of each problem was correct or incorrect. The first trial began with a fixation point in the middle of screen for 500 ms, followed by the arithmetic problem until the participant’s response. After giving the answer, the second trial appeared with the same sequence of events as that of the first trial: a fixation point for 500 ms and the arithmetic problem until the participant’s response. After each block of two trials, the participants were instructed to press the space bar to continue with the following block. Participants were instructed to respond by pressing the keys labeled as “correct” and “incorrect.” The duration of the experiment was approximately 25 minutes.

Results

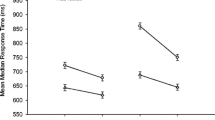
The percentage of errors was 2.67 %. Accuracy analyses were not performed due to the reduced variability of errors in two conditions of the study (only 3 out of 13 participants committed errors in the Unrelated 1 condition with digit numbers and only 5 out of 13 participants committed errors in the Unrelated 1 condition with verbal numbers). Data points below 200 ms and above 2,000 ms were considered outliers, and analyses of variance (ANOVAs) were performed on mean reaction times with trial (first and second trial) and relation (related and unrelated) as within-participant variables and the numerical format (digit vs. numerical words) as a between-participants variable. These analyses showed a main effect of relation, F(1, 24) = 25.22, p < .001, ηp 2 = .51, so that participants took more time to respond to related trials (M = 1,334 ms, SE = 27) relative to unrelated trials (M = 1,294 ms, SE = 25). Furthermore, there was a main effect of numerical format, F(1, 24) = 29.29, p < .001, ηp 2 = .55, such that responses in the word-format group were slower (M = 1,452 ms, SE = 40) in comparison to responses in the digit-format group (M = 1,176 ms, SE = 36). However, there was not a main effect of trial, F < 1. Importantly, the Relation × Format interaction was significant, F(1, 24) = 17.61, p < .001, ηp 2 = .42. Planned comparisons showed significant differences between the related condition (M = 1,213 ms, SE = 38) and the unrelated condition (M = 1,139 ms, SE = 35) in the digit-format group, F(1, 24) = 23.52, p < .001, ηp 2 = .49. However, in the word-format group, there were no differences between the related condition (M = 1,455 ms, SE = 38) and the unrelated condition (M = 1,448 ms, SE = 35), F < 1, ηp 2 = .03. Other effects were not significant (all ps > .27) (see Table 3)

Table 3 Results obtained in Experiment 1
Full size table

.

Further analyses were performed. First, we evaluated whether the interference effect depended on the problem size. To this end, the additions were categorized within each trial (Trial 1 and Trial 2) into small and large problems based on the size of the correct addition result (below and above the median problem size of the stimulus set). Afterwards, problem size (large and small) was introduced in the analyses along with trial (first, second), format (digit, words) and relation (related, unrelated). The outcome of this analysis showed a significant problem-size effect, F(1, 24) = 88.44, p < .001, ηp 2 = .78. Small problems were resolved faster (1,236 ms) than large problems (1,391 ms). However, problem size did not interact with any other variable (all ps > .12). Importantly, the Relation × Format interaction was significant again, F(1, 24) = 7.76, p = .01, ηp 2 = .24, indicating that after controlling for the problem size, the interference effect depended on the format of the addition problems. Second, we evaluated the possible relationship between the interference effect found in the first and second trial of the study. In the digit-format group, the correlation was not significant, r = -.06, p = .83. In the word-format condition, the correlation was not significant either, r = -.07, p = .83. Finally, the interference effect depended on the performance of participants in the experimental task. Thus, there was a negative correlation between the response time of participants to true addition problems in Trial 2 and the interference effect (difference between related minus unrelated trials), r = -.39, p = .05.

Discussion

In Experiment 1 we observed interference effects that were modulated by the format in which the addition problems were presented. In the first trial, the participants in the digit group were slower in the Related 1 condition relative to the Unrelated 1 condition, which seems to indicate that they coactivated the result of multiplying the operands. However, this effect was not observed with additions presented in the word format. Similarly, with Arabic digits, participants were slower in the Related 2 condition relative to the Unrelated 2 condition, suggesting that they inhibited the irrelevant result of multiplying the operands of the first trial, and so they needed additional time to reactivate it in the second trial. Again, this effect was not found with problems presented in the word format. The results obtained with problems presented in the digit format replicate the data reported by Megías et al. (2014) with the same paradigm and surface form of the problems. Hence, the effects found with the adaptation of the negative priming paradigm seem to be a reliable phenomenon. Additionally, the interference effect did not depend on the size of the addition problems presented in the experiment, which seems to indicate that, overall, the problem size of addition problems we used was small so the automatic processing of additions fostered the coactivation of related nodes in the network of arithmetic facts. Moreover, in the digit condition of this experiment, the interference effects in Trial 1 and Trial 2 were unrelated, which seems to indicate that, in the context of the current study, the inhibition applied to select the correct solution was not proportional to the amount of conflict among coactivated arithmetic facts. Furthermore, if we consider the interference effect found in this experiment as an index of the degree of activation spreading through the network of arithmetic facts, it was related to the proficiency of participants in resolving addition problems. A stronger interference effect was associated to faster responses given to correctly resolved additions.

Importantly, the current experiment suggested that coactivation and inhibition of irrelevant arithmetic facts depend on the degree of automaticity to which problems are retrieved from memory. Problems with Arabic digits would be more automatically recovered relative to problems presented in the word format. This automatic retrieval from memory would be accompanied by the spread of activation though the network of arithmetic facts, which would produce the coactivation of related nodes (i.e., multiplications) when participants verified addition problems. The results obtained in this experiment showed faster response times in the digit-format condition relative to the word-format condition. However, the format-dependent effect found here (interference effect in the digit-format group only) might be due to differences in response speed between the two format groups. In fact, it has been documented that negative priming effects are modulated by the time needed to perform the task (fast vs. slow responses, e.g., Neill & Westberry, 1987). Hence, in order to evaluate whether the presence or absence of interference was due to the format of the problem and not to differences in the speed of response, further analyses were performed. For each participant, the median RT was computed, and RT data above and below the median were assigned to a fast-speed condition and a slow-speed condition. This factor was introduced in the analyses as a within-participant variable (fast responses, slow responses) along with trial (first, second), relation (related, unrelated) and format (digit, words). None of the two-way interactions including processing speed were significant (all ps > .05), and the interaction among all factors was not significant, either, F < 1. Importantly, the critical Relation × Format interaction was marginal, F(1, 48) = 3.66, p = .06, ηp 2 = .07. The interference effect was significant in the digit format group, F(1, 48) = 7.65, p = .008, ηp 2 = .14, while it was not in the word format group F < 1. Therefore, the absence of interference effects obtained with problems presented in the word format seems to be not explained by the slow RT of participants in this condition.

The pattern of results obtained in this experiment fits well with the idea that the automaticity in the retrieval of arithmetic facts underlies the presence of interference obtained with problems in the digit format and its absence with problems in the word format.

Nevertheless, it could be argued that the absence of interference effects obtained with word-format operations were not due to a reduced automaticity in the retrieval of arithmetic facts but to the use of other ways to resolve these problems. The participants in the verbal format might be using nonretrieval strategies to verify the additions, and thus no evidence of coactivation and selection during the retrieval of arithmetic facts was observed. Previous proposals supposed that adult individuals always used direct retrieval from memory to resolve arithmetic problems such as additions and multiplications regardless of the numerical format (e.g., Ashcraft, 1992; Ashcraft & Christy, 1995; McCloskey, 1992). However, many recent studies have shown that even simple arithmetic problems might be solved with nonretrieval or procedural strategies such as counting (e.g., 4 + 3 = 4 + 1 + 1 + 1) and transformation (e.g., 4 + 7 = 4 + 4 + 3) (Campbell & Fugelsang, 2001; Fayol & Thevenot, 2012; Imbo & Vandierendonck, 2008; Metcalfe & Campbell, 2007; Thevenot, Fanget, & Fayol, 2007; see Ashcraft & Guillaume, 2009, for a review of strategies in mental arithmetic).

Campbell and Alberts (2009) evaluated whether the format of arithmetic problems (digit format and word format) influenced the degree to which participants used direct memory retrieval to resolve additions and subtractions. After performing these arithmetic problems, the participants indicated the way they resolved them. Overall, the participants used retrieval from memory to resolve problems presented in the digit format in 67 % of cases, while this percentage was reduced to 57 % with problems presented in the word format.

Therefore, the absence of interference effects obtained in the word-format group of Experiment 1 would be explained because participants were using nonretrieval (procedural) strategies to resolve the task, so potential effects associated to direct memory retrieval were not observed. Thus, in order to conclude that the modulation of the interference effect by the surface format was due to automaticity (less automatic retrieval in the word format group), this modulation should be found in participants from the digit and word format groups that used retrieval from memory to perform the task. In the next experiment, we directly addressed this issue.

Experiment 2

The goal of Experiment 2 was to evaluate whether differences due to the format of the problem modulated the activation and selection of arithmetic facts in participants that mainly used direct memory retrieval to resolve the task. A modulation of the interference effects due to the numerical format in these participants would indicate that differences in automaticity would be the underlying factor explaining the effect of the surface form of the problems found in Experiment 1.

Method

Participants

A new set of 60 students from the University of Granada (33 women and 27 men) took part in Experiment 2. None of them participated in Experiment 1. Thirty participants (18 women and 12 men) were assigned randomly to the group of digit format. Their mean age was 23 years (SD = 4.40). Twenty-eight participants of this condition were right-handed and two were left-handed. Thirty participants (15 women and 15 men) were assigned randomly to the group of word format. Their mean age was 23 years (SD = 4.45). In this group, 27 participants were right-handed and three were left-handed. All the participants gave informed consent to participate in the study at the beginning of the experimental session, and their participation was remunerated with academic credits.

In this experiment, we were interested in evaluating possible differences depending on the degree to which participants used direct memory retrieval to perform the task with problems presented in the digit format and word format. To this end, we formed a high retrieval usage group and a low retrieval usage group in each numerical format (digit and word) with the same sample size (15 participants of high retrieval usage and 15 of low retrieval usage in the digit- and word-format groups) by sorting the participants depending on the percentage of direct memory retrieval strategy reported after finishing the experimental task. The criterion of selection was established according to the median value of direct memory retrieval reported by the participants in each format group. In the digit format condition, there were differences in the use of direct memory retrieval between the high retrieval usage group (90 %) and the low retrieval usage group (44 %), F(1, 28) = 79.28, p < .001, η2 = .74. The same difference was found in the word format condition between the high-retrieval usage group (95 %) and the low retrieval usage group (50 %), F(1, 28) = 55.62, p < .001, η2 = .66. The interaction between format and strategy was not significant, F < 1, so the difference between the high retrieval usage group and the low retrieval usage group was similar in the two format groups.

Similarly to Experiment 1, the participants completed a questionnaire to determine their use of simple arithmetic (Colomé et al., 2011) before performing the experimental task (see Table 4). All the participants made simple calculations on a daily basis, most of the participants in both groups learned the multiplication tables orally, and no differences were found in other questions regarding additions and multiplications between the two format groups (all p values > .12). In addition, the participants of Experiments 1 and 2 were equated in the use of simple arithmetic (all ps > .12).

Table 4 Use of simple arithmetic of participants in Experiment 2
Full size table

As in Experiment 1, we evaluated the participants’ knowledge about multiplication tables with the multiplication production task. The mean correct responses in this task was similar in both format groups (92.46 % for the digit-format group and 91.30 % for the word-format group), t(58) = 0.67, p = .50. Response times were also similar in the digit- and word-format groups (1,086 ms and 1,114 ms, respectively), t(58) = 0.37, p = .70. Moreover, the percentage of correct responses in the multiplication product task was similar in participants of Experiment 1 (93.48 %) and participants of Experiment 2 (91.88 %), t(84) = -1.07, p = .29. Response times did not differ in participants of Experiment 1 and 2 (1,184 ms and 1,100 ms, respectively), t(84) = 1.19, p = .24.

Design and materials

The experimental task and the experimental conditions in the first and second trial of this experiment were the same as those of Experiment 1. Additionally, in this experiment we gathered information about the way participants performed the task at the end of the experiment through self-reports of strategies used to resolve arithmetic problems. The participants had to indicate the degree to which they used direct memory retrieval versus nonretrieval strategies in a 7-point Likert scale, from 0 (never used) to 7 (always used), to perform the experimental task.

Procedure

The same procedure employed in Experiment 1 was used here, except that in Experiment 2 participants had to indicate the degree to which they used retrieval from memory versus nonretrieval strategies (transformation and counting) to resolve the task. The use of retrieval from memory included this explanation: when a problem such as 2 + 3 = is presented, you know from memory that 5 is the correct answer. Nonretrieval strategies included the explanation for counting (when a problem such as 2 + 3 = is presented, you count mentally from 2 . . . 3, 4 and 5 to get the answer), transformation (when a problem such as 2 + 3 = is presented, you decompose it in other easy problems, e.g., 2 + 2 + 1) and other strategies different from those explained before.

Results

The mean percentage of incorrect responses was 3.18 %. The mean percentage with which participants used direct memory retrieval over procedural strategies was 70 %, and there were no differences between the digit-format group (67 %) and the word-format group (73 %), F < 1. Data points below 200 ms and above 2,000 ms were considered outliers and analyses of variance (ANOVAs) were performed on means of the reaction times with trial (first and second trial) and relation (related and unrelated) as within-participant variables (related and unrelated conditions), numerical format as a between-participants variable (digit format vs. word format) and direct memory retrieval usage as a between-participants variable (high retrieval usage vs. low retrieval usage). There was a main effect of relation, F(1, 56) = 53.00, p < .001, ηp 2 = .49. As in Experiment 1, responses to related trials were slower (M = 1,366 ms, SE = 21) than responses to unrelated trials (M = 1,321 ms, SE = 19). Similarly, differences between the two numerical formats were significant, F(1, 56) = 44.25, p < .001, ηp 2 = .44, so that participants in the word format group were slower to give the response (M = 1,473 ms, SE = 28) relative to participants in the digit format group (M = 1,213 ms, SE = 28). Furthermore, there was a main effect of direct memory retrieval usage, F(1, 56) = 12.31, p < .001, ηp 2 = .18, such that participants in the low retrieval usage group were slower to respond (M = 1,412 ms, SE = 28) in comparison to participants in the high retrieval usage group (M = 1,275 ms, SE = 28). On the other hand, the Format × Direct memory retrieval usage interaction effect was significant, F(1, 56) = 5.26, p = .02, ηp 2 = .09, as well as the Relation × Direct memory retrieval interaction, F(1, 56) = 5.59, p = .02, ηp 2 = .09.

In order to further investigate these interactions including “direct memory retrieval” as a variable, we conducted the same analyses performed in Experiment 1 for the two retrieval groups separately. The detailed results found in each cell of the current experiment are reported in Table 5.

Table 5 Results obtained in Experiment 2
Full size table

High retrieval usage group

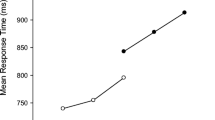
As done in Experiment 1, we performed an ANOVA with trial (first trial and second trial), relation (related condition, unrelated condition) and format (digit format vs. word format; see Table 5). The analyses showed a main effect of relation, F(1, 28) = 42.78, p < .001, ηp 2 = .60, such that related trials were answered to more slowly (M = 1,305 ms, SE = 31) than unrelated trials (M = 1,245 ms, SE = 28). On the other hand, there was a significant difference between the two numerical formats, F(1, 28) = 35.57, p < .001, ηp 2 = .56, so that participants in the word format group took more time to respond (M = 1,450 ms, SE = 41) than participants in the digit format group (M = 1,100 ms, SE = 41). Furthermore, the Relation × Format interaction effect was marginal, F(1, 28) = 3.58, p = .07, and it was associated to a medium effect size, ηp 2 = .11. Planned comparison showed a large relation effect in the digit format group, F(1, 28) = 35.56, p < .001, ηp 2 = .56 (77 ms difference); compared to the relation effect in the word format group, F(1, 28) = 10.81, p = .003, ηp 2 = .28 (42 ms difference). The Trial × Relation × Format interaction effect was not significant, F(1, 28) = 1.65, p = .21. No other effects were significant either (all ps > .41).

Low retrieval usage group

Regarding the analysis in the low retrieval usage group, there was a main effect of relation, F(1, 28) = 13.23, p = .001, ηp 2 = .32, so that participants took more time to respond to related trials (M = 1,427 ms, SE = 27) compared to unrelated trials (M = 1,397 ms, SE = 25). Furthermore, there was a main effect of numerical format, F(1, 28) = 10.85, p = .003, ηp 2 = .28, so that problems in the word format were answered to more slowly (M = 1,497 ms, SE = 37) than problems in the digit format (M = 1,327 ms, SE = 37). In this case, the Relation × Format interaction effect was significant, F(1, 28) = 4.46, p = .04, ηp 2 = .14. Planned comparison showed a relation effect in the digit format group, F(1, 28) = 16.53, p < .001, ηp 2 = .37 (48 ms difference); whereas the relation effect in the word format group was not significant, F(1, 28) = 1.16, p = .29. The Trial × Relation × Format interaction effect was not significant, F < 1. No other effects were significant either (all ps > .11).

Discussion

In Experiment 2, two interference effects were obtained when participants performed the verification of addition problems. These two effects seem to indicate, first, that participants coactivated multiplication facts when they checked the additions and second, that they used an inhibitory mechanism to suppress the activation of irrelevant arithmetic facts to correctly perform the task. However, these effects depended on the numerical format of the operations even in participants that mainly used direct memory retrieval to resolve the problem. In the next section we discuss this pattern of results in terms of the automaticity in the retrieval of arithmetic facts.

In the current experiment, we evaluated the way in which participants resolved the addition problems (memory retrieval, procedural strategies) by asking them to indicate how they accomplished the task at the end of the experiment. It might be argued that a final report is not valid to determine strategy use since traces in working memory of what participants did on each trial would not be available at the end of the task. Hence, a procedure in which participants reported the strategy used to resolve each trial would be preferred. However, negative priming effects strongly depend on the interstimulus interval (i.e., Martín, Macizo, & Bajo, 2010). Therefore, sequential negative priming effect required that problems were solved in succession without an interfering task in between. Moreover, in previous studies, the usual way of evaluating strategy selection is a choice procedure (e.g., Lemaire, Arnaud, & Lecacheur, 2004; Lemaire & Lecacheur, 2001, 2002; see Thevenot et al., 2007, for a critical discussion about the use of verbal reports), where participants have to indicate whether they solve a problem by retrieving the result from memory or by using procedures. However, in the current study, participants were asked to report the degree to which they used retrieval and procedures on a Likert scale. Hence, it could be argued also that the way in which we measured strategy selection with the use of a Likert scale was not appropriated.

We performed an additional control experiment to determine the validity of the self-report measure of strategy selection used in Experiment 2. We evaluated a new set of 60 students from the same pool that participated in Experiment 2. Individuals had to verify the correctness of all addition problems used in Experiment 1 and 2. Thirty participants performed the task with digit numbers and another 30 with number words. Since we were not interested in the responses to the addition problems but in the strategy used to resolve them, the addition problems were randomly presented. Participants reported the strategy used to resolve each problem on a trial-by-trial basis with a two-choice procedure: After the answer to each addition, individuals decided whether they resolved it by direct memory retrieval or by a nonretrieval strategy. Furthermore, in order to compare the two-choice report measure to that used in Experiment 2, participants had to indicate at the end of the arithmetic task the degree to which they used direct memory retrieval versus nonretrieval strategies in a 7-point Likert scale, from 0 (never used) to 7 (always used), a measure that was exactly the same as that used in Experiment 2. We examined possible differences in the percentage of retrieval from memory usage due to the measure of strategy selection (trial-by-trial vs. final report) and the possible interaction with format (digit format vs. word format). The participants reported the use of retrieval from memory to a greater extent in the final report test (72 %) than in the trial-by-trial test (65 %), F(1, 58) = 4.38, p = .04, ηp 2 = .07. The retrieval from memory percentage was similar in the digit-format group (69 %) and the word-format group (68 %), F < 1. Importantly, the Strategy test × Format interaction was not significant, F < 1. In the trial-by-trial test, the percentage of retrieval from memory was 66 % in the digit group and 65 % in the word group. In the final report test, these percentages were 71 % and 72 % for the digit and word groups, respectively. Moreover, the retrieval from memory percentage obtained in the trial-by-trial test (65 %) correlated with that obtained in the final report test (72 %), r = .44, p < .001, and this correlation was significant in the digit-format group, r = .38, p = .04 and in the word-format group, r = .49, p = .006. Furthermore, when we compared the final report of this control experiment with that of Experiment 2, there were no differences in the percentage of retrieval from memory (70 % and 72 %, respectively) nor the experiment interacted with format, Fs < 1. Thus, the measure used in Experiment 2 to evaluate strategy selection seems to be valid for the set of addition problems used in the study.

A fine-grained examination of the results obtained in Experiment 2 leaves another question that needs to be answered: There were no differences in the usage of direct retrieval between numerical formats. In fact, the use of direct memory retrieval was similar in the digit format (67 %) and the word format (73 %). This finding differs from previous studies showing that direct memory retrieval is more frequently used with word operands than with digit operands (Campbell, 1994; Campbell & Alberts, 2009; Campbell, Kanz, & Xue, 1999; McNeil & Warrington, 1994). For example, Campbell and Alberts showed that when addition problems were presented in digit format, participants reported the use of direct memory retrieval more often than the use of procedural strategies (i.e., counting); while the opposite was found when participants resolved operations in the word format. The lack of differences in the use of the direct memory retrieval strategy might be due to the small size of the problems we selected (the addends produced a result equal or less than 18). In fact, there is evidence of reduced format effects on direct retrieval usage for equations with small problem size. Additionally, differences between the current study and previous research might be due to the way of manipulating the format of the problem. Thus, numerical format is usually considered as a within-participants variable (Campbell & Alberts, 2009; Campbell & Fugelsang, 2001; Campbell, Kanz, & Xue, 1999; McNeil & Warrington, 1994) while it was a between-participants factor in our study.

General Discussion

The purpose of the current study was to evaluate if the retrieval and selection of arithmetic facts depended on the numerical surface format in which operations were presented. To this end, participants verified the correctness of simple additions presented in either a digit format or a word format. The results obtained in Experiment 1, with digits, showed that participants were slower to verify additions when the result was incorrect but was the result of multiplying the operands (2 + 4 = 8) relative to a control condition with an unrelated result (2 + 4 = 10). This interference effect is usually interpreted as due to the coactivation and competition of related multiplication answers when participants retrieve the addition facts needed to perform the task (Zbrodoff & Logan, 1986). Previous research has suggested that this competition is solved with the involvement of an inhibitory mechanism responsible to suppress the irrelevant arithmetic response (Campbell & Dowd, 2012; Campbell & Thompson, 2012; Megías et al., 2014). In the current study, this view would imply that participants inhibited the multiplication answer when they verified the correctness of addition problems in the first trial. As a consequence, participants would take additional time to resolve a subsequent addition when the result was that of multiplying the operands of the previous trial. In agreement with this hypothesis, participants responded more slowly to additions presented in the digit format when the result of multiplying the operands of the first trial (2 and 4) was the correct result of the problem presented in the second trial (2 + 6 = 8) relative to an unrelated condition.

Nevertheless, other explanations might account for the interference effects found in the current study when the additions were presented in the digit format. To illustrate, when an incorrect addition was presented in the first trial (e.g., 2 + 5 = 10), participants might coactivate and inhibit the multiplication fact (2 × 5 = 10) along with other addition facts to which the presented result was also true (e.g., 7 + 3 = 10). The current study cannot determine whether other addition facts were coactivated when participants performed the task. However, in our opinion, the interference effects obtained here mainly came from the competition associated to coactivated multiplication facts: First, the critical difference between the Related 1 trials (2 + 5 = 10) and Unrelated 1 trials (2 + 5 = 14) was that the result of a related addition was exactly the result of multiplying its operands while it was not the case in Unrelated 1 additions. On the contrary, the possible coactivation of related additions with the same result (e.g., 7 + 3 = 10) would occur in both a related condition (2 + 5 = 10) and an unrelated condition (e.g., 3 + 4 = 10). Second, coactivation of arithmetic facts directly depends on the strength of connections among problems, and it is assumed that multiplications, which are learned by rote in school, have a higher associative strength than additions (e.g., Ashcraft, 1992; Campbell & Xue, 2001). Therefore, it is reasonable to assume that coactivated multiplications might compete strongly relative to other additions potentially activated.

Another issue to be considered is that interference might not be located at the network of arithmetic facts but at the response level. Thus, in Related 1 trial (2 + 4 = 8), participants might learn the association 8-false, so when a Related 2 trial was presented afterwards (2 + 6 = 8), the result was associated to a true response (8-true), and thus it was hard to overcome the previous incongruous association. Nevertheless, this explanation is difficult to reconcile with previous research showing that interference effects do not depend on the congruency of responses (same/different) in the first and second trial of a negative priming paradigm (Macizo et al., 2010, Experiment 2).

The interference effects obtained in Experiment 1 were only observed when the additions appeared in the digit format but not when they were presented with words. Hence, these results seemed to indicate that coactivation and selection of arithmetic facts was determined by the numerical surface format of problems. We argued that the format effect in the coactivation and selection of arithmetic facts was related to the degree of automaticity to which arithmetic facts are retrieved from memory. It has been proposed that the retrieval and selection of arithmetic facts is associated to practice in the solution of everyday mathematical problems (Besner & Coltheart, 1979). Individual are encountered with operations in the digit format more often than with operations in the word format. Therefore, the resolution of arithmetic problems in the digit format would be associated to an effortless processing of the task and a ballistic retrieval of arithmetic facts from memory. This explanation would imply that when participants were presented with operations in the word format, the processing was less automatic so the spreading of activation in the network of arithmetic facts was reduced, and thus participants did not coactivate arithmetic facts and no inhibitory processes were needed to resolve competition. As a consequence, no interference effects were found in the first trial and second trial of Experiment 1 with equations presented with words.

Nevertheless, the absence of interference effects in the word-format group might be accounted simply by the fact that participants in this group did not use retrieval from memory as the way to resolve the problems. As a consequence, no interference effects would be expected. However, when we controlled for the way in which participants performed the arithmetic task in Experiment 2, the interference effects were still modulated by the numerical format. Specifically, the participants with a high use of retrieval from memory showed the interference effect in the first and second trial of the study. However, the magnitude of these effects was smaller in the word-format group (42 ms) relative to the digit-format group (77 ms). Since these participants were equated in their high use of direct retrieval to resolve the problems, the differences due to the numerical format seem to be related to the automaticity in the activation of arithmetic facts.

Moreover, we also considered participants with reduced use of direct memory retrieval (less than half of cases), and the interference effects were observed again in the digit format but were not present in the word format. This last result suggests that even when individuals used retrieval from memory to a lesser extent, the automatic access to the calculation network with digit problems sufficed to observe the interference effect due to the coactivation of arithmetic facts. In contrast, in the word format, the less automatic spreading of activation in the calculation network reduced the probability of finding this interference effect.

Together, the results found in the current study suggest that the format of arithmetic problems and the degree to which participants use retrieval from memory determine the resolution of simple additions. Both variables work together to foster the spread of activation in the network of arithmetic facts (coactivation effects) and the subsequent selection of what is needed to resolve the problem. The highest coactivation in the network of arithmetic facts is produced when the use of retrieval predominates and the problem is presented in the digit format. On the contrary, reduced or no coactivation of arithmetic facts is observed when the use of retrieval is low and additions are presented in the word format. From this view, we can explain the interference effect associated to problems presented in the word format (Experiment 2). Even when the automaticity to which these problems are solved is low relative to problems in the digit format, interference arises when participants prefer the use of retrieval from memory to perform the task.

Implications for perspectives of arithmetic processing

The results obtained in the current study have relevant implications for current models of arithmetic processing discussed in the introduction section. Overall, the amodal view of arithmetic processing (the abstract-modular model, McCloskey, 1992; see also, Blankenberger & Vorberg, 1997) would assume that the resolution of simple arithmetic would not depend on the surface form of the problem. In contrast, from a format-dependent perspective (i.e., the encoding complex view; Campbell & Clark, 1992; Campbell & Epp, 2004), arithmetic processing and representation would vary with the surface form.

The main effect of surface format observed in this study could be accommodated within the abstract perspective (Blankenberger & Vorberg, 1997; McCloskey, 1992). The participants were faster in verifying the correctness of additions when they were presented in the digit format relative to the word format. This faster response time associated to problems presented with digits might be due to the familiarity of this format, which would make it easier to process the problem at the initial encoding stage of processing. Nevertheless, the results found in this study, suggesting that the coactivation of arithmetic facts depended on the numerical format, is difficult to reconcile with the abstract perspective since these effects go beyond the encoding stage by impacting the retrieval of arithmetic facts. The abstract view assumes the existence of a problem-encoding mechanism to convert several numeral surface forms into a common internal code for calculation, and thus the retrieval of arithmetic facts is not expected to differ with surface form. Accordingly, regardless of the main effect of format, which could be explained by differences at the encoding stage of processing, no other differences would be observed in the coactivation of arithmetic facts across formats since coactivation is a direct image of how calculation knowledge is accessed within the network of arithmetic facts. In contrast, the surface format × relation interaction effects can be accommodated within a format-dependent perspective in arithmetic cognition (Campbell & Clark, 1992; Campbell & Epp, 2004). When individuals mainly use retrieval from memory to resolve simple addition problems, calculation is less automatic with written number words relative to problems presented with Arabic digits.

Overall, we can consider two stages of processing involved in the resolution of arithmetic problems: The encoding level, where the operands and the results are processed, and a central level, where activation spreads in the associative network of arithmetic facts. A main contribution of the current study is the demonstration of an interactive process by which encoding and central stages do not work in an independent manner. On the contrary, we observed an interaction between numerical formats, which tapped the encoding level, and coactivation and inhibition effects, which were located at the central level. This pattern of results suggests that the resolution of simple arithmetic do not involve strictly serial processes performed in isolation but it supports a dynamic view of simple arithmetic in which interactions between peripheral and central processes take place.