1 INTRODUCTION

In physically based rendering, the interaction of materials with light, in particular, by reflection, is very important. Reflection properties affect the visual appearance of objects [1–7]. Realistic visualization of materials with complex optical properties presents a major challenge. In [8], the bidirectional reflectance of surfaces having complex optical properties is described. The bidirectional scattering distribution function (BSDF)—two-beam scattering function—describes the scattering of light on a surface. Microfacet-based BSDF models use parameterized expressions to approximate reflective properties. In [9], a two-layer model of microfacet reflection is proposed, which combines both specular and diffuse diffraction effects. The paper [10] proposes a compact representation of bidirectional reflection data that combines accurate reconstruction with efficient visualization using the integrated reflectance interpolation. The bidirectional reflection distribution functions describe the interaction of light with a point on a surface. An overview of the methods used to evaluate representations of a bidirectional reflectance distribution function (BRDF—two-beam reflectance function) is given in [11]. For storage efficiency, reflection functions are often approximated by analytical formulas. These approximations are obtained by minimizing the weighted quadratic distances. However, these indices do not correlate well with perceptual quality when the BRDF is used in scene rendering. In [12], the evaluation of the perception quality for BRDF approximations as well as analytical BRDF models by their ability to approximate tabular BRDFs were studied. Most bidirectional scattering models are either based on geometric optics and include multiple scattering but no diffraction effects or based on wave optics and include diffraction but no multiple scattering effects. In [13], a method was proposed for combining the results from single scattering scalar diffraction theory with multiple scattering geometric optics. Monte Carlo integration is used. With considering a surface microgeometry, the method enables one to compute bidirectional scattering of the surfaces with small details. Thin volumes of semi-transparent nanostructures interact coherently with incident light waves to produce fine textural coloration. Such structures are complicated by incoherent scattering due to the accompanying microgeometry. Paper [14] presents a physically based approach to the use of submicroscopic scannings of quasi-periodic one-dimensional modulations in volumes for their realistic display images.

The proposed paper presents a method for physically based rendering of functionally defined objects. To properly generate diffraction effects, wave optics is applied in the rendering. The diffraction effects are caused by changes in surface altitudes [15]. To approximate the phase shifts introduced by the base altitude field, Gabor kernels are used [16]. As a result, an analytical solution is obtained for the spatially-variable detailed distribution wave functions of the BRDF reflection factor.

The aim of the present paper is to create a physically based rendering method for functionally defined objects using graphics processing units for rendering of high-realistic models.

2 FUNCTIONALLY DEFINED OBJECTS

To describe geometric objects, we use perturbation functions of the basic quadric [15, 17]:

$$F^{\prime}(x,y,z)=F(x,y,z)+\sum\limits_{i=1}^{N}f_{i}R_{i}(x,y,z),$$
(1)

where \(F^{\prime}(x,y,z)\) is a free form; \(F(x,y,z)\) is the basic quadric; \(f_{i}\) is the form factor; \(i=\ 1,\dots,N\) is the number of perturbation functions; \(R_{i}(x,y,z)\) is the perturbation:

$$R_{i}(x,y,z)=\begin{cases}Q_{i}^{3}(x,y,z),\quad\text{if}\quad Q_{i}(x,y,z)\geqslant 0;\\ 0,\quad\text{if}\quad Q_{i}(x,y,z)<0,\end{cases}$$
(2)

\(Q(x,y,z)\) is the perturbing quadric.

3 REFLECTANCE DISTRIBUTION WAVE FUNCTION

There are two main types of materials: dielectrics and metals. Their difference in interaction with lighting is that metals do not let light into themselves. Dielectrics have diffuse reflection when light rays penetrate the material and scatter, and then some of the light is absorbed and some emerges out. In addition, dielectrics have white highlights. Metals do not transmit light but reflect it partially or completely, which results in a colored glare. Dielectrics also reflect light, but to a much lesser extent than metals. When the light falls on materials of both types, the Fresnel effect occurs. According to this effect, the degree of reflection depends on the angle of light incidence on the surface. The more acute the angle, the more light will be reflected.

Diffraction models in wave optics are used to calculate the reflected field from a rough surface [18]. In wave optics, light is described by fields with a complex value to encode magnitude and phase.

Consider the altitude field \(h(\mathbf{s})\) [15] of a point \(\mathbf{s}=[s_{u},s_{v},h(\mathbf{s})]\) on a rough surface. The BRFD function is defined as the ratio between the incident radiation from the direction \({\omega}_{i}\) and the reflected radiation in the direction \({\omega}_{0}\). The light reflected from different points on the surface moves different distances depending on the local altitude of the surface. This causes phase shifts in the reflected waves; therefore, it must be taken into account that these waves interfere with each other.

The surface reflects light with a spatially changing phase shift, which is given by the reflection function [18]

$$r(\mathbf{s})=\mathbf{e}^{-i2\pi({\psi}\,\cdot\,\mathbf{n})h(\mathbf{s})/\lambda},$$
(3)

where \(\lambda\) is the wavelength, \({\psi}={\omega}_{i}+{\omega}_{0}\) is the projection, and \(\mathbf{n}\) is the normal.

Several BRDF scalar diffraction models are known [19]: the original Harvey–Shack model, the generalized Harvey–Shack model, two modifications of these models in which the Kirchhoff diffraction formula is applied instead of the Fourier formula, and Kirchhoff’s BRDF model—the base model. In this paper, a generalized Harvey–Shack model was used to strike a balance between computation time and image quality.

Let us define the directions \({\omega}_{i}\) and \({\omega}_{0}\) as three-dimensional unit vectors. The BRDF function is calculated using the surface integral [19]

$$f_{r}({\omega}_{i},{\omega}_{0})=\frac{F|{\omega}_{0}\cdot\mathbf{n}|}{A_{H}\lambda^{2}|{\omega}_{i}\cdot\mathbf{n}|}\,\Bigg{|}\int\limits_{H}r(\mathbf{s})\mathbf{e}^{-i2\pi({\psi}\,\cdot\,\mathbf{s})h(\mathbf{s})/\lambda}\,d\mathbf{s}\;\Bigg{|}^{2},$$
(4)

where \(H\) is the area of the altitude field (the projection of the rough surface onto the \(XY\)-plane), \(A_{H}\) is the projected area, \({\psi}\) is the 2\(D\)-projection of unit vectors, and \(F\) is the Fresnel reflection coefficient.

In Eq. (4), incident light with an infinite coherence region is used to calculate the BRDF. However, realistic light sources have finite regions, for example, inversely proportional to their solid angle.

We calculate the BRDF for a single coherence region as follows:

$$f_{r}({\omega}_{i},{\omega}_{0})=\frac{F|{\omega}_{0}\cdot\mathbf{n}|}{A_{c}\lambda^{2}|{\omega}_{i}\cdot\mathbf{n}|}\,\Bigg{|}\int\limits_{H_{c}}r^{*}(\mathbf{s})\mathbf{e}^{-i2\pi({\psi}\,\cdot\,\mathbf{s})h(\mathbf{s})/\lambda}\,d\mathbf{s}\;\Bigg{|}^{2},$$
(5)
$$r^{*}(\mathbf{s})=\omega(\mathbf{s}-\mathbf{x}_{c})r(\mathbf{s}),$$
(6)
$$A_{c}=\int|\omega(\mathbf{s})|^{2}\,d\mathbf{s},$$
(7)

where \(\omega(\mathbf{s})\) is the coherence kernel, \(H_{c}\) is the part of the projection of the rough surface onto the \(XY\)-plane in the region of the coherence kernel, \(\mathbf{x}_{c}\) is the center of the coherence kernel, \(A_{c}\) is the normalization coefficient, and \(r^{*}\) is the product of \(r(\mathbf{s})\) and the coherence kernel.

When rendering for \(\omega\) (6), we use a fixed size of the coherence region—Gauss with a deviation of 10 \(\mu\)m [20]. To effectively calculate the integral in Eq. (5), an approximation of the reflection function with a phase delay \(r^{*}(\mathbf{s})\) by a weighted combination of Gabor kernels is used. Gabor kernels are best suited for representing high-frequency functions typical for \(r^{*}(\mathbf{s})\).

The Gabor kernel is defined as the product of a two-dimensional Gaussian function and an exponential (plane wave):

$$g(\mathbf{s},\mathbf{c},\zeta,\mathbf{p})=G(\mathbf{s},\mathbf{c},\zeta)\mathbf{e}^{-i2\pi(\mathbf{p}\,\cdot\,\mathbf{s})},$$
(8)
$$G=\frac{1}{2\pi\zeta^{2}}\mathbf{e}^{-\|\mathbf{s}-\mathbf{c}\|^{2}/(2\zeta^{2})},$$
(9)

where \(\mathbf{c}\) is the center of the kernel, \(\zeta\) is the width, \(\mathbf{p}\) is the plane wave parameter, and \(G\) is the normalized two-dimensional isotropic Gaussian function.

Let us consider the approximation of phase shifts by Gabor kernels. Spatially changing phase shifts are introduced for different wavelengths (3). Since the function \(r(\mathbf{s})\) is difficult to calculate, we approximate it using Gabor kernels. To do this, we cover the area of the altitude field with a grid of cells. A uniform mesh is used. Grid cells are squares of the same size that correspond to the original texels of the altitude field. Next, a set of cells centered at \(\mathbf{c}_{k}\) is selected, which covers the current coherence kernel. The coherence kernel is approximated with a constant value for the cell \(w_{k}=w(\mathbf{c}_{k}-\mathbf{x}_{c})\) since the cells are smaller than the coherence region. The Gabor kernel is located in every cell of the grid for the approximation of \(r(\mathbf{s})\) in its neighborhood.

An approximation for \(r^{*}(\mathbf{s})\) can be written in the form

$$r^{*}(\mathbf{s})\approx\sum\limits_{k}w_{k}r_{k}(\mathbf{s})=\sum\limits_{k}w_{k}C_{k}g(\mathbf{s},\mathbf{c}_{k},\zeta_{k},\mathbf{p}_{k}),$$
(10)

where \(C_{k}\) is a complex constant:

$$C_{k}=l_{k}^{2}G(\mathbf{s},\mathbf{c}_{k},\zeta_{k})\mathbf{e}^{-i2\pi(\psi\mathbf{n})(h(\mathbf{c}_{k})-h^{\prime}(\mathbf{c}_{k})\mathbf{c}_{k})/\lambda};$$
(11)
$$\mathbf{p}_{k}=\frac{(\psi\mathbf{n})h^{\prime}(\mathbf{c}_{k})}{\lambda}.$$
(12)

The complex constant includes a scaling factor and a phase shift. Choose \(\zeta_{k}=l_{k}/2\), where \(l_{k}\) is the cell length.

Then the altitude field \(h(\mathbf{s})\) is approximated in each cell around \(\mathbf{c}_{k}\):

$$h(\mathbf{s})\approx h(\mathbf{c}_{k})+h^{\prime}(\mathbf{c}_{k})(\mathbf{s}-\mathbf{c}_{k})=h^{\prime}(\mathbf{c}_{k})\mathbf{s}+(h(\mathbf{c}_{k})-h^{\prime}(\mathbf{c}_{k})\mathbf{c}_{k}),$$
(13)

where \(h^{\prime}(\mathbf{c}_{k})\) is the altitude field gradient at \(\mathbf{c}_{k}\).

We substitute this approximation into \(r(\mathbf{s})\) and obtain an approximation to the contribution of one grid cell:

$$r_{k}(\mathbf{s})=b(\mathbf{s},\mathbf{c}_{k},l_{k})\mathbf{e}^{-i2\pi(\psi\mathbf{n})h(\mathbf{s})/\lambda}\approx l_{k}^{2}G(\mathbf{s},\mathbf{c}_{k},\zeta_{k})\mathbf{e}^{-i2\pi(\psi\mathbf{n})((h(\mathbf{c}_{k})-h^{\prime}(\mathbf{c}_{k})\mathbf{c}_{k})+h^{\prime}(\mathbf{c}_{k})\mathbf{s})/\lambda},$$
(14)

where \(b\) is a binary rectangular function and \(l_{k}^{2}\) is the cell area.

We use the Gabor kernel approximation to calculate the BRDF:

$$f_{r}({\omega}_{i},{\omega}_{0})=\frac{F|{\omega}_{0}\cdot\mathbf{n}|}{A_{c}\lambda^{2}|{\omega}_{i}\cdot\mathbf{n}|}\,\Big{|}\tilde{r}^{*}\Big{(}\frac{{\psi}}{\lambda}\Big{)}\Big{|}^{2}\approx\frac{F|{\omega}_{0}\cdot\mathbf{n}|}{A_{c}\lambda^{2}|{\omega}_{i}\cdot\mathbf{n}|}\,\Bigg{|}\sum\limits_{k}w_{k}C_{k}F_{T}\Big{[}g(\mathbf{s},\mathbf{c}_{k},\zeta_{k},\mathbf{p}_{k})\Big{(}\frac{{\psi}}{\lambda}\Big{)}\Big{]}\Bigg{|}^{2},$$
(15)

where \(F_{T}\) is the Fourier transform.

The Fourier transform of the Gabor kernel is written as another Gabor kernel:

$$F_{T}[(\mathbf{s},\mathbf{c},\zeta,\mathbf{p})](\mathbf{v})=\mathbf{e}^{-i2\pi(\mathbf{c}(\mathbf{v}+\mathbf{p}))}\mathbf{e}^{-i2\pi^{2}\zeta^{2}\|\mathbf{v}+\mathbf{p}\|^{2}}=\frac{1}{2\pi\zeta^{2}}\mathbf{e}^{-i2\pi(\mathbf{c}\,\cdot\,\mathbf{p})}g\Big{(}\mathbf{v};-\mathbf{p},\frac{1}{2\pi\zeta},\mathbf{c}\Big{)}.$$
(16)

Then, we calculate sum (15) running over all the cells in the coherence region.

4 SUBSURFACE SCATTERING

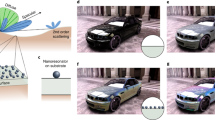
In addition to direct reflection at the point of shading, light can penetrate under the surface, scatter, and exit at another point, as shown in Fig. 1.

Fig. 1
figure 1

Subsurface light scattering.

Full size image

The amount of energy passing into the lower layers is [20]

$$E=(1-F(\alpha_{i}))(1-F(\alpha_{o})),$$
(17)

where \(F\) is the Fresnel reflection coefficient. For plastic, the reflection coefficient depends on the reflection coefficient \(\rho_{\textrm{d}}\) of the diffuse layer [21]:

$$\rho_{p}=E\frac{\rho_{\textrm{d}}}{\pi}\Big{(}1-\frac{\rho_{\textrm{d}}}{\pi}\,F_{\textrm{dr}}\Big{(}\frac{1}{\sigma}\Big{)}\Big{)}^{-1},$$
(18)

where \(F_{\textrm{dr}}\) is the diffuse Fresnel reflectance.

The diffuse Fresnel reflectance corresponds to the integral of the Fresnel reflectance multiplied by the cosine of the angle along the incoming directions.

For the subsurface layer, this depends on the albedo \(a\) of the scattering material [21]:

$$\rho_{\textrm{subsurf}}=E\,\frac{a}{4\pi}\Big{(}\frac{1}{\cos\alpha_{i}^{\prime}+\cos\alpha_{o}^{\prime}}\Big{)}+E\,\frac{a}{2\pi}\mathbf{e}^{-\sqrt{3(1-a)}}\mathbf{e}^{-(4/3)\sqrt{3(1-a)}\,(1-F_{\textrm{dr}})/(1+F_{\textrm{dr}})},$$
(19)

where \(\alpha_{i}^{\prime}\) and \(\alpha_{o}^{\prime}\) are the angles of refraction of the rays with the normal to the surface (see Fig. 1).

5 RESEARCH RESULTS

The high resolution \(8K\times 8K\) of the altitude field as texture maps is used to describe the microgeometry. The texel has a fixed size of one square micron of the real world. The altitude fields are covered with a grid of cells to achieve high surface resolution. Since the texels in the altitude field form a uniform grid, we convert each texel into a Gabor kernel.

To accelerate calculations, we previously create a hierarchy as a MIP-map for each altitude field [15]. Each node contains both the positional and directional bounding boxes of its four child nodes. For each BRDF request, this hierarchy is traversed from top to bottom. Nodes that are not within the coherence regions are discarded. For this, the positional bounding boxes, as well as the directional bounding boxes to remove nodes that do not affect the direction of the request, are used.

Using the Gabor kernels that represent the altitude fields, it is easy to compute the BRDF importance sampling, which is needed to find the outgoing global illumination ray. To do this, the Gabor kernel in the coherence region is randomly selected in accordance with the weight function.

To accelerate rendering, we separate direct lighting from point lights and lighting from other lights, including the environment. This separation makes it possible to use less samples per pixel; rendering requires four to twenty-five samples on a subpixel grid.

Figure 2 shows an anisotropic brushed metal object rendered with a point light source and ambient lighting.

This scene illustrates an object with a brushed metal body illuminated by a point light source and the environment. The altitude field is anisotropic. As shown in Fig. 2, the method is able to handle anisotropy, which results in vertical lines of highlights. It can be seen from the fragment (see Fig. 2, on the right) that the method is able to create widely distributed thin peaks.

Fig. 2
figure 2

Anisotropic brushed metal: the full model (left), fragment (right).

Full size image
Fig. 3
figure 3

An example of a material with subsurface light scattering.

Full size image

Figure 3 shows the result of subsurface scattering simulation.

Subsurface light transport is represented by the bidirectional scattering–surface reflectance distribution function (BSSRDF). The BSSRDFs lead to a generalized reflection equation.

To represent the BSSRDF, we specify the material properties that are responsible for the scattering behavior. Among these are absorption, scattering, attenuation, and albedo coefficients. The anisotropy coefficient is found for anisotropic scattering, leads to a decrease in scattering and attenuation coefficients and a reduced albedo value.

The results are obtained on the Intel Core i7-8700K 6-core CPU at 3.7 GHz and the GeForce GTX 690 (NVIDIA) GPU. The Compute Unified Device Architecture (CUDA) from NVIDIA was used for the implementation. The rendering time for the tested scenes averaged about 60–70 ms per frame.

6 CONCLUSIONS

A method for physically based rendering of functionally defined objects is presented. We have described a material reflection model based on the representation of the surface microgeometry, which allows for diffraction effects caused by smaller-scale details. The model provides a good approximation with the measured materials, including at grazing angles and away from the specular peak, and also explains the wavelength dependence observed in the measured materials. The method uses wave optics to generate diffraction effects. Gabor kernels are used to approximate the phase shifts introduced by the base altitude field. This results in an analytical solution obtained for the spatially-variable detailed wave BRDF.