INTRODUCTION

Computing 3D and range data is important for various applications: computer graphics, medicine, multimedia, machine vision, navigation, automotive safety, computer interaction, tracking, image recognition, and many others. Obtaining 3D geometric data from a complex environment has been a subject of research for many years. Computer graphics and image analysis are two methods for processing visual information. Computer graphics uses formal descriptions of objects to create their visual images. Image analysis systems use the images to create formalized models of objects. Recently, there has been a tendency to mutual integration of computer graphics and image analysis. This is due primarily to the development of virtual reality systems, which use 3D modeling of real objects, which is inefficient for complex 3D objects that require significant time and computing resources.

There are active and passive methods for reconstructing information about the depth of the real scene. Active methods, which output depth information, use laser illumination of the working space [1]. However, these methods have limitations with respect to measurement range and cost of hardware components.

Passive methods based on computer vision are implemented with simpler and more inexpensive distance sensors. Such methods can generate information about the depth by an obtained pair of images and parameters of two cameras [2].

Modeling the shape of real-world objects from a series of images has been investigated in recent years. One well-known approach to 3D modeling is shape generation from a silhouette, which reconstructs the shape of objects from their contours. This approach is popular because of its fast computation and high reliability. The construction of 3D models by multiple views was presented in [3]. The method [4] uses orthogonal projection to build 3D models. Numerous studies are devoted to creating shapes from silhouettes to convert visible contours into a visual form [5–7].

The aim of this work is to develop a method for reconstructing a 3D model of a real object by means of silhouettes and multiview depth maps, which are generated by means of a stereo pair with the subsequent transformation into a functional model.

In this article, a well-known method for creating shape from silhouettes [8] and a correlation algorithm [9] to calculate a depth map are used.

PERTURBATION FUNCTIONS

It is proposed to describe complex geometric objects by defining a perturbation function (second order) from a base quadric, which has the form of the following inequality

$$F(x,y,z)=Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Iz+K\geqslant 0.$$
(1)

Free forms are constructed on the basis of quadrics. A free form is a composition of the base quadric \(F(x,y,z)\) and perturbations [10]

$$F^{\prime}(x,y,z)=F(x,y,z)+\sum\limits_{i=1}^{N}f_{i}R_{i}(x,y,z),$$
(2)

where \(R(x,y,z)\) is the perturbation, and \(f_{i}\) is the form factor:

$$R_{i}(x,y,z)=\begin{cases}Q_{i}^{3}(x,y,z),\quad\textrm{if}\quad Q_{i}(x,y,z)\geqslant 0;\\ 0,\quad\textrm{if}\quad Q_{i}(x,y,z)<0,\end{cases}$$
(3)

where \(Q(x,y,z)\) is the perturbing quadric.

The resulting surface will be smooth and will require a small number of perturbation functions to create complex surface shapes; the amount of data is reduced by more than 100 times compared to a polygonal description [11].

OBJECT RECONSTRUCTION

Calibration of stereo cameras with calculation of such parameters as focal lengths, mutual position of cameras in space, optical curvature parameters, which all video cameras have, brightness distortion parameters, and others will not be considered in this work.

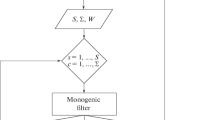
The method consists of three calculation steps:

(1) Computation of silhouettes, voxel model, and intersected nodes of the octree from root to leaves.

(2) Calculation of multiview depth maps, point clouds, merging of point clouds, construction of a triangle grid, and computation of normals.

(3) Transformation into a functional model.

In order to solve the problem of reconstruction of objects, the well-known method of 3D reconstruction using voxels [8], stereo reconstruction with the determination of depth and surface normals [12, 9], and transformation into a functionally defined description of the octree structure and calculated normals were used.

1. In the 3D reconstruction method using voxels, a rotating disk is rotated, video images are captured, and the contour of a real object is extracted (Fig. 1).

When the camera geometry is known, a bounding pyramid can be constructed for each image. This is done by sighting lines from the camera focus through all the contour points of the object silhouette. The shape is computed in 3D by a cut-out method to remove all voxels that are outside the projected silhouette cone. The intersection of all silhouette cones from several images defines the geometry of the object, which is called the visual shape [8].

Fig. 1
figure 1

Real object with shadows in different angles.

Full size image

If the image coordinate defines a background pixel, the voxel is marked as to be removed. After processing all voxels, the object is rotated and the algorithm goes to the next image.

The method is optimized based on voxel calculations using an octree structure. Voxels at the current level can be obtained from the results of the previous level by applying a modified algorithm. Constraints on the areas containing the corresponding information object significantly shorten the computation time. The use of such preprocessing greatly reduces the probability of depth calculation error.

Calculating normals to voxel surfaces is a nontrivial task. The scalar field of a voxel model is considered in its current state, i.e., its time dependence is not taken into account. The gradient of the scalar field \(\nabla f(x)\) is always perpendicular to the level surfaces, the set of points in space at which the scalar field takes the same value. Therefore, the normal to the voxel surface at a given point \(\textbf{n}(\textbf{x})\) can be calculated as a scalar field gradient, which is a vector of partial derivatives of the scalar field along the directions of the coordinate axes. The partial derivative \(\partial f(\textbf{x})/\partial x\) of the considered scalar field toward the \(i\)th axis of the coordinate system can be found as a convolution of the discrete function \(f[\textbf{k}]\) with a filter kernel of a special form. The sequence of operations is performed in one pass for one block of the voxel model. In order to obtain an image of the whole voxel model or its separate part from the camera, the procedure should be repeated for each block in the sample. The operation speed depends on the number and size of output blocks, pixel projection area, and camera orientation relative to the 3D grid (the number of voxel samples increases if projection beams pass through the blocks diagonally). The disadvantages of the method include noninteger processing of blocks. As a result, normals are calculated for block boundaries, while the integrity of the normal map of the monolithic body is not observed.

Therefore, in this work another method was used to calculate normals.

2. In addition to voxel shape generation, the method of reconstruction of the 3D scene from an image sequence is used for depth map computation.

For the calibrated stereo pair, we have two projective matrices [12]:

$$\left(\begin{matrix}u_{i}s_{i}\\ v_{i}s_{i}\\ s_{i}\end{matrix}\right)=M_{i}\left(\begin{matrix}X\\ Y\\ Z\\ 1\end{matrix}\right),$$
(4)

where \(X\), \(Y\), and \(Z\) are 3D coordinates of the point, \(u_{i}\) and \(v_{i}\) are their projections on the image and \(i\); \(s_{i}\), and is the scale factor. The stereo pair \(I=(u,v)\) is the point of the image plane and \(P=(x,y,z)\) is the point of the world coordinate system. From the calibrated stereo pair, the depth map of one perspective of an image is calculated using the correlation algorithm. In this work, the area-based algorithm with correlation of image intensity levels (grey levels) is used [9].

The number of perspectives is generated according to the number of silhouettes calculated earlier. Depth maps are projected back into the 3D space of the object. When reconstructing a 3D shape from multiview silhouettes and depth maps, a cloud of 3D points is first generated from each depth image with an appropriate camera setup. The combination of these point clouds is treated as an initial shape estimate. It is then refined by applying the previously calculated silhouettes to filter out the noise points. The point will be preserved only if all its multiview 2D-projections are inside the silhouettes. Then, a grid of triangles is constructed and the normals are calculated as described in [13].

3. The final shape based on perturbation functions is highly dependent on the accuracy of the normals, because the computation begins by traversing the leaves of the octree where they are stored. After calculating the voxel model and normals, all intersected nodes of the octree are marked at each point on the surface from the root to the leaves to create a functionally specified object (the leaves store the calculated normals).

The surface voxels (leaves of the octree) are matched with the image input signal. Functional objects consist of base quadrics and perturbation functions.

In order to distinguish between the base quadric and the perturbation functions, the coefficients of its equation are preliminary determined. To do this, the quadric should be written into the resulting structure of the octree model, and the coefficients of the base quadric should be determined by the 9 dimensional points of the surface voxels. We have the coefficients of perturbation function equations (1) \(A\), \(B\), \(C\), \(D\), \(E\), \(F\), \(G\), \(H\), \(I\), and \(K\) and coefficients of equations of the base quadric \(q\). At the next defining of the quadrics,

$$Q=\left(\begin{matrix}q_{xx}&q_{xy}/2&q_{xz}/2&q_{x}/2\\ q_{xy}/2&q_{yy}&q_{yz}/2&q_{y}/2\\ q_{xz}/2&q_{yz}/2&q_{zz}&q_{z}/2\\ q_{x}/2&q_{y}/2&q_{z}/2&q\end{matrix}\right).$$
(5)

The value of the function given by (5) at an arbitrary point \(P[x,y,z]\) will be written as follows

$$Q(P[x,y,z])=q_{xx}x^{2}+q_{yy}y^{2}+q_{zz}z^{2}+q_{xy}xy+q_{xz}xz+q_{yz}yz+q_{x}x+q_{y}y+q_{z}z+q.$$
(6)

Since the value of \(Q\) on the surface is zero, we have a system of linear equations to find the quadric coefficients by the 9 points \(P_{1}[x_{1},y_{1},z_{1}]{-}P_{9}[x_{9},y_{9},z_{9}]\)

$$\left\{\begin{matrix}Q(P_{1})=0\\ Q(P_{2})=0\\ \vdots\\ Q(P_{i})=0\\ \vdots\\ Q(P_{9})=0\end{matrix}\right\}.$$
(7)

Substituting (6), we obtain

$$\left\{\begin{matrix}q_{xx}x_{1}^{2}+q_{yy}y_{1}^{2}+q_{zz}z_{1}^{2}+q_{xy}x_{1}y_{1}+q_{xz}x_{1}z_{1}+q_{yz}y_{1}z_{1}+q_{x}x_{1}+q_{y}y_{1}+q_{z}z_{1}+q=0;\\ q_{xx}x_{2}^{2}+q_{yy}y_{2}^{2}+q_{zz}z_{2}^{2}+q_{xy}x_{2}y_{2}+q_{xz}x_{2}z_{2}+q_{yz}y_{2}z_{2}+q_{x}x_{2}+q_{y}y_{2}+q_{z}z_{2}+q=0;\\ \vdots\\ q_{xx}x_{i}^{2}+q_{yy}y_{i}^{2}+q_{zz}z_{i}^{2}+q_{xy}x_{i}y_{i}+q_{xz}x_{i}z_{i}+q_{yz}y_{i}z_{i}+q_{x}x_{i}+q_{y}y_{i}+q_{z}z_{i}+q=0;\\ \vdots\\ q_{xx}x_{9}^{2}+q_{yy}y_{9}^{2}+q_{zz}z_{9}^{2}+q_{xy}x_{9}y_{9}+q_{xz}x_{9}z_{9}+q_{yz}y_{9}z_{9}+q_{x}x_{9}+q_{y}y_{9}+q_{z}z_{9}+q=0.\end{matrix}\right\}.$$
(8)

The solution of the system of equations with the free term \(q\) (let us put it equal to \(K\)) and given \(P_{1}[x_{1},y_{1},z_{1}]\) — \(P_{9}[x_{9},y_{9},z_{9}]\) will be 9 required coefficients: \(q_{xx}\), \(q_{yy}\), \(q_{zz}\), \(q_{xy}\), \(q_{xz}\), \(q_{yz}\), \(q_{x}\), \(q_{y}\), \(q_{z}\).

Next, the coefficients of this quadric will be used when transforming to a functional model and calculated using the Cramer’s method:

$$\left[\begin{matrix}x_{1}^{2}&y_{1}^{2}&z_{1}^{2}&x_{1}y_{1}&x_{1}z_{1}&y_{1}z_{1}&x_{1}&y_{1}&z_{1}\\ x_{2}^{2}&y_{2}^{2}&z_{2}^{2}&x_{2}y_{2}&x_{2}z_{2}&y_{2}z_{2}&x_{2}&y_{2}&z_{2}\\ x_{3}^{2}&y_{3}^{2}&z_{3}^{2}&x_{3}y_{3}&x_{3}z_{3}&y_{3}z_{3}&x_{3}&y_{3}&z_{3}\\ x_{4}^{2}&y_{4}^{2}&z_{4}^{2}&x_{4}y_{4}&x_{4}z_{4}&y_{4}z_{4}&x_{4}&y_{4}&z_{4}\\ x_{5}^{2}&y_{5}^{2}&z_{5}^{2}&x_{5}y_{5}&x_{5}z_{5}&y_{5}z_{5}&x_{5}&y_{5}&z_{5}\\ x_{6}^{2}&y_{6}^{2}&z_{6}^{2}&x_{6}y_{6}&x_{6}z_{6}&y_{6}z_{6}&x_{6}&y_{6}&z_{6}\\ x_{7}^{2}&y_{7}^{2}&z_{7}^{2}&x_{7}y_{7}&x_{7}z_{7}&y_{7}z_{7}&x_{7}&y_{7}&z_{7}\\ x_{8}^{2}&y_{8}^{2}&z_{8}^{2}&x_{8}y_{8}&x_{8}z_{8}&y_{8}z_{8}&x_{8}&y_{8}&z_{8}\\ x_{9}^{2}&y_{9}^{2}&z_{9}^{2}&x_{9}y_{9}&x_{9}z_{9}&y_{9}z_{9}&x_{9}&y_{9}&z_{9}\end{matrix}\right]\left[\begin{matrix}q_{xx}\\ q_{yy}\\ q_{zz}\\ q_{xy}\\ q_{xz}\\ q_{yz}\\ q_{x}\\ q_{y}\\ q_{z}\end{matrix}\right]=\left[\begin{matrix}K\\ K\\ K\\ K\\ K\\ K\\ K\\ K\\ K\end{matrix}\right].$$
(9)
Fig. 2
figure 2

Virtual functionally defined object in different perspectives.

Full size image

Functionally, during rasterization the model is set in a cube with center \((0,0,0)\) and coordinates from \(-1\) to 1 along \(x,y\), and \(z\) in the object coordinate system. In octal division, the coefficients of the equation \(A\), \(B\), \(C\), \(D\), \(E\), and \(F\) are divided by 4 and the coefficients \(XYZ\) , by 2 (reducing the size of the cube). After that, a shift to vector \((\pm 0.5;\pm 0.5;\pm 0.5)\) (10) is made, where unprimed coefficients are taken from the previous recursion step:

$$A^{\prime}=A/4,\quad B^{\prime}=B/4,\quad C^{\prime}=C/4,\quad D^{\prime}=D/4,\quad E^{\prime}=E/4,\quad F^{\prime}=F/4,$$
$$G^{\prime}=G/2+iA/2+jD/4+kE/4,\quad H^{\prime}=H/2+iD/4+jB/2+kF/4,$$
$$I^{\prime}=I/2+iE/4+jF/4+kC/2,\quad K^{\prime}=K/2+iG/4+jH/4+kI/4,$$
$$K^{\prime\prime}=K^{\prime}/2+iG^{\prime}/2+jH^{\prime}/2+kI^{\prime}/2.$$
(10)

All surface points (surface voxels) are known and all branches and leaves of the tree where the model intersected with cubes of different levels of the octree representation of the object space took place as well as all intersected leaves of the tree. The main idea is as follows. If by means of recursive partitioning of the object space, we can visualize functionally defined objects (calculate surface points, normals at these points, illumination, etc.), then we can solve the following inverse problem:

$$N_{x}=\frac{G^{\prime}}{\sqrt{G^{\prime 2}+H^{\prime 2}+I^{\prime 2}}};$$
(11)
$$N_{y}=\frac{H^{\prime}}{\sqrt{G^{\prime 2}+H^{\prime 2}+I^{\prime 2}}};$$
(12)
$$N_{z}=\frac{I^{\prime}}{\sqrt{G^{\prime 2}+H^{\prime 2}+I^{\prime 2}}},$$
(13)

i.e., find functions describing a given object by the given points and normals (11), (12), and (13).

Systems of linear equations at each level of recursion are solved. The same coefficients of equations are determined (taking into account the set threshold of approximation accuracy), and the number of functions at each level is minimized. Only after all equations of a given level have been processed does the process move to the next upper level. This process is repeated up to the octree root and as a result obtains the required minimum of functions representing the given object in the format of description of functionally defined objects on the basis of quadrics with analytical perturbation functions (Fig. 2).

METHOD ANALYSIS AND RESULTS

A voxel model of 3D shape reconstruction using 30 images and \(512^{3}\) voxels was obtained from a real object. It does not have a good degree of smoothness to look realistic. Therefore, a stereo pair reconstruction method was used to calculate the normals more accurately. For the sake of brevity of description and smoothness of the surface, the model was transformed into a functional description. It required 104 perturbation functions. Hierarchical processing using the octree structure significantly shortens the computation time (Table 1).

Table 1 Computation time reduction using hierarchical processing
Full size table

The compression coefficient for transforming polygonal models into functional ones is more than two orders of magnitude, and for voxel models, more than three orders of magnitude. The method was tested for several real objects. This method can be used to transform polygonal and voxel models into functional objects without losses. Moreover, for smooth curvilinear surfaces, the image quality will improve. The objects are visualized using the method described in [14] and using graphics processors. It took from several milliseconds to one second to transform voxel models into functional ones. The testing was performed on an Intel Core2 CPU E8400 3.0 GHz. The known approaches to transform 3D models into implicit surfaces use iterative methods, which are approximate and slow. In the proposed method, the transformation to a functionally based model is carried out by a rigorous mathematical calculation without iterations.

CONCLUSIONS

This article proposed a method for reconstructing real objects from stereo images using the voxel structure of an octree and its transformation into a functional description based on perturbation functions. The transformation is performed by mathematical calculation rather than iteratively and with approximations which lead to a partial loss of information. Hierarchical processing significantly reduces the computation time of the voxel model. The proposed method of defining 3D objects and the method of geometric data transformation have advantages over known approaches.

The main advantages of the proposed method and technique include: the simplicity of transformation of voxel objects into a functional description with a fast search for describing functions as well as a significant reduction in the amount of data for defining curvilinear objects.