1 INTRODUCTION

Development of new nondestructing methods of investigating the stress-strain state of objects, as well as creation of information and measuring systems based on them is a topical problem of present-day instrument engineering. Among many existing nondestructing methods of control, special mention should go to a series of methods called optical.

If the object surface is optically smooth, one can use interference measurement methods. The radiation source wavelength, which is a physical constant, is used as a reference. These methods allow one to perform measurements with an accuracy of up to the hundredth and thousandth of the wavelength [1–4].

With the appearance of holography, it became possible to carry out interferometric measurements of the stress-strain state not only of transparent and reflecting objects (i.e., objects with an optically pure surface) but also diffusely reflecting objects. Holographic interferometry is one of most promising method of control of this state of objects [5–10]. However, the development of holographic interferometry is restricted by the necessity of using higher-resolution photographic materials for registering intermediate holograms. The use of photographic plates is connected with complex chemical processes during the treatment. In addition, it is very difficult to form a large-size reference beam for control of large objects. For this reason, measurement systems based on these methods are used mainly in laboratory conditions for the control of relatively small objects.

For optically rough surfaces, methods based on the moire effect show good results because they are less sensitive to the medium and their measurement range is significantly larger than in interference methods. However, moire methods rank below holographic interference in accuracy [2, 11]. Since the determination of deformations needs measurements of displacement field derivatives, using such methods for investigating the stress-strain state of objects is not realistic.

The structured illumination method is used mainly for measuring the relief profile of relatively small objects due to the insufficient sensitivity [12].

In this work, the possibility of determining deformations of large objects based on the phase method of structured illumination is considered. For this purpose, a new highly sensitive method for the formation of the phase difference field is proposed. Then, measuring the object before and after the action of a certain force on it, one can find the object deformation as the difference of its profiles before and after the loading.

2 PHASE METHOD OF STRUCTURED ILLUMINATION

The Hartmann method is one of earliest ways for determining the curvature of optical elements [13]. First Hartmann sensors were plane plates with small holes which operated as converging lenses. By the arrangement of spots in the focal plane (hartmannogram), one can judge about the wavefront curvature. The photogrammetry method, by use of which spatial coordinates of points of surface object are found by measurements performed by a series of object photographs taken from different locations, is also widely known. In doing this, common points are sought in each image. Then, the line of sight is drawn from the location of the photo camera to the point on the object. The intersection of these lines determines the position of the point in the space. To increase the accuracy in the determination of common points in photogrammetric methods, it is required to create special (in particular, light) spots. Detecting them is a difficult technical problem [14]. The error of photogrammetric measurement systems depends on the distance from the object. For example, for the photogrammetric system based on the V-STARS/N Platinum camera, the measurement accuracy is calculated by the formula 5 \(\mu\)m \(+\) 5 \(\mu\)m/m [15].

At present, reference patterns are most frequently projected using optical projection systems. A certain pattern (structured illumination) is projected on the object; pattern distortions caused by the object shape are recorded by a photo or video camera [12]. Present-day ways based on structured illumination project special patterns whose distortions determine the surface shape [16–19]. The simplest patterns include a set of points, lines, and grids. Lines can be projected using special laser pointers or slide projectors; the simplest way, however, is projection of lines on the object by a usual liquid crystal or laser projector. The camera situated overby the projector records the grid shape and calculates the distance for each point in the field of vision. However, the technique based on recording the displacement of points relative to the reference and finding the \(z\)-coordinate by the points using triangulation technologies does not allow one to determine the surface relief with an accuracy sufficient for determining the deformations.

Phase methods of structured illumination are very similar to methods of pattern projection [20] (in many sources, they are considered as a certain type of structured illumination) and consist in projecting a system of sinusoidal fringes on the object surface. Methods of calculating phase differences developed for interferential and holographic systems [21–23] are also suitable for methods of determining the profile when the object is illuminated by patterns of sinusoidal fringes. This is explained by the fact that the intensity pattern is characterized by the following expression both during interference and during projection of fringes:

$$I_{i}(x,y)=I_{0}(x,y)[1+V(x,y)\cos(\Delta\varphi(x,y)+\delta_{i})],$$
(1)

where \(I_{0}(x,y)\) is the average intensity; \(V(x,y)\) is the average visibility or contrast; \(\Delta\varphi\) is the phase difference between the investigated and ideal distribution of fringes; and \(\delta_{i}\) is the known phase shift. The change in the profile depends on the phase difference \(\Delta\varphi\) and geometry of the optical facility.

The phase shift interferometry (PSI) method proposed for the first time in [24, 25] attracted specialists’ attention by the possibility to obtain measurement information at each point of the interference pattern without analyzing the neighborhood of this point [21, 26, 27]. The step-by-step phase shift method consists in addition of a known phase shift to the distribution of sinusoids during projection of fringes. A series of sinusoidal patterns with a given phase shift is formed in optical projection systems. The general formula for computer simulation of sinusoidal patterns oriented along the \(x\) axis has the form

$$I_{i}(x,y)=a_{0}+a\cos((2\pi N_{p}/N_{x})x-\delta_{i}),$$
(2)

where \(a_{0}\) is the average brightness, \(a\) is the amplitude, \(N_{x}\) is the number of points in the array, \(N_{p}\) is the required number of fringes, and \(\delta_{i}\) is the phase shift.

To find the phase difference which is proportional to the relief of the object surface, we project the system of fringes (2) on the object, fix \(I_{i}(x,y)\), and solve system of equations (1) for \(\Delta\varphi=(2\pi N_{p}/N_{x})x\). In [28], the generalized algorithm for solving systems of transcendental equations (1) for arbitrary phase shifts was described.

3 MEASUREMENT SCHEME

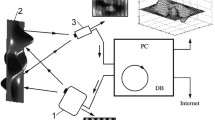
The object is a clamped cantilever beam one end of which is fixed and the other end of the beam is subjected to a load. This measurement scheme is well studied and, therefore, allows one to compare experimental data with results of theoretical calculations. For the beam, an extruded profile of aluminum alloys is used (Fig. 1). Its cross section has the shape of an L-bar with the shelf dimensions \(h=65\) mm, \(b=10\) mm, and the profile thickness \(\Delta=1{.}2\) mm. The elasticity modulus of the beam material \(E=7\cdot 10^{9}\) Pa. The length \(L=0{.}5\) m. The second area moment \(I=5{.}194\cdot 10^{-8}\) m\({}^{4}\) and the magnitude of the concentrated force \(P\) applied at the beam end is 4.5 N.

The loading device is a commercial micrometer which serves also for the control of the bend of the free beam end.

Fig. 1
figure 1

Scheme of loading and cross section shape of the sample under study.

Full size image

The scheme of measurements and the measuring system implementing them are shown in Fig. 2. Here, \(d=1{.}5\) m is the distance between the projector and camera, \(L=2\) m is the distance between the projector and object plane, and \(EF=500\) mm is the beam length.

With a decrease in the period of the projected sinusoidal pattern, one needs projectors with a higher spatial resolution. In this work, a VPL-VW260ES 4K projector was used. It provides a resolution of \(4096\times 2160\) pixels. For the record, a commercial CANON EOS M50 photo camera connected to a computer was used. The photo camera has a CMOS 24.1-MP matrix with dimensions of \(22{.}3\times 14{.}9\) mm (APS-C format). The maximum resolution in the process of frame input is \(6000\times 4000\).

4 DETERMINATION OF DEFORMATIONS

To find the surface deformation field, the phase difference of the profile of two object states is specified: before the deformation and after it.

The object profile is determined using images of the object illuminated by sinusoidal fringes. According to the set of sinusoidal fringes, the phase distribution of the field reflected from the object is found by the step-by-step phase shift method.

Let the area of object recording on the photoreceiver matrix along the \(X\) axis be 4000 pixels; we project 20 fringes (200 pixels per fringe). As a result of measurements, we obtain a phase field with a period determined by the size of the projected sinusoids (Fig. 3).

Fig. 2
figure 2

Measurement scheme (left) and general view of the facility (right).

Full size image
Fig. 3
figure 3

Phase distributions of object images when projecting 20 fringes on the object (a) before and (b) after loading.

Full size image

Phase distributions can be subtracted only after elimination of phase ambiguity. However, the presence of noises makes this procedure rather difficult. For elastic deformations, the displacement is small and one can use the procedure described in [29]. Let us calculate fringe patterns for phase shifts \(\delta_{i}\) using the expression

$$I_{i}(x,y)=\cos(\varphi_{p}(x,y)-\varphi_{r}(x,y)+\delta_{i}),$$
(3)

where \(\varphi_{p}(x,y)-\varphi_{r}(x,y)\) is the phase difference for the first and second states of the object and \(\delta_{i}\) are arbitrary phase shifts. For four shifts \(\delta_{i}=\{0^{\circ},90^{\circ},180^{\circ},270^{\circ}\}\), \(i=0,1,2,3\), we obtain a series of sinusoidal patterns shown in Fig. 4.

Fig. 4
figure 4

Series of sinusoidal patterns corresponding to the field of deformations obtained using expression (3).

Full size image
Fig. 5
figure 5

Plots of normal deformation curves at deflection of the free end of the beam by 0.5, 1.0, 2.0, and 3.0 mm.

Full size image
Fig. 6
figure 6

Plots of normal deformation curves at deflection of the free end of the beam by 10, 20, and 50 \(\mu\)m.

Full size image
Fig. 7
figure 7

Plot of the normal deformation curve of the beam.

Full size image

Then, using the step-by-step phase shift method, we obtain a phase distribution which has points of discontinuity only if the resulting phase distribution exceeds the phase difference of the projected fringes before and after loading of the object. This considerably reduces requirements to algorithms of phase ambiguity elimination. The interpretation formulas for each state of the object has the following form:

$$\begin{cases}\sin(\varphi)=\sqrt{2}(I_{1}-I_{5})+(I_{2}-I_{4}-I_{6}+I_{8}),\\ \cos(\varphi)=\sqrt{2}(-I_{3}+I_{7})-(I_{2}-I_{4}+I_{6}+I_{8}).\end{cases}$$
(4)

The phase shift between the patterns \(\delta_{i}-\delta_{i-1}\) is \(45^{\circ}\). Each of the presented formulas is a combination of two formulas whose reactions on nonlinearity of fringes projected on the object are equal in magnitude but opposite in sign. This makes it possible to reduce the phase determination error by an order of magnitude as compared to known interpretation formulas [4] and, correspondingly, to increase the measurement sensitivity. Then, using algorithm (3), we calculate the phase distribution proportional to the displacement field which coincides with the theoretical beam deflection plot up to a multiplier.

The method can be also used for investigating the stress-strain state of objects by methods of holographic interferometry.

5 DETERMINATION OF METHOD SENSITIVITY

A pattern of sinusoidal fringes is projected on a 430-mm-long beam. Totally, 3996 pixels are projected. Each fringe corresponds to 40 pixels. Thus, totally, we obtain 97.5 fringes. The size of a single fringe is 4.098 mm. When determining phase values which are proportional to the profile, one fringe corresponds to \(2\pi\) rad, which corresponds to 4098 \(\mu\)m. Both before and after object deformation, eight patterns were recorded. The phase shift between the patterns is 90\({}^{\circ}\). Geometric distortions and unevenness of illumination during projection and record of sinusoidal patterns were also eliminated [].

To determine the method sensitivity, different load was applied to the free end of the beam. The deflection of the end was measured by a micrometer with an accuracy of \(\pm 5\) \(\mu\)m. Figure 5 shows plots of the detected deformations when the free end of the beam is deflected by 0.5, 0.1, 2.0, and 3.0 mm, respectively. It is seen that the noise level during the determination of deformation is high. For this reason, here and during the determination of ultimate sensitivity, trends of deformation curves were distinguished.

Table 1

Deformation, \(\mu\)m

Measured value, \(\mu\)m

Absolute error, \(\mu\)m

Relative error

10

10.138

\(\pm 0.124\)

0.0132

20

19.77

\(\pm 0.232\)

0.0115

50

50.71

\(\pm 0.711\)

0.0142

500

487.899

\(\pm 11.102\)

0.0242

1000

1015.442

\(\pm 16.447\)

0.0154

2000

2025.808

\(\pm 25.633\)

0.0129

3000

3040.501

\(\pm 41.365\)

0.0135

To investigate the lower boundary of deformations, measurements under light loads were carried out. The deflection of the free end of the beam amounted to 10, 20, and 50 \(\mu\)m, respectively (Fig. 6). It follows from the figure that the method sensitivity allows one to perform measurements under light loads but the relative measurement error remains rather large. This is well seen in the plot of deformation when the free end of the beam is deflected by 10 \(\mu\)m (Fig. 7).

Table 1 presents results of deformation measurements and average values of the absolute and relative errors calculated over the whole cross section.

6 CONCLUSIONS

In this work, the possibility to determine deformations of large objects by phase structured illumination is considered. The method is based on projecting a series of sinusoidal fringes on the surface of the object under study. A new method for the formation of the phase difference field with a higher sensitivity to displacements is proposed. The method sensitivity is comparable with methods of holographic interferometry. It is shown experimentally that the proposed method allows one to determine deformations when the free end of a clamped beam with a length of 0.5 m is shifted to less than 10 \(\mu\)m.