Between 1970 and 2000, periodic errors in machining were intensely studied. Various models and formulas were proposed by methods such as correlation analysis [1] and spectral analysis [2] (Table 2, items 1 and 8).

Research expanded to embrace discontinuous cutting (Table 2, items 2 and 3) [3, 4]; grinding with submicronic accuracy [5]; and the influence of discontinuous wheels (Table 2, item 17) [6]. Two reasons were identified for the appearance of undulation (Table 2, item 12) [7]: (1) tool motion along specific tracks; (2) transfer of the tool’s geometric error to the workpiece. Computer calculation of complex dimensional chains was employed [8].

However, these examples relate only to errors corresponding to one or two periods. The prediction of machining errors over many periods (10–20 or more) is very difficult [9]. The description of the variational method used to calculate machining errors only includes one example relating to calculations for periodic machining errors and relates to ground surfaces of an uncommon type (produced by errors of the positional screw) [10].

Standardization, monitoring, prediction, and minimization of surface undulation were discussed concisely in [11].

In machine tools, the main reason for undulation of machined metal surfaces is vibration of the machining system. Forced or self-induced vibration may be responsible. Forced vibration is produced by centrifugal forces associated with imbalance of the rotating workpiece, the tool, and other system components (pulleys, gears, joints, shafts, etc.). Self-vibration is due to interaction (including frictional interaction) of the workpiece, the tool, and other system components.

Vibration cannot be eliminated but may be decreased. Devices have been proposed for decreasing vibration [11]. In turning and boring, such devices include a viscous-friction damper; a dynamic vibrational damper; a damping stay; a swinging damper; elastic elements at thin-walled parts; a Sheptalin damper; impact dampers; damping coatings; and specialized boring bars. Vibrationally stable sprung cutters developed by Lakur quench vibrations. The independent operation of two cutters has been proposed. An automatic system that damps cutter vibrations decreases undulation [12]. The dry-friction dampers used in milling contain frictional disks and sprung inertial masses. A flywheel on a machine-tool spindle and an elastically deformed element with a corner plate on the tool holder operate analogously. The flywheel housing is mounted on the spindle, while the damper (two suspension elements) is connected on the tool holder. In machining nonrigid parts, damping stays are employed.

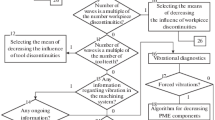
However, changes in the production technology are more effective [13–15].

Three basic approaches to decreasing the height of the surface undulation have been identified (Fig. 1) [11, 13, 15]: (1) adjustment of the mutual trajectory of the tool and workpiece; (2) change in the workpiece setup; (3) change in the discontinuity of the cutting process. The options in the first approach (Fig. 2) are to deform the mutual trajectory (I) and to change the positions of tool and workpiece (II). Deformation of the mutual trajectory may correspond to variation in factors such as the height or pitch of the undulation; the width and position of the troughs and peaks; and their radius of curvature. Possibilities include increase or decrease in the wavelength Lw; increase or decrease in half the pitch of the wave Lw/2 (extension or compression of the waist with corresponding change in inclination); change in peak position (displacement or suppression); trough displacement; and increase in radius of curvature of the troughs and peaks. Other approaches are also possible.

Fig. 1.
figure 1

Approaches to decreasing the undulation height [15]: (◻) UAPK algorithm; (△) UVPK algorithm; MT, mutual trajectory of the workpiece and tool.

Full size image
Fig. 2.
figure 2

Control of the mutual trajectory of the workpiece and tool and undulation profile on the basis of deformation (I) and change in position (II).

Full size image

Self-intersection of waves begins under the following condition [15]: Rto = R ≥ v2/(ν2Ak2) when Wz < 2A. Correspondingly, four possible control approaches are possible: increase in the vibrational frequency ν; increase in the amplitude А; decrease in the relative velocity v of the tool and workpiece; and closer values of the tool radius \({{R}_{{{\text{to}}}}}\) and the radius \({{R}_{{{\text{ms}}}}}\) of the machined surface.

The first two methods are appropriate for vibrational cutting. They are inapplicable to natural vibration, since they do not meet the second condition. Three approaches are of practical value: (1) А \( \to \) min; (2) V \( \to \) min; (3) \({{R}_{{{\text{to}}}}} \to {{R}_{{{\text{ms}}}}}\).

In grinding, the major source of forced vibrations is the imbalance of the wheel. At the workpiece surface, undulation is formed. The most intense harmonic is approximately equal to the ratio of rotational frequencies of the wheel and workpiece.

In centerless grinding, wheel imbalance of \( \pm \)800.375 g cm produces the most intense harmonics (harmonics 13–14). Their magnitude is proportional to the wheel imbalance Рim [16]: \({{\Delta }_{{{\text{pme}}}}} = 2.24 + 0.002{{P}_{{{\text{im}}}}}\). The periodic machining errors may be associated with vibration due to rotor imbalance of the wheel’s motor. Synphase rotation plays a significant role here.

The balancing of grinding wheels is a subject of intense interest [16]. This process calls for compactness, speed, high sensitivity, precision, reliability, and compatibility with automation. Such requirements may be met by devices in which the compensating mass is filtered working fluid [17, 18].

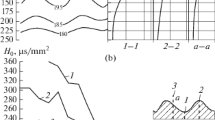
The relative velocity v of the tool and workpiece may be decreased by lowering the workpiece speed vwo in the final stage (dwelling). Continuous change in workpiece speed is more effective [15]. In that case, all except the third harmonics of the periodic machining errors may be decreased (Fig. 3).

Fig. 3.
figure 3

Spectrograms of the surface after external grinding with constant (1) and variable (2) workpiece speed [15]: (◻) UAPK algorithm; (△) VAPK algorithm.

Full size image

To more closely match the tool and workpiece radii, we use bars pressed against the machined surface by centrifugal forces—that is, centrifugal honing [15]. That sharply decreases the high- and moderate-frequency spectral components.

Research on surface undulation in machining was reviewed in detail in [19, 20]. To calculate the height of the undulation, we use three parameters associated with initial surface condition of the workpiece, the tool and workpiece wobble, and the tool’s geometry and kinematics. A calculation method has been proposed for the three main groups of machining methods (Table 2, item 21).

The periodic machining errors may be classified in terms of the ratio n of the wavelength Lw of the dominant vibrations to the length of the machined surface [21]. In other words, the ratio n corresponds to the number of waves of periodic machining errors within the machined surface. On the basis of n, the unity of all the periodic errors may be understood, and the arbitrariness of the familiar classification is apparent. The errors were divided into seven classes (in terms of n) in [21]. In each class, the size, shape, and positional errors are different. This corresponds to the surface extent.

In the first class, corresponding to several workpieces with small extent L of the machined surface, the high-speed process affects the dimensional, shape, and wave precision. Workpieces at the trough of the wave will be smaller than those at the peak of the wave.

For each part, the surface is of different shape. With a sinusoidal wave, the components at the peak of the wave are convex, while those at the trough are concave; those on the incline are nonparallel. In the third class, the surfaces of revolution are characterized by positional error: eccentricity. Those in the fourth class are characterized by shape error: oval or elliptical distortion. The fifth class is transitional. The sixth is characterized solely by undulation and the seventh by roughness. This is conditional, and the type of surfaces may be the same in the sixth and seven classes and even in the fifth class.

It is wrong to regard undulation as irregularity with a pitch greater than the base length [22]. Experience shows that the pitch in undulation may be less than the base length by an order of magnitude or more. Table 1 presents the relation between the periodic machining errors and the frequencies of the most powerful sources of vibration for internal grinding.

Table 1

Spectrogram

Wheel speed, rpm

Workpiece speed, rpm

Eigenfrequency, Hz

Ratio of wheel

and workpiece speeds

Most intense spectral components

298

6300

156

75

40.38

40, 80

299

6300

156

320

40.38

40, 80

300

11 760

156

150

75.38

75

301

11 760

156

320

75.38

75

303

16 000

400

280, 1200

40.42

42

304

10 500

400

105

26.25

27, 28

Table 2

Item

Operation, wave sources

Formulas for wave height and profile

Year, source

1

Any

Profile: Y(x) = Yβ(x) + Yγ(x), where Yβ(x) and Yγ(x) are the systematic and random components

1971

[1]

2

Tooth milling,

discontinuity

Facet height: \({{H}_{B}} = 1.9 \times {{10}^{{ - 5}}}{{m}_{n}}S_{0}^{2}{{\theta }_{Z}}\frac{{\cos a{\text{co}}{{{\text{s}}}^{{3~}}}\beta {\text{co}}{{{\text{t}}}^{2}}~\varphi }}{{\cos \varphi }}\)

1971

[3]

3

Slot milling,

vibration

Height of undulation: \(H = {{H}_{{{{\varphi }_{k}}}}} + {{H}_{{{{A}_{C}}}}} + {{H}_{\delta }}\cos {{\varphi }_{1}} + {{H}_{{{{e}_{1}}}}} = \xi \frac{D}{2}\left( {1 - \cos {\varphi }} \right)\)

1972

[4]

4

Plastic deformation (finishing)

Height of undulation: \({{H}_{2}} = 2{{C}_{0}}\left\{ {1 + {\text{cos}}\left[ {\left( {n - 1} \right)\frac{{180}}{n}} \right]} \right\}\)

1972

[23]

5

External grinding, wheel imbalance

Height of undulation: \({{H}_{B}} = H\left\{ {1 + \cos \left[ {\left( {p - 1} \right)180{\text{/}}\eta } \right]} \right\}\)

1972

[24]

6

Grinding,

vibration

Height of undulation: \({{H}_{1}} = {\Delta }{{Y}_{k}} + {\Delta }\left( {{{Y}_{{{\text{wo}}}}} + {{Y}_{k}}} \right),\) where \({\Delta }{{Y}_{k}} = \frac{{{\Delta }P\beta }}{B}\frac{1}{{K_{a}^{*}}};~\,\,\Delta \left( {{{Y}_{{{\text{wo}}}}} + {{Y}_{B}}} \right) = \frac{{\Delta {{P}_{y}}}}{{{{j}_{{{\text{sp}}}}}}}\)

1973

[25]

7

Machining, vibration

Height of undulation: \(H = {{C}_{0}}\left\{ {1 + \cos \left[ {\left( {p - 1} \right)180^\circ {\text{/}}m} \right]} \right\}\)

1973

[26]

8

Machining and grinding, vibration

Fourier-series description of profile: \(y\left( x \right) = \frac{{{{a}_{0}}}}{2} + \mathop \sum \limits_{n = 1}^\infty \left( {{{a}_{n}}\cos \frac{{n \times 2\pi x}}{{{{B}_{1}}}} + {{b}_{n}}{\text{sin}}\frac{{n \times 2\pi x}}{{{{B}_{1}}}}} \right)\)

1973

[2]

9

Thread grinding, vibration

Height of undulation: \(~H = \frac{2}{\pi }{{H}_{{{\text{max}}}}}\arctan \frac{{3.64}}{{{{H}_{{{\text{max}}}}}}};~\,\,{{H}_{{{\text{max}}}}} = \frac{{{{\lambda }^{2}}\sin \alpha {\text{/}}2}}{{8{{R}_{{{\text{re}}}}}}}\)

1974

[27]

10

External grinding, wheel imbalance

Height of undulation: \({{H}_{{\text{w}}}} = \frac{{{{l}^{2}}}}{8}\left( {\frac{{{{R}_{H}} - {{R}_{{{\text{cr}}}}}}}{{{{R}_{H}}{{R}_{{{\text{cr}}}}}}}} \right)\)

1974

[28]

11

Grinding, oval wheel

Maximum height of undulation: \({{H}_{{{\text{max}}}}} = \left\{ {\frac{{\Delta R}}{2}\left[ {1 + \sin \left( {{\text{arccos}}\frac{{ - t}}{{\Delta R{\text{sin}}\frac{\xi }{2}}} + \frac{\xi }{2}} \right)} \right] + t} \right\}\left( {1 - \frac{{{{C}_{y}}}}{f}} \right)\)

1975

[29]

12

Boring, variable rigidity

Shape error of hole: \(\Delta {\Phi} = 2{{A}_{2}},\)\({{A}_{2}} = \frac{{\left( {{{j}_{{{\text{max}}}}} - {{j}_{{{\text{min}}}}}} \right){{x}_{1}}t_{{{\text{me}}}}^{\alpha }}}{{{v}{{j}_{0}}\sqrt {{{{\left[ {{{j}_{0}} + {{x}_{1}}t_{{{\text{me}}}}^{{\alpha - 1}} - m\omega _{1}^{2}} \right]}}^{2}}{{\mu }^{2}}\omega _{1}^{2}} }}\)

1975

[7]

13

Internal grinding, trimming

Height of undulation: \(~{{H}_{{\text{w}}}} = {{10}^{{8.785}}}V_{n}^{{0.165}}V_{p}^{{9.99}}\)

1975

[30]

14

Plane grinding, wheel imbalance

Height of undulation: \(~H = \frac{{2h}}{{\sqrt {\left( {\omega _{c}^{2} - {{\omega }^{2}}} \right) + 4{{n}^{2}}{{\omega }^{2}}} }}{{K}_{i}}\)

1977

[31]

15

Wheel grinding, vibration, self-intersecting waves

Height of undulation: \(~{{H}_{{\text{w}}}}_{{_{n}}} = \frac{{{{H}_{{{{{\text{w}}}_{1}}}}}}}{2}\left[ {1 + {\text{sin}}\left( {\arctan \frac{{\sin {{\theta }_{n}}}}{{1 - \cos {{\theta }_{n}}}}} \right)} \right]\), \(R \leqslant {{\left( {\frac{{v}}{{2\pi \nu \times 60}}} \right)}^{2}}\frac{1}{A}\)

1978

[11]

16

Plane grinding, vibration

Height of undulation: \(~H = 2A{\text{si}}{{{\text{n}}}^{2}}\frac{{\pi {v}}}{{2\omega \sqrt {AR} }}\)

1980

[32]

17

Internal grinding, wheel

discontinuity

Height of undulation: \({{H}_{{\text{w}}}} = R + t - \frac{\tau }{{\sin \frac{\varphi }{2}}}\sin \left[ {\frac{\varphi }{2} + \arcsin \left( {\frac{{R + T - r}}{r}\sin \frac{\varphi }{2}} \right)} \right]\)

1981

[6]

18

Deep honing, initial undulation

Height of undulation: \({{W}_{Z}} = 2.578 \times {{10}^{3}}\frac{{{{S}^{{0.26\ln t + 0.16~ln}}}}}{{{{t}^{{ - 1.264}}}{{n}_{\sigma }}A}};\)

1985

[33]

19

Grinding by discontinuous wheels, vibration, discontinuity

Undulation profile: xw = xdyn+S; S = S ' + S '', yw = ydyn+H;

x dyn \( = \left( {{{A}_{i}} + {{u}_{{{{Z}_{i}}}}}{\text{sin}}{{\omega }_{{{{b}_{i}}}}}\tau } \right){\text{cos}}{{\omega }_{{{{c}_{i}}}}}\tau + {{\nu }_{g}}\tau \) + \(\frac{{{{R}_{{{\text{cr}}}}}\left( {{{B}_{i}} + {{u}_{{{{y}_{i}}}}}{\text{sin}}{{\omega }_{{{{b}_{i}}}}}\tau } \right){{\omega }_{i}}{\text{co}}{{{\text{s}}}_{{{{c}_{i}}}}}\tau }}{{v}}\)

y dyn \(~ = \left( {{{B}_{i}} + {{u}_{{{{y}_{i}}}}}{\text{sin}}{{\omega }_{{{{b}_{i}}}}}\tau } \right){\text{sin}}{{\omega }_{{{{c}_{i}}}}}\tau + {{\nu }_{g}}\tau + \) \(\,\frac{{{{R}_{{{\text{cr}}}}}\left( {{{u}_{{{{z}_{i}}}}}{{\omega }_{{{{b}_{i}}}}}{\text{cos}}\tau {\text{co}}{{{\text{s}}}_{{{{c}_{i}}}}}\tau } \right) + {{{v}}_{g}} - D}}{{v}}\)

1986

[34]

20

Plane grinding, vibration

Conditions of loop appearance: \(\frac{{{{{\left( {{{x}^{2}} + {{y}^{2}}} \right)}}^{{3/2}}}}}{{\dot {y}\ddot {x} - \ddot {y}\dot {x}}} \geqslant R,\)\(\frac{{{{{\left( {{{{v}}^{2}} + 2a\omega {v}{\text{cos}}\omega t + {{a}^{2}}{{\omega }^{2}}} \right)}}^{{3/2}}}}}{{a{{\omega }^{2}}\left( {a\omega + {v}{\text{cos}}\omega t} \right)}} \geqslant R\)

1987

[35]

21

Basic machining methods

Mean undulation height: \({{W}_{Z}} = 1.2\sqrt {H_{1}^{2} + H_{2}^{2} + H_{3}^{2}} \), where H1 is the initial state of the surface layer; H2 is the workpiece and tool wobble; and H3 takes account of the tool geometry and kinematics

1987

[19],

2000

[20]

 

Cutting (first group)

\({{H}_{1}} = \frac{{{{C}_{{y}}}{{S}^{{{{y}_{P}}_{y}}}}{{{v}}^{{{{Z}_{P}}_{y}}}}\left[ {HB_{{\max }}^{n}{{t}^{{{{x}_{P}}_{y}}}} - HB_{{\min }}^{n}{{{\left( {t - {{W}_{{{{Z}_{{{\text{in}}}}}}}} - {{R}_{{{{Z}_{{{\text{in}}}}}}}}} \right)}}^{{{{x}_{P}}_{y}}}}} \right]}}{{HB_{{{\text{me}}}}^{n}{{j}_{{{\text{sp}}}}}\sqrt {{{{\left( {1 - {{\lambda }^{2}}{\text{/}}{{\omega }^{2}}} \right)}}^{2}} + T{{n}^{2}}{{\lambda }^{2}}} }}\),\({{H}_{2}} = 2{{C}_{0}}\left\{ {1 + \cos \left[ {\left( {n - 1} \right)\frac{{180^\circ }}{n}} \right]} \right\}\delta ,~\)\(\delta = \frac{{180{{l}_{{bn}}}{{{v}}_{D}}}}{{\pi {{{v}}_{{{\text{cr}}}}}D}}~~\), \({{W}_{Z}} = \frac{{1.2{{C}_{{y}}}{{S}^{{{{y}_{P}}_{y}}}}{{{v}}^{{{{Z}_{P}}_{y}}}}\left[ {HB_{{\max }}^{n}{{t}^{{{{x}_{P}}_{y}}}} - HB_{{\min }}^{n}{{{\left( {t - {{W}_{{{{Z}_{{{\text{in}}}}}}}} - {{R}_{{{{Z}_{{{\text{in}}}}}}}}} \right)}}^{{{{x}_{P}}_{y}}}}} \right]}}{{HB_{{{\text{me}}}}^{n}{{j}_{{{\text{sp}}}}}\sqrt {{{{\left( {1 - {{\lambda }^{2}}{\text{/}}{{\omega }^{2}}} \right)}}^{2}} + {{T}_{n}}{{\lambda }^{2}}} }}\)

 
 

Diamond grinding (second group)

\({{H}_{1}} = \Delta {{y}_{{{\text{wh}}}}} + \Delta \left( {{{y}_{{\text{w}}}} + {{y}_{{\text{t}}}}} \right)\), \(\Delta \left( {{{y}_{{\text{w}}}} + {{y}_{{\text{t}}}}} \right) = \frac{{\Delta {{P}_{y}}}}{{{{J}_{{{\text{sp}}}}}}}\),

\(\Delta {{y}_{{{\text{wh}}}}} = \frac{{\Delta {{P}_{y}}\left[ {{{E}_{2}}\left( {1 - \mu _{1}^{2}} \right) + {{E}_{1}}\left( {1 - \mu _{2}^{2}} \right)} \right]}}{{\pi B{{E}_{1}}{{E}_{2}}}}\ln \frac{{2\pi B{{E}_{1}}{{E}_{2}}\left( {D + d} \right)}}{{\Delta {{P}_{y}}\left[ {{{E}_{2}}\left( {1 - \mu _{1}^{2}} \right) + {{E}_{1}}\left( {1 - \mu _{2}^{2}} \right)} \right]}}\),

\({{H}_{2}} = {{A}_{{{\text{cr}}}}}\left\{ {1 - \cos \left[ {13.2\frac{{{{V}_{D}}}}{{{{f}_{n}}}}\sqrt {\frac{1}{{{{A}_{{{\text{re}}}}}}}\left( {\frac{1}{D} + \frac{1}{d}} \right)} } \right]} \right\}\), \({{H}_{3}} = \frac{{D\left( {1 - \cos \delta } \right)}}{{2\cos \delta }},\)

\(\begin{gathered} {{W}_{Z}} = 1.2\left\{ {{{{\left[ {\frac{{\Delta {{P}_{y}}}}{{{{j}_{{{\text{sp}}}}}}}\frac{{{{E}_{1}}\left( {1 - \mu _{2}^{2}} \right)}}{{\pi B{{E}_{1}}{{E}_{2}}}}~\ln \frac{{2\pi {{E}_{1}}{{E}_{2}}\left( {D + d} \right)~~}}{{\Delta {{P}_{y}}{{E}_{1}}\left( {1 - \mu _{2}^{2}} \right)}}} \right]}}^{2}}} \right. + \hfill \\ {{\left. {_{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{}}}}^{{}}{{A}_{{{\text{cr}}}}}\left[ {1 - \cos \left( {13.2\frac{{{{{v}}_{D}}}}{{{{f}_{n}}}}\sqrt {\frac{1}{{{{A}_{{{\text{wh}}}}}}}\left( {\frac{1}{D} + \frac{1}{d}} \right)} } \right)} \right]} \right\}}^{{0.5}}} \hfill \\ \end{gathered} \)

 
 

Finishing (third group)

\({{H}_{1}} = {{W}_{{{{Z}_{{{\text{in}}}}}}}} - {{\left( {\frac{{PR_{{{{p}_{{in}}}}}^{2}}}{{\pi {{R}_{{{\text{re}}}}}HB}}} \right)}^{{0.25}}},\) \({{H}_{2}} = 1.4{{\left[ {\left( {1 + {{f}^{2}}} \right)\left( {W_{{{{Z}_{{{{{p}}_{{{\text{in}}}}}}}}}}^{2} + \Delta _{P}^{2}} \right)} \right]}^{{0.25}}} \times \)

 
  

\({{\left\{ {\frac{{{{j}_{{{\text{sp}}}}}}}{{\pi Rc{\kern 1pt} '{{\sigma }_{{\text{y}}}}\left[ {\frac{{180^\circ - \arccos \frac{{s - {{{a}}_{{{\text{pl}}}}}}}{{{{{a}}_{{{\text{pl}}}}}}}}}{{{{{a}}_{{{\text{pl}}}}}}}\left( {{{h}_{{{\text{kin}}}}} + {{h}_{{{\text{de}}}}}} \right) - 2{{h}_{{{\text{de}}}}}} \right]}}} \right\}}^{{0,5}}},\)

 
  

\({{H}_{3}} = {{h}_{{{\text{kin}}}}} - \left[ {1 - \frac{{f\left( {\sqrt {{{h}_{{{\text{kin}}}}}{\text{/}}2 + 1} } \right)}}{{\left( {\sqrt {{{h}_{{{\text{kin}}}}}{\text{/}}8r + 1} } \right)\left( {1 + {{f}^{2}}} \right)}}} \right]~,\)

\(\begin{gathered} {{W}_{Z}} = 1.2 \times \hfill \\ {{\left\{ {{{{\left[ {{{W}_{{{{Z}_{{{\text{in}}}}}}}} - {{{\left( {\frac{{9pRa_{{{{p}_{{{\text{in}}}}}}}^{2}}}{{\pi {{R}_{{{\text{re}}}}}HB}}} \right)}}^{{1/3}}}} \right]}}^{2}} + \left[ {\frac{{27{{f}_{{{\text{sp}}}}}{{{\left( {W_{{{{Z}_{p}}}}^{2} + \Delta _{P}^{2}} \right)}}^{{0,5}}}{{R}_{{{{a}_{{{\text{max}}}}}}}}}}{{\pi rc{\kern 1pt} ''{{\sigma }_{T}}\frac{{180^\circ - \arccos \frac{{s - {{{a}}_{{{\text{pl}}}}}}}{{{{{a}}_{{{\text{pl}}}}}}}}}{{{{a}_{{{\text{pl}}}}}}}\left( {{{h}_{{{\text{kin}}}}} - {{h}_{{{\text{de}}}}}} \right) - 2{{h}_{{{\text{de}}}}}}}} \right] + h_{{{\text{kin}}}}^{2}} \right\}}^{{0.5}}} \hfill \\ \end{gathered} \)

 

22

Wheel grinding, vibration, five frequency ranges

Range 1: 2\(\pi n \leqslant \omega \leqslant 4\pi n\)

Oval distortion: \(\Delta = {{y}_{{{\text{max}}}}}{\text{sin}}\left( {\omega + \varphi } \right)\);

Range 2: 4\(\pi n \leqslant \omega \leqslant 30\pi n\)

Facet height: \(\Delta = R\left( {1 - \frac{{{{V}_{{{{S}_{{{\text{cr}}}}}}}}}}{{\sqrt {{{A}^{2}}{{\omega }^{2}}{{{\cos }}^{2}}\omega {{\tau }_{x}} + V_{{{{S}_{{{\text{cr}}}}}}}^{2}} }}} \right) + A\left( {1 + {\text{sin}}\omega {{\tau }_{x}}} \right)\)

1988

[36]

  

Range 3: \(30\pi n \leqslant \omega \leqslant 2\pi n\sqrt {\frac{{\left( {R + \tau } \right)\tau }}{{AR}}} \)

Height of undulation: \(\Delta = 2A\sin \frac{{{{\pi }^{2}}n}}{{60}}\sqrt {\frac{{\left( {R + \tau } \right)\tau }}{{AR}}} ~,\)

Range 4: \(\omega \leqslant 0.02\pi {{V}_{{{{S}_{{{\text{cr}}}}}}}}{\text{/}}A.\)

Height of undulation: \(\Delta = R\left( {1 - \frac{{{{V}_{{{{S}_{{{\text{cr}}}}}}}}}}{{\sqrt {{{A}^{2}}{{\omega }^{2}}{{{\cos }}^{2}}\omega {{\tau }_{x}} + V_{{{{S}_{{{\text{cr}}}}}}}^{2}} }}} \right) + A\left( {1 + {\text{sin}}\omega {{\tau }_{x}}} \right)\)

Range 5: \(\omega \geqslant 0.02\pi {{V}_{{{{S}_{{{\text{cr}}}}}}}}{\text{/}}A\)

Height of undulation: \({{\Delta }_{n}} = \frac{\lambda }{{50}} = \frac{{0.08{{\pi }^{2}}n\tau }}{\omega }\)

 

23

Thread grinding, vibration

Height of undulation: \(H = \frac{{{{V}^{2}}}}{{4\pi \rho {{f}^{2}}}}{\text{arctan}}\frac{{29.2{{f}^{2}}a\rho }}{{{{V}^{2}}}}~\)

1982

[37]

24

Boring, displacement of cutter axes

Noncircularity: \({{\Delta }_{{{\text{cr}}}}} = 8.3{{e}^{{ - 1.428}}}\sqrt {{{R}^{2}} + {{e}^{2}}} - R\)

1998

[38] 1999

[39]

Table 2 presents mathematical models of the periodic machining errors.