INTRODUCTION

The effect of liquid electrodispersion (polydispersion) at realization of instability of its charged surface has been thoroughly examined both from a theoretical [1–7] and experimental [6–14] point of view since it is related to multiple academic, technical, and engineering applications. The problem of calculating parameters (dimensions and charges of progeny droplets) of electrostatic disintegration of a strongly charged drop, an uncharged drop in a strong electric field, or a charged drop in an electric field has also been investigated both experimentally [12–19] and theoretically [20–24]. In the noted experimental investigations, the instability of the liquid surface at its dispersion occurred in various external conditions: from the surface of suspended drops of various kinds [12–18], freely falling charged drop [10, 19, 25], and liquid meniscus at the end of the capillary through which the liquid is supplied to the discharge system [7, 8, 22, 26–32].

In this investigation, we focused on calculating disintegration parameters of a charged drop suspended motionlessly in a thunderstorm cloud in a superposition of aerodynamic, electrostatic, and gravitational fields. The general physical situation in this problem is similar to the problem studied experimentally in [14]: three fields—aerodynamic, electrostatic, and gravitational fields—are present there and influence the disintegration parameters, but its theoretical analysis was not discussed, though this situation is common in nature.

FORMULATION OF THE PROBLEM

In this paragraph, we describe a physical model of the phenomenon that we intend to calculate.

A spherical drop of incompressible electrically conducting liquid with a coefficient of interfacial tension σ, mass density ρ1, radius R, and charge Q located in a gravitational field \(\vec {g}\)and aired by an air flux with a velocity of \({{\vec {U}}_{0}}\left\| { - \vec {g}} \right.\) is primarily inserted in a uniform electrostatic field \({{\vec {E}}_{0}}\left\| {\vec {g}} \right.\). For definiteness, we assume the drop charge Q is negative so as the field \({{\vec {E}}_{0}}\) facilitates the aerodynamic field \({{\vec {U}}_{0}}\) to keep the drop in a suspended state.

Let us accept that, in the aforementioned conditions, the initial drop (further named a parent drop) acquires a spherical equilibrium shape in a linear approximation according to the value of its stationary deformation. Suppose that, due to realization of electrostatic instability of this drop, it projects in the direction \( - {{\vec {E}}_{0}}\left\| {{{{\vec {U}}}_{0}}} \right.\) a progeny droplet with a charge q and initial radius r that also possesses a spheroidal shape in the noted conditions whose eccentricity differs from that of the parent drop as it is represented in Fig. 1.

Fig. 1.
figure 1

Scheme of a drop suspended in a thunderstorm cloud.

Full size image

Note, that the progeny drop is projected from that end of the parent drop where the sign of the induced charge coincides with the sign of the intrinsic charge in the case under consideration. Taking into account the aforementioned, the progeny droplet will bear a negative charge and will be projected to the direction opposite to the direction of the gravitational field, that is, upward.

Note the parent drop eccentricity as e1: \({{e}_{1}} \equiv \sqrt {1 - {{{\left( {{{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}} \right)}}^{2}}} \), where b1 and a1 are the minor and major semiaxes of the spheroidal parent drop expressed in terms of the radius of the initial spherical drop R and the square eccentricity \(e_{1}^{2}\) by the equations

$${{a}_{1}} \equiv {R \mathord{\left/ {\vphantom {R {{{{\left( {1 - e_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \right. \kern-0em} {{{{\left( {1 - e_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}},\,\,\,\,{{b}_{1}} \equiv R{{\left( {1 - e_{1}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}.$$

The respective parameters of the progeny droplet are defined in a similar way

$$\begin{gathered} {{e}_{2}} \equiv \sqrt {1 - {{{\left( {{{b}_{2}}/{{a}_{2}}} \right)}}^{2}}} ,\,\,\,\,{{b}_{2}} \equiv r{{\left( {1 - e_{2}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}; \\ {{a}_{2}} \equiv {r \mathord{\left/ {\vphantom {r {{{{\left( {1 - e_{2}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \right. \kern-0em} {{{{\left( {1 - e_{2}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}. \\ \end{gathered} $$

The supposition of spheroidal shape of the parent and progeny drops is based on the results of [33] where the shape of the drop in an electrostatic suspension was evaluated. The range of dimensions of real cloud drops to which the following discussion refers amounts from \(3\) to 30 μm; they contain the main quantity of the cloud’s water [34, p. 131].

One should note that the problem of electrostatic disintegration of a strongly charged drop and of the charged drop in an external uniform electrostatic field was earlier discussed in [23, 24] on the basis of the principle of the least energy dissipation rate in nonequilibrium processes. However, the problem was considered there in the framework of quite idealized models and motionless drops (though a charged drop should move in the field with acceleration) whose positioning was not explained but adopted on default. In the present work, a charged drop is in a dynamic state under the action of electrostatic, gravitational, and aerodynamic forces.

In the qualitative evaluation, we calculate the force acting on the drop from the side of the air stream in the cloud according to the Stokes formula.

The condition of immobility of the parent drop in a superposition of aerodynamic, electrostatic, and gravitational fields is in the form

$$Q \times {{\vec {E}}_{0}} + 6\pi R{{\mu }_{2}}{{\vec {U}}_{0}} = \frac{4}{3}\pi {{R}^{3}}{{\rho }_{1}}\vec {g},$$
(1)

where μ2 is the coefficient of dynamic viscosity of the medium (air).

Let us project the relationship (1) on the direction \({{\vec {E}}_{0}}\). Then we obtain a condition of immobility of the parent drop in the terms of unitless Rayleigh (\(W \equiv {{{{Q}^{2}}} \mathord{\left/ {\vphantom {{{{Q}^{2}}} {16\pi {{R}^{3}}\sigma }}} \right. \kern-0em} {16\pi {{R}^{3}}\sigma }}\)) [1, 23, 33] and Taylor (\(w \equiv {{RE_{0}^{2}} \mathord{\left/ {\vphantom {{RE_{0}^{2}} {16\pi \sigma }}} \right. \kern-0em} {16\pi \sigma }}\)) [5, 23, 33] parameters, which characterize the electrostatic stability of the drop surface in relation to the intrinsic charge Q and the charge induced by the external field \({{\vec {E}}_{0}}\), respectively, in the form

$$\begin{gathered} \sqrt {wW} + \frac{3}{8}\gamma - \frac{1}{{12}}\eta = 0;\,\,\,\,\gamma \equiv {{{{\mu }_{2}}{{U}_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}{{U}_{0}}} \sigma }} \right. \kern-0em} \sigma }; \\ \eta \equiv {{{{\rho }_{1}}g{{R}^{2}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}g{{R}^{2}}} \sigma }} \right. \kern-0em} \sigma }. \\ \end{gathered} $$
(1a)

For the case of emission of a progeny drop, the free energy of the system changes. Assuming that the system’s temperature, the total volume, and electric charge of the liquid phase remain constant, we can write down the variation of the system’s energy as

$$\begin{gathered} \Delta F \equiv {{F}_{f}} - {{F}_{{{\text{in}}}}} \equiv 4\pi {{r}^{2}}\sigma \left[ {{{{\text{A}}}_{2}} - \frac{{2r{{{\text{A}}}_{1}}}}{{3R}}} \right] \\ + \,\,{{{\text{B}}}_{2}}\frac{{{{q}^{2}}}}{{2r}} - {{{\text{B}}}_{1}}\frac{{\left( {Q - q} \right)q}}{{2R}} - \\ \end{gathered} $$
(2)
$$\begin{gathered} + \,\,K\frac{{\left( {Q - q} \right)q}}{R} - {{E}_{0}}Rq{{\varphi }_{e}}(\zeta ) \\ + \,\,\frac{{2\pi {{r}^{3}}{{\rho }_{1}}{{U}^{2}}}}{3} + \frac{4}{3}\pi {{r}^{3}}{{\rho }_{1}}gL; \\ \end{gathered} $$
$${{\varphi }_{e}}(\zeta ) \equiv \frac{{\zeta {\text{arctanh}}\left( {{{e}_{1}}\frac{{\zeta - 1}}{{\zeta - e_{1}^{2}}}} \right) - {{e}_{1}}(\zeta - 1)}}{{\left( {{\text{arctanh}}{{e}_{1}} - {{e}_{1}}} \right){{{\left( {1 - e_{{1\,}}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}};$$
$$K \equiv \frac{{{{{\left( {1 - e_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{arctanh}}\left( {\frac{{{{e}_{1}}}}{\zeta }} \right)}}{{{{e}_{1}}}};$$
$${{A}_{i}} \equiv \frac{1}{2}\left( {{{{\left( {1 - e_{i}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + e_{i}^{{ - 1}}{\text{arc}}\sin{{e}_{{i\,}}}} \right)\frac{1}{{{{{\left( {1 - e_{i}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}}};$$
$${{B}_{i}} \equiv \frac{{{{{\left( {1 - e_{i}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{{{e}_{i}}}}{\text{arctanh}}\left( {{{e}_{i}}} \right).$$

In Eqs. (2), \({{E}_{0}}R{{\varphi }_{e}}(\zeta )\) is the electrostatic potential of the uncharged parent drop in an external uniform electrostatic field \({{\vec {E}}_{0}}\), in the center of the droplet, written using a unitless distance between the drops \(\zeta = {{\left( {1 + {\xi \mathord{\left/ {\vphantom {\xi {a_{2}^{2}}}} \right. \kern-0em} {a_{2}^{2}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\) in the moment when the contact between the drops is breaking (ξ = 0 or ζ = 1 correspond to the parent drop surface); L is the dimension distance between the parent drop top and the center of the progeny drop in the breaking moment; Fin and Ff are the initial and final values of the potential energy of the system.

The equation for φe(ζ) is put down on the basis of the analytical relationship for the potential of the charges induced by a uniform external electrostatic field \({{\vec {E}}_{0}}\) in the parent drop in spherical coordinates ([35, p. 48, problem 5]) and the relationship for the difference of hyperbolic arctangents ([36, p. 284]) taking into account the circumstance that the vertical coordinate is counted off in the direction opposite to \({{\vec {E}}_{0}}\).

In Eqs. (2), the first term defines the free energy variation of the forces of surface tension of the system during emission of a single droplet; the second and third terms are variation of the intrinsic electrostatic energy of the system taking into account the charges of the progeny and parent drops—the second term defines the appearance of the intrinsic electrostatic energy of the progeny droplet charge and the third term defines the variation of the intrinsic electrostatic energy of the parent drop charge. The fourth term provides the variation of the energy of electrostatic interaction of the progeny droplet charge with remains of the parent drop charge; the fifth term is the appearance of the energy of electrostatic interaction of the progeny droplet charge with the electric field of the charges induced in the parent drop by the field \({{\vec {E}}_{0}}\) (the minus sign before this term notes the fact that the charge of the progeny droplet is negative). The sixth term describes the appearance of the kinetic energy of the progeny droplet acquired in the air stream. It is assumed that the parent drop is at rest relative to the earth, but the progeny droplet with dimensions of the order of tenth parts of a micrometer and less [23] is virtually motionless relative to the air stream [34, p. 260]. The last term presents the variation of the progeny droplet potential energy in a gravitational field.

Introducing the ratio of the progeny droplet charge to the parent drop charge Y ≡ (q/Q), we obtain a unitless charge of the progeny droplet. Then we do the same for the radius X ≡ (r/R) and obtain its unitless characteristic radius—unitless relative to the parent drop radius. As the similar calculations for disintegration of a strongly charged drop have demonstrated [23, 24], these values are rather small parameters, much less than unity; X and Y are different. Equation (2) is valid only in a quadratic approximation over X and Y as well as over their product. There is no sense to put down the variation of the system’s free energy with greater accuracy to avoid cumbersome expressions since the respective terms are small.

Let us rewrite Eq. (2) taking into account the small introduced parameters as well as unitless parameters w and W that characterize the electrostatic stability of the parent drop with respect to the external electrostatic field strength and the intrinsic charge value

$$\begin{gathered} \Delta F \equiv {{X}^{2}}\left[ {{{A}_{2}} - \frac{2}{3}X{{A}_{1}}} \right] + 2W \\ \times \,\,{{B}_{2}}\frac{{{{Y}^{2}}}}{X} - 2W{{B}_{1}}\left( {1 - Y} \right)Y \\ \end{gathered} $$
$$\begin{gathered} + \,\,4WK(1 - Y)Y - 4\sqrt {wW} {{\varphi }_{e}}(\zeta ) \\ \times \,\,Y + \left( {\frac{1}{6}{\text{We}} + \frac{1}{3}{{\eta }}\Lambda } \right){{X}^{3}}; \\ \end{gathered} $$
(2а)
$$\begin{gathered} {\text{We}} \equiv \frac{{R{{\rho }_{1}}{{U}^{2}}}}{\sigma }; \\ \Lambda \equiv \frac{L}{R} \equiv \frac{{{{a}_{1}}(\zeta - 1)}}{R} \equiv \frac{{(\zeta - 1)}}{{{{{\left( {1 - e_{{1\,}}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}, \\ \end{gathered} $$

where We is the Weber parameter, Λ is the unitless distance between the parent drop top where the progeny droplet separates and the center of the progeny droplet.

Variation of the system energy (2) (or (2а)) is associated with the appearance of a new surface due to the emission of a progeny droplet, i.e., with variation of the potential energy value of the forces of surface tension, potential energy of the progeny droplet in the field of gravitation forces, acquiring of kinetic energy by it that can be expressed through the progeny droplet radius r and variation of the electric field potential energy expressed through its charge q. Let us demand that this variation is extremal due to the principle of the least energy dissipation rate [23, 37, 38], i.e., the conditions \({{\partial (\Delta F)} \mathord{\left/ {\vphantom {{\partial (\Delta F)} {\partial r = 0}}} \right. \kern-0em} {\partial r = 0}}\) (or \({{\partial (\Delta F)} \mathord{\left/ {\vphantom {{\partial (\Delta F)} {\partial X = 0}}} \right. \kern-0em} {\partial X = 0}}\) that means the same) and \({{\partial (\Delta F)} \mathord{\left/ {\vphantom {{\partial (\Delta F)} {\partial q = 0}}} \right. \kern-0em} {\partial q = 0}}\) (or \({{\partial (\Delta F)} \mathord{\left/ {\vphantom {{\partial (\Delta F)} {\partial Y = 0}}} \right. \kern-0em} {\partial Y = 0}}\)) are fulfilled, from which it is easy to obtain equations for r (or X) and q (or Y)

$$\left\{ {{{A}_{2}} - {{A}_{1}}X - {{B}_{2}}W\frac{{{{Y}^{2}}}}{{{{X}^{3}}}} - \left( {\frac{1}{4}{\text{We}} + {{\eta }}\frac{{(\zeta - 1)}}{{2{{{\left( {1 - e_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \right)X} \right\} = 0;$$
(3)
$$\left\{ {{{B}_{2}}W\frac{Y}{X} - {{B}_{1}}W\frac{{\left( {1 - 2Y} \right)}}{2} + KW\left( {1 - 2Y} \right) - \sqrt {wW} {{{{\varphi }}}_{e}}} \right\} = 0.$$
(4)

Let us assume that the separation of the progeny drop occurs from the top spike that grows on top of the parent drop along \({{\vec {E}}_{0}}\) when the instability develops in it. Furthermore, the spike of the top together with the charge that it bears separates due to the electrostatic interaction of the charge of the top spike and electrostatic field of the parent drop (see [35, p. 55, problem 1]). This occurs just when the sum of the electric repulsion force and the Stokes force of interaction of the progeny drop with the air stream exceeds the sum of the surface tension forces in the narrowest place of the neck 2π\({{r}_{*}}\)σ and the progeny drop gravitational force that holds the top’s spike (\({{r}_{*}}\) is the radius of the neck that links the drops in the narrowest place).

It should be noted that the shape of the neck that links the parent and progeny droplets has to be very close to a catenoid to ensure the free energy minimum [39, p. 338, problem 1]. At the fixed linear dimensions of the parent and progeny droplets, there should exist a minimal neck radius \({{r}_{*}}\) for which the equality occurs between the Laplace force in the neck 2π\({{r}_{*}}\)σ and the progeny droplet weight mg, which keep the drops together, and the sum of the forces of electrical repulsion of the parent and progeny droplets and the Stokes force that acts on the progeny drop from the air stream side 6πb2μU0 that disrupt the contact

$$2\pi {{r}_{*}}\sigma + \frac{4}{3}\pi {{r}^{3}}\rho g = Eq + 6\pi {{b}_{2}}{{\mu }_{2}}{{U}_{0}}.$$
(5)

Here, E is the strength of the superposition field of the intrinsic charge of the parent drop and the charge induced in it by an external uniform electrostatic field in the center of location of the small droplet; b2 functions as a characteristic linear lateral dimension of the separating drop. Note, the first term to the right defining the electrostatic force that disrupts the progeny droplet is calculated on the basis of the solution similar to that provided in [35, p. 53, problem 1].

To find the charge of the progeny drop, let us specify a model of its separation from the parent drop. As was noted above, the progeny droplet separates from the spike growing on the oriented upward top of the parent drop (where the surface charge density is maximal) when the electrostatic instability realizes in it. To perform an estimative analysis, we assume a cylindrical shape of the nonequilibrium spike and model it using a semispheroid elongated along the field for convenience of analytical calculations (the exact shape of the spike is not substantial for the reasoning). Due to its large curvature, a charge is accumulated on the spike that interacts with the electrostatic field of the parent drop. At a certain length of the spike, when the force of its repulsion from the parent drop increases, a part of it separates and forms a progeny droplet. In other words, the initial cylindrical spike, when it separates, contracts under the action of capillary forces into a droplet bearing the charge that existed on the separated part of the spike.

Equation (5) is an equation for determining parameter ζ that characterizes the distance between the drops in the moment when the neck disrupts. In a unitless form, Eq. (5) is as follows

$$\begin{gathered} X\frac{\alpha }{8} + {{X}^{3}}\frac{\eta }{{12}} = Y\frac{{{{{\left( {1 - e_{1}^{2}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{\zeta }^{2}}}} \\ \left\{ {W{{{{\varphi }}}_{q}} + \sqrt {wW} \frac{{{{{{\varphi }}}_{e}}}}{{{{{\left( {1 - e_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \right\} + \frac{{3\gamma }}{8}{{\left( {1 - e_{2}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}; \\ \end{gathered} $$
(5а)
$${{{{\varphi }}}_{q}} \equiv \frac{{{\text{arctanh}}\left( {{{e}_{1}}\frac{{\zeta - 1}}{{\zeta - e_{1}^{2}}}} \right)}}{{{\text{arctanh}}{{e}_{1}}}};$$
$${{{{\varphi }}}_{e}} \equiv \frac{{\zeta \arctan {\text{h}}\left( {{{e}_{1}}\frac{{\zeta - 1}}{{\zeta - e_{1}^{2}}}} \right) - {{e}_{1}}(\zeta - 1)}}{{\left( {\arctan {\text{h}}{{e}_{1}} - {{e}_{1}}} \right){{{\left( {1 - e_{{1\,}}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}};\,\,\,\,\alpha \equiv \frac{{{{r}_{*}}}}{r}.$$

Solving the system of Eqs. (3)–(4) and (5а), one can find the dimensions and charges of the emitted droplets versus the value of the velocity of the ascending air stream in [23, 38]. Concerning the condition of suspension of the parent drop in a thunderstorm cloud (1а), one should not demand that it equals to zero. When the equality (1а) is strictly fulfilled, the drop will be motionless. But a real cloud is a dynamic system: the strength of the external electric field and velocity of the air stream blowing it are continuously varying in a small neighborhood of any drop. The intrinsic charge of the drop also changes due to multiple elementary processes of charging of cloud drops that occur in a thunderstorm cloud (see, e.g., [40, Ch. 10, pp. 426–460] or [41]). But we assume that the velocity of motion of the parent drop in the cloud is low, of the order of tens of centimeters per second.

The preliminary calculations demonstrated that the dimensions and charges of the emitted droplets in conditions when the drop is suspended in a thunderstorm cloud is by two orders lesser than was earlier obtained in the model calculations for a motionless charged drop in [23, 42].

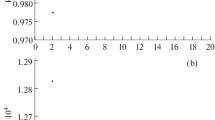
The results of the numerical calculations according to Eqs. (3)–(4) and (5а) for σ = 77 g/s2, μ2 = 1.6 × 10–4 g/s cm, R = 30 μm, ρ1 = 1 g/cm3, U0 = 100 cm/s, Q = 10–2 CGSE, E0 = 3 CGSE are presented in Figs. 2–3. In these figures, the dependences of the following calculated unitless parameters of the emitted progeny droplet versus its sequence number n are shown: the equivalent radius \({{X}_{*}}\) ≡ (X – 0.000678) × 107, charge \({{Y}_{*}}\) ≡ (Y – 0.000019) × 106, distance \({{\zeta }_{*}}\) ≡ (ζ – 2.116) × 102, Rayleigh parameter Wd as well as of the dimensional radius \({{R}_{*}}\) ≡ (R – 0.0029999 cm) × 109 and charge \({{Q}_{*}}\) ≡ (Q – 0.0088 CGSE) × 104 of the remains of the parent drop. These values are plotted in the ordinate axis in Figs. 2–3 since the variation of the respective parameters for the two subsequently emitted progeny drops is small. For example, one can determine the genuine radius of the progeny droplet according to Fig. 2 using the relationship \({{X}_{*}}\) ≡ (X – 0.000678) × 107 as: X ≡ 10–7\({{X}_{*}}\) + 0.000678.

Fig. 2.
figure 2

(a) Dependence of the unitless radius \({{X}_{*}}\) of the progeny droplet vs. the sequence number n of the emission event. (b) Dependence of the unitless charge \({{Y}_{*}}\) of the progeny droplet vs. the sequence number n of the emission event. (c) Dependence of the unitless distance \({{\zeta }_{*}}\) that describes the location of the progeny droplet vs. the sequence number n of the emission event. (d) Dependence of the Rayleigh parameter Wd of the progeny droplet vs. the sequence number n of the emission event.

Full size image
Fig. 3.
figure 3

(a) Dependence of the dimensional radius \({{R}_{*}}\) of the parent droplet’s remains vs. the sequence number n of the emission event. The radius is measured in centimeters. (b) Dependence of the dimensional charge \({{Q}_{*}}\) of the parent droplet’s remains vs. the sequence number n of the emission event. The charge is measured in CGSE units.

Full size image

In can be seen that the characteristic linear dimension \({{X}_{*}}\) decreases when \(n\) increases, but \({{Y}_{*}}\), \({{\zeta }_{*}}\), and Wd increase. One more distinctive feature is also evident between the model calculations of the disintegration parameters for the charged drop [23, 42] and for the thunderstorm cloud conditions—this is the difference of the quantity of the emitted progeny drops—their quantity amounted to two hundred for the charged drop [23, 42], while it amounts to several thousands in the present calculation.

The Rayleigh parameter of the progeny droplet Wd expressed via unitless magnitudes W, X, and Y is in the form

$${{W}_{d}} \equiv {{{{W{{Y}^{2}}} \mathord{\left/ {\vphantom {{W{{Y}^{2}}} X}} \right. \kern-0em} X}}^{3}},$$
(6)

where W is the Rayleigh parameter of the parent drop. The increasing of Wd with increasing of n is explained by the decreasing of the denominator and increasing of numerator in Eq. (6).

The circumstance that Wd exceeds unity (is greater that the Rayleigh critical value [1]) and increases with the increasing of the sequence number should be commented.

We should recall again that, due to considerable variations in the cloud’s medium [34, 40], the performed calculations are qualitative and are valid only within the order of value.

ANALYSIS OF STABILITY OF THE EMITTED DROPLET

An isolated spherical droplet with radius r bearing a charge q possesses a free energy F that presents the sum of the energy of the surface tension forces and intrinsic energy of the electric charge

$$F = 4\pi {{r}^{2}}\sigma + \frac{{{{q}^{2}}}}{{2r}}.$$

The extremum of the potential energy of this droplet occurs for

$$\frac{{\partial F}}{{\partial r}} = 8\pi r\sigma - \frac{{{{q}^{2}}}}{{2{{r}^{2}}}} = 0$$

or for

$$\frac{{{{q}^{2}}}}{{16\pi \sigma {{r}^{3}}}} \equiv {{W}_{*}} = 1,$$

i.e., when the droplet is near the Rayleigh’s threshold of electrostatic stability [1].

If we take the second derivative of F with respect to r, we obtain \(\left( {{{{{\partial }^{2}}F} \mathord{\left/ {\vphantom {{{{\partial }^{2}}F} {\partial r{}^{2}}}} \right. \kern-0em} {\partial r{}^{2}}}} \right) > 0\). In other words, minimum corresponds to the extremum of F, and the presence of the Rayleigh limit charge (for the specified radius) on the progeny drop is the most advantageous from the thermodynamic point of view.

It is natural to consider a problem: how the drop charge changes when an electrostatic field is present in its location point. This problem is reasonable since the progeny droplets are formed in the electrostatic field of the parent drop (or in the electrostatic field of the discharge system) during electrodispersion of the parent drop (or of the liquid from the capillary end through which it is supplied into the discharge system [23]). Thus, let this droplet be in a uniform (within the droplet) electrostatic field with its strength E. In this case, the total potential energy of the droplet \({{F}_{*}}\) can be written as

$${{F}_{*}} = 4\pi {{r}^{2}}\sigma + \frac{{{{q}^{2}}}}{{2r}} + \frac{{{{E}^{2}}}}{2}\left( {\frac{{{{r}^{3}}}}{3} + C} \right) + q{{\varphi }_{*}}.$$

In this relationship, C is a constant dependent on the geometry of the space occupied by the electrostatic field; \({{\varphi }_{*}}\) is the total potential of the electrostatic field where the drop is located. Since our analysis is qualitative, we neglect the spheroidal deformation of the drop surface since it is insignificant.

By finding the first derivative of \({{F}_{*}}\) with respect to r and setting it equal to zero, as above, one can get the condition of the extremal (minimal, as earlier) value of the Rayleigh parameter for the progeny droplet in the form

$${{W}_{*}} = 1 + \frac{{{{E}^{2}}r}}{{16\pi \sigma }} \equiv 1 + w,$$

where the unitless parameter w characterizes the drop’s stability relative to the induction charge [5, 23]. Similar to the case of the isolated charged spherical droplet, we obtain that the value of the Rayleigh parameter W+ exceeding unity corresponds to the minimum of the potential energy of the system and, hence, the limits in terms of electrostatic stability relative to the intrinsic charge (the lower “asterisk” index distinguishes the isolated drop from the droplet in the electrostatic field). It is easy to see that taking into consideration the spheroidal form of the droplet in the external electrostatic field does not change the qualitative result.

Let us discuss a more general situation described in the formulation of the problem on the disintegration of the charged motionless drop in a thunderstorm cloud in a superposition of aerodynamic, electrostatic, and gravitational fields. In other words, let us consider a situation when a progeny droplet is formed in the presence of gravitational and aerodynamic fields added to the electrostatic field. In this case, variation of the potential energy of the system during emission of the progeny droplet ΔF+ is as follows

$$\begin{gathered} \Delta {{F}_{ + }} = 4\pi {{r}^{2}}\sigma + \frac{{{{q}^{2}}}}{{2r}} + \frac{{{{E}^{2}}}}{2}\left( {\frac{{{{r}^{3}}}}{3} + C} \right) \\ + \,\,q{{\varphi }_{ + }} + \frac{4}{3}\pi {{r}^{3}}{{\rho }_{1}}\left( {2{{U}^{2}} + g\,L} \right), \\ \end{gathered} $$

where φ+ is the total electrostatic field potential where the droplet is located. By finding the first derivative of ΔF+ with respect to r and setting it equal to zero, we obtain the condition for determining the minimal Rayleigh parameter value for the progeny droplet in the form

$${{W}_{*}} = 1 + w + \left( {{\text{We}} + \frac{1}{2}{{\eta }}\Lambda } \right)X.$$

It is easy to see that the value of the Rayleigh parameter W+ of the progeny droplet exceeding unity also corresponds in this case to the minimum of the potential energy of the system.

One can arrive to the same conclusion by analyzing the adopted model of the droplet separation. In the adopted model, the breaking up spike initially possesses a semispherical shape, and the charge accumulated on it is defined by its electric capacitance that increases with the increasing of the spheroid’s eccentricity (Fig. 4). When the spike separates, it contracts under the action of capillary forces into a drop, its eccentricity decreases, and the charge of the formed drop exceeds the critical limits.

Fig. 4.
figure 4

Dependence of the electrocapacity of spheroid vs. the square of its eccentricity.

Full size image

It follows from the comparison of all the situations discussed that the progeny droplet bears the charge that exceeds the limit one in the terms of electrostatic stability relative to the intrinsic charge, and the droplet will disintegrate over a certain time period of the order of the characteristic time of realization of electrostatic stability. Since the progeny droplets are very small, a field charge emission or fission into the parts of comparable dimensions will be the most probable channels of transition to a stable state [43].

CONCLUSIONS

The regularities of the electrostatic disintegration of the cloud drop suspended in a superposition of electric, gravitational, and aerodynamic fields were investigated. It is shown that, as opposed to the disintegration of a strongly charged drop in the studied case, the emitted droplets possess substantially lesser dimensions and charges, though their quantity is much greater. It was also demonstrated that the emitted droplets are unstable in terms of realization of the electrostatic instability.