Sensorless Vector Control of a Permanent-Magnet Synchronous Motor Based on an Extended Adaptive Kalman Filter

Abstract

The application of an adaptive extended Kalman filter as an optimal observer for recovering electromechanical coordinates in the sensorless vector-control system of a permanent-magnet synchronous motor is considered. The mathematical description is represented as a discrete vector matrix model of a permanent-magnet synchronous motor in a rotating synchronous frame of rotor coordinates. An approach to synthesizing an extended adaptive Kalman filter by extended linearization and sequential recursive method is proposed. The modeling of the Kalman filter is conducted in MATLAB/Simulink for checking its functionality to estimate the angular velocity and position of the rotor in different working modes of the permanent-magnet synchronous motor.

Alternating-current rectifier drives based on three-phase permanent-magnet synchronous motors (PMSMs) have a high specific torque with a high performance coefficient. The electric motors of such electric drives have a larger gap and smaller dimensions when compared against other types of electric motors of similar power. For that reason, they are broadly used in high-capacity electric-drive systems of commercial machines and processing complexes [1, 2].

The vector control of the PMSM electric drive is a closed nonlinear automatic control system (ACS) with feedback by electromechanical coordinates from mechanical-coordinate sensors such as angular rotor-speed sensors and position sensors [2, 3]; these are one of the most expensive devices in a PMSM ACS. For this reason, it is a relevant task to construct a sensorless vector-control system for a PMSM in the event of physical inaccessibility for measuring electromechanical coordinates. According to a large number of works [4, 5], in systems with Luenberger observers and Kalman filters (KFs), the recovery of nonmeasurable electromechanical PMSM coordinates is used, in which the available noises have an unsatisfactory influence on the accuracy of estimating internal states.

This paper considers a sensorless vector-control system for a permanent-magnet synchronous motor using an extended adaptive Kalman filter (EAKF) as an optimal observer of electromechanical coordinates. This filter allows indirectly determining important PMSM parameters, such as rotor position and frequency (speed), as well as switch phases, not only in steady-state modes but also at low speeds, taking into account the influence of measurement noises.

MATHEMATICAL DESCRIPTION OF A PMSM RECTIFIER DRIVE

The mathematical description of the PMSM as a control object is necessary for synthesizing ACS performance algorithms. The mathematical description of the rectifier drive can be considered in a stationary system of α–β coordinates [1, 2] or in a rotating system of d–q coordinates [5, 6]. The PMSM model in a rotating system of d–q coordinates is used for a more convenient synthesis of a sensorless vector-control system for high-precision commercial electric drives.

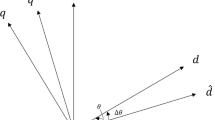
The position of the coordinate axes of the three-phase permanent-magnet synchronous motor is shown in Fig. 1.

Fig. 1.

Positions of the coordinate axes of the three-phase permanent-magnet synchronous motor: A, B, and C are the PMSM stator phases; U_A,U_B, and U_C are the PMSM stator phase voltages; and d–q are the rotating coordinate axes aligned along the magnet axis of the rotor.

It is assumed in the mathematical description of the PMSM that the magnetic circuit of the electric motor is unsaturated, stator windings are symmetrical, and scattered inductance does not depend on the position of the rotor. This having been stated, the mathematical description of the PMSM in the rotating system of d–q coordinates (with the d axis aligned along the magnetic axis of the rotor) is recorded, as in [2], as

$$\left\{ \begin{gathered} {{u}_{{sd}}} = {{R}_{s}}{{i}_{{sd}}} + \frac{{d{{{{\psi }}}_{{sd}}}}}{{dt}} - {{{{\omega }}}_{e}}{{{{\psi }}}_{{sq}}}; \hfill \\ {{u}_{{sq}}} = {{R}_{s}}{{i}_{{sq}}} + \frac{{d{{{{\psi }}}_{{sq}}}}}{{dt}}\,\,{\text{ + }}\,\,{{{{\omega }}}_{e}}{{{{\psi }}}_{{sd}}}; \hfill \\ {{{{\psi }}}_{{sd}}} = {{L}_{{sd}}}{{i}_{{sd}}} + {{{{\psi }}}_{r}};\,\,\,\,{{{{\psi }}}_{{sq}}} = {{L}_{{sq}}}{{i}_{{sq}}}; \hfill \\ {{M}_{{\text{m}}}} = \frac{3}{2}{{p}_{{{\text{pr}}}}}\left[ {{{{{\psi }}}_{r}}{{i}_{{sq}}} + \left( {{{L}_{{sd}}} - {{L}_{{sq}}}} \right){{i}_{{sd}}}{{i}_{{sd}}}} \right]; \hfill \\ \frac{{d{{{{\omega }}}_{r}}}}{{dt}} = \frac{1}{J}\left( {{{M}_{{\text{m}}}} - {{M}_{{{\text{ld}}}}} - b{{{{\omega }}}_{e}}} \right); \hfill \\ \frac{{d{{{{\theta }}}_{e}}}}{{dt}} = {{{{\omega }}}_{e}};\,\,\,\,{{{{\omega }}}_{e}} = {{p}_{{{\text{pr}}}}}{{{{\omega }}}_{r}}; \hfill \\ \end{gathered} \right.$$

(1)

where ${{u}_{{sd}}},\,\,{{u}_{{sq}}},\,\,{{i}_{{sd}}},\,\,{{i}_{{sq}}}$, and ${{{{\psi }}}_{{sd}}},\,\,{{{{\psi }}}_{{sq}}},\,\,{{{{\psi }}}_{r}}$ are the stator voltages and currents, stator flux linkages, and rotor magnetic flux linkages; M_m, M_ld, J, and b are the electromagnetic and load torques of the motor, motor rotor inertia torque, and ductile friction coefficient; ω_e, ω_r, and θ_e are the electric and angular rotation frequencies of the rotor and the electric-rotor turning angle; p_pr is the number of pole pairs; R_s, L_sd, and L_sq is the active resistance of the stator winding and the stator inductance along the longitudinal and transverse axes of the rotor (with a smooth rotor, L_sd = L_sq = L_s).

Synthesis of the EAKF algorithm is carried out taking into account mathematical PMSM model (1) in the stationary system of α–β coordinates [1] recorded as

$$\left\{ \begin{gathered} \frac{{d{{i}_{{s\alpha }}}}}{{dt}} = - \frac{{{{R}_{s}}}}{{{{L}_{s}}}}{{i}_{{s\alpha }}} + \frac{{{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}}}{{{{L}_{s}}}}{{{{\omega }}}_{r}}\sin {\kern 1pt} {{{{\theta }}}_{e}} + \frac{{{{u}_{{s\alpha }}}}}{{{{L}_{s}}}}; \hfill \\ \frac{{d{{i}_{{s\beta }}}}}{{dt}} = - \frac{{{{R}_{s}}}}{{{{L}_{s}}}}{{i}_{{s\beta }}} - \frac{{{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}}}{{{{L}_{s}}}}{{{{\omega }}}_{r}}{\text{cos}}{{{{\theta }}}_{e}} + \frac{{{{u}_{{s\beta }}}}}{{{{L}_{s}}}}; \hfill \\ \frac{{d{{{{\omega }}}_{r}}}}{{dt}} = \frac{1}{J}\left( {{{M}_{{\text{m}}}} - {{M}_{{{\text{ld}}}}} - b{{{{\omega }}}_{r}}} \right); \hfill \\ \frac{{d{{{{\theta }}}_{e}}}}{{dt}} = {{p}_{{{\text{pr}}}}}{{{{\omega }}}_{r}}; \hfill \\ \end{gathered} \right.$$

(2)

where u_sα, u_sβ, i_sα, and i_sβ are the stator currents and voltages along axes α–β.

Assume that, during the EAKF synthesis, angular rotor speed ω_r is maintained constant during the forecasting process; that is (dω_r/(dt) ≈ 0. In this case, system (2) is recorded as the following differential equations:

$$\begin{gathered} \frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {{{i}_{{s\alpha }}}} \\ {{{i}_{{s\beta }}}} \\ {{{{{\omega }}}_{r}}} \\ {{{{{\theta }}}_{e}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - L_{s}^{{ - 1}}{{R}_{s}}}&0&{L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}\sin {\kern 1pt} {{{{\theta }}}_{e}}}&0 \\ 0&{ - L_{s}^{{ - 1}}{{R}_{s}}}&{ - L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}{\text{cos}}{{{{\theta }}}_{e}}}&0 \\ 0&0&0&0 \\ 0&0&{{{p}_{{{\text{pr}}}}}}&0 \end{array}} \right] \\ \times \,\,\left[ {\begin{array}{*{20}{c}} {{{i}_{{s\alpha }}}} \\ {{{i}_{{s\beta }}}} \\ {{{{{\omega }}}_{r}}} \\ {{{{{\theta }}}_{e}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {L_{s}^{{ - 1}}}&0 \\ 0&{L_{s}^{{ - 1}}} \\ 0&0 \\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{u}_{{s\alpha }}}} \\ {{{u}_{{s\beta }}}} \end{array}} \right]. \\ \end{gathered} $$

(3)

Model (3) is a simplified mathematical description of the control object suitable for developing the sensorless vector control of the rectifier drive and synthesizing the EAKF.

EAKF SYNTHESIS ALGORITHM

The Kalman filter is an optimal stochastic observer for an ACS of nonlinear objects and is designed for estimating the variable states vector of the CO exposed to random disturbances and for measuring these disturbances [4–6]. For the function chart of estimating the variable states vector of the CO, see Fig. 2.

Fig. 2.

Function chart of estimation of the vector of control-object state variables.

It is assumed that the CO is exposed to state noises w(t) and output sensor signals are exposed to measurement noises v(t) (Fig. 2). Assume that CO (3) is described by the following nonlinear model:

$$\left\{ \begin{gathered} {\mathbf{\dot {x}}}(t) = {\mathbf{f}}\left[ {{\mathbf{x}}(t),} \right] + {\mathbf{Bu}}(t) + {\mathbf{w}}(t); \hfill \\ {\mathbf{y}}(t) = {\mathbf{h}}\left[ {{\mathbf{x}}(t)} \right] + {\mathbf{v}}(t), \hfill \\ \end{gathered} \right.$$

(4)

where ${\mathbf{x}}(t) = {{\left[ {\begin{array}{*{20}{c}} {{{i}_{{s\alpha }}}}&{{{i}_{{s\beta }}}}&{{{{{\omega }}}_{r}}}&{{{{{\theta }}}_{e}}} \end{array}} \right]}^{T}}$ is the variable-state vector of the CO, ${\mathbf{u}}(t) = {{\left[ {\begin{array}{*{20}{c}} {{{u}_{{s\alpha }}}}&{{{u}_{{s\beta }}}} \end{array}} \right]}^{T}}$ is the control-action vector, ${\mathbf{y}}(t) = {{\left[ {\begin{array}{*{20}{c}} {{{i}_{{s\alpha }}}}&{{{i}_{{s\beta }}}} \end{array}} \right]}^{T}}$ is the output-variable vector, ${\mathbf{h}}\left[ {{\mathbf{x}}(t)} \right] = \left[ {\begin{array}{*{20}{c}} {{{i}_{{s\alpha }}}} \\ {{{i}_{{s\beta }}}} \end{array}} \right]$ is a nonlinear function of nonlinear variables,

$${\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} {L_{s}^{{ - 1}}}&0 \\ 0&{L_{s}^{{ - 1}}} \\ 0&0 \\ 0&0 \end{array}} \right]$$

is the control matrix, and

$${\mathbf{f}}\left[ {{\mathbf{x}}(t)} \right] = \left[ {\begin{array}{*{20}{c}} {{{f}_{1}}} \\ {{{f}_{1}}} \\ {{{f}_{1}}} \\ {{{f}_{1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{{R}_{s}}}}{{{{L}_{s}}}}{{i}_{{s\alpha }}} + \frac{{{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}}}{{{{L}_{s}}}}{{{{\omega }}}_{r}}\sin {\kern 1pt} {{{{\theta }}}_{e}}} \\ { - \frac{{{{R}_{s}}}}{{{{L}_{s}}}}{{i}_{{s\beta }}} - \frac{{{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}}}{{{{L}_{s}}}}{{{{\omega }}}_{r}}{\text{cos}}{\kern 1pt} {{{{\theta }}}_{e}}} \\ 0 \\ {{{p}_{{{\text{pr}}}}}{{{{\omega }}}_{r}}} \end{array}} \right]$$

is the nonlinear functions of the CO.

Vectors w(t) and v(t) in Eq. (4) are described as white noise, as random Gaussian processes with zero average value and respective diagonal covariation matrices Q and R. Assume that weight matrices Q and R are known and independent of each other; that is,

$$\left\{ \begin{gathered} {\mathbf{w}}(k) \sim N\left( {0,{\mathbf{Q}}} \right),\,\,{\mathbf{Q}} \geqslant 0; \hfill \\ {\mathbf{v}}(k) \sim N\left( {0,{\mathbf{R}}} \right),\,\,{\mathbf{R}} > 0. \hfill \\ \end{gathered} \right.$$

To synthesize the EAKF algorithm, it is necessary to linearize nonlinear system of equations (4) to pseudolinear models with the help of Taylor series. In this case, system of equations (4) is recorded as Jacobi matrices:

$$\left\{ \begin{gathered} {\mathbf{\dot {x}}}(t) = {\mathbf{A}}\left( {{\mathbf{x}}(t)} \right){\mathbf{x}}(t) + {\mathbf{Bu}}(t) + {\mathbf{w}}(t); \hfill \\ {\mathbf{y}}(t) = {\mathbf{C}}\left( {{\mathbf{x}}(t)} \right){\mathbf{x}}(t) + {\mathbf{v}}(t), \hfill \\ \end{gathered} \right.$$

(5)

where

$$\begin{gathered} {\mathbf{A}}\left( {{\mathbf{x}}(t)} \right) = {{\left. {\frac{{\partial {\mathbf{f}}}}{{\partial {\mathbf{x}}}}} \right|}_{{{\mathbf{x}} = {\mathbf{x}}(t)}}} \\ = \left[ {\begin{array}{*{20}{c}} { - L_{s}^{{ - 1}}{{R}_{s}}}&0&{L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}\sin {\kern 1pt} {{{{\theta }}}_{e}}}&{L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}{\text{cos}}{{{{\theta }}}_{e}}} \\ 0&{ - L_{s}^{{ - 1}}{{R}_{s}}}&{ - L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{\text{cos}}{\kern 1pt} {{{{\theta }}}_{e}}}&{L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}{\text{sin}}{{{{\theta }}}_{e}}} \\ 0&0&0&0 \\ 0&0&{{{p}_{{{\text{pr}}}}}}&0 \end{array}} \right] \\ \end{gathered} $$

is the parametric state matrix of the CO and

$${\mathbf{C}}\left( {{\mathbf{x}}(t)} \right) = {{\left. {\frac{{\partial {\mathbf{h}}}}{{\partial {\mathbf{x}}}}} \right|}_{{{\mathbf{x}} = {\mathbf{x}}(t)}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \end{array}} \right]$$

is the parametric matrix of the CO output.

Euler’s method of linearizing and sampling the CO with sampling period T_s allows recording system of equations (5) as

$$\left\{ \begin{gathered} {\mathbf{x}}(k + 1) = {\mathbf{A}}(k){\mathbf{x}}(k) + {\mathbf{B}}(k){\mathbf{u}}(k) + {\mathbf{w}}(k); \hfill \\ {\mathbf{y}}(k) = {\mathbf{C}}(k){\mathbf{x}}(k) + {\mathbf{v}}(k), \hfill \\ \end{gathered} \right.$$

(6)

$${\mathbf{x}}(k) = {{\left[ {\begin{array}{*{20}{c}} {{{i}_{{s\alpha }}}(k)}&{{{i}_{{s\beta }}}(k)}&{{{{{\omega }}}_{r}}(k)}&{{{{{\theta }}}_{e}}(k)} \end{array}} \right]}^{T}};$$

where

$${\mathbf{u}}(k) = {{\left[ {\begin{array}{*{20}{c}} {{{u}_{{s\alpha }}}(k)}&{{{u}_{{s\beta }}}(k)} \end{array}} \right]}^{T}}$$

$${\mathbf{A}}(k) = {\mathbf{I}} + {{T}_{s}}{\mathbf{A}}\left( {{\mathbf{x}}(t)} \right) = \left[ {\begin{array}{*{20}{c}} {1 - {{T}_{s}}L_{s}^{{ - 1}}{{R}_{s}}}&0&{{{T}_{s}}L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}\sin {\kern 1pt} {{{{\theta }}}_{e}}}&{{{T}_{s}}L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}{\text{cos}}{{{{\theta }}}_{e}}} \\ 0&{1 - {{T}_{s}}L_{s}^{{ - 1}}{{R}_{s}}}&{ - {{T}_{s}}L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{\text{cos}}{{{{\theta }}}_{e}}}&{{{T}_{s}}L_{s}^{{ - 1}}{{p}_{{{\text{pr}}}}}{{{{\psi }}}_{r}}{\text{sin}}{{{{\theta }}}_{e}}} \\ 0&0&1&0 \\ 0&0&{{{T}_{s}}{{p}_{{{\text{pr}}}}}}&1 \end{array}} \right],$$

$${\mathbf{B}}(k) = {{T}_{s}}{\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} {{{T}_{s}}L_{s}^{{ - 1}}}&0 \\ 0&{{{T}_{s}}L_{s}^{{ - 1}}} \\ 0&0 \\ 0&0 \end{array}} \right],$$

$${\mathbf{C}}(k) = {\mathbf{C}}\left( {{\mathbf{x}}(t)} \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \end{array}} \right]$$

is the unit diagonal matrix.

Discrete model (6) can be used for calculating the amplification coefficient matrix of the optimal KF. When deriving estimate $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$(k) of the KF state vector, the composite quality function of the mean square error recorded as

$$J = E\left\{ {\left[ {{\mathbf{x}}(k) - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k)} \right]{{{\left[ {{\mathbf{x}}(k) - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k)} \right]}}^{T}}} \right\} \to \min $$

(7)

is minimized.

The KF is implemented by recursion with the processing of random data mined by minimizing composite quality function (7). The process of synthesizing the KF performance algorithm consists of forecasting and correction [5]. The optimal estimate of state vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$(k) is derived from:

forecast equations (step 1)

$${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}^{ - }}(k) = {\mathbf{A}}(k){\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k - 1),$$

(8)

$${{{\mathbf{P}}}^{ - }}(k) = {\mathbf{A}}(k - 1){\mathbf{P}}(k - 1){{{\mathbf{A}}}^{T}}(k - 1) + {\mathbf{Q}}(k - 1),$$

(9)

$${\mathbf{\hat {y}}}(k) = {\mathbf{C}}(k){{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}^{ - }}(k).$$

(10)

and correction equations (step 2) recorded as

$${\mathbf{e}}(k) = {\mathbf{\hat {y}}}(k) - {\mathbf{C}}(k){{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}^{ - }}(k),$$

(11)

$${\mathbf{L}}(k) = {{{\mathbf{P}}}^{ - }}(k){{{\mathbf{C}}}^{T}}(k){{\left[ {{\mathbf{C}}(k){{{\mathbf{P}}}^{ - }}(k){{{\mathbf{C}}}^{T}}(k) + {\mathbf{R}}(k)} \right]}^{{ - 1}}},$$

(12)

$${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k) = {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}^{ - }}(k) + {\mathbf{L}}(k){\mathbf{e}}(k),$$

(13)

$${\mathbf{P}}(k) = \left[ {{\mathbf{I}} - {\mathbf{L}}(k){\mathbf{C}}(k)} \right]{{{\mathbf{P}}}^{ - }}(k),$$

(14)

where ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}^{ - }}(k)$, ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k)$, ${{{\mathbf{P}}}^{ - }}(k)$ and ${\mathbf{P}}(k)$ are the a priori and a posteriori estimates of the state-variable vector and the error covariation matrix, L(k) is the KF amplification coefficient matrix, and e(k) is the measurement error matrix.

In practice, however, random noise values frequently change, which makes it more complicated to determine weight matrices Q(k) and R(k). Their instability causes a large estimation error in the application of the KF in nonlinear systems, and divergence can occur during filtration. The estimation accuracy requirements are satisfied by using the EAKF as a filter that is adaptive to noise and estimates covariation state noise and measurement matrices Q(k) and R(k).

Equation (11) can be recorded as

$${\mathbf{e}}(k) \approx {\mathbf{C}}(k)\left( {{\mathbf{x}}(k) - {{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}}^{ - }}(k)} \right) + {\mathbf{v}}(k).$$

(15)

Covariations are derived by using the dispersion from both parts of Eq. (15):

$${{{\mathbf{\Phi }}}_{e}}(k) = \frac{1}{k}\sum\limits_{i = 1}^k {\mathbf{e}} (k){{{\mathbf{e}}}^{T}}(k) = {\mathbf{C}}(k){{{\mathbf{P}}}^{ - }}(k){{{\mathbf{C}}}^{T}}(k) + {\mathbf{R}}(k).$$

(16)

The measurement noise covariation estimate is

$${\mathbf{R}}(k) = {{{\mathbf{\Phi }}}_{e}}(k) - {\mathbf{C}}(k){{{\mathbf{P}}}^{ - }}(k){{{\mathbf{C}}}^{T}}(k).$$

(17)

The state noise covariation estimate is

$${\mathbf{Q}}(k) = {\mathbf{L}}(k){{{\mathbf{\Phi }}}_{e}}(k){{{\mathbf{L}}}^{T}}(k).$$

(18)

The parameters of the covariation state and measurement matrices are adaptively upgraded by Eqs. (17) and (18) in each integration k. Equations (8)–(18) are appropriate for deriving optimal EAKF observer coefficient vector (12).

A function chart of the synthesis of optimal EAKF observer coefficients and state vector estimation vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$(k) is shown in Fig. 3.

Fig. 3.

Function chart of the synthesis of the optimal coefficient vector of the EAKF observer and state vector estimator vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mathbf{x}}$(k).

The sensorless vector-control system of the rectifier drive of the PMSM is modeled in MATLAB/Simulink using the Delta ECMA-Series synchronous motor the parameters of which in nominal mode are shown in Table 1.

Table 1

Parameter	Value
Shaft power, W	1500
Feeding voltage, V	380
Effective phase current, A	8.3
Shaft torque, N m	7.16
Rotor inertia torque, ×10−4 kg m2	11.18
Rotor frequency, rad/s	200
Stator-phase resistance, Ω	0.26
Stator-phase inductance, ×10–3 H	4.01
Viscous friction coefficient, N m s/rad	0.001
Performance	0.91
Load torque, N m	1.5
Pole pairs	4

Consider the sensorless vector-control system of the rectifier drive of the PMSM with an extended adaptive Kalman filter as the observer of the angular speed and position of the rotor. The function chart for modeling such a system is shown in Fig. 4.

Fig. 4.

Function chart of the sensorless vector-control system of a permanent-magnet synchronous motor with an extended adaptive Kalman filter: CCDC is the converter of coordinates in the direct channel, CCFC is the converter of coordinates in the feedback channel, AVR is the active voltage rectifier, and FC is the frequency converter.

It is seen from Fig. 4 that the PMSM is powered by a frequency converter with an active voltage rectifier. The vector system of controlling the speed of the PMSM rectifier drive consists from two loops. The internal loop has independent PI controllers of current PI_d and PI_q. The external loop is PI speed controller PI_ω. Rotor speed ${{{{\hat {\omega }}}}_{r}}$ and electric angle ${{{{\hat {\theta }}}}_{e}}$ of rotor flux linkage are assessed using the EAKF observer.

The parameters for modeling the work of the EAKF observer are

$${\mathbf{Q}}{\text{(}}0{\text{)}} = \text{diag}\left[ {\begin{array}{*{20}{c}} {0.05}&{0.05}&{0.01}&{0.01} \end{array}} \right];$$

$${\mathbf{R}}(0) = \text{diag}(0.01,{\text{ }}0.05);\,\,\,\,{{T}_{s}} = {{10}^{{ - 6}}}\,{\text{s}}{\text{.}}$$

The initial value of the state and matrix of error covariation is

$${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}^{ - }}(0) = 0;$$

$${{{\mathbf{P}}}^{ - }}(0) = \text{diag}\left[ {\begin{array}{*{20}{c}} {0.001}&{0.001}&{0.005}&{0.001} \end{array}} \right].$$

The results of modeling the work of the sensorless control system are considered for two modes.

(1) Using the sensorless control system of the PMSM rectifier drive with an EAKF in a low-speed mode. The modeling results are estimated by components of the transient process of the angular speed and angular position of the rotor and stator phase currents (Figs. 5–7). In this case, the design angular speed at inlet of the PI speed controller is 10 rad/s.

Fig. 5.

Oscillograms of the rotor speed refinement by the EAKF observer: (1) target angular speed, (2) transient rotor-speed process in the case of using a mechanical speed sensor, and (3) transient rotor-speed process in the case of using the EAKF observer.

Fig. 6.

Observer of the estimate of the angular position of the EAKF-based rotor: (1) angular speed of the rotor in the case of using a mechanical position sensor; (2) angular position estimation with the help of an EAKF observer.

Fig. 7.

PMSM stator-phase currents. Curves 1, 2, and 3 correspond to stator-winding phase currents i_A, i_B, and i_C.

The oscillograms of the rotor speed refinement by the EAKF observer are shown in Fig. 5.

For the results of the EAKF observer of the angular rotor-position estimate, see Fig. 6.

The phase currents of the PMSM stator are shown in Fig. 7. The phase currents depend on load torque. In this case, the load torque on the motor shaft within 0.1 s after startup is 1.5 N m and i_ABC ≈ 3.

(2) The second mode is the work of the EAKF observer of the PMSM sensorless rectifier drive in normal mode. In this case, a preset speed signal is transmitted to the speed loop inlet as a rectangular pulse with an amplitude of 200 rad/s. The reactions of the closed speed loop are shown in Figs. 8–10.

Fig. 8.

Normal mode of running the EAKF observer of the system of the PMSM sensorless electric drive: (1) target angular speed, (2) rotor-speed reaction in the case of using mechanical speed sensor, and (3) rotor-speed estimate reaction in the case of using the EAKF observer.

Fig. 9.

Normal mode of running the EAKF observer of the system of the PMSM sensorless electric drive: (1) angular position of the rotor in the case of using the mechanical position sensor; (2) estimate of the angular position of the rotor in the case of using the EAKF observer.

Fig. 10.

Curves of phase currents of PMSM stator windings: curves 1–3 correspond to phases A–C.

In Fig. 9, curve 1 corresponds to the angular position of the rotor in case of using the mechanical position sensor and curve 2 corresponds to the estimate of the angular position of the motor rotor in the case of using the EAKF observer.

The curves of the phase currents in the PMSM stator windings are shown in Fig. 10 (curves 1–3 correspond to phases A–C).

The values of the integral estimation error (IEE) of the angular speed and position of the rotor in the low-speed and normal modes of using the rectifier drive are shown in Table 2. The IEE parameters are calculated as

$${{I}_{{{{{{\omega }}}_{r}}}}}(\% ) = \frac{{\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left| {{{{{\omega }}}_{r}} - {{{{{\hat {\omega }}}}}_{r}}} \right|} dt}}{{\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left| {{{{{\omega }}}_{r}}} \right|dt} }} \cdot 100\% ;$$

$${{I}_{{{{{{\theta }}}_{e}}}}}(\% ) = \frac{{\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left| {{{{{\theta }}}_{e}} - {{{{{\hat {\theta }}}}}_{e}}} \right|} dt}}{{\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left| {{{{{\theta }}}_{e}}} \right|dt} }} \cdot 100\% ,$$

where ${{{{\hat {\omega }}}}_{r}}{\text{ and}}\,\,{{{{\hat {\theta }}}}_{e}}$ are the estimates of the angular speed and position of the rotor.

Table 2

Rectifier-drive operation mode	Angular rotor speed IEE, ${{I}_{{{{\omega }_{r}}}}}$ (%)	Angular rotor position IEE, ${{I}_{{{{\theta }_{e}}}}}$ (%)
Low-speed	2.32	3.29
Normal	2.16	3.02

According to the modeling results in Figs. 5–10 and Table 2, the integral errors in estimating the angular speed and position of the rotor were much less critical in the case of using the EAKF observer. This observer based on the extended adaptive Kalman filter is a good method of recovering electromechanical state variables in the electric-drive control system of complex control objects.

CONCLUSIONS

A sensorless vector-control system for a PMSM rectifier drive and synthesis of an EAKF observer without conventional sensors allow making the control system less expensive and improving the reliability of the PMSM vector-control system.