Calculation of Transient Modes in Semiconductor Converters Using Static Resistances and the Implicit Euler Method

Abstract

The article proposes a new method for numerical analysis of processes in nonlinear electrical circuits with switchings. It is based on use of the implicit Euler method at the moments of switchings and immediately after them, as well as use of static resistances for linearization of the nonlinear resistors equations. In the intervals between commutations, systems of the electrical circuit equations can be solved by the trapezoid method or by the method based on backward differentiation formulas, as well as by more precise methods. The proposed method is highly stable and reliable.

INTRODUCTION

The known methods for the numerical analysis of processes in electrical circuits, as well as computer programs based on these methods, often reveal a large discrepancy between the results of calculations and physical reality. The development of power electronics and the growth in the complexity of products are imposing increased requirements on the methods of their calculation and design. This applies fully to the modeling of processes in converters operating in autonomous power plants based on renewable energy sources—in particular, sources based on hydrogen fuel cells. In this case, the absence of gross distortions of numerical solutions is critically important. The purpose of the article was not to carry out a detailed study of existing methods and programs, as well as the reasons why they fail. The defect of a known program was shown only to clarify the existing problem and show its relevance.

For numerical analysis of processes in electrical circuits, well-known methods are mainly used. Popular programs such as PSpice, Multisim, PSIM, Micro-Cap, and a few others seem to work on the basis of backward differentiation formulas (BDFs) or the trapezoidal method. The LT-spice program definitely uses the trapezoidal method; in the Fastmean program, the solution of systems of ordinary differential equations (ODEs) is carried out by summing the Taylor series and doubling the integration step.

For numerical methods for solving systems of ODEs and differential-algebraic systems of equations (DASEs), a very valuable property is absolute stability (A-stability) [1]. A-stable methods have no restrictions on the integration step. BDF-based methods are A‑stable only for orders of accuracy 1 and 2 (“Dahlquist barrier”). In addition, BDFs of an order higher than first are multipoint. They are derived for smooth functions; therefore, their application to rigid systems, for discontinuous functions, and for functions with discontinuous derivatives leads to false impulses and oscillations.

The trapezoidal method is an A-stable method of the second order of accuracy; however, it is not suitable for rigid ODE systems, since it is not L-stable (its local error tends to unity with increasing numerical solution step) [2]. L-stability allows good damping of false oscillations when the number of integration points is insufficient to adequately calculate the rigid component of the solution. The lack of L-stability leads to a sharp increase in the error if the initial integration step exceeds the smallest time constant of the circuit.

The method based on the Taylor series and step doubling refers to explicit methods and therefore is not A-stable. To calculate circuits with small time constants, it is necessary to increase the number of members of the Taylor series and the number of doubling of the integration step. In addition, the method is poorly adapted to the calculations of nonlinear circuits, since it requires repeating all the work that was carried out in preparing the matrices at each interval of circuit linearization.

In [3], nonsmooth modeling of switched circuits is considered in detail. Numerical models are developed using convex analysis, complementarity theory, variational inequalities, and differential measures. However, to simulate switching elements in [3], the simplest ideal model is usually used.

Most of methods and programs for calculating nonlinear electrical circuits use the Newton–Raphson method as a basis. However, it is sensitive to the choice of the initial guess and often fails. In general, the existing methods are not sufficiently adapted to the calculation of nonlinear-parametric rigid-oscillatory electric circuits with frequent switchings, which are relevant for practice, the time between which is several orders of magnitude less than the calculated interval. This is manifested either in the fundamental inability to solve such problems or in the inability to combine high accuracy with economical computations.

AN EXAMPLE OF INCORRECTNESS IN THE CALCULATION OF ELECTRICAL CIRCUITS

Unfortunately, all seven programs studied lead to some kind of gross distortion of solutions even on simple test circuits. Most often, they produce false high-frequency oscillations or short high-voltage pulses. For example, consider the program Micro-Cap 12.0.2.1 (32 bit) Evaluation Version (https://micro-cap.informer.com/download/#downloading).

The test circuit diagram is shown in Fig. 1. The source gives a symmetrical rectangular meander with a frequency of 50 Hz with a duty cycle of 0.5 and an amplitude of 30 V. The resistance of the resistor is 5 Ohm, the inductances of the coils are L₁ = 0.02 and L₂ = 0.2 H. A generic first level diode model is used; integration step is 10 μs. Figure 2 shows the voltage across diode VD₂ with false oscillations typical for calculating a rigid circuit using the trapezoidal method.

Fig. 1.

Test circuit diagram for the Micro-Cap 12.0.2.1 program.

Fig. 2.

Micro-Cap 12.0.2.1 program. Voltage on diode VD₂ and source voltage, V; current of diode VD₂, A, multiplied by 10. False high-frequency voltage fluctuations on diode VD₂ are shown in a general plan and in the insert with magnification. Screenshot of the program with explanations. The insert was received separately and added in a graphic editor.

The task is complicated by the fact that diode switching occurs in a circuit in which there is a series connection of inductors. This connection represents the simplest case of a cross section consisting only of coils and current sources. Such sections, as well as circuits consisting only of capacitors and EMF sources, lead to DASE of electrical circuits with an index of 2 [2, 4]. Solving such systems by standard methods can lead to errors. The given example (one of many similar ones) testifies that, at the current global level, the methods and programs for the numerical analysis of processes in electrical circuits give unacceptably large, qualitative errors; therefore, it is necessary to develop new reliable methods.

CALCULATION OF CIRCUITS WITH NONLINEAR RESISTORS

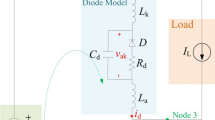
The iterative method based on static resistances provides convergence for a wide class of current–voltage characteristics of nonlinear resistors, but this method is rarely used and has not been sufficiently studied. The description of this method is given in [5]. To analyze it, the theorem on the equivalent generator is used, the nonlinear resistor is set off into a separate branch, and the rest of the circuit, possibly including other linearized nonlinear elements, is represented as a series connection of the EMF source and linear resistor R_i (Fig. 3).

Fig. 3.

Equivalent nonlinear circuit model.

The calculation scheme of the method for nonlinear current-controlled resistors is determined by the equation (here, ${{R}_{{st}}}(i) = \frac{{u(i)}}{i}$ is the static resistance of the nonlinear resistor)

$${{i}_{{k + 1}}} = \frac{e}{{{{R}_{i}} + {{R}_{{st}}}({{i}_{k}})}} = F({{i}_{k}}).$$

(1)

In [5], the sufficient condition for the convergence of process (1) has the form

$$\left| {\frac{{dF(i)}}{{di}}} \right| = \left| {\frac{{{{R}_{d}} - {{R}_{{st}}}}}{{{{R}_{i}} + {{R}_{{st}}}}}} \right| < 1,$$

(2)

where R_d = $\frac{{du}}{{di}}$ is the differential resistance of the nonlinear resistor. Moreover, it was noted that, for nonlinear two-terminal networks with decreasing static resistance, in which, in addition, 0 < R_d < R_st, the process converges for any values ​​of R_i. However, this estimate can be expanded and refined. Consider the most unfavorable case R_i = 0. Obviously, inequality (2) is satisfied under the condition

$$0 < {{R}_{d}} < 2{{R}_{{st}}}.$$

(3)

The differential equation R_d = 2R_st for the current–voltage characteristics of a nonlinear resistor has the form

$$\frac{{du}}{{di}} = 2\frac{u}{i}.$$

Solving it, we obtain u = ci², where c is any constant. Accordingly, inequalities (2) and (3) are satisfied for the current–voltage characteristics of the form u(i) = ci^k for 0 < k <2, 0 ≤ i. Hereinafter, we will consider nonlinear elements with positive values ​​of static and differential resistance; therefore, 0 < c.

Adding a positive constant to the voltage of the nonlinear resistor increases the static resistance and does not affect the differential resistance. Therefore, for resistors for which the current–voltage characteristic has the form of inequalities (2) and (3) is also satisfied, u(i) = c₁ + c₂i^k; 0 ≤ i, 0 < k < 2; 0 ≤ c₁, 0 < c₂, as a result of which iterative process (1) is guaranteed to converge for any positive initial approximations of the current. The forward branches of the current–voltage characteristics of diodes, transistors, and many other elements can be described with good accuracy by functions of this type.

Numerical experiments show that process (1) rapidly converges for any nonzero initial approximation and any sign of the current for resistors as well, the current–voltage characteristics of which have the form

$$\begin{gathered} u(i) = {\text{sign}}(i)\left( {{{c}_{1}} + {{c}_{2}}|{\kern 1pt} i{\kern 1pt} {{|}^{k}}} \right){\text{ or}} \hfill \\ u{\text{(}}i{\text{)}} = \left\{ \begin{gathered} {{c}_{1}} + {{c}_{2}}{\kern 1pt} i{\kern 1pt} {{|}^{k}},\,\,i > 0 \hfill \\ {{R}_{r}}i,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i \leqslant 0 \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered} $$

where R_r is a positive constant (reverse resistance), 0 < k < 2; 0 ≤ c₁, 0 < c₂.

Obviously, a linear combination of such characteristics also satisfies inequality (3) if its coefficients are positive. Thus, the new result for current-controlled nonlinear resistors can be formulated as follows:

convergence of process (1) for nonlinear resistors, the current–voltage characteristic of which has the form

$$\begin{gathered} u(i) = {\text{sign}}(i)\left( {{{c}_{1}} + \sum\limits_{n = 2}^N {{{c}_{n}}|{\kern 1pt} i{\kern 1pt} {{|}^{{k(n)}}}} } \right){\text{ or}} \hfill \\ u{\text{(}}i{\text{)}} = \left\{ \begin{gathered} {{c}_{1}} + \sum\limits_{n = 2}^N {{{c}_{n}}|{\kern 1pt} i{\kern 1pt} {{|}^{{k(n)}}}} ,\,\,\,\,i > 0 \hfill \\ {{R}_{r}}i,\,\,\,\,i \leqslant 0 \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered} $$

is guaranteed for 0 < k(n) < 2; 0 ≤ c_k and any nonzero initial approximation regardless of the rest of the circuit.

Similarly, for nonlinear voltage-controlled resistors, an iterative process can be specified in the form:

$${{u}_{{k + 1}}} = e\frac{{{{R}_{{st}}}({{u}_{k}})}}{{{{R}_{i}} + {{R}_{{st}}}({{u}_{k}})}} = F({{u}_{k}}),$$

(4)

where R_st(u) = $\frac{u}{{i(u)}}$ is static resistance. It is not difficult to derive the convergence condition for this process in the form indicated in [5]:

$$\left| {\frac{{dF(u)}}{{du}}} \right| = \frac{{{{R}_{i}}\left| {1 - \frac{{{{R}_{{st}}}}}{{{{R}_{d}}}}} \right|}}{{{{R}_{i}} + {{R}_{{st}}}}} < 1.$$

(5)

Performing transformations similar to the above, we obtain the convergence condition for nonlinear voltage-controlled resistors:

convergence of process (4) for nonlinear resistors, the current–voltage characteristic of which has the form

$$\begin{gathered} i(u) = {\text{sign}}(u)\left( {{{c}_{1}} + \sum\limits_{n = 2}^N {{{c}_{n}}|{\kern 1pt} u{\kern 1pt} {{|}^{{k(n)}}}} } \right){\text{ or}} \hfill \\ i{\text{(}}u{\text{)}} = \left\{ \begin{gathered} {{c}_{1}} + \sum\limits_{n = 2}^N {{{c}_{n}}u{{{\kern 1pt} }^{{k(n)}}}} ,\,\,\,\,u > 0 \hfill \\ \frac{u}{{{{R}_{r}}}},\,\,\,\,u \leqslant 0 \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered} $$

at 0 < k(n) ≤ 2; 0 ≤ c_k and any nonzero initial approximation is guaranteed regardless of the rest of the circuit.

The static resistance method can be easily generalized to circuits with an arbitrary number of nonlinear resistors, provided that the above conditions for the convergence of processes (1) or (4) are fulfilled for them. It is enough to use the corresponding static resistances instead of nonlinear resistances at each step of the iterative process and solve the resulting linear system of circuit equations. Numerous calculations of circuits with diodes and transistors show that, to achieve a relative error of no more than 10^–3, as a rule, no more than from one to three iterations are required. This method can also be used for a circuit containing reactive elements, since most numerical methods reduce the calculation of any circuit to the calculation of resistive circuits.

NUMERICAL PROCESSING OF SWITCHING MOMENTS

A model of an ideal diode and similar models with nonlinear resistive current–voltage characteristics are considered without taking into account the dynamic processes when switching on and off. Modeling such processes is a separate task, the solution of which gives a more accurate approximation to physical reality. A special problem in the calculations of nonlinear circuits is the numerical processing of the switching moments—that is, mathematical techniques and algorithms for the numerical solution of the equations of electrical circuits with an abrupt change in the parameters or configuration of the circuit. In this problem, a typical case can be distinguished, in which a diode connected in series with an inductor is closed. If a diode closes when a current is flowing in the coil, then this current, multiplied by the large reverse resistance of the diode, produces significant false overvoltages. As a rule, in existing methods and programs, the problem of abrupt changes in the system is solved by calculating the moment of such events with the subsequent adjustment of the integration step [6]. However, this moment cannot be determined with absolutely accuracy; therefore, some current in the diode and the coil connected in series with it will remain. In addition, in the presence of impulse sources in the circuit, such a forecast becomes much more complicated. The commutation of the remaining circuit elements (not diodes) usually does not cause such problems, since they are usually synchronized with the integration step.

The iterative method described above for nonlinear resistive circuits can be used to solve the diode switching problem. This method should be supplemented with a special simple procedure that allows one to determine the state of the diode at the moment immediately after switching and calculate the state of the circuit at this moment, as well as damp false overvoltages and oscillations in the vicinity of the switching point.

An important fact was noted in [3]: the classical implicit Euler method automatically calculates switching of circuit elements in unstable states. Therefore, at the moments after switching, the state of the circuit should be calculated by the implicit Euler method, switching to it from the main numerical method for calculating the circuit. It is possible to detect the moment of diode switching in a simple way: if the signs of the diode current in the previous and present moments are different, then switching occurs in the current interval. In addition to switching to the implicit Euler method, the iterative algorithm described above should be used to determine the state of the diode and the entire circuit at the moment after switching. For a nonlinear diode model, it is used at each integration step.

There is another problem that is connected with commutations—the inability of many numerical methods to calculate rigid circuits and circuits with discontinuous solutions and their derivatives, as well as circuits the original DASEs of which have an index of 2 and higher. In particular, index 2 is of circuits containing contours only from capacitors and EMF sources, or sections only from inductors and current sources. In the cases listed above, such widely used methods as the trapezoidal method and BDF-based methods yield significant false oscillations. This problem can be solved by calculating the state of the circuit not only at the moment of switching, but also during three to four integration steps after switching by the implicit Euler method in combination with an iterative solution of nonlinear equations. This method differs from others in increased stability; moreover, it is L‑stable and, therefore, dampens well the false oscillations of the solution [1].

Low accuracy is a well-known drawback of the explicit and implicit Euler methods. However, in three to four steps, there is no significant loss of accuracy and the rigid part of the solution, if it exists and if there are not enough integration points for its adequate calculation, is well damped. As a result, the circuit is brought to a state from which until the next switching, less universal, but more accurate, methods can be applied. For example, one can use the trapezoidal method and BDF-based methods, which work well on the intervals of solution smoothness, including for circuits with DASE with index 2.

EXAMPLES OF CALCULATIONS USING THE NEW METHOD

Figure 4 shows the correct calculation of the processes in the test circuit (Fig. 1) using the Elektroskop program, which implements the above algorithm. In areas of smoothness of the solution, the trapezoidal method was used. A diode model APTGT150DH120G with a piecewise linear forward-bias region and a reverse-bias region of the current–voltage characteristic in the form of a linear resistance of 100 kOhm is used; the time step was 10 μs. The permissible relative error for nonlinear equations is set equal to 10^–4. The proposed method and program have been tested many times when creating more than 30 different energy converters and electric drives.

Fig. 4.

Elektroskop program. Correct calculation of the test circuit (Fig. 1). On the abscissa axis, time, ms; on the ordinate axis, voltage of diode VD₂, V, source voltage, V, and current of diode VD₂, A (multiplied by 10).

To demonstrate the capabilities of the proposed algorithm and the corresponding program, in addition to calculating the test circuits, the processes in the step-down transformerless converter of constant voltage of the power plant on fuel cells for an unmanned aerial vehicle were calculated [7–9]. The circuit of the converter taking into account the parasitic parameters of the circuit is shown in Fig. 5.

Fig. 5.

Circuit of a transformerless dc voltage converter taking into account parasitic parameters.

For a pulse (PWM) connection of the choke L₁ = 3.13 μH to the source, IAUT300N10S5N015 transistors are used that are connected in parallel. The PWM frequency is 108 kHz. The circuit parameters for simulating a laboratory experiment are shown in the diagram in SI units. The E₁ source provides a constant voltage of 36.7 V. The duty cycle of the PWM converter is 0.724, and the rated load voltage is 27.03 V. Figure 6 shows a comparison of the calculated and experimental oscillograms of the voltage of transistors 1 and 3 of the converter.

The calculated oscillogram was obtained using the Elektroskop software. A constant integration step of 48 ns was chosen, which is equal to the switching-off time of the transistors. The experimental oscillogram was obtained using a DSO1014A oscilloscope. The supply voltage is 36.7 V, the load voltage is 27 V, and the load resistance is 28.3 Ohm. The slight difference in frequency, as well as in the width of the calculated and experimental pulses, is explained by the operation of the voltage regulator on a real physical device; there is no regulator in the calculated model. The relative error of the peak values ​​of the voltage across the transistors is 1.4%, and there are no gross calculation defects.

Fig. 6.

Calculated and experimental oscillograms of the voltage of transistors 1 and 3.