Study of Continuous-Wave Single-Mode Lasing Efficiency in a Longitudinally Pumped YLF:Nd³⁺ Laser

Abstract

We report a theoretical and experimental study of the effect of up-conversion on the efficiency of continuous-wave generation of the fundamental TEM₀₀ mode in a YLF:Nd³⁺ laser longitudinally pumped by laser diode radiation. It is shown that up-conversion is not the reason for the dependence of the single-mode output power of a YLF:Nd³⁺ laser on the output mirror reflectance at a constant pump power.

1 INTRODUCTION

Longitudinal pumping of the active element (AE) with radiation from laser diodes (LDs) in solid-state lasers makes it possible to effectively implement continuous-wave generation of single-mode beams with a high power and low divergence, corresponding to the diffraction limit with M² ≈ 1 [1]. Moreover, due to a number of properties—a high absorption coefficient at a wavelength of 0.8 μm, an effective four-level generation scheme at a wavelength of 1 μm, optical quality, and mechanical strength—YAG:Nd³⁺, YLF:Nd³⁺, and YVO₄:Nd³⁺ crystals doped with neodymium ions are most often chosen as AEs. The possibility of expanding the areas of application of this type of laser, especially for technological purposes, requires a consistent increase in the power of the generated continuous-wave single-mode radiation. To solve this problem, the most promising is the use of a yttrium–lithium fluoride crystal in combination with sources of continuous-wave pump radiation having a power of up to several tens of watts, since, firstly, YLF:Nd³⁺ is a uniaxial crystal with natural birefringence and, secondly, for the wavelength λ = 1.053 μm, the effect of thermo-optical distortions arising under the influence of high-power LD radiation in the YLF:Nd³⁺ crystal on the beam quality is significantly less than that in crystals of yttrium aluminum garnet and yttrium vanadate under similar conditions [2]. However, as has been shown in a number of studies, with increasing pump radiation power density in a YLF:Nd³⁺ crystal, the lifetime of the upper laser level and the energy storage efficiency significantly decrease [3]. The reason for this effect is the up-conversion process, which consists in the interaction of two neighboring Nd³⁺ ions located at the metastable ⁴F_3/2 level, followed by the energy exchange between these ions. In this case, one of the ions undergoes a transition to one of the lower levels, i.e., ⁴I_9/2, ⁴I_11/2, ⁴I_13/2, and ⁴I_15/2, while the second ions undergoes a transition to a higher energy level, the decay of which, in turn, results in luminescence in the visible region spectrum observed in a YLF:Nd³⁺ crystal under the action of focused pump radiation [4]. The rate of the up-conversion process is proportional to the square of the inverse population density, and therefore its negative effect on the laser parameters in both main regimes—cavity Q-switching and continuous-wave lasing—increases rapidly with increasing pump radiation power density [5].

An important consequence of up-conversion, in addition to the accelerated decay of the upper ⁴F_3/2 laser level population, is the release of additional heat due to an increase in the number of nonradiative transitions, implemented in accordance with the above-described scheme. Pollnau et al. [4] studied in detail the dynamics of up-conversion in YLF:Nd³⁺ and YAG:Nd³⁺ crystals, as well as its influence on the upper laser level population, on the amount of heat generated, and on the parameters of the AE thermo-optical lens under conditions of the presence and absence of lasing. In particular, Pollnau et al. [4] showed that multiphonon relaxation accompanying each of the up-conversion transitions in the absence of lasing leads to significantly greater heat release in the AE compared to heat release under stationary lasing conditions. Chen et al. [6] studied theoretically and experimentally the effect of up-conversion on the efficiency of continuous-wave single-mode generation in lasers based on YAG:Nd³⁺ and YVO₄:Nd³⁺ crystals longitudinally pumped LD radiation. In the calculations, use was made of a model of rate equations written taking into account the inhomogeneous spatial distribution of pump radiation and the fundamental TEM₀₀ mode of the cavity [7]. The correspondence of the results of calculations and experiments indicates the admissibility of the chosen calculation model. However, the approximation of the pump beam by a Gaussian beam with a constant radius, used in [6] and some other works (see, for example, [8, 9]), did not make it possible to study the effect of up-conversion on the laser parameters under different focusing conditions. Laporta and Brussard [10] showed that in lasers with longitudinal pumping of the AE by LD radiation, there is an optimal focusing at which the output power has a maximum value. However, because at the time when Laporta and Brussard [10] performed their investigation, the LDs used in the experiments had a relatively low radiation power, and the threshold and slope efficiency were calculated without taking up-conversion into account. With an increase in the radiation power of LDs used as a pump source, in particular, in continuous-wave YLF:Nd³⁺ lasers, it became necessary to take into account the influence of up-conversion when considering processes in AEs. This explains the relevance of choosing a pump scheme and cavity elements that make it possible to increase the single-mode output power of a YLF:Nd³⁺ laser, taking into account the possible influence of up-conversion.

In this work, we studied theoretically and experimentally the efficiency of continuous-wave generation of the fundamental TEM₀₀ mode in a YLF:Nd³⁺ laser with variations in the parameters of its elements. For the calculations, we chose a mathematical model used earlier in [6], which takes into account the up-conversion process, but is written with allowance for a change in the diameter of the Gaussian pump beam along the AE length. In this case, the parameters of the elements of a single-mode continuous-wave YLF:Nd³⁺ laser used in the calculations and experiments corresponded to each other. This made it possible to evaluate the correctness of the description of processes in the laser cavity by comparing the results of calculations and measurements. The purpose of the work was to study the effect of up-conversion on the efficiency of single-mode generation in a YLF:Nd³⁺ laser longitudinally pumped by continuous-wave LD radiation. As a result of the calculations and measurements, it was shown in particular that up-conversion is not the reason, as noted by Chen et al. [6], for the dependence of the single-mode output power of a YLF:Nd³⁺ laser on the output mirror reflectance at a constant pump power.

2 STATIONARY SINGLE-MODE LASING IN A LONGITUDINALLY PUMPED LASER. BASIC EQUATIONS TAKING INTO ACCOUNT UP-CONVERSION

To calculate the main parameters—power and lasing threshold—we will use the following mathematical model of a single-mode longitudinally pumped laser. The LD radiation propagates along the z axis of the cylindrical AE and is focused in a certain region, the diameter of which is much smaller than the AE diameter, at a distance z₀ from the input plane. The spatial distribution of pump radiation in the AE is described by a Gaussian function. However, since the LD radiation along the “fast” and “slow” axes is single-mode and multimode, respectively, the change in the diameter of the pump beam with distance is complex. Measurements of a typical pump beam profile showed that it corresponds to a Gaussian beam, the diameter of which (at the e^–1 intensity level) varies with distance from the waist in accordance with the expression

$$w_{{\text{p}}}^{2}(z) = w_{{{\text{p0}}}}^{2}\left[ {1 + {{{\left( {{{M}^{2}}\frac{{{{\lambda }_{{\text{p}}}}(z - {{z}_{0}})}}{{\pi w_{{{\text{p}}0}}^{2}}}} \right)}}^{2}}} \right],$$

(1)

where w_p0 is the waist radius of the pump beam (at the e^–1 intensity level) [cm], λ_p is the pump wavelength [cm], (z – z₀) is the distance to the waist [cm], and M² is a parameter characterizing the beam quality.

Thus, the pump intensity changes with distance due to absorption in the AE and variations in the cross-sectional area of the beam:

$${{r}_{{\text{p}}}}(x,y,z) \sim \exp \left( { - {{\alpha }_{{{\text{abs}}}}}z - \frac{{{{x}^{2}} + {{y}^{2}}}}{{w_{{\text{p}}}^{2}(z)}}} \right),$$

(2)

$$\int\limits_{{\text{active}}} {{{r}_{{\text{p}}}}(x,y,z){\text{d}}V = {\text{1,}}} $$

(3)

where α_abs is the radiation absorption coefficient [cm^–1], and x and y are coordinates in the plane orthogonal to the axis of the cylindrical AE.

To find the normalization factor, we divide the AE along the z axis into a finite number N of small regions of length Δz. Then the normalized distribution function of the pump radiation in the AE has the form

$$\begin{gathered} {{r}_{{\text{p}}}}(x,y,z) = {{\alpha }_{{{\text{abs}}}}}\exp \left( { - {{\alpha }_{{{\text{abs}}}}}z - \frac{{{{x}^{2}} + {{y}^{2}}}}{{w_{{\text{p}}}^{2}(z)}}} \right) \\ \times {{\left\{ {[1 - \exp ( - {{\alpha }_{{{\text{abs}}}}}\Delta z)]\sum\limits_{i = 0}^{N - 1} {\pi w_{{\text{p}}}^{2}({{z}_{i}})\exp ( - {{\alpha }_{{{\text{abs}}}}}{{z}_{i}})} } \right\}}^{{ - 1}}}, \\ \end{gathered} $$

(4)

where z_i is the distance from the input plane to the ith element [cm].

The spatial distribution of laser radiation photons, corresponding to the fundamental TEM₀₀ mode of the resonator, is described by a Gaussian function, the parameters of which in the region of the active element will be considered constant:

$$S(x,y,z,{{P}_{{{\text{pump}}}}}) = S({{P}_{{{\text{pump}}}}}){{s}_{0}}(x,y,z),$$

(5)

$${{s}_{0}}(x,y,z) = \frac{1}{{\pi w_{{\text{s}}}^{2}{{L}_{{\text{r}}}}}}\exp \left( { - \frac{{2({{x}^{2}} + {{y}^{2}})}}{{w_{{\text{s}}}^{2}}}} \right),$$

(6)

$$\int\limits_{{\text{active}}} {{{s}_{{\text{0}}}}(x,y,z){\text{d}}V = {\text{1,}}} $$

(7)

where s₀(x, y, z) is the spatial distribution function of photons in the fundamental mode normalized to the resonator volume [cm^–3]; w_s is the radius of the fundamental mode beam (at the e^–2 level) in the AE region [cm]; S(P_pump) is the equilibrium number of photons in the fundamental mode, corresponding to the pump power level; P_pump is the continuous-wave pump power [W]; and L_r is the resonator length [cm].

Using the general form of balance equations for a single-mode laser, written taking into account the up-conversion process (see, for example, [6]), we find the relationships between the main parameters and lasing characteristics of the laser:

$$\begin{gathered} \int\limits_{{\text{active}}} {4R_{{\text{p}}}^{{{\text{th}}}}{{r}_{{\text{p}}}}(x,y,z){{\tau }_{{\text{f}}}}\exp \left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{w_{0}^{2}}}} \right)} \\ \times \;{{\left[ {1 + \sqrt {1 + 4R_{{\text{p}}}^{{{\text{th}}}}{{r}_{{\text{p}}}}(x,y,z)\gamma \tau _{{\text{f}}}^{2}} } \right]}^{{ - 1}}}{\text{d}}x{\text{d}}y{\text{d}}z = {{\delta }_{{{\text{in}}}}}\frac{{\pi w_{{\text{s}}}^{2}}}{\sigma }, \\ \end{gathered} $$

(8)

$$F(x,y,z,{{P}_{{{\text{pump}}}}}) = c\sigma {{\tau }_{{\text{f}}}}{{s}_{0}}(x,y,z)S({{P}_{{{\text{pump}}}}}),$$

(9)

$$\begin{gathered} \int\limits_{{\text{active}}} {4{{R}_{{\text{p}}}}{{r}_{{\text{p}}}}(x,y,z){{\tau }_{{\text{f}}}}\exp \left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{w_{{\text{s}}}^{2}}}} \right)} \left\{ {{{{[1 + F(x,y,z,{{P}_{{{\text{pump}}}}})]}}^{{^{{^{{}}}}}}}} \right. \\ {{\left. { + \sqrt {{{{[1 + F(x,y,z,{{P}_{{{\text{pump}}}}})]}}^{2}} + 4{{R}_{{\text{p}}}}{{r}_{{\text{p}}}}(x,y,z)\gamma \tau _{{\text{f}}}^{2}} } \right\}}^{{ - 1}}}{\text{d}}x{\text{d}}y{\text{d}}z = {{\delta }_{{{\text{in}}}}}\frac{{\pi w_{{\text{s}}}^{2}}}{\sigma }, \\ \end{gathered} $$

(10)

$${{P}_{{{\text{abs}}}}} = {{R}_{{\text{p}}}}h{{\nu }_{{\text{p}}}},$$

(11)

$$P_{{{\text{pump}}}}^{{{\text{th}}}} = \frac{{R_{{\text{p}}}^{{{\text{th}}}}h{{\nu }_{{\text{p}}}}}}{{{{\eta }_{{{\text{abs}}}}}}},$$

(12)

$${{P}_{{{\text{out}}}}}({{P}_{{{\text{pump}}}}}) = S({{P}_{{{\text{pump}}}}})h{{\nu }_{{\text{s}}}}T\frac{c}{{2{{L}_{{\text{r}}}}}},$$

(13)

where R_p is the pump speed [s^–1]; P_abs is the absorbed pump power in the AE [W]; hν_p is the pump photon energy [J]; $R_{{\text{p}}}^{{{\text{th}}}}$ is the threshold pump speed; P_pump is the pump radiation power [W]; $P_{{{\text{pump}}}}^{{{\text{th}}}}$ is the threshold pump power [W]; τ_f is the lifetime of the upper laser level [s]; σ is the cross-sectional area of the induced transition [cm²]; c is the speed of light [cm/s]; δ_in is the total radiation loss per round-trip transit of radiation in the resonator, which consists of useful losses on the output mirror [T = ln(1/R₁), R₁ is the output mirror reflectance] and losses in the remaining elements of the resonator; γ is the rate of the up-conversion process [cm^–3 s^–1]; P_out(t) is the laser radiation power [W]; hν_s is the photon energy of laser radiation; and η_abs is the absorption efficiency of pump radiation in the AE.

Thus, expressions (8)–(13) will be the basic equations of the mathematical model of a continuous-wave single-mode longitudinally pumped laser, used in the calculations. When calculating the integrals in (8) and (10), we apply the above-mentioned division of the AE into elementary regions Δz, in each of which the value of w_p(z_i) is assumed to be constant. To find solutions to these equations, we used the method of successive iterations. As a first approximation, the values of S(P_pump) and $R_{{\text{p}}}^{{{\text{th}}}}$ were calculated for the case when γ = 0; i.e., there is no up-conversion. In particular, S(P_pump) was calculated as a first approximation from the expression obtained by linearizing equation (1.10) from [6], written without taking up-conversion into account:

$$S({{P}_{{{\text{pump}}}}}) = \frac{1}{{T + {{\delta }_{{{\text{in}}}}}}}\frac{{2{{L}_{{\text{r}}}}}}{c}{{\eta }_{{{\text{abs}}}}}{{\eta }_{{{\text{overlap}}}}}\frac{{{{P}_{{{\text{pump}}}}} - P_{{{\text{pump}}}}^{{{\text{th}}}}}}{{h{{\nu }_{{\text{p}}}}}},$$

(14)

$$\begin{gathered} {{\eta }_{{{\text{overlap}}}}} = {{\left[ {\int\limits_{{\text{active}}} {{{s}_{0}}(x,y,z){{r}_{{\text{p}}}}(x,y,z){\text{d}}V} } \right]}^{2}} \\ \times {{\left[\;\; {\int\limits_{{\text{active}}} {s_{0}^{2}(x,y,z){{r}_{{\text{p}}}}(x,y,z){\text{d}}V} } \right]}^{{ - 1}}}, \\ \end{gathered} $$

(15)

where η_overlap is the efficiency of spatial matching of the pump beams and the fundamental mode of the resonator.

Equations (8) and (10) with the updated values of S(P_pump) and $R_{{\text{p}}}^{{{\text{th}}}}$ were numerically integrated sequentially until the relative difference between the right- and left-hand sides in the equations did not exceed 5 × 10^–4. The values of S(P_pump) and $R_{{\text{p}}}^{{{\text{th}}}}$ at which this condition was satisfied were the sought solutions to (8) and (10). Then the threshold pump power and continuous-wave lasing power under stationary conditions were calculated from relations (12) and (13) using the found solutions to (8) and (10).

Note that from relations (13) and (14) one can obtain known expressions for the linear dependence of the output power on the pump power and the slope efficiency, which characterize the efficiency of using pump radiation to generate single-mode radiation [10]:

$${{P}_{{{\text{out}}}}}({{P}_{{{\text{pump}}}}}) = \frac{T}{{T + {{\delta }_{{{\text{in}}}}}}}\frac{{{{\nu }_{{\text{s}}}}}}{{{{\nu }_{{\text{p}}}}}}{{\eta }_{{{\text{abs}}}}}{{\eta }_{{{\text{overlap}}}}}({{P}_{{{\text{pump}}}}} - P_{{{\text{pump}}}}^{{{\text{th}}}}),$$

(16)

$${{P}_{{{\text{out}}}}}({{P}_{{{\text{pump}}}}}) = {{\eta }_{{{\text{slope}}}}}({{P}_{{{\text{pump}}}}} - P_{{{\text{pump}}}}^{{{\text{th}}}}),$$

(17)

where η_slope is the slope generation efficiency.

3 EXPERIMENTAL STUDY AND COMPARISON WITH CALCULATION RESULTS

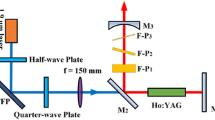
During the experiments, we studied a continuous-wave single-mode YLF:Nd³⁺ laser longitudinally pumped by radiation from laser diodes, with the laser resonator having a flat-spherical design. The resonator was formed by a flat output mirror with reflectance R₁ and a highly reflecting spherical mirror with a radius of curvature r₂ = 200 mm. The geometric length of the resonator was 53 mm; the beam radius of the fundamental mode in the AE region was w_s = 0.185 mm. The LD radiation was coupled into the AE through a spherical mirror; the dielectric coating deposited on its flat and concave surfaces provided a transmittance of more than 98% at a wavelength of 800 nm. The pump radiation was focused by a lens with a focal length of 70 mm into a beam with a complex profile, which can be approximated by a Gaussian beam with w_p0 = 0.05 mm and M² = 8 [see (4)]. A cylindrical AE—a YLF:Nd³⁺ crystal (a-cut, С_Nd = 1.2 at %) with a diameter of 5 mm and a length of 10 or 15 mm—was installed close to the highly reflecting spherical mirror. To remove heat, it was mounted through indium foil in a copper flange on an electric microcooler that maintained a constant temperature level of 30°C. A plane-parallel glass plate 2 mm thick was positioned at the Brewster angle in the horizontal plane, which ensured (when consistent with the AE orientation) generation of σ-polarized radiation by the YLF:Nd³⁺ crystal at a wavelength of 1.053 μm. The radiation from two LDs in the wavelength range of 802–805 nm with a nominal power of 4 W in each LD was combined into a single beam in such a way that it consisted of two orthogonally polarized components, the directions of which coincided with the a and c axes of the YLF:Nd³⁺ crystal. In this case, the average absorption coefficient was ∼2 cm^–1, which ensured (taking into account the low mechanical strength of YLF:Nd³⁺ crystals) the pump power density in the AE below the damage threshold. The use of shorter wavelength LDs, the radiation of which corresponded to a stronger absorption band by neodymium ions in the YLF:Nd³⁺ crystal, led to the damage of the AE at a beam power of less than 3 W. The ratio of the radii of the TEM₀₀-mode and pump beams w_s/($\sqrt 2 {{w}_{{{\text{p0}}}}}$) ≈ 2.5 ensured generation of only the fundamental transverse mode with stability of the spatial parameters of the beam over the entire range of changes in the pump power. To implement the conditions for optimal matching of the LD radiation and the resonator mode, ensuring maximum efficiency in the free generation regime [10], the experiment provided for the possibility of varying the distance between the front end of the AE and the waist plane of the Gaussian pump beam. In addition, moving the pump beam waist plane from the optimal location towards the output end of the AE made it possible to equalize the inverse population density along the crystal axis, reducing its average level.

In the entire series of experiments, we measured the dependence of the power of a single-mode continuous-wave generation of a YLF:Nd³⁺ laser on the pump power for various values of several parameters of the scheme, namely, output mirror reflectance, AE length, and distance between the input plane of the AE and the waist plane w_p0 of the pump beam. As an example, Figs. 1 and 2 present the results of measuring and calculating the radiation power of a YLF:Nd³⁺ laser in the form of linear functions, carried out at minimum and maximum reflectances of the output mirror with optimal focusing of the pump radiation in an AE with a length of 10 and 15 mm, respectively. In other cases, with other values of the varied parameters, the corresponding characteristics were also linear. Therefore, to describe the single-mode lasing of a YLF:Nd³⁺ laser, it is sufficient to use two characteristics: the threshold pump power and the slope lasing efficiency. Figures 3–6 show the dependences of these characteristics on the output mirror reflectance, constructed from the results of processing the corresponding data. It is clear from Figs. 3 and 4 that the values of the threshold pump power calculated taking into account up-conversion correspond with good accuracy to the experimental values over the entire range of changes in useful losses, while the values calculated without taking into account up-conversion are expectedly less than those in the experiment. Moreover, with increasing losses at the output mirror, this difference increases monotonically. In addition, moving the waist plane deep into the AE from the optimal position, both in experiment and in calculations taking into account up-conversion, does not lead to an increase in lasing thresholds, since the decrease in the influence of this effect is compensated for by a decrease in the efficiency of matching the pump beams and the fundamental mode. For the slope lasing efficiency (Figs. 5 and 6), the situation is more complicated. From a comparison of the graphs in Figs. 1 and 2, it follows that for output mirrors with maximum reflectance, the experimental and calculated (with and without up-conversion) values of the lasing power are close; i.e., the characteristics at the same slope differ only in the lasing threshold. With increasing losses on the output mirror, the dependences obtained in the calculations remain parallel to each other, and the slope of the curves constructed from the experimental results monotonically decreases.

Fig. 1.

Dependences of the radiation power of a YLF:Nd³⁺ laser on the pump power, obtained in the experiment and calculations for a 1-cm-long AE with reflectance R₁ = (a) 82% and (b) 33%. Loss per round-trip transit of radiation in the resonator is 0.03, and the absorption coefficient is 2 cm^–1; the pump focusing is optimal, i.e., 0.5 cm in AE.

Fig. 2.

Dependences of the radiation power of a YLF:Nd³⁺ laser on the pump power, obtained in the experiment and calculations for a 1.5-cm-long AE with reflectance R₁ = (a) 82% and (b) 55%. Loss per round-trip transit of radiation in the resonator is 0.03, and the absorption coefficient is 2 cm^–1; the pump focusing is optimal, i.e., 0.5 cm in AE.

Fig. 3.

Experimental and calculated dependences of the threshold pump power on losses on the output mirror of a continuous-wave YLF:Nd³⁺ laser with an AE 1 cm long: (a) optimal focusing of 0.5 cm in the AE and the resonator round-trip losses of 0.03, and (b) nonoptimal focusing of 1 cm in the AE and the resonator round-trip losses of 0.07.

Fig. 4.

Experimental and calculated dependences of the threshold pump power on losses on the output mirror of a continuous-wave YLF:Nd³⁺ laser with an AE 1.5 cm long: (a) optimal focusing of 0.5 cm in the AE and the resonator round-trip losses of 0.03, and (b) nonoptimal focusing of 1.6 cm in the AE and the resonator round-trip losses of 0.03.

Fig. 5.

Dependences of the slope lasing efficiency on the useful loss coefficient of a continuous-wave YLF:Nd³⁺ laser with an AE 1 cm long: (a) optimal focusing of 0.5 cm in the AE and resonator round-trip losses of 0.03, and (b) nonoptimal focusing of 1 cm in the AE and resonator round-trip losses of 0.07.

Fig. 6.

Dependences of the slope lasing efficiency on the useful loss coefficient of a continuous-wave YLF:Nd³⁺ laser with an AE 1.5 cm long: (a) optimal focusing of 0.5 cm in the AE and resonator round-trip losses of 0.03, and (b) nonoptimal focusing of 1.6 cm in the AE and resonator round-trip losses of 0.03.

Thus, in the entire series of experiments, regardless of the method of LD radiation focusing in the AE and the intracavity losses, the slope efficiency of continuous-wave single-mode lasing decreased with decreasing output mirror reflectance. The calculated values of the slope efficiency, while remaining constant, coincided with good accuracy with those calculated using the approximate formula (16). Due to this behavior of the characteristics, the relative difference between the calculated P_calc and measured P_exp output powers of the YLF:Nd³⁺ laser at a certain pump power, (P_calc – P_exp)/P_calc, monotonically increased with increasing losses on the output mirror (Fig. 7) regardless of the pump focusing method and intracavity losses. These results indicate a decrease in the efficiency of single-mode lasing with increasing losses on the output mirror. Up-conversion increases the decay rate of the population inversion only in the absence of fundamental mode radiation in the resonator, which slightly increases the lasing threshold. After reaching the lasing threshold, the rate of decay of the population inversion due to stimulated emission significantly exceeds the rate of up-conversion {see (1) in [6]}, and the influence of the latter on the single-mode lasing power turns out to be negligible. Consequently, the discrepancy between the experimental and calculated values of the slope efficiency was not a consequence of up-conversion, but of a process not taken into account in the system of balance equations and relation (10). The results of calculations of the power of continuous-wave single-mode lasing at a fixed pump power obtained in [6] were in good agreement with experimental values in a wider range of changes in reflectance of the output mirror, i.e., from 98% to 50% than in our case. However, in [6], the ratio of the radii of the pump beams and the fundamental mode is w_s/($\sqrt 2 {{w}_{{{\text{p0}}}}}$) ≈ 1.25, i.e., two times less than in our experiment. This may be significant, since the configuration of the plane-spherical resonator used in the present experiments was close to the degeneracy point at which the condition

$$\arccos \sqrt {{{g}_{1}}{{g}_{2}}} = \pi \frac{m}{n},$$

(18)

is met (where m and n are natural numbers; g_{1, 2} = 1 – L_r/r_{1, 2}; and r_{1, 2} is the curvature of the output and spherical mirrors of the resonator) with m = 1 and n = 6. Indeed, as was shown by the authors of works [11, 12], with an increase in the pump radiation concentration near the resonator axis with g_{1, 2} satisfying (18), a significant deviation of the fundamental mode shape from a Gaussian one is possible. These deviations were especially significant in the vicinity of the points corresponding to the pairs of numbers m = 1, n = 3 and m = 4, n = 6 in (18), and the size of these vicinities Δg_{1, 2} expanded with increasing unsaturated gain.

Fig. 7.

Dependences of the relative difference between the experimental and calculated values of the radiation power of a continuous-wave YLF:Nd³⁺ laser at a pump power of 6 W on the value of losses on the output mirror.

In addition, when conditions (18) are met and at a certain distribution of pump radiation relative to the axis of the plane-spherical resonator, conditions are created for the generation of off-axis beams, which Dingjan et al. [13] call geometric modes rather than the fundamental Hermite–Gaussian TEM₀₀ mode. In using optimal output mirrors with R₁ = 75–83%, the spatial distribution of radiation corresponded to the Hermite–Gaussian TEM₀₀ mode with fairly good accuracy, which is confirmed by measurements of the diameter and divergence of the laser beam. Moreover, the calculation results are consistent with experiment over the entire range of pump power variations. As the output mirror reflectance decreases, as is known, the stationary values of the inverse population density and the gain in the AE increase, and the number of photons in the Gaussian TEM₀₀ mode decreases. Under the conditions of our experiments, when the resonator configuration was close to the degenerate one at m = 1 and n = 6 in (18), these factors, according to the results of [12], created conditions for expanding the regions Δg_{1, 2}, in which the deviation of the fundamental mode from the Gaussian shape could be the reason for a significant decrease in the lasing efficiency with a decrease in reflectance of the output mirror. The above-mentioned increase in the difference between the calculated and experimental values of the slope efficiency for an AE length of 1.5 cm (see Fig. 6) could be a consequence of a more accurate correspondence of the optical length of the resonator to condition (18).

4 CONCLUSIONS

We have calculated the output power of a continuous-wave single-mode YLF:Nd³⁺ laser using a model based on the search for a stationary solution to a system of rate equations written taking into account up-conversion and spatial distributions of the inverse population density and radiation intensity. The calculation results correspond to the values of the continuous-wave output power of the YLF:Nd³⁺ laser, obtained during the experiments over the entire range of changes in the LD power at a low level of useful losses in the resonator, when the output mirror reflectance is at least 75%. Under the conditions of the studies, the effect of up-conversion in the YLF:Nd³⁺ crystal on the laser efficiency is to increase the lasing thresholds, and at the optimal level of useful losses this change is small compared to the value of the threshold power. The slope efficiency values calculated using approximate formulas and obtained by solving a system of rate equations that took into account up-conversion, coincided with good accuracy, but differed from the experimental ones. A comparison of the above and previously published research results suggest that the reason for a decrease in the slope efficiency observed in experiment, but not confirmed by calculations, with increasing transparency of the output mirror is a change in the shape of the distribution of the fundamental mode of the resonator near the degeneracy point. However, additional research is needed to examine this assumption.