Mathematical Model of Magnetic Hydrodynamics and Heat Transfer in an Aluminum Reduction Cell

Abstract

A new nonstationary three-dimensional mathematical model of an aluminum reduction cell which makes it possible to perform coupled thermoelectric and magneto-hydrodynamic calculation while taking into account sideledge formation is presented. The model takes into account the nonlinear dependence of the coefficients of electrical conductivity and thermal conductivity of materials on temperature, as well as, for ferromagnetic materials, the nonlinear dependence of magnetization on the magnetic field strength. The heat-transfer coefficients on the outer surfaces include radiant and convective components of heat transfer and are functions of the ambient temperature and the local surface temperature. In the energy equation, internal sources of heat are taken into account due to the flow of electric current, exothermic reactions, and additional thermal effects associated with the raw material loading and phase transitions. To obtain a numerical solution, the control volume method is applied. Experimental testing of the developed mathematical model is performed on the S8BME aluminum reduction cell. This paper presents the calculated and experimental data of magnetic, electric, thermal, and hydrodynamic fields. A comparison of the calculation results with the results of industrial experiments shows that the model reflects the physical processes taking place in the aluminum reduction cell with accuracy sufficient for engineering calculations. The calculated values of electrical voltage, magnetic induction, and temperature practically coincide with the measured ones. Values obtained from calculating the direction of velocity in the metal pad and the shape of the sideledge profile differ insignificantly from the experimental values. This model can be used to estimate the performance and design parameters of the operation of new and modernized aluminum electrolysis cells. Further studies will be aimed at clarifying the calculated results by improving the mathematical model.

INTRODUCTION

The improvement of tools for mathematically simulating the physical fields of an aluminum reduction cell (ARC) is due to the necessity for a detailed study of physicochemical processes under various regime and structural changes of its operation. The aluminum reduction cell refers to facilities where multiplysical processes with complicated interconnection take place. Presently, the mathematical simulation of physical fields of ARC allows accounting many physical processes with a sufficient accuracy.

A number of works are devoted to simulating magnetic hydrodynamics (MHD) in ARC [1–6 and related references]. As a rule, MHD is computed in the approximation of shallow water without taking heat exchange and the shape of operation cavity (SOC) into account. Works [7, 8] present the results of a three-dimensional simulation of APXe and AP6X reduction cells obtained using the ALUCELL package, whose main purpose is the possibility of the coupled computation of MHD stability of the bath, dissolution, and the transfer of alumina in electrolyte, as well as heat fields.

The authors of [9] presented a three-dimensional model assigned for determining SOC and optimization of ARC construction. This work includes a computational study of three busbar designs for thermal and hydrodynamic states of reduction cell operating at a current strength of 400 kA. The software solution is performed as follows: first, electromagnetic and thermal problems are solved in the Ansys package; then inner heat sources and magnetic Lorentz forces are passed to the Fluent application. The hydrodynamic problem taking into account the crystallization of the electrolyte is solved in Fluent. SOC is determined by the introduction of an additional component into the Navier–Stokes equation, which represents the volume force responsible for slowing down the melt. In this way, solutions to thermoelectric and hydrodynamic problems in [9] are not coupled, which in our opinion may lead to inaccurate results.

In our work, we suggest a new three-dimensional nonstationary mathematical model that allows performing a coupled computational analysis of electrolyte and metal flow under magnetic and gravitational forces, as well as smelting chamber shape. At the same time, we applied the Ansys CFX commercial software system, assigned for solving problems of computational hydrodynamics, and specific application Blums 5.07, which allows computing magnetic fields in the volume of a reduction cell. Computation results were compared with data from industrial experiments.

MATHEMATICAL MODEL

Motion of metal and electrolyte is simulated using a homogeneous model, according to which both phases have identical fields of velocity, temperature, and turbulence. A change in the phase content is simulated by the introduction of additional variables r_α—the volume fraction of each phase at a given point. Electrolyte and metal are counted incompressible liquids. The following equations of hydrodynamics are used [10, 11].

• Continuity equation of phase α:

$$\frac{\partial }{{\partial t}}\left( {\rho {{r}_{\alpha }}} \right) + \nabla \left( {\rho {\mathbf{u}}{{r}_{\alpha }}} \right) = 0\,\,\left( {\alpha = 1,2} \right),$$

(1)

where ρ is the density of mixture and u is its average velocity.

• Continuity equation of mixture:

$$\frac{\partial }{{\partial t}}\left( \rho \right) + \nabla \left( {\rho {\mathbf{u}}} \right) = 0;$$

(2)

• Navier–Stokes equation taking turbulence into account in the Reynolds approximation and stress tensor:

$$\begin{gathered} \frac{\partial }{{\partial t}}\left( {\rho {{u}_{i}}} \right) + \frac{\partial }{{\partial {{x}_{j}}}}\left( {\rho {{u}_{i}}{{u}_{j}}} \right) \\ = - \frac{{\partial p}}{{\partial {{x}_{j}}}} + \frac{\partial }{{\partial {{x}_{j}}}}\left[ {\mu \left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}} - \frac{2}{3}{{\delta }_{{ij}}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}}} \right)} \right] \\ - \,\,\frac{\partial }{{\partial {{x}_{j}}}}\left( {\rho \overline {u_{i}^{'}u_{j}^{'}} } \right) + {{{\mathbf{F}}}_{e}} + {{{\mathbf{F}}}_{b}} + {{{\mathbf{F}}}_{s}}, \\ \end{gathered} $$

(3)

$$ - \rho \overline {u_{i}^{'}u_{j}^{'}} = {{\mu }_{{\text{t}}}}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right) - \frac{2}{3}\left( {\rho k + {{\mu }_{t}}\frac{{\partial {{u}_{k}}}}{{\partial {{x}_{k}}}}} \right){{\delta }_{{ij}}}.$$

Here u_i, u_j are components of average velocity vector; u′ is fluctuation velocity; r_α is volume fraction of phase α; k is turbulent kinetic energy; μ, μ_t are coefficients of dynamic and turbulent viscosity, correspondingly; δ_ij is the Kronecker symbol; p is static pressure; and F_e is the electromagnetic Lorentz force:

$${{{\mathbf{F}}}_{{\text{e}}}} = {\mathbf{J}} \times {\mathbf{B}},$$

where J is current density; B is magnetic induction; and F_b is the volume force, which determines buoyancy:

$${{{\mathbf{F}}}_{{\text{b}}}} = \left( {{{\rho }_{\alpha }} - {{\rho }_{{{\text{ref}}}}}} \right){\mathbf{g}},$$

where ρ_α is the density of component α; ρ_ref is reference density; F_s is the force slowing the flow down at temperatures below that of electrolyte liquidus:

$${{{\mathbf{F}}}_{{\text{s}}}} = - h(T){\mathbf{u}},$$

where $h(T)$ is the function of temperature, which takes values 0 and 10⁶ kg/(m³ s) at temperatures above and below temperature of electrolyte liquidus correspondingly.

This model of crystallization was suggested in work [12] for the first time and has been successfully applied in many computational problems with phase transitions since then, for example in [1].

Parameters of two-phase mixture in equations are computed as follows:

$$\rho = \sum\limits_{\alpha = 1}^2 {{{r}_{\alpha }}{{\rho }_{\alpha }}} ,\,\,\,\,\mu = \sum\limits_{\alpha = 1}^2 {{{r}_{\alpha }}{{\mu }_{\alpha }}} .$$

(4)

Heat exchange and crystallization in the melt are determined from the solution of energy equation

$$\begin{gathered} \frac{\partial }{{\partial t}}\sum\limits_{\alpha = 1}^2 {\left( {{{r}_{\alpha }}{{\rho }_{\alpha }}{{h}_{\alpha }}} \right)} + \frac{\partial }{{\partial {{x}_{i}}}}\sum\limits_{\alpha = 1}^2 {\left( {{{r}_{\alpha }}{\mathbf{u}}{{\rho }_{\alpha }}{{h}_{\alpha }}} \right)} \\ = \frac{\partial }{{\partial {{x}_{j}}}}\left( {{{\lambda }_{{{\text{eff}}}}}\frac{{\partial T}}{{\partial {{x}_{j}}}}} \right) + {{Q}_{J}} + {{Q}_{{{\text{chem}}}}}. \\ \end{gathered} $$

(5)

Here h is enthalpy; Q_J is the heat effect, which is responsible for heat release in control volumes of the model caused by the flowing of the electric current:

$${{Q}_{J}} = {{{\mathbf{J}} \cdot {\mathbf{J}}} \mathord{\left/ {\vphantom {{{\mathbf{J}} \cdot {\mathbf{J}}} \sigma }} \right. \kern-0em} \sigma },$$

(6)

where σ is electric conductivity; Q_chem is the heat effect from exothermal chemical reactions flowing in liquid electrolyte and metal, as well as additional thermal effects; and λ_eff is the coefficient of efficient heat conductivity:

$${{\lambda }_{{{\text{eff}}}}} = \sum\limits_{\alpha = 1}^2 {{{r}_{\alpha }}\left( {{{\lambda }_{\alpha }} + {{\lambda }_{{\text{t}}}}} \right)} ,$$

(7)

where λ_α is the coefficient of heat conductivity of phase α; λ_t is the turbulent coefficient of heat conductivity:

$${{\lambda }_{{\text{t}}}} = \frac{{{{c}_{p}}{{\mu }_{{\text{t}}}}}}{{{\text{P}}{{{\text{r}}}_{{\text{t}}}}}},$$

(8)

where Pr_t is the turbulent Prandtl number; с_р is isobaric heat capacity.

Table 1 presents thermal effects of chemical reactions and their areas. Additional thermal effects appear at the expense of heating of alumina and aluminum fluoride, heat of water evaporation, and heat of phase transition Al₂O₃ (γ → α). Work [13] describes the mentioned heat effects and simulation methodology in more detail.

Table 1.   Thermal effects of the main reactions

We used the Shear Stress Transport (SST) k–ω turbulence model in computations [10].

Magnetic fields on the volume of reduction cell were accepted as constant in time. The electric field was determined from equation

$${\mathbf{E}} = - \nabla \cdot \varphi ,$$

(9)

where φ is the electric potential.

To compute the distribution of the density of the electric current in the volume of the bath and magnetic induction, we need a solution of Maxwell’s equation set. They are represented below in stationary form:

• Faraday’s induction law:

$$\nabla \times {\mathbf{E}} = 0;$$

(10)

• theorem about circulation of magnetic field:

$$\nabla \times {{\mathbf{B}} \mathord{\left/ {\vphantom {{\mathbf{B}} {\chi }}} \right. \kern-0em} {\chi }} = {{{\chi }}_{0}}{\mathbf{J}},$$

(11)

• Gaussian theorem for electric charge:

$$\nabla \cdot {\mathbf{E}} = {q \mathord{\left/ {\vphantom {q {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}},$$

(12)

• Gaussian theorem for magnetic field:

$$\nabla \cdot {\mathbf{B}} = 0.$$

(13)

Here, E is the strength of electric field, B is magnetic induction, q is the volume density of the electric charge, χ₀ = 4π × 10^–7 H/m is the magnetic constant, and χ is the magnetic permeability of medium.

The density of the electric current is connected with the strength of the electric field, as well as the velocity of melt motion and magnetic induction, by the following dependency:

$${\mathbf{J}} = \sigma \left( {{\mathbf{E}} + {\mathbf{v}} \times {\mathbf{B}}} \right).$$

(14)

The electric conductivity of materials (σ) is a function of temperature. The continuity equation of the electric current is denoted as

$$\nabla \cdot {\mathbf{J}} = 0.$$

(15)

When solving the magnetic problem for ferromagnetic materials (steel anode and cathode shell, steel conductor wires located in bake blocks, steel riffled sheets for providing motion of transport in the body of reduction cell and cooling of lateral surfaces of cathode cover at the expense of natural convection), the nonlinear dependence of magnetization on the magnetic field was taken into account.

BOUNDARY CONDITIONS

For solving thermal problem on outer surfaces contacting with air, we set an effective coefficient of heat release which accounts for convective and radiation components. Coefficients of heat release were functions of temperature of surrounding environment, local temperature, and orientation of the outer surface. Computations were performed for an environmental temperature of 0°C. For the electric problem, we set a current intensity of 170 kA on an anode busbar and zero electric potential on cathode busbar.

The normal component of current density was equal to zero on all outer surfaces of the model. At the border exceeding the sizes of three electrolysis cells, the normal component of magnetic induction is also taken equal to zero. To solve the hydrodynamic problem on the inner surfaces of the lining in contact with metal and electrolyte, the conditions are set for the normal and tangent components of the velocity to be equal to zero.

SOFTWARE SOLUTION

Reduction cell S8BME with the following technological parameters was chosen for simulation:

Current intensity, kA	170
Metal level, mm	300
Electrolyte level, mm	200

Initially magnetic fields were computed in Blums, from where values of magnetic induction in the volume of electrolyte and metal were defined and imported to ANSYS CFX, where a coupled solution of thermal and electric problems, as well as magnetic hydrodynamics, was performed taking free surface metal–electrolyte and formation of SOC into account.

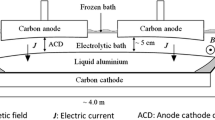
Figure 1 presents the model created in Blums 5.07. Busbar with three pipes was used for simulation. The influence of magnetic fields of neighbor reduction cells and reduction cells of neighbor row was accounted in computation. The magnetization curve, representing the dependency of induction on the strength of magnetic field B(H), was used for ferromagnetic materials. Detailed description of package Blums and its application methods for simulating magnetic fields is presented in [14].

Fig. 1.

General view of the model for computing magnetic fields in Blums 5.07.

Figure 2 presents finite element mesh used for coupled computations in ANSYS CFX, which consists of 3 × 10⁶ elements and 2.5 × 10⁶ nodes.

Fig. 2.

Grid used for the complex model.

All the computations were carried out in nonstationary formulation. Values of coefficients of thermal and electric conductivity of materials were accepted as dependencies on temperature.

RESULTS AND DISCUSSION

Computations allowed determining the temperature and electric and magnetic fields, as well as the velocity field in metal and electrolyte, shape of the metal–electrolyte boundary, and SCS. It can be seen in Fig. 3 that the vertical component of magnetic induction, which, together with horizontal currents in metal is the main reason for horizontal Lorentz forces and thus plays the main role in the MHD stability of reduction cell, is in the range B_z = –0.012–0.011 T.

Fig. 3.

Magnetic induction on metal–electrolyte interface with measurement points 1–6 (inlet edge on the bottom).

The model was verified by a comparison of computed data with experimental results. Magnetic induction was measured using a MAL-3.2 magnetometer by blank and front sides at 3 points located at identical distances in space between border and anode (Fig. 3). The results are gathered in Table 2. A comparison of computed and experimental values of magnetic induction is presented in Table 3, where it can be seen that they qualitatively correlate with each other.

Table 2.   Results of a measurement of magnetic induction in the space of cathode metal of reduction cells

Table 3.   Computed and experimental average values of magnetic induction

In order to estimate the correctness of the solution to the problem of distribution of electric potential, computed and experimental values of voltage loss in the reduction cell were compared. It can be seen from Fig. 4 that values of voltage drop are almost identical in all respects, which is also an indirect indicator of the correctness of dependencies of electric conductivity on the temperature set in the model. The computation methodology of the average voltage presented in Table 4 is described in [15].

Fig. 4.

Velocity field and circulation contours on metal–electrolyte interface (inlet edge on the left).

Table 4. Computed and experimental values of a potential drop in the reduction cell

Computations showed the formation of the four main stationary vortices in the corners of the bath (Fig. 4). The maximal value of the computed velocity constituted v = 31 cm/s. The industrial measurement of velocities in metal is very approximate. It is performed by the immersion of steel bars into liquid aluminum for some time; then, by the shape of their erosive damage, directions and values of the average velocity are determined during the experiment [16].

Experimentally obtained directions of the average velocity are presented in Fig. 4 by black and white arrows. Black arrows do not deviate by more than 90° from the direction of computed velocities, while white arrows exceed this value. It can be seen that 8 out of 25 experimental values deviate from computed directions of metal motion by more than 90°.

Figure 5 presents the metal–electrolyte interface. Static skewness of levels of cathode metal has maximum of 6 cm and minimum of –5 cm with respect to relatively initial level. The highest level of liquid metal is reached at the collision site of two flows from opposite vortices, and the lowest value is observed in the centers of the vortices.

Fig. 5.

Static skewness of cathode metal levels.

Figure 6 presents the computed shape of the lower ledge and upper ledge. The upper ledge is a frozen electrolyte above the level of liquid metal and below this level it is an lower ledge. According to computations, lower ledge falls under the projection of the anode, which is confirmed by multiple measurements on existing S8BME reduction cells, which operate at parameters close to the ones accepted in the model. The shape and sizes of the upper ledge also correspond to measured values. The computed thickness of lower ledge in the space between the border and anode turned out to be 3–7 cm less than the experimental value, which is on average 14 cm.

Fig. 6.

Shape of operation space of reduction cell S8BME.

Such a difference in values of thickness of lower ledge can be explained as follows. There are two main mathematical models describing the process of formation of lower ledge. The first is concluded in the fact that heat transfer from the inner melt to the surrounding environment is checked and the metal–lower ledge interface is estimated by the temperature of the liquidus of the electrolyte in the area of the liquid metal. In particular, the estimate of SOC was determined in this way in works [17–19]. Data obtained on the basis of the second model imply that the formation of lower ledge may significantly influence the presence of a thin electrolyte film between the lower ledge and metal. This model is described in more detail in [20, 21].

The computed and experimental temperatures of electrolyte in the space between the border block and anode coincide and constitute 949°С. Figure 7 presents the temperature field of the cathode cover. It can be seen that it is heated nonuniformly due to various (by the surface of borders and bottom blocks) values of coefficient of convective heat exchange and temperature of metal. It may be noted that temperatures of lateral walls of the cover are several degrees higher where vortices form in metal or electrolyte, which is explained by the effective transfer of heat from the center of the bath to border walls. The maximal temperature of the cover constituted 317°С.

Fig. 7.

Distribution of temperature in shell (inlet edge on the right).

Figure 8 shows the computed temperature at the bottom of the cover and the point where industrial measurements were performed. Table 5 presents a comparison of computed and experimental values of temperature of the cover bottom obtained for three reduction cells at a temperature of the surrounding air of 0°С. It can be seen from Table 5 and Fig. 8 that computed temperatures on the bottom of the cover turned out to be symmetrically distributed with respect to the center; this means the alignment of the temperature field by the thickness of reduction cell base.

Fig. 8.

Distribution of temperature in the bottom side of the shell (inlet edge on the left).

Table 5.   Computed and experimental values of temperature (°С) of the bottom side of the shell, averaged by three aluminum reduction cells

CONCLUSIONS

Our mathematical model of the aluminum reduction cell made it possible to determine the magnetic, temperature, and electric fields, as well as the velocity field, in volumes of metal and electrolyte. The model can be used to approximately estimate the shape of the operation space. Accounting for thermal sources from chemical reactions and raw materials loaded to electrolyte makes it possible to forecast the technical–chemical characteristics of the designed and upgraded reduction cells of various powers. The mathematical model of physical fields also allows a detailed determination of local perturbations connected with technological operations or their operational disorders and propagation in time and space of the reduction cell.

An analysis of the results showed a good agreement with experimental data, which implies the possibility of application and appropriateness of further improving the mathematical model.