Calculating the Neutron Radiation in the Spent Nuclear Fuel of VVER-1200 Reactors

Abstract

Results are presented from calculating the neutron radiation of spent nuclear fuel (SNF) from stationary campaigns of VVER-1000 and VVER-1200 reactors due to spontaneous fission and (α, n) reactions. An analytical dependence is obtained for the average number of neutrons produced in spent nuclear fuel per α-particle on the particle’s energy. The neutron radiation of VVER-1200 spent nuclear fuel is several times higher than that of a VVER-1000 reactor, due primarily to the increased number of ²⁴⁴Cm isotopes produced in high-burnup fuel.

INTRODUCTION

The handling of spent nuclear fuel (SNF) is a critical issue not only of nuclear and radiation safety but of closing a nuclear fuel cycle as well [1], which is one of the key problems in the development of nuclear power industry. The handling of spent nuclear fuel is one of the most important issues that attract the attention of environmental organizations and the public. This is of great important in today’s world and largely determines the attitude to nuclear power and its development in different countries and regions.

Spent nuclear fuel is characterized by a high degree of radioactivity. Fission products disintegrate due to β-decays accompanied by γ-radiation. Actinides are predominantly α-emitters. Actinides can decay with a low degree of probability, due to spontaneous fission emitting 2–3 neutrons on average [2]. This determines the main neutron radiation of spent fuel in the first decades after the end of a reactor campaign [3]. However, substantial amounts of neutron radiation are created by (α, n) reactions on the nuclei of oxygen contained in UO₂ uranium fuel [3].

In this work, we investigate neutron radiation from the spent fuel of a stationary campaign of a VVER-1200 reactor. Our findings are compared to those from similar calculations for a VVER-1000 reactor.

CONTRIBUTION FROM REACTIONS OF SPONTANEOUS FISSION TO THE NEUTRON RADIATION OF SPENT NUCLEAR FUEL

The chief nuclides that make a substantial contribution to neutral radiation caused by spontaneous fission are ²³⁸Pu, ²⁴⁰Pu, ²⁴²Pu, ²⁴²Cm, and ²⁴⁴Cm. Reference data on these nuclides are given in Table 1 [4]. Table 2 presents data on the production of these nuclides in VVER-1000 and VVER-1200 reactors [5‒7].

Table 1.   Main nuclides that contribute to SNF neutron radiation caused by spontaneous fission [4]

Table 2.   Production of actinides that make substantial contributions to the neutron radiation of VVER-1000 and VVER‑1200 SNF [5–7]

The great increase in the production of ²⁴⁴Cm isotope in a VVER-1200 relative to a VVER-1000 reactor is worthy of attention. ²⁴⁴Cm isotope is produced along the ²³⁸U → ²³⁹Pu → ²⁴⁰Pu → ²⁴¹Pu → ²⁴²Pu → ²⁴³Am → ²⁴⁴Cm chain by the sequential capture of six neutrons. The rate of production of every subsequent nuclide in the chain depends on the actual number of the precursor element, so a considerable rate of production of a specific element in the chain is observed only after the entire chain of its precursors has been formed. This results in strong nonlinear dynamics of the production of ²⁴⁴Cm.

Neutron radiation caused by spontaneous fissions is described as

$${{A}_{n}}(t) = \sum\limits_i {{{\chi }_{i}} \cdot {{A}_{i}}{{e}^{{ - {{\lambda }_{i}}t}}}} ,$$

(1)

where χ_i is the probability of spontaneous fission, A_i is the radiation, and λ_i is the constant of the decay of the i-th nuclide.

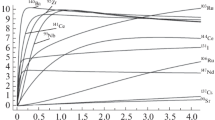
The graphs of neutron radiation caused by spontaneous fissions as a function of the period of storage of the spent fuel from stationary campaigns of VVER-1000 and VVER-1200 reactors are shown in Fig. 1. The dynamic process at the beginning of storage is caused by fast decay of the ²⁴²Cm isotope.

Fig. 1.

Dependences of neutron radiation caused by spontaneous fission reactions on the period of storage of spent fuel from stationary VVER-1000 and VVER-1200 reactor campaigns.

At burnup rates of 40 MW day t⁻¹ in a VVER-1000 reactor and 70 MW day t⁻¹ in a VVER-1200 reactor, the neutron radiation caused by spontaneous fission in the first 100 years of cooling differs by 6–7 times. The basic contribution to neutron radiation comes from the spontaneous fission of ²⁴⁴Cm.

CONTRIBUTION FROM (α, n) REACTIONS TO THE NEUTRON RADIATION OF SPENT FUEL

Considerable neutron radiation is also caused by (α, n) reactions on the oxygen contained in UO₂ uranium fuel. The cross sections of the radiative (n, γ) capture of ¹⁶O, ¹⁷O, and ¹⁸O nuclei are negligible at hundredths of barns and lower [8], so changes in the ratios between different oxygen isotopes during the operation of a reactor can be ignored. The ¹⁶O(α, n)¹⁹Ne reaction has a threshold that exceeds the energy of α-decays. so it does not proceed in spent fuel. Neutrons form mainly due to the ¹⁸O(α, n)²¹Ne reaction, with the fraction of ¹⁸O in natural oxygen being 0.2% [9]. The content of ¹⁷O in natural oxygen is considerably lower: 0.038%. In other words, there is approximately one ¹⁷O atom for every five ¹⁸O atoms. The cross sections of the (α, n) reactions of ¹⁷O and ¹⁸O in the range of the possible energies of α-particles are comparable (Fig. 2) [8], so the ¹⁷O(α, n)²⁰Ne reaction must also be considered. In the range of possible α-particle energies, the cross sections of the (α, n) reactions change in an approximately linear fashion, which allows us to use an approximation of functions of this kind. Linear approximations of the dependences of the cross sections of (α, n) reactions on ¹⁷O and ¹⁸O produce formulas (2) and (3), respectively:

$$\begin{gathered} \sigma _{{(\alpha ,n)}}^{{{\text{17O}}}} = 0.063{{E}_{\alpha }} - 0.126\,\,({\text{barn}}), \\ 2\,\,{\text{MeV}} \leqslant {{E}_{\alpha }} \leqslant 6\,\,{\text{MeV}}{\text{,}} \\ \end{gathered} $$

(2)

$$\begin{gathered} \sigma _{{(\alpha ,n)}}^{{{\text{17O}}}} = 0.063{{E}_{\alpha }} - 0.126\,\,({\text{barn}}), \\ 2.5\,\,{\text{MeV}} \leqslant {{E}_{\alpha }} \leqslant 6\,\,{\text{MeV}}{\text{,}} \\ \end{gathered} $$

(3)

Fig. 2.

Cross section of (α, n) reactions on ¹⁷O and ¹⁸O isotopes [7].

where E_α is the kinetic energy of an α-particle. Below these ranges, the cross sections are considered to be equal to zero.

As an α-particle slows, it loses small amounts of energy: at an energy of 5 MeV, ~10⁴ ionization events are required to slow an α-particle. We may therefore consider that the particle loses energy continuously, creating fluence throughout the range of possible energies (from the initial energy to zero). The path of an α-particle in a solid substance is several micrometers long, so we may assume that an α-particle produced in the medium creates fluence throughout the range of energies approximately at the point of its production.

According to the Bethe formula [10], the linear energy losses of a nonrelativistic α-particle are

$$\begin{gathered} - \frac{{dE}}{{dx}} = \frac{{4\pi z_{\alpha }^{2}{{n}_{e}}r_{0}^{2}{{m}_{e}}{{c}^{2}}}}{{{{\beta }^{2}}}} \\ \times \,\,\left[ {\ln \left( {\frac{{2{{m}_{e}}{{c}^{2}}{{\beta }^{2}}}}{{\bar {J}}}} \right) - \ln \left( {1 - {{\beta }^{2}}} \right) - {{\beta }^{2}}} \right], \\ \end{gathered} $$

(4)

where $\bar {J} = 13.5{{Z}_{{{\text{eff}}}}}$ is the mean ionization potential in terms of electron volts; Z_eff is the effective charge of the substance; m_e is the mass of the electron; z_α = 2 is the charge of the α-particle in terms of electron charge units; r₀ is the classical electron radius; ρ is the density of the substance in terms of (g cm⁻³); and β = υ/c is the velocity of the α-particle in terms of the speed of light.

A formula convenient for numerical calculations is [11]

$$\begin{gathered} - \frac{{dE}}{{dx}} = 3.1 \times {{10}^{{ - 2}}}\frac{{{{z}_{\alpha }}\rho }}{{{{\beta }^{2}}}}\frac{{{{Z}_{{{\text{eff}}}}}}}{{{{A}_{{{\text{eff}}}}}}} \\ \times \,\,\left[ {11.2 + \ln \left( {\frac{{{{\beta }^{2}}}}{{{{Z}_{{{\text{eff}}}}}(1 - {{\beta }^{2}})}}} \right) - {{\beta }^{2}}} \right]\,\,{\text{MeV }}{{{\text{m}}}^{{ - 1}}}, \\ \end{gathered} $$

(5)

where A_eff is the effective mass number of the substance and ρ is the fuel density in terms of kg/m³. The Z_eff/A_eff ratio is a quantity that changes much less than each of the Z_eff or A_eff parameters individually: at a maximum fuel burnup rate of 70 MW day t⁻¹, Z_eff/A_eff changes by ~0.7%. This allows us to ignore the change in the fuel composition during burnup without causing any significant losses.

The fluence of α-particles with energy E_α (in the range of E_α to E_α + dE_α) is determined as the total pathlength of particles with the above energy to the volume in which the particle travels. Since the formulation of the problem requires that the fluence be found in a mass unit of the spent fuel (we find the number of the neutrons produced in a unit of time in a mass unit of fuel as a result of the (α, n) reaction) this allows us to exclude from consideration the density of the substance when considering the mass to be ρ = m_f/V_f, where subscript “f” denotes the fuel.

In Eq. (5), we move from velocity β = υ/c to energy E_α:

$$\begin{gathered} - \frac{{dE}}{{dx}} = 3.1 \times {{10}^{{ - 2}}}\frac{{{{E}_{{0\alpha }}}{{m}_{{\text{f}}}}}}{{{{E}_{\alpha }}{{V}_{{\text{f}}}}}}\frac{{{{Z}_{{{\text{eff}}}}}}}{{{{A}_{{{\text{eff}}}}}}} \\ \times \,\,\left[ {11.2 + \ln \left( {\frac{{2{{E}_{\alpha }}}}{{{{Z}_{{{\text{eff}}}}}({{E}_{{0\alpha }}} - 2{{E}_{\alpha }})}}} \right) - \frac{{2{{E}_{\alpha }}}}{{{{E}_{{0\alpha }}}}}} \right]. \\ \end{gathered} $$

(6)

From Eq. (6), we obtain the expression for the distribution of the fluence over energies dx/V_т (the minus sign can be omitted):

$$\frac{{dx}}{{{{V}_{{\text{f}}}}}} = \frac{{dE}}{{\varphi ({{E}_{\alpha }})}}.$$

(7)

Since E_α $\ll$ E_0α = M_αc²,

$$\begin{gathered} \varphi ({{E}_{\alpha }}) = 3.1 \times {{10}^{{ - 2}}}\frac{{{{E}_{{0\alpha }}}{{m}_{{\text{f}}}}}}{{{{E}_{\alpha }}}} \\ \times \,\,\frac{{{{Z}_{{{\text{eff}}}}}}}{{{{A}_{{{\text{eff}}}}}}}\left[ {11.2 + \ln \left( {\frac{{2{{E}_{\alpha }}}}{{{{Z}_{{{\text{eff}}}}}{{E}_{{0\alpha }}}}}} \right)} \right]. \\ \end{gathered} $$

(8)

Function φ(E_α) can be rewritten after calculating the constants and Z_eff/A_eff values for UO₂. Its final form is

$$\begin{gathered} \varphi ({{E}_{\alpha }}) = \frac{{5.8 \times {{{10}}^{2}}}}{{{{E}_{\alpha }}}} \\ \times \,\,\left[ {11.2 + \ln \left( {\frac{{{{E}_{\alpha }}}}{{4.0}}} \right)} \right]{\text{MeV }}{{{\text{m}}}^{2}}{\text{ k}}{{{\text{g}}}^{{ - 1}}}, \\ \end{gathered} $$

(9)

where E_α is given in terms of MeV.

According to (7), 1/φ(E_α) shows the magnitude of the elementary fluence created by one α-particle in the (E_α, E_α + dE_α) range of energies. 1/φ(E_α) is virtually a linear dependence, and approximating it with the least squares approach yields a function in simple form:

$$f({{E}_{\alpha }}) = (1.41{{E}_{\alpha }} + 0.51) \times {{10}^{{ - 4}}}\,\,{\text{Me}}{{{\text{V}}}^{{ - 1}}}{\text{ }}{{{\text{m}}}^{{ - 2}}}{\text{ kg}},$$

(10)

with approximation (10) deviating from 1/φ(E_α) by no more than 1.5%. Given (10), expression (7) can be rewritten as

$$\frac{{dx}}{{{{V}_{{\text{f}}}}}} = \left( {1.41{{E}_{\alpha }} + 0.51} \right) \times {{10}^{{ - 4}}}dE,$$

(11)

The number of the (α, n) reactions per α-decay on X nuclei is

$$\begin{gathered} N_{{1\alpha }}^{X} = \int\limits_{E{\kern 1pt} '}^{{{E}_{{0\alpha }}}} {{{N}_{X}}f(E)\sigma _{{(\alpha ,n)}}^{X}} dE \\ = {{N}_{X}} \times {{10}^{{ - 4}}}\int\limits_{E{\kern 1pt} '}^{{{E}_{{0\alpha }}}} {(1.41E + 0.51)\sigma _{{(\alpha ,n)}}^{X}} dE, \\ \end{gathered} $$

(12)

where N_X is the number of X nuclei in a kilogram of the UO₂ fuel and E' is the beginning of the range of integration at which the reaction cross section differs from zero (2 MeV for ¹⁷O and 2.5 MeV for ¹⁸O) (see Fig. 2).

Substituting cross sections (2) and (3), calculating N_17O and N_18O according to their contents in natural oxygen, and integrating (12), we obtain the expression for the number of neutrons formed in the spent fuel per α-particle with energy E_α:

$$\begin{gathered} \nu ({{E}_{\alpha }}) = 3.86 \times {{10}^{{ - 8}}} \\ \times \,\,(1 - 0.167{{E}_{\alpha }} - 0.207E_{\alpha }^{2} + 0.051E_{\alpha }^{3}), \\ \end{gathered} $$

(13)

Expression (13) can be simplified by approximating it with a quadratic function:

$$\nu ({{E}_{\alpha }}) = (2.52E_{\alpha }^{2} - 19.28{{E}_{\alpha }} + 38.71) \times {{10}^{{ - 8}}}.$$

(14)

The maximum discrepancy between (13) and (14) in the 5.2–6.2 MeV range of energies is 0.13%.

It should be noted that at a difference between the energies of α-particles of ~19% (5.2 and 6.2 MeV), the average number of the neutrons formed by them differs by more than two times (Eq. (14)). It would therefore be incorrect to average the energies of α-particles and then use Eq. (14).

When analyzing the way in which Eq. (14) was obtained, note that the main source of potential errors is the accuracy of determining the cross sections of (α, n) reactions in the nuclear data libraries (Fig. 2). This error is irreducible and the proposed procedure is not at all inferior in terms of accuracy to numerical calculations performed using the Monte Carlo codes. In the considered range of energies, Bethe’s formula is of practical accuracy [12].

The neutron radiation caused by (α, n) reactions is

$${{A}_{{(\alpha ,n)}}}(t) = \sum\limits_i {\nu ({{E}_{{\alpha ,i}}}) \cdot {{A}_{i}}} ,$$

(15)

where A_i is the radiation and E_α,i is the energy of the α‑decay of the i-th nuclide.

With the exception of ²⁴¹Am, the nuclides presented in Table 2 decay according to an exponential law. ²⁴¹Am is produced due to the β-decay of ²⁴¹Pu, so the dynamics of its change is described in a slightly more complex way:

$$\begin{gathered} A({}^{{241}}{\text{Am}},t) = \alpha \cdot {{A}_{0}}({}^{{241}}{\text{Pu}}) \cdot {{e}^{{ - \lambda ({}^{{241}}{\text{Pu}})t}}} \\ + \,\,\left[ {{{A}_{0}}({}^{{241}}{\text{Am}}) - \alpha \cdot {{A}_{0}}({}^{{241}}{\text{Pu}})} \right] \cdot {{e}^{{ - \lambda ({}^{{241}}{\text{Am}})t}}}, \\ \end{gathered} $$

(16)

where $\alpha = \frac{{\lambda ({}^{{241}}{\text{Am}})}}{{\lambda ({}^{{241}}{\text{Am}}) - \lambda ({}^{{241}}{\text{Pu}})}}$.

The initial radiation of ²⁴¹Pu in spent fuel of the VVER-1000 and VVER-1200 reactors equal 5.86 × 10¹⁵ and 8.64 × 10¹⁵ Bq t^–1, respectively [5].

Dependences of the neutron radiation caused by (α, n) reactions on the storage time of spent fuel from stationary campaigns of VVER-1000 and VVER-1200 reactors are shown in Fig. 3a. The total neutron radiation caused by spontaneous fission and (α, n) reactions is presented in Fig. 3b. As with spontaneous fission, the dynamic sections in the first 2–2.5 years are caused by the decay of high-activity ²⁴²Cm. During this period, the material is kept in a spent fuel pool, so this isotope does not cause any additional problems in handling it.

Fig. 3.

Dependences of (a) neutron radiation caused by (α, n) reactions and (b) total neutron radiation on the period of storage of spent fuel from stationary VVER-1000 and VVER-1200 reactor campaigns.

Figure 4 shows the relative contribution from curium isotopes ²⁴²Cm and ²⁴⁴Cm to the total neutron radiation. As can be seen, almost all of the neutron radiation caused by spontaneous fission and (α, n) reactions in the first decades of storing the spent fuel of a VVER-1200 reactor comes from curium isotopes. As the above calculations show, the problem of a great increase in neutron radiation is critical when dealing with high-burnup uranium fuel.

Fig. 4.

Relative contribution from ²⁴²Cm and ²⁴⁴Cm isotopes to the total neutron radiation.

CONCLUSIONS

We obtained values of the neutron radiation of spent nuclear fuel from VVER-1000 and VVER-1200 reactors caused by spontaneous fission and (α, n) reactions.

We used an analytical approach whose accuracy was not inferior to numerical calculations for determining the neutron radiation of spent fuel caused by (α, n) reactions. It was shown that the average number of neutrons produced per α-decay in the spent fuel was almost entirely determined by the energy of α-particles.

In a VVER-1200 reactor at a burnup rate of 70 MW day t⁻¹, ²⁴⁴Cm isotope is produced in numbers one order of magnitude higher than in a VVER-1000 reactor. This isotope makes the main contribution to the neutron radiation of the spent fuel in the first decades of fuel storage.