INTRODUCTION

The development of experimental quantum optics and laser physics has allowed us to generate different types of nonclassical light fields in the laboratory. Such nonclassical fields as biphotonic pairs, single-photon states [1–4], and squeezed states of light [5–9] can now be generated in experiments. A field in the state of a squeezed vacuum [10–12] that has a wide distribution in terms of the number of photons is currently one of the most promising and widely studied nonclassical objects. The most widely used ways of obtaining this field are based on parametric scattering with \({{\chi }^{{(2)}}}\) nonlinear crystals and four-wave mixing with \({{\chi }^{{(3)}}}\) nonlinear crystals. Such a field also has suppressed dispersion along one direction, which is very important for certain metrological applications. Finally, such a field retains its considerable nonclassical properties even with a large mean number of photons and is characterized by multiple entanglements between signal and idle photon beams.

Interaction between such fields and atomic and molecular systems is an important problem, not only from a fundamental point of view, but also in light of various practical applications. The fundamental novelty introduced by a quantum field is an additional degree of freedom that results in a completely different character of the processes that proceed, compared to a classical field [12–14]. This feature requires completely new ways of describing the interaction between such nonclassical fields and atomic and molecular systems. Quantum correlations (entanglements) between subsystems, which greatly influence the dynamics of both atomic and field subsystems, are an important factor when considering nonclassical fields and their interaction with atomic and molecular systems. Entanglement is the impossibility of factoring the wave function of a compound system into a product of single-particle wave functions of individual subsystems. We therefore can obtain information about one subsystem by measuring the parameters of another [13, 14]. Such a property of entangled systems is very important not only for certain metrological measurements (for example, measuring quantum frequency standards [15]); it is also widely used in the problem of forming so-called q-bits and q-trits. Protocols for the storing and transmission of quantum information are constructed on their basis. The question of describing the dynamics of atomic and molecular systems that interact with different nonclassical fields is thus relevant but poorly understood today.

In this work, we investigate the interaction between a two-level atom and a resonant nonclassical electromagnetic field. Features of the dynamics of an atomic subsystem are analyzed for different initial states of a quantum field. There is strong entanglement of the atomic and field subsystems during their interaction. A substantial change in the photon statistics due to the interaction between atomic and field systems is observed.

THEORETICAL APPROACH

Our theoretical approach to solving this problem is based on the solution to the nonstationary Schrödinger equation with Hamiltonian operator

$${\text{i}}\hbar \frac{\partial }{{\partial t}}\Psi = \left[ {\mathop \sum \limits_{i = 1}^2 {{E}_{i}}~\left| i \right\rangle \left\langle i \right| + \hbar \omega \left( {{{{\hat {a}}}^{ + }}\hat {a} + \frac{1}{2}} \right) - \left( {\widehat {\vec {d}},{{\varepsilon }_{0}}\hat {q}} \right)} \right]\Psi .$$
((1))

The first term on the right characterizes the atomic subsystem; the second term, one mode of the quantum field; and the third term, their interaction, which is considered in the dipole approximation. Here, \(\hat {q} = {{\left( {{{{\hat {a}}}^{ + }} + \hat {a}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\hat {a}}}^{ + }} + \hat {a}} \right)} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}~\) is the field coordinate, and \({{\varepsilon }_{0}} = \sqrt {\frac{{4\pi \hbar \omega }}{{{{L}^{3}}}}} \) is a dimensionless constant in effective volume of interaction \({{L}^{3}}\). We solve the problem in the Fock representation.

For simplicity, the initial condition is chosen such that the probability of finding an electron at the lower level is equal to unity, and the field subsystem is decomposed according to Fock states in an arbitrary way:

$${\Psi\text{}}\left( {t = 0} \right) = {{\chi }_{{{\text{at}}}}}\mathop \sum \limits_{n = 0}^\infty {{C}_{n}}~\left| {n~} \right\rangle ,{{\chi }_{{{\text{at}}}}} = ~\left| 1 \right\rangle .$$
((2))

Here, \({{C}_{n}}\) denotes the expansion coefficients of the field in the Fock basis. We then seek a solution to Eq. (1) in the form

$${\Psi\text{}}\left( t \right) = \mathop \sum \limits_{i = 1}^2 \mathop \sum \limits_n {{C}_{{in}}}\left( t \right){{e}^{{ - \frac{{i\left( {{{E}_{i}} + \widetilde {{{E}_{n}}}} \right)t}}{\hbar }}}}\left| {in} \right\rangle ,$$
((3))

where \({{E}_{i}}\) is the energy of the upper or lower level of the atom; \(\widetilde {{{E}_{n}}}\) is the energy of the Fock state of field mode; and \({{C}_{{in}}}\left( t \right)\) denotes the amplitudes of the probability of finding the system in a given state. We obtain the system for the coefficients after substituting solution (3) into the equation. A system of time-differential equations for the probability amplitudes, which are factorized into pairs of related equations that depend on number \(n\), is obtained after averaging over high-frequency oscillations:

$$\left\{ {\begin{array}{*{20}{c}} {iC_{{1,n + 1}}^{'}\left( t \right) = \Omega \sqrt {k + 1} {{C}_{{2,n}}}} \\ {iC_{{2,n}}^{'}\left( t \right) = \Omega \sqrt {k + 1} {{C}_{{1,n + 1}}}} \end{array}} \right.,$$
((4))

where \(\Omega = \frac{{{{\varepsilon }_{0}}d}}{{\hbar \sqrt 2 }}\) is the frequency of oscillation in the system.

We next find the form of the wave function, solving this system with allowance for the initial condition. All information can be obtained from this wave function:

$$\begin{gathered} {\Psi\text{}}\left( t \right) = \mathop \sum \limits_{k = 0}^\infty {{C}_{k}}\cos \Omega \sqrt k t~{{e}^{{ - \frac{i}{\hbar }\left( {{{E}_{1}} + \widetilde {{{E}_{k}}}} \right)t}}}~\left| {k,~1} \right\rangle \\ + \,\,~i\mathop \sum \limits_{k = 0}^\infty {{C}_{{k + 1}}}\sin \Omega \sqrt {k + 1} t{{e}^{{ - \frac{i}{\hbar }\left( {{{E}_{2}} + \widetilde {{{E}_{k}}}} \right)t}}}\left| {k,~2} \right\rangle . \\ \end{gathered} $$
((5))

The population of the atomic level is determined by summing the squares of moduli \({{C}_{{in}}}\left( t \right)\) over all possible field states:

$${{W}_{1}}\left( t \right) = ~\mathop \sum \limits_{k = 0}^\infty C_{k}^{2}{{\cos }^{2}}\Omega \sqrt k t,$$
((6))
$${{W}_{2}}\left( t \right) = ~\mathop \sum \limits_{k = 0}^\infty C_{{k + 1}}^{2}{{\sin }^{2}}\Omega \sqrt {k + 1} t.$$
((7))

It is not difficult to see that the sum of the populations at the upper and lower levels is equal to unity, as it should be.

The wave function obtained above does not factor separately for the wave functions of the atomic and field subsystems. This means the subsystems are entangled.

$${\Psi\text{}}\left( {\vec {r},~q} \right) \ne ~\varphi \left( {\vec {r}} \right)F\left( q \right).$$
((8))

The total density matrix must be reduced over all possible states of another subsystem so that a particular subsystem is considered:

$${{\rho }^{{{\text{total}}}}} = \left| {\Psi\text{}} \right\rangle \left\langle {\Psi\text{}} \right|,$$
((9))
$${{\rho }_{{{\text{red}}}}} = {\text{Sp}}{{\left( {{{\rho }^{{{\text{total}}}}}} \right)}_{{{\text{second}}\,{\text{system}}}}}.$$
((10))

If the total two-particle wave function is factorized, there is no entanglement. Each of the subsystems is then in a pure state. It is known that if the state of the system is pure, the density matrix is a projection; i.e., the trace of the matrix’s square is unity.

$${{\rho }^{2}} = ~\,\,\rho ,$$
((11))
$${\text{Sp}}\left( \rho \right) = 1.$$
((12))

If there is no initial factorization (3), each subsystem will be in a mixed state separately. A coefficient of purity is introduced to determine the degree of entanglement of the two-particle state:

$$\mathcal{P} = ~\,\,{\text{Sp}}\left( {\rho _{{{\text{red}}}}^{2}} \right).$$
((13))

Note that this coefficient is inversely proportional to the Schmidt coefficient used to describe the entanglement of quantum states:

$$\mathcal{K} = ~\,\,\frac{1}{\mathcal{P}} = \frac{1}{{{\text{Sp}}\left( {\rho _{{{\text{red}}}}^{2}} \right)}}.$$
((14))

In this work, the dependence of the Schmidt parameter on time characterizes the system’s degree of entanglement.

Let us consider the explicit 𝒦 dependence on time on the example of a two-level system. Reducing this matrix over the field variables, we have

$${{\rho }_{{{\text{red}}}}} = \mathop \sum \limits_n \left\langle n \right|\left| {\Psi\text{}} \right\rangle \left\langle {\Psi\text{}} \right|\left| n \right\rangle ,$$
((15))
$${{\rho }_{{{\text{red}}}}} = \left( {\begin{array}{*{20}{c}} {{{\rho }_{{11}}}}&{{{\rho }_{{12}}}} \\ {{{\rho }_{{21}}}}&{{{\rho }_{{22}}}} \end{array}} \right).$$
((16))

Taking the square of this matrix and its trace, we get

$$\mathcal{K} = ~\frac{1}{{\rho _{{11}}^{2} + \rho _{{22}}^{2} + 2{{\rho }_{{21}}}{{\rho }_{{12}}}}},$$
((17))

where \({{\rho }_{{ij}}}\) obeys the relations

$${{\rho }_{{11}}} = ~\mathop \sum \limits_{k = 0}^\infty C_{k}^{2}{{\cos }^{2}}\Omega \sqrt k t,$$
((18))
$${{\rho }_{{22}}} = \mathop \sum \limits_{k = 0}^\infty C_{{k + 1}}^{2}{{\sin }^{2}}\Omega \sqrt {k + 1} t,$$
((19))
$$\begin{gathered} {{\rho }_{{12}}} = \rho _{{21}}^{*} \\ = \,\,\mathop \sum \limits_{k = 0}^\infty {{C}_{k}}{{C}_{{k + 1}}}\sin \Omega \sqrt {k + 1} t\cos \Omega \sqrt k t. \\ \end{gathered} $$
((20))

We write the expansion coefficients in the Fock basis for certain types of nonclassical fields at the initial time to determine the explicit form of the Schmidt coefficient and the population of the atomic levels.

The coherent state of the field is

$${{C}_{n}} = {{e}^{{ - \frac{{\bar {n}}}{2} + i\varphi }}}\frac{{{{{\sqrt {\bar {n}} }}^{n}}}}{{\sqrt {n!} }}.$$
((21))

A squeezed vacuum is

$${{C}_{{2n}}} = {{\left( { - 1} \right)}^{n}}{{\left( {\frac{{1 - {\alpha\text{}}}}{{1 + {\alpha\text{}}}}} \right)}^{n}}\sqrt {\mathop \prod \limits_{m = 1}^n \left( {1 - \frac{1}{{2m}}} \right)} \sqrt {\frac{{2\sqrt {\alpha\text{}} }}{{1 + {\alpha\text{}}}}} ,$$
((22))

where only even Fock states are populated in the case of squeezed light, and \({\alpha\text{}}\) is the squeeze coefficient, as can be seen from (22). This parameter can be associated with the mean number of photons by considering the relation

$${{\left| {{{C}_{0}}} \right|}^{2}} = \frac{{2\sqrt {\alpha\text{}} }}{{1 + {\alpha\text{}}}} = \frac{1}{{1 + \bar {n}}}~.$$
((23))

Schrödinger’s cats are

$${{C}_{n}} = {{e}^{{ - \frac{{\bar {n}}}{2}}}}\frac{{{{{\sqrt {\bar {n}} }}^{n}}}}{{\sqrt {n!} }}\left( {1 \pm {{{\left( { - 1} \right)}}^{n}}} \right)\mathcal{N},$$
((24))

where 𝒩 is the normalization constant. Another behavior of the atomic subsystem and entanglement in such fields is based on the considerable difference in the distribution of the number of photons for the initial states of the field.

RESULTS AND DISCUSSION

Quantum Population and Quantum Entanglement

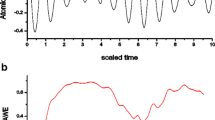
Let us first consider the interaction between an atom and coherent light. It was discovered experimentally in [16] that there is a quantum collapse and revival of the inverse population when a Rydberg atom is irradiated by coherent light with a low mean number of photons. The population dependence of the lower level for a model two-level atom upon irradiation with coherent light with \(\bar {n} = 100\) is shown in Fig. 1a, which demonstrates this effect. The initial Rabi oscillations are replaced by relatively long intervals of time in which the population does not change. This phase is referred to as collapse. The Rabi oscillations are renewed, characterizing the revival. This effect is actually due to the oscillating terms in (6) and (7) being initially phased in; the difference between the Rabi quantum frequencies for different \(n\) leads to compensation for different terms in sums (6), (7). Further partial phasing is again possible, but it will not occur for long periods of time due to irrationality in the argument, so the effect is destroyed over time. Let us compare the dependences for Schmidt’s coefficient and population for the same system. The dependence of entanglement on time for this atomic and field system is shown in Fig. 1b. Comparing these graphs, we may conclude that the evolution of the field subsystem, which leads to the revival of population oscillations, occurs even when there are no transitions in the system. Note too that the entanglement of the system tends to a maximum for long periods of time. We may therefore conclude that coherent radiation is not classical even with a large mean number of photons.

Fig. 1.
figure 1

(a) Population of the lower level and (b) entanglement of the atomic and field subsystems as a function of time for the coherent initial state of a field.

Full size image

Let us turn to a more exotic type of nonclassical light: Schrödinger’s cat. Its distribution over the number of photons has a Poisson profile (along with coherent radiation). However, only even (or odd) numbers make non-zero contributions. The nature of the dependence of population on time does not change, in comparison to coherent light; i.e., quantum collapse and the revival effect are also observed (see Fig. 2a). However, the dependence of the Schmidt coefficient on time does change, which is interesting. Entanglement does not now change during the collapse of the inverse population; instead, it corresponds to its maximum (see Fig. 2b). In this case, the revival of atomic transitions arises for this field state twice as often as for the coherent state, due apparently only to odd (or even) Fock states in the initial field distribution over photons.

Fig. 2.
figure 2

(a) Population of the lower level and (b) entanglement of the atomic and field subsystems as a function of time for a field initially in the squeezed vacuum state.

Full size image

The dynamics when considering squeezed light must differ fundamentally, since the distribution on the number of photons is much broader than in the previous two cases. Let us consider the population dependence of an atom excited by a squeezed vacuum (Fig. 3a). There is no collapse or revival effect in this case since there are many functions of the same order that oscillate with different frequencies in the population expression, even at brief periods of time. The Schmidt coefficient also has no clear profile. However, its mean value is considerably higher in comparison to the above types of nonclassical field (Fig. 3b).

Fig. 3.
figure 3

(a) Population of the lower level and (b) entanglement of the atomic and field subsystems as a function of time for a field initially in a Schrodinger’s cat–type state.

Full size image

Photon Statistics

The features of the considered nonclassical fields allowed us to find the moments in time where the distribution with respect to the number of photons for the interacting field varies substantially, compared to the initial moment of time. In the case of a coherent field, the distribution profile curves smoothly over time and becomes very jagged in the vicinity of the entanglement minima. The field of a squeezed vacuum behaves much more interestingly. Since only even Fock states are populated at the initial moment in time, odd photon states should appear in the field statistics during the evolution of the system. We can indeed find the moment in time when all the populated states in the distribution become odd Fock states (Fig. 4). This situation apparently characterizes the emergence of a field in a nongaussian state (with a negative Wigner function), which requires further investigation.

Fig. 4.
figure 4

Photon statistics of a quantum field, calculated at the time corresponding to the minimum of entanglement. The quantum field is described at the initial moment in time, in the form of a squeezed vacuum state and interacts with an atom.

Full size image

CONCLUSIONS

In this work, we studied the interaction between different types of nonclassical fields and a model two-level system. The onset of quantum collapse and the revival effect of the inverse population for the atomic system was analyzed for different initial states of the quantum field. It was shown that collapse and the revival effect is observed for the initial states of a field of the Schrödinger’s cat type, as in the case of a coherent field. No such effect was observed for the squeezed states of light. Strong entanglement of the atomic and field subsystems (which turned out to be greatest for the action of compressed nonclassical fields) was observed. A change in the photon statistics during interaction between the field and an atom was investigated. There was a substantial population of odd Fock states during evolution, which could indicate the formation of nongaussian field states.