Maintaining Resonant Modes of Vibration Transport and Production Machines with Unbalance Vibration Exciters

Abstract

This article is about solving the problem of maintaining the resonant vibration mode in a vibration transport and production machine with self-synchronizing vibration exciters at an undetermined mass of work material. An algorithm for maintaining automatic resonant mode maintenance is proposed. This algorithm is based on using preliminary numerical modeling (dynamic portrait) results and allows calculating the natural frequency (work material mass) in the real-time mode and implementing the necessary control over the vibration exciter rotation frequency according to the phase difference between the perturbation force and the oscillations of the working body. The results of numerically modeling the tuning of the vibration machine to the resonant mode while using the developed algorithm with variations in the mass of the work material are provided. A laboratory oscillation wobbler screen prototype is designed and equipped with an automatic resonant mode maintenance system. The operational ability and efficiency of the proposed solutions is confirmed by numerical and full-scale test results.

Vibration production processes and machines are widely used in various industries.

Using oscillations permits significantly intensifying various transportation and process operations, such as adoption, partitioning/blending, separation, compaction/loosening, degassing, orienting, and crushing, among others [1–3].

This article considers the increase in the energy efficiency of machines designed for implementing production processes, such as vibration displacement and screen sizing of discrete and lumpy materials and media.

Nowadays, machine building, metallurgy, mining, road construction, and other industries make wide use of sizing screens and oscillating conveyors with unbalanced vibration exciters driven by AC induction motors [4–8]. To generate a unidirectional action, two identical unbalanced vibration exciters are usually installed on the working body and synchronously rotate in opposite directions. In certain cases, the equality of angular velocities and the required phase difference among eccentric weights of vibration exciters are implemented through the self-synchronization of the vibration exciters of a vibration machine that run in the region of super resonant excitation frequencies, which ensures their consistent operation irrespective of variations in the work material mass and various nonlinear interactions of the whole vibration exciter-working body-work material dynamic system. However, to achieve the super resonant oscillation mode, it is necessary to pass through the region of resonant frequencies, which requires applying the vibration approach with redundant power. As a consequence, electric motors run outside their nominal mode at operating frequencies and the range of synchronous unbalanced rotation frequencies is narrowed by using self-synchronizing vibration exciters [10, 11].

One of the ways of making vibration machines more energy efficient is to use the resonant mode of oscillations in the working body [10, 12, 13]. However, the application of the resonant mode, especially in nonlinear dynamic systems, is related to ensuring its steadiness. The nonlinear properties of the dynamic vibration machine system result from the potential nonlinearity of elastic properties, the peculiarities of the contact of the working body with oscillation vibration exciters and the processed medium, and the variations in the work material mass. The integration of the vibration machine with the regulation system with feedback allows controlling the oscillation parameters of the working body in real-time mode thus stabilizing the resonant oscillation mode of vibration machines [14, 15].

This article is aimed at making vibration processing machines with self-synchronizing unbalanced vibration exciters more energy efficient by using resonant oscillations of the working body.

In this article, resonant tuning is implemented by employing a synchronous rotation frequency of eccentric weights and, respectively, the perturbing effect frequency, closer to the natural oscillation frequency of the working body with the work material while using an automatic control system.

ALGORITHM FOR THE RESONANT MODE MAINTENANCE SYSTEM

For the flowchart of the resonant tuning system, see Fig. 1. Phase difference ε between disturbing force F(t) and vibration accelerations $\ddot {q}(t)$ of the working body in a chosen direction is used as the controlled parameter.

Fig. 1.

Resonant mode tuning and maintenance algorithm.

Working body vibration acceleration $\ddot {q}(t)$ is determined by information read from the acceleration meters. Angular velocities of vibration exciters are determined by information read from encoders as average for the preceding rotation. That said, disturbing force F(t) is found as the sum of centrifugal forces of eccentric weights projected to a chosen acceleration measurement direction. In the case of the synchronization of vibration exciters that ensures a unidirectional influence on the working body (counterphase synchronization at zero phase displacement of the eccentric mass rotation), the resulting function of disturbing force F(t) is considered harmonic. Otherwise, when the eccentric weight rotation speeds are equal and their shift phase differs from zero, the aggregate signal is filtered for generating a harmonic signal.

Phase difference ε is determined by signals $\ddot {q}(t)$ and F(t) preliminarily filtered from high-frequency constituents in the steady-state oscillation mode of the working body. The phase difference is calculated as ε = Δt/T. In this case, oscillation period T is determined as the time between two successive acceleration meter signal values at $\dddot q(t) < 0$; Δt is determined as the time between two successive zero acceleration meter signal values and the coercive force at $\dddot q(t) < 0$ and $\dot {F}(t) > 0$ (Fig. 2, where the dashed line shows the case at the resonant phase shift value ε = ε*).

Fig. 2.

Diagram of the calculation of phase shift ε, with dashes showing the case at phase shift ε equal to resonant value ε*.

The criterion for tuning the system to resonance is the proximity of phase difference ε to resonant phase difference ε*. The condition under which oscillations are considered steady-state is the constancy of the phase difference averaged for n measurements: $\left| {\overline {{{\varepsilon }_{t}}} - \overline {{{\varepsilon }_{{t - 1}}}} } \right| < {{\Delta }_{1}}\overline {{{\varepsilon }_{t}}}$, where $\overline {{{\varepsilon }_{t}}}$, $\overline {{{\varepsilon }_{{t - 1}}}}$ is the average phase difference ε for n previous and subsequent periods, respectively; Δ₁ is the allowed relative deviation. The condition under which the eccentric weight rotation frequency must be adjusted is the difference in the phase shift averaged for n periods from resonant value $\left| {\varepsilon {\kern 1pt} \text{*} - \;{{{\bar {\varepsilon }}}_{t}}} \right| > {{\Delta }_{2}}\varepsilon {\kern 1pt} \text{*}$, where Δ₂ is the allowed relative deviation.

The controlling parameter of the considered system is the vibration exciter supply frequency f. The main element of the control system is the unit for calculating the adjusting supply frequency value necessary for tuning the system to resonance. In this case, adjusting frequency f * can be calculated by various methods.

One of the ways of varying the eccentric weight rotation frequency is the iteration adjustment of the supply frequency with a certain pitch. The pitch size can be chosen on the basis of a preselected stability margin of the algorithm or be adaptable; that is, it can decrease with the approximation of phase shift ε to the required value ε*. In both cases, the required phase shift values are reached by adjusting the supply frequency in several iterations.

PID control is the most popular iteration algorithm. That being said, the adjusting supply frequency value at each iteration is calculated as the sum of the proportional, integral, and differential constituents of the controlling parameter, which is recorded as

$$f\text{*} = {{K}_{p}}(\varepsilon {\kern 1pt} \text{*} - \;\varepsilon (t)) + {{K}_{i}}\int\limits_0^t {(\varepsilon {\kern 1pt} \text{*} - \;\varepsilon (\tau ))d\tau } + {{K}_{d}}\frac{{d(\varepsilon {\kern 1pt} \text{*} - \;\varepsilon (t))}}{{dt}}.$$

Each of the summands depends on the difference ε* – ε(t), whereas the level of its influence on the calculation of the adjusting supply frequency value is controlled with the help of coefficients K_p, K_i, and K_d, the values of which are selected most frequently in an empirical manner by the Ziegler–Nichols algorithm [16].

Since the controlled parameter is not a continuous function of time, in this article, differentiation and integration are replaced with differencing calculation sequences. In this case, the controlling parameter is adjusted only after determining the oscillations, whereas it is not required for the controlled parameter to leave the range of allowed values (Δ₂ = 0).

It should be noted that the PID controller does not allow tracking in the real-time mode variations in the factors that have caused the deviation of the controlled parameter, in particular, the current mass work material mass and the resonance frequency of the system.

In addition to iterative approximation algorithms, there are also resonant mode maintenance algorithms based on the dynamic portrait of the system [17].

This portrait is the design dependence of the phase difference between the coercive force and the working body oscillations on the process load weight (natural frequency of the system) and the supply frequency of the vibration exciter. The current value of natural frequency p of the system is determined by the current values of phase shift ε and the electric motor supply frequency f, whereas the required electric motor supply frequency f* is determined from a series of possible states of the system.

However, to make up a dynamic portrait, it is required to elaborate a detailed mathematical model of the vibration machine.

MATHEMATICAL MODEL OF THE VIBRATION MACHINE

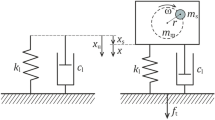
The considered transport and production machine (Fig. 3) consists of working body 1, mounted on springs 2, 3, two self-synchronizing unbalanced vibration exciters 4, and control system parts 5–8. The axes of the vibration exciter shafts lie in vertical planes parallel to the process axis of the machine (Fig. 3, axis X). The chosen vibration machine layout allows considering both wobbling screens and shaking conveyors.

Fig. 3.

Design of the vibration machine with an automatic resonant oscillation maintenance system.

According to Fig. 3, the resonant oscillation maintenance system consists of encoders 5, mounted on the vibration exciter shafts; acceleration meter 6, mounted on the working body of the vibration machine; control system controller 7, responsible for processing sensor signals and calculating the adjusting supply frequency values; and frequency converter 8, controlling the vibration exciter rotation speed.

The stiffness of the elastic support springs was chosen proceeding from the following considerations: (1) the perturbing action frequency must be similar to the first natural oscillation frequency of the working body (resonant mode energy efficiency condition); (2) the first oscillation mode must correspond to the translational vibrations towards the process axis of the machine. A synchronous counterphase rotation of the eccentric weights must be ensured, which is necessary for applying a unidirectional perturbation force; (3) the first resonant frequency value must correspond to the recommended oscillation frequency of the working body for the production process; (4) the wobble action and potential change in the oscillation mode due to the influence of the subsequent natural frequency must be excluded.

Because of the symmetry of the vibration machine relative to the upright plane crossing the process axis of the machine, Fig. 4 shows only one (right) half of the design diagram.

Fig. 4.

Design diagram of the vibration machine.

The motion of the working body is described relative to the OXYZ global frame of reference, the beginning of which coincides with the position of the mass center of the system at point C at a standstill, where the OZ axis is vertical. The working body is modeled as an absolutely solid body with mass M, length 2L_x, and width 2L_y. The position of the eccentric weights and spring attachment points are preset in the O′xyz local frame of reference, rigidly connected with the solid body, and by the datum point coinciding with zero point of the OXYZ frame of reference. Moreover, at a standstill the axes of the local and global frames of reference coincide.

The inertia torques of the working body around the O′x, O′y, and O′z axis are indicated as J_x, J_y, and J_z, respectively. The reciprocal turn of the global and the local frames of references is described with the help of Krylov–Bulgakov angles [18] that are represented for simplicity as α, β, and γ (Fig. 4). As a result, the position of the working body relative to the global frame of reference is preset with the help of three displacements x, y, and z and three angular rotations α, β, and γ.

The variation in the process load mass is modeled by slow variations in attached mass m. It is accepted that the process load is evenly distributed across the working body and carries out movements without separation. In this case, the coordinate of the mass center along the O′z process load axis varies as

$${{z}_{m}}(t) = \frac{{m(t)}}{{8\rho {{L}_{x}}{{L}_{y}}}},$$

where ρ is the bulk density of the work material and the coordinates are x_m(t) = y_m(t) = 0.

The spring attachment points are located in the angles of the working body and shifted by distance z_p along the O′z axis. Each of the elastic support springs is considered to exhibit linear stiffness in three mutual perpendicular directions with coefficients k_z, k_x, and k_y. The damping in the system is conditioned by the dissipation of energy in the springs and described by the linearly viscous friction model with coefficients b_x, b_y, and b_z.

Oscillations are excited using two unbalanced vibration exciters driven by induction motors energized by a common frequency changer that regulates the motor supply according to the proportional law recorded as U/f = const. The eccentric weight of each vibration exciter has mass m_i with eccentricity r_i and inertia torque J_di (i = 1, 2 is the vibration exciter number). The position of each of the eccentric weights in the O′xyz local frame of reference is described with the help of an additional local frame of reference O_iξ_iη_iζ_i. The position of the O_iξ_iη_iζ_i local frame of reference is preset by radius vector ${{{\boldsymbol{\rho }}}_{i}} = \left( {\begin{array}{*{20}{c}} {0,}&{{{\rho }_{i}}\cos {{\delta }_{i}}}&{{{\rho }_{i}}\sin {{\delta }_{i}}} \end{array}} \right)$, where ρ_i and δ_i are the module and the tilt of the radius vector to the positive direction of the O′y axis, and by tilt θ_i of the O_iξ_i axis to the O′x axis; the latter tilt is counted from the positive direction of the O′x axis counterclockwise. Angles φ_i of the eccentric weight rotation around the O_iξ_i axis are counted from the negative counterclockwise direction of the O_iζ_i axis. To determine the directions of rotation, let us use the parameter σ_i = ±1, where the positive value corresponds to the rotational direction of the ith eccentric weight and the negative value corresponds to clockwise rotation. The induction motors of vibration exciters have torque characteristics M_i preset as modified Kloss formulas [19] that consider the shift in the torque characteristic with proportional frequency regulation, which is recorded as

$${{M}_{i}}({{\dot {\varphi }}_{i}}) = \frac{{2{{M}_{{Cr}}}\left( {{{\omega }_{s}} - {{\omega }_{{Cr}}}} \right)\left( {\pi {{f}_{0}} - {{{\dot {\varphi }}}_{i}} - \Delta \omega } \right)}}{{{{{\left( {\pi {{f}_{0}} - {{{\dot {\varphi }}}_{i}} - \Delta \omega } \right)}}^{2}} + {{{\left( {{{\omega }_{s}} - {{\omega }_{{Cr}}}} \right)}}^{2}}}},$$

where M_Cr is the critical motor torque; ω_Cr is the critical torque frequency; ω_s = 2πf₀/K is the idle frequency, where f₀ is the nominal supply voltage frequency of the electric motor; K is the number of poles in the electric motor; Δω = 2πf/K; and f is the current supply voltage frequency. There are minor differences in the motor specs; that is, M₁ = $\varkappa$M₂, where $\varkappa$ ≈ 1.

The motion of the working body is described by the following system of differential equations:

$${\mathbf{M\ddot {q}}} + {\mathbf{B\dot {q}}} + {\mathbf{Kq}} = {\mathbf{F}}({\mathbf{q}},{\mathbf{\dot {q}}},{\mathbf{\ddot {q}}}),$$

(1)

where ${{{\mathbf{q}}}^{T}} = \left( {\begin{array}{*{20}{c}} x&y&z&\alpha &\beta &\gamma &{{{\varphi }_{1}}}&{{{\varphi }_{2}}} \end{array}} \right)$; М is the mass matrix; В is the damping matrix; K is the stiffness matrix; and ${\mathbf{F}}({\mathbf{q}},{\mathbf{\dot {q}}},{\mathbf{\ddot {q}}})$ is the column vector of external forces.

For a detailed description of the derivation and verification of the equations of motion, see work [20], which is why they are not provided in this study.

MAKING UP THE DYNAMIC PORTRAIT OF THE SYSTEM

In systems with potential spatial oscillations of the working body, phase difference ε is calculated while measuring oscillations in any direction. According to the preliminary analysis of the numerical model, at the first resonant frequency, the working body carries out a plane movement in the XOZ plane. In addition, the amplitudes of oscillations towards the OX axis are maximal (main oscillations), whereas the oscillations along the OZ axis are generated due to the fact that the aggregate perturbing force of both eccentric weights is directed at a certain angle to the process axis. Phase difference ε is measured between oscillations of the center of mass of the system along the OX axis and by aggregate projections φ_i of the eccentric weight coordinates on the O_iζ_i axis. Since the direction of the OX axis is the direction of the main translational oscillations of the system in the first natural mode shape, the resonant phase difference along this direction is ε* = π/2, which is confirmed by the results of full-scale tests of the laboratory wobbling screen prototype.

In the system with unbalanced vibration exciters, phase shift ε reaches resonant value ε* under the influence of damping on natural frequency p₀ of the system, not on resonant frequency ω > p₀. Thus, damping is a sort of stability margin for resonance tuning.

Motion equations (1) are solved by calculating phase shift ε and natural frequency p of the system, depending on vibration exciter supply frequencies f and mass m of the work material.

The results of the calculations at f and m varying within their possible variation ranges form an array of system states; in this array, each string is space point P(p, f, ε).

The resulting array is approximated by the following function:

$$\varepsilon (f,p) = a \cdot {{e}^{{b{{f}^{2}} + cp + d}}},$$

(2)

where a, b, c, and d are the approximation parameters.

For a functional dynamic portrait of the machine considered, see Fig. 5. The black line shows the portrait points corresponding to phase difference ε* of resonant tuning.

Fig. 5.

Dynamic portrait of the system.

NUMERICAL TEST

The algorithms proposed for maintaining the resonant mode of control systems were integrated with the mathematical model of the vibration machine. The system parameters at which the calculations were made were as follows: L_x = 0.23 m, L_y = 0.21 m, M = 25.67 kg, m_i = 0.52 kg, r_i = 0.01 m, J_x = 0.685 kg m², J_y = 0.597 kg m², J_z = 0.860 kg m², k_x = 91 744 N m^–1, k_y = 175 676 N m^–1, k_z = 152 075 N m^–1, z_p = 0.012 m, b_x = 90 N s m^–1, b_y = 125 N s m^–1, b_z = 117 N s m^–1, ρ_i = 0.23 m, δ₁ = –0.07 rad, δ₂ = π + 0.07, $\varkappa$ = 0.97, M_Cr = 1.233 N m, ω_Cr = 115 rad s^–1, ω_s = 2πf₀/K = 157 rad s^–1, f₀ = 50 Hz, K = 2, f = 26–38 Hz, m = 0–6 kg, ρ = 1400 kg m^–3, n = 3, Δ₁ = 0.02ε_i, Δ₂ = 0.01ε* for the algorithm based on the dynamic portrait, and Δ₂ = 0 for the algorithm based on the PID controller.

According to (2), the dynamic portrait approximation coefficients are a = 10 820 rad, b = 8.571 × 10^–3 Hz^–2, с = –1.243 Hz^–1, and d = 1.828. The PID controller coefficients are K_p = 0.712 Hz/rad, K_i = 0.532 rad^–1, and K_d = 0.110 Hz rad^–1 s^–1.

In the numerical test, the variation in the handled material mass was preset by the piecewise linear law (Fig. 6).

Fig. 6.

Time relation of process duty changes.

The accepted law of mass variation allows studying the system reaching the resonant mode and the maintenance of maximal oscillation amplitudes.

Despite insignificant variations in the natural frequency at a preset variation in the work material mass, the maximal oscillation amplitudes at the tuning of an unloaded machine for resonance (at m = 0 kg) and at full loading (at m = 6 kg) exhibit a nearly twofold difference, which is caused by the steepness of the resonant peak of the frequency response function.

For the curves of variations in the controlling parameter (supply frequency) and the controlled parameter (Fig. 7c), depending on time at the tuning with the help of PID control (Fig. 7a) and with the help of a dynamic portrait (Fig. 7b), see Fig. 7. During PID control, resonance (Figs. 7a, 7c) is reached in steps, which takes about 20 iterations. At a smooth variation in the work material mass, the controlling parameter changes almost monotonically, in which case the controlled parameter deviation falls within 5% of the resonant value, whereas at sharp changes an explicitly oscillatory transient is observed.

Fig. 7.

Numerical test results: (a) variation in the controlling parameter over time with PID control; (b) with the use of a dynamic portrait; (c) variation in the controlled parameter over time.

When a dynamic portrait is used (Fig. 7b), the resonance is achieved in one iteration for a considerably shorter time than under PID control. Smooth variations in the work material mass make possible a more precise adjustment for resonance against PID control (Fig. 7c); in the case of sharp changes, however, a rapidly fading aperiodic transient is observed.

Under sharp variations in the load mass, the controlled parameter leaves the limits of the allowed range due to the slow response of the system and the peculiarities of calculating this parameter.

EXPERIMENTAL

The experiments were conducted on the designed lab vibration machine prototype (Fig. 3) equipped with an automatic system of maintaining the resonant mode.

The system was launched in the preresonant frequency mode ( f_s = 24 Hz), and the working body was loaded after entering the resonant oscillation mode. Brazen granules were used as the work material; every ten seconds zero to eight kilograms of these granules were poured into a box attached to the working body (position 9 in Fig. 3). Then the material was manually bailed out with the help of a measuring jar, which simulated the unloading of the working body. For the law of variations in the work material mass over time, see Figs. 8a and 8b. For the experimental results, see Figs. 8c–8f.

Fig. 8.

(a) Variation in the work material mass over time under machine loading; (b) for machine unloading; (c) variation in the controlled parameter over time for machine loading; (d) for machine unloading; (e) variation in the controlling parameter over time for machine loading; and (f) for machine unloading.

RESULTS AND DISCUSSION

This article describes the implementation of a steady resonant oscillation mode of the working body of a vibration transport production machine with two self-synchronizing unbalanced vibration exciters with the fluctuation of the work material mass by automatically controlling the eccentric mass rotation speeds.

In the course of solving the problem formulated, a resonant frequency maintenance algorithm was developed on the basis of the dynamic portrait of the system and conclusions were made about the possibility of using PID controllers for these purposes. The mathematical model of the laboratory wobbling screen prototype has been used for deriving the function of the system’s dynamic portrait.

This article provides the results of numerical tests conducted to maintain the resonant oscillation mode under variations in the work material mass on the working body of the vibration transport production machine with the help of both the earlier derived dynamic portrait of the system and the PID controller.

As shown by comparing the calculation results, both algorithms used for maintaining the resonant oscillation mode maintain the deviation of the controlled parameter within 5% of the resonant value under slow variations in the load weight. However, the maintenance of the resonant mode using the algorithm based on the dynamic portrait is more precise and significantly faster and allows determining the current work material mass and the resonant frequency of the plant in real-time mode.

The operational ability of the suggested algorithm for maintaining the resonant mode based on the dynamic portrait of the system is shown by the test results. Under loading of the working body, the control system maintained the controlled parameter within the five-percent deviation range. The fact that the rotation speed was regulated by the design dependences obtained by mathematically modeling the plant shows that correct assumptions were chosen for deriving the equations of motion of the working body and the formula of the dynamic portrait function. The periodic overruns of the controlled parameter beyond the five-percent deviation in the case of unloading the working body are conditioned by the influence of process factors at the loadout of the material.

It should be noted that these short-time overruns beyond the preset range do not cause any disruption to the region of super resonant frequencies due to the detention lag of the system and the availability of a sufficient stability margin related to the decrement in the system.