It is known that cavitation of a fluid is accompanied by numerous effects. In particular, when a bubble with a spherical form or a shape close to spherical collapses, radially converging shock waves can arise in its cavity [1], causing a strong increase in pressure, temperature, and density [2], and a glow may appear [3]. At the end of the collapse being close to spherical, the pressure in the liquid layer surrounding the bubble can increase significantly [4], and radially diverging acoustic and shock waves can be emitted into the liquid [5]. Under nonspherical collapse, high-speed cumulative streams can form on the surface of the bubble [6], etc.

In practice, cavitation effects often cause problems. So, it is known that cavitation can lead to damage to the surfaces of bodies [7, 8], noise [9], reduced efficiency of devices [10], etc. However, the effects of cavitation are widely used. For example, cavitation is used to clean deposits from heat exchanger tubes [11], increase the efficiency of wave technologies [12], and heat liquids using vortex heat generators [13, 14].

In this article we discuss the effects of fluid heating and acoustic radiation when collapsing a single cavitation bubble in an unlimited volume of a stationary liquid.

STATEMENT OF THE PROBLEM

The values of thermal and acoustic energies released during the collapse of a single spherical cavitation (vapor) bubble in liquid (water) are calculated. Initially, at instant of time t = 0, the vapor of a bubble and the surrounding liquid are at rest, the temperature of the vapor and liquid is T0 = 20°С, and the vapor is in a state of saturation at the pressure pS(T0) = 0.022 bar. Far away from the bubble, the pressure of the liquid is p∞ = 10 bar. The collapse of the bubble is due to the fact that the fluid pressure p∞ is much higher than the initial pressure pS(T0) in the bubble.

In this article, when modeling collapse of a bubble, we assume that the vapor in its cavity and the surrounding liquid are heat-conducting, and processes of heat and mass transfer occur on the surface of the bubble. The vapor in the bubble is assumed to be a perfect gas with a pressure that depends only on time. The liquid is assumed to be slightly compressible, which enables us to take into account the effect of acoustic radiation. The viscosity effect of liquid on the conversion of radial pulsation energy of a bubble into thermal energy is not taken into account.

Mathematical model. The mathematical formulation of the problem is a system of differential equations [15]

$$\begin{gathered} \left( {1 - \frac{{{{u}^{ + }}}}{{{{c}_{L}}}}} \right)R{{{\dot {u}}}^{ + }} + \frac{3}{2}\left( {1 - \frac{{{{u}^{ + }}}}{{3{{c}_{L}}}}} \right){{u}^{ + }}^{2} + 2\left( {1 - \frac{{{{u}^{ + }}}}{{4{{c}_{L}}}}} \right){{u}^{ + }}\left( {\dot {R} - {{u}^{ + }}} \right) \\ = \left( {1 + \frac{{\dot {R}}}{{{{c}_{L}}}}} \right)\frac{{{{p}^{ + }} - {{p}_{\infty }}}}{{{{\rho }_{L}}}} + \frac{R}{{{{c}_{L}}}}\frac{{{{{\dot {p}}}^{ + }} - {{{\dot {p}}}_{\infty }}}}{{{{\rho }_{L}}}}, \\ \end{gathered} $$
(1)
$${{\dot {p}}^{ - }} = \frac{3}{R}[(\gamma - 1){{({{\kappa }_{{v}}}{{T}_{r}})}^{ - }} - \gamma p{{u}^{ - }}],$$
(2)
$$\dot {R} = {{u}^{ + }} + \frac{j}{{{{\rho }_{L}}}},$$
(3)
$${{T}_{t}} + u{{T}_{r}} = \frac{{(\gamma - 1)T}}{{\gamma p}}\left( {{{{\dot {p}}}^{ - }} + \frac{1}{{{{r}^{2}}}}{{{({{r}^{2}}{{\kappa }_{{v}}}{{T}_{r}})}}_{r}}} \right),$$
(4)
$${{\rho }_{L}}C{{r}^{2}}\left( {{{T}_{t}} + \frac{{{{R}^{2}}}}{{{{r}^{2}}}}{{u}^{ + }}{{T}_{r}}} \right) = {{({{\kappa }_{L}}{{r}^{2}}{{T}_{r}})}_{r}},$$
(5)

where the dot above means the derivative with respect to time t, r is the distance to the center of the bubble, R is the bubble radius, u is the velocity, p is the pressure, T is the temperature, ρ is the density, с is the speed of sound, κ is the heat conductivity coefficient. Subscripts L and \({v}\) indicate the liquid and vapor, respectively, and superscripts + and – indicate the relation to the surface of the bubble on the sides of liquid and vapor, respectively, γ is the vapor adiabat index, and С is the specific heat of the liquid. Moreover, we have

$${{p}^{ + }} = {{p}^{ - }} - \frac{{2\sigma }}{R} - \frac{{4\mu }}{R}{{u}^{ + }},\quad u = \frac{r}{R}{{u}^{ - }} + \frac{{\gamma - 1}}{{\gamma p}}\left( {{{\kappa }_{v}}{{T}_{r}} - \frac{r}{R}{{{({{\kappa }_{v}}{{T}_{r}})}}^{ - }}} \right),$$
$${{u}^{ - }} = \frac{j}{{{{\rho }^{ - }}}} - \dot {R},\quad {{\rho }^{ - }} = \frac{{{{p}^{ - }}}}{{{{R}_{v}}T{\kern 1pt} *}},\quad j = \frac{{{{\alpha }_{M}}}}{{\sqrt {2\pi {{R}_{v}}} }}\left( {\frac{{{{p}_{S}}(T{\kern 1pt} *)}}{{\sqrt {T{\kern 1pt} *} }} - \frac{{\Gamma {{p}^{ - }}}}{{\sqrt {T{\kern 1pt} *} }}} \right),$$
$$\Gamma = {{{\text{e}}}^{{ - {{\Omega }^{2}}}}} - \Omega \sqrt \pi \left( {1 - \frac{2}{{\sqrt \pi }}\mathop {\mathop \smallint \limits_0 }\limits^\Omega {{{\text{e}}}^{{ - {{x}^{2}}}}}{\text{d}}x} \right),\quad \Omega = \frac{j}{{{{p}^{ - }}}}\sqrt {\frac{{{{R}_{v}}T{\kern 1pt} *}}{2}} ,$$

where σ is the surface tension coefficient, μ is the viscosity coefficient of liquid, \({{R}_{v}}\) is the vapor gas constant, αM is the accommodation coefficient (evaporation/ condensation), Т* is the temperature on the surface of the bubble, and \({{p}_{S}}\)(T) is the saturated vapor pressure at temperature T.

The boundary conditions for the equations of thermal conductivity of the vapor (4) and liquid (5) are given by

$$r = 0{\kern 1pt} :\;\;{{T}_{r}} = 0,$$
(6)
$$r = \infty {\kern 1pt} :\;\;T = {{T}_{0}},\quad p = {{p}_{\infty }},$$
(7)
$$r = R{\kern 1pt} :\;\;{{({{\kappa }_{L}}{{T}_{r}})}^{ + }} - {{({{\kappa }_{v}}{{T}_{r}})}^{ - }} = jl({{p}^{ - }}),\quad {{T}^{ + }} = {{T}^{ - }} = T{\kern 1pt} *{\kern 1pt} .$$
(8)

Here l(p–) is the latent vaporization heat at pressure р–.

The boundary conditions at \(t = 0\) for equations (1)–(5) have the form

$${{u}^{ + }} = 0,\quad {{p}^{ - }} = {{p}_{S}}({{T}_{0}}),\quad R = {{R}_{0}};\quad T = {{T}_{0}}\quad {\text{for}}\quad 0{\text{ }} \leqslant r < \infty .$$
(9)

Within the framework of the accepted conditions, we have ρL = 998.2 kg/m3, сL = 1483 m/s, κL = 0.5984 W/(m K), \({{\kappa }_{v}}\) = 0.018222 W/(m K), γ = 1.325, С = 4150 J/(kg K), σ = 0.0725 N/m, μ = 103 kg/(m s), \({{R}_{v}}\) = 461.912 J/(kg K), and αM = 0.04.

The main statements of the technique of the numerical solution. In the numerical method for solving problem (1)–(9), a change of variables is used r = Rη, t = τ. As a result, we have for the arbitrary function f

$${{f}_{t}} = {{f}_{\tau }} - \eta \frac{{\dot {R}}}{R}{{f}_{\eta }},\quad {{f}_{r}} = \frac{1}{R}{{f}_{\eta }},\quad \left. {{{f}_{r}}} \right|_{{r = R}}^{ - } = {{\left. {\frac{1}{R}{{f}_{\eta }}} \right|}_{{\eta = 1}}}.$$

In terms of coordinate η, the region of the bubble corresponds to the interval 0 ≤ η < 1, while the region of the liquid corresponds to the interval 1 < η ≤ ηL, where ηL determines the position of the outer boundary of the calculated region of the liquid. In the vicinity of the surface of a bubble, very thin thermal boundary layers can arise on both sides of the surface during radial pulsations of the bubble. With this in mind, the numerical meshs are chosen to be exponentially denser toward the bubble surface.

The algorithm for solving problem (1)–(9) using these new variables is based on the finite difference method. In addition, the spatial derivatives are approximated by central differences everywhere, with the exception of the bubble surface. On the surface of the bubble, one-sided approximations of the second order of accuracy are used. Replacing the spatial derivatives with finite differences reduces partial differential equations (4), (5) to a system of ordinary differential equations for temperature T at the nodes of the difference mesh. This system turns out to be related to ordinary differential equations (1)–(3) with respect to u+, \(\dot {R}\), and p– only through parameters j(T*), \(\kappa {{T}_{r}}{{{\text{|}}}^{ - }}\), and l(p–). Equations (1)–(3) are solved by the Dorman–Prince method [16], which is a high-precision option of the Runge–Kutta method with automatic selection of the integration step over time. The above-mentioned system relative to temperature T at the nodes of the difference mesh is solved implicitly in part using five-point sweeping.

The calculation is carried out using a single time step. In this case, at the next time step, when calculating new values of variables u+, \(\dot {R}\), and p–, the temperature T– and its gradient \(T_{r}^{ - }\) on the surface of the bubble are assumed to be constant. At the same time, when calculating the new temperature field T in the bubble and liquid, the pressure p– is taken as unchanged. When using this approach, there are no problems with stability of calculations. At the same time, the accuracy of the solution is determined by the accuracy of the solution of equations (4), (5), which is not automatically controlled. Therefore, the required calculation accuracy is achieved by successive partitioning of the spatial mesh used to solve equations (4), (5).

RESULTS

The results presented in Sections 1–3 were obtained for the initial bubble radius R0 = 0.5 mm.

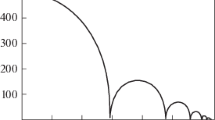
(1) Features of bubble collapse. Figure 1 demonstrates the change in the bubble radius during its collapse.

Fig. 1.
figure 1

Decrease in the bubble radius upon collapse.

Full size image

We can see that the collapse occurs in the form of a series of rapidly decaying radial pulsations, at the end of which the bubble disappears. The rather rapid collapse of the bubble is mainly due to the fluid compressibility and condensation of vapor at the interface.

Figure 2 shows the change in the vapor temperature in the central region of the bubble, where the effect of heat exchange with liquid and the pressure of the vapor are insignificant. The pressure of vapor within the framework of the adopted model depends only on time (it is constant over the entire volume of the bubble). One can see that at the moments of local extreme compression of the bubble, the temperature and vapor pressure gradually decrease. At the moments of maximum expansion of the bubble after the first two compressions, the temperature increases slightly and then decreases, while the pressure increases monotonically all the time.

Fig. 2.
figure 2

Change in temperature (a) at the center of the bubble and (b) the pressure in the cavity during collapse.

Full size image

(2) Evaluation of thermal energy entering the liquid. The energy qR coming from the bubble and spent on heating the liquid can be calculated by the formula

$${{\dot {q}}_{R}} = - 4\pi {{\kappa }_{L}}\left. {{{T}_{r}}} \right|_{{r = R}}^{ + }{{R}^{2}},$$
(10)

where \(\left. {{{T}_{r}}} \right|_{{r = R}}^{ + }\) is the temperature gradient on the surface of the bubble.

Figure 3 demonstrates the change in qR according to (10) during the collapse of the bubble. We can see that the value of qR increases monotonically during the collapse. In this case, its maximum growth is observed during the first compression and subsequent expansion of the bubble. After the second expansion, the value of qR increases insignificantly. This is apparently due to a rather rapid decrease in the bubble surface area through which heat exchange between the bubble and the liquid occurs. According to Fig. 3, the energy E spent for heating the liquid is approximately equal to 27 μJ.

Fig. 3.
figure 3

Change in thermal energy escaping from the bubble into the liquid in the process of its collapse.

Full size image

(3) Estimation of the energy of acoustic radiation. To estimate the energy of acoustic radiation, the solution of the problem under consideration was obtained without taking into account the influence of the fluid compressibility determining the acoustic radiation. For this purpose, we put cL = ∞ in Eq. (1). Figure 4 plots the calculation results. Disregarding acoustic radiation, the main process that determines the rate of bubble collapse is the effect of evaporation/condensation. Figure 4a shows that in this case the bubble collapse slows down by more than 1000 times. The moment of disappearance of a bubble with allowance for acoustic radiation (in calculations without it) corresponds approximately to the moment when the bubble radius reaches its maximum value during the first local expansion of the bubble following its first local compression. The given maximum value of the radius differs very little from its original value. This, along with Fig. 4a, indicates slow damping of the radial bubble pulsations.

Fig. 4.
figure 4

Variation in bubble radius R ((а), (b)) and thermal energy qR of liquid escaping the bubble ((c), (d)) during the entire process of the bubble collapse ((а), (c)), and at its initial stage ((b), (d)) without taking into account the fluid viscosity (cL = ∞). The dotted lines in ((b), (d)) correspond to a compressible fluid (Figs. 1, 3).

Full size image

From Figs. 4c and 4d, it follows that, without taking into account acoustic radiation, the outgoing thermal energy Enoac of the bubble (the maximum of qR calculated at cL = ∞) turns out to be about ten times greater than when acoustic radiation is accounted for, whence it follows that the acoustic radiation energy is Eac = E noac – E ≈ 9E. Figure 4d shows that neglecting acoustic radiation also changes the character of heat exchange between the liquid and the bubble. If, when acoustic radiation is accounted for, the thermal energy value increases monotonically, then without taking it into account the thermal energy grows in the form of oscillations (with a decreasing amplitude). This means that when acoustic radiation is taken into account, the flow of thermal energy during the entire collapse of the bubble is directed from the bubble to the liquid. Without taking into account acoustic radiation, the heat flux is directed to the liquid only in the greater part of each local compression of the bubble. On the contrary, in most of each local expansion, the thermal energy goes back from the liquid to the bubble.

(4) The impact of bubble size. To assess the influence of the bubble size on its energy spent on heating of the liquid by the end of the bubble collapse, and on the acoustic radiation energy, calculations were performed for a number of values of the initial bubble radius R0 (Fig. 5).

Fig. 5.
figure 5

Influence of the initial bubble radius R0 on its energy E spent on heating the liquid by the end of bubble collapse with allowance for (points connected by a dashed curve) and without allowance for acoustic radiation (points connected by a solid curve).

Full size image

In logarithmic scales, both dependences on the bubble radius prove to be close to linear. An analysis shows that both dependences are close to cubic.

It should also be noted that model (1)–(9) takes into account the dissipation of energy of the radial pulsations of the bubble due to the fluid viscosity. In reality, this energy is transformed into the thermal energy of liquid. This transformation is not taken into account in the model of this work. To assess the thermal energy losses of the liquid, which were not taken into account during the aforementioned transformation, we carried out the calculations without taking into account the influence of the fluid viscosity, i.e., at μL = 0. Calculations show that, in model (1)–(9), the loss of thermal energy of the liquid due to the absence of transformation of the viscous dissipation energy of the radial pulsations of the bubble is insignificant.

CONCLUSIONS

We present the results of a numerical study of the thermal and acoustic energies released during the collapse of a single spherical cavitation (vapor) bubble in a liquid (water). The fluid pressure is 10 bar, and the temperature is 20°С. A physical model is used in which the vapor in the bubble and the surrounding liquid are considered to be heat-conducting, and heat and mass transfer occur on the bubble surface. We take into account acoustic radiation due to the fluid compressibility, but the effect of viscosity outside the bubble surface on the conversion of mechanical energy into heat is not accounted for. The vapor in the bubble is considered a perfect gas with a pressure that depends only on time.

It is shown that, when a bubble with an initial radius of 0.5 mm collapses, an energy of about 25 μJ comes into the liquid, which is spent on heating. In this case, an energy that is nearly nine times higher goes out by means of acoustic radiation resulting from radial oscillations of the bubble. At the same time, the energy caused by the dissipation of radial oscillations of the bubble due to the fluid viscosity is insignificant (in the model of this work, the transformation of this energy into heat is not taken into account). It is found that the energy spent on heating the liquid and the energy carried away by acoustic radiation are proportional to the cube of the initial bubble radius.

It should be noted that the model used does not take into account the influence of a number of important factors, in particular, the deformation of the bubble, the dependence of the thermal conductivity coefficients on temperature, vapor imperfection, etc. Taking these effects into account is a quite nontrivial task. In this sense, the results presented can be treated as the first approximation, which provides a good guideline for further research using more adequate models.