MIMO Semi-blind Channel Estimation by using Tikhonov Regularized MMSE and MAP Algorithms with Householder Transformation based QR Decomposition

Abstract

In this paper, we present novel semi-blind channel estimation schemes for Rayleigh fading Multi-Input Multi-Output (MIMO) channel. Here channel matrix H is decomposed as an upper triangular matrix R, which can be estimated blindly using the Householder transformation based QR decomposition of received output covariance matrix and Q matrix, which can be estimated using the Tikhonov regularization-based MAP (maximum a posteriori) and MMSE (minimum mean square error) techniques with the help of singular value decomposed orthogonal pilot symbols. Simulation results in terms of BER performance obtained for BPSK and 4-PSK data modulation schemes using Alamouti coded 2×6 (2 transmitter and 6 receiver antennas) and 2×8 (2 transmitter and 8 receiver antennas) cases by choosing different values of regularization parameter λ. Appropriate choice of regularization parameter can be calculated using discrepancy principles that gives better performance in terms of BER. The paper proposes the novel semi-blind channel estimation approach using the Householder QR decomposition based blind estimation of R and Tikhonov regularized based MMSE and MAP algorithms using pilot symbols for estimation of Q will yield good results in channel estimation methods.

1. Introduction

In this modern and high-tech world of communication, there is a requirement to deploy a robust and efficient wireless system to support high data rates with less errors. MIMO wireless communications have become an integral part of the most forthcoming commercial and next generation wireless data communication systems. These systems offer an increase in the data throughput and link robustness without any need for additional bandwidth or transmitting power [1]–[4].

MIMO antenna technology achieves this objective by spreading the same total transmit power over several antennas to accomplish an array gain that recovers the spectral efficiency (more bits per second per Hertz of bandwidth) or to achieve a diversity gain that increases the link reliability, i.e. resulting in a reduced fading [5]–[8].

Many techniques like pilot, blind, semi-based transmission methods have been explored for channel estimation, as a robust channel estimation method plays a very crucial role in the performance of MIMO system. Pilot-based channel algorithms may have a disadvantage as compared to blind channel estimation methods, which were shown to provide better spectral efficiencies since it uses received data statistics and does not requir pilot symbols [9], [10]. Hence, as a trade-off to balance both above techniques, semi-blind methods have been thoroughly studied.

The approaches for semi-blind channel estimation using a combination of few pilot-based symbols with blind statistical information make it possible to solve the poor convergence speed and high complexity problems of blind estimators [11]–[13].

Here we propose and present a novel semi-blind channel estimation scheme. The main steps of this novel scheme are as follows:

Step 1. From the received output data covariance matrix, it is necessary to estimate R matrix blindly using Householder transformation based QR decomposition method.

Step 2. From the orthogonal pilot symbols, it is necessary to estimate Q matrix using the Tikhonov regularization-based MAP and MMSE techniques with the help of singular value decomposition of orthogonal pilots and by choosing appropriate regularization parameter λ using discrepancy principal method [4], [14]–[16].

Final channel estimate will be calculated as follows:

$$ \hat{\mathbf{H }} = \mathbf{R}{\hat{\mathbf{Q}}}^{\rm H}. $$

Tikhonov’s regularization is a method that works well in case of a matrix with ill-conditioned inverse problems [4]. Tikhonov’s regularization is usually helpful in mitigating the problem in linear regression. This paper explores the use of Tikhonov regularized LS and MAP, both training-based methods to find the unitary matrix Q [17]–[20].

2. System Model

The MIMO system exploits the advantages of spatial diversity by playing with the number of transmitting and receiving antennas.

The basic model of a spatially multiplexed MIMO system (Fig. 1) includes the number of transmitting antennas Tx and the number of receiving antennas Rx, and Rx ≥ Tx. The general equation for the received signal matrix Y is given as

$$ \mathbf{Y=HX+n}, $$

(1)

where X is the input signal matrix, H is the channel matrix and n is the noise matrix.

Fig. 1.

Basic block diagram for MIMO system [6].

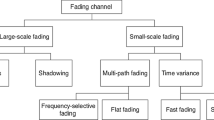
The channel is modelled as H, which is a matrix. Here a flat fading scenario is considered where the channel characteristics remain constant for a block or a frame of certain symbols.

3. Proposed Semi-Blind Channel Estimation Technique

3.1. Householder QR Decomposition Based Blind Matrix Calculation

Here MIMO channel matrix H can be decomposed as a product $\hat{\mathbf{H }} = \mathbf{R}{\hat{\mathbf{Q}}}^{\rm H}$ , where R denotes the upper triangular matrix, which is estimated blindly using the Householder decomposition of output covariance matrix and Q is estimated by using the Tikhonov regularized MAP and MMSE pilot-based methods.

Now using (1), we can write output covariance matrix ${{\mathbf{R}}_{\mathbf{YY}}}$ as

$$ {{\mathbf{R}}_{\mathbf{YY}}}={\rm E}[{{\mathbf{Y}}_{{b}}}{{\mathbf{Y}}_{{b}}}^{{\rm H}}\mathbf{]=H}{{\mathbf{X}}_{{b}}}{{{(\bf H}{{\mathbf{X}}_{{b}}}{)}}^{{\rm H}}}+\sigma _{n}^{2}\mathbf{I}, $$

(2)

where ${{\mathbf{Y}}_{{b}}}$ are the received output data, ${{\mathbf{X}}_{{b}}}$ are the blind input data, $\sigma _{n}^{2}$ is the noise power, and ( )^H is hermitian matrix.

Next, we can write output covariance matrix ${{\mathbf{R}}_{\mathbf{YY}}}$ as

$$ {{\mathbf{R}}_{\mathbf{YY}}}=\mathbf{H}{{\mathbf{H}}^{{\rm H}}}+\sigma _{n}^{2}\mathbf{I}. $$

(3)

Now using the Householder QR transformation of output covariance matrix, a series of reflection matrices are applied to matrix ${{\mathbf{R}}_{\mathbf{YY}}}$ column by column to annihilate the lower triangular elements. The orthonormal reflection transformations can be written as follows:

$$ \mathbf{A}=(1+\beta \mathbf{g}{{\mathbf{g}}^{{\rm H}}}), $$

(4)

where g is the Householder vector and $\beta =-2\left\| \mathbf{g} \right\|_{2}^{2}$ .

For matrix ${{\mathbf{R}}_{\mathbf{YY}}}$ to annihilate the lower elements of the K-th column, matrix ${{\mathbf{A}}_{{K}}}$ is constructed as follows:

1. Let g will be the K-th column of ${{\mathbf{R}}_{\mathbf{YY}}}$ .

2. Update the g value by using expression

$$ \mathbf{g}={{\mathbf{R}}_{\mathbf{YY}}}+{{\left\| {{\mathbf{R}}_{\mathbf{YY}}} \right\|}_{2}}\boldsymbol{\psi }, $$

where $\boldsymbol{\psi }={{[1,\,0,\,0,\,0]}^{\rm T}}$ .

3. Determine $\beta$ to be equal to $\beta =-2\left\| \mathbf{g} \right\|_{2}^{2}$ .

4. A is calculated as $\mathbf{A}=(1+\beta \mathbf{g}{{\mathbf{g}}^{{\rm H}}})$ .

Further results are pre-multiplied by ${{\mathbf{R}}_{\mathbf{YY}}}$ sequentially as follows:

$$ {{\mathbf{A}}_{{n}},..,}{{\mathbf{A}}_{\mathbf{1}}}{{\mathbf{R}}_{\mathbf{YY}}}=\left[ \begin{aligned} &\mathbf{R} \\ &\mathbf{0} \\ \end{aligned} \right], $$

where R is the $n\times n$ upper triangular matrix and 0 is the null matrix.

So, we can estimate R blindly using the Householder transformation based QR decomposition method.

Using the QR decomposition based semi-blind method, it is possible to determine the MIMO channel [17]

$$ \mathbf{H=R}{{\mathbf{Q}}^{{\rm H}}}. $$

(5)

3.2. Tikhonov’s Regularization-based Cost Function for Pilot-based Channel Estimation

When using the Tikhonov regularization based constrained ML estimate to find matrix Q, the cost function is given as follows:

$$ \left\| {\mathbf{Y}_p-\mathbf{HX}_p} \right\|_F^2+{{\lambda }^{2}}\left\| \mathbf{H} \right\|_F^2 , $$

(6)

where $||\;||_F$ is Frobenius norm, λ is the regularization parameter, ${\mathbf X}_p$ is the matrix of orthogonal pilot symbols and ${\mathbf Y}_p$ is the output matrix of pilot symbols. Hence, using (5) we can write:

$$ {{\left\| {\mathbf{Y}_p-\mathbf{HX}_p} \right\|}_F^2}+{{\lambda }^{2}}\left\| \mathbf{H} \right\|_F^2={\left\| {\mathbf{Y}_p-\mathbf{R}}{{\mathbf{Q}}^{{\rm H}}}{\mathbf{X}_p} \right\|}_F^2+\lambda^2\left\| \mathbf{R}{{\mathbf{Q}}^{{\rm H}}} \right\|_{{F}}^{2}. $$

(7)

3.2.1. Tikhonov regularized MAP algorithm

Using MAP algorithm [7] (2008) in conjunction with the Tikhonov regularization method, the channel matrix can be calculated as follows

$$ {{{\mathbf H}}_{{\rm TMAP}}}\mathbf{=(}{{{\mathbf R}}_{nn}^{{-1}}} + {{{\mathbf R}}_{hh}}{{\mathbf{)}}^{-1}}{{{\mathbf R}}_{{nn}}^{-1}}{{\mathbf{(}{{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{{\rm H}}} + {{\lambda }^{2}}\mathbf{I})}^{{-1}}}{{{\mathbf X}}_{{p}}^{{\rm H}}}{{\mathbf{Y}}_{{p}}}, $$

(8)

where ${\mathbf R}_{hh}$ is the channel covariance matrix and ${\mathbf R}_{nn}$ is the noise covariance matrix.

Using MAP analysis we can write equation of channel matrix as

$$ {{{\mathbf H}}_{{\rm TMAP}}}\mathbf{=(}{{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{\mathbf{)}}^{{-1}}}{{{\mathbf R}}_{{nn}}^{-1}}{{{\mathbf Y}}_{{p}}}{{{\mathbf X}}_p^{\ne }} $$

(9)

where ${{{\mathbf X}}_{p}^{\ne }}$ is the regularized inverse matrix given as follows

$$ {{{\mathbf X}}_{p}^{\ne }}\mathbf{=(}{{{\mathbf X}}_{p}^{{\rm H}}}{{{\mathbf X}}_{p}} + {{\lambda }^{2}}\mathbf{I}{{\mathbf{)}}^{\mathbf{-1}}}{{{\mathbf X}}_{p}^{{\rm H}}}. $$

(10)

Now we can take SVD of ${\mathbf X}_p$ and write the following equations

$$ \begin{aligned} {\rm SVD(}{{{\mathbf X}}_{p}}) &= {{{\mathbf U}}_{{x}}}{{{\mathbf \Sigma }}_{{x}}}{{{\mathbf V}}_{{x}}^{{\rm H}}}, \\ {\mathbf H}_{\rm TMAP} &= ({{{\mathbf R}}_{nn}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{{nn}}^{{-1}}}{{({{{\mathbf U}}_{{x}}^{{\rm H}}}{{{\mathbf U}}_{x}}{{{\mathbf \Sigma }}_{{x}}^{{\rm H}}}{{{\mathbf \Sigma }}_{x}} {{{\mathbf V}}_{x}^{{\rm H}}}{{{\mathbf V}}_{x}} + {{\lambda }^{2}}\mathbf{I)}}^{-1}}({{{\mathbf U}}_{x}^{{\rm H}}}{{{\mathbf \Sigma }}_{x}^{{\rm H}}}{{{\mathbf V}}_{x}}){{{\mathbf Y}}_{p}} \\ &=({{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{{nn}}^{-1}}{{({{{\mathbf \Sigma }}_{x}^{2}}\mathbf{+}{{\lambda }^{2}}\mathbf{I)}}^{{-1}}}({{{\mathbf U}}_{x}^{\rm H}}{{{\mathbf \Sigma }}_{x}^{\rm H}}{{{\mathbf V}}_{{x}}}){{{\mathbf Y}}_{{p}}} \\ &= (({{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{{nn}}^{-1}}) \frac{{{{\mathbf \Sigma }}_{{x}}^{\rm H}}}{({{{\mathbf \Sigma }}_{x}^{2}} + {{\lambda }^{2}})}{{{\mathbf U}}_{x}^{\rm H}}{{{\mathbf Y}}_{p}}{{{\mathbf V}}_{x}} \\ &=(({{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{-1}}{{{\mathbf R}}_{nn}^{{-1}}})\frac{{{{\mathbf \Sigma }}_{{x}}^{2}}}{({{{\mathbf \Sigma }}_{x}^{2}} + {{\lambda }^{2}})}\frac{{{{\mathbf U}}_{x}^{\rm H}}{{{\mathbf Y}}_{p}}}{{{{\mathbf \Sigma }}_{x}}}{{{\mathbf V}}_{{x}}} \\ &=(({{{\mathbf R}}_{{nn}}^{-1}}+{{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{nn}^{-1}})\sum\limits_{i=1}^{n}{\frac{{{\sigma }_i^2}}{{{\sigma }_i^2}+{{\lambda }^2}}}\frac{{{u}_i^{\rm H}}{{{\mathbf Y}}_{{p}}}}{{{\sigma }_{i}}}{{v}_{i}}, \end{aligned} $$

(11)

where $\sigma_i$ are the singular values of matrix ${\mathbf \Sigma }_x$ , and $u_i$ and $v_i$ are values of ${\mathbf U}_x$ and ${\mathbf V}_x$ orthonormal matrices.

Using Tikhonov filter factors

$$ f_i=\frac{\sigma_i^2}{\sigma_i^2+\lambda^2}\cong \left\{ \begin{aligned} &1, & \sigma_i &\gg \lambda , \\ &\sigma_i/\lambda^2, & \sigma_i &\ll \lambda \end{aligned} \right . $$

(12)

we obtain

$$ {{{\mathbf H}}_{{\rm TMAP}}} = (({{{\mathbf R}}_{nn}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{{nn}}^{-1}})\sum\limits_{i=1}^{n}{{{f}_{i}}}\frac{{{u}_i^{\rm H}}{{{\mathbf Y}}_{p}}}{{{\sigma }_{i}}}{{v}_{i}}. $$

(13)

Now we can write

$$ {{{\mathbf Y}}_{{p}}}={\mathbf H}{{{\mathbf X}}_{{p}}}={\mathbf R}{{{\mathbf Q}}^{{\rm H}}}{{{\mathbf X}}_{{p}}} $$

then Q can be estimated as follows:

$$ \begin{aligned} {\hat{{{{\mathbf Q}}}}^{{\rm H}}}&={{{\mathbf R}}^{{\dagger }}}{{{\mathbf Y}}_{{p}}}{{{\mathbf X}}_p^{\ne }} ={{{\mathbf R}}^{{\dagger }}}{{{\mathbf H}}_{{\rm TMAP}}} \\ &= {{{\mathbf R}}^{{\dagger}}} (( {{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}} {{{\mathbf R}}_{{nn}}^{-1}})({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}} + {{\lambda }^{2}}{\mathbf I}{{)}^{{-1}}}{{{\mathbf X}}_{{p}}^{\rm H}}{{{\mathbf Y}}_{{p}}} \\ &= {{{\mathbf R}}^{{\dagger}}} (({{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{{nn}}^{-1}}){{{\mathbf Y}}_{{p}}}{{{\mathbf X}}_{p}^{\ne }} \\ &= {{{\mathbf R}}^{{\dagger}}} (({{{\mathbf R}}_{{nn}}^{-1}} + {{{\mathbf R}}_{{hh}}}{{)}^{{-1}}}{{{\mathbf R}}_{{nn}}^{-1}}) \sum\limits_{i=1}^{n}{\frac{{{\sigma }_{i}^2}}{{{\sigma }_{i}^2}+{{\lambda }^{2}}}}\frac{{{u}_i^{\rm H}}{{{\mathbf Y}}_{{p}}}}{{{\sigma }_{i}}}{{v}_{i}}, \end{aligned} $$

(14)

where $(\,)^{\dagger }$ denotes pseudo inverse (moore- penrose inverse)

$$ {\hat{\mathbf{H}}}={\mathbf R}{{{\hat{{\mathbf Q}}}}^{\rm H}}. $$

(15)

3.2.2. Tikhonov regularized MMSE algorithm

Using MMSE algorithm [7] in conjunction with Tikhonov’s method, the channel matrix can be calculated as follows:

$$ \begin{aligned} {{{\mathbf H}}_{{\rm TMMSE}}} &= {{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}} + \sigma _{n}^{2}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}})}^{{-1}}}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}} + {{\lambda }^{2}}{\mathbf I)}}^{{-1}}}{{{\mathbf X}}_{{p}}^{\rm H}}{{{\mathbf Y}}_{{p}}} \\ & = {{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}}+\sigma _{n}^{2}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}})}^{{-1}}}{{{\mathbf Y}}_{{p}}}{{{\mathbf X}}_{p}^{\ne }} \\ & = ({{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}} + \sigma _{n}^{2}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}})}^{{-1}}})\frac{{{{\mathbf \Sigma }}_{{x}}^2}}{({{{\mathbf \Sigma }}_{{x}}^{2}} + {{\lambda }^{2}})}\frac{{{{\mathbf U}}_{{x}}^{\rm H}}{{{\mathbf Y}}_{{p}}}}{{{{\mathbf \Sigma }}_{{x}}}}{{{\mathbf V}}_{{x}}} \\ & = ({{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}} + \sigma _{n}^{2}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}} )}^{{-1}}})\sum\limits_{i=1}^{n}{\frac{{{\sigma }_{i}^2}}{{{\sigma }_{i}^2}+{{\lambda }^{2}}}}\frac{{{u}_{i}^{\rm H}}{{{\mathbf Y}}_{{p}}}}{{{\sigma }_{i}}}{{v}_{i}}, \end{aligned} $$

(16)

$$ \begin{aligned} {\hat{{{{\mathbf Q}}}}^{{\rm H}}} &= {{{\mathbf R}}^{{\dagger }}}({{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}} + \sigma _{n}^{2}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}})}^{{-1}}})({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}} + {{\lambda }^{2}}{\mathbf I}{{)}^{{-1}}}{{{\mathbf X}}_{{p}}^{\rm H}}{{{\mathbf Y}}_{{p}}} \\ & = {{\mathbf{R}}^{{\dagger }}}({{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}}+\sigma _{n}^{2} {{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}})}^{{-1}}})\sum\limits_{i=1}^{n}{\frac{{{\sigma }_{i}^2}}{{{\sigma }_{i}^2}+{{\lambda }^{2}}}}\frac{{{u}_{i}^{\rm H}}{{{\mathbf Y}}_{{p}}}}{{{\sigma }_{i}}}{{v}_{i}}. \end{aligned} $$

(17)

Using the same analysis that was applied for MAP, we can write:

$$ {\hat{\mathbf{H }}} ={\mathbf R}{{{\hat{{\mathbf Q}}}}^{\rm H}}. $$

The choice of regularization parameter λ is one of important points that will be discussed in the next section.

3.2.3. Choosing regularization parameter λ while using discrepancy principle

We can write the solution norm in the form:

$$ {{\left\| {{{\mathbf H}}^{{\lambda }}}{{{\mathbf X}}_{{p}}} - {{{\mathbf Y}}_{{p}}} \right\|}_{{2}}}{=}{{\delta }_{e}}, $$

(18)

where $||e||_2\le\delta_e$ , ${{{\mathbf H}}^{{\lambda }}}$ is the estimated channel for particular regularization value λ and $\delta_e$ is the error of the norm, which minimizes the cost function. Estimation error can be found as

$$ {{\left\| {{{\mathbf H}}^{{\lambda }}}-{{{\mathbf H}}^{{\rm perfect}}} \right\|}_{{2}}}{=}{{\left\| e \right\|}_{2}}. $$

For the MAP method we can write the equation in the form

$$ \left\| {{{\mathbf H}}^{{\lambda }}}{{{\mathbf X}}_{p}}{-}{{{\mathbf Y}}_{{p}}} \right\|_{{2}}^{{2}} =(( {{{\mathbf R}}_{{nn}}^{-1}}+{{{\mathbf R}}_{{hh}}}{)^{-1}}{{{\mathbf R}}_{{nn}}^{-1}})\sum\limits_{i=1}^{n}{((1-{{f}_{i}}}){{u}_{i}^{\rm H}}{{{\mathbf Y}}_{{p}}})^2. $$

(19)

Next for the MMSE method, we can write the equation in the form

$$ \left\| {{{\mathbf H}}^{{\lambda }}}{{{\mathbf X}}_{p}} - {{{\mathbf Y}}_{{p}}} \right\|_{{2}}^{{2}}= ({{{\mathbf R}}_{{hh}}}{{({{{\mathbf R}}_{{hh}}} + \sigma _{n}^{2}{{({{{\mathbf X}}_{{p}}}{{{\mathbf X}}_{{p}}^{\rm H}})}^{{-1}}})}^{{-1}}})\sum\limits_{i=1}^{n}{((1-{{f}_{i}}}){{u}_{i}^{\rm H}}{{{\mathbf Y}}_{{p}}}{{)}^{2}}. $$

(20)

Now choosing λ in such way that

$$ {{\left\| {{{\mathbf H}}^{{\lambda }}}{{{\mathbf X}}_{{p}}}-{{{\mathbf Y}}_{{p}}} \right\|}_{{2}}}={{({{\left\| e \right\|}_{2}}-{{\alpha }^{2}}{{\rm trace}(\mathbf X}_{{p}}^{{{\ne}}}{{{\mathbf X}}_{{p}}}{))}}^{{1/2}}}, $$

(21)

where ${{{\mathbf H}}^{{\lambda }}}={\mathbf X}_{{p}}^{\ne }{{{\mathbf Y}}_{{p}}}$ , ${{\alpha }^{2}}=\operatorname{cov}({{{\mathbf Y}}_{{p}}})$ , and cov represents covariance of (Y_p).

Next, using the generalized cross validation (GCV), we select parameter λ in such a way that minimizes function $G(\lambda )$

$$ {G(\lambda )=}\frac{\left\| {{{\mathbf H}}^{{\lambda }}}{{{\mathbf X}}_{{p}}}-{{{\mathbf Y}}_{{p}}} \right\|_{{2}}^{{2}}}{{\rm trace}({\mathbf I- \mathbf X}_{{p}}^{\ne }{{{\mathbf X}}_{{p}}}{{)}^2}}. $$

(22)

4. Simulation Results

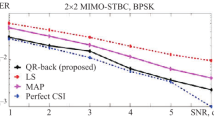
Extensive simulation has been conducted to demonstrate the bit error rate (BER) performance of proposed novel semi-blind channel estimation techniques.

Results are obtained for BPSK and 4-PSK data modulation schemes with 100 orthogonal pilot symbols using Alamouti coded 2 transmitter antennas and 6 or 8 receiver antennas cases by choosing and deriving values of regularization parameter λ equal to 0.5 and 0.1 using the discrepancy principle method.

Figures 2 and 3 demonstrate the performance of Tikhonov regularized MMSE channel estimation technique using 4-PSK modulation scheme for 6 and 8 receiver antennas for with and without noise cases. We can see that performance is improved by 1 dB for regularization factor equal to 0.5 compare to 1 for both cases and further performance is better by using 8 antennas in the same case. Figures 4 and 5 demonstrate the same analysis using BPSK modulation system, which depicts that performance is better compare to 4-PSK modulation scheme with overall analysis almost 2 to 3 dB improvements compare to the previous case.

Fig. 2.

Tikhonov regularized MMSE for 4-PSK with 6 receiver antennas.

Fig. 3.

Tikhonov regularized MMSE for 4-PSK with 8 receiver antennas.

Fig. 4.

Tikhonov regularized MMSE for BPSK with 6 receiver antennas.

Fig. 5.

Tikhonov regularized MMSE for BPSK with 8 receiver antennas.

Figures 6 to 9 demonstrate the performance analysis of Tikhonov regularized MAP channel estimation technique using 4-PSK and BPSK for 6 and 8 receiver antennas. We can further depict that better results can be observed with improvement of 1.5 dB for BPSK scheme and for 8 receiver antennas compare to 4-PSK scheme and with 6 receiver antennas for regularization factor equal to 0.1 compare to 0.5.

Fig. 6.

Tikhonov regularized MAP for 4-PSK with 6 receiver antennas.

Fig. 7.

Tikhonov regularized MAP for 4-PSK with 8 receiver antennas.

Fig. 8.

Tikhonov regularized MAP for BPSK with 6 receiver antennas.

Fig. 9.

Tikhonov regularized MAP for BPSK with 8 receiver antennas.

Here a Rayleigh fading MIMO channel has been considered for simulations with noise (practical case) and without noise criterion.

5. Conclusions

The results have shown that the chosen values of parameter λ equal to 0.1 and less yield the best results in terms of the BER vs SNR relationship. In case of increasing the number of receive antennas, the improvement in results was due to the MIMO advantage related to the spatial diversity.

The selection of the BPSK modulation scheme has given better results since the complexity involved in higher modulation schemes has been removed. However, with the demands that the evolving technology put on MIMO, the selection of higher modulation schemes will be a necessity for supporting the higher data rates with lesser interferences and robust link coverage.

The comparison with the perfect channel showed that the results for the simulations run without noise were closer to and at times the same as for the perfect channel case. However, in practical cases, the noise will be present no matter how good the environment conditions are. Hence, the simulations with noise should be considered for studying the schemes that can be proposed to obtain better channel estimation methods.

This paper proposes a novel semi-blind channel estimation scheme using Householder QR decomposition based blind estimation of matrix R and Tikhonov regularized based MMSE and MAP algorithms using pilot symbols for estimation of matrix Q will yield good results in channel estimation methods.