1 INTRODUCTION

Currently, the use of unmanned aerial vehicles (UAVs) on ships is given considerable attention. The sea fleet is interested in using UAVs with vertical take-off and landing capable of automatically performing take-off and landing on a limited area.

Due to the unique operational and technical features encountered by the sea fleet when using UAVs on civilian ships which are not adapted for landing aircraft, it is important to find a design solution by a ship’s developer to provide necessary take-off and landing facilities on board. However, the solution of this issue in most cases is associated with the need to significantly change the external design of the vessel (change the position of superstructures, navigation equipment, means of loading, etc.) in order to find the necessary areas.

This is not always acceptable to a ship’s designer due to possible significant changes in some of its operational and technical characteristics. Therefore, the solution to the problem of landing can be reduced to the need to find other ways with application of special tools (movable or immovable nets, ropes, etc.). When floating the device onto the water with a parachute or balloon, the device needs to be repaired due to corrosion that occurs in salt water, which is associated with significant costs. Landing of the device by a “dry” method allows avoiding this problem. In this regard, various methods of landing vehicles on deck of the ship are constantly worked out. Some of them are based on methods developed for landing UAVs: landing UAVs in a vertical net, using a wing parachute, and picking up with a rod mounted on a vertical pole on board of the ship [1–4].

Further research is aimed at creating the technology for designing a system for stabilizing angular position of the platform, designed to ensure the take-off and landing of an unmanned aerial vehicle from the deck of a ship in the high sea.

The success of landing on deck of a ship is complicated by a number of factors, namely, the limited area of the landing platform (deck), the movement of the landing point, uncontrolled movements caused by the ship’s motion, intense atmospheric phenomena due to changes in airflow on the ship. The most important factor that determines the complexity of landing onto a ship is the oscillating motions. The action of these factors causes not only a decrease in the accuracy of stabilization of the platform in the horizon plane in the conditions of accidental oscillation, but also the output of control actions at the boundary limits of the operating zone of the hexapod.

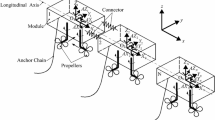
To compensate the impact of the motions, it is proposed to use Stewart platform (hexapod) as a take-off and landing table (Fig. 1) [5]. It consists of a movable platform and a base, which are mechanically connected by means of six identical actuators (or “legs”). Each leg acts as a linear actuator and contains two half-rods that are hinged to the base and platform.

Fig. 1.
figure 1

Example of using Stewart platform as a runway [5].

Full size image

The task of stabilizing the angular position of the hexapod platform is to provide small angles of its deviation in the horizon plane under conditions of nondeterministic external disturbances and factors, namely, in the conditions of the sea motions, with significant fluctuations in wind force and wind direction.

A review of the literature [6, 7] showed that the hexapod is a multidimensional object, the dynamics of which depends on its application.

As mentioned above, the task of the position control system of the hexapod platform is to practice the positions given in Cartesian coordinates and the orientation of the moving platform relative to the base with certain accuracy.

The main difficulty of control is that when adjusting in Cartesian coordinates it is necessary to generate forces in linear actuators—the legs of the hexapod [8]. The simplest and most popular approach to solve this problem is the implementation of separate control of the length of the hexapod legs, in which the control system is divided into six regulators on each leg. The signal of the required leg length is given to the input of each controller, which is calculated on the basis of solving the inverse problem of kinematics; the control is formed on the basis of the signal from the feedback sensor of the linear drive. The disadvantages of separate control are particularly acute in the positioning and orientation of a large object with large moments of inertia and a remote center of mass.

The disadvantages of existing hexapod position control systems reduce the efficiency of the use of marine aircraft in difficult hydrometeorological conditions and can lead to accidents.

Analysis of the results of modern research in the sphere of hexapod control systems [7, 9, 10] allowed us to conclude that overcoming the shortcomings of existing systems and achieving the highest accuracy of stabilization of the angular position of the platform can be done using multidimensional optimal stochastic stabilization systems. One of the effective methodologies for creating systems of this class is based on the use of models of the dynamics of the control object and the existing disturbances and the quadratic quality criterion [11].

Therefore, the research is relevant and has been aimed at creating a control system for the angular position of the platform for takeoff and landing of UAVs and helicopters from the surfaces of ships in the high sea, which will ensure the required accuracy of orientation in the conditions of oscillation.

2 PROBLEM STATEMENT

To identify the matrix of transfer functions of the system “hexapod + regulator,” as well as the matrix of the spectral density of disturbances acting at the centered stationary random oscillations of the platform, the experimental device at Fig. 2 was used [9].

Fig. 2.
figure 2

Experimental installation for identification of the system “hexapod + regulator”: 1—drives to change the length of the rods; 2—movable platform; 3—computer-integrated system; 4—controller; 5—fixed base.

Full size image

Consideration of its design showed that it is a mechatronic system, which is designed to change the position of the movable platform 2 relative to the fixed base 5. In addition to these elements, it also includes six drives 1, which can change the length of the rods 6 by signals from the controller 4. Orientation of platform 2 relative to base 5 can be determined using MEMS gyroscope mpu-6050 3 [12].

The drives are controlled by a computer-integrated control system 4 via Mesa 5i25 + 7i77 control interface.

As a result of structural identification [9, 13], it is determined that the system “hexapod + regulator” is a linear two-dimensional control object, the motion of which is described by a system of ordinary differential equations represented in Laplace transform under zero initial conditions:

$$Px = Mu + y,$$
(1)

where P is matrix of size 2 × 2, the elements of which are operator polynomials from the differentiation operator; x is a 2-dimensional vector of output signals of the control object; u is a 2-dimensional vector of control signals; M is a polynomial matrix of size 2 × 2, which determines the sensitivity of the object to changes in the control signal; and ψ is a disturbance vector of appropriate size, which belongs to the set of centered random processes. The disturbance dynamics is characterized by a known fractional rational matrix of spectral densities Sψψ.

The synthesis problem is formulated as follows.

According to the known matrices P, M, Sψψ, the structure and parameters of the control law of the additional controller W, the connection of which to the feedback circuit (Fig. 3) ensures the stability of a closed control system and delivers a minimum sum of weighted variances of control signal vectors u and output x (Ju and Jx, respectively), represented as the following functional

$$J = R{{J}_{x}} + C{{J}_{u}},$$
(2)
Fig. 3.
figure 3

The block diagram of a multidimensional stabilization system.

Full size image

where R is a positively defined diagonal weight matrix and C is an inseparably given diagonal weight matrix.

The analysis of the literature has shown that there are several methods of synthesis of stabilization systems, but they all require cumbersome calculations, which can negatively affect the accuracy of calculations. In connection with the above-mentioned fact, it was decided to use the method of synthesis of the optimal system of stochastic stabilization, which is described in [10, 11, 14], which fully takes into account the dynamics of the object, and reduces the number of calculations without reducing their accuracy.

3 DESCRIPTION OF THE ALGORITHM FOR AN OPTIMAL SYSTEM’S SYNTHESIS

In terms of [11], we denote the transfer function of a closed system from the disturbance input ψ to the output x through \(F_{x}^{\psi }\), and the transfer function of the system from the input ψ to the output u through \(F_{u}^{\psi }\).

As is known [11], matrices \(F_{x}^{\psi }\) and \(F_{u}^{\psi }\) are related by equation

$$PF_{x}^{\psi } - MF_{u}^{\psi } = {{E}_{n}},$$
(3)

at the same time, the structure and parameters of these matrices depend [10, 11] on the dynamics of the object and the controller as:

$$F_{u}^{\psi } = W{{(P - MW)}^{{ - 1}}}\,\,{\text{and}}\,\,F_{x}^{\psi } = {{(P - MW)}^{{ - 1}}}.$$
(4)

Then the quality functional in the frequency domain can be represented as:

$$J = \frac{1}{j}\int\limits_{ - j\omega }^{j\omega } {{\text{tr}}\left[ {\left( {F_{{x^{*}}}^{\psi }RF_{x}^{\psi }x + F_{{u^{*}}}^{\psi }{{u}_{*}}F_{{u^{*}}}^{\psi }} \right)S_{{\psi \psi }}^{/}} \right]ds} .$$
(5)

It is necessary to choose the structure and parameters of the matrix of transfer functions \(F_{u}^{\psi }\) to ensure the stability of a closed system “object-controller” and provide minimum to quality functional (2) based on the original data, which are listed above. The search for the algorithm to determine the structure and parameters of the matrix of transfer functions W occurs as a result of minimizing the functional on the class of stable and physically realizable varied matrices Φ using the Wiener–Kolmogorov procedure.

In accordance with this algorithm, the desired matrix of transfer functions can be found if \(F_{u}^{\psi }\) and \(F_{x}^{\psi }\) are known. Then, taking into account relations (4), it is possible to write:

$$W = F_{u}^{\psi }{{(F_{x}^{\psi })}^{{ - 1}}}.$$
(6)

When using the known algorithm for the synthesis of a stochastic stabilization system for a non-minimum phase object with full measurement of its initial reactions, the optimal physically feasible matrices \(F_{u}^{\psi }\) and \(F_{x}^{\psi }\) are determined by the formulas [10, 11]:

$$F_{x}^{\psi } = {{P}^{{ - 1}}}({{E}_{n}} + M\Phi ),$$
(7)
$$F_{u}^{\psi } = - {{\Gamma }^{{ - 1}}}({{T}_{0}} + {{T}_{ + }}){{D}^{{ - 1}}},$$
(8)

where Г is the result of factorization [15–17] of the expression

$${{\Gamma }_{*}}\Gamma = {{M}_{*}}P_{*}^{{ - 1}}R{{P}^{{ - 1}}}M + C,$$
(9)

D is the result of factorization [15–17] of the spectral density of disturbance

$$D{{D}_{*}} = S_{{\psi \psi }}^{/},$$
(10)

\({{T}_{0}} + {{T}_{ + }}\) is a fractional-rational matrix, which is a stable part of the result of separation [15–17] (splitting) of the matrix T.

$$T = \Gamma _{*}^{{ - 1}}{{M}_{*}}P_{*}^{{ - 1}}R{{P}^{{ - 1}}}D.$$
(11)

Thus, the synthesis technique according to the selected algorithm will contain the following steps:

(1) choose weight matrices R, C;

(2) according to the known matrices M, P, R, C, determine the sum (9) and factorize it;

(3) factorize the fractional-rational transposed matrix of spectral densities of generalized disturbances (10);

(4) on the basis of algorithm (11), form a fractional-rational matrix T and carry out its separation;

(5) find the optimal variable matrix Φ, reduce it by expressions (7), (8) to obtain matrices \(F_{x}^{\psi }\) and \(F_{u}^{\psi }\);

(6) calculate the transfer function of the optimal controller using Eq. (6);

(7) assess the quality of the stabilization system by the indicator (5).

4 THE RESULTS OF AN OPTIMAL SYSTEM’S SYNTHESIS

The initial data for the synthesis of the optimal structure of the system of stochastic stabilization of the angular position of the platform are the models of dynamics of the system “hexapod + regulator” as a control object, as well as the spectral density of the active disturbances, which were determined by actual tests using special techniques and algorithms [9, 11].

$$P = \left[ {\begin{array}{*{20}{c}} {{{s}^{2}} + 0.0042s + 4.5e - 05}&0 \\ 0&{{{s}^{2}} + 0.0065s + 4.225e - 05} \end{array}} \right];$$
$$M = \left[ {\begin{array}{*{20}{c}} {{{s}^{2}} + 0.0042s + 4.5e - 05}&{ - 0.23333(s - 0.03)(s - 0.007)} \\ {0.37477({{s}^{2}} - 0.02s + 0.0004)}&{0.6({{s}^{2}} + 0.0065s + 4.225e - 05)} \end{array}} \right];$$
$$S\psi \psi = \left[ {\begin{array}{*{20}{c}} {\frac{{0.21746({{s}^{2}} + 0.0042s + 4.5e - 05)({{s}^{2}} - 0.0042s + 4.5e - 05)}}{{(s + 0.6)(s - 0.6)(s + 2)(s - 2)}}} \\ {\frac{{0.053189({{s}^{2}} + 0.0065s + 4.225e - 05)({{s}^{2}} - 0.0042s + 4.5e - 05)}}{{(s + 0.6)(s - 0.6)(s + 2)\,(s - 2)}}} \end{array}} \right.$$
$$\left. {\begin{array}{*{20}{c}} {\frac{{0.53189({{s}^{2}} - 0.0065s + 4.225e - 05)({{s}^{2}} + 0.0042s + 4.5e - 05)}}{{(s + 0.6)\,(s - 0.6)\,(s + 2)\,(s - 2)}}} \\ {\frac{{0.078212({{s}^{2}} + 0.0065s + 4.225e - 05)({{s}^{2}} - 0.0065s + 4.225e - 05)}}{{(s + 0.6)(s - 0.6)(s + 2)(s - 2)}}} \end{array}} \right].$$

As a result of the first stage of the synthesis technique, the weight matrices R, C were determined. Their determination was carried out empirically taking into account the recommendations given in the literature [10, 11, 14]:

Weight matrices R, C are defined as

$$R = \left[ {\begin{array}{*{20}{c}} {0.2}&0 \\ 0&{0.2} \end{array}} \right],\,\,\,\,C = \left[ {\begin{array}{*{20}{c}} {0.1}&0 \\ 0&{0.1} \end{array}} \right].$$
(12)

According to this method of synthesis by the known matrices M, P, R, C the sum (9) and its factorization were determined:

$$\Gamma = \left[ {\begin{array}{*{20}{c}} {\frac{{1.068({{s}^{2}} + 0.008619s + 0.0001418)}}{{({{s}^{2}} + 0.0065s + 4.225e - 05)}}}&{\frac{{ - 0.0079291(s - 0.9358)(s + 0.003388)}}{{({{s}^{2}} + 0.0042s + 4.5e - 05)}}} \\ {\frac{{ - 0.01184(s + 0.003091)}}{{({{s}^{2}} + 0.0065s + 4.225e - 05)}}}&{\frac{{0.6438({{s}^{2}} + 0.009176s + 7.763e - 05)}}{{({{s}^{2}} + 0.0042s + 4.5e - 05)}}} \end{array}} \right].$$
(13)

The result of factorization of fractional-rational transposed matrix of spectral densities of generalized disturbances:

$$D = \left[ {\begin{array}{*{20}{c}} {\frac{{0.42({{s}^{2}} + 0.0042s + 4.5e - 05)}}{{(s + 0.6)(s + 2)}}}&0 \\ {\frac{{0.19({{s}^{2}} + 0.0042s + 4.5e - 05)}}{{(s + 0.6)(s + 2)}}}&{\frac{{0.28({{s}^{2}} + 0.0065s + 4.225e - 05)}}{{(s + 0.6)(s + 2)}}} \end{array}} \right].$$
(14)

The formation of the matrix T is carried out by substituting the necessary initial data for expression (11). Separation of the obtained result relative to a single circle is carried out using the stabsep function of the Matlab system (Matrix Laboratory) with selected C, R. The result of separation:

$${{T}_{0}} + {{T}_{ + }} = \left[ {\begin{array}{*{20}{c}} {\frac{{ - 0.25826(s + 0.1841)(s + 1.404)({{s}^{2}} - 0.004193s + 7.856e - 05)}}{{(s + 0.001923)(s + 0.07652)(s + 0.1546)(s + 1.449)(s + 2.394)({{s}^{2}} + 0.0042s + 4.5e - 05)}}} \\ {\frac{{0.48034(s + 0.06451)({{s}^{2}} + 0.02125s + 0.000116)}}{{(s + 0.0005919)(s + 0.07652)(s + 0.1546)(s + 1.449)({{s}^{2}} + 0.004166s + 4.225e - 05)}}} \end{array}} \right.$$
$$\left. {\begin{array}{*{20}{c}} {\frac{{ - 0.64579(s + 0.1583)(s + 1.445)({{s}^{2}} + 0.007647s + 0.0001286)}}{{(s + 0.001923)(s + 0.07652)(s + 0.1546)(s + 1.449)(s + 2.394)({{s}^{2}} + 0.0065s + 4.225e - 05)}}} \\ {\frac{{0.11557(s + 2.409)({{s}^{2}} + 0.1007s + 0.006714)}}{{(s + 0.07652)(s + 0.1546)(s + 1.449)(s + 2.394)({{s}^{2}} + 0.0065s + 4.225e - 05)}}} \end{array}} \right].$$
(15)

Then by expression (7) the transfer function \(F_{u}^{\psi }\) is obtained. After reduction by the method [10, 11, 14] \(F_{u}^{\psi }\) can be represented as

$$F_{u}^{\psi } = \left[ {\begin{array}{*{20}{c}} {\frac{{ - 0.6751(s + 0.0007954)(s + 0.2145)(s + 1.361)({{s}^{2}} + 0.0065s + 4.225e - 05)}}{{(s + 1.449)(s + 2.394)(s + 0.1546)(s + 0.07655)(s + 0.001916)(s + 0.000532)}}} \\ {\frac{{2.1317(s + 0.002075)({{s}^{{}}} + 0.07285)(s + 2.393)({{s}^{2}} + 0.0042s + 4.9e - 05)}}{{(s + 1.449)(s + 2.394)(s + 0.1546)(s + 0.07655)(s + 0.001916)(s + 0.000532)}}} \end{array}} \right.$$
$$\left. {\begin{array}{*{20}{c}} {\frac{{ - 2.1317(s + 0.1507)(s + 1.457){\text{ }}({{s}^{2}} + 0.0065s + 4.225e - 005){\text{ }}}}{{(s + 1.449){\text{ }}(s + 2.394){\text{ }}(s + 0.1546){\text{ }}(s + 0.07655){\text{ }}(s + 0.001916){\text{ }}}}} \\ {\frac{{ - 0.6751{\text{ }}(s + 0.001189)(s + 0.09763)(s + 2.401)({{s}^{2}} + 0.0042s + 4.9e - 05)}}{{(s + 1.449){\text{ }}(s + 2.394){\text{ }}(s + 0.1546){\text{ }}(s + 0.07655){\text{ }}(s + 0.001916){\text{ }}(s + 0.000532)}}} \end{array}} \right].$$
(16)

Using expression (8), the transfer function \(F_{x}^{\psi }\) is calculated in this form

$$F_{x}^{\psi } = \left[ {\begin{array}{*{20}{c}} {\frac{{s(s + 2)(s + 0.1038)({{s}^{2}} + 0.7981s + 0.209)}}{{(s + 2.394)(s + 1.449)(s + 0.1546)(s + 0.07655)(s + 0.000532)}}} \\ {\frac{{1.026s(s - 0.004244)(s + 2.633)({{s}^{2}} + 0.06915s + 0.001345)}}{{(s + 2.394)(s + 1.449)(s + 0.1546)(s + 0.07655)(s + 0.001916)(s + 0.000532)}}} \end{array}} \right.$$
$$\left. {\begin{array}{*{20}{c}} {\frac{{ - 1.9742s(s + 0.1611)(s + 1.376)({{s}^{2}} + 0.0105s + 3.237e - 05)}}{{(s + 2.394)(s + 1.449)(s + 0.1546)(s + 0.07655)(s + 0.001916)(s + 0.000532)}}} \\ {\frac{{s(s + 0.1107)(s + 1.952)({{s}^{2}} + 0.8087s + 0.2088)}}{{(s + 2.394)(s + 1.449)(s + 0.1546)(s + 0.07655)(s + 0.001916)}}} \end{array}} \right].$$
(17)

Figure 4 shows the frequency characteristics of the optimal system.

Fig. 4.
figure 4

Frequency characteristics of the optimal system.

Full size image

According to the defined transfer functions \(F_{x}^{\psi }\) and \(F_{u}^{\psi }\) on the basis of (6) the matrix of transfer functions of the optimal controller is calculated, which after reduction has the form

$$W = \left[ {\begin{array}{*{20}{c}} {\frac{{0.6751(s - 2.769)(s - 0.09909)({{s}^{2}} + 0.0065s + 4.225e - 05)}}{{s({{s}^{2}} + 0.1112s + 0.01561)({{s}^{2}} + 1.589s + 3.063)}}} \\ {\frac{{ - 2.1317(s + 1.453)(s + 0.1355)({{s}^{2}} + 0.0042s + 4.9e - 05)}}{{s({{s}^{2}} + 0.1112s + 0.01561)({{s}^{2}} + 1.589s + 3.063)}}} \end{array}} \right.$$
$$\left. {\begin{array}{*{20}{c}} {\frac{{2.1317(s + 0.3286)(s + 0.7326)({{s}^{2}} + 0.0065s + 4.225e - 05)}}{{s({{s}^{2}} + 0.1112s + 0.01561)({{s}^{2}} + 1.589s + 3.063)}}} \\ {\frac{{0.6751(s - 4.867)(s - 0.03887)({{s}^{2}} + 0.0042s + 4.9e - 05)}}{{s({{s}^{2}} + 0.1112s + 0.01561)({{s}^{2}} + 1.589s + 3.063)}}} \end{array}} \right].$$
(18)

In Fig. 5 the frequency characteristics of the optimal controller are shown.

Fig. 5.
figure 5

Frequency characteristics of the controller.

Full size image

The regulator with a matrix of transfer functions W provides stability of the closed stabilization system.

The values of the quality indicator and its components are determined by expression (5):

$$\begin{gathered} J = 0.3132; \\ {{J}_{x}} = \left[ {\begin{array}{*{20}{c}} {0.1904}&0 \\ 0&{0.0939} \end{array}} \right];\,\,\,\,{{J}_{u}} = \left[ {\begin{array}{*{20}{c}} {0.0196}&0 \\ 0&{0.0083} \end{array}} \right]. \\ \end{gathered} $$

5 DISCUSSION

Thus, the structure and parameters of the control law of the additional controller which to provide stability of a closed control system and provides a minimum of the sum of weight variances of the components of the control signal vectors \({{J}_{u}} = \left[ {\begin{array}{*{20}{c}} {0.0196}&0 \\ 0&{0.0083} \end{array}} \right]\), variances at the angles of the trim 0.1904 and the list 0.0939 of the output signal and the value of the quality indicator J = 0.3132.

This allowed providing small angles of deflection of Stewart platform (hexapod) in the horizon plane under the conditions of the sea motions, with significant fluctuations in wind force and direction to ensure the take-off and landing of unmanned aerial vehicles from deck of the ship in the high sea.

6 CONCLUSIONS

When developing the state space method, R. Kalman repeatedly noted that he had developed an approach designed for optimal synthesis of control systems for non-stationary objects, which operate under the action of random useful signals and interference in the form of white noise.

N. Wiener’s frequency synthesis method is designed for optimal synthesis of control systems with stationary objects that operate under the influence of random useful signals and interference in the form of colored noise. As V. Kuchera proved, in the case of solving Wiener’s problems, the action of the state space method requires the expansion of the order of the control object and the development of the observer and can cause the so-called curse of dimension.

Consequently, under the conditions of action of useful signals and noises, which belong to stationary color random processes, it is advisable to use frequency methods.