1 INTRODUCTION

Concrete and mortar are some most widely used construction materials for numerous civil engineering applications subjected to impact load, accidental load, and blast/explosion load, mostly for critical infrastructure protection all over the world. Critical infrastructures are defined as the physical structures essential for a society’s functioning and national security. These infrastructures included energy infrastructures (power generation plants, fuel storage facilities), transport infrastructures (airport, seaports, railways, bridges), water infrastructures (reservoirs, dams), healthcare infrastructures (hospitals, medical laboratories, clinics, medicine manufacturing facilities), Emergency services infrastructures (police departments, fire stations, disaster response agencies) and government infrastructures (government buildings, military buildings, nuclear power plants). The functionality of these structures significantly affects the critical situation during an emergency. Vehicle impact, missile impact, projectile or aircraft impact, protective layers of nuclear power plants, runways for repeat loading, etc., are responsible for high strain rate loading on the infrastructures, especially concrete structures. Concrete subjected to high strain rate dynamic loading has drastically different response characteristics and damage mechanisms from those static or low strain rate loading. Hence, dynamic characterization is essential because the behavior of materials can significantly differ under dynamic loading as compared to static loading. The dynamic mechanical response of a material is more complex and exhibits different characteristics, such as strain rate sensitivity, rate-dependent plasticity, and energy dissipation. Understanding these dynamic mechanical properties is crucial in various engineering applications, such as designing structures, safety systems, impact-resistant materials, and optimizing performance in high-speed applications.

Numerous experimental techniques have been designed and developed to characterize dynamic material properties. Based on the investigation requirement and strain rate sensitivity, the experimental techniques varied from laboratory to laboratory. Drop weight hammer test (10–2 to 10 s–1), Ballistic impact method (101 to 103 s–1), split hopkinson pressure bar technique (101 to 104 s–1), expanding ring technique (10–3 to 103 s–1), the cam plastometer (102 to 104 s–1), taylor impact test (104 to 106 s–1) and plate impact test (104 to 106 s–1) are important techniques used for dynamic loading. When the strain rate is more than 1 s–1 is defined as dynamic, although, Lindholm, U. S. (1971) [1] suggested strain rate 10 s–1 as the lower limit. The split hopkinson pressure bar technique [2] is a popular experimental technique to investigate the dynamic behaviour of materials subjected the high strain rates (10–104 s–1). SHPB technique improved daily for validating and accuracy of resulting data used for dynamic material characterization [3, 4]. Studies have been performed experimentally and numerically on cement-based brittle materials, i.e., mortar, normal concrete, high-strength concrete, high-performance concrete, and ultra-high-performance concrete, to investigate the strain rate sensitivity and size effect dependency of dynamic material properties. It isn’t easy to maintain the experimental conditions during the high loading rate when the specimen has a larger dimension. Additionally, the dynamic behaviour cannot be predicted during the explosive loads. To predict the actual material properties and failure mechanism, numerical simulation is the best alternative option for various dynamic loading conditions. Various numerical tools based on finite element methods like ABAQUS/Explicit code, LS-DYNA, ANSYS/Explicit Dynamic, AUTODYN, etc., are available for simulation by numerical modeling under these circumstances. These numerical tools are based on the empirical equations proposed by the researchers based on experimental investigation. Concrete and concrete-like materials showed strain rate sensitivity during experimentation [5–6]. The various material models like Holmquist Johnson Cook (HJC) [7], riedel hiermaier thoma (RHT) [8, 9], concrete damage plasticity (CDP) [10], drunker prager model [11], and Kamran and Iqbal (K and I) [12] has been incorporated in these finite element-based tools to investigate the dynamic response of cement-based brittle materials subjected to high strain rate and large strain during ballistic and impact. The strain rate effect has been considered in terms of the dynamic increase factor (DIF) for the dynamic compressive and tensile behaviour, which is defined as the ratio of dynamic strength to the quasi-static strength as a function of strain rate. These DIF equations are either based on logarithm trends or power law variation obtained from the best fitting curves on the results data obtained experimentally. Numerical simulation and experimentation performed by using SHPB to predict the response of concrete under high strain rate show complex deformation and formulate a compressive strength constitutive model based on the strain rate effect and the damage effect [13]. Many researchers performed numerical and experimental studies to predict the response of plain concrete, mortar, and high-strength concrete under a high strain rate and evaluate the mechanical response in terms of the compressive strength, Dynamic Increase Factor (DIF), energy absorption, and fragmentation with consideration of strain rate effect, inertia effect, and geometry effect [14–16]. Numerical investigation performed on heterogeneous materials like concrete, mortar, and composite material by using the material model like the Drucker-Prager model in ABAQUS and Concrete Damage model in LS-DYNA with the help of SHPB predicts that the DIF of concrete is not only enhanced by material effects but also by structural effects (Interface friction, material inertia, specimen geometry) [17]. Most researchers described the development and validation of empirical equations with DIFs as a function of strain rate-sensitivity only, but DIFs are also affected by structural effects [18–20]. However, there are many DIF equations proposed to predict the dynamic behaviour of materials, but the equation obtained is based on the regression analysis for the brittle materials. The trends of these equations varied from material to material, from linear to non-linear. Despite significant progresses in the proposal of DIF models for strength enhancement, proper design codes and guidelines are still lacking. Numerous institutions and international committees, such as the American Concrete Institute (ACI349-13) [21], United States Integrated Facility Standards (UFC 3-340-02) [22], and Euro-International Committee for Concrete and International Federation for Pre-stressing (CEB–FIP) [19, 23], have announced numerous DIF prediction models for concrete-like brittle materials since the late 1980s. However, these models do not effectively address the need for comprehensive design codes and guidelines regarding strength improvement. In the field of dynamic material characterization, the experimentally and numerically proposed dynamic increase factor models are commonly used to describe the behavior of brittle materials under compression and tension loading conditions. These models aim to capture the dynamic behaviour, as well as the ultimate dynamic material strength. The objective of this study is to provide a comprehensive explanation of the commonly used DIF models in numerical investigations, specifically about the generation of a specific equation for a particular material. This research focuses on enhancing our understanding of the empirical DIF equation proposed for brittle materials based on cement, through a study of the numerical and experimental analyses conducted under compression and tension loading conditions.

2 SPLIT HOPKINSON PRESSURE BAR (SHPB) TEST APPARATUS

2.1 SHPB Setup

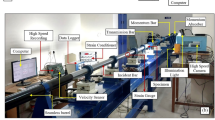
SHPB is the most widely used experimental technique for the dynamic material characterization of concrete-like materials under compression at high strain rates in the range of 10 to 10000 1/s and for tension at a high strain rate in the range of 1 to 100 1/s. John Hopkinson was the first person to conduct dynamic load testing in 1872 on materials by dropping the weight on the wire to reveal the challenging task of measuring the stress wave in the wire [23]. Kolsky, in 1949, extended the concept of the Hopkinson pressure bar with a new technique to measure the stress-strain response of the material under dynamic loading [24]. In 1964, Lindholm merged all previous improvements and presented the most updated version of SHPB [1]. In 2009, Song replicated the Kolsky bar apparatus for material characterization at high strain rates, incorporating significant advancements and modifications suggested in the 20th century to improve its mechanical testing capabilities [2, 3, 26]. The Kolsky compression bar apparatus comprises three main elements: a loading device, bar components, and a data acquisition and recording system, as illustrated in Fig. 1. The specimen is sandwiched between the incident bar and transmission bar. The striker bar is launched by the gas gun at a known incident velocity in order to generate the trapezoidal compressive stress waves in the incident bar shown in Fig. 1. This compressive stress wave, referred to as the incident wave and propagates in the incident bar towards the specimen. At the interface of the incident bar and specimen, some portion of the compressive wave is reflected in the incident bar due to a difference in the mechanical impedance of the bar and testing specimen, mentioned as a reflected wave with tensile nature, and the remaining portion of the compressive stress wave is transmitted through the specimen into the transmission bar, referred as transmission stress waves shown in Fig. 2a. The impedance of a material is defined as the property of the material that resists deformation under the application of force. Both incident and reflected stress waves are recorded by the strain gauge mounted at the center of the incident bar, and the transmitted wave is measured by the strain gauge mounted at the center of the transmission bar with the help of DAQS. The strain pulse propagation shows in Fig. 2b. These recorded pulses are used to analyze the mechanical properties of the tested specimen.

Fig. 1.
figure 1

A schematic Klosky compression bar apparatus.

Full size image
Fig. 2.
figure 2

(a) Wave propagation in the bars. (b) Schematic diagram of strain wave in the bars.

Full size image

Split–Hopkinson Pressure Bar (SHPB) testing is the most widely used experimental technique for determining stress, strain, and strain rate behavior in materials under high-rate of loading conditions. To ensure valid, precise, and consistent results of the materials, specific criteria must be followed during the SHPB testing process. Here are some of the essential criteria are as follows:

1. The elastic stress wave propagation within Kolsky bars must be the 1-D elastic wave.

2. The incident, transmission, and striker bars must remain elastic, and centric during the entire testing.

3. Deformation of the specimen should be uniform during testing.

4. The end friction at the interfaces of the testing specimen and pressure bars should be negligible during the testing.

5. The specimen must attain the equilibrium conditions during failure for valid results.

2.2 Working Principle of SHPB Setup

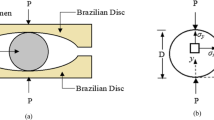
SHPB working principle is based on the concept of 1-D elastic stress wave propagation theory in the bar. The strain associated with the incident stress wave is referred to as εI, the strain associated with the reflected stress wave as εR in the incident bar, and the strain associated with the transmitted stress wave are referred to as εT respectively. The amplitude of the stress wave depends upon the striker impact incident velocity, while the loading duration of this stress wave depends upon the length of the striker bar. The incident, transmission, and striker bars must remain linear elastic, and centric during the test, and friction acting at the interfaces of the testing specimens and bars should be insignificant so that no end friction confinement will exist. The working principle for dynamic compression and dynamic splitting tensile test is the same, only the difference in the placement of the specimen. The specimen was placed along the length/thickness for the dynamic compression test see Fig. 3a; for the splitting tensile test, the specimen was placed along the diameter see Fig. 3b.

Fig. 3.
figure 3

(a) Concrete specimen under dynamic compression test. Fig. 3. (b) Concrete specimen under dynamic Split Tensile Test.

Full size image

2.3 Dynamic Compression Test

Based on the 1-D elastic stress wave propagation theory in the bar [4] and stress equilibrium in the specimen during the testing [5], stress-time histories, strain-time histories, and strain rate-time histories in the specimen for compression were determined by using the following equation

$${{{{\sigma }}}_{{\text{c}}}}\left( {\text{t}} \right) = {{{\text{E}}}_{{\text{b}}}}\left( {\frac{{2{{{\text{A}}}_{{\text{b}}}}}}{{{{{\text{A}}}_{{\text{s}}}}}}} \right)({{\varepsilon }_{{\text{I}}}} + {{\varepsilon }_{{\text{R}}}} + {{\varepsilon }_{{\text{T}}}}),$$
(2.1)
$${{\varepsilon }_{{\text{c}}}}\left( {\text{t}} \right) = \frac{{{{{\text{C}}}_{{\text{o}}}}}}{{{{{\text{L}}}_{{\text{o}}}}}}\mathop \smallint \limits_0^{\text{t}} ({{\varepsilon }_{{\text{I}}}} - {{\varepsilon }_{{\text{R}}}} - {{\varepsilon }_{{\text{T}}}}){\text{dt,}}$$
(2.2)
$${{\dot {\varepsilon }}_{c}}\left( {\text{t}} \right) = \frac{{{{{\text{C}}}_{{\text{o}}}}}}{{{{{\text{L}}}_{{\text{o}}}}}}({{\varepsilon }_{{\text{I}}}} - {{\varepsilon }_{{\text{R}}}} - {{\varepsilon }_{{\text{T}}}}).$$
(2.3)

The specimen is assumed to be stress equilibrated and apply the boundary conditions as shown in Fig. 4.

Fig. 4.
figure 4

Free body diagram of the specimen in compression.

Full size image

Bars should be linear elastic in nature and hence obey Hook’s law \(\sigma = E\varepsilon \), the stress on the interfaces of specimen and bars are as below

$${{{{\sigma }}}_{1}} = \frac{{{{{\text{F}}}_{1}}}}{{{{{\text{A}}}_{{\text{I}}}}}}\quad {\text{and}}\quad {{{{\sigma }}}_{2}} = \frac{{{{{\text{F}}}_{2}}}}{{{{{\text{A}}}_{{\text{T}}}}}},$$
(2.4)

where \({{F}_{1}}~{\text{is the}}\) force on the incident bar-specimen interface, and \({{F}_{2}}\) is the forces at the specimen-transmitted bar interface represented in terms of measured strains as

$${{{\text{F}}}_{1}} = {{{\text{A}}}_{{\text{I}}}}{{{\text{E}}}_{{\text{I}}}}({{\varepsilon }_{{\text{I}}}} + {{\varepsilon }_{{\text{R}}}})\quad {\text{and}}\quad {{{\text{F}}}_{2}} = {{{\text{A}}}_{{\text{T}}}}{{{\text{E}}}_{{\text{T}}}}({{\varepsilon }_{{\text{T}}}}),$$
(2.5)

where \({{A}_{I}}\) and \({{A}_{T}}\) are the cross-sectional areas of incident and transmission bars, respectively. \({{E}_{I}}\) and \({{E}_{T}}\) are the elastic moduli of incident and transmitter bars, respectively. If the equilibrium condition achieved in the specimen during the testing and the cross-sectional area of the incident and transmission bar are equal, then

$${{F}_{1}} = {{F}_{2}} \Rightarrow {{\varepsilon }_{{\text{I}}}} + {{\varepsilon }_{{\text{R}}}} = {{\varepsilon }_{{\text{T}}}}.$$
(2.6)

Hence the stress, strain, and strain time histories in the specimen were determined by using the following equations

$${{\varepsilon }_{{\text{c}}}} = - \frac{{2{{{\text{C}}}_{{\text{o}}}}}}{{{{{\text{L}}}_{{\text{o}}}}}}\mathop \smallint \limits_0^{\text{t}} {{\varepsilon }_{{\text{R}}}}{\text{dt,}}$$
(2.7)
$${{\dot {\varepsilon }}_{c}} = - \frac{{2{{{\text{C}}}_{{\text{o}}}}}}{{{{{\text{L}}}_{{\text{o}}}}}}{{\varepsilon }_{{\text{R}}}},$$
(2.8)
$${{{{\sigma }}}_{{\text{c}}}} = {{{\text{E}}}_{{\text{b}}}}\left( {\frac{{{{{\text{A}}}_{{\text{b}}}}}}{{{{{\text{A}}}_{{\text{s}}}}}}} \right){{\varepsilon }_{{\text{T}}}},$$
(2.9)

where \({{\sigma }_{d}}\), \({{\varepsilon }_{c}}\), and \({{\dot {\varepsilon }}_{c}}\) are the stress-time history, strain-time history, and strain rate-time history in the tested specimen, respectively. \({{A}_{b}}\) is the bar cross-sectional area, and \({{A}_{s}}\) is the cylindrical specimen cross-sectional area. \({{E}_{b}}\) is the modulus of elasticity of the pressure bar, \({{C}_{o}}\) is the wave velocity in the pressure bar. \({{L}_{o}}\) is the initial length of the specimen. During the uniform distribution of compressive stress wave across the specimen, the stress in the specimen is directly proportional to the transmitted wave strain, while the strain and strain rate in the specimen is directly proportional to the reflected wave strain. A dynamic stress-strain curve of the specimen is generated by using these stress and strain time histories for a given strain rate.

2.4 Dynamic Splitting Tensile Test

Various experimental techniques have been used to determine the tensile strength of concrete, including the direct tension test, three-point bending test, and splitting tensile test (Brazilian Disc Test). The Brazilian disc test is the most suitable method for determining the tensile strength and is extended to determine the dynamic tensile strength using the SHPB test apparatus. If the dynamic stress equilibrium condition is achieved in the specimen, the dynamic splitting tensile strength of concrete is proportional to the peak value of the transmitted wave obtained by using the following expression

$${{{{\sigma }}}_{{\text{t}}}} = \left( {\frac{{{{{\text{E}}}_{{\text{b}}}}{\text{D}}_{{\text{b}}}^{2}}}{{2{{{\text{L}}}_{{\text{o}}}}{{{\text{d}}}_{{\text{s}}}}}}} \right){{\varepsilon }_{{\text{T}}}},$$
(2.10)

where \({{\sigma }_{{td}}}\) is the dynamic splitting tensile strength, \({{D}_{b}}\) is the diameter of bars, \({{d}_{s}}\) is the diameter of the concrete specimen. The strain rate is not constant in the specimen during the loading hence the average strain rate used by Tedesco and Ross [27] and the loading rate in the dynamic tensile test adopted as

$${{\dot {\varepsilon }}_{t}} = - \frac{{{{{{\sigma }}}_{{\text{t}}}}}}{{{{{\text{E}}}_{{\text{s}}}}{\text{T}}}},$$
(2.11)
$${{{{\dot {\sigma }}}}_{t}} = - \frac{{{{{{\sigma }}}_{{\text{t}}}}}}{{\text{T}}},$$
(2.12)

where \({{\dot {\varepsilon }}_{t}}\) is the tensile strain rate, \({{E}_{s}}\) is Young’s modulus of elasticity of the specimen, \({{{{\dot {\sigma }}}}_{t}}\) is the loading rate in the specimen, and T is defined as the time interval between the start of the transmitted wave and maximum value of transmitted wave. Based on the experimental data obtained, it has been shown that the elastic modulus of concrete is not strain rate sensitive as compared to the tensile strength sensitivity to the strain rate; therefore, the quasi-static elastic modulus used in the Eq. (4) [28, 29].

3 STRAIN RATE DEPENDENCY OF CONCRETE STRENGTH

3.1 Strain Rate Dependency of DIF under Compression

Researchers conducted comprehensive experimental studies on concrete and concrete-like brittle materials tested in the range of high strain rate 101–104 s–1 by using the SHPB technique. Researchers have proposed several empirical equations to predict the dynamic mechanical response of materials in terms of DIF (Dynamic Increase Factor) relative to the high strain rate. These proposed empirical equations are typically derived from logarithmic trends or power law variations. The empirical equation used for the DIF is also implemented in the various numerical material models based on the finite element method. There are some other numerical methods also used to solve differential equations apart from the Finite Element Method (FEM), such as Finite Difference Method (FDM), Boundary Element Method (BEM), Finite Volume Method (FVM), and meshless methods. The most common empirical equation proposed for the concrete-like brittle material is given in the CEB - FIP model code 1993 [19]. This model code suggested the important guidelines used in the scientific and technical development of the proposed material models used for the safety, security, analysis, and design of important concrete structures. The DIF equation gives the dependency for two-stage strain rates of concrete by the following expression

$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}}{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1.026{{\alpha }_{s}}}}}\quad {\text{for}}\quad \dot {\varepsilon }~~ \leqslant 30{\text{ }}{{{\text{s}}}^{{ - 1}}},~$$
(3.1)
$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}} = {{\gamma }_{s}}{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1/3}}}\quad {\text{ for}}\quad \dot {\varepsilon }~~ > 30\,\,{{{\text{s}}}^{{ - 1}}},~$$
(3.2)

where \({{f}_{{cd}}}\) is the dynamic compressive strength and \({{f}_{{cs}}}\) is the quasi-static compressive strength of the brittle materials. \(\dot {\varepsilon }\) is the strain rate during dynamic loading in s–1, \({{\alpha }_{s}}\) = 1/(5 + 9(\({{f}_{{cs}}}\)/\({{f}_{{co}}}\))); where \({{f}_{{co}}}\) = 10 MPa, \({{\gamma }_{s}}\) = \({{10}^{{(6.156{{\alpha }_{s}} + 2.0)}}}\) and \({{\dot {\varepsilon }}_{S}}\) = 30 × 10–6 s–1 for static loading. The strain rate 30 s–1 was found to be a transition point for the two-stage behavior of concrete for DIF. Beyond this transition strain rate value, the DIF is highly sensitive to strain rate and increases exponentially, describing the high compressive strength for dynamic loading.

Except for the CEB FIP Model code, some other experimental and numerical-based DIF models have been proposed following the power law distribution trends. The constitutive equation of the material model used to describe the DIF model of the compressive strength of concrete as a function of strain rate proposed by the Fujikake et al. [30] is given by the following expression

$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}} = {{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{0.006{{{\left[ {{\text{log}}\left( {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right)} \right]}}^{{1.05}}}}}},$$
(3.3)

where \({{\dot {\varepsilon }}_{S}}\) is the quasi-static strain rate, and \(\dot {\varepsilon }\) is the high strain rate under static and dynamic loading conditions, respectively.

Another numerical model for DIF is also proposed, utilizing data obtained from earlier studies on concrete under high-rate loading conditions by Hartmann et al. [31]. This model incorporates a power law relationship that demonstrates an increase in DIF with an increase in the strain rate and is expressed by the following equation

$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}}0.05{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{o}}}}} \right]}^{{0.13}}} + 0.9,$$
(3.4)

where \({{\dot {\varepsilon }}_{o}} = 1~\) s–1 is defined as the transition strain rate.

A series of dynamic compression tests were conducted on the SHPB setup by Tedesco and Ross [33] to investigate the effect of different concrete strengths, moisture content, and strain rate on the dynamic mechanical behaviour of concrete. Statistical analysis yielded strain-rate-dependent constitutive equations, applied to modify nonlinear concrete material models. Two-stage transition behaviors were observed at a strain rate of around 63.1 s–1. A higher increment in compressive strength is observed beyond this transition strain rate. The DIF increases rapidly beyond this transition point, expressed by the following equation

$${\text{DIF}} = 0.00965{\text{log}}(\dot {\varepsilon }) + 1.058 \geqslant 1.0\quad {\text{for}}\quad \dot {\varepsilon } \leqslant 63.1{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.5)
$${\text{DIF}} = 0.758{\text{log}}(\dot {\varepsilon }) + 0.289 \leqslant 2.5\quad {\text{for}}\quad \dot {\varepsilon }~~ > 63.1{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.6)

The transition point is defined as the point below which the DIF is less sensitive, while above this point, the DIF is highly sensible to strain rate. The transition strain rate from low to high strain rate dependency is slightly higher than given by the CEB-FIP material model code [29].

The DIF equation proposed by CEB-FIP 2010 [23] was reviewed by Guo et al. [33] and concluded that the equation needed to be more suitable for investigating the dynamic response of high-strength concrete tested through high-speed SBPB impact test of concrete with different quasi-static compressive strength. Based on the resulting output, an equation has been proposed as follows

$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}} = {{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{0.014}}}\quad {\text{for }}\quad \dot {\varepsilon } \leqslant {{\dot {\varepsilon }}_{{TR}}}\,\,{{{\text{s}}}^{{ - 1}}},$$
(3.7)
$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}} = A{{\log }_{{10}}}{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{1}} + B\quad {\text{for }}\quad \dot {\varepsilon } \geqslant {{\dot {\varepsilon }}_{{TR}}}\,\,{{{\text{s}}}^{{ - 1}}},$$
(3.8)

where \({{\dot {\varepsilon }}_{{TR}}}\) is defined as the transition strain rate. A and B are the material constants obtained through experimental study.

Ngo et al. [34] performed blast tests on the ultra-high-strength concrete panel to investigate the explosive resistance. Based on the resulting output, it has been summarized that there is a logarithmic relation has been established between DIF and high strain rate with the following formula

$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}} = {{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1.026\alpha }}}\quad {\text{for }}\quad \dot {\varepsilon } \leqslant {{\dot {\varepsilon }}_{c}}\,\,{{{\text{s}}}^{{ - 1}}},$$
(3.9)
$${\text{DIF}} = \frac{{{{f}_{{cd}}}}}{{{{f}_{{cs}}}}} = {{A}_{1}}\ln (\dot {\varepsilon }) - {{A}_{2}}\quad {\text{for }}\quad \dot {\varepsilon } > {{\dot {\varepsilon }}_{c}}\,\,{{{\text{s}}}^{{ - 1}}},$$
(3.10)

where, \({{\dot {\varepsilon }}_{s}}\) = 3 × 10–5 s–1 quasi-static strain rate, α = 1/(20 + fc/2) is the strain rate exponent; \({{\dot {\varepsilon }}_{c}}\) = 0.0022\(f_{{cs}}^{2}\) – 0.1989\({{f}_{{cs}}}\) + 46.137 is the critical strain rate, \({{A}_{1}}\) = –0.0044\({{f}_{{cs}}}\) + 0.9866, and \({{A}_{2}}\) = –0.0128\({{f}_{{cs}}}\) + 2.1396 are the material parameters.

Based on the experimental investigation of concrete by using SHPB, Al-Salloum et al. [35] also proposed the DIF model as a function of strain rate by the simple rational expression. This expression was obtained using MATLAB such that both the numerator and denominator were represented using the single degree of polynomial equation, and the coefficient was obtained by the least square method with 95% assured limits. The expression has been shown by the rational formulation with the linear expression of numeration and denominator as follows

$$DIF = \frac{{3.54\dot {\varepsilon } + 430.6}}{{\dot {\varepsilon } + 447.3}}.$$
(3.11)

Based on experimental investigation, it has been summarized that the concrete is highly sensitive to strain rate. Hence to describe this, a model has been presented by Lu and Xu [36] for damage and fracture behaviour of cement-based brittle materials under dynamic loading conditions. The development of an accurate model for analyzing the response of concrete structures subjected to blast loading necessitates incorporating dynamic compressive strength, dynamic increase factor, and other strain rate-dependent mechanical properties of the concrete material. Hence the dynamic behaviour of brittle materials is modeled by the following expression

$${\text{DIF}} = 0.0013{{(\dot {\varepsilon })}^{{0.2}}} + 0.113{{(\dot {\varepsilon })}^{{0.2}}} + 1.$$
(3.12)

Based on the research, it has been shown that the linear and power exponent functions need to be revised in precisely describing the relationship between the DIF and the strain rate at high rates of loading. To achieve a more accurate definition, scholars and investigators have turned to two or three-degree polynomial equations to describe the relationship between DIF and high strain rate more precisely. These equations help in properly describing the dynamic increase factor of the logarithmic strain rate. Moreover, experimental studies have led to the proposal of varying transition strain rates for different concrete materials.

Grote et al. [37] experimentally studied the behavior of concrete and concrete mortar at a strain rate of 104 s–1 and under high hydrostatic pressure. The experimental test on cement mortar specimens by SHPB techniques shows significantly rate-sensitive in the strain rate ranging from 250 to 1700 s–1. There is a sharp increase in the dependency on DIF at a high strain rate of around 102 s–1. It shows a weaker dependence for strain rate below 266 s–1 but stronger rate dependence above this transition point. This might be due to the complex microstructure of mortar and concrete, deformation phenomenon, stresses distribution phenomenon, and material inhomogeneity at a high strain rate. They proposed an empirical equation to measure the response of DIF at a high strain rate as follows

$${\text{DIF}} = 0.0235{\text{log}}(\dot {\varepsilon }) + {\text{ }}1.07\quad {\text{for}}\quad \dot {\varepsilon } \leqslant 266{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.13)
$${\text{DIF}} = 0.882{{(\log \dot {\varepsilon })}^{3}}-4.48{{(\log \dot {\varepsilon })}^{2}} + 7.22(\log \dot {\varepsilon }) - 2.64~\quad {\text{for}}\quad \dot {\varepsilon } > 266{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.14)

Li et al. [38] conducted a series of SHPB experimental tests and numerical simulations on mortar specimens at a strain rate of approximately 102 s–1. The results confirmed the apparent DIF enhancement for the concrete-like brittle materials beyond the transition strain rate quantitatively. The lateral inertia confinement mainly governs the dynamic compressive strength increments due to the mass density and size of the tested specimen. They proposed the DIF empirical equation based on the results outcomes as follows

$${\text{DIF}} = 0.03438{\text{ }}({\text{log}}(\dot {\varepsilon }) + 3) + 1\quad {\text{for}}\quad \dot {\varepsilon } \leqslant 100{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.15)
$${\text{DIF}} = 1.729{{(\log \dot {\varepsilon })}^{2}} - 7.1372(\log \dot {\varepsilon }) + 8.5303~\quad {\text{for}}\quad ~\dot {\varepsilon } > 100{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.16)

Zhou and Hao [39] conducted a series of compression and tension tests by SHPB apparatus on concrete-like brittle materials at varying strain rates. Numerical simulation of concrete is also carried out under compression at various strain rates. The concrete specimen is assumed to be homogeneous/composite with strain rate sensitive/insensitive material in the simulation. They proposed a two-stage empirical equation with a transition point at a 10 s–1 strain rate based on experimental and numerical results are as follows

$${\text{DIF}} = 0.0225{\text{log}}(\dot {\varepsilon }) + 1.12\quad {\text{for}}\quad \dot {\varepsilon } \leqslant 10{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.17)
$${\text{DIF}} = 0.2713{{(\log \dot {\varepsilon })}^{2}}~-{\text{ }}0.3563(\log \dot {\varepsilon }) + 1.2275\quad {\text{for}}\quad 10 \leqslant ~~\dot {\varepsilon } \leqslant 2000{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.18)

Katayama et al. [40] proposed an alternative DIF model that maintains the inertia conservation and spatial continuity of inertia based on the condition that mass is preserved and proposed the following expression

$${\text{DIF}} = 0.2583(\log \dot {\varepsilon })-0.05076(\log \dot {\varepsilon }) + 1.021.$$
(3.19)

In the experimental study performed on concrete, it is widely acknowledged that the lateral inertia effect is also generated due to the friction at the interface of bar and specimen, hence the end friction cannot be neglected high-speed SHPB impact test suggested as suggested by Hao et al. [41]. Hence, they have proposed an empirical equation for the DIF model as a function of strain rate to remove the effect of end friction confinement on the dynamic increase factor (DIF) as follows

$${\text{DI}}{{{\text{F}}}_{{\mu = 0}}}~ = {\text{ }}0.6346~{{(\log \varepsilon )}^{2}}-1.0835(\log \varepsilon )~~ + {\text{ }}2.0558\quad {\text{for}}\quad 10 \leqslant \dot {\varepsilon } \leqslant 600{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.20)

Hao et al. [42, 43] also concluded that the end friction confinement at the interfaces of the specimen and bar ends also disturbed the lateral inertia confinement effect of the concrete specimen. They proposed the empirical equation for mortar and concrete separately to remove the confinement effect generated due to friction on the dynamic compressive strength enhancement of the tested materials as follows

$${\text{DI}}{{{\text{F}}}_{{{\text{mortar}}}}} = 0.0419(\log \dot {\varepsilon }) + {\text{ }}1.2165\quad {\text{for}}\quad 1\,{{{\text{s}}}^{{ - 1}}} < \dot {\varepsilon } \leqslant 10{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.21)
$${\text{DI}}{{{\text{F}}}_{{{\text{mortar}}}}} = 0.8988~2(\log \dot {\varepsilon }) + 0.2.8255(\log \dot {\varepsilon }) + 3.4907\quad {\text{for}}\quad 10{\text{ }}{{{\text{s}}}^{{ - 1}}} < \dot {\varepsilon } \leqslant 1000{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.22)
$${\text{DI}}{{{\text{F}}}_{{{\text{Aggregate}}}}} = 0.0191~~ + {\text{ }}1.2222(\log \dot {\varepsilon })\quad {\text{for}}\quad 1{\text{ }}{{{\text{s}}}^{{ - 1}}} < \dot {\varepsilon } \leqslant {\text{ }}220{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.23)
$${\text{DI}}{{{\text{F}}}_{{{\text{Aggregate}}}}} = 1.66607~2(\log \dot {\varepsilon }) - 6.9122(\log \dot {\varepsilon }) + 8.346\quad {\text{for}}\quad 200{\text{ }}{{{\text{s}}}^{{ - 1}}} < \dot {\varepsilon } \leqslant 1000{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.24)

where \({\text{DI}}{{{\text{F}}}_{{{\text{mortar}}}}}\) and \({\text{DI}}{{{\text{F}}}_{{{\text{Aggregate}}}}}\) are the dynamic increase factor mortar and concrete with aggregates, respectively.

Table 1 represents the conclusive DIF model equations, which encapsulate the nature of trend and transition strain rate for concrete-like brittle materials under high-rate loading conditions, as derived from the earlier empirical equations.

Table 1. DIF model equation proposed by researchers for dynamic compression
Full size table

Based on the summarized Table 1, it has been observed that the proposed equation follows either power law variation trends [19, 29, 30, 31–34] or logarithm variation with linear and polynomial equations to represent the results more accurately and precisely [37–43]. DIF equation following the power law variation only considering the strain rate dependency irrespective of the inertia and end friction confinement. The end friction between the bars and specimen interfaces restrains the lateral deformation of the specimen and induces the end friction confinement, which increases the strength of the concrete material. Similarly, due to the poison’s effect on concrete material, the inertial force was generated in the direction opposite the lateral deformation of the specimen, and lateral inertia confinement occurred, further increasing the strength of the material. Additionally, water in the material generates resistance in generating and propagating cracks in the concrete matrix due to water viscosity, further increasing the concrete strength. With an increase in the strength, the dynamic increase factor also increases due to the described factors.

The lateral inertia effect and end friction effect have been included for the polynomial-based DIF models based on the numerical investigation by using the different proposed models, but it is impossible to separate the end friction effect and lateral inertia effect of concrete experimentally. The proposed DIF model are either based on numerical or experimental studies, but the different material behaves differently concerning high strain rate. The suggested DIF results are scattered due to different quasi-static compressive strengths of materials: mortar, normal concrete, high-strength concrete, and fiber reinforcement concrete. The authors are defining the DIF empirical equation based on their tested materials, as a result, the DIFs are satisfying properly with their results rather than with the results of other researchers. This might be due to different experimental techniques, cement-based brittle materials, high-strength materials, and fiber-reinforced concrete materials. Additionally, the results mismatching may also be due to the structural effect generated due to end friction confinement and geometry of the specimen, which constrain the lateral expansion of the specimen in the radial direction due to the poison’s effect and further increases the dynamic compressive strength. From the above experimental and numerical studies, it has been concluded that the DIF showed strain rate dependency and was significantly affected by the strain rate. However, the DIF showed a wide range of variation under high strain rates might be due to strain sensitivity, end friction, lateral inertia, and the presence of water. Moreover, the DIF becomes more sensitive to strain rate beyond the transition strain rate due to the dominancy of the above mention factors.

Besides the material properties and structural effect, fire also significantly affects structures and their materials, particularly when it is subjected to blasts or explosions. When a blast happens, it can create a fireball, intense heat, high temperature, and a shock that can cause extensive damage to the building’s infrastructure and its materials. The combination of blast effects and subsequent fire is often called a fire dynamic load. The effects of fire on materials of structure and its elements can be relatively severe. High temperatures generated by the fire can weaken or melt structural materials, such as steel or concrete, leading to structural failure due to a significant decrease in the compressive tensile and shear strength [44, 45]. The heat can cause expansion and subsequent contraction, generating the loading and unloading situation, resulting in warping, buckling, or collapse of building components [46, 47]. Hence, the effect of high temperature must include in the DIF of materials, and deep study is required.

3.2 Strain Rate Dependency of DIF under Tension

Like dynamic compression tests on concrete-like brittle materials by SHPB, many investigators and researchers also performed many experiments on concrete and concrete-like materials to investigate the strain rate effects using direct or indirect tensile tests. The critical review conducted on preceding research revealed a greater emphasis on reporting experimental data associated with the dynamic strength of concrete, while comparatively less attention has been given to the tensile strength. Based on the review study, it was concluded that the tensile strength of concrete under dynamic loading conditions exhibits a higher sensitivity to strain rate when compared to its compressive strength. The dynamic tensile strength of brittle materials showed a higher sensitivity to the strain rate above a transition strain rate, which is typically between 1 to 10 s–1, as indicated by the dynamic tensile results [2, 6, 9]. Based on the experimental data, researchers have proposed various curves to describe the enhancement of the tensile strength with the strain rates, which is explained in this section.

Most of the DIF models for high strain rate enhancement of concrete are presented by the European CEB-FIP Model code [19]. DIF equation for concrete tensile strength up to the strain rate 30 s–1 is given by the expression

$${\text{DIF}} = {{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1.016{{{{\alpha }}}_{{\text{s}}}}}}}\quad {\text{for}}\quad {{\dot {\varepsilon }}_{S}} < \dot {\varepsilon } \leqslant 30{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.25)
$${\text{DIF}} = {{{{\gamma }}}_{{\text{s}}}}{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1/3}}}\quad {\text{for}}\quad \dot {\varepsilon } > 30{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.26)

where \({{\alpha }_{s}}\) = 1/(10 + 6(\({{f}_{{cs}}}\)/\({{f}_{{co}}}\))); where \({{f}_{{cs}}}\)=unconfined quasi-static uniaxial compressive strength, \({{f}_{{co}}}\) = 10 MPa, \({{\gamma }_{s}}\) = \({{10}^{{(7.11{{\alpha }_{s}} + 2.33)}}}\) and \({{\dot {\varepsilon }}_{S}}\) = 3 × 10–6 s–1 for static loading. Later the CEB-FIP model code modify the DIF equation more precisely to investigate the strain rate sensitivity base on the experimental and numerical study by using the expression [48]

$${\text{DIF}} = {{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{0.018}}}\quad {\text{for}}\quad {{\dot {\varepsilon }}_{S}} < \dot {\varepsilon } \leqslant 10{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.27)
$${\text{DIF}} = 0.0062{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1/3}}}\quad {\text{for}}\quad \dot {\varepsilon }~~ > 10{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.28)

where \(\dot {\varepsilon }\) defined as the transition strain rate and \({{\dot {\varepsilon }}_{S}}\) = 1 × 10–6 as the quasi-static strain rate.

The experimental data have been reviewed to investigate the strain-rate effects on the dynamic tensile strength of concrete. The modification in the DIF expression presented by CEB-FIP suggested by Malvar and Ross [49] are as follows

$$\text{DIF}={{\left[ \frac{{{\dot{ }\!\!\varepsilon\!\!\text{ }}}}{\overset{}{\mathop{{{\text{ }\!\!\varepsilon\!\!\text{ }}_{\text{s}}}}}\,} \right]}^{{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{s}}}}}\quad \text{for}\quad ~{{\dot{\varepsilon }}_{S}}<\dot{\varepsilon }\le 1\text{ }{{\text{s}}^{-1}},$$
(3.29)
$${\text{DIF}} = {{{{\gamma }}}_{{\text{s}}}}{{\left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{S}}}}} \right]}^{{1/3}}}\quad {\text{for}}\quad \dot {\varepsilon }~~ > 1{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.30)

\({{\alpha }_{s}}\) = 1/(1 + 8(\({{f}_{{cs}}}\)/\({{f}_{{co}}}\))); \({{\gamma }_{s}}\) = \({{10}^{{(6{{\alpha }_{s}} + 2)}}}\) and \({{\dot {\varepsilon }}_{S}}\) = 1 × 10–6 s–1 for static loading.

Based on the experimental data reported by different investigations in the past, Soroushian et al. [50] suggested an empirical equation of DIF. The suggested equation used to develop a constitutive model to determine the dynamic response of concrete is as follows;

$${\text{DIF}} = 0.0154{{\left( {\log \dot {\varepsilon }} \right)}^{2}} + 0.219\left( {\log \dot {\varepsilon }} \right) + 1.77.$$
(3.31)

The experimental and numerical study performed by Tedesco et al. [27] used the SHPB setup to determine the Splitting tensile strength of different compressive strengths. Based on the test results obtained, a bilinear equation of DIF was suggested are as following

$${\text{DIF}} = 0.1425\left[ {\left( {\log \dot {\varepsilon }} \right) + 5.8456} \right] + 1 \geqslant 1.0\quad {\text{for}}\quad \dot {\varepsilon } \leqslant 2.32{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.32)
$${\text{DIF}} = 0.1425\left[ {\left( {\log \dot {\varepsilon }} \right) + 5.8456} \right] + 1 \leqslant 6.0\quad {\text{for}}\quad \dot {\varepsilon } > 2.32{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.33)

Based on the curve fitted on the experimental data, Zhou and Hao [39] suggested the DIF expression for mesoscale modeling of concrete-like materials and used it for numerical analysis. They suggested a tensile DIF fitting curve based on experimental results as follows

$${\text{DIF}} = 0.0225\left( {\log \dot {\varepsilon }} \right) + 1.12\quad {\text{for}}\quad \dot {\varepsilon } \leqslant 0.1{\text{ }}{{{\text{s}}}^{{ - 1}}},$$
(3.34)
$${\text{DIF}} = 0.7325{{\left( {\log \dot {\varepsilon }} \right)}^{2}} + 1.235\left( {\log \dot {\varepsilon }} \right) + 1.6\quad {\text{for}}\quad \dot {\varepsilon } > 0.1{\text{ }}{{{\text{s}}}^{{ - 1}}}.$$
(3.35)

Katayama et al. [40] also suggested a DIF equation to predict the tensile response of concrete. The suggested equation was parabolic in nature and introduced in the Drucker–Prager’s material model as follows

$${\text{DIF}} = 1.4379{{\left( {\log \dot {\varepsilon }} \right)}^{2}} - 0.02987\left( {\log \dot {\varepsilon }} \right) + 0.8267.$$
(3.36)

The direct tensile behaviors of different concrete mixed were studied by Komlos [51] under different strain rates. He conducted the under different strain rates by varying the cement content, water cement ratio, and aggregates cement ratio and developed the experimental-based formula of DIF as follows

$${\text{DIF}} = 1.0 + 0.1\log \left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{s}}}}} \right].$$
(3.37)

Xiao [52] conducted the experimental study on concrete under direct tension test on dumbbell-shaped specimens by using the servo-hydraulic testing machine. They proposed a linear-logarithmic relationship between tensile strength with the increasing strain rate as follows

$${\text{DIF}} = 1 + 0.0653\log \left[ {\frac{{\dot {\varepsilon }}}{{{{{\dot {\varepsilon }}}_{s}}}}} \right].$$
(3.38)

The DIF model obtained for tensile behaviour by using experimentally and numerically has been summarized in Table 2, describing the transition strain rate and nature of the equation.

Table 2. DIF model equation proposed by researchers for dynamic Tension
Full size table

The dynamic tensile strength’s dependence on strain rate is significantly pronounced, as its transition point occurs at significantly lower strain rates compared to compression. Based on the summarized Table 2, it has been observed that the proposed equation follows either power law variation trends [19, 48, 49] or logarithm variation with linear and quadratic polynomial equations to represent the results more accurately and precisely [27, 32, 39, 40, 50–54]. For dynamic tensile strength, a suggested transition strain rate is approximately 1 s–1, beyond this, the tensile strength increases significantly. Several DIF models for dynamic tensile have been proposed for normal concrete. Still, robust DIF models are lacking specifically designed for high-strength concrete with fiber content because fibers increase the tensile strength effectively.

4 CONCLUSIONS

Based on the above critical study, the following conclusion has been derived

I. This paper examines the available experimental and numerical data concerning DIF models measured under high strain rates. However, the analysis needs to sufficiently address the impact of concrete matrix strength and specimen geometry on the dynamic compressive and tensile DIF model.

II. The DIF models used for normal concrete cannot apply to high-strength concrete, ultra-high-performance concrete (UHPC), and fiber-reinforced concrete (FRC) because they may overestimate the dynamic increase factor of compressive and tensile strength.

III. The transition strain rate for dynamic strength in compression is predominantly observed to be above 10 s–1, whereas, for tensile strength, the transition strain rate is approximately 1 s–1, described that the tensile behaviour of concrete is more sensitive to the strain rate.

IV. The lateral inertia confinement increases the load-carrying capacity and DIF under compression at a high strain rate. However, it is also observed from the above study that there is dramatically changed in DIFs for concrete-like material beyond the transition point. The inertial confinement becomes more significant beyond the transition point under a high strain rate.

V. Concrete subjecting to high-speed impact loading, the lateral inertial force of the specimen increase. This inertial force increases the lateral inertia confinement in a SHPB test. This lateral inertia effect restricts the expansion of the specimen in a radial direction under a high strain rate. Hence there is a rapid increase in dynamic material properties of material subjected to a high strain rate.

VI. The dynamic compressive strength of the cement-based brittle materials is also influenced by end friction confinement, moisture content, porosity, lateral inertia confinement, and high strain rate. However, the existing DIF strength models need to differentiate these influencing factors.

VII. DIF model follows the linear-based single-degree equation with a logarithmic strain rate before the transition strain rate mostly, while beyond this point, the DIF model follows the two-degree polynomial equation, and dynamic compressive strength increases significantly.

VIII. The Power Law-based DIF model focused solely on the strain rate effect, without addressing the impact of friction between bars and specimen, and lateral inertia effects.