1 INTRODUCTION

The study of dynamic characteristics or response of elastic structures has inspired and attracted engineers, mathematicians and researchers in related fields for more than a century. This is due largely to its wide range of applications in transportation and construction industry. [1–5]. One of the widely studied elastic structures is a beam; among the earliest investigations concerning the dynamic characteristics of an elastic beam under travelling loads are the works of Ayre et al. [6] who studied the transverse vibration of one-end of two-span beams under the action of a moving load. The exact solution for the resulting partial differential equation is obtained by using infinite series method and the effect of the mass ratio of the system is presented. Fryba [7] who also investigated the vibration of solids and structures under moving loads of beams due to a moving arbitrary force. He considered the effect of beam damping, travelling loads speed, and the structure end conditions on the vibrating system. Gbadeyan and Oni [8] who considered dynamic behaviour of beams and rectangular plates under moving loads, in this study different options was adopted to obtain the analytical solution to this problem. Rao [9] who studied linear dynamics of an elastic beam under moving loads. The normalized maximum deflection of the structure for each moving load velocity in the range 1 to 100 m/s is given in graphical form at two different positions of the beam, namely at \(x = 0.25L\) and \(x = 0.5L\). Pesterev et al. [10] who in their work entitled “Revisiting the moving force problem” developed tools for finding the maximum deflection of a beam for any given velocity of the travelling force. Many other useful results also were presented. Wodek [11] also, who presented advanced structural dynamics and active control of structures. Evidently, from all these aforementioned studies, the velocity of the travelling load has been generally considered constant along the span of the beam. Generally speaking, in the open literature, most of the investigations concerning the dynamic behaviour of a structural member under moving load has been commonly considered for a load travelling at constant velocity. For instance, among several other authors who have made significant contributions in this area of important study are Duplyakin [12] who studied the motion of a carriage with constant velocity along a beam of infinite length resting on a base with two elastic characteristics, Aleksandrov and Duplyakin [13] who investigated the dynamics of an endless Timoshenko beam lying on a base with two elastic characteristics during the movement of a deformable crew and more recently, Erofeev et al. [14] who considered the dynamic behavior of a beam laying on a generalized elastic basis, with moving load.

On the other hand, studies concerning dynamical system involving accelerating or decelerating loads are not so common in literature. Previous studies where efforts were made to tackle the problem of the transverse vibration of elastic beam under accelerating masses include the works of Wand [15] who studied the dynamical analysis of finite inextensible beam with an attached accelerating mass. In this study, it was reported that applied forward force amplifies the speed of the mass and the displacement of the beam. Oni and Omolofe [16] who study the flexural motions under accelerating load of structurally prestressed beams with general boundary conditions. The authors developed an elegant analytical procedure involving the generalized finite integral transform in conjunction with the Struble’s asymptotic technique to obtain solutions to this class of problem. Lee [17] tackled the transverse vibration of a Timoshenko beam under the actions of an accelerating mass. In his study, he presented numerical results for a prescribed constant acceleration or deceleration and the slenderness ratio of the beam. He figured-out that the separation of the mass from the beam may occur for a Timoshenko beam when the traveling speed of the mass is large due to large initial traveling speed or large prescribed acceleration. Nevertheless, these studies though impressive, the authors over looked the possibility of investigation the effects of some vital structural parameters on the dynamic characteristics and stability of of the dynamical system.

Hilal and Ziddeh [18] investigated the vibration analysis of beams with general boundary conditions traversed by a single point force traveling with variable velocity type of motion. They obtained analytical solution to the beam problem and compared the results with same beam under the actions of a concentrated force traveling at constant velocity. Their method of solution is only suitable to handle an approximate model in which the vehicle-structure interaction is completely neglected; this type of beam model has been described in [19] as the crudest approximation known to the literature of assessing the dynamic response of an elastic system which supports moving concentrated masses.

Huang and Thambiratnam [20] investigated the deflection response of plate on Winkler foundation to moving accelerated loads. They developed a solution procedure involving finite strip method with a spring system and applied it to treat the response of a plate structure resting on elastic foundation. Dynamic response to moving accelerated point loads was investigated and the effects of initial moving velocity, acceleration and initial load position on the response were discussed. Their results show that the initial velocity and acceleration have great influence on the dynamic response. They equally figured out that the response of the plate away from the boundaries resembles that of an infinite plate and might have practical applications.

In a more recent development, Niki et al. [21] investigated the dynamic response of a simply supported elastic beam resting on an elastic foundation of Winkler’s type with viscous damping to a point load moving with variable speed on the surface of the beam. They employed combined analytically and numerical method to obtain the dynamic response of the Bernoulli-Euler beam. Effects of the various parameters, like foundation stiffness and damping, beam damping and acceleration or deceleration of the moving load or loads, on the response of the beam are assessed through extensive parametric studies and useful practical conclusions are presented.

Ivanchenko [22] developed a method to treat the problem of rods under an inertial load moving with variable speed. As an illustrative example, they considered the motion of a force or a load with variable speeds along a pin-ended beam and also on the motion of a high-speed train at braking across a bridge consisting of four beam spans.

Fang et al. [23] used the method that combines the finite difference method and the Fourier transform method to solve the numerical solutions of the dynamic response of a beam resting on a Vlazov foundation subjected to a load moving with uniform variable velocity. They verified this method by comparing it with theoretical solutions of the dynamic deflection of a beam on a homogeneous elastic foundation under one-axle load moving with constant speed. The effects of load acceleration, deceleration, and initial velocity on the dynamic deflection of the beam are also investigated. Their results show that, with the increase of the load movement distance, a larger initial velocity can lead to a greater effect of acceleration or deceleration on the peak value of the dynamic deflection of the beam. To the authors best of knowledge, extensive study concerning elastic structures under accelerating, decelerating and uniform velocity-type of motions for all pertinent boundary conditions is not known in literature.

This study therefore concerns the dynamic characteristics of elastic structure resting on non-winkler type foundation and under compressive axial force and masses travelling with three different types of motion namely, accelerating, decelerating and uniform velocity type of motion. Effects of various structural parameters on the response characteristics of the beam are thoroughly scrutinized. Solution procedure proposed in [24] is adopted in this study to obtain the transverse displacement response of the beam under the actions of travelling loads which is considered to be travelling with either accelerating or decelerating or uniform velocity type of motion.

2 THE GOVERNING EQUATION OF MOTION

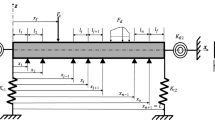
Axially prestressed isotropic beam resting on elastic foundation and traversed by concentrated mass M travelling with a varying speed is considered. Neglecting the effect of damping parameters, the equation prescribing the flexural motion of the homogenous beam is given by

$$EJ\frac{{{{\partial }^{4}}\mathbb{Z}\left( {x,t} \right)}}{{\partial {{x}^{4}}}} - {{A}_{f}}\frac{{{{\partial }^{2}}\mathbb{Z}\left( {x,t} \right)}}{{\partial {{x}^{2}}}} + \varpi \frac{{{{\partial }^{2}}\mathbb{Z}\left( {x,t} \right)}}{{\partial {{t}^{2}}}} + F\mathbb{Z}\left( {x,t} \right) - S\frac{{{{\partial }^{2}}\mathbb{Z}\left( {x,t} \right)}}{{\partial {{x}^{2}}}} = {{{{\Phi }}}_{f}}\left( {x,t} \right)\left[ {1 - \frac{{{\Theta }}}{g}\mathbb{Z}\left( {x,t} \right)} \right],$$
(1)

where \(x\) represents the position coordinate in the axial direction, \(t\) represents the time, EJ is the flexural stiffness, \(\frac{\partial }{{\partial x}}\) and \(\frac{\partial }{{\partial t}}\) are partial derivatives with respect to the position coordinate x and time \(t\) respectively. \(\mathbb{Z}\left( {x,t} \right)\) is the transverse displacement, \({{{{\Phi }}}_{f}}\left( {x,t} \right)\) is the moving force, \({{A}_{f}}\) is the axial force and \(\varpi \) is the constant mass per unit length of the beam, \(F\) and \(S\) are respectively foundation and shear rigidity.

The structural member which has simple support at both ends is assumed to be under a compressive force and executing vibrations according to simple Bernoulli-Euler beam theory of flexure.

Thus the boundary conditions are given as

$$\mathbb{Z}\left( {0,t} \right) = 0 = \mathbb{Z}\left( {L,t} \right),\quad \frac{{{{\partial }^{2}}\mathbb{Z}\left( {0,t} \right)}}{{\partial {{x}^{2}}}} = 0 = \frac{{{{\partial }^{2}}\mathbb{Z}\left( {L,t} \right)}}{{\partial {{x}^{2}}}}$$
(2)

and the initial conditions are

$$\mathbb{Z}\left( {x,0} \right) = 0 = \frac{{\partial \mathbb{Z}\left( {x,0} \right)}}{{\partial t}}.$$
(3)

Θ is and operator define as

$${{\Theta }} = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + 2\frac{d}{{dt}}f\left( t \right)\frac{{{{\partial }^{2}}}}{{\partial x\partial t}} + {{\left( {\frac{d}{{dt}}f\left( t \right)} \right)}^{2}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{d}^{2}}f\left( t \right)}}{{d{{t}^{2}}}}\frac{\partial }{{\partial x}}.$$
(4)

The time varying function f(t) which describes the motion of the travelling load at any instance of time is given by

$$f\left( t \right) = {{x}_{o}} + ut + \frac{1}{2}a{{t}^{2}}.$$
(5)

where \({{x}_{o}}\) is the point of application of the force \({{{{\Phi }}}_{f}}\) at the instance \(t = 0\), u is the initial velocity and a is the constant acceleration of motion. Equation (5) depicts a uniform accelerating or decelerating type of motion. Thus, for the uniform velocity type of motion, the function f(t) reduces to

$$f\left( t \right) = ut.$$
(6)

The continuous moving force \({{{{\Phi }}}_{f}}\left( {x,t} \right)\) acting on the slender member is given as

$${{{{\Phi }}}_{f}}\left( {x,t} \right) = Mg\delta \left( {x - f\left( t \right)} \right),$$
(7)

where g is the acceleration due to gravity and \(\delta \left( \bullet \right)\) represent the well-known Dirac delta which as an even function is expressed as

$$\delta \left( x-f\left( t \right) \right)=\frac{1}{L}+\frac{2}{L}\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\text{cos}\frac{n\pi }{L}\text{cos}\frac{n\pi x}{L}.$$
(8)

Substituting (4), (5), (6) and (8) into Eq. (1) leads to

$$\begin{gathered} EJ\frac{{{{\partial }^{4}}\mathbb{Z}(x,t)}}{{\partial {{x}^{4}}}} - {{A}_{f}}\frac{{{{\partial }^{2}}\mathbb{Z}(x,t)}}{{\partial {{x}^{2}}}} + \varpi \frac{{{{\partial }^{2}}\mathbb{Z}(x,t)}}{{\partial {{x}^{2}}}} + F\mathbb{Z}(x,t) - S\frac{{{{\partial }^{2}}\mathbb{Z}(x,t)}}{{\partial {{x}^{2}}}} + M\delta \left[ {x - \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)} \right] \\ \times \left[ {\frac{{{{\partial }^{2}}\mathbb{Z}(x,t)}}{{\partial {{t}^{2}}}} + 2(u + at)\frac{{{{\partial }^{2}}\mathbb{Z}(x,t)}}{{\partial x\partial t}} + {{{(u + at)}}^{2}}\frac{{{{\partial }^{2}}\mathbb{Z}(x,t)}}{{\partial {{x}^{2}}}} + a\frac{{\partial \mathbb{Z}(x,t)}}{{\partial x}}} \right] = M\delta \left[ {x - \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)} \right]. \\ \end{gathered} $$
(9)

3 SOLUTION PROCEDURES

By mode superimposition technique, the transverse displacement \(\mathbb{Z}\left( {x,t} \right)\) of the vibrating beam with simple supports at ends x = 0 and \(x = L\), can be written as

$${{\mathbb{Z}}_{m}}\left( {x,t} \right) = \mathop \sum \limits_{m = 1}^N {{Z}_{m}}\left( t \right){\text{sin}}\frac{{m\pi x}}{L}.$$
(10)

Substituting (10) into (9) and taking into account (8), one obtains

$$\begin{gathered} \sum\limits_{m = 1}^\infty {\left\{ {EJ{{{\left( {\frac{{m\pi }}{L}} \right)}}^{4}}\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(y) + {{A}_{f}}{{{\left( {\frac{{m\pi }}{L}} \right)}}^{2}}\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(t) + \varpi \left( {\sin \frac{{m\pi x}}{L}} \right){{{\ddot {Z}}}_{m}}(t)} \right.} \\ + F\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(y) + S{{\left( {\frac{{m\pi }}{L}} \right)}^{2}}\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(t) \\ + \frac{M}{L}\left( {\sin \frac{{m\pi x}}{L}{{{\ddot {Z}}}_{m}}(t) + 2\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}{{{\ddot {Z}}}_{m}}(t)} } \right. \\ + 2(u + at)\cos \frac{{m\pi x}}{L}{{{\dot {Z}}}_{m}}(t) + 4(u + at)\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}{{{\dot {Z}}}_{m}}(t)} \\ - {{(u + at)}^{2}}\sin \frac{{m\pi x}}{L}{{Z}_{m}}(t) - 2{{(u + at)}^{2}}\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}{{Z}_{m}}(t)} \\ \left. {\left. { + a\cos \frac{{m\pi x}}{L}{{Z}_{m}}(t) + 2a\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}{{{\dot {Z}}}_{m}}(t)} } \right)} \right\} \\ - Mg\delta \left[ {x - \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)} \right] = 0. \\ \end{gathered} $$
(11)

The solution technique require that the expression on the left hand side of Eq. (11) be orthogonal to the function

$${{V}_{k}}\left( x \right) = {\text{sin}}\frac{{k\pi x}}{L}.$$
(12)

Thus multiplying (11) by (12) and integrating from x = 0 to \(x = L\), one obtains

$$\begin{gathered} \int\limits_0^L {\left[ {\sum\limits_{m = 1}^\infty {\left\{ {EJ{{{\left( {\frac{{m\pi }}{L}} \right)}}^{4}}\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(t) + {{A}_{f}}{{{\left( {\frac{{m\pi }}{L}} \right)}}^{2}}\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(t) + \varpi \left( {\sin \frac{{m\pi x}}{L}} \right){{{\ddot {Z}}}_{m}}{{{(t)}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right.} } \right.} \\ + \,F\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(t) + S{{\left( {\frac{{m\pi }}{L}} \right)}^{2}}\left( {\sin \frac{{m\pi x}}{L}} \right){{Z}_{m}}(t) \\ \end{gathered} $$
$$\begin{gathered} + \frac{M}{L}\left( {\sin \frac{{m\pi x}}{L}{{{\ddot {Z}}}_{m}}(t) + 2\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}{{{\ddot {Z}}}_{m}}(t)} + 2(u + at)\cos \frac{{m\pi x}}{L}{{{\dot {Z}}}_{m}}(t)} \right. \\ + \,4(u + at)\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\cos \frac{{m\pi x}}{L}{{{\dot {Z}}}_{m}}(t) - {{{(u + at)}}^{2}}\sin \frac{{m\pi x}}{L}{{Z}_{m}}(t)} \\ - \,2{{(u + at)}^{2}}\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} \cos \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}{{Z}_{m}}(t) \\ \left. {\left. { + \,a\cos \frac{{m\pi x}}{L}{{Z}_{m}}(t) + 2a\sum\limits_{m = 1}^\infty {\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}\cos \frac{{n\pi x}}{L}\cos \frac{{m\pi x}}{L}{{{\dot {Z}}}_{m}}(t)} } \right)} \right\} \\ - \,Mg\delta \left[ {x - \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)} \right]\sin \frac{{k\pi x}}{L}dx = 0. \\ \end{gathered} $$
(13)

Equation (13) after some simplifications and rearrangements leads to

$$\begin{gathered} \sum\limits_{m = 1}^\infty {\left\{ {{{R}_{0}}{{{\ddot {Z}}}_{m}}(t) + ({{R}_{1}} + {{R}_{2}} + {{R}_{3}} + {{R}_{4}}){{Z}_{m}}{{{(t)}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right.} \\ + \frac{M}{{\varpi L}}\left( {{{R}_{5}}{{{\ddot {Z}}}_{m}}(t) + 2\sum\limits_{n = 1}^\infty {{{R}_{6}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{{\ddot {Z}}}_{m}}(t) + {{R}_{7}}(u + at){{{\dot {Z}}}_{m}}(t)} } \right. \\ \, + \sum\limits_{n = 1}^\infty {{{R}_{8}}(u + at)\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{{\dot {Z}}}_{m}}(t) - {{R}_{9}}{{{(u + at)}}^{2}}{{Z}_{m}}(t)} \\ \, - \sum\limits_{n = 1}^\infty {{{R}_{{10}}}{{{(u + at)}}^{2}}} \cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{Z}_{m}}(t) + {{R}_{{11}}}{{Z}_{m}}(t) \\ \left. {\left. { + \,\sum\limits_{n = 1}^\infty {{{R}_{{10}}}\cos } \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{Z}_{m}}(t)} \right)} \right\} = \frac{{Mg}}{\varpi }\int\limits_0^\infty {\delta \left[ {x - \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)} \right]} \sin \frac{{k\pi x}}{L}dx, \\ \end{gathered} $$
(14)

where

$${{R}_{0}} = \mathop \smallint \limits_0^L {\text{sin}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx,$$
$${{R}_{1}}=\frac{{{A}_{f}}}{\varpi }{{\left( \frac{m\pi }{L} \right)}^{2}}\int\limits_{0}^{L}{\text{sin}\frac{m\pi x}{L}\text{sin}\frac{k\pi x}{L}dx},$$
$${{R}_{2}} = \frac{F}{\varpi }\int\limits_0^L {{\text{sin}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{3}} = \frac{S}{\varpi }{{\left( {\frac{{m\pi }}{L}} \right)}^{2}}\int\limits_0^L {{\text{sin}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{4}} = \int\limits_0^L {{\text{sin}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{5}}=2\int\limits_{0}^{L}{\text{cos}\frac{n\pi x}{L}\text{sin}\frac{m\pi x}{L}\text{sin}\frac{k\pi x}{L}dx},$$
$${{R}_{6}} = 2\int\limits_0^L {{\text{cos}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{7}}=4\int\limits_{0}^{L}{\text{cos}\frac{n\pi x}{L}\text{cos}\frac{m\pi x}{L}\text{sin}\frac{k\pi x}{L}dx},$$
$${{R}_{8}} = \int\limits_0^L {{\text{sin}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{9}} = \int\limits_0^L {{\text{cos}}\frac{{n\pi x}}{L}{\text{sin}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{{10}}} = a\int\limits_0^L {{\text{cos}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} ,$$
$${{R}_{{11}}} = 2a\int\limits_0^L {{\text{cos}}\frac{{n\pi x}}{L}{\text{cos}}\frac{{m\pi x}}{L}{\text{sin}}\frac{{k\pi x}}{L}dx} .$$

Equation (13) can further be rearranged to take the form

$$\begin{gathered} \sum\limits_{m = 1}^\infty {\left\{ {{{{\ddot {Z}}}_{m}}(t) + \varphi _{{mf}}^{2}{{Z}_{m}}(t) + {{\varepsilon }_{0}}\left( {{{\Omega }_{0}}{{{\ddot {Z}}}_{m}}(t) + \sum\limits_{n = 1}^\infty {{{\Omega }_{1}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{{\ddot {Z}}}_{m}}(t) + {{\Omega }_{2}}(u + at){{{\dot {Z}}}_{m}}(t)} } \right.} \right.} \\ + \,\sum\limits_{n = 1}^\infty {{{\Omega }_{3}}(u + at)\cos } \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{{\dot {Z}}}_{m}}(t) - {{\Omega }_{4}}{{(u + at)}^{2}}{{Z}_{m}}(t) - \sum\limits_{n = 1}^\infty {{{\Omega }_{5}}{{{(u + at)}}^{2}}} \\ \left. {\left. { \times \cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{Z}_{m}}(t) + {{\Omega }_{6}}{{Z}_{m}}(t) + \sum\limits_{n = 1}^\infty {{{\Omega }_{7}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}{{Z}_{m}}(t)} } \right)} \right\} \\ = \frac{{Mg}}{{\varpi {{R}_{0}}}}\sin \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}, \\ \end{gathered} $$
(15)

where

$$\begin{gathered} \varphi _{{mf}}^{2} = \left( {\frac{{{{R}_{1}} + {{R}_{2}} + {{R}_{3}} + {{R}_{4}}}}{{{{R}_{0}}}}} \right),\quad {{\varepsilon }_{0}} = \frac{M}{{\varpi L}},\quad {{\Omega }_{0}} = \frac{{{{R}_{5}}}}{{{{R}_{0}}}},\quad {{\Omega }_{1}} = \frac{{{{R}_{6}}}}{{{{R}_{0}}}},\quad {{\Omega }_{2}} = \frac{{{{R}_{7}}}}{{{{R}_{0}}}}, \\ {{\Omega }_{3}} = \frac{{{{R}_{8}}}}{{{{R}_{0}}}},\quad {{\Omega }_{4}} = \frac{{{{R}_{9}}}}{{{{R}_{0}}}},\quad {{\Omega }_{5}} = \frac{{{{R}_{{10}}}}}{{{{R}_{0}}}},\quad {{\Omega }_{6}} = \frac{{{{R}_{{11}}}}}{{{{R}_{0}}}},\quad {{\Omega }_{7}} = \frac{{{{R}_{{10}}}}}{{{{R}_{0}}}}. \\ \end{gathered} $$
(16)

Equation (15) is the transformed equation governing the motion of the simply supported beam subjected to accelerating loads. In what follows, two special cases of Eq. (15) will be discussed. Namely (i) elastic beam traversed by a moving force and (ii) elastic beam traversed by a moving mass.

3.1 Case I: A Beam Traversed by a Moving Force

If the inertia or mass effect of the travelling load is considered negligible, the mass ratio \({{\varepsilon }_{0}}\) in the governing equation (15) is set to zero and considering only the mth particle of the system, the entire Eq. (15) thus reduces to

$${{\ddot {Z}}_{m}}\left( t \right) + \varphi _{{mf}}^{2}{{Z}_{m}}\left( t \right) = \frac{{Mg}}{{\varpi {{R}_{0}}}}{\text{sin}}\frac{{k\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}.$$
(17)

To obtain the solution of Eq. (17), the impulse response function known as Duhamel’s integral is employed. By this technique, the solution of the beam-force system (17) may be written as

$${{Z}_{m}}\left( t \right) = \int\limits_0^t {{{h}_{m}}\left( {t - \tau } \right){{Q}_{m}}\left( \tau \right)d\tau } .$$
(18)

The impulse response function \({{h}_{m}}\left( t \right)\) is defined as

$${{h}_{m}}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{\varphi }_{{dm}}}}}{{e}^{{ - {{\epsilon }_{m}}{{\varphi }_{m}}t}}}{\text{sin}}{{\varphi }_{{dm}}}t}&{t \geqslant 0} \\ 0&{t < 0} \end{array}} \right..$$
(19)

And the damped circular frequency of the mth mode of the beam, \({{\varphi }_{{dm}}}\) is given as

$${{\varphi }_{{dm}}} = {{\varphi }_{{mf}}}\sqrt {1 - \epsilon _{m}^{2}} .$$
(20)

It is well known that when considering dynamic responses, the effect of damping parameters is most often considered insignificant, thus setting the damping parameter \({{\epsilon }_{m}} = 0\) in (20) implies

$${{\varphi }_{{dm}}} = {{\varphi }_{{mf}}}.$$
(21)

And this leads to

$${{Z}_{m}}\left( t \right)=\frac{Mg}{\varpi {{R}_{0}}{{\varphi }_{mf}}}\int\limits_{0}^{t}{\text{sin}k\pi \left( {{x}_{0}}+ut+\frac{1}{2}a{{t}^{2}} \right)\text{sin}{{\varphi }_{mf}}\left( t-\tau \right)d\tau }\text{}\text{.}$$
(22)

Equation (10) in view of the integral (22) yields

$$\begin{gathered} {{\mathbb{Z}}_{m}}(x,t) = \sum\limits_{m = 1}^N {\frac{{Mg}}{{8\varpi {{\varphi }_{{mf}}}}}\operatorname{Re} \text{[}{{G}_{1}}{{U}_{1}}\{ (\cos {{\phi }_{1}} - i\sin {{\phi }_{1}})[{\text{erf}}({{T}_{2}} - {{T}_{3}}t) - {\text{erf}}({{T}_{2}})]} \\ - \,(\cos {{\phi }_{2}} - i\sin {{\phi }_{2}})[{\text{erf}}({{T}_{5}} - {{T}_{3}}t) - {\text{erf}}({{T}_{5}})]\} \\ + \,{{G}_{2}}{{U}_{1}}\{ (\cos {{\phi }_{3}} - i\sin {{\phi }_{3}})[{\text{erf}}({{T}_{7}} - {{T}_{8}}t) - {\text{erf}}({{T}_{7}})] \\ - \,(\cos {{\phi }_{4}} - i\sin {{\phi }_{4}})[{\text{erf}}({{T}_{{10}}} - {{T}_{8}}t) - {\text{erf}}({{T}_{{10}}})]\} ] \times \left( {\sin \frac{{m\pi x}}{L}} \right) \\ \end{gathered} $$
(23)

Which is the expression depicting the response of the structurally prestressed beam to accelerating moving forces.

Where

$${{G}_{1}} = (1 + i),\quad {{G}_{2}} = (1 - i),\quad {{U}_{1}} = \sqrt {\frac{\pi }{{k\pi a}}} ,\quad {{T}_{2}} = \frac{1}{{2\sqrt {k\pi a} }}[({{\varphi }_{{mf}}} - k\pi u) + i(k\pi u - {{\varphi }_{{mf}}})],$$
$${{T}_{3}} = \frac{{1 - i}}{2}\sqrt {k\pi a} ,\quad {{T}_{5}} = \frac{1}{{2\sqrt {k\pi a} }}[ - ({{\varphi }_{{mf}}} + k\pi u) + i(k\pi u + {{\varphi }_{{mf}}})],$$
$$\begin{gathered} {{T}_{7}} = \frac{1}{{2\sqrt {k\pi a} }}[({{\varphi }_{{mf}}} + k\pi u) + i(k\pi u + {{\varphi }_{{mf}}})],\quad {{T}_{8}} = \frac{{1 + i}}{2}\sqrt {k\pi a} , \\ {{T}_{{10}}} = \frac{1}{{2\sqrt {k\pi a} }}[({{\varphi }_{{mf}}} - k\pi u) + i({{\varphi }_{{mf}}} - k\pi u)],\quad {{\phi }_{1}} = \frac{{ - {{k}^{2}}{{\pi }^{2}}(2a{{x}_{0}} - {{u}^{2}}) - 2k\pi {{\varphi }_{{mf}}}(u + at) + \varphi _{{mf}}^{2}}}{{2\pi ka}} \\ \end{gathered} $$
(24)
$$\begin{gathered} {{\phi }_{2}} = \frac{{{{k}^{2}}{{\pi }^{2}}(2a{{x}_{0}} - {{u}^{2}}) - 2k\pi {{\varphi }_{{mf}}}(u + at) - \varphi _{{mf}}^{2}}}{{2\pi ka}},\quad {{\phi }_{3}} = \frac{{{{k}^{2}}{{\pi }^{2}}(2a{{x}_{0}} - {{u}^{2}}) - 2k\pi {{\varphi }_{{mf}}}(u + at) - \varphi _{{mf}}^{2}}}{{2\pi ka}}, \\ {{\phi }_{4}} = \frac{{{{k}^{2}}{{\pi }^{2}}(2a{{x}_{0}} - {{u}^{2}}) + 2k\pi {{\varphi }_{{mf}}}(u + at) - \varphi _{{mf}}^{2}}}{{2\pi ka}}. \\ \end{gathered} $$

For a constant velocity type of motion, the response characteristics of axially prestressed structural member subjected to a moving force is similarly obtained as

$$\begin{array}{*{20}{l}} {{{\mathbb{Z}}_{m}}\left( {x,t} \right) = }&{\mathop \sum \limits_{m = 1}^N \frac{{Mg}}{{8\varpi {{\varphi }_{{mf}}}}}\left[ {\frac{{k\pi u{\text{sin}}{{\varphi }_{{mf}}}t - {{\varphi }_{{mf}}}{\text{sin}}k\pi ut}}{{k\pi {{u}^{2}} - \varphi _{{mf}}^{2}}}} \right] \times \left( {{\text{sin}}\frac{{m\pi x}}{L}} \right)} \end{array}.$$
(25)

3.2 Case II: A Beam Traversed by a Moving Mass

If the inertia or mass effect of the travelling load is considered as an essential components of the system, then the mass or slenderness ratio \({{\varepsilon }_{0}} \ne 0\) all the inertia terms are retained in the governing differential equation which give a more accurate model. Thus, the solution of the entire equation (15) is desirable.

To this effect, Eq. (15) is rearranged to take the form

$${{\ddot {Z}}_{m}}(t) + \frac{{{{\varepsilon }_{0}}\left[ {{{\Omega }_{2}}(u + at) + \sum\limits_{n = 1}^\infty {{{\Omega }_{3}}(u + at)\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right]}}{{\left[ {1 + {{\varepsilon }_{0}}\left( {{{\Omega }_{0}} + \sum\limits_{n = 1}^\infty {{{\Omega }_{1}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right)} \right]}}{{\dot {Z}}_{m}}(t)$$
$$\begin{gathered} + \frac{{{{\varepsilon }_{0}}\left[ {\varphi _{{fm}}^{2} + \left( {{{\Omega }_{4}}{{{(u + at)}}^{2}} + \sum\limits_{n = 1}^\infty {{{\Omega }_{5}}{{{(u + at)}}^{2}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right)} \right]}}{{\left[ {1 + {{\varepsilon }_{0}}\left( {{{\Omega }_{0}} + \sum\limits_{n = 1}^\infty {{{\Omega }_{1}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right)} \right]}}{{Z}_{m}}(t) \\ + \frac{{{{\varepsilon }_{0}}\left[ {\varphi _{{fm}}^{2} + \left( {{{\Omega }_{6}} + \sum\limits_{n = 1}^\infty {{{\Omega }_{7}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right)} \right]}}{{\left[ {1 + {{\varepsilon }_{0}}\left( {{{\Omega }_{0}} + \sum\limits_{n = 1}^\infty {{{\Omega }_{1}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right)} \right]}}{{Z}_{m}}(t) \\ \end{gathered} $$
(26)
$$ = \frac{{{{\varepsilon }_{0}}Lg}}{{\left[ {1 + {{\varepsilon }_{0}}\left( {{{\Omega }_{0}} + \sum\limits_{n = 1}^\infty {{{\Omega }_{1}}\cos \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}} } \right)} \right]}}\sin \frac{{n\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L}.$$

Clearly, Eq. (26) in its present form is not amenable to any known conventional method of solution. To treat Eq. (26) therefore, a modification of an asymptotic method developed by Struble extensively discussed in Omolofe and Adeloye [1] shall be employed. By this technique, a parameter \(\varrho < 1\) is considered for any arbitrary mass ratio \({{\varepsilon }_{0}}\)

$$\varrho = \frac{{{{\varepsilon }_{0}}}}{{1 + {{\varepsilon }_{0}}}}$$
(27)

and

$${{\varepsilon }_{0}} = \varrho + o{{(\varrho )}^{2}}.$$
(28)

Substituting (28) into (26) and after some simplifications, the entire equation (26) reduces to a second order ordinary differential equation

$$\frac{{{{d}^{2}}{{Z}_{m}}\left( t \right)}}{{d{{t}^{2}}}} + \varphi _{{mm}}^{2}{{Z}_{m}}\left( t \right) = \frac{{\varrho Lg}}{{\varpi {{R}_{0}}}}{\text{sin}}\frac{{k\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right)}}{L},$$
(29)

where

$${{\varphi }_{{mm}}} = \left\{ {1 - \frac{\varrho }{2}\left[ {{{{{\Omega }}}_{0}} - \frac{{\{ {{u}^{2}}{{{{\Omega }}}_{4}} + a{{{{\Omega }}}_{6}}\} }}{{\varphi _{{mf}}^{2}}}} \right]} \right\}.$$
(30)

Expression (30) represents the modified natural frequency due to the inertia effect of the moving mass.

Equation (29) is analogous to equation (17). Thus, the solution of (29) is obtained as

$${{Z}_{m}}\left( t \right) = \frac{{\varrho Lg}}{{\varpi {{R}_{0}}{{\varphi }_{{mm}}}}}\int\limits_0^t {{\text{sin}}k\pi \left( {{{x}_{0}} + ut + \frac{1}{2}a{{t}^{2}}} \right){\text{sin}}{{\varphi }_{{mm}}}\left( {t - \tau } \right)d\tau } .$$
(31)

Equation (10) in view of Eq. (31) thus becomes

$$\begin{gathered} {{\mathbb{Z}}_{m}}(x,t) = \sum\limits_{m = 1}^N {\frac{{\varrho Lg}}{{8\varpi {{\varphi }_{{mm}}}}}\operatorname{Re} \text{[}{{G}_{1}}{{U}_{1}}\{ (\cos {{\phi }_{1}} - i\sin {{\phi }_{1}})[{\text{erf}}({{T}_{2}} - {{T}_{3}}t) - {\text{erf}}({{T}_{2}})]} \\ - \,(\cos {{\phi }_{2}} - i\sin {{\phi }_{2}})[{\text{erf}}({{T}_{5}} - {{T}_{3}}t) - {\text{erf}}({{T}_{5}})]\} \\ + \,{{G}_{2}}{{U}_{1}}\{ (\cos {{\phi }_{3}} - i\sin {{\phi }_{3}})[{\text{erf}}({{T}_{7}} - {{T}_{8}}t) - {\text{erf}}({{T}_{7}})] \\ - \,(\cos {{\phi }_{4}} - i\sin {{\phi }_{4}})[{\text{erf}}({{T}_{{10}}} - {{T}_{8}}t) - {\text{erf}}({{T}_{{10}}})]\} ] \times \left( {\sin \frac{{m\pi x}}{L}} \right), \\ \end{gathered} $$
(32)

which represents the response characteristics of the beam resting on elastic foundation and traversed by accelerating mass.

Similarly, for the same beam under mass travelling at constant velocity, the solution is obtained as

$$\begin{array}{*{20}{l}} {{{\mathbb{Z}}_{m}}\left( {x,t} \right) = }&{\mathop \sum \limits_{m = 1}^N \frac{{\varrho Lg}}{{8\varpi {{\varphi }_{{mm}}}}}\left[ {\frac{{k\pi u{\text{sin}}{{\varphi }_{{mm}}}t - {{\varphi }_{{mm}}}{\text{sin}}k\pi ut}}{{k\pi {{u}^{2}} - \varphi _{{mm}}^{2}}}} \right] \times \left( {{\text{sin}}\frac{{m\pi x}}{L}} \right)} \end{array}.$$
(33)

4 RESULTS AND DISCUSSIONS

The analysis proposed in this study is illustrated in this section by considering a homogeneous beam of modulus of elasticity \(E = 3.9012 \times {{10}^{9}}\) N/m3, the moment of inertial \(J = 2.87698 \times {{10}^{{ - 3}}}{{m}^{4}}\), the beam span \(L = 30m\) and the mass per unit length of the beam \(\varpi = 2758.291\) kg/m. The values of foundation moduli are varied between 0 N/m3 and \(400000\) N/m3, the values of axial force \({{A}_{f}}\) are varied between 0N and \(2.0 \times {{10}^{8}}N\).

The analysis in this study is applied to homogeneous beam subjected to concentrated loads moving with uniformly accelerated, decelerated or uniform velocity type of motion.

Figures 1a–1c show the dimensionless mid-span dynamic deflection of a pinned-pinned uniform beam under the action of concentrated forces travelling with accelerating, decelerating or uniform velocity type of motion for the various values of axial force \({{A}_{f}}\) and for fixed values of subgrade moduli \(F = 40000\) and shear modulus \(S = 30000\). The figures show that as \({{A}_{f}}\) increases, the response amplitude of the beam decreases for all the three type of motions considered. It is observed that the maximum deflection occurs under decelerated type of motion.

Fig. 1.
figure 1

Dynamic deflection profile for a pinned-pinned beam; (a) accelerated motion; (b) decelerated motion; (c) uniform motion; for moving force; (——) \({{A}_{f}} = 0\); (– – –)\({{A}_{f}} = 200000\); (……) \({{A}_{f}} = 2000000\).

Full size image

The mid-span deflection profile of a pinned-pinned uniform beam under the action of accelerating, decelerating and uniform velocity type of motion for the travelling concentrated force is shown in Fig. 2 (a–c). The figures show that for various values of foundation subgrade moduli F and for fixed values of axial force \({{A}_{f}} = 200000\) and shear modulus \(S = 30000\) as the values of the foundation modulus \(F\) increases, the deflection of the beam decreases.

Fig. 2.
figure 2

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving force;(——) \(F = 0\); (– – –)\(F = 40000\); (……) \(F = 400000\).

Full size image

In Figures 3a–3c, effect of shear modulus on the mid-span deflection of a pinned-pinned uniform beam for the moving force system under the action of accelerating, decelerating and uniform velocity type of motion is shown. It is observed that the deflection of the beam decreases as the values of the shear modulus increases.

Fig. 3.
figure 3

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving force; (——) \(S = 0\); (– – –)\(S = 30000\); (……) \(S = 300000\).

Full size image

Figures 4a–4c depict the dimensionless dynamic displacement of a the uniform beam at mid-span under the action of accelerating, decelerating and uniform velocity type of motion for the travelling concentrated force for the various values of span length \(L\). The figures reveal that as the span length \(L\) increases, the response amplitude of the beam decreases for all the three type of motions considered.

Fig. 4.
figure 4

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving force; (——) \(L = 20m\); (– – –) \(L = 30m\); (……) \(L = 40m\).

Full size image

Figures 5a–5c show the mid span deflection of the simply supported uniform beam under the action of accelerating, decelerating and uniform velocity type of motion for a concentrated moving force. For various values of load velocity V, fixed values of axial force \({{A}_{f}} = 200000\), foundation modulus \(F = 40000\) and shear modulus \(S = 30000\). These figures clearly show that as the velocity of the moving force increases the deflection of the vibrating beam increases. It is observed that under the uniform velocity type of motion, the deflection increases as the velocity increases until it gets to a certain point and start decreasing.

Fig. 5.
figure 5

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving force;(——) \(V = 10\) m/s; (– – –) \(V = 20m/s\); (……) V = 30 m/s.

Full size image

Figures 6a–6c showcased the dimensionless mid-span dynamic displacement of a pinned-pinned uniform beam under the action of accelerating, decelerating or uniform velocity type of motion for various values of axial force Af and for fixed values of subgrade moduli \(F = 40000\) and shear modulus \(S = 30000\). The figures show that as Af increases, the response amplitude of the beam decreases for all the three type of motions considered. It is observed that the maximum deflection occurs under the decelerated type of motion.

Fig. 6.
figure 6

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving mass; (——) \({{A}_{f}} = 0\); (– – –)\({{A}_{f}} = 200000\); (……) \({{A}_{f}} = 2000000\).

Full size image

The mid-span defection profile of the Pinned-pinned uniform beam under the action of accelerating, decelerating or uniform velocity type of motion for the travelling concentrated force for various values of foundation subgrade moduli \(F\) and for fixed values of axial force \({{A}_{f}} = 200000\) and shear modulus \(S = 30000\) is displayed in Figures 7 (a–c). These figures clearly show that as we increase the values of the foundation modulus \(F\), the deflection of the beam decreases.

Fig. 7.
figure 7

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving mass; (——) \(F = 0\); (– – –)\(F = 40000\); (……) \(F = 400000\).

Full size image

Figures 8a–8c depict the effect of shear modulus on the mid-span deflection of a pinned-pinned uniform beam of the moving mass system under the action of accelerating, decelerating or uniform velocity type of motion. It is observed that the deflection of the beam decreases as the value of shear modulus increases when values of foundation subgrade moduli \(F\) and that of axial force are fixed.

Fig. 8.
figure 8

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving mass;(——) \(S = 0\); (– – –) \(S = 30000\); (……) \(S = 300000\).

Full size image

In Figures 9a–9c the displacement response of the vibrating beam for the three type of motions is displayed. It is seen from the figures that as the value of the beam span length \(L\) increases, for fixed values of foundation moduli \(F\) and shear modulus, the response amplitude of the beam decreases significantly for all the three type of motions considered.

Fig. 9.
figure 9

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving mass; (——) \(L = 20m\); (– – –) \(L = 30m\); (……) \(L = 40m\).

Full size image

Figures 10a–10c display the mid-span deflection profile of the pinned-pinned uniform beam under the action of accelerating, decelerating or uniform velocity type of motion for the travelling concentrated mass. It is shown that for various values of velocity \(V\), for fixed values of axial force Af, foundation modulus \(F\) and shear modulus \(S\) the deflection of the beam increases as the value of the velocity increases. It is observed that under uniform velocity-type of motion the deflection increases as the velocity increases until it get to a certain point and start decreasing.

Fig. 10.
figure 10

Dynamic deflection profile for a pinned-pinned beam;(a) accelerated motion;(b) decelerated motion; (c) uniform motion; for moving mass; (——) \(V = 10\) m/s; (– – –) \(V = 20\) m/s; (……) V = 30 m/s.

Full size image

5 CONCLUSIONS

In this present study, dynamic characteristics of an elastic beam under compressive axial force and subjected to masses travelling with accelerating, decelerating, and uniform velocity type of motion is investigated. Galerkin’s Method is used to transform the fourth order partial differerential equation governing the motion of the elastic structural member to a set of second order ordinary differential equations. This system of equations called Galerkin’s equations is further simplified using asymptotic method of Struble. Duhamel integral transform (also known as impulse response function) is further employed to obtain solution representing the response of this structural member to accelerating masses. Effects of various vital structural parameters and dynamic characteristics exhibited by the beam-mass system are extensively scrutinized. It is discovered that incorporating these parameters sufficiently into the governing equation of motion enhances the dynamic stability of the beam vibrating due to compressive axial force and accelerating masses.

Analysis and various results further show that:

• as the axial force Af increases, the response amplitude of the beam decreases for all the three type of motions considered. It is observed that the maximum deflection occurs under the decelerating masses;

• as the values of the foundation moduli \(F\) increases, the deflection of the beam decreases for both the moving force and moving mass systems for all the three type of motions considered;

• as the value of shear modulus \(S\) increases, the mid-span deflection of the beam decreases;

• for fixed values of foundation moduli \(F\), shear moduli \(S\) and axial force Af, as the span length \(L\) increases, the response amplitude of the beam decreases for all the three type of motions considered and

• as the velocity of the travelling masses increases, the deflection of the beam increases for both the moving force and the moving mass problem. This is true for all the three types of motion considered. It is however observed that for the uniform velocity type of motion, the deflection increases as the velocity increases until it get to a certain point and start decreasing for both the moving force and moving mass systems.

In addition to the above, effects of various boundary conditions, type of motion and the beam span length on the dynamic characteristics of the beam were investigated. Results obtained in this present study are readily applicable to further investigations in this area of research. For example, effect of damping is considered negligible in this work. Incorporating this may form the basis for future work. Results of this study form the basis for the authors ongoing research and evidently, researchers in this area of study will no doubt find the results very relevant and useful. Finally, this study provides deep insight and vital information about the complex interaction of structure-load system. The method of solution can handle this class of problems for all pertinent boundary conditions.