INTRODUCTION

Non-stationary and asymmetric cyclic deformation processes consist of a sequence of monotonic and cyclic loading modes. Mathematical modeling of such processes under conditions of hard (controlled deformations) loading and especially soft (controlled stresses) loading is a very difficult task. In addition, when such modes are implemented, difficult to describe processes of landing and ratcheting the hysteresis loop arise. As for the assessment and prediction of the resource under the conditions of unsteady and asymmetric cyclic loading, then in these cases the accumulation of damage must be determined throughout the deformation process, taking into account that the accumulation of damage is substantially nonlinear.

Mathematical modeling of deformation and damage accumulation under cyclic loading is based mainly on versions of plasticity theories belonging to the class of plastic flow theories with combined (isotropic and anisotropic) hardening, a review and analysis of which are contained in [1–12]. In this article, mathematical modeling of deformation and damage accumulation processes is based on the version of the theory of plasticity [1, 9], which, as shown in [10], is the most adequate option for describing deformation and fracture processes under cyclic loading in comparison with the Korotkikh [2] and Shabosh [6–8] models.

To identify the features of deformation under non-stationary and asymmetric cyclic loading, rigid loading under tension-compression conditions for specimens made of 12Х18Н10Т stainless steel is considered, which is a sequence of five stages: cyclic, monotonic, cyclic, monotonic, cyclic up to fracture. Analysis of transient processes from cyclic to monotonic and from monotonic to cyclic shows the need to separate the processes of monotonic and cyclic deformation. For this, in the space of plastic deformations, a criterion for changing the direction of plastic deformation and a memory surface separating cyclic and monotonic deformation processes are introduced. Further, equations of the evolution of parameters of isotropic and anisotropic hardening for monotonic and cyclic loading modes are introduced into the equations of the theory of plasticity.

The separation of the processes of monotonic and cyclic deformation also takes place in the Korotkikh model [2–4], but only to describe the evolution of isotropic hardening. The memory surface in this model is built in the space of the microstress deviator with the determination of the maximum value of the microstress intensity in the process of deformation. In [2, 11], to describe the evolution of anisotropic hardening in the space of the deviator of plastic deformations, a memory surface is introduced with the determination of the intensity of the maximum amplitude of plastic deformation in the process of deformation. Further, in [12], to describe the evolution of anisotropic hardening, the same memory surface is used as before for isotropic hardening. All these approaches [2, 11, 12] have one significant drawback, that is, the achieved size of the memory surface has the ability to decrease and increase at the end of the cycle, and this leads to the fact that at the end of each cycle both monotonic and cyclic loading is possible. In addition, according to the evolutionary equation for the maximum intensity of microstresses under cyclic loading, this value always decreases, although it should remain constant during the stabilized cycle. In conclusion, it should also be said that there is insufficient substantiation of the considered approaches [2, 11, 12] in the literature.

Taking into account the revealed features of monotonic and cyclic loading for the refined equations of the modified theory of plasticity, a basic experiment is determined and a method for identifying material functions is formulated. The material functions of 12Х18Н10Т stainless steel at room temperature are obtained. A comparison of the results of calculated and experimental studies of stainless steel 12Х18Н10Т under rigid loading, consisting of a sequence of monotonic and cyclic loading modes, is given. The kinetics of the stress-strain state is analyzed, the changes in the range and average stress of the cycle during the stages of cyclic loading are considered.

1 BASIC EQUATIONS OF THE THEORY OF PLASTICITY

We consider a very simple version of the theory of plasticity [9, 10], which is a partial version of the theory of inelasticity [1]. The version of the theory of plasticity belongs to the class of one-surface flow theories with combined hardening. The range of applicability of the version of the theory of plasticity is limited to small deformations of initially isotropic metals at temperatures, when there are no phase transformations, and strain rates, when the dynamic and rheological effects can be neglected.

The following is a summary of the basic equations of a variant of the theory of plasticity.

$$\dot {\boldsymbol{\varepsilon}} = \dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{e}}} + \dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}},$$
(1.1)
$${{\dot{\boldsymbol{\varepsilon}}}^{{\mathbf{e}}}} = \frac{{1 + \nu }}{E}\dot{\boldsymbol{\sigma}} - \frac{\nu }{E}{\text{tr}}\left( {\dot{\boldsymbol{\sigma}}} \right){\mathbf{I}},$$
(1.2)
$$f\left( \boldsymbol{\sigma} \right) = \frac{3}{2}\left( {{\mathbf{s}} - {\mathbf{a}}} \right):\left( {{\mathbf{s}} - {\mathbf{a}}} \right) - {{C}^{2}} = 0,$$
(1.3)
$$\dot {C} = {{q}_{\varepsilon }}\dot {\varepsilon }_{{u\text{*}}}^{p},\quad \dot {\varepsilon }_{{u\text{*}}}^{p} = {{\left( {\frac{2}{3}\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}}:\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}}} \right)}^{{\frac{1}{2}}}},$$
(1.4)
$${\mathbf{\dot {a}}} = \sum\limits_{m = 1}^M {{\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{m}} \right)}}} ,$$
(1.5)
$${\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{1}} \right)}} = \frac{2}{3}{{g}^{{\left( 1 \right)}}}\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}} + g_{a}^{{\left( 1 \right)}}{\mathbf{a}}_{{}}^{{\left( {\mathbf{1}} \right)}}\dot {\varepsilon }_{{u\text{*}}}^{p},$$
(1.6)
$${\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{2}} \right)}} = \frac{2}{3}{{g}^{{\left( 2 \right)}}}\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}} + g_{a}^{{\left( 2 \right)}}{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}\dot {\varepsilon }_{{u\text{*}}}^{p},$$
(1.7)
$${\mathbf{\dot {a}}}_{{}}^{{\left( {\mathbf{m}} \right)}} = \frac{2}{3}{{g}^{{\left( m \right)}}}\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}}\quad \left( {m = 3,...,M} \right),$$
(1.8)
$${\mathbf{\dot{\boldsymbol{\varepsilon}}}}_{{}}^{{\mathbf{p}}} = \frac{{\partial f}}{{\partial \boldsymbol{\sigma}}}\lambda = \frac{3}{2}\frac{{{\mathbf{s}}\text{*}}}{{\sigma _{u}^{*}}}\dot {\varepsilon }_{{u\text{*}}}^{p},\quad {\mathbf{s}}\text{*} = {\mathbf{s}} - {\mathbf{a}},\quad \sigma _{u}^{*} = {{\left( {\frac{3}{2}{\mathbf{s}}\text{*}:{\mathbf{s}}\text{*}} \right)}^{{\frac{1}{2}}}},$$
(1.9)
$$\dot {\varepsilon }_{{u{\kern 1pt} \text{*}}}^{p} = \frac{1}{{{{E}_{*}}}}\frac{3}{2}\frac{{{\mathbf{s}}\text{*}:{{\dot{\boldsymbol{\sigma}}}}}}{{{\sigma} _{u}^{*}}},\quad {{E}_{*}} = {{q}_{\varepsilon }}\sum\limits_{m = 1}^M {{{g}^{{\left( m \right)}}}} + \sum\limits_{m = 1}^2 {g_{a}^{{\left( m \right)}}} a_{u}^{{\left( m \right)\text{*}}},\quad a_{u}^{{\left( m \right)\text{*}}} = \frac{3}{2}\frac{{{\mathbf{s}}\text{*}:{\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}}}{{\sigma _{u}^{*}}},$$
(1.10)
$$\dot {\varepsilon }_{{u\text{*}}}^{p} = \frac{1}{{{{E}_{*}} + 3G}}3G\frac{{{\mathbf{s}}\text{*}:{\mathbf{\dot {\varepsilon }}}}}{{\sigma _{u}^{*}}},\quad G = \frac{E}{{2\left( {1 + \nu } \right)}},$$
(1.11)
$$\begin{gathered} \sigma _{u}^{*} < C \cup \dot {\varepsilon }_{{u\text{*}}}^{p} \leqslant 0{-}{\text{elasticity,}} \\ \sigma _{u}^{*} = C \cap \dot {\varepsilon }_{{u\text{*}}}^{p} > 0{-}{\text{elastoplasticity,}} \\ \end{gathered} $$
(1.12)
$$\dot {\omega } = \alpha {{\omega }^{{\frac{{\alpha - 1}}{\alpha }}}}\frac{{{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}:\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}}}}{{{{W}_{a}}}},\quad \alpha = {{(\sigma _{a}^{{\left( 2 \right)}}{\text{/}}a_{u}^{{\left( 2 \right)}})}^{{{{n}_{\alpha }}}}},\quad a_{u}^{{\left( 2 \right)}} = {{\left( {\frac{3}{2}{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}:{\mathbf{a}}_{{}}^{{\left( {\mathbf{2}} \right)}}} \right)}^{{\frac{1}{2}}}}.$$
(1.13)

Here, \(\dot{\boldsymbol{\varepsilon}},\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{e}}},\dot{\boldsymbol{\varepsilon}}_{{}}^{{\mathbf{p}}}\) are the tensors of the rates of total, elastic and plastic deformations; \(\boldsymbol{\sigma},{\mathbf{s}},{\mathbf{s}}\text{*}\), a are the stress tensor, deviators of stresses, active stresses and microstresses; \(\varepsilon _{{u\text{*}}}^{p}\) is the accumulated plastic deformation; ω is damage; E, ν are the Young’s modulus and Poisson’s ratio; C is the radius (size) of the loading surface; \({{{\mathbf{a}}}^{{({\mathbf{1}})}}},{{{\mathbf{a}}}^{{({\mathbf{2}})}}},{{{\mathbf{a}}}^{{({\mathbf{m}})}}}\) are the microstresses (deviator of displacement of the center of the loading surface) of the first, second and third types; \({{q}_{\varepsilon }},{{g}^{{(m)}}},g_{a}^{{(m)}}\) are defining functions, the connection of which with material ones will be given below.

2 EXPERIMENT

The article discusses the results of experimental studies of samples of stainless steel 12Х18Н10Т. The chemical composition and mechanical properties of steel are presented in Table 1.

Table 1

C

Si

Mn

Ni

S

P

Cr

Cu

Ti

Fe

<0.12

<0.8

<2

9–11

<0.02

<0.035

17–19

<0.3

0.4–1

~67

Young’s modulus (GPa)

Poisson’s

ratio

Yield strength

(MPa)

Tensile strength (MPa)

Relative elongation

at break (%)

198

0.28

196

510

40

The tests were carried out on a Zwick Z100 universal testing machine. The geometry and dimensions of the tested samples are in accordance with the requirements of ASTM E606. The diameter of the working part of the sample is 8 mm, the length is 24 mm, the radius of transition from the working part to the gripping part is 32 mm (Fig. 1). Deformation during the test was measured and controlled using a mounted extensometer with a measuring base of 10 mm.

figure 1

Fig. 1

3 MONOTONIC AND CYCLIC LOADING OF STAINLESS STEEL 12Х18Н10Т

The results of experimental studies of 12Х18Н10Т stainless steel under uniaxial rigid loading, including the stages of monotonic and cyclic loading, are considered. The experiment consists of 5 stages of loading:

– Stage 1 includes cyclic loading with a frequency of 0.2 Hz at \(\varepsilon _{m}^{{\left( 1 \right)}} = 0,\) \(\Delta {{\varepsilon }^{{\left( 1 \right)}}} = 0.016\) and \({{N}^{{\left( 1 \right)}}} = 20\) cycles;

– Stage 2 includes monotonic stretching up to \({{\varepsilon }^{{\left( 2 \right)}}} = 0.05\);

– Stage 3 includes cyclic loading with a frequency of 0.4 Hz at \(\varepsilon _{m}^{{\left( 3 \right)}} = 0.05,\) \(\Delta {{\varepsilon }^{{\left( 3 \right)}}} = 0.012\) and \({{N}^{{\left( 3 \right)}}} = 200\) cycles;

– Stage 4 includes monotonic stretching up to \({{\varepsilon }^{{\left( 4 \right)}}} = 0.1\);

– Stage 5 includes cyclic loading with a frequency of 0.4 Hz at \(\varepsilon _{m}^{{\left( 5 \right)}} = 0.1\), \(\Delta {{\varepsilon }^{{\left( 5 \right)}}} = 0.012\,\,\,\)and \({{N}^{{\left( 5 \right)}}} = {{N}_{f}}\) cycles until fracture.

Here, \(\varepsilon _{m}^{{\left( i \right)}}\,\) is the average deformation of the cycle; \(\Delta {{\varepsilon }^{{\left( i \right)}}}\) is the cycle deformation range; ε(i) is the attainable strain under monotonic loading; N(i) is the number of cycles.

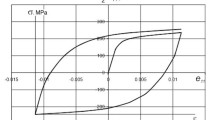
Figure 2 shows an experimental diagram of deformation of 12Х18Н10Т steel, including all five stages of loading. The cycle diagrams of the first, third, and fifth stages show the loops for the first and last cycles. Further, the obtained experimental results are analyzed.

figure 2

Fig. 2

Cyclic deformation at the first stage shows that 12Х18Н10Т steel at the initial stage is cyclically hardened with a subsequent deceleration of the cyclic hardening process to insignificant (\(d{{C}_{p}}{\text{/}}d\varepsilon _{{u * }}^{p} \approx 1\) MPa) and the steel becomes almost cyclically stable.

At the third and fifth stages of cyclic deformation, the hysteresis loop fits. Moreover, the planting processes at these stages are identical, as if there was no preliminary history of deformation. Thus, the modulus Ea, which is included in the evolutionary equation for microstresses of the first type and provides the loop fitting process, must have the same initial value \({{E}_{a}} = {{E}_{{a0}}}\). Т That is, at the stages of monotonic loading after cyclic loading, at which Ea falls almost to zero, the module Ea should quickly return to its initial value\({{E}_{{a0}}}\).

At the second and fourth stages of monotonic loading, the hardening is the same and constant. The hardening here is determined by the modulus Ea0 and, to a lesser extent, by some modulus of monotonic isotropic hardening.

Thus, the behavior of the modulus Ea, which characterizes the anisotropic hardening, and, accordingly, the behavior of the isotropic hardening parameters substantially depends on the mode of the deformation process, that is, cyclic or monotonic.

To separate the processes of monotonic and cyclic deformation in the space of the tensor of plastic deformations \(\boldsymbol{\varepsilon} _{{}}^{{\mathbf{p}}}\), a memory surface is introduced that limits the region of cyclic deformation. The surface is determined by the position of its center ξ and its radius (size) \({{C}_{\varepsilon }}\). To calculate the center and size of the surface, two plastic strain tensors \(\boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}}\) and \(\boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}\) are introduced, which define the surface boundaries. At the beginning of deformation, these variables are equal to zero. Determination of the displacement and size of the memory surface occurs when the direction of plastic deformation changes. The following condition is accepted as a criterion for changing direction:

$$\dot{\boldsymbol{\varepsilon}}_{{\left( {{\mathbf{t}} - {\mathbf{0}}} \right)}}^{{\mathbf{p}}}:\dot{\boldsymbol{\varepsilon}}_{{\left( {\mathbf{t}} \right)}}^{{\mathbf{p}}} < 0,$$

where \(\dot{\boldsymbol{\varepsilon}}_{{\left( {\mathbf{t}} \right)}}^{{\mathbf{p}}}\) is the plastic strain rate tensor at the current moment of time; \(\dot{\boldsymbol{\varepsilon}}_{{\left( {{\mathbf{t}} - {\mathbf{0}}} \right)}}^{{\mathbf{p}}}\) is the plastic strain rate tensor at the previous moment of time.

At this moment, the change in the boundaries, center and size of the loading surface is described based on the following relationships:

$$\boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}} = \boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}},\quad \boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} = \boldsymbol{\varepsilon} _{{}}^{{\mathbf{p}}},\quad \xi = \frac{{\boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} + \boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}}}{2},\quad {{C}_{\varepsilon }} = {{\left[ {\frac{2}{3}\left( {\frac{{\boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} - \boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}}}{2}} \right):\left( {\frac{{\boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{1}} \right)}} - \boldsymbol{\varepsilon} _{{}}^{{{\mathbf{p}}\left( {\mathbf{2}} \right)}}}}{2}} \right)} \right]}^{{\frac{1}{2}}}}$$

Then the condition for cyclic deformation is deformation within the memory surface

$${{\left[ {\frac{2}{3}(\boldsymbol{\varepsilon} _{{}}^{{\mathbf{p}}} - \boldsymbol{\xi} ):(\boldsymbol{\varepsilon} _{{}}^{{\mathbf{p}}} - \boldsymbol{\xi})} \right]}^{{\frac{1}{2}}}} \leqslant {{C}_{\varepsilon }}.$$

Outside the memory surface, deformation is monotonic.

Based on the above features of monotonic and cyclic loads for the modulus Ea and the determining functions for microstresses, the following equations are formulated:

$${{g}^{{\left( 1 \right)}}} = {{E}_{a}},\quad {{g}^{{\left( 2 \right)}}} = {{\beta }^{{\left( 2 \right)}}}\sigma _{a}^{{\left( 2 \right)}},\quad g_{a}^{{\left( 2 \right)}} = - {{\beta }^{{\left( 2 \right)}}},$$
$${{g}^{{\left( m \right)}}} = \left\{ {\begin{array}{*{20}{l}} {{{\beta }^{{\left( m \right)}}}\sigma _{a}^{{\left( m \right)}}} \\ {0,\,\,{\text{if}}\,\,a_{u}^{{\left( m \right)}} \geqslant \sigma _{a}^{{\left( m \right)}} \cap {\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}:{\mathbf{s}}\text{*} > 0,} \end{array}} \right.\quad a_{u}^{{\left( m \right)}} = {{\left( {\frac{3}{2}{\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}{\mathbf{a}}_{{}}^{{\left( {\mathbf{m}} \right)}}} \right)}^{{\frac{1}{2}}}}\quad \left( {m = 3,...,M} \right),$$
$${{\dot {E}}_{a}} = \left\{ {\begin{array}{*{20}{l}} { - {{K}_{E}}{{{\left( {\frac{{{{E}_{a}}}}{{{{E}_{{a0}}}}}} \right)}}^{{{{n}_{E}}}}}\dot {\varepsilon }_{{u\text{*}}}^{p}\quad {\text{under cyclic loading,}}} \\ {{{M}_{E}}\left( {\frac{{{{E}_{{a0}}} - {{E}_{a}}}}{{{{E}_{{a0}}}}}} \right)\dot {\varepsilon }_{{u\text{*}}}^{p}\quad {\text{under monotonic loading,}}} \end{array}} \right.$$
$$g_{a}^{{\left( 1 \right)}} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{E}_{a}}}}\frac{{d{{E}_{a}}}}{{d\varepsilon _{{u\text{*}}}^{p}}}\quad {\text{under cyclic loading,}}} \\ {0\quad {\text{under monotonic loading}}{\text{.}}} \end{array}} \right.$$

So, to describe microstresses, it is necessary to define the following material functions:

\({{E}_{{a0}}},\sigma _{a}^{{(m)}},{{\beta }^{{(m)}}}\) are modules of anisotropic hardening;

\({{K}_{E}},{{n}_{E}},{{M}_{E}}\) are parameters of anisotropic hardening during cyclic and monotonic deformation.

To determine these material functions, the results of the experiment in Fig. 2 are used.

The modulus of anisotropic hardening is determined by the formula

$${{E}_{{a0}}} = \frac{{\sigma _{m}^{{\left( 3 \right)}}}}{{\varepsilon _{m}^{{p\left( 3 \right)}}}}\,,$$

where \(\sigma _{m}^{{\left( 3 \right)}}\) is the average stress in the first cycle of the third stage; \(\varepsilon _{m}^{{p\left( 3 \right)}}\) is the average plastic deformation in the first cycle of the third stage.

Modules of anisotropic hardening \(\sigma _{a}^{{\left( m \right)}}\) and β(m) are determined from processing the cyclic diagram of the last half-cycle of the first stage according to the method described in [1, 9].

The parameters of anisotropic hardening KE and nE are determined based on the results of the fitting of the hysteresis loop at the third and fifth stages. For this, a dependence is built in coordinates

$${{Y}_{E}} = \ln \left[ {\frac{{{{\sigma }_{m}}\left( {N - 1} \right) - {{\sigma }_{m}}\left( N \right)}}{{2\Delta {{\varepsilon }^{p}}\varepsilon _{m}^{p}}}} \right],\quad {{X}_{E}} = \ln \left[ {\frac{{{{\sigma }_{m}}\left( N \right)}}{{\varepsilon _{m}^{p}{{E}_{{a0}}}}}} \right],$$

where N is the cycle number; \({{\sigma }_{m}}\left( N \right)\) is the average stress of the Nth cycle; \(\Delta {{\varepsilon }^{p}}\) is the range of plastic deformation; \(\varepsilon _{m}^{p}\) is the average plastic deformation. The resulting dependence is approximated by a linear function

$${{Y}_{E}} = {{a}_{E}}{{X}_{E}} + {{b}_{E}},\quad {{K}_{E}} = \exp \left( {{{b}_{E}}} \right),\quad {{n}_{E}} = {{a}_{E}}.$$

The anisotropic hardening parameter ME under monotonic loading is determined from the consideration of restoring the parameter Ea from 0 to the value \({{E}_{{a0}}}\) when the plastic deformation changes under monotonic loading for \(\varepsilon _{{st}}^{p}\). Then the parameter ME will be determined by the formula

$${{M}_{E}} = \frac{{{{E}_{{a0}}}}}{{\varepsilon _{{st}}^{p}}}.$$

Having determined the microstresses throughout the entire process from the first to the fifth stage of loading, it is possible to determine the behavior of the size (radius) of the loading surface, i.e., the change in isotropic hardening in transient processes from cyclic to monotonic and from monotonic to cyclic deformation.

Figure 3 shows the change in the size of the loading surface (functional C) throughout the deformation process from the first to the fifth stage of loading. The dotted line in Figure 3 shows the isotropic hardening function \(C = {{C}_{p}}(\varepsilon _{{u\text{*}}}^{p})\) under cyclic loading.

figure 3

Fig. 3

An analysis of the results shown in Fig. 3 shows that, when passing from cyclic to monotonic deformation (stages two and four), an increase in the intensity of isotropic hardening occurs, and when passing from monotonic to cyclic (stages three and five), isotropic hardening slowly decreases and it tends to isotropic \(C = {{C}_{p}}(\varepsilon _{{u\text{*}}}^{p})\) during cyclic deformation.

Based on the above, the features of the change in isotropic hardening under cyclic and monotonic loading, the following dependence is taken for the determining function of isotropic hardening:

$${{q}_{\varepsilon }} = \left\{ {\begin{array}{*{20}{l}} {\left[ {\frac{{d{{C}_{p}}}}{{d\varepsilon _{{u\text{*}}}^{p}}} - {{K}_{C}}{{{\left( {\frac{{C - {{C}_{p}}}}{{{{C}_{p}}}}} \right)}}^{{{{n}_{C}}}}}} \right]\quad {\text{under cyclic loading,}}} \\ {\left[ {\frac{{d{{C}_{p}}}}{{d\varepsilon _{{u\text{*}}}^{p}}} + {{M}_{C}}} \right]\quad {\text{under monotonic loading}}{\text{.}}} \end{array}} \right.$$

So, to describe isotropic hardening, it is necessary to determine the following material functions:

\({{C}_{p}}(\varepsilon _{{u\text{*}}}^{p})\) is the isotropic hardening function under cyclic loading;

\({{K}_{C}},{{n}_{C}},{{M}_{C}}\) are the moduli of isotropic hardening under cyclic and monotonic loading.

To determine these material functions, the results of the experiment in Fig. 3 are used.

The isotropic hardening function under cyclic loading \({{C}_{p}}(\varepsilon _{{u\text{*}}}^{p})\) is determined based on the change in the surface size at the first, third and fifth stages (dashed curve in Fig. 3).

The isotropic hardening parameters KC and nC under cyclic loading are determined based on the results of a decrease in the size of the loading surface at the third and fifth stages of loading. For this, a dependence is built in coordinates

$${{Y}_{C}} = \ln \left[ {\frac{{d\left( {{{C}_{p}} - C} \right)}}{{d\varepsilon _{{u\text{*}}}^{p}}}} \right],\quad {{X}_{C}} = \ln \left[ {\frac{{\left( {C - {{C}_{p}}} \right)}}{{{{C}_{p}}}}} \right].$$

The resulting dependence is approximated by a linear function

$$Y = {{a}_{C}}{{X}_{C}} + {{b}_{C}},\quad {{K}_{C}} = \exp \left( {{{b}_{C}}} \right),\quad {{n}_{C}} = {{a}_{C}}.$$

The isotropic hardening parameter MC under monotonic loading is determined from the slope of the deformation curve at the second and fourth stages by the formula

$${{M}_{C}} = \frac{{d\sigma }}{{d{{\varepsilon }^{p}}}} - {{E}_{{a0}}} - \frac{{d{{C}_{p}}}}{{d{{\varepsilon }^{p}}}}.$$

4 VERIFICATION OF THE MODIFIED THEORY OF PLASTICITY

In order to verify the modified theory of plasticity and verify the adequacy of approximations of material functions, the kinetics of the stress-strain state of stainless steel 12Х18Н10Т is calculated under rigid cyclic and monotonic loading according to the program (five stages) described in the second section. For the calculations, we used the material functions obtained on the basis of the experimental data in Fig. 2. Comparisons of the calculated (solid curves) and experimental (open circles) results are shown in Figs. 4–7. Dashed curves show the results of calculations based on the variant [10]. Figure 4 shows the cyclic diagram of the 20th cycle of the (last) first stage, monotonic loading in the second stage and the first cycle of the third stage. Figure 5 shows the cyclic diagram of the 200th cycle of the (last) third stage, monotonic loading at the fourth stage and the first cycle of the fifth stage. Changes in the stress swing and average stress of cycles at the first, third and fifth stages of loading are shown in Figs. 6, 7.

figure 4

Fig. 4

figure 5

Fig. 5

figure 6

Fig. 6

figure 7

Fig. 7

A significant improvement is observed in the description of the kinetics of the stress-strain state on the basis of the variant proposed here in comparison with the previous one [10]. As for the changes in the range and average stress of the cycles, the proposed version adequately describes these rather complex processes.

CONCLUSIONS

Based on the analysis of the results of experimental studies of stainless steel, it has been established that isotropic and anisotropic hardening are significantly different during monotonic and cyclic deformation. Also, there are transient hardening processes when changing the processes of monotonic and cyclic, cyclic and monotonic deformation.

Taking into account the revealed features of monotonic and cyclic loading, the equations of the modified theory of plasticity are refined. The basic experiment is determined, a method for identifying material functions is formulated, and material functions of stainless steel 12Х18Н10Т at room temperature are obtained.

Comparison of the results of calculated and experimental studies of stainless steel 12Х18Н10Т under rigid loading, consisting of a sequence of monotonic and cyclic loading modes. The kinetics of the stress-strain state was analyzed, the changes in the range and average stress of the cycle during cyclic loading were considered. A reliable agreement between the calculated and experimental results was obtained.

A sufficiently adequate description by the theory of the processes of change in the kinetics, range and average stress of the cycle under hard loading allows us to assume the possibility of a more adequate description of soft loading processes, especially under nonstationary asymmetric loading modes.