Relaxation of Residual Stresses in a Surface-Hardened Cylinder under Creep Conditions and Rigid Restrictions on Linear and Angular Deformations

Abstract—

A method for solving the boundary value problem of a residual stress relaxation in a surface-hardened solid cylinder under creep conditions with initially defined and rigidly fixed axial deformation and torsion angle has been developed. It includes a phenomenological methodology for reconstructing the stress-strain state after hardening and its kinetics during relaxation of axial load and torsional moment due to creep. In order to illustrate the method, a cylindrical specimen made of ZhS6KP alloy after pneumo-shot peening is considered. A detailed investigation of the residual stress relaxation has been performed for various combinations of initially defined and fixed axial and angular deformations at temperature of 900°C. The results of a comparative analysis of obtained data with data for the residual stress relaxation under pure temperature loading in the absence of mechanical loads are presented.

INTRODUCTION

Surface hardening of parts that is a standard technology in aircraft engine building, power engineering, aircraft manufacturing, and other industries is one of the methods for increasing product reliability indicators (fatigue resistance, wear resistance, microhardness, and other characteristics). The positive effect of surface plastic deformation is associated with the creation of compressive residual stresses (RS) in a thin near-surface layer. They result in an increase in the lifetime of hardened parts in comparison with unhardened ones. This circumstance is shown in the vast number of publications of domestic and foreign researchers, for example, in [1–4].

One of the important problems is the reconstruction of the stress-strain state after hardening, since this information is decisive in the development of methods for solving boundary value problems for hardened structural elements under creep conditions. Various experimental methods applied to cylindrical and prismatic parts make it possible to determine the distribution of only one or two components of the RS tensor over the hardened layer thickness [2]; however, they do not allow for establishing the distribution of the components of the residual plastic strain (PS) tensor.

The development of theoretical methods for reconstruction of RS and PS fields on the basis of direct modeling of a specific technological process is primarily associated with the emergence of powerful computing systems, which stimulated a number of studies where the solution of contact dynamic and quasi-static elastoplastic problems is considered [5–7]. However, it is practically impossible to take into account the full range of parameters in technologies for hardening the surface of parts. Therefore, the obtained results are mainly of a qualitative nature.

The second important problem is the estimation of the kinetics of induced residual stresses in the field of temperature-force (operational) loads, since the relaxation of RS occurs due to creep. As a consequence, it becomes necessary to develop methods for solving boundary value problems with an initial stress-strain state under creep conditions. An analysis of publications shows that this subject is in nascent stage and being developed mainly in the scientific school of Samara State Technical University with the participation of the authors of this article. Let us stress out the article [8], in which the method for solving the boundary value problem on RS relaxation in a hardened cylinder under a tensile axial load and torsional moment is implemented. However, in applied researches, there is another kind of problems, where surface-hardened rods at the initial moment are exposed to axial and circumferential deformations that are then rigidly fixed. A technical example of such a mode of operation is the shrouded blades of the compressor and turbine of an aircraft engine (certainly, with a more complex geometric design). In connection with the above, the purpose of this article is to generalize the method proposed in [8] to the case of RS relaxation in a solid surface-hardened cylindrical specimen under creep conditions with rigid (fixed) constraints on linear and angular deformations.

1 STATEMENT OF THE PROBLEM

We consider a solid cylindrical specimen of radius R, in the surface layer of which RS and PS are induced by surface plastic deformation at normal (“room”) temperature T = T₀. At the first stage, the inverse boundary value problem of reconstruction of the RS and PS fields is solved using partially known (experimental) information on one or two (depending on the hardening technology) components of the RS tensor. Next, the temperature increases up to the operational one T = T₁ $({{T}_{1}} > {{T}_{0}})$; an axial tensile load F₀ and a torsional moment M₀ are applied leading to linear uniform axial and angular deformations (respectively), which are then rigidly fixed. Then the boundary value problem on the relaxation of forces $F = F\left( t \right)$ ($F\left( 0 \right) = {{F}_{0}}$) and $M = M\left( t \right)$ ($M\left( 0 \right) = {{M}_{0}})~$is solved. Against the background of this problem, the RS relaxation occurs in the near-surface layer of the cylinder due to creep of the material. An axisymmetric statement in a cylindrical coordinate system $\left( {r,~{\theta },~z} \right)$ is considered, therefore all components of stress and strain tensors depend only on the coordinate $r \in \left[ {0,~R} \right]$.

2 RECONSTRUCTION OF THE STRESS-STRAIN STATE IN A SOLID CYLINDER AFTER HARDENING

The first stage in solving the problem is to reconstruct the RS and PS fields after hardening. We denote the radial, circumferential, and axial components of the RS tensor by ${\sigma }_{r}^{{{\text{res}}}}$, ${\sigma }_{{\theta }}^{{{\text{res}}}}$, ${\sigma }_{z}^{{{\text{res}}}}$, respectively, and the corresponding components of the PS tensor by q_r, ${{q}_{{\theta }}}$, q_z, respectively. To determine RS and PS, we use the phenomenological method [9], the initial data for which, depending on the hardening technology, are one (${\sigma }_{{\theta }}^{{{\text{res}}}}$) or two (${\sigma }_{{\theta }}^{{{\text{res}}}}$ and ${\sigma }_{z}^{{{\text{res}}}}$) experimentally determined RS diagrams over the hardened layer thickness.

As for any inverse boundary value problem, it is necessary to introduce a number of restrictions on the components of RS and PS tensors to obtain a unique solution. In this method the following hypotheses are introduced: (1) off-diagonal components of the RS and PS tensors are an order of magnitude or more smaller (in absolute value) than the normal components [10], thus they can be neglected; (2) axial and circumferential components of the PS tensor are proportional: ${{q}_{z}}\left( r \right) = {\alpha }{{q}_{{\theta }}}\left( r \right)$, where α is the phenomenological parameter of the hardening anisotropy [9]; (3) there are no secondary plastic deformations in the material compression area. Then the following relations are valid for the components of the RS and PS tensors [9]:

$$\begin{array}{*{20}{c}} {{\sigma }_{r}^{{{\text{res}}}}\left( r \right) = \frac{1}{r}\mathop \smallint \limits_0^r {\sigma }_{{\theta }}^{{{\text{res}}}}\left( {\xi } \right)d\xi } \end{array},$$

(2.1)

$$\begin{gathered} {{q}_{\theta }}(r) = \frac{{(1 + \mu )(1 - 2\mu )}}{{{{E}_{0}}{{{(1 + \alpha \mu )}}^{2}}}}{{r}^{{ - \nu }}}\int\limits_0^r {{{\xi }^{{\nu - 1}}}[\sigma _{r}^{{{\text{res}}}}(\xi ) + (1 + \alpha )\sigma _{\theta }^{{{\text{res}}}}(\xi )]} d\xi \\ - \frac{{1 + \mu }}{{{{E}_{0}}(1 + \alpha \mu )}}[(1 - \mu )\sigma _{\theta }^{{{\text{res}}}}(r) - \mu \sigma _{r}^{{{\text{res}}}}(r)],\quad \nu = \frac{{2 + \alpha }}{{1 + \alpha \mu }}, \\ \end{gathered} $$

(2.2)

$$\begin{array}{*{20}{c}} {{{q}_{z}}\left( r \right) = \alpha {{q}_{{\theta }}}\left( r \right),\quad {{q}_{r}}\left( r \right) = - \left( {1 + {\alpha }} \right){{q}_{{\theta }}}\left( r \right)} \end{array},$$

(2.3)

$$\begin{array}{*{20}{c}} {{\varepsilon }_{z}^{0} = \frac{2}{{{{R}^{2}}}}\mathop \smallint \limits_0^R r\left\{ {{{q}_{z}}\left( r \right) - \frac{{\mu }}{{{{E}_{0}}}}[{\sigma }_{r}^{{{\text{res}}}}\left( r \right) + {\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right)]} \right\}dr} \end{array},$$

(2.4)

$$\begin{array}{*{20}{c}} {{\sigma }_{z}^{{{\text{res}}}}\left( r \right) = {{E}_{0}}[{\varepsilon }_{z}^{0} - {{q}_{z}}\left( r \right)] + \mu [{\sigma }_{r}^{{{\text{res}}}}\left( r \right) + {\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right)]} \end{array},$$

(2.5)

where E₀ is the Young’s modulus of the material at hardening temperature T₀; µ is Poisson’s ratio.

The required components of the RS and PS tensors in a surface-hardened solid cylinder are determined in the following sequence:

$$\begin{array}{*{20}{c}} {{\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right),~\alpha \mathop \to \limits^{\left( {2.1} \right)} ~{\sigma }_{r}^{{{\text{res}}}}\left( r \right)\mathop \to \limits^{\left( {2.2} \right)} {{q}_{{\theta }}}\left( r \right)\mathop \to \limits^{\left( {2.3} \right)} {{q}_{r}}\left( r \right),~{{q}_{z}}\left( r \right)\mathop \to \limits^{\left( {2.4} \right)} {\varepsilon }_{z}^{0}\mathop \to \limits^{\left( {2.5} \right)} {\sigma }_{z}^{{{\text{res}}}}\left( r \right)} \end{array}.$$

(2.6)

Here, above the arrows, there are the numbers of the formulas using which the corresponding values are calculated.

The initial data for applying scheme (2.6) are the dependence for the circumferential component of the residual stress tensor ${\sigma }_{{\theta }}^{{{\text{res}}}} = {\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right)$ and the hardening anisotropy parameter α.

The distribution of the component ${\sigma }_{{\theta }}^{{{\text{res}}}} = {\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right)$ can be determined by experimental methods only in a thin surface layer. To obtain continuous fields for RS and PS according to the scheme (2.6), this information must be extrapolated to the entire region of integration r ∈ [0, R]. To this end, the following approximation is proposed:

$$\begin{array}{*{20}{c}} {{\sigma }_{{\theta }}^{{{\text{res}}}}(r) = {{{\sigma }}_{0}} - {{{\sigma }}_{1}}\exp \left( { - \frac{{{{{(R - h{\text{*}} - r)}}^{2}}}}{{{{b}^{2}}}}} \right)} \end{array},$$

(2.7)

where ${{{\sigma }}_{0}}$, ${{{\sigma }}_{1}}$, h*, b are the parameters to be determined.

The method for identifying the parameter α is also described in [9]. For methods of isotropic surface hardening (pneumo-shot peening, ultrasonic hardening, etc.), the value α = 1 and stress diagrams ${\sigma }_{{\theta }}^{{{\text{res}}}} = {\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right)$ and ${\sigma }_{z}^{{{\text{res}}}} = {\sigma }_{z}^{{{\text{res}}}}\left( r \right)$ practically coincide, and for the methods of anisotropic hardening (roller strengthening, diamond smoothing, etc.), the parameter α ≠ 1 and there is a significant difference in the diagrams for the axial and circumferential components of the RS tensor in the hardened layer [9].

3 DETERMINATION OF THE CHARACTERISTICS OF THE STRESS-STRAIN STATE IN A SURFACE-HARDENED SOLID CYLINDER UNDER TEMPERATURE-FORCE LOADING

First, we consider the temperature loading mode for a cylindrical specimen being heated from the temperature of hardening T₀ (as a rule, the “room” temperature), at which the Young’s modulus of the material is equal to E₀, up to the “operational” temperature T₁ $({{T}_{1}} > {{T}_{0}})$, at which creep deformations develop in the material and which corresponds to the value of Young’s modulus E₁ $({{E}_{1}} < {{E}_{0}})$.

Assuming that no additional plastic deformations arise under temperature loading and, therefore, the quantity ${{q}_{{\theta }}} = {{q}_{{\theta }}}\left( r \right)$ does not depend on temperature, we write relation (2.2) for the moment of complete heating of the specimen up to the temperature T₁ in the form

$$\begin{array}{*{20}{c}} {{{q}_{{\theta }}}\left( r \right) = \frac{{\left( {1 + {\mu }} \right)\left( {1 - 2{\mu }} \right)}}{{{{E}_{1}}{{{\left( {1 + {\alpha \mu }} \right)}}^{2}}}}{{r}^{{ - {\nu }}}}\mathop \smallint \limits_0^r {{{\xi }}^{{{\nu } - 1}}}\frac{{{{E}_{1}}}}{{{{E}_{0}}}}[{\sigma }_{r}^{{{\text{res}}}}\left( {\xi } \right) + \left( {1 + {\alpha }} \right){\sigma }_{{\theta }}^{{{\text{res}}}}\left( {\xi } \right)]d{\xi }~} \\ { - \frac{{1 + {\mu }}}{{{{E}_{1}}\left( {1 + {\alpha \mu }} \right)}}\frac{{{{E}_{1}}}}{{{{E}_{0}}}}[\left( {1 - {\mu }} \right){\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right) - {\mu \sigma }_{r}^{{{\text{res}}}}\left( r \right)].} \end{array}$$

(3.1)

The form of relation (3.1) is similar to (2.2) if all RS diagrams after the hardening are multiplied by the coefficient ${{E}_{1}}{\text{/}}{{E}_{0}}$. Thus, we obtain the RS distribution at the temperature T₁. Note that temperature deformations are not taken into account here, since we conventionally assume that the heating of the sample has been carried out instantaneously, and a uniform temperature field only leads to a bulk change in the geometry of the sample and does not affect the stress state.

Now, we consider the loading of a hardened cylinder by the axial force F₀ and the torsional moment M₀ at time $t = 0 + 0$. It is assumed that after additional loading of a cylindrical specimen (after hardening), its material is in the elastic region. In this case, there is a stepwise change in axial and tangential stresses by the amount of “operational” stresses arising due to external loads, and the stress state is given by the relations:

$$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{\sigma }}_{z}}\left( {r,0 + 0} \right) = \frac{{{{E}_{1}}}}{{{{E}_{0}}}}{\sigma }_{z}^{{{\text{res}}}}\left( r \right) + \frac{{{{F}_{0}}}}{{{\pi }{{R}^{2}}}},\quad {{{\sigma }}_{{\theta }}}\left( {r,0 + 0} \right) = \frac{{{{E}_{1}}}}{{{{E}_{0}}}}{\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right),} \\ {{{{\sigma }}_{r}}\left( {r,0 + 0} \right) = \frac{{{{E}_{1}}}}{{{{E}_{0}}}}{\sigma }_{r}^{{{\text{res}}}}\left( r \right),\quad {\tau }\left( {r,0 + 0} \right) = \frac{{{{M}_{0}}}}{J}r,} \end{array}} \end{array}$$

(3.2)

and the components of the total strain tensor have the form:

$$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{\varepsilon }}_{i}}\left( {r,0 + 0} \right) = \frac{1}{{{{E}_{1}}}}\left[ {\left( {1 + {\mu }} \right){{{\sigma }}_{i}}\left( {r,0 + 0} \right) - {\mu \sigma *}} \right] + {{q}_{i}}\left( r \right)~~~\left( {i = r,~{\theta },z} \right),} \\ {{\gamma }\left( {r,0 + 0} \right) = \frac{{{\tau }\left( {r,0 + 0} \right)}}{{{{G}_{1}}}},\quad {{G}_{1}} = \frac{{{{E}_{1}}}}{{2\left( {1 + {\mu }} \right)}}.} \end{array}} \end{array}$$

(3.3)

Hereinafter, ${{{\sigma }}_{i}} = {{{\sigma }}_{i}}\left( {r,t} \right)$ and ${{{\varepsilon }}_{i}} = {{{\varepsilon }}_{i}}\left( {r,t} \right)$ $\left( {i = r,~{\theta },{\text{z}}} \right)$ denote the dependences for the components of the stress and total strain tensors on the spatial and temporal coordinates; σ* = σ_z(r, 0 + 0) + σ_θ(r, 0 + 0) + ${{{\sigma }}_{r}}(r,0 + 0)$; ${\tau }\left( {r,t} \right) = {{{\sigma }}_{{{\theta }z}}}\left( {r,t} \right)$ is the shear stress; ${\gamma }(r,t) = 2{{{\varepsilon }}_{{{\theta }z}}}(r,t)$ is shear deformation; $J = {\pi }{{R}^{4}}{\text{/}}2$ is the moment of inertia of the cross section about the cylinder axis; G₁ is the shear modulus of the material at temperature T₁.

To describe the process of relaxation of residual stresses, axial force, and torsional moment, it is necessary to solve the boundary value problem on creep of a surface-hardened cylinder at temperature ${{T}_{1}}~$ in the case of rigid constraints on axial deformation and torsion angle with an initial stress-strain state determined by stresses (3.2) and deformations (3.3).

4 METHOD FOR SOLVING THE BOUNDARY VALUE PROBLEM ON CREEP OF A SURFACE-HARDENED SOLID CYLINDER LOADED BY AN AXIAL FORCE AND TORSIONAL MOMENT IN THE CASE OF RIGID CONSTRAINTS ON LINEAR AND ANGULAR DEFORMATIONS

Let us describe the process of relaxation of residual stresses, axial force F = F(t) and torsional moment M = M(t) during the creep of a surface-hardened solid cylinder under rigid loading mode, when the total axial deformation ${{{\varepsilon }}_{z}}\left( {r,t} \right) = {{{\varepsilon }}_{z}}\left( {r,0 + 0} \right) = {\varepsilon }_{z}^{*} = {\text{const}}$ and the torsion angle ${\varphi }\left( t \right) = {\varphi }\left( {0 + 0} \right) = {\varphi\text{*}}$ = const are set. The formulation of the corresponding boundary value problem on creep includes the following relations:

—equilibrium equations:

$$\begin{array}{*{20}{c}} {r\frac{{d{{{\sigma }}_{r}}\left( {r,t} \right)}}{{dr}} + {{{\sigma }}_{r}}\left( {r,t} \right) = {{{\sigma }}_{{\theta }}}\left( {r,t} \right)} \end{array},$$

(4.1)

$$\begin{array}{*{20}{c}} {2\pi \mathop \smallint \limits_0^R {{{\sigma }}_{z}}\left( {r,t} \right)r~dr = F\left( t \right)} \end{array},$$

(4.2)

$$\begin{array}{*{20}{c}} {2\pi \mathop \smallint \limits_0^R {\tau }\left( {r,t} \right){{r}^{2}}~dr = M\left( t \right)} \end{array};$$

(4.3)

—equation of strain compatibility:

$$r\frac{{d{{{\varepsilon }}_{{\theta }}}\left( {r,t} \right)}}{{dr}} + {{{\varepsilon }}_{{\theta }}}\left( {r,t} \right) = {{{\varepsilon }}_{r}}\left( {r,t} \right);$$

(4.4)

—plane section hypothesis:

$$\begin{array}{*{20}{c}} {{{{\varepsilon }}_{z}}\left( {r,t} \right) = {\varepsilon }_{z}^{*}} \end{array};$$

(4.5)

—hypothesis of straight radii:

$$\begin{array}{*{20}{c}} {\gamma \left( {r,t} \right) = r{\varphi \text{*}}} \end{array},$$

(4.6)

where ${\varphi \text{*}} = {\gamma }\left( {r,0 + 0} \right){\text{/}}r = {\text{const;}}$

—boundary conditions:

$$\begin{array}{*{20}{c}} {\mathop {\lim }\limits_{r \to 0} \frac{{d{{{\sigma }}_{r}}\left( {r,t} \right)}}{{dr}} = 0,~~{{{\sigma }}_{r}}\left( {R,t} \right) = 0} \end{array}.$$

(4.7)

Since the time t is a parameter in the relations (4.1)–(4.7), hereinafter we use the operator of the total derivative for the derivatives of the components of the stress and strain tensors with respect to r.

Let us describe the process of relaxation of residual stresses due to creep at a temperature $T = {{T}_{1}}$. We write the relations for the components of the total strain tensor in the form

$$\begin{array}{*{20}{c}} {{{{\varepsilon }}_{i}}\left( {r,t} \right) = {{e}_{i}}\left( {r,t} \right) + {{q}_{i}}\left( r \right) + {{p}_{i}}\left( {r,t} \right)~~~~\left( {i = r,~\theta ,~z} \right)} \end{array},$$

(4.8)

$$\begin{array}{*{20}{c}} {\gamma \left( {r,t} \right) = {{{\gamma }}^{e}}\left( {r,t} \right) + {{{\gamma }}^{p}}\left( {r,t} \right)} \end{array},$$

(4.9)

where ${{e}_{z}}$, ${{e}_{{\theta }}}$, ${{e}_{r}}$, γ^e are the components of the elastic strain tensor; ${{p}_{z}}$, ${{p}_{{\theta }}}$, ${{p}_{r}}$, γ^p are the components of the creep strain tensor. Moreover, at the initial moment of time, the components of the creep strain tensor are equal to zero for all r ∈ [0, R]:

$${{p}_{z}}\left( {r,0} \right) = 0;\quad {{p}_{{\theta }}}\left( {r,0} \right) = 0;\quad {{p}_{r}}\left( {r,0} \right) = 0;\quad {{{\gamma }}^{p}}\left( {r,0} \right) = 0.$$

The problem is reduced to resolving system (4.8) and (4.9) with respect to the stress tensor components.

Let’s write Hooke’s law for elastic deformations:

$$\begin{array}{*{20}{c}} {{{e}_{i}}\left( {r,t} \right) = \frac{1}{{{{E}_{1}}}}\left[ {\left( {1 + {\mu }} \right){{{\sigma }}_{i}}\left( {r,t} \right) - {\mu \bar {\sigma }}} \right]~~~~\left( {i = r,~\theta ,~z} \right)} \end{array},$$

(4.10)

$$\begin{array}{*{20}{c}} {{{{\gamma }}^{e}}\left( {r,t} \right) = \frac{1}{{{{G}_{1}}}}\tau \left( {r,t} \right)} \end{array},$$

(4.11)

where ${\bar {\sigma }} = {{{\sigma }}_{z}}\left( {r,t} \right) + {{{\sigma }}_{{\theta }}}\left( {r,t} \right) + {{{\sigma }}_{r}}\left( {r,t} \right)$.

Substituting (4.5) and (4.10) at i = z into relation (4.8) at i = z, we find the dependence for the axial component of the stress tensor:

$$\begin{array}{*{20}{c}} {{{{\sigma }}_{z}}\left( {r,t} \right) = {{E}_{1}}[{\varepsilon }_{z}^{*} - {{q}_{z}}\left( r \right) - {{p}_{z}}\left( {r,t} \right)] + \mu \left[ {{{{\sigma }}_{{\theta }}}\left( {r,t} \right) + {{{\sigma }}_{r}}\left( {r,t} \right)} \right]} \end{array}.$$

(4.12)

Further applying the procedure from [8] that implements the method for solving the boundary value problem of RS relaxation in a hardened cylinder under a tensile axial load and torsional moment and using (4.1), (4.4), (4.5), (4.12) in the system of Eqs. (4.8) and (4.9), the stress tensor components σ_θ and σ_z are successively eliminated. As a result, we get an inhomogeneous differential equation of the second order with respect to σ_r:

$$\begin{array}{*{20}{c}} {{{r}^{2}}\frac{{{{d}^{2}}{{{\sigma }}_{r}}\left( {r,t} \right)}}{{d{{r}^{2}}}} + 3r\frac{{d{{{\sigma }}_{r}}\left( {r,t} \right)}}{{dr}} = g\left( {r,t} \right)} \end{array}$$

(4.13)

that has the following right-hand side:

$$\begin{array}{*{20}{c}} {g\left( {r,t} \right) = \frac{{{{E}_{1}}}}{{1 - {{{\mu }}^{2}}}}\left[ {\frac{{2 + {\alpha }}}{{1 + {\alpha }}}{{q}_{r}}\left( r \right) + {{p}_{r}}\left( {r,t} \right) - {{p}_{{\theta }}}\left( {r,t} \right)} \right.~} \\ {\left. {\, - r\left( {\frac{{d{{p}_{{\theta }}}\left( {r,t} \right)}}{{dr}} + {\mu }\frac{{d{{p}_{z}}\left( {r,t} \right)}}{{dr}}} \right) + \frac{{r\left( {1 + {\alpha \mu }} \right)}}{{1 + {\alpha }}}\frac{{d{{q}_{r}}\left( r \right)}}{{dr}}} \right].} \end{array}$$

The solution of the equation (4.13) under boundary conditions (4.7) is written as follows:

$${{{\sigma }}_{r}}\left( {r,t} \right) = - \mathop \smallint \limits_r^R \frac{1}{{{{{\xi }}^{3}}}}\mathop \smallint \limits_0^{\xi } g\left( {{\eta },t} \right){\eta }d{\eta }d{\xi }{\text{.}}$$

With the known σ_r from equation (4.1), we find the dependence for the circumferential component of the stress tensor:

$${{{\sigma }}_{{\theta }}}\left( {r,t} \right) = \frac{d}{{dr}}\left[ {r{{{\sigma }}_{r}}\left( {r,t} \right)} \right].$$

Knowing the quantities σ_r and ${{{\sigma }}_{{\theta }}}$, we can determine σ_z by the formula (4.12) and then the value of F(t) from equation (4.2).

Substituting (4.11) into relation (4.9) and taking into account (4.6), we obtain the distribution of the tangential component of the stress tensor:

$${\tau }\left( {r,t} \right) = {{G}_{1}}[r{\varphi \text{*}} - {{{\gamma }}^{p}}\left( {r,t} \right)]$$

after which we determine the value of M(t) from the relation (4.3).

5 CALCULATION RESULTS AND THEIR ANALYSIS

In the model calculations, we have used cylindrical specimens made of ZhS6KP alloy of radius R = 3.76 mm (r ∈ [0, 3.76] mm) and have been hardened by pneumo-shot peening of the surface, which is a standard technology for hardening parts made of this alloy, for example, in engine building.

In the calculations, we have adopted the following values: ${{T}_{0}} = 20~^\circ {\text{C}}$, ${{T}_{1}} = 900~^\circ {\text{C}}$, ${{E}_{0}} = 2~$ × 10⁵ MPа, ${{E}_{1}} = 1.364~$ × 10⁵ MPa, μ = 0.3. The experimental data for the component ${\sigma }_{z}^{{{\text{res}}}} = {\sigma }_{z}^{{{\text{res}}}}\left( r \right)~$ in the surface layer that are given in [8] have been used as the initial information. For pneumo-shot peening of the surface, the coefficient of anisotropy hardening is α = 1 and the diagrams for circumferential and axial RS are close to each other. Therefore, to identify the parameters of relation (2.7) in the first approximation, we have used the experimental data for the axial component of the RS tensor (points in Fig. 1). Next, the parameters ${{{\sigma }}_{0}}$, ${{{\sigma }}_{1}}$, and $b$ in (2.7) have been varied and for each of their sets, the algorithm (6) has been implemented until the minimum of the functional of the mean square deviation of the calculated data for ${\sigma }_{z}^{{{\text{res}}}}$ from the experimental values has been reached. As a result, the following values of the approximation parameters (2.7) for ${\sigma }_{{\theta }}^{{{\text{res}}}}$ have been obtained: ${{{\sigma }}_{0}} = 22.554$ MPа, ${{{\sigma }}_{1}} = 1027.454$ MPа, and $b = 9.313$ × 10^–2 mm. The quantity h* is initially equal to zero (h* = 0), since the case h* ≠ 0 is possible only if the extremum of the dependence ${\sigma }_{{\theta }}^{{{\text{res}}}} = {\sigma }_{{\theta }}^{{{\text{res}}}}\left( r \right)~$ is not on the surface, but in the subsurface layer [9]. In Fig. 1, the solid line shows the dependence for ${\sigma }_{z}^{{{\text{res}}}} = {\sigma }_{z}^{{{\text{res}}}}\left( r \right)$ (MPa).

Fig. 1.

The theory of steady-state creep has been used to simulate the relaxation process for RS and the forces $F = F\left( t \right)$ and $M = M\left( t \right)$:

$$\begin{array}{*{20}{c}} {{{{\dot {p}}}_{{ij}}} = \frac{3}{2}c{{S}^{{m - 1}}}\left( {{{{\sigma }}_{{ij}}} - \frac{1}{3}{{{\delta }}_{{ij}}}{{{\sigma }}_{{kk}}}} \right)\quad \left( {i,j,k = 1,2,3} \right)} \end{array},$$

(5.1)

where $S$ is the stress intensity; c, m are the material constants. For the ZhS6KP alloy at a temperature of ${{T}_{1}} = 900~^\circ {\text{C}}$ we have [8]: $c = 1.5$ × 10^–20 (MPа)^–m h^–1, m = 6.62.

Note that the creep problem has been solved numerically using the well-known “time steps” method [8] and relations (5.1) being integrated by the Euler method.

Calculations are performed with various combinations of initial tensile load ${{F}_{0}}~$ and torsional moment M₀. Figure 2 shows a typical picture of the relaxation of the axial force $F = F\left( t \right)$ ($t \in \left[ {0,~100} \right]$ h) at a fixed value of the initial torsion angle by the moment ${{M}_{0}} = 16700$ N mm. Solid lines 1, 2, 3 correspond to the values of $~F = F\left( t \right)~$ with the initial values ${{F}_{0}} = \left\{ {0,~~4441.5,\,\,~8882.9} \right\}$ N, respectively.

Fig. 2.

In Fig. 3, as an illustration of the calculation results, the solid lines show the typical distribution of σ_z = ${{{\sigma }}_{z}}(r,t)$ (MPa) for ${{F}_{0}} = 8882.9$ N, ${{M}_{0}} = 16700$ N mm at different moments of time. Number 1 corresponds to the initial state after hardening (t = 0–0), 2 is for the temperature loading, 3 is for force loading (t = 0 + 0), 4 and 5 are for the time t = 20 h and t = 100 h, respectively. Here, the dashed lines show the distribution of the same component of the RS tensor under conditions of pure thermal exposure at ${{T}_{1}} = 900~^\circ {\text{C}}$.

Fig. 3.

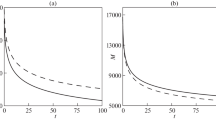
In Fig. 4, solid lines show the dependences for stress ${{{\sigma }}_{z}} = {{{\sigma }}_{z}}\left( {R,t} \right)$ (MPa) on the cylinder surface after temperature-force loading at t ∈ [0, 100] h (numbers 1, 2, 3 correspond to loading modes in Fig. 2). Here, for comparison, the dashed line shows the dependence for the same stress under thermal exposure conditions (purely temperature loading at ${{F}_{0}} = 0$, ${{M}_{0}} = 0$ and ${{T}_{1}} = 900~^\circ {\text{C}}$). Note that for the circumferential component, there is a stepwise change in its value only due to a change in temperature, and when external force disturbances are applied, there is no stepwise change in ${{{\sigma }}_{{\theta }}} = {{{\sigma }}_{{\theta }}}\left( {r,t} \right)~$ in contrast to the component ${{{\sigma }}_{z}} = {{{\sigma }}_{z}}\left( {r,t} \right)$.

Fig. 4.

A detailed parametric study of the RS relaxation problem for ${{{\sigma }}_{z}}$, ${{{\sigma }}_{{\theta }}}$, ${{{\sigma }}_{r}}~$ has shown an insignificant effect of the initially specified (and rigidly fixed) elastic axial and angular deformations on the kinetics of all components of the RS tensor.

CONCLUSIONS

A technique has been developed for solving boundary value problems of RS relaxation in surface-hardened solid cylinders under creep conditions with an initial stress-strain state caused by given (and rigidly fixed) axial and angular deformations. An analysis of the model calculations for hardened specimens made of ZhS6KP alloy at T = 900°C has shown an insignificant effect of the initial stress-strain state on the RS relaxation process in relation to the case of pure thermal exposure. This is a positive factor in the applied aspect from the point of view of engineering practice, for example, in aircraft engine building, where surface plastic hardening is a regular technological operation.