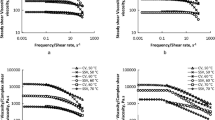1 Introduction

An asphalt binder can exhibit non-Newtonian behavior at a certain temperature range. It has been identified that liquids exhibiting non-Newtonian behavior can be divided into three types, which are shear-thinning liquids, shear-thickening liquids and Bingham plastics [1]. As a non-Newtonian liquid, an asphalt binder is of the shear-thinning type [1,2,3]. The shear-thinning or pseudo-plastic behavior of an asphalt binder is characterized by the dependence of shear viscosity on the shear rate; specifically, the measured shear viscosity shows a decreasing tendency as the applied shear rate increases [2]. A comprehensive understanding of such a behavior is crucial for the development of test methods to evaluate the rutting potential and predict the mixing and compaction temperatures of asphalt binders.

The shear viscosity versus shear rate curve, known as flow curve, is normally employed to investigate the shear-thinning behavior of asphalt binders [1]. The flow curve describes the evolution of steady-state shear viscosity with the growth of shear rate. It is generally believed that the flow curve reaches an upper asymptote when the shear rate approaches zero and a lower asymptote at infinitely high shear rate [2]. The viscosity value corresponding to the upper asymptote, named as zero shear viscosity (ZSV), is a rheological parameter that gives an indication of the Newtonian behavior exhibited by asphalt binders within a certain shear rate range [1,2,3]. The ZSV is now widely utilized to evaluate the rutting potential of asphalt binders [4,5,6,7]. It was found that for both conventional and polymer-modified asphalt binders, the ZSV measured at 60 °C had a close correlation with the results of wheel tracking tests performed on asphalt mixtures [8].

As a crucial step in determining the ZSV, the flow curve of an asphalt binder can be established using the shear rate sweep test, which consists of a series of constant strain rate tests [7, 9, 10]. The shear rate sweep test provides the most direct measurement of the ZSV. At each shear rate, the shear viscosity is recorded when the asphalt binder reaches a steady-state flow. After the test is completed, a rheological model, such as the Cross model, the Carreau model or the Carreau-Yasuda model, is employed to fit the flow curve in order to estimate the ZSV with better accuracy [1, 11, 12]. In addition to the shear rate sweep test, the flow curve can be also obtained by conducting creep tests at multiple stress levels [3, 7]. For each creep test, the steady-state shear viscosity is measured when a linear growth of the shear strain is observed with the increasing creep time. The flow curve is then established by plotting the steady-state shear viscosity versus the shear rate, and the ZSV can be determined accordingly. It is noted that both the shear rate sweep test and the creep test can be seen as steady-state flow tests because of the required steady-state flow in each test method.

The shear-thinning behavior of asphalt binders can be also investigated with the application of frequency sweep test [4,5,6,7]. The viscosity measured in oscillation mode is termed as complex viscosity, which is calculated as the ratio of complex modulus to angular frequency. The Cox–Merz rule builds the connection between the complex viscosity and the steady-state shear viscosity, as presented in Eq. (1) [13]. It is an empirical relationship that is widely used in polymeric systems [14, 15].

$$\left| {\eta^{ *} \left( \omega \right)} \right|{ = }\eta \left( {\dot{\gamma }} \right)$$
(1)

where: \(\omega\) = angular frequency, rad/s; \(\left| {\eta^{ *} \left( \omega \right)} \right|\) = complex viscosity, \({\text{pa}} \cdot {\text{s}}\); \(\dot{\gamma }\) = shear rate, s−1; and \(\eta \left( {\dot{\gamma }} \right)\) = steady-state shear viscosity, \({\text{pa}} \cdot {\text{s}}\). As is seen from Eq. (1), the Cox–Merz rule states the equivalency between the complex viscosity and the steady-state shear viscosity in the case that the angular frequency is numerically identical to the shear rate. In accordance with this rule, the ZSV of an asphalt binder can be determined by establishing a \(\left| {\eta^{ *} \left( \omega \right)} \right|\) versus \(\omega\) curve. Models analogous to those used for describing the flow curve can be also applied to the \(\left| {\eta^{ *} \left( \omega \right)} \right|\) versus \(\omega\) curve. As a result of the model fitting, the ZSV of the tested asphalt binder can be readily obtained.

It can be summarized that the shear thinning behavior of asphalt binders can be investigated in the steady-state shear domain and in the oscillatory shear domain. The developed test methods mentioned previously are used widely in the pavement society, among which the creep test and the frequency sweep test have been accepted in the European standards to determine the ZSV and the equiviscous temperature of asphalt binders, respectively [2, 3]. However, there are still some concerns over the use of the ZSV that need to be further addressed: (1) whether a yield stress exists at relatively low shear rates; and (2) whether the Cox–Merz rule is applicable to asphalt binders. In recent years, lots of efforts have been devoted to verifying the applicability of the Cox–Merz rule [9, 10, 15,16,17,18,19], while limited attention has been paid to investigating the yield stress that an asphalt binder may exhibit at low shear rates [11].

Unlike what is commonly believed, the flow curve of an asphalt binder will not reach an upper asymptote if the asphalt binder behaves as a shear-thinning liquid with yield stress. In this case, only when the shear stress is larger than the yield stress will the asphalt binder start to flow [11]. Therefore, a linear growth in the shear viscosity can be observed with the decrease of shear rate within the yield stress region. Li et al. conducted an extensive experimental study on such a topic. Shear rate sweep tests were performed on ten different types of asphalt binders at 60 °C in order to measure the steady-state shear viscosities at the shear rates ranging from 1.25 × 10−6–1.25 × 103 s−1 [11]. The test results confirmed the existence of yield stress with respect to each asphalt binder. The Herschel–Bulkley model was employed to characterize the evolution of shear stress with the increase of shear rate and to further quantify the yield stress at each test condition. However, the Carreau model with no consideration of yield stress was applied to part of the flow curve so as to determine the ZSV. Therefore, an improved rheological model is needed that takes into account the yield stress.

As for the second concern, many attempts were made to verify the applicability of the Cox-Merx rule to asphalt binders. However, inconsistent conclusions were obtained [9, 10, 15,16,17,18,19]. In addition, none of these attempts investigated the possible yield stress of asphalt binders. Shan et al. conducted shear rate sweep tests and frequency sweep tests on three types of unmodified asphalt binders at multiple temperatures [9]. They found that the Cox–Merz rule was followed in the shear-thinning region but not always followed in the ZSV region. A different conclusion was drawn by Pérez-Lepe et al., who performed shear rate sweep tests and frequency sweep tests on asphalt binders modified by high-density polyethylene (HDPE) [17]. They observed that the Cox–Merz rule was not followed at shear rates and frequencies outside the ZSV region for all tested asphalt binders. Apparently, these inconsistent conclusions limit the use of the Cox–Merz rule for asphalt binders.

This study focused on characterizing the shear-thinning behavior of asphalt binders with two objectives: (1) identify the existence of yield stress behavior and employ an improved rheological model to describe the flow curve of asphalt binders; and (2) verify the applicability of the Cox–Merz rule to asphalt binders with consideration of yield stress. This paper is organized as follows. The next section describes the test materials and the test protocol developed for the characterization of the shear thinning behavior of asphalt binders. Based on the test results, Sect. 3 identifies the existence of yield stress from the developed test protocol. An improved rheological model is adopted in Sect. 4 to describe the flow curve and the \(\left| {\eta^{ *} \left( \omega \right)} \right|\) versus \(\omega\) curve and to further determine the ZSV. The applicability of the Cox–Merz rule is verified in Sect. 5 with consideration of yield stress. The final section summarizes the major findings of this study.

2 Materials and laboratory tests

2.1 Test materials

Three types of neat asphalt binders were selected as the test materials, referred to as N1, N2 and N3, respectively. These asphalt binders were initially graded based on penetration. In this study, the high-temperature PG grade and true PG grade of each asphalt binder were determined following the guidelines detailed in ASTM D7175 and ASTM D7643 [20] [21]. Therefore, N1, N2 and N3 were identified as PG 64-XX, PG 70-XX and PG 64-XX, respectively, and the high-temperature true PG grade of each asphalt binder was 67.2, 70.6 and 64.5 °C, respectively. The neat asphalt binders were chosen in this study because they were the base asphalt binders for future modification. If yield stress is observed for the neat asphalt binders, the modified asphalt binders would exhibit such a behavior as well. Afterwards, multiple specimens were prepared for each asphalt binder using the silicon mold method illustrated in ASTM D7175 [20].

2.2 Test protocol

In this study, a Dynamic Shear Rheometer (DSR) was employed to characterize the shear-thinning behavior of asphalt binders. Two types of rheological tests were performed on asphalt binder specimens, including frequency sweep test and shear rate sweep test. The 25 mm parallel-plate geometry and a 1 mm gap were adopted for both tests. The DSR was able to apply a torque ranging from 10 nNm to 200 mNm in the frequency sweep test with a resolution of 0.1 nNm, and the torque range became 20 nNm to 200 mNm in the shear rate sweep test with the same torque resolution. With respect to each asphalt binder, these two tests were conducted at three temperature levels, namely 50, 60 and 70 °C. As mentioned previously, the ZSV is a rheological parameter widely utilized to evaluate the high temperature performance of asphalt binders. The temperature 60 °C was selected for the rheological tests in this study because it is generally seen as a representative temperature for the temperature range in which rutting occurs [22]. The temperatures 50 and 70 °C were chosen to obtain test data at a wider temperature range in order to validate the accuracy of the rheological model adopted in this study.

The frequency sweep test was conducted under controlled-strain mode with an angular frequency range of 1.25 × 10−2–1.25 × 102 rad/s. Prior to the frequency sweep test, a strain amplitude sweep test was carried out at the lowest test temperature (i.e. 50 °C) and at the highest frequency (i.e. 1.25 × 102 rad/s) to determine the appropriate strain amplitude that could ensure the linear viscoelastic state of each asphalt binder [23]. It was found that a strain amplitude of 0.5% was applicable to all of the three asphalt binders. Therefore, the controlled-strain frequency sweep test was performed on each asphalt binder with a strain amplitude of 0.5% at three temperatures. Regarding each frequency sweep test, a logarithmic sampling method was used to collect five data points of \(\left| {\eta^{ *} \left( \omega \right)} \right|\) per decade, which produced a total of 21 data points of \(\left| {\eta^{ *} \left( \omega \right)} \right|\) at the end of the test.

As for the shear rate sweep test, the asphalt binder specimen was sheared at a series of shear rates that stepped up from 1.25 × 10−5 to 1.25 × 102 s−1 for asphalt binder N1 and N2 at all three temperatures and asphalt binder N3 at 50 and 60 °C. The selected shear rate range was 1.25 × 10−3 to 1.25 × 102 s−1 for asphalt binder N3 tested at 70 °C because the steady-state equilibrium could not be reached at vanishing small shear rates. The DSR apparatus sampled five data points of \(\eta \left( {\dot{\gamma }} \right)\) per decade logarithmically. At each shear rate, the equilibrium viscosity was recorded by the DSR when the test specimen reached a steady-state flow. It should be noted that the 1.25 × 102 s−1 was not necessarily required because the shear rate sweep test was terminated once a sudden drop in shear stress was observed during each test [9]. According to the research conducted by Shan et al., the sudden drop in shear stress indicated that damage occurred at this shear rate, which resulted in a reduction of the load-bearing capacity of the test specimen [9]. As a consequence, only the measured data before the critical shear rate would be used in the subsequent analysis.

The frequency sweep test was performed when the test specimen stayed in the linear viscoelastic state, which introduced no damage into the specimen. However, the shear rate sweep test was not terminated until the test specimen was damaged. In order to eliminate the effect of sample-to-sample variability on the verification of the Cox–Merz rule, the two types of tests were performed successively on the same asphalt binder specimen. Specifically, the frequency sweep test was conducted first, followed by the shear rate sweep test, and no rest period was allowed between these two tests. With respect to each asphalt binder, two replicates were used at each temperature for the proposed test protocol in order to verify the repeatability of the test results. Considering all test results, the flow curves and the \(\left| {\eta^{ *} \left( \omega \right)} \right|\) versus \(\omega\) curves were established, from which the yield stress behavior could be confirmed.

3 Identification of yield stress behavior

In this study, the frequency sweep test and the shear rate sweep test were performed successively on the same specimen in order to investigate the shear-thinning behavior of selected asphalt binders in the oscillatory shear domain and in the steady-state shear domain, respectively. As mentioned previously, the shear rate sweep test is capable of providing the most direct measurement of the ZSV of an asphalt binder. Thus, the test results obtained from the shear rate sweep tests were analyzed first.

3.1 Identification of yield stress behavior from Shear rate sweep test

Using the major outputs of each shear rate sweep test, the steady-state shear viscosity and the shear stress were plotted against the corresponding shear rate in the same graph but using different vertical axes. Double logarithmic coordinates were adopted in such a graph. The steady-state shear viscosity is related to the shear stress by the following relationship:

$$\eta \left( {\dot{\gamma }} \right) = \frac{{\tau \left( {\dot{\gamma }} \right)}}{{\dot{\gamma }}}$$
(2)

where: \(\tau \left( {\dot{\gamma }} \right)\) = measured shear stress when the asphalt binder reached a steady-state flow at a certain shear rate, \({\text{pa}}\). The flow curve and the log–log plot of shear stress versus shear rate were then utilized to identify the possible yield stress behavior. Figure 1 presents the test results of asphalt binder N3 measured at three test temperatures (e.g. 50, 60 and 70 °C) as an example. In this study, the specimen number was named as Binder Type–Temperature–Replicate Number. For example, N3–50 °C–1 indicated the asphalt binder N3 was tested at the temperature of 50 °C using the first replicate specimen.

Fig. 1
figure 1

Evolution of steady-state shear viscosity and shear stress with shear rate at different temperatures

Full size image

It was observed from the flow curves shown in Fig. 1 that the steady-state shear viscosity reached a Newtonian plateau within a specific range of shear rates at each temperature. At this Newtonian plateau, the shear viscosity remained approximately the same irrespective of the applied shear rate. However, such a plateau failed to represent an upper asymptote by which the ZSV was defined. This was because the shear viscosity increased with the reduction of shear rate before the Newtonian plateau region. This fact demonstrated that the asphalt binder exhibited the yield stress behavior at all three temperatures although no clear yield stress was observed because of the insufficient shear rate range limited by the DSR capacity. It was also observed from Table 1 that the ZSV of an asphalt binder decreased as the test temperature increased. The yield stress behavior suggested that it was infeasible to use the shear viscosity at a vanishingly small shear rate as a rutting indicator.

Table 1 Determined model parameters using the modified Carreau model
Full size table

Due to space limitations, the test results of asphalt binders N1 and N2 are not presented in this paper. With respect to these two asphalt binders, yield stress behavior was also observed at each test condition. As a consequence, the asphalt binders were classified as shear-thinning liquids with yield stress (or equivalently yield stress shear-thinning liquids). As pointed out by Doraiswamy et al., the ZSV of a yield stress shear-thinning liquid was not the shear viscosity at zero shear rate; instead, it corresponded to the shear viscosity of a Newtonian plateau at low shear rates [24]. It can be more accurate to use the term Newtonian plateau viscosity in lieu of ZSV. The shear rate range corresponding to the Newtonian plateau is dependent on the test temperature.

3.2 Identification of yield stress behavior from frequency sweep test

In this subsection, the test results of complex viscosity and complex modulus obtained from the frequency sweep tests were employed to characterize the shear-thinning behavior of selected asphalt binders. The complex viscosity is calculated as the ratio of complex modulus to angular frequency, as shown in Eq. (3).

$$\left| {\eta^{*} \left( \omega \right)} \right| = \frac{{\left| {G^{*} \left( \omega \right)} \right|}}{\omega }$$
(3)

where: \(\left| {G^{*} \left( \omega \right)} \right|\) = complex modulus, \({\text{pa}}\). With respect to the test results at each test condition, two log–log plots were built in the same graph but using different vertical axes, namely, the log–log plot of \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) and the log–log plot of \(\left| {G^{*} \left( \omega \right)} \right|\) versus \(\omega\). The test results of asphalt binder N3 measured at three test temperatures are illustrated in Fig. 2 as an example.

Fig. 2
figure 2

Evolution of complex viscosity and complex modulus with angular frequency at different temperatures

Full size image

It was found from Fig. 2 that for each \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve, the complex viscosity remained basically unchanged within a certain range of angular frequencies, which indicated the existence of a Newtonian plateau. Such a Newtonian plateau provided a means to determine the ZSV from the frequency sweep test. Similar to what was observed in the flow curves shown in Fig. 1, the complex viscosity in Fig. 2b, c didn’t reach an upper asymptote at infinitely small angular frequencies; instead, it kept increasing with the decrease of angular frequency prior to the Newtonian plateau region, which therefore demonstrated the yield stress behavior of asphalt binder N3 in the frequency sweep test. In addition, the yield stress could be visually confirmed via the \(\left| {G^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve shown in Fig. 2c, in which the measured complex modulus stayed almost constant at the angular frequencies ranging from 1.25 × 10−2 to 1.25 × 10−1 rad/s.

As for Fig. 2a, within the selected angular frequency range, no yield stress behavior was observed, which, however, was attributed to the insufficient frequency range limited by the DSR capacity. It was concluded that the yield stress behavior became more significant as the test temperature increased. Similar findings were obtained from the test results of the other two asphalt binders. Accordingly, the yield stress behavior of the three asphalt binders could also be confirmed by using the frequency sweep tests.

3.3 Effect of yield stress behavior on ZSV determination

Both the shear rate sweep tests and the frequency sweep tests confirmed the yield stress behavior of selected asphalt binders. The asphalt binders were then classified as shear-thinning liquids with yield stress. As a result, the ZSV was no longer an indicator of the shear viscosity at zero shear rate but represented the viscosity of a Newtonian plateau at low shear rates.

In recent years, the concept of low shear viscosity (LSV) was proposed in lieu of the ZSV, where “low” indicates close to zero [2, 5, 7]. Based on the LSV, a test protocol for determination of equiviscous temperature was developed using the DSR in low frequency oscillation mode, as detailed in the CEN/TS 15324 (2008) [2]. The LSV is applicable when a Newtonian plateau doesn’t exist in the \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve. In this case, the complex viscosity measured at the frequency of 10−3 rad/s or 10−4 Hz is considered as an approximation of the ZSV, as recommended by De Visscher and CEN/TS 15324 (2008), respectively [2, 5]. It is believed that the LSV is more representative of the ZSV of an asphalt binder when the frequency is closer to zero [2]. Apparently, the LSV concept was put forward without awareness of the yield stress behavior of asphalt binders. The determined LSV is likely to be larger than the ZSV if the frequency 10−3 rad/s or 10−4 Hz corresponds to the yield stress region. The yield stress behavior of asphalt binders highlights the importance of determining the ZSV from a Newtonian plateau [25].

4 Modeling of flow curve and determination of ZSV

4.1 Herschel–Bulkley model

A rheological model is required for an accurate determination of the ZSV from the flow curve or the \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve. The asphalt binders were classified as shear-thinning liquids with yield stress in the previous section. However, none of the commonly used rheological models, including the Cross model, the Carreau model and the Carreau-Yasuda model, are able to describe the yield stress behavior [1, 11, 12]. Li et al. employed the Herschel–Bulkley model to characterize the evolution of shear stress with the increase of shear rate [11]. The fitting results demonstrated that the Herschel–Bulkley model was able to describe the yield stress behavior well. The Herschel–Bulkley model is of the following form:

$$\left\{ \begin{array}{ll} \tau \left( {\dot{\gamma }} \right) = \tau_{0} + K\dot{\gamma }^{n},& \tau > \tau_{0} \hfill \\ \dot{\gamma } = 0, &\tau \le \tau_{0} \hfill \\ \end{array} \right.$$
(4)

where: \(\tau_{0}\) = yield stress, P.a; \(K\) = consistency factor; and \(n\) = flow index.

In addition to the Herschel–Bulkley model, the Carreau model with no consideration of yield stress was applied by Li et al. to part of the flow curve so as to determine the ZSV [11]. As a matter of fact, a model analogous to Eq. (4) can be obtained for the shear viscosity versus shear rate in accordance with Eq. (2), as shown in Eq. (5).

$$\eta \left( {\dot{\gamma }} \right) = \frac{{\tau_{0} }}{{\dot{\gamma }}} + K\dot{\gamma }^{n - 1}$$
(5)

In an attempt to characterize the yield stress shear-thinning behavior of asphalt binders, Eqs. (4) and (5) were employed in this study to model the test results obtained from the shear rate sweep test. The model parameters were determined by fitting Eq. (4) to the shear stress versus shear rate curve and then substituted into Eq. (5) to model the flow curve. It was found that although Eq. (4) provided a satisfactory fit of the shear stress versus shear rate curve, Eq. (5) failed to account for the Newtonian behavior which exhibited at low shear rates in the flow curve. Figure 3 presents the fitted flow curve of asphalt binder specimen N3–50 °C–1 as an example. Although the yield stress region could be well described by the model, no Newtonian plateau was observed in the fitted flow curve because the fitted shear viscosity kept decreasing with the growth of shear rate.

Fig. 3
figure 3

Fitted flow curve of specimen N3–50 °C–1 using Eq. (4)

Full size image

The absence of the Newtonian plateau in Fig. 3 demonstrated the inability of the Herschel–Bulkley model to characterize the yield stress shear-thinning behavior of asphalt binders. In addition, the Herschel–Bulkley model lacked of a parameter that was directly related to the ZSV of asphalt binders, which made it difficult to determine the ZSV after curve fitting. Therefore, an improved rheological model is needed.

4.2 Modified Carreau model

In this study, a modified Carreau model was employed to characterize the yield stress shear-thinning behavior of asphalt binders. The traditional Carreau model, as presented in Eq. (6), has been utilized by many researchers to determine the ZSV of asphalt binders when the test results show no yield stress within selected shear rate or frequency range [11]. This model can well describe the Newtonian behavior at low shear rates and the power-law behavior at high shear rates of asphalt binders.

$$\frac{{\eta \left( {\dot{\gamma }} \right) - \eta_{\infty } }}{{\eta_{0} - \eta_{\infty } }} = \frac{1}{{\left[ {1 + \left( {a\dot{\gamma }} \right)^{2} } \right]^{{{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0pt} 2}}} }}$$
(6)

where: \(\eta_{0}\) = ZSV, \({\text{pa}} \cdot {\text{s}}\); \(\eta_{\infty }\) = limiting shear viscosity at infinitely high shear rate, \({\text{pa}} \cdot {\text{s}}\); \(a\) = shear rate coefficient, s; and \(b\) = shear rate index. The flow curves shown in Fig. 1 indicated that the limiting shear rate viscosity was not achieved in the shear rate sweep test because the test specimen was damaged at the critical shear rate. The parameter included in Eq. (6) was therefore omitted in this study, which led to:

$$\eta \left( {\dot{\gamma }} \right) = \frac{{\eta_{0} }}{{\left[ {1 + \left( {a\dot{\gamma }} \right)^{2} } \right]^{{{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0pt} 2}}} }}$$
(7)

As stated previously, the traditional Carreau model fails to take the yield stress into account. In accordance with the Herschel–Bulkley model, the term \({{\tau_{0} } \mathord{\left/ {\vphantom {{\tau_{0} } {\dot{\gamma }}}} \right. \kern-0pt} {\dot{\gamma }}}\) was added to Eq. (7) in order to characterize the yield stress behavior of asphalt binders. Accordingly, a modified Carreau model was formulated as Eq. (8). This modified Carreau was initially developed by Poslinski et al. to investigate the shear-thinning behavior of filled polymeric systems [26]. On the basis of Eqs. (2) and (8), the shear stress corresponding to each steady-state shear viscosity could be determined using Eq. (9).

$$\eta \left( {\dot{\gamma }} \right) = \frac{{\tau_{0} }}{{\dot{\gamma }}} + \frac{{\eta_{0} }}{{\left[ {1 + \left( {a\dot{\gamma }} \right)^{2} } \right]^{{{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0pt} 2}}} }}$$
(8)
$$\tau \left( {\dot{\gamma }} \right) = \tau_{0} + \frac{{\eta_{0} \dot{\gamma }}}{{\left[ {1 + \left( {a\dot{\gamma }} \right)^{2} } \right]^{{{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0pt} 2}}} }}$$
(9)

The modified Carreau model was developed for modeling the flow curve of asphalt binders. Hence, with respect to each test condition, the model parameters were determined by fitting Eq. (8) to the flow curve using the target error function shown in Eq. (10).

$${\text{Error}}_{1} = \sum\limits_{i = 1}^{N} {\left( {\frac{{\eta \left( {\dot{\gamma }} \right)_{m,i} - \eta \left( {\dot{\gamma }} \right)_{p,i} }}{{\eta \left( {\dot{\gamma }} \right)_{m,i} }}} \right)^{2} }$$
(10)

where: \(N\) = number of the measured data points; \(\eta \left( {\dot{\gamma }} \right)_{m,i}\) = measured steady-state shear viscosity, \({\text{pa}} \cdot {\text{s}}\); and \(\eta \left( {\dot{\gamma }} \right)_{p,i}\) = fitted steady-state shear viscosity, \({\text{pa}} \cdot {\text{s}}\). The determined model parameters were then substituted into Eq. (9) to characterize the evolution of shear stress with the increase of shear rate. Table 1 lists the ZSV determined at each test condition, the coefficient of determination (R2) between the measured and predicated values of \(\eta \left( {\dot{\gamma }} \right)\) and the R2 between the measured and predicated values of \(\tau \left( {\dot{\gamma }} \right)\).

It was seen from Table 1 that the values of \(R^{2}_{{\eta \left( {\dot{\gamma }} \right)}}\) and \(R^{2}_{{\tau \left( {\dot{\gamma }} \right)}}\) were larger than 0.96 at all test conditions, which proved the accuracy of Eqs. (8) and (9). The fitted curves of asphalt binder specimen N3–70 °C–1 was illustrated in Fig. 4 as an example to demonstrate the excellent agreement between the measured and fitted values. The yield stress behavior was well captured by Eq. (9), as exhibited in Fig. 4b. Therefore, the modified Carreau model was able to account for the yield stress behavior at low shear rates, the Newtonian behavior at medium shear rates and the power-law behavior at high shear rates.

Fig. 4
figure 4

Fitted curves of specimen N3–70 °C–1 using the modified Carreau model (shear rate sweep test)

Full size image

Analogous to Eqs. (8) and (9), Eqs. (11) and (12) expressed in the form of the modified Carreau model were adopted to model the log–log plot of \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) and the log–log plot of \(\left| {G^{*} \left( \omega \right)} \right|\) versus \(\omega\), respectively. The target error function shown in Eq. (13) was utilized to solve the unknown parameters in Eq. (11) through nonlinear regression.

$$\left| {\eta^{*} \left( \omega \right)} \right| = \frac{{\tau_{0} }}{\omega } + \frac{{\eta_{0} }}{{\left[ {1 + \left( {a\omega } \right)^{2} } \right]^{{{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0pt} 2}}} }}$$
(11)
$$\left| {G^{*} \left( \omega \right)} \right| = \tau_{0} + \frac{{\eta_{0} \omega }}{{\left[ {1 + \left( {a\omega } \right)^{2} } \right]^{{{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0pt} 2}}} }}$$
(12)
$${\text{Error}}_{2} = \left( {\frac{{\left| {\eta^{*} \left( \omega \right)} \right|_{m} - \left| {\eta^{*} \left( \omega \right)} \right|_{p} }}{{\left| {\eta^{*} \left( \omega \right)} \right|_{m} }}} \right)^{2}$$
(13)

where: \(\eta \left( {\dot{\gamma }} \right)_{m,i}\) = measured complex viscosity, \({\text{pa}} \cdot {\text{s}}\); and \(\eta \left( {\dot{\gamma }} \right)_{p,i}\) = fitted complex viscosity, \({\text{pa}} \cdot {\text{s}}\). The determined ZSV, the R2 between the measured and fitted values of \(\left| {\eta^{*} \left( \omega \right)} \right|\) and the R2 between the measured and fitted values of \(\left| {G^{*} \left( \omega \right)} \right|\) are also summarized in Table 1. The accuracy of Eqs. (11) and (12) was validated by the calculated values of \(R^{2}_{{\left| {\eta^{*} \left( \omega \right)} \right|}}\) and \(R^{2}_{{\left| {G^{*} \left( \omega \right)} \right|}}\). Figure 5 presents the fitted curves of asphalt binder specimen N3–70 °C–1 as an example to demonstrate the closeness between the measured and fitted values. It was observed from Fig. 5b that the fitted curve showed a plateau value of complex modulus at small angular frequencies. Thus, the modified Carreau model was capable of accurately characterizing the yield stress shear-thinning behavior of asphalt binders.

Fig. 5
figure 5

Fitted curves of specimen N3–70 °C–1 using the modified Carreau model (frequency sweep test)

Full size image

It should be noted that after the curve fitting, the value of \(\tau_{0}\) was reliable only when the test data of \(\tau \left( {\dot{\gamma }} \right)\) or \(\left| {G^{*} \left( \omega \right)} \right|\) showed an obvious plateau, whereas the ZSV was regarded reliable and accurate in all cases due to the Newtonian plateau observed in the test data of \(\eta \left( {\dot{\gamma }} \right)\) and \(\left| {\eta^{*} \left( \omega \right)} \right|\) at each test condition. In order to verify the repeatability of the developed test protocol, the coefficient of variation (COV) of the two ZSV values of each pair of replicates were further calculated and are summarized in Table 1. The low COV values (less than 5%) statistically demonstrated the good repeatability of the test results in terms of the ZSV. As a consequence, the two ZSV values at each test condition were averaged and considered as the final ZSV.

5 Verification of the Cox–Merz rule

In accordance with Eq. (1), the Cox–Merz rule is an empirical relationship that states the equivalency between \(\left| {\eta^{*} \left( \omega \right)} \right|\) and \(\eta \left( {\dot{\gamma }} \right)\) when the angular frequency is numerically identical to the shear rate [13]. In order to verify the applicability of the Cox–Merz rule to asphalt binders, this study performed the frequency sweep test and the shear rate sweep test on the same asphalt binder specimen at three temperatures. As a nondestructive test, the frequency sweep test was conducted first, followed by the shear rate sweep test that was terminated when damage was introduced into the test specimen. This test protocol highlighted the importance of the yield stress behavior of asphalt binders, and effectively eliminated the effect of sample-to-sample variability on the verification of the Cox–Merz rule. As a result, the applicability of the Cox–Merz rule was examined by establishing the flow curve and the \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve in the same graph with respect to each replicate at each temperature.

Figure 6 presents the test results of asphalt binder N3 as an example to compare the flow curve with the \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve. All the three graphs in Fig. 6 indicated that there was an overlap between the flow curve and the \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve. The following conclusions were drawn from Fig. 6 and Table 1 that:

Fig. 6
figure 6

Comparisons between flow curve and \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve

Full size image
  1. (1)

    The Cox–Merz rule was not followed in the yield stress region. The \(\tau_{ 0}\) determined from the shear rate sweep test was remarkably different from that determined from the frequency sweep test in regard to each replicate;

  2. (2)

    The Cox–Merz rule was followed in part of the ZSV region. It was confirmed from Table 1 that the ZSV obtained from the shear rate sweep test and that obtained from the frequency sweep test were very close to each other. However, the ZSV region determined from the shear rate sweep test was wider than that determined from the frequency sweep test; and

  3. (3)

    The Cox–Merz rule was followed in part of the shear-thinning region. As the shear rate sweep test was terminated once a sudden drop in shear stress was observed, the corresponding shear-thinning region was observed to be narrower than that determined from the frequency sweep test.

As stated previously, the ZSV is employed as a rutting indicator of asphalt binders in the pavement society. Of the three conclusions, the second conclusion proved the validity of determining the ZSV in the steady-state shear domain and in the oscillatory shear domain. The ZSV values determined from the frequency sweep tests were plotted against those determined from the shear rate sweep tests with regard to all specimens, which resulted in a total of 18 data points. It was found that those data points lied close to the equivalence line with a coefficient of correlation (r) of 0.9994, which demonstrated the closeness between the ZSV values obtained from the two test methods. Therefore, it was reasonable to determine the ZSV of an asphalt binder using either test method.

6 Conclusions

This study focused on the characterization of the shear-thinning behavior of asphalt binders. The frequency sweep test and the shear rate sweep test were performed on three types of neat asphalt binders at 50, 60 and 70 °C. These two types of tests were carried out successively on the same asphalt binder specimen in order to eliminate the effect of sample-to-sample variability on the verification of the Cox–Merz rule. Specifically, the frequency sweep test was conducted first, followed by the shear rate sweep test, and no rest period was allowed between these two tests. The major findings of this present study are summarized as follows based on the test results of the developed test protocol:

  1. (1)

    The steady-state shear viscosity or the complex viscosity reached a Newtonian plateau within a specific range of shear rates or angular frequencies at each temperature. Such a plateau failed to represent an upper asymptote because the viscosity increased with the reduction of shear rate or angular frequency before the Newtonian plateau region. This fact demonstrated that the selected asphalt binders exhibited the yield stress behavior at all three temperatures;

  2. (2)

    The asphalt binders were classified as shear-thinning liquids with yield stress. As a result, the ZSV was not the shear viscosity at zero shear rate but represented the viscosity of a Newtonian plateau at low shear rates. It can be more accurate to use the term Newtonian plateau viscosity in lieu of ZSV;

  3. (3)

    Although the Herschel–Bulkley model provided a satisfactory fit of the shear stress versus shear rate curve, it failed to account for the Newtonian behavior which exhibited at low shear rates in the flow curve. Similar findings were obtained when the Herschel–Bulkley model was applied to the test results obtained from the frequency sweep tests;

  4. (4)

    A modified Carreau model was employed to characterize the yield stress shear-thinning behavior of asphalt binders. The modified Carreau model was proved able to account for the yield stress behavior at low shear rates or angular frequencies, the Newtonian behavior at medium shear rates or angular frequencies and the power-law behavior at high shear rates or angular frequencies; and

  5. (5)

    There was an overlap between the flow curve and the \(\left| {\eta^{*} \left( \omega \right)} \right|\) versus \(\omega\) curve. It was demonstrated that the Cox–Merz rule was followed in part of the ZSV region and part of the shear-thinning region but not followed in the yield stress region. The ZSV values determined from the frequency sweep tests were close to those determined from the shear rate sweep tests with a coefficient of correlation of 0.9994. Therefore, it was reasonable to determine the ZSV of an asphalt binder using either the shear rate sweep test or the frequency sweep test.