1 Introduction

It is critically important to repair concrete cracks, which seriously deteriorate concrete’s strength, performance and durability [1]. As a promising approach to repair the concrete cracks, electrochemical deposition method (EDM) has been applied to marine structures or other situations in which the traditional repairing methods are not adequate [2–5]. The healing effects of this method are due to the fact that the electrochemical deposition products can fill the (micro-)cracks and (micro-)voids in the concrete [2–18]. During the past 20 years, numerous works have been conducted on the EDM, which include different ways to produce damaged specimens, factors influencing the healing effectiveness of the EDM and assessing methods on the healing effectiveness [2–18]. However, existing literatures mainly focus on the experimental procedures, and few studies have disclosed the healing mechanism of the EDM with rigorous analytical models, particularly the micromechanical models at the microstructural level. To address these issues, the authors have recently proposed micromechanical models for saturated concrete repaired by the EDM [19]. Specifically, the healed saturated concrete is described at the micro level and represented by a three-phase composite made up of the water, the deposition products and the intrinsic concrete. Meanwhile, the Mori–Tanaka method based multilevel homogenization scheme is utilized to predict the effective properties of the saturated concrete during the healing process [19].

As an extension of our latest works [19, 20], a differential-scheme based micromechanical framework is proposed to quantitatively characterize and predict the mechanical performance of concrete healed by the EDM in this paper. Three different states of the healing process, including no healing, partial healing and complete healing, are quantitatively investigated by incorporating the differential-scheme and the generalized self-consistent method together based on the multiphase healing model we presented recently. The rest of this paper is organized as follows. Section 2 introduces the differential-scheme for the two-phase composite. The effective properties at three different states of the healing process are quantitatively predicted by modifying the differential-scheme for saturated concrete repaired by EDM. Meanwhile, modification procedures are adopted to consider the water effects and shapes of the pores in the healed concrete in Sect. 3. Numerical examples including experimental validations and comparisons with existing micromechanical models are presented in Sect. 4. Some conclusions are reached in the final section.

2 The differential-scheme for two-phase composite

2.1 The effective properties of a composite

One goal of continuum micromechanics is to estimate the effective elastic properties of a material defined over the representative volume element (RVE). The RVE is based on a ‘mesoscopic’ length scale, which is considerably larger than the characteristic length scale of particles (inhomogeneities) but smaller than the characteristic length scale of a macroscopic specimen [21]. Take a two-phase composite as an example, the effective elastic stiffness tensor \(\mathbf{D}\) of the composite is defined through

$${\bar{\varvec{\sigma }}} = \mathbf{D:}{\bar{\varvec{\varepsilon }}}\;$$
(1)

with

$${\bar{\varvec{\sigma }}} \equiv \frac{1}{V}\int\limits_{V} {{\varvec{\upsigma}}\left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} = \frac{1}{V}\left[ {\int\limits_{{V_{0} }} {{\varvec{\upsigma}}\left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} + \int\limits_{{V_{1} }} {{\varvec{\upsigma}}\left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} } \right]$$
(2)
$${\bar{\varvec{\varepsilon }}} \equiv \frac{1}{V}\int\limits_{V} {{\varvec{\upvarepsilon}}\left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} = \frac{1}{V}\left[ {\int\limits_{{V_{0} }} {{\varvec{\upvarepsilon}}\left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} + \int\limits_{{V_{1} }} {{\varvec{\upvarepsilon}}\left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} } \right]$$
(3)

where V is the volume of an RVE, V 0 is the volume of the matrix, and \(V_{1}\) is the volume of the inhomogeneity; \({\bar{\varvec{\sigma }}}\) and \({\bar{\varvec{\varepsilon }}}\) are volume averaged stress and strain of the RVE, respectively.

2.2 The differential scheme

In terms of the inclusion-based micromechanical theory and the average stress method [21–24], the effective elastic stiffness tensor of the two-phase composite can be rephrased as Eq. (4):

$$\mathbf{D} = \mathbf{D}_{0} + \phi \left( {\mathbf{D}_{\text{I}} - \mathbf{D}_{0} } \right){\mathbf{A}}\;$$
(4)

where \(\mathbf{D}_{\mathbf{0}}\) is the elastic stiffness tensor of the matrix phase, \(\mathbf{D}_{\text{I}}\) is the elastic stiffness tensor of the inhomogeneity, \({\mathbf{A}}\) is the strain concentration tensor for the inhomogeneity; \(\phi\) denotes the volume fraction of the inhomogeneity.

Let us define \(\phi = \varOmega_{1} /\left( {\varOmega_{0} + \varOmega_{1} } \right)\) and \(\phi + \Delta \phi = \left( {\varOmega_{1} + \Delta \varOmega } \right)/\left( {\varOmega_{0} + \varOmega_{1} + \Delta \varOmega } \right)\), where \(\varOmega_{0}\) and \(\varOmega_{1}\) represent the volume of the matrix phase and the inclusion phase in the current composite, respectively; \(\Delta \varOmega\) denotes the increment of inclusion volume. For the differential method, a composite with the volume fraction of inclusion equal to \(\, \phi + \Delta \phi\), can be treated as the equivalent composite with the volume fraction of inclusion equal to \(\Delta \varOmega /\left( {\varOmega_{0} + \varOmega_{1} + \Delta \varOmega } \right)\). It is noted that the matrix phase in the equivalent composite is the current composite, which includes the current matrix (\(\varOmega_{0}\)) and current inclusion (\(\varOmega_{1}\)). According to Eq. (4), the effective properties of the material can be obtained [22, 23, 25, 26]

$$\mathbf{D}\left( {\phi + \Delta \phi } \right) = \mathbf{D}\left( \phi \right) + \frac{\Delta \varOmega }{{\left( {\varOmega_{0} + \varOmega_{1} + \Delta \varOmega } \right)}}\left( {\mathbf{D}_{I} - \mathbf{D}\left( \phi \right)} \right){\mathbf{A}}\left( {\mathbf{D}\left( \phi \right)} \right)\;$$
(5)

Equation (5) can be rephrased as below through the simple derivation

$$\frac{{\mathbf{D}\left( {\phi + \Delta \phi } \right) - \mathbf{D}\left( \phi \right)}}{\Delta \phi } = \frac{1}{1 - \phi }\left( {\mathbf{D}_{\text{I}} - \mathbf{D}\left( \phi \right)} \right){\mathbf{A}}\left( {\mathbf{D}\left( \phi \right)} \right)\;$$
(6)

with

$$\Delta \phi = \frac{{\varOmega_{1} + \Delta \varOmega }}{{\varOmega_{0} + \varOmega_{1} + \Delta \varOmega }} - \frac{{\varOmega_{1} }}{{\varOmega_{0} + \varOmega_{1} }} = \frac{{\left( {1 - \phi } \right)\Delta \varOmega }}{{\left( {\varOmega_{0} + \varOmega_{1} + \Delta \varOmega } \right)}}$$
(7)

When \(\Delta \phi \to 0\), Eq. (6) can be expressed as

$$\frac{{{\text{d}}{\mathbf{D}}\left( \phi \right)}}{{{\text{d}}\phi }} = \frac{1}{1 - \phi } \, \cdot \left( {{\mathbf{D}}_{\text{I}} - {\mathbf{D}}\left( \phi \right)} \right):{\mathbf{A}}\left( {{\mathbf{D}}\left( \phi \right)} \right) \,$$
(8)

The composite effective properties with no inclusion effects should be the same as those of the matrix phase, which implies

$${\mathbf{D}}\left( \phi \right)\left| {_{\phi = 0}} = \right.{\mathbf{D}}_{0}$$
(9)

When the Eshelby method is considered, we write

$${\mathbf{A}} = \;\left[ {\mathbf{I} + \mathbf{SD}\left( \phi \right)^{ - 1} (\mathbf{D}_{\text{I}} - \mathbf{D}\left( \phi \right))} \right]^{ - 1}$$
(10)

where \(\mathbf{S}\) is Eshelby’s tensor, which depends on \({\mathbf{D}}\left( \phi \right)\) and the shape of the inclusions; \(\mathbf{I}\) defines the fourth-order isotropic identity tensor.

3 Differential-scheme based micromechanical predictions for the effective properties of saturated concrete repaired by the EDM

3.1 Micromechanical model for saturated concrete repaired by the EDM

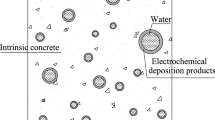
At the micro level, the healed saturated concrete element is composed of water, the deposition products, mortar, coarse aggregates, micro-cracks, micro-voids, and the constituent interfaces [19, 20, 27, 28]. To study the deposition product’s healing effects through micromechanical framework, the three traditional solid phases, including the mortar, coarse aggregates and their interfaces, are merged into one matrix phase, namely the “intrinsic” concrete, in the RVE [19, 20, 27, 28]; the deposition products and the water phase (occupying the spaces of micro-cracks and micro-voids) are accordingly considered as the inclusion phases in the saturated concrete element. Furthermore, following assumptions are adopted to set up our micromechanical model: (1) The shape of the water-filled cracks or voids within the healed concrete is spherical, (2) during the healing process the volume of the deposition products is proportional to the volume of the spherical pore, and (3) the interfaces are perfect (well bonded) between the deposition products and the intrinsic concrete matrix [19, 20, 27–30].

According to the above assumptions, a micromechanical model for the saturated concrete element healed by the EDM can be proposed, as exhibited in Fig. 1a [19]. The equivalent inclusion can be obtained by homogenization of the two-phase composite made up of the water and the deposition products, as shown in Fig. 1b. During the healing process of saturated concrete, the water phase is replaced by the deposition products phase. By predicting the effective properties using our micromechanical model, the mechanical performance of the concrete can be quantitatively assessed during the healing process. Different with our recent work [19, 20, 27, 28], a differential-scheme based homogenization process is utilized to obtain the properties of the healed saturated concrete according to [31–45]. Furthermore, three different states of the healing process, including no healing, partial healing and complete healing, are quantitatively investigated based on our proposed multiphase healing model.

Fig. 1
figure 1

Micromechanical representations: a the multiphase micromechanical model for saturated concrete healed by the EDM; b the equivalent inclusion

Full size image

3.2 The effective properties of saturated healed concrete at two extreme states

The first extreme state is that there is no electrochemical deposition product (no healing process) in the concrete at all (which is equal to a saturated concrete). Therefore, the only inclusion phase in our proposed model is water itself. Let \(\mathbf{D}_{1}\) and \(\mathbf{D}_{3}\) represent the stiffness tensor of the water phase and the intrinsic concrete; Let \(\mathbf{D}_{\text{e1}}\) be the stiffness tensor of the equivalent composite of the saturated concrete predicted by the differential scheme;\(\;\phi_{F}\) denote the volume fraction of water in the saturated concrete. For the isotropic matrix and spherical equivalent inclusions, the tensorial components of \(\mathbf{I}, \; \mathbf{D}_{1}, \; \mathbf{D}_{3},\) and \({\mathbf{D}}_{\text{e1}}\) are as follows:

$$I_{ijkl} = \frac{1}{3}\delta_{ij} \delta_{kl} + \frac{1}{2}\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} - \frac{2}{3}\delta_{ij} \delta_{kl} } \right)$$
(11)
$$D_{3ijkl} = K_{3} \delta_{ij} \delta_{kl} + \mu_{3} \left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} - \frac{2}{3}\delta_{ij} \delta_{kl} } \right)$$
(12)
$$D_{1ijkl} = K_{1} \delta_{ij} \delta_{kl} + \mu_{1} \left(\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} - \frac{2}{3}\delta_{ij} \delta_{kl}\right )$$
(13)
$$D_{{{\text{e}}1ijkl}} = K_{{{\text{e}}1}} \delta_{ij} \delta_{kl} + \mu_{{{\text{e}}1}} \left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} - \frac{2}{3}\delta_{ij} \delta_{kl} } \right)$$
(14)

where \(\delta_{ij}\) is the Kronecker delta. \(K_{3}\), \(\mu_{3}\) (\(K_{1}\), \(\mu_{1}\)) are respectively the bulk modulus and shear modulus of the intrinsic concrete (water), and \(K_{{{\text{e}}1}}\), \(\mu_{\text{e1}}\) are those of the equivalent composite of the saturated concrete predicted by the differential scheme, correspondingly.

By replacing the matrix phase and inhomogeneities (inclusion phase) with the intrinsic concrete and water, the differential-scheme is modified to obtain the effective properties of the saturated concrete. By substituting Eqs. (11)–(14) into Eqs. (8)–(10), the effective bulk modulus and shear modulus of the saturated concrete are obtained by solving the following nonlinear ordinary differential equations after some derivations:

$$\frac{{{\text{d}}K_{\text{e1}} }}{{d\phi_{\text{F}} }} + \frac{{(K_{\text{e1}} - K_{1} )\left( {3K_{\text{e1}} + 4\mu_{\text{e1}} } \right)}}{{\left( {1 - \phi_{\text{F}} } \right)\left( {3K_{1} + 4\mu_{\text{e1}} } \right)}} = 0$$
(15)
$$\frac{{{\text{d}}\mu_{\text{e1}} }}{{{\text{d}}\phi_{\text{F}} }} + \frac{{5\mu_{\text{e1}} \left( {\mu_{\text{e1}} - \mu_{1} } \right)\left( {3K_{\text{e1}} + 4\mu_{\text{e1}} } \right)}}{{\left( {1 - \phi_{\text{F}} } \right)\left[ {3K_{\text{e1}} \left( {3\mu_{\text{e1}} + 2\mu_{1} } \right) + 4\mu_{\text{e1}} \left( {2\mu_{\text{e1}} + 3\mu_{1} } \right)} \right]}} = 0$$
(16)

When the porosity is zero, the properties of the saturated concrete should be equal to those of intrinsic concrete, which implies the initial conditions as below

$$K_{\text{e1}} \left( 0 \right) = K_{3}$$
(17)
$$\mu_{\text{e1}} \left( 0 \right) = \mu_{3}$$
(18)

The second extreme state is that the saturated concrete has been completely healed by the EDM. Therefore, the healed concrete is effectively a two-phase composite with isotropic spherical deposition products as the inclusion phase. Suppose that \(K_{\text{e2}}\) and \(\mu_{\text{e2}}\) (\(K_{2}\) and \(\mu_{2}\)) are the bulk modulus and shear modulus of the completely healed concrete (deposition products). By respectively replacing \(K_{\text{e1}}\), \(\mu_{\text{e1}}\) and \(K_{1}\), \(\mu_{1}\) in Eqs. (15)–(18) with \(K_{\text{e2}}\), \(\mu_{\text{e2}}\) and \(K_{2}\), \(\mu_{2}\), the effective properties of completely healed concrete can be similarly achieved with the differential scheme, which can be expressed as below

$$\frac{{{\text{d}}K_{\text{e2}} }}{{{\text{d}}\phi_{\text{F}} }} + \frac{{(K_{\text{e2}} - K_{2} )\left( {3K_{\text{e2}} + 4\mu_{\text{e2}} } \right)}}{{\left( {1 - \phi_{\text{F}} } \right)\left( {3K_{2} + 4\mu_{\text{e2}} } \right)}} = 0$$
(19)
$$\frac{{{\text{d}}\mu_{\text{e2}} }}{{{\text{d}}\phi_{\text{F}} }} + \frac{{5\mu_{\text{e2}} \left( {\mu_{\text{e2}} - \mu_{2} } \right)\left( {3K_{\text{e2}} + 4\mu_{\text{e2}} } \right)}}{{\left( {1 - \phi_{\text{F}} } \right)\left[ {3K_{\text{e2}} \left( {3\mu_{\text{e2}} + 2\mu_{2} } \right) + 4\mu_{\text{e2}} \left( {2\mu_{\text{e2}} + 3\mu_{2} } \right)} \right]}} = 0$$
(20)

with the initial conditions as below

$$K_{\text{e2}} \left( 0 \right) = K_{3}$$
(21)
$$\mu_{\text{e2}} \left( 0 \right) = \mu_{3}$$
(22)

3.3 The effective properties of saturated concreted partially healed by EDM

As to saturated concrete partially healed by EDM, the two inclusion phases (water and deposition products) should be taken into considerations. According to [31–45], the differential-scheme based two-level homogenization scheme is employed to attain the effective properties of the saturated healed concrete, which is a three-phase composite made up of the intrinsic concrete, the deposition products and the water phase. Through the first level homogenization, as shown in Fig. 1b, the equivalent inclusion can be obtained with the generalized self-consist model by modifying its inner- and outer-layer phases into the water phase and the deposition products, respectively [46, 47]. Accordingly, the effective bulk modulus and shear modulus for the equivalent inclusion can be expressed by Eqs. (23) and (24), correspondingly:

$$K_{\text{F}} = K_{2} + \frac{{\phi_{\text{FD}} (K_{1} - K_{2} )\;(3K_{2} + 4\mu_{2} )}}{{3K_{2} + 4\mu_{2} + 3\;(1 - \phi_{\text{FD}} )\;(K_{1} - K_{2} )}}$$
(23)
$$A\left( {\frac{{\mu_{\text{F}} }}{{\mu_{2}}}}\right)^{2} + B\left( {\frac{{\mu_{\text{F}} }}{{\mu_{2} }}} \right) + C = 0$$
(24)

where \(\phi_{\text{FD}}\) is the volume fraction of the water phase in the two-phase composite composed by the water and the deposition products. Further, \(K_{1}\), \(K_{2}\) and \(K_{\text{F}}\)(\(\mu_{1}\), \(\mu_{2}\) and \(\mu_{\text{F}}\)) denote the bulk modulus (the shear modulus) for the water, the deposition products and the equivalent inclusion after the first level homogenization, respectively. \(A\), \(B\), \(C\) are parameters dependent on \(\phi_{\text{FD}}\), the properties of the water and those of deposition products. See details in our previous work [19, 20, 27, 28].

Let us define \(K_{S}\) and \(\mu_{S}\) as the effective bulk modulus and shear modulus of the saturated healed concrete. In this differential-scheme based micromechanical framework, these two effective properties can be obtained with the second level homogenization. Specifically, by replacing \(K_{\text{e1}}\), \(\mu_{\text{e1}}\), \(K_{1}\), and \(\mu_{1}\) in Eqs. (15)–(18) with \(K_{\text{S}}\), \(\mu_{\text{S}}\), \(K_{\text{F}}\), and \(\mu_{\text{F}}\), the effective properties of the partially healed concrete (\(K_{\text{S}}\) and \(\mu_{\text{S}}\)) can be calculated by solving the following nonlinear ordinary differential equations

$$\frac{{{\text{d}}K_{\text{S}} }}{{{\text{d}}\phi_{\text{F}} }} + \frac{{(K_{\text{S}} - K_{\text{F}} )\left( {3K_{\text{S}} + 4\mu_{\text{S}} } \right)}}{{\left( {1 - \phi_{\text{F}} } \right)\left( {3K_{\text{F}} + 4\mu_{\text{S}} } \right)}} = 0$$
(25)
$$\frac{{{\text{d}}\mu_{\text{S}} }}{{{\text{d}}\phi_{\text{F}} }} + \frac{{5\mu_{\text{S}} \left( {\mu_{\text{S}} - \mu_{\text{F}} } \right)\left( {3K_{\text{S}} + 4\mu_{\text{S}} } \right)}}{{\left( {1 - \phi_{\text{F}} } \right)\left[ {3K_{\text{S}} \left( {3\mu_{\text{S}} + 2\mu_{\text{F}} } \right) + 4\mu_{\text{S}} \left( {2\mu_{\text{S}} + 3\mu_{\text{F}} } \right)} \right]}} = 0$$
(26)

with the initial conditions as below

$$K_{\text{S}} \left( 0 \right) = K_{3}$$
(27)
$$\mu_{\text{S}} \left( 0 \right) = \mu_{3}$$
(28)

With the bulk modulus and shear modulus, the material’s Young’s modulus and Poisson’s ratio can be computed from the following well-known expression:

$$E = \frac{9K\mu }{3K + \mu }$$
(29)
$$\nu = \frac{1 - 2\mu /3K}{2 + 2\mu /3K}$$
(30)

where \(K\), \(\mu\), \(E\) and \(\nu\) are the material bulk modulus, shear modulus, Young’s modulus and Poisson’s ratio, respectively.

3.4 Modifications to the differential-scheme based predictions

The following two procedures are performed to consider the water effects. On one hand, further hydration occurs when the concrete is saturated [48, 49]. Like previous works [19, 20, 48, 49], \(\phi_{\text{F}}\) in Eqs. (15)–(16) and Eqs. (25)–(26) should be replaced by the effective porosity of saturated concrete \(\phi_{\text{EF}} = m\phi_{\text{F}}\) to consider these impacts, where m is a coefficient, and \(m < 1\). On the other hand, the water viscosity improves the shear modulus of the concrete [48, 49]. The similar function \(f(\phi_{\text{F}} ) = a\,\phi_{\text{F}}^{2} + b\,\phi_{\text{F}} + 1\) from [19, 20, 48, 49] is adopted to modify the micromechanical estimations of the shear modulus [19, 49]. See details in [19, 49].

The pores can’t be assumed to be spherical any more for the dried specimen [19, 20, 29, 49]. From the view point of micromechanics, (micro-)cracks or (micro-)voids within concrete can be classified as ‘‘stiff’’ pores and ‘‘soft’’ pores, respectively. The former can be represented as a sphere, and the latter can be signified as an ellipse or a disk, which generally decrease the stiffness of the concrete [19, 20, 29, 49]. All pores in the saturated concrete are assumed to be spherical since the water is able to resist the deformations of the specimen [19, 20, 29, 49]. However, this assumption is not reasonable when the specimen is dried; i.e., the influence of the pore shape should be considered [19, 20, 29, 49]. Based on [19, 50], three modification coefficients, \(\chi_{K}\), \(\chi_{\mu }\) and \(\chi_{E}\), are similarly employed in the extension:

$$\chi_{K} = \frac{{K_{\alpha }^{*} }}{{K_{\alpha = 1}^{*} }}$$
(31)
$$\chi_{\mu } = \frac{{\mu_{\alpha }^{*} }}{{\mu_{\alpha = 1}^{*} }}$$
(32)
$$\chi_{E} = \frac{{E_{\alpha }^{*} }}{{E_{\alpha = 1}^{*} }}$$
(33)
$$\alpha = \frac{1}{N}\;\sum\limits_{i = 1}^{N} {\,\frac{{a_{i} }}{{b_{i} }}}$$
(34)

where \(a_{i}\) and \(b_{i}\) are the lengths of the pores’ minor and major axes, respectively, and N is the number of different pores within the concrete specimens; \(\alpha\) is the equivalent aspect ratio; \(K_{\alpha = 1}^{*}\), \(\mu_{\alpha = 1}^{*}\) and \(E_{\alpha = 1}^{*}\) (\(K_{\alpha }^{*}\), \(\mu_{\alpha }^{*}\) and \(E_{\alpha }^{*}\)) are respectively the predicted effective bulk modulus, the effective shear modulus and Young’s modulus, when \(\alpha = 1\) (\(\alpha < 1\)). The effective properties \(K_{\alpha = 1}^{*}\), \(\mu_{\alpha = 1}^{*}\), \(E_{\alpha = 1}^{*}\), \(K_{\alpha }^{*}\), \(\mu_{\alpha }^{*}\) and \(E_{\alpha }^{*}\) of the dry healed concrete can be obtained using the micromechanical iteration schemes [50]. See details in [19, 50].

It is noted that Eqs. (37)–(43) in [19] are derived based on the assumption that the properties of deposition products and intrinsic concrete are the same with each other. The homogenization process should be utilized when this assumption does not hold. It implies that \(K_{2}\) and \(\mu_{2}\) in Eqs. (37)–(43) of [19] should be replaced by \(K_{\text{av}}\) and \(\mu_{\text{av}}\), which are obtained by the following expressions:

$$K_{\text{av}} = 0.5\;\,[\phi_{\text{G}} K_{2} + (1 - \phi_{\text{G}} )K_{3} ] + 0.5\;\left[ {\frac{{K_{2} K_{3} }}{{\phi_{\text{G}} K_{3} + (1 - \phi_{\text{G}} )K_{2} }}} \right]$$
(35)
$$\mu_{\text{av}} = 0.5\;[\phi_{\text{G}} \mu_{2} + (1 - \phi_{\text{G}} )\mu_{3} ] + 0.5\left[ {\frac{{\mu_{2} \mu_{3} }}{{\phi_{\text{G}} \mu_{3} + (1 - \phi_{\text{G}} )\mu_{2} }}} \right]$$
(36)
$$\phi_{\text{G}} = \frac{{V_{\text{de}} }}{{V_{\text{de}} + V_{\text{in}} }}$$
(37)

where \(K_{\text{av}}\), \(\mu_{\text{av}}\) are the effective bulk modulus and shear modulus of the equivalent material made up of the deposition products and the intrinsic concrete. \(\phi_{\text{G}}\) is the volume fraction of the deposition product in the equivalent composite; \(V_{\text{de}}\) and \(V_{\text{in}}\) are the volume of deposition products and intrinsic concrete.

So the effective properties of the healed saturated concrete in the dry state can be obtained as follows: Firstly, the properties of water should be replaced by those of air in the first step homogenization; secondly, the water viscosity in pores should be ignored in the second step homogenization; thirdly, with the results calculated by Eqs. (37)–(43) of [19], the properties of the healed saturated concrete in the dry state can be obtained by multiplying the results of the second step homogenization and the modifying coefficients obtained with Eqs. (31)–(34).

Furthermore, if the nondestructive testing methods, such as the ultrasonic waves, are employed to test the effective dynamic properties of concrete repaired by the EDM, the static properties should be modified into dynamic properties according to the relationships between the two types [19, 51].

4 Verifications

4.1 Comparisons with experiments and existing models of the EDM

Our predictions are compared with the experimental data and the estimations of the existing models to verify the capacity of the proposed differential-scheme based micromechanical framework for saturated concrete repaired by the EDM.

Firstly, with the modifications in Sect. 3.4, the differential-scheme based micromechanical model for the healed saturated concrete can be modified to predict the properties of the healed specimen when they are dried. Here, the dynamic Young’s moduli in the dry state of the specimen before and after healing in Chen’s experiment [28] are adopted to validate the proposed micromechanical model. The average initial porosity of the specimen is 0.299. The average pulse-velocity of its intrinsic concrete is 5134.5 m/s. The density is 2537.9 kg/m3 and the Poisson’s ratio is 0.229. As exhibited in Fig. 2, the predictions obtained from the micromechanical model correspond well with those obtained experimentally with the maximum relative difference between the experimental data and our results being 16.3 %. Overall, the predictions in this paper are still close to those of Zhu et al. [19].

Fig. 2
figure 2

The comparisons among our predictions, results of [19] and those obtained experimentally [28]

Full size image

Secondly, the existing models [19] are utilized to verify our proposed differential-scheme based micromechanical framework. The predicting results of the different models are compared using three types of deposition products, whose properties are listed in Table 1 [19]. The properties of the intrinsic concrete and water are listed in Table 2 according to [19].

Table 1 Properties of three types of deposition products [19]
Full size table
Table 2 Properties of intrinsic concrete and water [19]
Full size table

Figure 3a–c present the comparisons of mechanical properties between our predictions and those of [19] during healing process. From Fig. 3a, it can be observed that our predictions for the shear modulus of the equivalent composite are very close to those of [19], which means our proposed differential-scheme based micromechanical model is also capable of describing the healing process from the micro-scale level. Meanwhile, the results of the two different micromechanical models show that the values of effective shear modulus gradually increase during the healing process due to the accumulation of deposition products. The stronger the deposition product is, the greater the equivalent composite becomes during the healing process. As to the effective bulk modulus and Young’s modulus, predictions in this paper are also similar to those obtained by [19], which are exhibited by Fig. 3b, c, respectively. Moreover, the properties of the deposition products still play an important role in the mechanical properties of the concrete during the healing process.

Fig. 3
figure 3

The comparisons of mechanical properties between our predictions and those of Zhu et al. [19] with \(\phi_{\text{D}}\) denoting the volume fraction of deposition products in the equivalent inclusion, −1, −2 and −3 representing the results obtained with the first, second and third type of deposition products, respectively

Full size image

Thirdly, the Voigt upper bound and Reuss lower bound [22, 23] of the effective properties of concrete during the healing process are employed to validate our predictive results. Figure 4a, b present the comparisons among the results obtained with the proposed micromechanical model, the Voigt lower bounds and the Reuss upper bounds during the healing process for the effective properties. It can be found from Fig. 4a that the predictions of the shear modulus of the healed concrete lie between the upper and lower bounds reasonably. When the bulk modulus are considered, similar conclusions can be reached in Fig. 4b.

Fig. 4
figure 4

The comparisons among the results obtained with the proposed micromechanical model, the Voigt lower bounds and the Reuss upper bounds during the healing process for the effective properties, with \(\phi_{\text{D}}\) denoting the volume fraction of deposition products in the equivalent inclusion, −1, −2 and −3 representing the results obtained with the first, second and third type of deposition products, respectively

Full size image

In summary, the comparisons between our predicting results and those obtained experimentally, and those reached by the existing models show that the proposed differential-scheme based micromechanical model can quantitatively describe the healing process reasonably well at the micro-scale level.

4.2 Comparison with experiments and existing models at two extreme states of the EDM

In this section, our predictions at two extreme states of the EDM are examined to further validate the proposed differential-scheme based micromechanical framework.

The first extreme state is that there is absolutely no healing process in the concrete. Figure 5 exhibits the comparisons among our results, those obtained by [19], the upper bounds, lower bounds and the experimental data of Yaman et al. [52]. The comparison shows that our predictions and those of Zhu et al. [19] agree well with the experimental data when the porosity is low. These two predictions are between the upper bounds and lower bounds reasonably. With the increase of the porosity, our predictions correspond with the experimental data better than those of Zhu et al. [19].

Fig. 5
figure 5

The comparison among the results obtained with the different micromechanical models and those obtained experimentally for the static Young’s modulus of saturated concrete

Full size image

The second extreme state is that the saturated concrete has been completely healed by the EDM. Therefore, there is no water effect and the healed concrete is effectively a two-phase composite with the isotropic spherical inclusion phase. The works done by Smith [53] are employed to verify our proposed model at the second extreme state. Figures 6 and 7 present the comparisons among our results, those obtained by Zhu et al. [19], the upper bounds, the lower bounds and the experimental data of Smith [53]. From Fig. 6, it can be found that our predictions for the Young’s modulus and those of Zhu et al. [19] agree well with the experimental data when the volume fraction of the particle is low. These two predictions lie between the upper bounds and lower bounds reasonably. However, our predictions correspond much better with the experimental data than those of Zhu et al. [19] when the volume fraction of the particle increases to 0.4–0.5. Similar conclusion can be reached when the shear modulus is considered according to Fig. 7.

Fig. 6
figure 6

The comparisons among our results, those obtained by Zhu et al. [19], the upper bounds, the lower bounds and the experimental data of Smith [53] for the Young’s modulus of two-phase composite

Full size image
Fig. 7
figure 7

The comparisons among our results, those obtained by Zhu et al. [19], the upper bounds, the lower bounds and the experimental data of Smith [53] for the shear modulus of two-phase composite

Full size image

In summary, our proposed differential-scheme based micromechanical framework for saturated concrete repaired by the EDM can predict the properties of the saturated concrete or the spherical particle reinforced composite at the extreme states. Compared with the previous models [19], the predictions of this new framework agree well with the experimental data better when the volume fraction of the inclusion is higher.

5 Conclusions

The EDM is a newly developed healing method for cracked concrete under a water environment. Many meaningful experimental studies have been performed to evaluate its healing effectiveness. However, there are limited theoretical models, especially the micromechanical models, available for describing the healing process of the concrete repaired by the EDM at the micro-scale level. As an extension of our latest work, the differential-scheme based micromechanical framework is proposed in this paper to quantitatively describe the healing process of concrete healed by the EDM. Three different states for the healing process are quantitatively investigated with different types of deposition products. Furthermore, our predictions are compared with those of the existing micromechanical models and the experimental data. The following conclusions can be reached:

  1. (1)

    The proposed differential-scheme based micromechanical models can quantitatively predict the mechanical properties of saturated concrete repaired by the EDM during the entire healing process. As a special case, the micromechanical framework can accurately estimate the effective properties of two-phase composites, including the saturated concrete.

  2. (2)

    The deposition products properties play an important role in determining the mechanical properties of concrete during the healing process. With the increase of the bulk modulus or shear modulus of the deposition products, the healed saturated concrete will enjoy higher mechanical properties.

  3. (3)

    Compared with the results of our latest models, the estimations of this differential-scheme based framework agree well with the experimental data better when the volume fraction of the inclusion is higher.

It is noted that the concrete element is assumed to be fully saturated for simplifications in this paper [19]. Actually concrete pores are rarely saturated in practice. With the decrease of the saturation degree, the mechanical performance of the healed specimen will reduce. See details for [54].