Introduction

The remarkable physical properties and possible applications of lead-free halide perovskites have inspired many researchers. Perovskites are employed in numerous optoelectronic devices, including solar cells. These materials have important optoelectronic properties, such as strong optical absorption, carrier mobility, charge diffusion, residual point defects, an adjustable band gap, and a small effective mass of the carriers. Additionally, these inexpensive materials are widely available, promoting research into them to build affordable solar cells rather than depending on costly Si materials [1, 2]. Regardless of several exceptional qualities, lead halide perovskites have two major challenges that significantly limit their effectiveness in applications: the toxicity brought on by the presence of lead and material instability under ambient circumstances [3,4,5]. Therefore, the creation of lead-free perovskites presents a useful and efficient means of overcoming these limitations [6,7,8,9,10,11]. Typically, toxic-free metal halide perovskites have low reflectivity, high optical conductivity, and high absorptivity, making them suitable for commercial utilization in solar cells, thermoelectric, and optoelectronic devices [12]. One of the most effective ways to get lead-free perovskites is the process of exchanging two Pb2+ cations for two metal cations, with one being monovalent [M (I)] and the other being trivalent [M (III)]. This substitution produces the A2M(I)M(III)X6 perovskites, which contain a stable cubic structure [13]. Bi- and Sb-based perovskites such as Na2CuMCl6 (M = Bi, Sb), Na2AgSbX6 (F, Cl, Br, I), and Cs2CuMCl6 (M = Bi, Sb) have attracted the most interest within this group of materials because of their increased stability, distinctive electronic properties, and photoluminescence [13,14,15]. DFT-based theoretical studies have recently indicated that the cubic crystal structure of lead-free double perovskites exhibits greater stability compared to the hexagonal structure. [16].

Numerous DFT computations have been carried out as a consequence of improvements in computing techniques and the expanding accessibility of computational facilities. Structure prediction is a rapidly expanding area of research as a result of the addition of increasingly sophisticated and accurate minimization techniques to DFT [17]. DFT has been used in computational methods to explain a lot about the chemical and physical properties of organic, inorganic, and hybrid perovskites [18]. Tang et al. investigated the variation in optical properties of A2CuSbX6 (A = Cs, Rb, and K; X = Cl, Br) and concluded that K2CuSbCl6 is a potential candidate for solar cells [19]. Kumari, Sunita, et al. computed the optical and thermoelectric features of Na2AgSbX6 (F, Cl, Br, and I) for their utilization in thermoelectric and photovoltaic devices [15]. The applications of Rb2ScAgX6 (X = Cl, Br, and I) materials in PV cells and thermoelectric generators have also been discussed by Asghar et al. [20]. Most recently, the physical features of Cs2GeSnX6 (X = Cl, Br) were investigated employing DFT analysis for their potential applications in photovoltaics [21].

In this context, we examined the structural, elastic, optoelectronic, and transport characteristics using WIEN2K and BoltzTraP codes according to the perspective of the available literature. The outline of this study is: “Introduction” section provides a broad introduction, whereas “Results and discussion” section includes the results. The overall conclusion of this work is covered in “Conclusion” and “Computational details” sections provides computation details. Future studies into the disciplines of solar cells and thermoelectric generators will be contributed by our results for applications in renewable energy.

Results and discussion

Structural properties

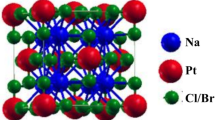
The materials Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) exhibit a cubic structure belonging to the space group Fm-3 m (#225). One of these families of double perovskite compounds, Na2CuMX6, exhibits sp3–d2 hybridization and in this structure, the cations Cu1+ and M3+ occupy alternating positions, forming a rock salt superstructure [22]. Halide double perovskites are known to have this rock-salt superstructure phase as their ground state [23]. Six halide ions (Cl−and Br−) surround the Cu1+ and M3+ (Sb3+ and Bi3+) cations in the center of the octahedral to form CuX6 and MX6 octahedral complexes, respectively. Figure 1(a) depicts the arrangement of these substances in a crystalline structure, where they form octahedral complexes that share corners with the Cs cation positioned at the center of the cuboctahedral [24]. The Location of the Na atom in the unit cell is (3/4, 1/4, 1/4), the Cu atom is at (0, 0, 0,), the M (Sb and Bi) atom is at (1/2, 0, 0), and the X (Br and Cl) anion is at (3/4, 0, 0). Goldschmidt’s tolerance factor is employed to investigate the structural stability or degree of distortion of all compounds using the following expression [25].

Figure 1
figure 1

(a) The rock salt structure (b–e) the volume optimization against energy of Na2CuMX6 (M = Sb, Bi, and X = Cl, Br).

Full size image
$$\uptau =\frac{{\mathrm{r}}_{\mathrm{Na}}+{\mathrm{r}}_{\mathrm{X}}}{\sqrt{2}(\frac{{\mathrm{r}}_{\mathrm{Cu}}+{\mathrm{r}}_{\mathrm{M}}}{2}+{\mathrm{r}}_{\mathrm{X}})}$$
(1)

Here, \({r}_{Na}\), \({r}_{Cu}\), \({r}_{M}\), and \({r}_{X}\) represent the corresponding atomic radii of the Na, Cu, M (Sb and Bi), and X (Cl and Br) atoms. Fedorovskiy et al. reported that a tolerance factor of 0.7 ≪ 1.2 is allowed to generate stable crystal structures [26]. Therefore, all the compounds have stable cubic structures whose values lie within the allowed range (see Table 1). We also computed the formation energy to evaluate the stability of the material. To estimate the formation energy, we utilized the expression [27]:

TABLE 1 The parameters of Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) obtained by utilizing PBE-GGA.
Full size table
$${\mathrm{E}}_{\mathrm{f}}={\mathrm{E}}_{\mathrm{Na}2\mathrm{CuMX}6}-\left(2{\mathrm{E}}_{\mathrm{Na}}+{\mathrm{E}}_{\mathrm{Cu}}+{\mathrm{E}}_{\mathrm{M}}+6{\mathrm{E}}_{\mathrm{X}}\right)$$
(2)

Here \({E}_{\mathrm{Na}2\mathrm{CuMX}6}\) is the total energy of Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) compounds, and the ENa, ECu, EM, and EX are the energies of the atoms individually. The confirmation of the thermodynamic stability of the double perovskites being investigated is evidenced by the presence of negative values for their formation energy, as depicted in Table 1 [28]. Furthermore, thermodynamic stability can be investigated through the computation of Gibbs free energy using the GIBBS2 computational mode [29]. The estimated Gibbs free energy (G) values were − 2.95 × 107 kJ/mol, − 6.33 × 107 kJ/mol, − 6.91 × 107 kJ/mol, and − 1.03 × 107 kJ/mol for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6, respectively. These negative results once again provide evidence of the thermodynamic stability of both double perovskites.

The structural parameters such as equilibrium lattice parameter, bulk modulus (B), bulk modulus derivative \({(\mathrm{B}}^{\mathrm{^{\prime}}})\), volume at ground state (V0), and ground state energy (E0) are optimized by implementing the Murnaghan equation of state [30]:

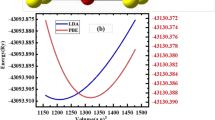
$$\mathrm{E}\left(\mathrm{V}\right)={E}_{0}\left(V\right)+\left[\frac{{B}_{0}V}{{{B}^{\mathrm{^{\prime}}}}_{0}\left({{B}^{\mathrm{^{\prime}}}}_{0}-1\right)}\right]\times \left[{B}_{0}\left(1-\frac{{V}_{0}}{V}\right)+{\left(\frac{{V}_{0}}{V}\right)}^{{{B}^{\mathrm{^{\prime}}}}_{0}}-1\right]$$
(3)

Here V0 is the ground state volume of the unit cell, B represents Bulk modulus, and \({B }{\prime}\) is the pressure associated with unit cell volume. With the use of a volume optimization procedure for each compound as shown in Fig. 1(b–e), the total energy is changed against the volume of the unit cell, and by putting in the equation, structural parameters (a, B, \({B}^{\mathrm{^{\prime}}}\),\({E}_{0}\) and V0) are determined as shown in Table 1.

Elastic properties

The mechanical stability was evaluated by measuring mechanical properties such anisotropy (A), shear modulus (G), bulk modulus (B), and second-order elastic constants (Cij). The elastic constants C11, C12, and C44 govern the dimensional structural strength of cubic perovskite materials. Where C11 represents material resistance to strain, C12 represents shear stress, and C44 represents resistance to shear deformation [21, 31]. The Born-Huang stability criteria, which is C11 > 0, C12 > 0, C44 > 0, C11 + 2C12 > 0, and C11–C12 > 0, is used to determine the structural stability of Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6 [32]. This leads us to conclude that the mechanical stability of halide-double perovskite material structures is high. The two models used to calculate shear modulus Voigt’s (GV) and Reuss’ (GR), were used to measure a material’s resistance to reversible deformation. Hill GH, on the other hand, is computed by taking the arithmetic mean of GV and GR [33]:

$${\mathrm{G}}_{\mathrm{H}}=\frac{\left({\mathrm{G}}_{\mathrm{V}}+{\mathrm{G}}_{\mathrm{R}}\right)}{2}$$
(4)

The determination of Young’s modulus is often used to determine the response of a crystalline substance to a linear deformation, and bulk modulus was obtained by using the following formula [34]:

$$\mathrm{Y}=\frac{9{\mathrm{BG}}_{\mathrm{V}}}{3\mathrm{B}+{\mathrm{G}}_{\mathrm{V}}}$$
(5)
$$\mathrm{B}=\frac{{\mathrm{C}}_{11}+{2\mathrm{C}}_{12}}{3}$$
(6)

The capacity to withstand variations in volume during compression is determined by Bulk modulus (B) of materials. Strong crystals are indicated by high B values, whereas resistance to deformation from plasticity is measured by shear modulus (G). The values of B determined for compounds Na2CuBiCl6 and Na2CuBiBr6 are 10.72 GPa and 10.32 GPa, respectively, while those for Na2CuSbCl6 and Na2CuSbBr6 are 10.293 GPa and 8.438. Cl-based compounds are more resistant to volume change than Br-based compounds due to their greater B value, and similarly, Cl-based compounds that have a high G value have high resistance to transverse bending. The Pugh’s ratio (B/G) can be used to reveal ductility or brittleness [35]. Materials with a B/G value beyond 1.75 are classified as ductile, whilst those exhibiting a value below 1.75 are categorized as brittle [36]. The calculated B/G values for all compounds show a brittle nature except Na2CuSbCl6, which exhibits ductile nature. Poisson’s ratio (ʋ) is another parameter that differentiates between the brittle and ductile behavior of materials. A ductile compound has a Poisson’s ratio (ʋ) larger than 0.26, whereas a brittle one has a value less than 0.26 [37]. All of the anticipated values of ʋ for the compounds indicate that the materials are brittle except for Na2CuSbCl6, which reveals a ductile nature. Furthermore, an anisotropy factor (A) has been calculated, with unity representing isotropic behavior and deviations from this value representing anisotropic behavior [38, 39]. All calculated values shown in the table indicate that all compounds are anisotropic. Cauchy’s pressure, calculated from Cp = C12–C44 was used to derive information about the type of bonding. Cp values that are positive signify ionic nature, whereas negative value denotes covalent bonding [40]. The negative values of Cp reveal the covalent nature of materials. Another term is shear constant Cʹ which gives information about the stability of a compound if Cʹ >0, and its formula is:

$$\mathrm{C{\prime}}=\frac{\left({\mathrm{C}}_{11}-{\mathrm{C}}_{12}\right)}{2}$$
(7)

Based on the estimated values, it can be determined that all substances exhibit dynamic stability. In addition, we investigated Debye temperature, which is related to elastic properties calculated as [41]:

$${\uptheta }_{\mathrm{D}}={\frac{\mathrm{h}}{{\mathrm{K}}_{\mathrm{B}}}\left[\frac{3\mathrm{n}}{4\uppi }\left(\frac{{\mathrm{N}}_{\mathrm{A\rho }}}{\mathrm{M}}\right)\right]}^{-1/3}{\mathrm{V}}_{\mathrm{m}}$$
(8)

Elastic anisotropy

Materials anisotropy is essential for understanding their mechanical strength and estimating microhardness. The formation of cracks at the micro level in the compounds might be caused by a considerable elastic anisotropy [42]. Using the ELATE program, contour graphs in three dimensions have been generated for further analyzing the elastic anisotropy of crystals through their respective moduli [43]. For Na2CuMX6 (M = Sb, Bi, and X = Cl, Br), double perovskite materials, elastic modulus graphs involving linear compressibility (β), Young’s modulus (Y), shear modulus (G), and Poisson’s ratio (ʋ), are obtained from the computed Cij and shown in Figs. 2 and 3. Isotropic elastic behavior does not always manifest in cubic crystals. The Zener anisotropic factor (A) is a measure of the degree of elastic anisotropy of the material. When A = 1, a crystal is said to be entirely isotropic, and variations in the given value indicate the presence of elastic anisotropy [39]. Elastic anisotropy (A) is determined for cubic crystals as follows [44]:

Figure 2
figure 2

A three-dimensional illustration of linear compressibility, Young’s modulus, shear modulus, and Poisson’s ratio for (a–d) Na2CuSbCl6 (e, f) Na2CuSbBr6.

Full size image
Figure 3
figure 3

A three-dimensional illustration of linear compressibility, Young’s modulus, shear modulus, and Poisson’s ratio for (a–d) Na2CuBiCl6 (e, f) Na2CuBiBr6.

Full size image
$$\mathrm{A}=\frac{2{\mathrm{C}}_{44}}{{\mathrm{C}}_{11}-{\mathrm{C}}_{12}}$$
(9)

In addition, the maximum ranges are shown by the blue curves in Figs. 2 and 3, while the lowest values are represented by the green curves for linear compressibility (β), Young’s modulus (Y), and shear modulus (G). Whereas, for Poisson’s ratio, maximum ranges are represented by blue and minimum values by red curves.

The results suggest that the linear compressibility, as seen in Figs. 2 and 3, exhibits isotropic properties when the value of A is equal to one, as indicated in Table 2. In contrast, it can be shown that Young’s modulus, Shear modulus, and Poisson’s ratio (ʋ) exhibit anisotropic characteristics across all compounds that have been investigated. The depiction of Young’s modulus illustrates that Na2CuBiBr6 exhibits the highest level of anisotropy compared to Na2CuSbCl6, Na2CuSbBr6, and Na2CuBiCl6. The shear modulus follows the same trend as that for Young’s modulus. Furthermore, the Poisson’s ratio shows the sequence: Na2CuBiCl6 > Na2CuBiBr6 > Na2CuBiCl6 > Na2CuBiBr6. Table 2 presents the values of elastic moduli together with their corresponding anisotropy values.

TABLE 2 Elastic parameters and variations in elastic moduli of all compounds.
Full size table

Electronic properties

The material’s electronic characteristics dictate how well it may be used in different optoelectronic devices. The Trans–Blaha modified Becke–Johnson (TB-mBJ) potential is used to figure out the energy band structure, total density of states (TDOS), and partial density of states (PDOS) to describe the electronic properties [32]. The current study uses PBE-GGA, PBEsol-GGA, and mBJ to identify the band structures of Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) while considering the optimized unit cell. Figure 4 depicts the calculated band structures across the Fermi energy level in the Brillouin zone along the high-symmetry path W → L → Γ → X → W → K with energies between − 4 eV and 8 eV. The band structures of Na2CuSbCl6 and Na2CuSbBr6 as determined by the PBE-GGA, PBEsol-GGA, and TB-mBJ functionals are shown in Fig. 4(a–f). The X-point was determined as the location of the valence band maximum (VBM), while the L-point was identified as the position of the conduction band minimum (CBM) revealing an indirect band gap for all compounds. The bandgap computed by PBE-GGA for Na2CuSbCl6 and Na2CuSbBr6 was 0.83 eV and 0.6 eV, respectively. By employing PBEsol-GGA, the band gap was found to be 0.79 eV and 0.56 eV for both compounds. The indirect band gaps were improved to 1.26 eV for Na2CuSbCl6 and 1.3 eV for Na2CuSbCl6 when GGA combined with mBJ potential was employed. By shifting the Cu-d and Cl-p dominated energy bands away from the Fermi level, the mBJ-potential broadened the bandgap. Similarly, the comparison between the band structures calculated using PBE-GGA, PBEsol-GGA, and mBJ for Na2CuBiCl6 and Na2CuBiBr6 is presented in Fig. 4(g–l). The band gaps of both materials have indirect nature. Bandstucure plotting reported the band gap (Eg) for Na2CuBiCl6 is 1.62 eV (L–X) while decreases to 1.57 eV (L–X) for Na2CuBiBr6 double perovskites using TB-mBJ functional due to increase in atomic radius. The calculated band gaps were slightly higher than the previously reported band gaps of Na2CuBiCl6 and Na2CuSbCl6 [14].

Figure 4
figure 4

Comparison between the band structures calculated utilizing PBE-GGA, PBEsol-GGA, and mBJ for (a–c) Na2CuSbCl6 (d–f) Na2CuSbBr6 (g–i) Na2CuBiCl6 (j–l) Na2CuBiBr6.

Full size image

Furthermore, the density of states illustrated in Fig. 5(a–d) depicts the distribution of electrons in Na2CuMX6 (M = Sb, Bi, and X = Cl, Br), Na, Cu, Sb/Br, and Cl/Br atoms. The DOS plots provide evidence for the band structure as well as the semiconducting characteristics [45]. The DOS plots of compounds under study show identical behavior with band structure. The electrons of the sodium (Na) atom are situated in the inner region, distanced from the valence and conduction bands, which have negligible impact on the transition mechanism. The transitions and recombination of electrons in Cu are primarily influenced by the d-state electrons, while in Sb/Bi and Cl/Br, the electrons in the p-state have a considerable contribution. The maximum contribution in the valence band (VB) and the formation of conduction band (CB) minima are primarily attributed to the presence of 3d-Cu and p-Cl/Br; Consequently, electrons also transition between the halide ions and 3d-Cu states.

Figure 5
figure 5

DOS plots of materials and individual components Na, Cu, Sb/Br, and Cl/Br of (a) Na2CuSbCl6 (b) Na2CuSbBr6 (c) Na2CuBiCl6 (d) Na2CuBiBr6.

Full size image

To get a comprehensive understanding of the electronic characteristics, an investigation was conducted to estimate the charge density profile within the (110) plane in a cross-section, as shown in Fig. 6. The Pauling electronegativity values of all elements are Na (0.93), Cu (1.90), Sb (2.05), Bi (1.9), Cl (3.16), and Br (2.96). The transition metal Cu, Sb and Bi atoms with Cl and Br atoms have lesser electronegativity differences, which is evidence of covalent bonds like Cu–Cl, Cu–Br, Sb–Cl, Sb–Br, Bi–Cl, and Bi–Br for the respective compounds. While there is ionic bonding between Na and Cl/Br due to their large electronegativity differences. The covalence nature is attributed to hybridization between the Cu-3d and Cl-3p, Cu-3d and Br-4p, Sb-5p and Cl-3p, Sb-5p and Br-4p, Bi-6p and Cl-3p, and Bi-6p and Br-4p state for their respective compounds, according to the PDOS spectra as expressed in Fig. 5.

Figure 6
figure 6

The electronic charge density (ECD) within the (110) plane for (a) Na2CuSbCl6 (b) Na2CuSbBr6 (c) Na2CuBiCl6 (d) Na2CuBiBr6.

Full size image

Optical properties

The band gap, absorption of energy, and efficiency of materials for converting light into electrical power determine the optoelectronic and solar cell properties of materials [46]. The material interaction with light can result in either an intra-band or an inter-band transition; the latter is responsible for excitations and recombination. In optical applications, this transition is valuable [47]. As a result, Fig. 7 shows the optical characteristics of the investigated compounds as estimated within the region of 0–6 eV energy. The optical behavior of Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) has been described by the real and imaginary dielectric functions dependent on energy as follows:

Figure 7
figure 7

Optical parameters (a) real part of dielectric function (b) imaginary part of dielectric function (c) refractive index (d) extinction coefficient (e) absorption coefficient (f) optical conductivity (g) reflectivity (h) energy loss for Na2CuMX6 (M = Sb, Bi, and X = Cl, Br).

Full size image
$$\upvarepsilon \left(\upomega \right)={\upvarepsilon }_{1}\left(\upomega \right)+\mathrm{i}{\upvarepsilon }_{2}\left(\upomega \right)$$

Here \({\varepsilon }_{1}\left(\omega \right)\) specifies the real part of the dielectric function and \({\varepsilon }_{2}\left(\omega \right)\) denotes the imaginary part of the dielectric function. The \({\varepsilon }_{1}\left(\omega \right)\) defines a certain amount of polarization within a material when light interacts and the quantity of light lost caused by dispersion is denoted by \({\varepsilon }_{2}\left(\omega \right)\). This is also expressed concerning the energy that the materials attenuate or absorb [48,49,50,51,52,53].

The computed real component of the dielectric function \({\varepsilon }_{1}\left(\omega \right)\) for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6 are displayed in Fig. 7(a). This component describes the dispersive behavior of the material to incoming photons [54]. The static value of \({\varepsilon }_{1}\left(\omega \right)\) is highest for Na2CuSbBr6 (3.44) in comparison to Na2CuBiBr6 (3.05), Na2CuSbCl6 (2.88), and Na2CuBiCl6 (2.45). This value rises as the band gap narrows [55]. Additionally, the values of \({\varepsilon }_{1}\left(\omega \right)\) are positive throughout the whole energy region, which justifies the fact that none of the Na2CuMX6 double perovskites reflects photons in the 0–6 eV range [56]. Furthermore, for the investigated perovskites, the maximum \({\varepsilon }_{1}\left(\omega \right)\) values lie inside the visible region. This confirms that these substances respond to the visible spectrum most strongly.

The relationship between the value of \({\varepsilon }_{2}\left(\omega \right)\) and the energy is illustrated in Fig. 7(b). The \({\varepsilon }_{2}\left(\omega \right)\) represents the optical band gap and absorption properties [57]. There is no evidence of absorption up to 1.2 eV, 1.4 eV, 1.6 eV, and 1.7 eV for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6, respectively, proving that the predicted electrical bandgap and optical bandgap are almost identical.

The refractive index \(\mathrm{n}\left(\upomega \right)\) represents the process in which light propagates through the materials under investigation [58]. The static refractive indices, \(\mathrm{n}\left(0\right)\), for the spectra of Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6 are 1.7, 1.85, 1.56, and 1.75. The peak values of \(n\left(\omega \right)\) are 2.14, 2.25, 1.87, and 2.05 for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6, respectively, in the 1.7–2.0 eV photon energy range, as shown in Fig. 7(c). The same patterns of graphs with increased energy are shown by the correspondence between \({\upvarepsilon }_{1}\left(\upomega \right)\) and \(\mathrm{n}\left(\upomega \right)\), which is essential for the validity of the findings. Additionally, the decay of light energy is indicated by the extinction coefficient \(\mathrm{k}\left(\upomega \right)\), which is illustrated as an imaginary part of the refraction of light [46]. The values of \(\mathrm{k}\left(\upomega \right)\) depicted in Fig. 7(d) consolidate with the values of \({\upvarepsilon }_{2}\left(\upomega \right)\) and \(\mathrm{\alpha }\left(\upomega \right)\).

A significant parameter that illustrates the transport of charge carriers to optical frequencies is optical conductivity \(\upsigma \left(\upomega \right)\) [47]. Figure 7(f) shows the simulated graphs of \(\upsigma \left(\upomega \right)\) for Na2CuMX6 double perovskites. The values of σ(ω) exhibit a value of zero within the frequency range beyond the optical band gap. The charge carriers are excited by the optical photon, possessing energy equivalent to the optical band gap. Na2CuSbBr6 exhibits the highest optical conductivity of 1100 Ω−1 cm−1 at the energy of 2.3 eV, followed by Na2CuBiBr6, having optical conductivity of 970.8 Ω−1 cm−1.

Reflectivity is the ratio of the intensity of radiation striking a surface to the intensity of light reflecting [59]. In Fig. 7(g), the pattern of \(\mathrm{R}\left(\upomega \right)\) is shown. The static reflectance values R(0) calculated for Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) were less than 10%. The values for the \(\mathrm{R}\left(\upomega \right)\) in the visible range are less than 20%. This indicates that all of the investigated double perovskites, Na2CuMX6, can absorb the greatest amount of visible photons. So, we recommend these materials for use in solar cell applications. Moreover, some of the light energy is lost through dispersion and many other losses. As a result, A graph of the optical energy loss L(\(\upomega\)) has been depicted in Fig. 7(h), demonstrating extremely low for the Na2CuSbBr6 and Na2CuBiBr6 double perovskites. These materials absorb the majority of the incident energy. It has been determined that all investigated perovskite materials, especially Na2CuSbBr6 and Na2CuBiBr6, are significant for solar cells based on a detailed investigation of the optical response of these materials.

Transport properties

Utilizing thermoelectric materials, waste heat may be converted into valuable electrical energy. Perovskites are especially advantageous for this purpose because of their accessibility, affordability, excellent electrical conductivity, and environmental friendliness [60]. The essential transport characteristics were computed against temperature in the 200–800 K range, by using the WIEN2k output files as the input files in the BoltzTraP code, with the assumption of a constant relaxation time (\(\uptau )\) [61, 62]. In the BoltzTraP code, its value is maintained constant at 10–14. The perturbing duration of lattice vibration is measured by this relaxation time [63]. The figure of merit \(ZT=\frac{{S}^{2}\sigma T}{\kappa } ,\) where “S” stands for the Seebeck coefficient, which is determined by the potential gradient between different metals, “ σ” for electrical conductivity, which controls carrier movement, and “κ” for thermal conductivity, which is determined by lattice vibration, is used to analyze the efficiency of thermoelectric materials. For optimal performance, the S and must be as high as possible, and the k as low as possible [63,64,65]. The computed output data obtained using the BoltzTraP code is plotted in Fig. 8.

Figure 8
figure 8

Temperature-dependent thermoelectric parameters (a) Seebeck coefficient (b) electrical conductivity (c) thermal conductivity (d) power factor (e) figure of merit for Na2CuMX6 (M = Sb, Bi, and X = Cl, Br).

Full size image

The Seebeck effect is the electric potential that arises due to a temperature differential in different electrical conductors or semiconductors. The measured value of the Seebeck coefficient, as mentioned in Fig. 8(a) dropped exponentially with temperature for all compounds, peaking at 200 K with a value of 226 µV/K for Na2CuSbCl6, 239 µV/K for Na2CuSbBr6, 220 µV/K for Na2CuBiCl6, and 235 µV/K for Na2CuBiBr6. The positive “S” values of the compounds show their p-type nature, which makes them active thermoelectric materialsThe Seebeck coefficient was found to be maximum at 300 K (room temperature) for Na2CuSbBr6 and Na2CuBiBr6.

The electrical conductivity (σ) enables us to understand how charge carriers and electric current relate to one another in materials. Electrical conductivity is highly desirable in a thermoelectric material since it lessens the Joule-heating impact [63]. The temperature-dependent σ in the 200–800 K range is shown in Fig. 8(b), and it rises linearly as the temperature rises. The calculated values of σ for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6 at room temperature are 1.96 × 1018, 2.15 × 1018, 1.81 × 1018, and 2.13 × 1018 Ω−1 m−1 s−1, respectively. This indicates that electrical conductivity has larger values for Na2CuSbBr6 and Na2CuBiBr6.

Electrons and lattice vibration both contribute to thermal conductivity (κe and κph) [66, 67]. In our calculations, we didn’t take into account the effect of phonons caused by the very low thermal conductivity of the lattice in double perovskites, as reported for Cs2PtI6 [68], as well as complicated calculations and the limitations of the BoltzTraP code [46]. As a result, Fig. 8(c) shows a graph of the computed κe for the investigated double perovskites. Graph observation of κe assures identical behavior to that of σ as the room temperature values of Br-based Na2CuSbBr6 and Na2CuBiBr6 are higher than Cl-based compounds. The ratio κe /σ has been determined for the investigation of efficiency and confirms that s is 105 times larger than κe, making them highly important materials for thermoelectric generators [69].

The power factor (PF = S2σ) is a fundamental factor to ensure thermoelectric material utilization for potential applications. Figure 8(d) plots the temperature-dependent power factor for all compounds. The PF values at room temperature (300 K) are 8.9 × 1010, 10.8 × 1010, 8.0 × 1010, and 10.6 × 1010 W/mK2s for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6, respectively. At higher temperatures (800 K), these values decrease to 3.1 × 1010, 9.0 × 1010, 1.86 × 1010 and 6.2 × 1010 W/mK2s, respectively. The Plots depict the rising PF behavior with temperature and illustrate these materials as suitable for thermoelectricity.

The figure of merit \(ZT=\frac{{S}^{2}\sigma T}{\kappa }\) defines the most effective thermoelectric properties of any material. The relation for the figure of merit reveals the value of ZT varies directly with the Seebeck coefficient. A material that is ideal for thermoelectric use must have a ZT value equal to one that provides a better energy conversion efficiency (> 25%) at the ideal operating temperature [58]. Figure 8(e) shows that the highest ZT values found to be 0.82, 0.79, 0.85, and 0.81 for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6, respectively, at room temperature were increased to 0.87, 0.83, 0.88, and 0.86, respectively, with an increase in temperature up to 800 K. This shows that all materials under study are efficient thermoelectrics. These results suggest that all investigated compounds have remarkable thermoelectric characteristics, especially Na2CuBiCl6, which has slightly higher ZT values, making them suitable for potential use in thermoelectric devices.

Conclusion

The computational investigation involved the utilization of the WIEN2k software package to analyze the elastic, structural, optoelectronic, and transport properties of Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) double perovskites. The double perovskites under investigation exhibit stable cubic structures. The indirect band gap when considering the symmetry points (L–X) indicates that all the materials possess semiconductor properties. The brittle or ductile nature, anisotropy, and elastic stability of the Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) double perovskites are evident from their mechanical properties. All the materials exhibit brittle nature except Na2CuSbCl6, which was ductile. The calculated band gap (Eg) for Na2CuSbCl6, Na2CuSbBr6, Na2CuBiCl6, and Na2CuBiBr6 double perovskites were determined to be 1.26 eV, 1.3 eV, 1.62 eV, and 1.57 eV using the TB-mBJ functional. The optical properties estimated within the range of energies of 0–6 eV possess the potential to be utilized in optoelectronic and photovoltaic devices due to their anticipated maximum optical conductivity, lower reflectivity (less than 20%), and ability to absorb incident photons within the visible region. Moreover, these materials exhibit a significantly high “S” and “ZT” (figure of merit), indicating their potential for thermoelectric applications. The results reveal that the perovskites under investigation have promising characteristics for use in solar and thermoelectric applications.

Computational details

To examine the physical characteristics of the Na2CuMX6 (M = Sb, Bi, and X = Cl, Br) materials, we conducted Density Functional Theory (DFT) calculations using the full-potential linearized augmented plane wave (FP-LAPW) technique included in the WIEN2k interface [70, 71]. The exchange–correlation functional of Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) was used to optimize the structures of all the compounds in the cubic phase [72]. The structural characteristics are obtained accurately using the PBE-GGA. The Generalized gradient approximation (GGA) is used to determine electronic properties both with and without the Tran and Blaha modified Becke and Johnson potential (TB-mBJ). The GGA approximation underestimating the Eg was compensated by employing the TB-mBJ functional [72,73,74]. The TB-mBJ has been utilized to eliminate the underestimation problem of band gap, which was identified by the PBE-GGA and PBEsol-GGA functionals [75]. The wave functions were produced using a foundation of plane waves with the value of the product of the cut-off reciprocal lattice vector and RminMT was adjusted to 10, where RminMT indicates the minimum muffin-tin sphere radius (RMT). The RMT was set as high as possible for atoms i.e. \({\mathrm{R}}_{\mathrm{MT}}^{\mathrm{Na}}=2.0, {\mathrm{R}}_{\mathrm{MT}}^{\mathrm{Cu}}=1.5, {\mathrm{R}}_{\mathrm{MT}}^{\mathrm{M}}=1.9,\mathrm{ and }{\mathrm{R}}_{\mathrm{MT}}^{\mathrm{X}}=2.0\) to prevent spheres from overlapping. To ensure convergence, we also sampled the Brillion Zone (BZ) utilizing a dense mesh of 100 k points. Energy and charge convergence between consecutive cycles converged to a value of 0.0001 Ry and 0.0001 e, respectively, which improved results. The optical characteristics were calculated using the OPTIC package within the WIEN2k framework [76, 77]. The thermoelectric characteristics were calculated using the BoltzTraP algorithm using an estimate of constant relaxation time (τ) [61, 78, 79].